Optimizing Coalition Formation Strategies for Scalable Multi-Robot Task Allocation: A Comprehensive Survey of Methods and Mechanisms
Abstract
1. Introduction
- (a)
- MRS enables parallel task execution, leading to accelerated goal attainment.
- (b)
- Heterogeneity in robot capabilities can be accommodated within MRS.
- (c)
- MRS effectively handles tasks distributed across large spatial domains.
- (d)
- Inherent robustness in fault tolerance is a characteristic feature of MRS.
2. MRTA and CF
2.1. Multi-Robot Task Allocation (MRTA)
2.2. Coalition Formation (CF)
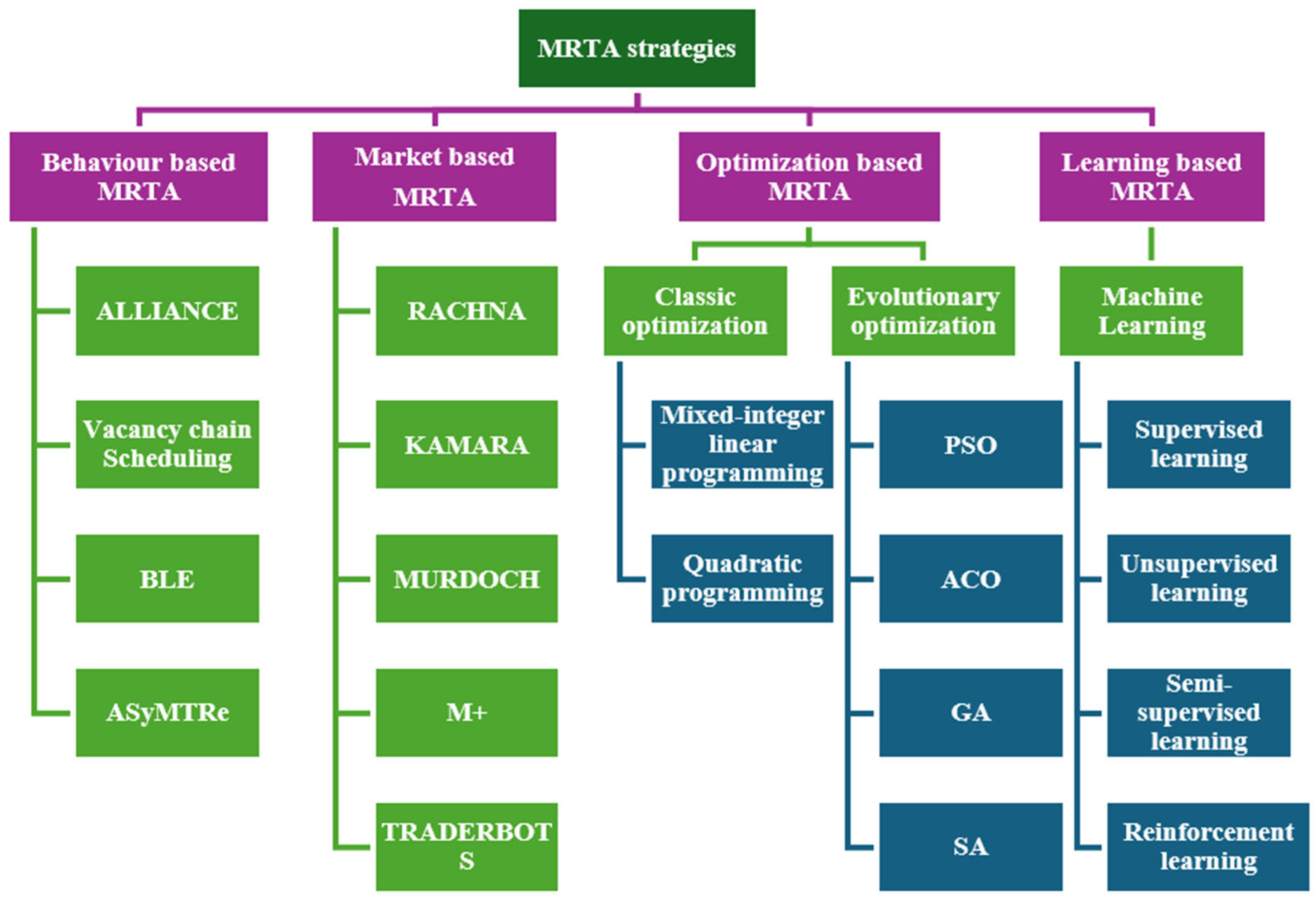
3. MRTA Classification
3.1. Behavior-Based MRTA
3.1.1. Alliance
3.1.2. Vacancy Chain Scheduling
3.1.3. Broadcast of Local Eligibility (BLE)
3.1.4. Automated Synthesis of Multi-Robot Task Solutions Through Software Reconfiguration (ASyMTRe)
3.2. Market-Based MRTA
3.2.1. RACHNA
3.2.2. KAMARA (KAMRO’s Multi-Agent Robot Architecture)
3.2.3. MURDOCH
3.2.4. M+
3.2.5. TraderBots
3.3. Optimization-Based MRTA
3.3.1. Traditional Optimization
3.3.2. Evolutionary Optimization
- PSO seeks global optima while navigating exploration and exploitation trade-offs.
- ACO emphasizes pheromone-guided exploration and solution construction.
- GA balances diversity through mutation and convergence via crossover.
- SA transitions from high-temperature exploration to low-temperature exploitation.
- LP targets linear relationships, and QP handles quadratic ones, both optimized for resource allocation.
3.4. Learning-Based MRTA
Machine Learning
3.5. Comparison with Different MRTA Approaches
4. Simulation and Results
- Robots are aware of the values of M (the total number of objects) and N (the total number of robots).
- Robots possess knowledge of both the current and desired positions of all M objects.
- Robots are capable of communicating with each other as needed.
- We assume that all robots are operating within a workspace where communication between robots is feasible.
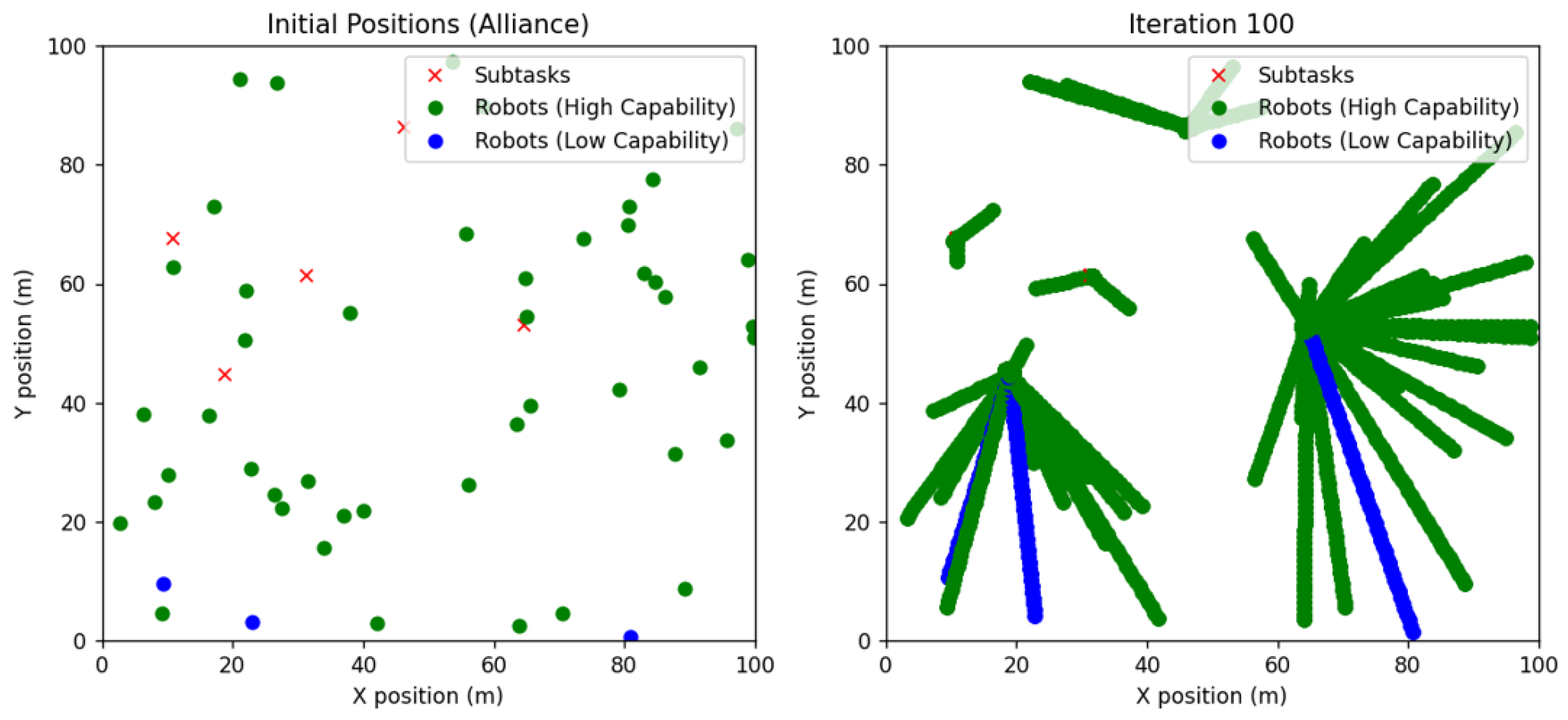
4.1. Behavior-Based: Alliance Architecture
4.2. Market-Based: M+ Algorithm
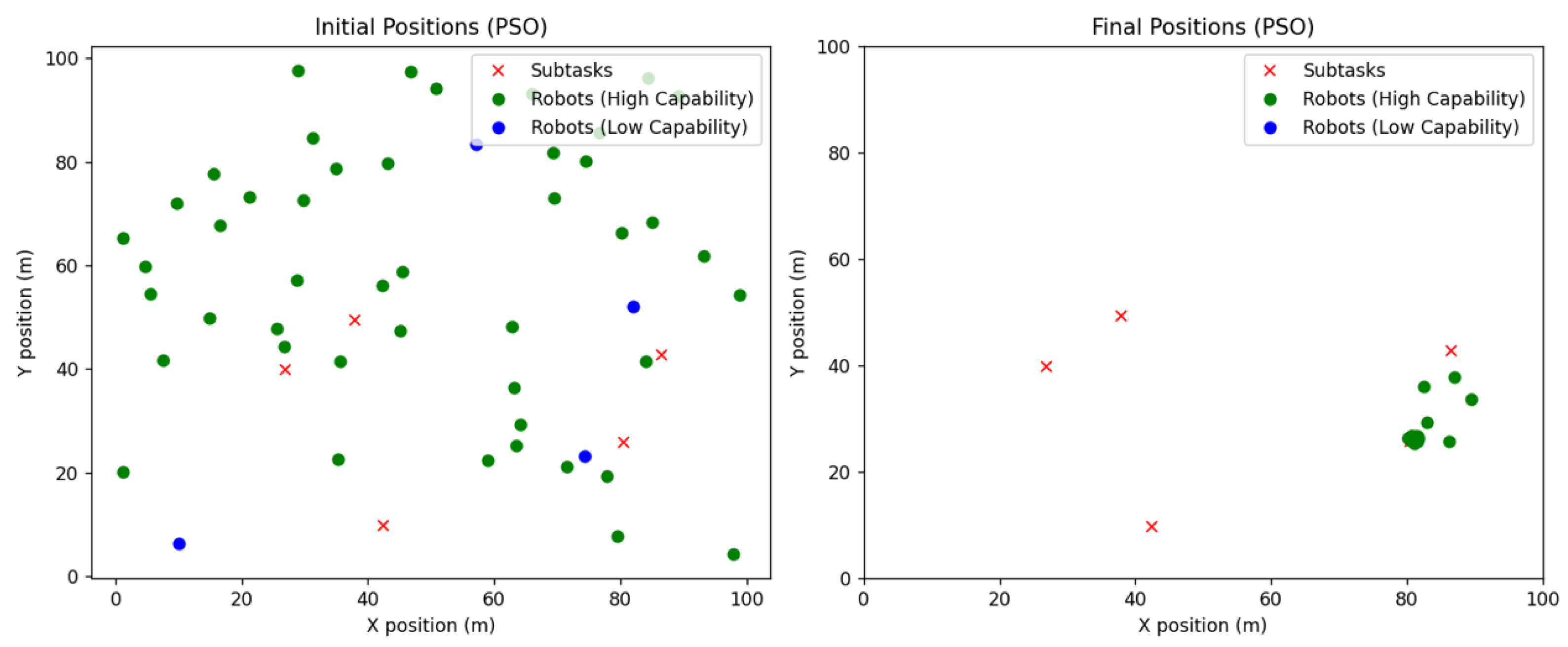
4.3. Optimization-Based: PSO Algorithm
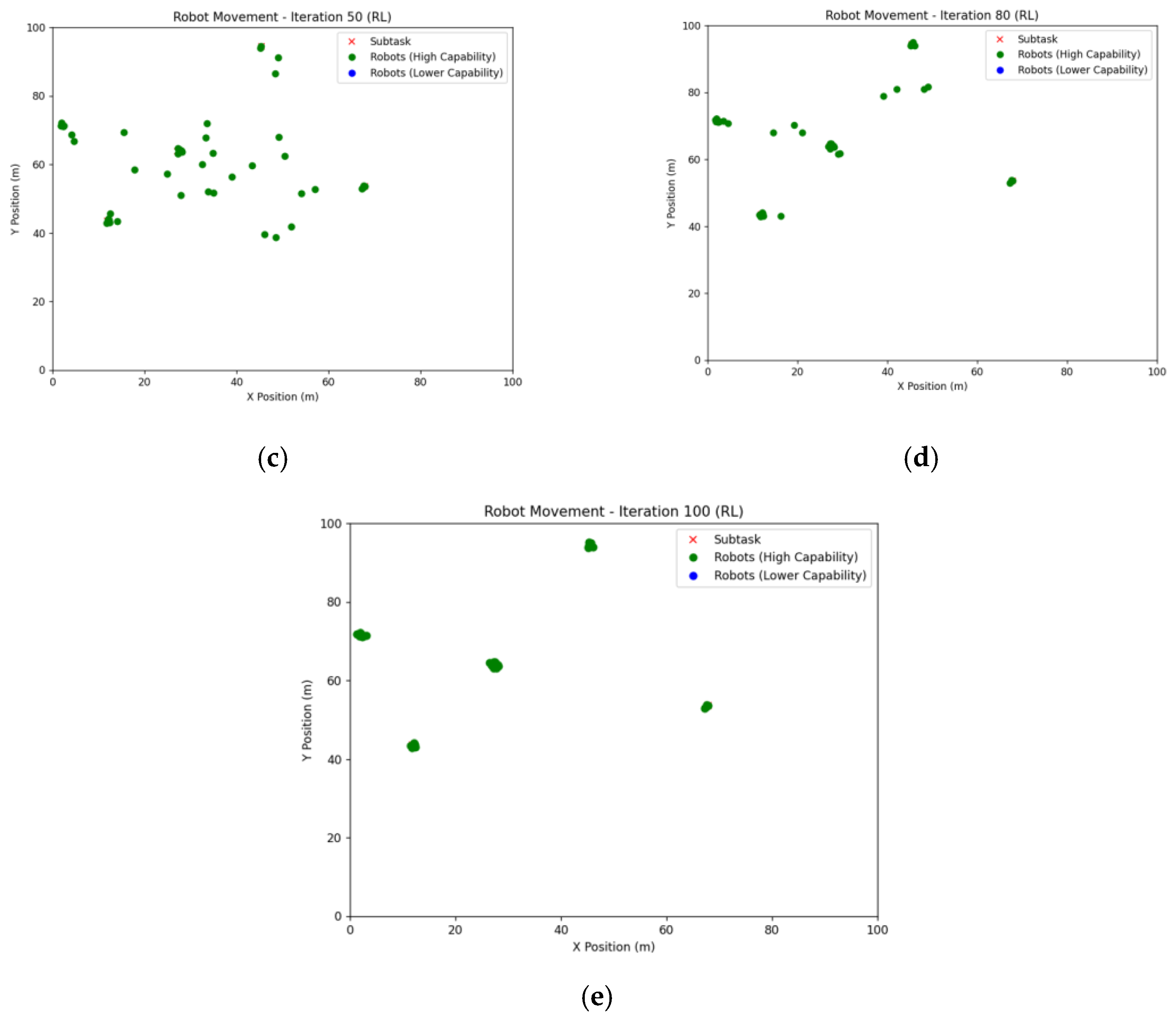
4.4. Learning-Based: Reinforcement Learning
4.5. Statistical Analysis
4.5.1. Quantitative Results and Statistical Comparison of Alliance, M+, PSO, and RL
4.5.2. Analysis of Convergence Time in Coalition Formation Algorithms Using ANOVA
4.5.3. Computation Cost Analysis of MRTA Strategies
4.5.4. Scalability Comparison of RL and Alliance Algorithms
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gautam, A.; Mohan, S. A review of research in multi-robot systems. In Proceedings of the 2012 IEEE 7th International Conference on Industrial and Information Systems (ICIIS), Chennai, India, 6–9 August 2012. [Google Scholar]
- Parker, L. Distributed intelligence: Overview of the field and its application in multi-robot systems. J. Phys. Agents 2008, 2, 5–14. [Google Scholar] [CrossRef]
- Arai, T.; Parker, L. Editorial: Advances in multi-robot systems. IEEE Trans. Robot. Autom. 2003, 18, 655–661. [Google Scholar] [CrossRef]
- Ahmad, A.; Walter, V.; Petráček, P.; Petrlík, M.; Báča, T.; Žaitlík, D.; Saska, M. Autonomous aerial swarming in GNSS-denied environments with high obstacle density. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9561284/ (accessed on 13 May 2024).
- Team CERBERUS Wins the DARPA Subterranean Challenge. Autonomous Robots Lab. Available online: https://www.autonomousrobotslab.com/ (accessed on 13 May 2024).
- Autonomous Mobile Robots (AMR) for Factory Floors: Key Driving Factors. 2021. Roboticsbiz. Available online: https://roboticsbiz.com/autonomous-mobile-robots-amr-for-factory-floors-key-driving-factors/ (accessed on 13 May 2024).
- Different Types of Robots Transforming the Construction Industry. 2020. Roboticsbiz. Available online: https://roboticsbiz.com/different-types-of-robots-transforming-the-construction-industry/ (accessed on 13 June 2024).
- Robocup Soccer Small-Size League. Robocup. Available online: https://robocupthailand.org/services/robocup-soccer-small-size-league/ (accessed on 13 May 2024).
- Robots in Agriculture and Farming. 2022. Cyber-Weld Robotic System Integrators. Available online: https://www.cyberweld.co.uk/robots-in-agriculture-and-farming/ (accessed on 13 May 2024).
- Roldán Gómez, J.; Barrientos, A. Special issue on multi-robot systems: Challenges, trends, and applications. Appl. Sci. 2021, 11, 11861. [Google Scholar] [CrossRef]
- Khamis, A.; Hussein, A.; Elmogy, A. Multi-robot task allocation: A review of the state-of-the-art. In Cooperative Robots and Sensor Networks 2015; Springer: Cham, Switzerland, 2015; pp. 31–51. [Google Scholar]
- Arjun, K.; Parlevliet, D.; Wang, H.; Yazdani, A. Analyzing multi-robot task allocation and coalition formation methods: A comparative study. In Proceedings of the 2024 International Conference on Advanced Robotics, Control, and Artificial Intelligence, Perth, Australia, 9–12 December 2024. [Google Scholar]
- Gerkey, B.P.; Mataric, M.J. Multi-robot task allocation: Analyzing the complexity and optimality of key architectures. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 19 September 2003. [Google Scholar]
- Bai, X.; Li, C.; Zhang, B.; Wu, Z.; Ge, S.S. Efficient performance impact algorithms for multirobot task assignment with deadlines. IEEE Trans. Ind. Electron. 2024, 71, 14373–14382. [Google Scholar] [CrossRef]
- Bai, X.; Yan, W.; Ge, S.S. Efficient task assignment for multiple vehicles with partially unreachable target locations. IEEE Internet Things J. 2021, 8, 3730–3742. [Google Scholar] [CrossRef]
- Bai, X.; Jiang, H.; Li, C.; Ullah, I.; Al Dabel, M.M.; Bashir, A.K.; Wu, Z.; Sam, S. Efficient hybrid multi-population genetic algorithm for multi-UAV task assignment in consumer electronics applications. IEEE Trans. Consum. Electron. 2025, 1–12. [Google Scholar] [CrossRef]
- Gerkey, B.; Mataric, M. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Korsah, G.; Stentz, A.; Dias, M. A comprehensive taxonomy for multi-robot task allocation. Int. J. Robot. Res. 2013, 32, 1495–1512. [Google Scholar] [CrossRef]
- Saravanan, S.; Ramanathan KC Mm, R.; Janardhanan, M.N. Review on state-of-the-art dynamic task allocation strategies for multiple-robot systems. Ind. Robot. Int. J. Robot. Res. Appl. 2020, 47, 929–942. [Google Scholar]
- Wen, X.; Zhao, Z.G. Multi-robot task allocation based on combinatorial auction. In Proceedings of the 2021 9th International Conference on Control, Mechatronics and Automation (ICCMA), Esch-sur-Alzette, Luxembourg, 11–14 November 2021. [Google Scholar]
- Chakraa, H.; Guérin FLeclercq, E.; Lefebvre, D. Optimization techniques for multi-robot task allocation problems: Review on the state-of-the-art. Robot. Auton. Syst. 2023, 168, 104492. [Google Scholar] [CrossRef]
- Dos Reis, W.P.N.; Lopes, G.L.; Bastos, G.S. An arrovian analysis on the multi-robot task allocation problem: Analyzing a behavior-based architecture. Robot. Auton. Syst. 2021, 144, 103839. [Google Scholar] [CrossRef]
- Agrawal, A.; Bedi, A.; Manocha, D. RTAW: An attention inspired reinforcement learning method for multi-robot task allocation in warehouse environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 1393–1399. [Google Scholar]
- Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the multiple traveling salesman problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 40, 100369. [Google Scholar] [CrossRef]
- Deng, P.; Amirjamshidi, G.; Roorda, M. A vehicle routing problem with movement synchronization of drones, sidewalk robots, or foot-walkers. Transp. Res. Procedia 2020, 46, 29–36. [Google Scholar] [CrossRef]
- Sun, Y.; Chung, S.-H.; Wen, X.; Ma, H.-L. Novel robotic job-shop scheduling models with deadlock and robot movement considerations. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102273. [Google Scholar] [CrossRef]
- Santana, K.A.; Pinto, V.P.; Souza DAd Torres, J.L.O.; Teles, I.A.G. (Eds.) New GA Applied Route Calculation for Multiple Robots with Energy Restrictions; EasyChair: Manchester, UK, 2020. [Google Scholar]
- Jorgensen, R.; Larsen, J.; Bergvinsdottir, K. Solving the dial-a-ride problem using genetic algorithms. J. Oper. Res. Soc. 2007, 58, 1321–1331. [Google Scholar] [CrossRef]
- Hussein, A.; Khamis, A. Market-based approach to multi-robot task allocation. In Proceedings of the 2013 International Conference on Individual and Collective Behaviors in Robotics (ICBR), Sousse, Tunisia, 15–17 December 2013. [Google Scholar]
- Ramanathan, K.C.; Singaperumal, M.; Nagarajan, T. Cooperative formation planning and control of multiple mobile robots. In Mobile Robots—Control Architectures, Bio-Interfacing, Navigation, Multi Robot Motion Planning and Operator Training; IntechOpen Limited: London, UK, 2011. [Google Scholar]
- Aziz, H.; Pal, A.; Pourmiri, A.; Ramezani, F.; Sims, B. Task allocation using a team of robots. Curr. Robot. Rep. 2022, 3, 227–238. [Google Scholar] [CrossRef]
- Zitouni, F.; Harous, S.; Maamri, R. A distributed approach to the multi-robot task allocation problem using the consensus-based bundle algorithm and ant colony system. IEEE Access 2020, 8, 27479–27494. [Google Scholar] [CrossRef]
- Rauniyar, A.; Muhuri, P.K. Multi-robot coalition formation problem: Task allocation with adaptive immigrants based genetic algorithms. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016. [Google Scholar]
- Kraus, S. Negotiation and cooperation in multi-agent environments. Artif. Intell. 1997, 94, 79–97. [Google Scholar] [CrossRef]
- Tosic, P.; Ordonez, C. Distributed protocols for multi-agent coalition formation: A negotiation perspective. In Proceedings of the 8th International Conference, AMT 2012, Macau, China, 4–7 December 2012. [Google Scholar]
- Selseleh Jonban, M.; Akbarimajd, A.; Hassanpour, M. A combinatorial auction algorithm for a multi-robot transportation problem. In Proceedings of the 3rd International Conference on Machine Learning and Computer Science (IMLCS’2014), Dubai, United Arab Emirates, 5–6 January 2014. [Google Scholar]
- Capitan, J.; Spaan, M.T.J.; Merino, L.; Ollero, A. Decentralized multi-robot cooperation with auctioned POMDPs. Int. J. Robot. Res. 2013, 32, 650–671. [Google Scholar] [CrossRef]
- Hernandez-Leal, P.; Kaisers, M.; Baarslag, T.; Munoz de Cote, E. A Survey of Learning in Multiagent Environments: Dealing with Non-Stationarity; Cornell University: New York, NY, USA, 2017. [Google Scholar]
- Vig, L.; Adams, J.A. Multi-robot coalition formation. IEEE Trans. Robot. 2006, 22, 637–649. [Google Scholar] [CrossRef]
- Guerrero, J.; Oliver, G. Multi-robot coalition formation in real-time scenarios. Robot. Auton. Syst. 2012, 60, 1295–1307. [Google Scholar] [CrossRef]
- Rizk, Y.; Awad, M.; Tunstel, E. Cooperative heterogeneous multi-robot systems: A Survey. ACM Comput. Surv. 2019, 52, 1–31. [Google Scholar] [CrossRef]
- Ramanathan, K.C.; Singaperumal, M.; Nagarajan, T. Behaviour based planning and control of leader follower formations in wheeled mobile robots. Int. J. Adv. Mechatron. Syst. 2010, 2, 281. [Google Scholar]
- Schillinger, P.; Bürger, M.; Dimarogonas, D. Simultaneous task allocation and planning for temporal logic goals in heterogeneous multi-robot systems. Int. J. Robot. Res. 2018, 37, 818–838. [Google Scholar] [CrossRef]
- Parker, L.E. ALLIANCE: An architecture for fault tolerant multirobot cooperation. IEEE Trans. Robot. Autom. 1998, 14, 220–240. [Google Scholar] [CrossRef]
- Parker, L.E. ALLIANCE: An architecture for fault tolerant, cooperative control of heterogeneous mobile robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994. [Google Scholar]
- Parker, L. L-ALLIANCE: A Mechanism for Adaptive Action Selection in Heterogeneous Multi-Robot Teams; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1996. [Google Scholar]
- Parker, L. Evaluating success in autonomous multi-robot teams: Experiences from ALLIANCE architecture implementations. J. Exp. Theor. Artif. Intell. 2000, 13, 95–98. [Google Scholar] [CrossRef]
- Parker, L. On the design of behavior-based multi-robot teams. Adv. Robot. 2002, 10, 547–578. [Google Scholar] [CrossRef]
- Parker, L.E. Task-oriented multi-robot learning in behavior-based systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. IROS ’96, Osaka, Japan, 8 November 1996. [Google Scholar]
- Mesterton-Gibbons, M.; Gavrilets, S.; Gravner, J.; Akçay, E. Models of coalition or alliance formation. J. Theor. Biol. 2011, 274, 187–204. [Google Scholar] [CrossRef]
- Dahl, T.; Matarić, M.; Sukhatme, G. Multi-robot task allocation through vacancy chain scheduling. Robot. Auton. Syst. 2009, 57, 674–687. [Google Scholar] [CrossRef]
- Lerman, K.; Galstyan, A.; Martinoli, A.; Ijspeert, A.J. A macroscopic analytical model of collaboration in distributed robotic systems. Artif. Life 2001, 7, 375–393. [Google Scholar] [CrossRef]
- Jia, X.; Meng, M.Q.H. A survey and analysis of task allocation algorithms in multi-robot systems. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013. [Google Scholar]
- Werger, B.; Mataric, M. Broadcast of local eligibility: Behavior-based control for strongly cooperative robot teams. In Proceedings of the Fourth International Conference on Autonomous Agents, Barcelona, Spain, 3–7 June 2000. [Google Scholar]
- Werger, B.; Mataric, M. Broadcast of local eligibility for multi-target observation. In Distributed Autonomous Robotic Systems 4; Springer: Tokyo, Japan, 2000; pp. 347–356. [Google Scholar]
- Faigl, J.; Kulich, M.; Preucil, L. Goal assignment using distance cost in multi-robot exploration. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 3741–3746. [Google Scholar]
- Tang, F.; Parker, L. ASyMTRe: Automated synthesis of multi-robot task solutions through software reconfiguration. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1501–1508. [Google Scholar][Green Version]
- Fang, T.; Parker, L.E. Coalescent multi-robot teaming through ASyMTRe: A formal analysis. In Proceedings of the ICAR ‘05. Proceedings, 12th International Conference on Advanced Robotics, Piscataway, NJ, USA, 18–20 July 2005. [Google Scholar][Green Version]
- Fang, G.; Dissanayake, G.; Lau, H. A behaviour-based optimisation strategy for multi-robot exploration. In Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics, Singapore, 1–3 December 2004; Volume 2, pp. 875–879. [Google Scholar][Green Version]
- Trigui, S.; Koubaa, A.; Cheikhrouhou, O.; Youssef, H.; Bennaceur, H.; Sriti, M.-F.; Javed, Y. A distributed market-based algorithm for the multi-robot assignment problem. Procedia Comput. Sci. 2014, 32, 1108–1114. [Google Scholar] [CrossRef]
- Badreldin, M.; Hussein, A.; Khamis, A. A comparative study between optimization and market-based approaches to multi-robot task allocation. Adv. Artif. Intell. 2013, 2013, 256524. [Google Scholar] [CrossRef]
- Service, T.C.; Sen, S.D.; Adams, J.A. A simultaneous descending auction for task allocation. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014. [Google Scholar][Green Version]
- Vig, L.; Adams, J. A Framework for Multi-Robot Coalition Formation. In Proceedings of the 2nd Indian International Conference on Artificial Intelligence, Pune, India, 20–22 December 2005; pp. 347–363. [Google Scholar][Green Version]
- Vig, L.; Adams, J. Market-based multi-robot coalition formation. In Distributed Autonomous Robotic Systems 7; Springer: Tokyo, Japan, 2007; pp. 227–236. [Google Scholar][Green Version]
- Vig, L.; Adams, J.A. Coalition formation: From software agents to robots. J. Intell. Robot. Syst. 2007, 50, 85–118. [Google Scholar] [CrossRef]
- Lueth, T.; Längle, T. Task description, decomposition, and allocation in a distributed autonomous multi-agent robot system. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994. [Google Scholar][Green Version]
- Längle, T.; Lueth, T.; Rembold, U. A distributed control architecture for autonomous robot systems. In Modelling and Planning for Sensor Based Intelligent Robot Systems; World Scientific Publishing Co Pte Ltd.: Singapore, 1995; pp. 384–402. [Google Scholar][Green Version]
- Gerkey, B.P.; Mataric, M.J. Sold!: Auction methods for multirobot coordination. IEEE Trans. Robot. Autom. 2002, 18, 758–768. [Google Scholar] [CrossRef]
- Guidotti, C.F.; Baião ATBastos, G.S.; Leite, A.H.R. A murdoch-based ROS package for multi-robot task allocation. In Proceedings of the 2018 Latin American Robotic Symposium 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE), Joao Pessoa, Brazil, 6–10 November 2018. [Google Scholar][Green Version]
- Lagoudakis, M.G.; Markakis, E.; Kempe, D.; Keskinocak, P.; Kleywegt, A.; Koenig, S.; Tovey, C.; Meyerson, A.; Jain, S. Auction-based multi-robot routing. In Proceedings of the 2005 International Conference on Robotics: Science and Systems I, Cambridge, MA, USA, 8–11 June 2005. [Google Scholar][Green Version]
- Lin, L.; Zheng, Z. Combinatorial bids based multi-robot task allocation method. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar][Green Version]
- Sheng, W.; Yang, Q.; Tan, J.; Xi, N. Distributed multi-robot coordination in area exploration. Robot. Auton. Syst. 2006, 54, 945–955. [Google Scholar] [CrossRef]
- Gerkey, B.; Matari, M. MURDOCH: Publish/subscribe task allocation for heterogeneous agents. In Proceedings of the National Conference on Artificial Intelligence, AAAI 2000 (Student Abstract), Austin, TX, USA, 30 July–3 August 2000. [Google Scholar][Green Version]
- Alami, R.; Fleury, S.; Herrb, M.; Ingrand, F.; Robert, F. Multi-robot cooperation in the MARTHA project. IEEE Robot. Autom. Mag. 1998, 5, 36–47. [Google Scholar] [CrossRef]
- Botelho, S.; Alami, R. M+: A scheme for multi-robot cooperation through negotiated task allocation and achievement. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; Volume 2, pp. 1234–1239. [Google Scholar][Green Version]
- Botelho, S.C.; Alami, R. A multi-robot cooperative task achievement system. In Proceedings of the 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000. [Google Scholar][Green Version]
- Smith. The contract net protocol: High-level communication and control in a distributed problem solver. IEEE Trans. Comput. 1980, C-29, 1104–1113. [Google Scholar] [CrossRef]
- Dias, M.B.; Zlot, R.; Zinck, M.; Gonzalez, J.P.; Stentz, A. A Versatile Implementation of the Traderbots Approach for Multirobot Coordination; Carnegie Mellon University: Pittsburgh, PA, USA, 29 June 2018. [Google Scholar] [CrossRef]
- Dias, M.B.; Stentz, A. A Free Market Architecture for Distributed Control of a Multirobot System; Computer Science, Engineering: Dalian, China, 2000. [Google Scholar]
- Zlot, R.; Stentz ADias, M.B.; Thayer, S. Multi-robot exploration controlled by a market economy. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002. [Google Scholar]
- Dias, M.B.; Stentz, A. Traderbots: A New Paradigm for Robust and Efficient Multirobot Coordination in Dynamic Environments; Carnegie Mellon University: Pittsburgh, PA, USA, 2004. [Google Scholar]
- Hussein, A.; Marín-Plaza, P.; García, F.; Armingol, J.M. Hybrid optimization-based approach for multiple intelligent vehicles requests allocation. J. Adv. Transp. 2018, 2018, 2493401. [Google Scholar] [CrossRef]
- Shelkamy, M.; Elias CMMahfouz, D.M.; Shehata, O.M. Comparative analysis of various optimization techniques for solving multi-robot task allocation problem. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020. [Google Scholar]
- Atay, N.; Bayazit, B. Mixed-Integer Linear Programming Solution to Multi-Robot Task Allocation Problem; Washington University in St Louis: St Louis, MO, USA, 2006. [Google Scholar]
- Bouyarmane, K.; Vaillant, J.; Chappellet, K.; Kheddar, A. Multi-Robot and Task-Space Force Control with Quadratic Programming. 2017. [Google Scholar]
- Pugh, J.; Martinoli, A. Inspiring and modeling multi-robot search with particle swarm optimization. In Proceedings of the 2007 IEEE Swarm Intelligence Symposium, Washington, DC, USA, 1–5 April 2007. [Google Scholar]
- Imran, M.; Hashim, R.; Khalid, N.E.A. An overview of particle swarm optimization variants. Procedia Eng. 2013, 53, 491–496. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.X. Particle swarm optimization based multi-robot task allocation using wireless sensor network. In Proceedings of the 2008 International Conference on Information and Automation, Hunan, China, 20–23 June 2008. [Google Scholar]
- Nedjah, N.; Mendonc¸a, R.; Mourelle, L. PSO-based distributed algorithm for dynamic task allocation in a robotic swarm. Procedia Comput. Sci. 2015, 51, 326–335. [Google Scholar] [CrossRef]
- Pendharkar, P.C. An ant colony optimization heuristic for constrained task allocation problem. J. Comput. Sci. 2015, 7, 37–47. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant colony optimization: Artificial ants as a computational intelligence technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Agarwal, M.; Agrawal, N.; Sharma, S.; Vig, L.; Kumar, N. Parallel multi-objective multi-robot coalition formation. Expert Syst. Appl. 2015, 42, 7797–7811. [Google Scholar] [CrossRef]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Wang, J.; Gu, Y.; Li, X. Multi-robot task allocation based on ant colony algorithm. J. Comput. 2012, 7, 2160–2167. [Google Scholar] [CrossRef]
- Jianping, C.; Yimin, Y.; Yunbiao, W. Multi-robot task allocation based on robotic utility value and genetic algorithm. In Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; pp. 256–260. [Google Scholar]
- Haghi Kashani, M.; Jahanshahi, M. Using simulated annealing for task scheduling in distributed systems. In Proceedings of the 2009 International Conference on Computational Intelligence, Modelling and Simulation, Brno, Czech Republic, 7–9 September 2009; pp. 265–269. [Google Scholar]
- Mosteo, A.; Montano, L. Simulated Annealing for Multi-Robot Hierarchical Task Allocation with Flexible Constraints and Objective Functions. In Proceedings of the Workshop on Network Robot Systems: Toward Intelligent Robotic Systems Integrated with Environments, IROS, Beijing, China, 9–15 October 2006. [Google Scholar]
- Chakraborty, S.; Bhowmik, S. Job shop scheduling using simulated annealing. In Proceedings of the 1st International Conference on Computation & Communication Advancement, West Bengal, India, 11–12 January 2013. [Google Scholar]
- Elfakharany, A.; Yusof, R.; Ismail, Z. Towards multi robot task allocation and navigation using deep reinforcement learning. J. Phys. Conf. Ser. 2020, 1447, 012045. [Google Scholar] [CrossRef]
- Dahl, T.; Mataric, M.; Sukhatme, G. A machine learning method for improving task allocation in distributed multi-robot transportation. In Complex Engineered Systems; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Wang, Y.; Silva, C. A machine-learning approach to multi-robot coordination. Eng. Appl. Artif. Intell. 2008, 21, 470–484. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, Q.; Jiang, Q.; Fan, Q. A deep reinforcement learning-assisted multimodal multiobjective bilevel optimization method for multirobot task allocation. IEEE Trans. Evol. Comput. 2025, 29, 574–588. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, X.; Yang, Z.; Ma, S.; Chen, J.; Sun, W. Scalable multi-robot task allocation using graph deep reinforcement learning with graph normalization. Electronics 2024, 13, 1561. [Google Scholar] [CrossRef]
- Cunningham, P.; Cord, M.; Delany, S. Supervised Learning; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar]
- Sermanet, P.; Lynch CHsu, J.; Levine, S. Time-contrastive networks: Self-supervised learning from multi-view observation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Teichman, A.; Thrun, S. Tracking-based semi-supervised learning. Int. J. Robot. Res. 2012, 31, 804–818. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, S.; Guo, H.; Wu, S. Automated labeling for robotic autonomous navigation through multi-sensory semi-supervised learning on big data. IEEE Trans. Big Data 2021, 7, 93–101. [Google Scholar] [CrossRef]
- Bousquet, O.; Luxburg, U.; Rätsch, G. Advanced lectures on machine learning. In ML Summer Schools 2003, Canberra, Australia, 2–14 February 2003, Tübingen, Germany, 4–16 August 2003, Revised Lectures; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Arel, I.; Liu, C.; Urbanik, T.; Kohls, A. Reinforcement learning-based multi-agent system for network traffic signal control. Intell. Transp. Syst. IET 2010, 4, 128–135. [Google Scholar] [CrossRef]
- Verma, J.; Ranga, V. Multi-robot coordination analysis, taxonomy, challenges and future scope. J. Intell. Robot. Syst. 2021, 102, 10. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Silva, C.W.D. Multi-robot box-pushing: Single-agent Q-learning vs. team Q-learning. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006. [Google Scholar]
- Guo, H.; Meng, Y. Dynamic correlation matrix based multi-Q learning for a multi-robot system. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008. [Google Scholar]












| Algorithm | Efficiency | Advantages | Disadvantages |
|---|---|---|---|
| Alliance | High | Scalable, adaptable to dynamic environments, provide a higher degree of stability in coalition | Requires effective communication and coordination |
| Optimal allocation | Medium | Low communication overhead, stable coalitions | Limited scalability, sensitive to changes in the team |
| Cooperation | Medium to high | Efficient, distributed, Low communication | Tends to form smaller coalitions |
| Vacancy Chain | High | Adaptive, efficient task allocation | Requires sophisticated negotiation mechanisms |
| Characteristics | Alliance | Vacancy Chain | BLE | ASyMTRE |
|---|---|---|---|---|
| Homogenous/ Heterogenous | Heterogeneous | Heterogeneous | Heterogeneous | Heterogeneous |
| Optimal allocation | Guarantee optimal allocation | Guarantee (Minimal) | Does not Guarantee | Guarantee (Minimal) |
| Cooperation | Strongly cooperative | Weak cooperation | Strongly cooperative | Strongly cooperative |
| Communicatiom | Strong | Limited | Strong | Limited |
| Hierarchy | Fully distributed | Not fully distributed | Fully distributed | Not fully distributed |
| Task reassignment | Possible through coalition reconfiguration) | Possible (via vacancy announcement) | (Possible based on dynamic eligibility) | (Possibly based on genetic optimization) |
| Characteristics | RACHNA | KAMARA | MURDOCH | M+ | TraderBots |
|---|---|---|---|---|---|
| Market-based | Negotiation-based | Market-based | Market-based | Negotiation-based | Auction-based |
| Bidding method | Uses a genetic algorithm to optimize bids | Bids are based on utility functions that consider the cost and quality of the task | Bids based on a simple cost function | Form coalitions to bid on tasks together | Bids are based on a reinforcement learning algorithm |
| Homogenous/ Heterogenous | Heterogeneous | Heterogeneous | Heterogeneous | Heterogeneous | Homogeneous robots |
| Fault tolerance | Not fault-tolerant | Fault-tolerant | Not fault-tolerant | Fault-tolerant | Fault-tolerant |
| Optimal allocation | Can guarantee depending on the fitness function | Can guarantee based on the utility function | Not Guaranteed | Can guarantee based on the coalition formation algorithm | Can guarantee |
| Cooperation | Cooperative | Cooperative | Strong cooperation | Cooperative | Strongly cooperative |
| Communication | Limited (Global communication) | Limited (Local communication) | Strong (Global communication) | Strong (Local communication) | Strong (Local communication) |
| Hierarchy | Distributed | Hybrid | Distributed (Loosely coupled) | Fully distributed | Combination of a distributed and centralized approach |
| Task reassignment | Not Possible | Possible | Not possible | Possible | Possible |
| Complexity | Moderate | Moderate | Simple | High | High |
| Cost | Moderate | Moderate | Low | High | High |
| Scalability | Limited | Highly scalable | Limited | Highly scalable | Highly scalable |
| Coalition formation | Yes | Possible | Yes, and dynamically adaptable | Yes, and dynamically adaptable | Yes |
| Approach | Optimization Technique | Advantages | Disadvantages |
|---|---|---|---|
| PSO [75,76,77,78] | Swarm intelligence |
|
|
| ACO [79,80,81,82,83] | Swarm intelligence |
|
|
| GA [84,85] | Evolutionary |
|
|
| SA [86,87,88] | Stochastic |
|
|
| MILP [72,73] | Mathematical Programming |
|
|
| QP [74] | Mathematical Programming |
|
|
| Characteristics | Particle Swarm Optimization (PSO)/Ant Colony Optimization (ACO)/Genetic Algorithm (GA)/Simulated Annealing (SA) | Mixed Integer Linear Programming (M ILP) | Quadratic Programming (QP) |
|---|---|---|---|
| Fault tolerance | Robust to individual robot failures but not to system-wide failures | Not inherently fault-tolerant | Not inherently fault-tolerant |
| Optimal allocation | May converge to local optima and be able to handle multiple objectives | Can find globally optimal solutions, but computational complexity may increase with problem size. | Can find globally optimal solutions, but computational complexity may increase with problem size. |
| Scalability | Can handle significant problems efficiently but requires extensive parameter tuning. | Small-medium-sized problems | Can handle significant problems efficiently but requires extensive parameter tuning |
| Task reassignment | Can handle by updating the objective functions and constraints | Can handle by updating the objective functions and constraints | Can handle by updating the objective functions and constraints |
| Coalition formation | Can handle by adding appropriate terms to the objective functions and constraints | Can handle by adding appropriate terms to the objective functions and constraints | Can handle by adding appropriate terms to the objective functions and constraints |
| Complexity | Can handle complex optimization problems with non-linearities and multiple objectives | Can handle linear and non-linear constraints. | Can handle linear and non-linear constraints. |
| Cost | It can be less expensive than MILP and QP but requires extensive parameter tuning. | It can be expensive due to the computational complexity | It can be expensive due to the computational complexity |
| Factors | Supervised Learning | Unsupervised Learning | Semi-Supervised Learning | Reinforcement Learning |
|---|---|---|---|---|
| Fault tolerance | Low, sensitive to errors in the labels as it relies on labeled data for training | Low, may handle noise and outliers better as it does not require labels. | More fault-tolerant by leveraging both labeled and unlabeled data. | Medium, through exploration-exploitation trade-offs |
| Optimal allocation | Can achieve optimal allocation by learning from labeled data and mapping inputs to correct outputs. | No, mostly aims to discover patterns and relationships in the data. | Partially, it may require more specialized approaches | Partially, it may require more specialized approaches |
| Scalability | High, may face challenges due to the need for labeled data and computational complexity. | High as it does not require labeled data. | High, by utilizing both labeled and unlabeled data. | Medium-high, may face challenges due to the need for labeled data and computational complexity. |
| Task reassignment | Difficult, not inherently designed for it, may require additional mechanisms. | Yes, it naturally clusters data into groups. | Yes, can leverage both labeled and unlabeled data to handle task reassignment. | Yes, equipped to handle task reassignment in sequential decision-making problems. |
| Coalition formation | Not specifically tailored, may need additional considerations and adaptations. | Same as Supervised learning | Same as Supervised learning and Unsupervised Learning | Possible in situations where agents make sequential decisions in coalition formation tasks. |
| Complexity | Lower, but based on the specific algorithm and techniques used within | Same as Supervised learning | Same as Supervised learning and Unsupervised Learning | Higher due to the need to learn policies for sequential decision-making. |
| Cost | Lower for simple models but varies depending on the complexity of the model and size of the data. | Same as Supervised learning | Same as Supervised learning and Unsupervised Learning | High due to learning and exploration process. |
| Method | Efficiency | Advantages | Disadvantages |
|---|---|---|---|
| Supervised Learning | Low-Medium |
|
|
| Semi-Supervised learning | Low-Medium |
|
|
| Unsupervised learning | Low-Medium |
|
|
| Reinforcement learning | Medium-High |
|
|
| Factors | Behavior-Based Methods | Market-Based Method | Optimization-Based Methods | Learning-Based Methods |
|---|---|---|---|---|
| Scalability | Scalable for small- to moderate-sized systems | Scalable for small- to moderate-sized systems | Scalable for large systems | Can scale to large and complex systems |
| Complexity | Can handle simple to moderately complex tasks | Can handle complex tasks and heterogeneous robots | Can handle complex tasks and constraints | Can handle complex tasks, constraints, and heterogeneous robots |
| Optimality | May not always achieve optimality | Can achieve Pareto efficiency under certain conditions | Can achieve optimality under certain conditions. | Can achieve optimality under certain conditions. But guaranteed for good optimal allocation all the time. |
| Flexibility | Limited flexibility to adapt to new tasks or situations | Can be flexible and adaptable to changing market conditions | May be flexible depending on the optimization method used | Can be flexible and adaptable to changing environment |
| Robustness | May be robust to some degree of uncertainty or failures | Can be robust to some degree of market uncertainty and failures | May not be robust to uncertainty or failures. | Can improve robustness through learning from experience and failures. |
| Communication | Local communication among neighbor robots. | Multiple times broadcasting of winner robot details after bidding | Local communication among neighbour robots. | Local/Global communication |
| Objective function | Single/multiple objectives Implicit or ad hoc | Single/multiple objectives Optimization | Single/multiple objectives Mathematical | Single/multiple objectives Learning from data |
| Coordination type | Centralized/distributed | Centralized/distributed | Centralized/distributed | Decentralized |
| task reallocation method | Heuristics ruled searching/Bayesian Nash equilibrium | Iterative auctioning methods | Iterative searching and allocation | Reinforcement learning |
| Uncertainty handling techniques | Game theory/probabilistic predictive modelling | Iterative auctioning methods | Difficult to handle uncertainty | Adaptive models |
| Constraints | Can be handled in a collective manner | Difficult to conduct auctions | Complex and difficult to solve due to multiple decision variables | Varies based on learning algorithms |
| Computational cost | Higher than optimization-based strategy | Lower than optimization strategy | Higher than market-based strategy | High; needs large amount of data |
| Coalition formation | Low efficiency as the approach is based on local rules without a global optimization perspective. | Moderate efficiency due to negotiation and market mechanisms | High efficiency through global optimization approaches | Moderate efficiency as it relies on learning and adaptive algorithms. |
| Task reallocation | Limited ability to perform task reallocation dynamically as it relies on predefined rules. | Efficient task reallocation due to negotiation and the market mechanism | Efficient reallocation due to optimization algorithms and centralized coordination | Adaptive due to learning algorithms and flexible decision-making |
| Collision avoidance | Limited capability due to lack of sophisticated coordination mechanism | Effective collision avoidance due to price-based mechanisms and negotiations. | Effective due to optimized task allocation and coordination | Adaptive due to learning and sensor-based approaches |
| Dynamic decision-making | Limited adaptability due to its rule-based and reactive characteristics | Limited adaptability as it relies on predefined market rules. | Flexible due to mathematical optimization and modeling | Flexible through adaptive learning algorithms |
| Temporal constraints | Limited support due to a lack of coordinated decision-making | Moderate support due to negotiation and the market mechanism | Highly support handling temporal constraints through optimization techniques and advanced scheduling algorithms. | Highly support handling temporal constraints through learning and scheduling algorithms. |
| Algorithm | CPU Time for 100 Iterations (Seconds) |
|---|---|
| Alliance | 289.7019 |
| M+ | 70.5721 |
| PSO | 0.051051 |
| RL | 26.3469 |
| Team Size | Alliance Average Final Distance | RL Average Final Distance | Alliance CPU Time (s) | RL CPU Time (s) |
|---|---|---|---|---|
| 10 | 36.94 | 11.49 | 0.0031 | 0.0014 |
| 25 | 49.54 | 12.69 | 0.0081 | 0.0028 |
| 50 | 29.04 | 10.64 | 0.0172 | 0.0064 |
| 75 | 36.62 | 9.31 | 0.0286 | 0.0098 |
| 100 | 40.16 | 12.20 | 0.0437 | 0.0158 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arjun, K.; Parlevliet, D.; Wang, H.; Yazdani, A. Optimizing Coalition Formation Strategies for Scalable Multi-Robot Task Allocation: A Comprehensive Survey of Methods and Mechanisms. Robotics 2025, 14, 93. https://doi.org/10.3390/robotics14070093
Arjun K, Parlevliet D, Wang H, Yazdani A. Optimizing Coalition Formation Strategies for Scalable Multi-Robot Task Allocation: A Comprehensive Survey of Methods and Mechanisms. Robotics. 2025; 14(7):93. https://doi.org/10.3390/robotics14070093
Chicago/Turabian StyleArjun, Krishna, David Parlevliet, Hai Wang, and Amirmehdi Yazdani. 2025. "Optimizing Coalition Formation Strategies for Scalable Multi-Robot Task Allocation: A Comprehensive Survey of Methods and Mechanisms" Robotics 14, no. 7: 93. https://doi.org/10.3390/robotics14070093
APA StyleArjun, K., Parlevliet, D., Wang, H., & Yazdani, A. (2025). Optimizing Coalition Formation Strategies for Scalable Multi-Robot Task Allocation: A Comprehensive Survey of Methods and Mechanisms. Robotics, 14(7), 93. https://doi.org/10.3390/robotics14070093









