An Improved DHA Star and ADA-DWA Fusion Algorithm for Robot Path Planning

Abstract

The advancement of mobile robot technology has made path planning a necessary condition for autonomous navigation, but traditional algorithms have issues with efficiency and reliability in dynamic and unstructured environments. This study proposes a Dynamic Hybrid A* (DHA*)–Adaptive Dynamic Window Approach (ADA-DWA) fusion algorithm for efficient and reliable path planning in dynamic unstructured environments. This paper improves the A* algorithm by introducing a dynamic hybrid heuristic function, optimizing the selection of key nodes, and enhancing the neighborhood search strategy, and collaboratively optimizes the search efficiency and path smoothness through curvature optimization. On this basis, the local planning layer introduces a self-adjusting weight-adaptive system in the DWA framework to dynamically optimize the speed, sampling distribution, and trajectory evaluation metrics, achieving a balance between obstacle avoidance and environmental adaptability. The proposed fusion algorithm’s comprehensive advantages over traditional methods in key operational indicators, including path optimality, computational efficiency, and obstacle avoidance capability, have been widely verified through numerical simulations and physical platforms. This method successfully resolves the inherent trade-off between efficiency and reliability in complex robot navigation scenarios, providing enhanced operational robustness for practical applications ranging from industrial logistics to field robots.

1. Introduction

With the rapid development of automation technology, mobile robots have become key platforms in industrial and service applications, gradually replacing traditional manual labor. Path planning algorithms, as the core technology of autonomous navigation systems, play a decisive role in ensuring the movement efficiency and safety of robots in complex environments [1,2,3,4]. The main goal of these algorithms goes beyond achieving spatial connection between the origin and destination; they need to perform multi-constraint optimization in dynamic scenarios, such as balancing, real-time obstacle avoidance, and energy consumption [5]. In recent years, the increasing demand for intelligent mobile robots has driven significant progress in path planning research [6,7]. Current methods adopt a hierarchical framework that integrates global path planning and local path planning [8,9,10]. Global planning utilizes the previous environmental map to generate the optimal trajectory through graph search or mathematical optimization, offering advantages in terms of path length and computational efficiency. In contrast, local planning dynamically adjusts the path based on real-time sensor data, prioritizing robustness and adaptability to unforeseen obstacles [11].

Current global path planning algorithms can be systematically classified into two categories based on the coverage characteristics of their solution spaces: complete planning algorithms and probabilistic complete algorithms [12]. Complete algorithms adopt deterministic mathematical methods to ensure the existence of solutions. Typical representatives are the A* algorithm, Dijkstra’s algorithm, and heuristic methods such as Genetic Algorithm (GA) and Ant Colony Optimization (ACO) [13,14,15,16]. Probabilistic complete algorithms include sample-based methods, such as Fast Exploration Random Tree (RRT) and probabilistic roadmap [17]. Local path planning algorithms, such as Time Elastic Band (TEB), Artificial Potential Field (APF), and Dynamic Window Method (DWA), are mainly used for real-time obstacle avoidance [18]. Although the A* algorithm has global optimality in a static environment, due to the fixed search neighborhood of the A* algorithm and the monotonic heuristic function, it often generates non-smooth paths with redundant nodes and sudden directions in the grid map. These restrictions not only reduce the movement efficiency, but also increase the computational cost [19,20,21]. Although the DWA algorithm can effectively handle dynamic obstacle avoidance problems, due to the lack of a global guiding vector, local optima are prone to occurring in complex obstacle distributions, resulting in potential collisions or unattainable targets [22,23,24,25].

The collaborative optimization and performance enhancement of the A* algorithm and the DWA algorithm have attracted extensive attention in the field of robot research. Xu et al. [26] improved the adaptive cost function in the A* algorithm and the corner-smoothing strategy of nodes, thereby enhancing its search efficiency. However, their method did not solve the reliability problem in complex dynamic environments. Wang et al. [27] introduced the heading-angle variation factor into the DWA evaluation function, which improved flexibility and efficiency. However, this method may converge to a local minimum in scenarios with dense and chaotic obstacles, resulting in an unfeasible path. Zhen et al. [28] integrated the improved versions of A* and DWA to achieve higher efficiency and stability. However, their framework neither optimized the search neighborhood of the A* algorithm (resulting in computational bottlenecks) nor verified the results through actual experiments. Jiang et al. [29] proposed a hybrid method that combines DWA and A* for segmented local path optimization, improving adaptability. However, their method failed to significantly reduce node redundancy or computing time. Wang et al. [30] enhanced the A* algorithm by improving neighborhood search and angle optimization, and combined it with the improved DWA for dynamic environments. Despite these improvements, persistent redundant nodes have reduced computational efficiency and increased planning time.

Existing path planning methods have serious drawbacks, such as excessive redundant nodes, rough trajectories, low search efficiency, poor adaptability to dynamic environments, and delayed obstacle avoidance responses, which seriously restrict their application in real-world scenarios. To solve these problems, this paper proposes a new fusion framework that integrates the DHA* and ADA-DWA algorithms. This method improves the DHA* algorithm through dynamic heuristic function adaptation, elimination of redundant nodes, and optimization of the neighborhood search mechanism, effectively reducing the path redundancy and improving the trajectory smoothness. Adaptive factors are embedded in the evaluation function of the DWA to achieve a dynamic balance between obstacle avoidance and global path consistency. The key nodes extracted from the global path generated by DHA* are used as intermediate guidance points of the DWA, thereby enabling real-time adaptation to environmental uncertainties. The synergy between the enhanced DHA* and ADA-DWA algorithms ensures robust and efficient navigation in complex dynamic environments, demonstrating superior adaptability and computational performance compared to traditional methods.

The remainder of this paper is organized as follows: Section 2 details the materials and methods, presenting the proposed DHA* algorithm with its enhanced heuristic function, key node selection, and neighborhood search strategy, followed by the ADA-DWA algorithm incorporating auto-tuning weight adaptation. The fusion framework integrating DHA* and ADA-DWA is also elaborated. Section 3 presents the results and discussion, including numerical simulations of DHA* and the fusion algorithm in both static and dynamic environments, as well as real-world evaluations on a mobile robot platform. Finally, Section 4 concludes the paper by summarizing the key findings and contributions.

2. Materials and Methods

2.1. DHA* Algorithm

2.1.1. A* Algorithm Principles

The A* pathfinding algorithm, a classic application of heuristic search, discretizes the search area into grid cells as illustrated in Figure 1b, transforming the path planning problem into an optimal connectivity search among these grid units. The resulting path is composed of a sequence of interconnected grid cells. During this process, each node is assigned an estimated cost value, derived from the heuristic function. The A* algorithm adheres to the “minimum estimated cost priority” principle, iteratively expanding the node with the smallest estimated value until the goal is reached, as illustrated in Figure 1c. Consequently, the definition of the heuristic function critically determines the algorithm’s efficiency. In the A* algorithm, the heuristic function is formulated as

$$f\left(n\right)=g\left(n\right)+h\left(n\right)$$

(1)

In Equation (1), $n$ represents the current node; $g\left(n\right)$ denotes the actual cost from the start node to the current node; and $h\left(n\right)$ indicates the estimated cost from $n$ to the goal node. To ensure the effectiveness of the A* algorithm, guarantee computational efficiency, and achieve optimal path planning, it is essential to balance the design of the evaluation function. Since the exact path from node S to the goal node G is unknown, a heuristic method must be utilized to compute $h\left(n\right)$, as depicted in Figure 1d. The traditional evaluation function employs the Euclidean distance:

$$h\left(n\right)=\sqrt{{\left(x_s-x_g\right)}^2+{\left(y_s-y_g\right)}^2}$$

(2)

In Equation (2), $x_s$ and $x_g$ represent the x-coordinates of the current node and the goal node, respectively. $y_s$ and $y_g$ denote the y-coordinates of the current node and the goal node, respectively.

2.1.2. Evaluation Function of DHA* Algorithm

The efficacy of the A* algorithm hinges critically on the choice of $h\left(n\right)$. An appropriately formulated heuristic function significantly boosts both search efficiency and path accuracy through targeted exploration and cost minimization [31]. However, traditional heuristic functions often lead the A* algorithm to converge to suboptimal solutions or explore excessively large search spaces. To address these limitations, this paper proposes a dynamic weighting strategy that synergistically combines the Chebyshev distance and Manhattan distance, adjusting their weights based on real-time pathfinding costs. The core principles of this strategy are as follows:

(1)

Early Stage (Global Exploration):

The Chebyshev distance provides a lower-bound estimation of the minimum distance, ensuring globally optimal path discovery when nodes are far from the goal.

(2)

Intermediate Stage (Balanced Search):

The weights of the Chebyshev and Manhattan distances are coordinated to balance exploration and exploitation.

(3)

Final Stage (Local Convergence):

The Manhattan distance dominates to accelerate convergence when nodes approach the goal.

The hybrid heuristic function is formulated as follows:

$$d_1=max\left\{\left|x_n-x_g\right|,\left|y_n-y_g\right|\right\}$$

(3)

$$d_2=\left|x_n-x_g\right|+\left|y_n-y_g\right|$$

(4)

$$d_3=\left|x_s-x_g\right|+\left|y_s-y_g\right|$$

(5)

$$h\left(n\right)=d_1·\left(1+(d_2/d_3)·w\right)$$

(6)

where ${(x}_n,y_n)$, ${(x}_g,y_g)$, and ${(x}_s,y_s)$ denote the coordinates of the current node, goal node, and start node, respectively. The parameter $w$ is an adaptive scaling factor that dynamically adjusts the heuristic function to balance exploration efficiency and path optimality.

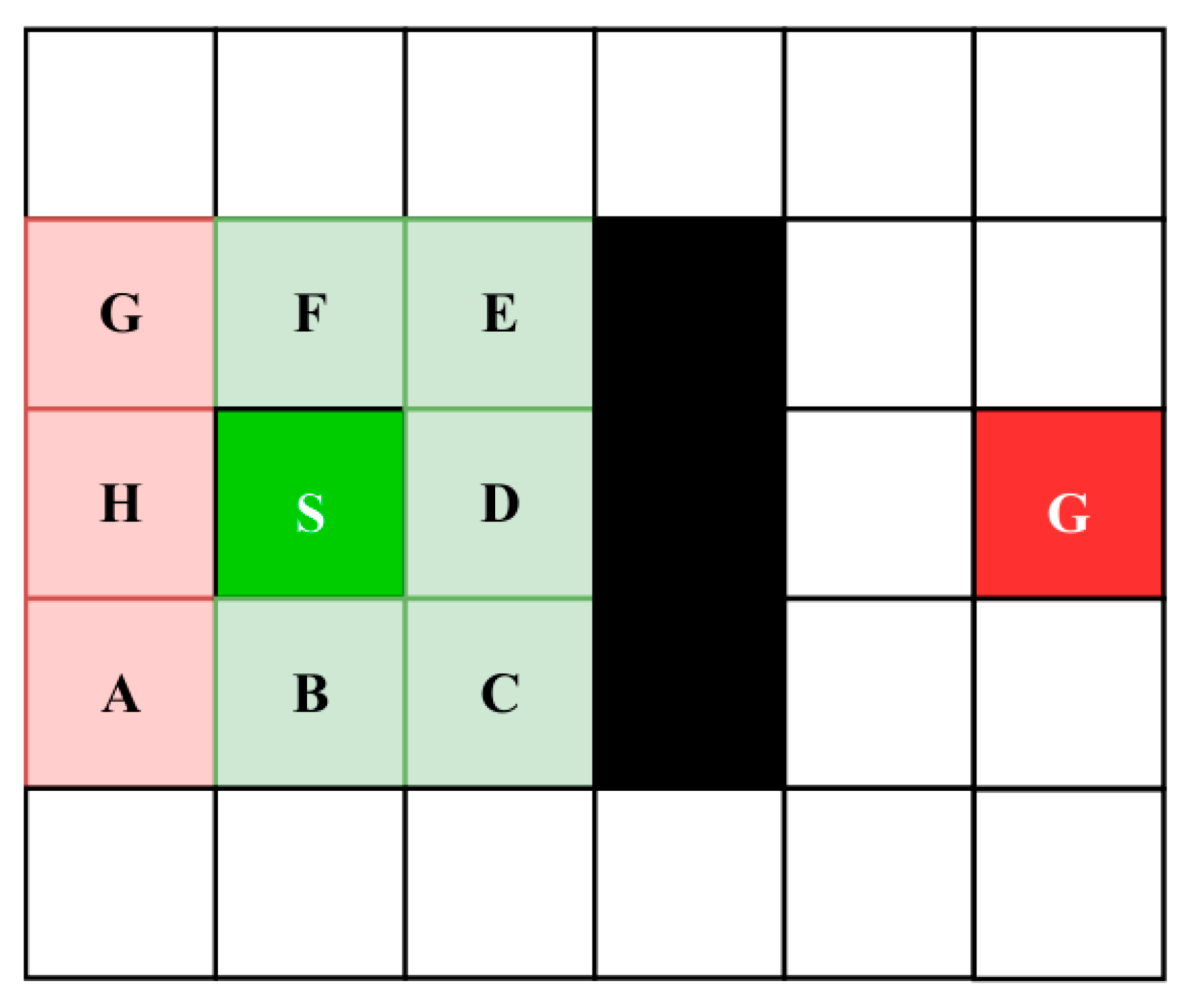
2.1.3. Key-Node Selection Strategy for DHA* Algorithm

Traditional A* algorithms generate paths with excessive redundant nodes and abrupt directional changes during grid-based node expansions [32], significantly degrading computational efficiency and inducing non-smooth motions in robotic navigation. To address these limitations, this paper proposes a key-node selection strategy to optimize path topology. The KNSS operates through two core mechanisms: Collision-Free Redundancy Pruning: Starting from the initial node, the algorithm checks for obstacle intersections between parent and current nodes. If no collision exists, intermediate nodes are eliminated, directly connecting the parent and current nodes. Safety Margin Validation: For retained nodes, the minimum distance between the line segment connecting consecutive nodes and nearby obstacles is calculated. If this distance exceeds a predefined safety threshold, intermediate nodes are pruned to ensure kinematic feasibility, as depicted in Figure 2.

The Safety Margin Validation function is formulated as follows: for consecutive nodes A $\left(x_a,y_a\right)$ and B $\left(x_b,y_b\right)$ the minimum distance to obstacles is computed as

$$d_{min}=\underset{O_i}{\min }\left(\underset{(x,y)\in \overline{\mathit{AB}}}{\min }\sqrt{{(x-x_{O_i})}^2+{(y-y_{O_i})}^2}\right)$$

(7)

where $(x_{O_i},y_{O_i})$ are the coordinates of obstacle $O_i$. If $d_{min}\ge d_{safe}$, intermediate nodes are pruned. The $d_{safe}$ needs to be set according to the environment and robot parameters.

2.1.4. Direction-Aware Neighborhood Search Strategy for DHA* Algorithm

The conventional A* algorithm employs an 8-neighborhood search strategy, expanding eight adjacent nodes around the parent node during exploration. However, this approach indiscriminately evaluates nodes irrespective of their alignment with the goal direction, leading to redundant computations and suboptimal search efficiency [33]. To mitigate this limitation, this paper proposes an optimized method based on the Direction–Target (D-T) principle that prioritizes goal-oriented nodes through vector alignment analysis.

D-T Rule: Given the current node $S$ and the goal node $G$, the 8-neighborhood nodes of $S$ form a candidate set $N_s$. For each node $A\in N_s$, the vector $\overrightarrow{SA}$ and the target vector $\overrightarrow{SG}$ are computed. The cosine of the angle between $\overrightarrow{SA}$ and $\overrightarrow{SG}$ is calculated. If this cosine value is greater than or equal to 0, the corresponding neighbor node $A$ is considered to lie in the direction of the goal, and is retained for further exploration. Nodes failing this criterion are pruned, ensuring that the search prioritizes goal-oriented paths while significantly reducing computational redundancy. As shown in Figure 3, let the current coordinates of node $S$ be ${(x}_s,y_s)$, the neighboring node $A$ be ${(x}_A,y_A)$, and the goal node $G$ be ${(x}_G,y_G)$. The vectors $\overrightarrow{SA}$ and $\overrightarrow{SG}$ are derived, and the angle between these vectors is computed. Here, $i$ and $j$ denote the unit vectors along the $x$- and $y$-axes, respectively.

$$SA=\left(x_A-x_S\right)i+\left(y_A-y_S\right)j$$

(8)

$$SG=\left(x_G-x_S\right)i+\left(y_G-y_S\right)j$$

(9)

$$\cos \theta =SA\times SG/\sqrt{\left|SA\right|\times \left|SG\right|}$$

(10)

As illustrated in Figure 3, the cosine values of the vector angles formed between the current node and nodes $A$, $H$, and $G$ are calculated to be less than zero. Consequently, these three nodes are excluded from subsequent computational evaluations to prioritize directional efficiency and avoid backward exploration.

2.2. Adaptive Dynamic Window Approach (ADA-DWA) Algorithm

The conventional DWA algorithm is prone to suboptimal path selection, including local minima entrapment, poor obstacle avoidance performance, and cumbersome parameter-tuning processes [34]. To overcome these limitations, this paper proposes an enhanced evaluation function that adaptively adjusts the velocity, heading angle, and positional parameters in response to environmental dynamics. This modification allows the robot to navigate at higher speeds while ensuring collision-free trajectories, thereby achieving both stability and efficiency in reaching the target.

2.2.1. Robot Kinematic Model and Velocity Sampling

The DWA algorithm is a local path planning algorithm based on velocity-space sampling. By performing multiple sampling iterations within the robot’s velocity space, it determines the feasible velocity range for the robot and generates multiple local trajectories within this range [35]. The robot’s pose in the world coordinate system at time $t+1$, denoted as ${\left[\begin{array}{ccc}{x}_{t+1}& y_{t+1}& {\theta }_{t+1}\end{array}\right]}^T$, is determined by its linear velocity $v$ and angular velocity $\omega$ at time $t$, with the kinematic model expressed as

$$\left\{\begin{array}{c}{x}_{t+1}=x_t+v∆t·\cos {\theta }_t\\ y_{t+1}=y_t+v∆t·\sin {\theta }_t\\ {\theta }_{t+1}={\theta }_t+\omega ∆t\end{array}\right.$$

(11)

where ${\left[\begin{array}{ccc}{x}_{t+1}& y_{t+1}& {\theta }_{t+1}\end{array}\right]}^T$ represents the robot’s pose at time $t$, and $∆t$ is the time interval.

Within the robot’s velocity space $\left(v,\omega \right)$, multiple velocity samples are generated, but constrained by three criteria to form a dynamic window:

(1)

Maximum Velocity Constraints:

$$V_s=\left(v,\omega \right)\in \left\{\left(v,\omega \right)|v\in \left[v_{min},v_{max}\right],w\in \left[{\omega }_{min}{,\omega }_{max}\right]\right\}$$

(12)

where $v_{min}$ and $v_{max}$ denote the robot’s minimum and maximum linear velocities, while ${\omega }_{min}$ and ${,\omega }_{max}$ represents the minimum and maximum angular velocities.

(2)

Acceleration/Deceleration Constraints:

$$V_d\in \left\{\left(v,\omega \right)|v\in \left[v_c-{\dot{v}}_b∆t,v_c+{\dot{v}}_b∆t\right],\omega \in \left[{\omega }_c-{\dot{\omega }}_b∆t,{\omega }_c+{\dot{\omega }}_b∆t\right]\right\}$$

(13)

where $v_b$ and ${\omega }_c$ denote the robot’s current linear velocity and angular velocity, ${\dot{v}}_b$ represents the maximum linear acceleration/deceleration, and ${\dot{\omega }}_b$ represents the maximum angular acceleration/deceleration.

(3)

Safety-Constrained Velocity Bounds:

$$V_a\in \left\{\left(v,\omega \right)|v\le \sqrt{2·dist\left(v,\omega \right)·{\dot{v}}_b},\omega \le \sqrt{2·dist\left(v,\omega \right)·{\dot{\omega }}_b}\right\}$$

(14)

where $dist\left(v,\omega \right)$ represents the minimum distance to obstacles along the predicted trajectory, and ${\dot{v}}_b$ and ${\dot{\omega }}_b$ are the values of maximum deceleration for linear and angular motion, respectively.

The final dynamic window velocity space is defined as the intersection of these constraints:

$$V_r=V_s\cap V_d\cap V_a$$

(15)

2.2.2. Adaptive Evaluation Function of ADA-DWA

To ensure the safety of mobile robots on global paths, the traditional DWA algorithm assigns a consistently higher weight to the minimum-distance evaluation sub-function (measuring the distance between the robot and obstacles) compared to other sub-functions. However, in densely cluttered obstacle environments, this priority may cause the robot to prefer local optima, leading to increased travel distances and degraded path efficiency [36]. To address this limitation, this paper introduces an adaptive factor into the evaluation function, dynamically adjusting the weights of sub-functions (e.g., speed, heading angle, and position) to achieve a balance between path safety and navigation efficiency. The enhanced evaluation function is formulated as

$$G(v,\omega )=\alpha ·disto\left(v,\omega \right)+\beta ·g(v,\omega )+\gamma ·vel\left(v\right)+\mu ·distg(v,\omega )$$

(16)

In the evaluation function, $disto\left(v,\omega \right)$ denotes the minimum distance to the nearest obstacle, $g(v,\omega )$ indicates alignment between the trajectory’s terminal direction and the goal direction, $vel\left(v\right)$ represents the absolute value of the robot’s linear velocity, $distg(v,\omega )$ is the distance from the robot’s current position to the goal, and α, β, γ, and μ are adaptive weights for each sub-function. The weights are dynamically adjusted based on environmental feedback:

(1)

Obstacle Avoidance Priority $\left(\alpha \right)$:

(2)

When the robot’s distance to obstacles exceeds a predefined threshold, $\alpha$ is increased to prioritize collision avoidance and maintain a safe margin.

(3)

Directional Consistency $\left(\beta \right)$:

(4)

If the predicted trajectory deviates from the goal direction by more than an angular threshold, $\beta$ is automatically amplified to realign the robot toward the target.

(5)

Velocity Optimization $\left(\gamma \right)$:

(6)

Within a safety margin, $\gamma$ is elevated to maximize velocity.

(7)

Goal Convergence $\left(\mu \right)$:

As the robot approaches the goal, $\mu$ is adaptively increased to minimize terminal oscillations and ensure smooth arrival.

This hierarchical weighting strategy enables the robot to dynamically balance safety, efficiency, and precision across diverse navigation scenarios. As shown in Figure 4, the traditional DWA algorithm may collide with moving obstacles due to its inflexible weight allocation across evaluation sub-functions. In contrast, Figure 4b demonstrates the proposed ADA-DWA algorithm, which ensures safe avoidance of unknown dynamic obstacles and successful goal attainment through adaptive weight adjustments of evaluation metrics.

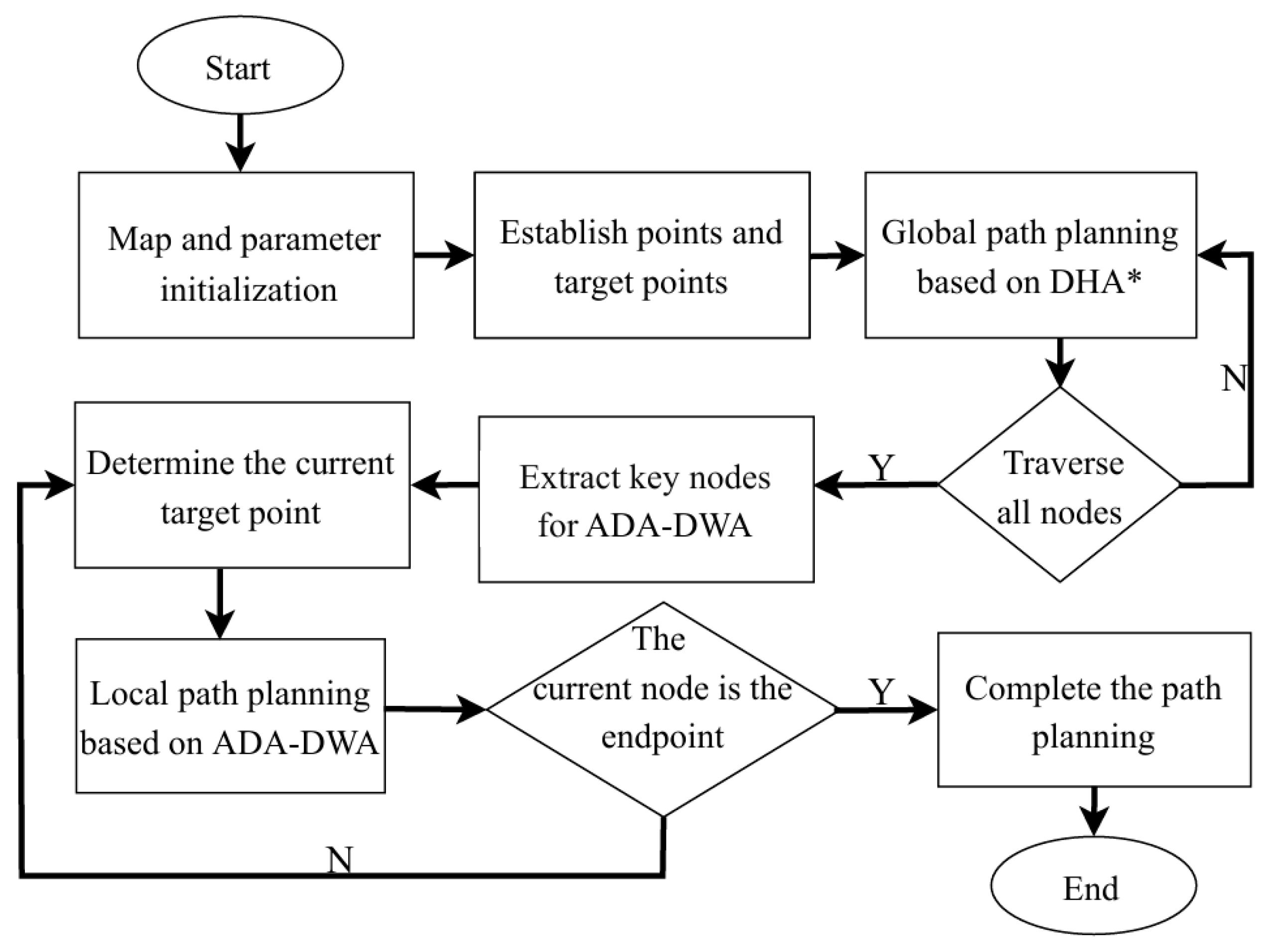
2.3. Fusion of DHA* and ADA-DWA Algorithms

Building upon of the DHA* and ADA-DWA algorithms, this paper proposes a novel fusion framework that synergizes global and local planning. The DHA* algorithm generates an optimal global path in static environments, while ADA-DWA focuses on real-time obstacle avoidance to ensure local path safety. Key nodes extracted from the DHA*-planned global path serve as intermediate guidance points for ADA-DWA, balancing global optimality with local reactivity [37]. As illustrated in Figure 5, this hierarchical architecture leverages the computational efficiency of DHA* for global exploration and enhances local maneuverability through ADA-DWA’s adaptive obstacle avoidance capabilities, enabling robust navigation in dynamic scenarios.

During the fusion of global and local path planning, the framework leverages seamless integration between DHA’s optimized global exploration (identifying the optimal path) and ADA-DWA’s real-time reactivity (collision avoidance in dynamic environments). Each key node generated by DHA serves as an intermediate target for ADA-DWA’s local planning. Through iterative progression between these key nodes, the robot sequentially navigates toward successive sub-goals. This hierarchical architecture demonstrates particularly robust performance in cluttered environments.

3. Results and Discussion

3.1. Numerical Simulation of DHA* Algorithm

To evaluate the performance enhancement of the DHA* algorithm, experiments were conducted using the numerical simulation platform MWORKS.Syslab, developed by Suzhou Tongyuan Soft Control Information Technology Co., Ltd. Comparative simulations were performed on the traditional A algorithm*, the DHA algorithm*, and other improved algorithms. The experimental platform was configured on a computer with 8GB RAM and a 64-bit Windows 11 operating system. Diverse 2D grid maps were designed to simulate environments with varying complexity levels. To comprehensively assess the dynamic obstacle avoidance capability of the proposed algorithm, randomly moving obstacles were introduced into the simulation, and the algorithm’s performance was analyzed under different obstacle interaction scenarios.

In this study, the performance of the traditional A* algorithm, other improved A* variants, and the DHA* algorithm was evaluated in two grid-based simulated environments. The simulation results are illustrated in Figure 6, and a detailed comparison of performance metrics across the algorithms is summarized in

Table 1. Comparison of algorithm performance.

Maps	Algorithms	$\mathit{P}$ $\left(\mathbf{Average}\right)$	$\mathit{L}/\mathbf{m}$ $\left(\mathbf{Average}\right)$	$\mathit{T}/\mathbf{s}$ $\left(\mathbf{Average}\right)$	$\mathit{N}$ $\left(\mathbf{Average}\right)$
20 × 20	Traditional A* Algorithm	$11$	$33.41$	$0.0455$	$31.25$
	Reference [31] Algorithm	$9.5$	$26.67$	$0.0281$	$20.5$
	Reference [32] Algorithm	$8$	$24.98$	$0.0272$	$18$
	DHA* Algorithm	$7.5$	$21.38$	$0.0208$	$12.5$
20 × 20	Traditional A* Algorithm	$17$	$61.28$	$1.147$	$61.5$
	Reference [31] Algorithm	$15.5$	$50.98$	$0.271$	$51.75$
	Reference [32] Algorithm	$12$	$56.16$	$0.297$	$46$
	DHA* Algorithm	$10$	$45.95$	$0.124$	$34.5$

, where $P$ is the number of traversed nodes, $L$ represents the path length, $T$ indicates the search time, and $N$ is the number of traversed nodes. The visual and numerical analyses demonstrate that the DHA* algorithm achieves significant improvements: it reduces the number of nodes by an average of 51.952%, 36.143%, and 27.655% compared to the traditional A* algorithm and the methods from references [31,32], respectively. Furthermore, the total path length generated by DHA* is shortened by an average of 30.517%, 14.851%, and 16.297% relative to the same baseline algorithms. In terms of search time, DHA* outperforms the traditional A* algorithm and the approaches in [31,32], with average reductions of 71.694%, 39.926%, and 40.889%, respectively. These comparative results validate the feasibility and effectiveness of the DHA* algorithm in path planning applications.

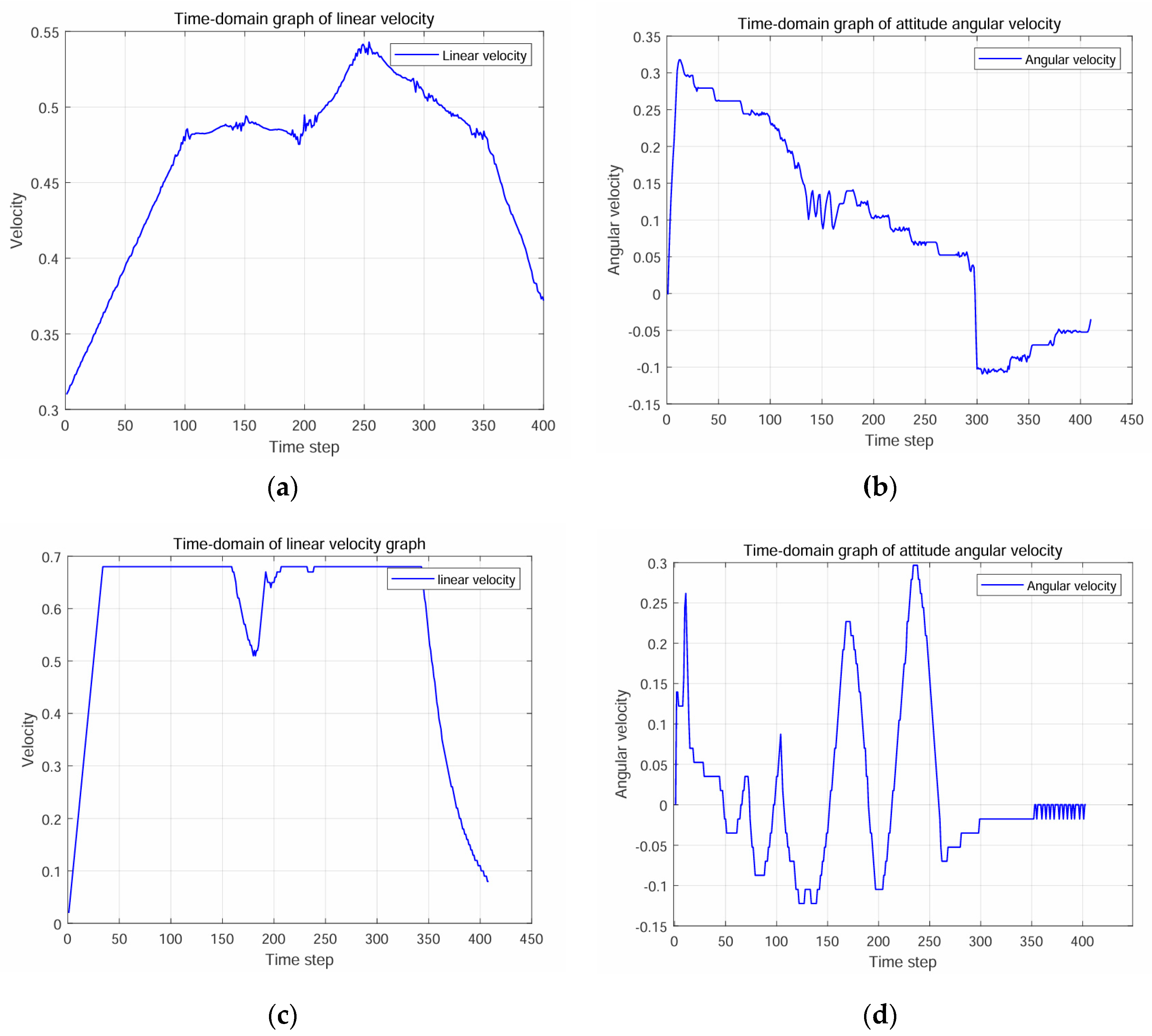
3.2. Numerical Simulation of DHA* and ADA-DWA Fusion Algorithm

To comprehensively evaluate the performance of the proposed fusion algorithm in both static and dynamic scenarios, its dynamic obstacle avoidance capability was rigorously tested by introducing three randomly moving obstacles into the simulation environment. The algorithm’s adaptability to stochastic obstacles was analyzed under varying conditions. Key parameters of the evaluation function, including adaptive weights adjusted in response to environmental changes, are summarized in

Table 2. Robot parameters.

${\mathit{v}}_{\mathit{m}\mathit{a}\mathit{x}}/\left(\mathbf{m}·\mathbf{s}\right)$	${\mathit{a}}_{\mathit{m}\mathit{a}\mathit{x}}/\left(\mathbf{m}·{\mathbf{s}}^2\right)$	${\mathit{\beta }}_{\mathit{m}\mathit{a}\mathit{x}}/\left(\left(°\right)·{\mathbf{s}}^{-}\right)$	${\mathit{w}}_{\mathit{m}\mathit{a}\mathit{x}}/\left(\mathbf{r}\mathbf{a}\mathbf{d}·\mathbf{s}\right)$
2.0	0.2	45	45

and

Table 3. Algorithm setting parameters.

${\mathit{v}}_{\mathit{r}\mathit{e}\mathit{s}}/\left(\mathbf{m}·\mathbf{s}\right)$	${\mathit{T}}_{\mathit{r}\mathit{e}\mathit{s}}/\mathbf{s}$	${\mathit{w}}_{\mathit{r}\mathit{e}\mathit{s}}/\left(\mathbf{r}\mathbf{a}\mathbf{d}·\mathbf{s}\right)$	${\mathit{T}}_{\mathit{p}\mathit{r}\mathit{e}\mathit{d}}/\mathbf{s}$
0.1	0.1	0.05	3.0

. Table 2 lists the robot’s kinematic constraints: $v_{max}$ (maximum linear velocity), $a_{max}$ (maximum linear acceleration), ${\beta }_{max}$ (maximum angular acceleration), and $w_{max}$ (maximum angular velocity). Table 3 details the algorithmic configurations: $v_{res}$ (linear velocity resolution), $T_{res}$ (sampling interval), $w_{res}$ (angular velocity resolution), and $T_{pred}$ (trajectory prediction horizon).

When the dynamic obstacles were set to a speed of 0.05 m/s, the robot successfully detected and avoided them in real time. The global path (dashed line) and the fusion algorithm’s real-time trajectory (solid line) are illustrated in Figure 7, while Figure 8 presents the corresponding velocity profiles and obstacle distance metrics, demonstrating the algorithm’s robustness in dynamic navigation tasks.

As shown in the second subfigure of Figure 7, the robot immediately prunes hazardous trajectory segments upon detecting reduced separation distance from moving obstacles, adjusts its motion trajectory to execute evasion maneuvers, and consequently contracts its feasible velocity-sampling space during collision avoidance. Following successful obstacle avoidance, the robot rapidly reconverges to the global reference path, leveraging guidance from key nodes generated by the DHA* algorithm. Figure 7 demonstrates the fusion algorithm’s capability to navigate around two unknown dynamic obstacles while maintaining a collision-free path to the goal. The real-time motion states of the robot during these maneuvers, including velocity and orientation changes, are detailed in Figure 8. A comparative analysis of the traditional DWA, ADA-DWA, and the fusion DHA*-ADA-DWA algorithm reveals that the hybrid method achieves the shortest planned path (24.08 m) and minimal computation time (20.32 s), with a peak average speed of 0.68 m/s. Specifically, the hybrid algorithm reduces the path length by 15.68% compared to conventional methods, and by 8.92% compared to improved DWA variants, while cutting the planning time by 32.16% and 16.34%, respectively. These results, visualized in Figure 9, underscore the hybrid algorithm’s superior efficiency and robustness in dynamic environments, validating its practical advantages for real-world robotic navigation.

To validate the superiority of the paths planned by the fusion algorithm, comparative simulations were conducted in the aforementioned complex dynamic-obstacle environment using the Dijkstra algorithm, the Ant Colony algorithm, and the traditional A* algorithm. The resulting trajectories are illustrated in Figure 10, highlighting the fusion algorithm’s enhanced adaptability and efficiency in cluttered scenarios.

As shown in

Table 4. Performance parameters of different algorithms.

Maps	Algorithms	$\mathit{P}$	$\mathit{L}/\mathbf{m}$	$\mathit{T}/\mathbf{s}$	Collision Occurred
$20\times 20$	Traditional A* algorithm	$9$	$25.38$	$26.63$	$Y$
	Dijkstra algorithm	$8$	$25.97$	$21.75$	$Y$
	Ant Colony algorithm	$9$	$26.68$	$29.24$	$Y$
	DHA*-ADA-DWA algorithm	$4$	$24.08$	$20.32$	$N$

, the performance comparison of the four algorithms reveals that, except for the fusion algorithm, the other three traditional algorithms generate collision-prone paths when encountering unknown dynamic obstacles. Only the fusion algorithm successfully plans safe and collision-free paths. Furthermore, compared to conventional methods, the fusion algorithm achieves shorter path lengths, fewer turns, and smoother trajectories, while maintaining higher computational efficiency. These results fully validate the effectiveness of the improved fusion algorithm in dynamic environments.

In this study, a series of experiments were conducted under identical environmental conditions to validate the effectiveness of the improved fusion algorithm in handling unknown dynamic obstacles. The results demonstrate that the proposed fusion method outperforms several traditional algorithms in navigating environments with unforeseen static and dynamic obstacles. Specifically, conventional methods such as A* struggle to avoid unanticipated obstacles effectively, while DWA tends to suffer from performance degradation in large-scale environments due to local optima. In contrast, the improved fusion algorithm not only overcomes these limitations, but also exhibits exceptional adaptability and robustness. The experimental findings confirm that the proposed approach successfully addresses the shortcomings of traditional navigation algorithms, thereby verifying its efficacy and generalizability in complex scenarios.

3.3. DHA*-ADA-DWA Evaluation in Real Environment

To validate the practical effectiveness of the improved fusion algorithm, real-world experiments were conducted on a Limo omnidirectional mobile robot. The platform features four wheels with independent steering control, enabling holonomic motion within a compact form factor (body dimensions: 520 × 500 × 200 mm, payload capacity: 15 kg). The system utilized Ubuntu 16.04 and the Robot Operating System (ROS Kinetic) middleware for autonomous navigation. Environmental perception was facilitated by an integrated RPLIDAR A1 360° laser scanner, with laboratory mapping accomplished via the Cartographer SLAM algorithm. Network communication between the host workstation (Intel Core i7-10700K, 32GB RAM) and the robot was established through a dedicated IEEE 802.11ac wireless local-area network. The experimental parameters of the mobile robot were configured as follows: a maximum linear velocity of 0.55 m/s, a maximum linear acceleration of 1.5 m/s², a maximum angular velocity of 1.0 rad/s, a maximum angular acceleration of 1.0 rad/s², and a prediction horizon of 1.7 s. The experimental setup and testing environment are illustrated in Figure 11, showcasing the hardware configuration and the obstacle layout in the lab.

The path planning results and experimental data for the improved fusion algorithm in this paper are illustrated in Figure 12 and

Table 5. Comparison of fusion algorithm’s performance.

Algorithms	$\mathit{L}/\mathbf{m}$	$\mathit{T}/\mathbf{s}$	Collision Occurred
Reference [38] algorithm	$8.74$	$10.41$	$N$
Reference [39] algorithm	$7.68$	$8.35$	$N$
Fusion algorithm in this article	$6.19$	$6.49$	$N$

. The experimental results demonstrate that, compared to the reference [38] and reference [39] algorithms, the proposed fusion algorithm reduced the path length by 29.176% and 19.401%, respectively. The running time was also reduced by 37.656% and 22.275%, respectively, compared with the algorithms from the above two references. These improvements indicate that the proposed algorithm generates smoother trajectories while ensuring global optimality, effectively avoiding dynamic obstacles in real time and enhancing the robot’s adaptability in complex environments.

4. Conclusions

Current robotic path planning methods, which rely exclusively on either global or local planning strategies, often fail to meet real-time and efficiency demands in complex and dynamic environments. To address these limitations, this paper proposes a novel fusion framework integrating the DHA* and ADA-DWA algorithms. The experimental results demonstrate significant improvements across multiple metrics. Compared to traditional A*, reference [31], and reference [32], the DHA* algorithm reduces the number of nodes by an average of 51.952%, 36.142%, and 27.655%, shortens the total path length by 30.517%, 14.851%, and 16.297%, and decreases the search time by 71.694%, 39.926%, and 40.889%, respectively. These enhancements highlight DHA*’s superior performance in terms of path length, planning time, and smoothness. Furthermore, the fused DHA*-ADA-DWA algorithm outperforms the traditional A*, Dijkstra, and Ant Colony algorithms, achieving path length reductions of 4.609%, 6.775%, and 9.257%, and computation time reductions of 23.695%, 6.574%, and 30.506%, respectively. Real-world experiments verify the practical effectiveness of the proposed method, showing that compared with the methods in [38,39], the path length is reduced by 29.176% and 19.401%, and the running time is reduced by 37.656% and 22.275%. Overall, the hybrid algorithm enables efficient path planning, robust dynamic obstacle avoidance, and enhanced adaptability, effectively overcoming the limitations of traditional methods.

The significance of this work lies in its innovative integration of DHA* and ADA-DWA, enabling the robot to perform fast and reliable navigation in highly complex environments while maintaining excellent obstacle avoidance capabilities. This advancement provides crucial technical support for the development of autonomous robot systems in practical applications.