Distributed Monitoring of Moving Thermal Targets Using Unmanned Aerial Vehicles and Gaussian Mixture Models

Abstract

This paper contributes a two-step approach to monitor clusters of thermal targets on the ground using unmanned aerial vehicles (UAVs) and Gaussian mixture models (GMMs) in a distributed manner. The approach is tailored to networks of UAVs that establish a flying ad hoc network (FANET) and operate without central command. The first step is a monitoring algorithm that determines if the GMM corresponds to the current spatial distribution of clusters of thermal targets on the ground. UAVs make this determination using local data and a sequence of data exchanges with UAVs that are one-hop neighbors in the FANET. The second step is the calculation of a new GMM when the current GMM is found to be unfit, i.e., the GMM no longer corresponds to the new distribution of clusters on the ground due to the movement of thermal targets. A distributed expectation-maximization algorithm is developed for this purpose, and it operates on local data and data exchanged with one-hop neighbors only. Simulation results evaluate the performance of both algorithms in terms of the number of communication exchanges. This evaluation is completed for an increasing number of clusters of thermal targets and an increasing number of UAVs. The performance is compared with well-known solutions to the monitoring and GMM calculation problems, demonstrating convergence with a lower number of communication exchanges.

1. Introduction

Unmanned aerial vehicles (UAVs) are powerful tools for monitoring ground activity that is costly to reach, such as wildfires and high-risk urban areas, among others. This paper considers a flying ad hoc network (FANET) of UAVs that capture images over an area of interest. Multiple UAVs are considered for three reasons: (1) the area can be scanned faster, (2) the airspace is restricted above a certain altitude according to local regulations, and (3) the altitude of UAVs is also limited by the resolution of the camera and its sensitivity. For example, in our open source UAV platform developed in [1], thermal cameras have a resolution of $256\times 192$ pixels with vertical and horizontal fields of view of 56.0° and 42.2°, respectively, so when the altitude is maximum at $120\mathrm{m}$ based on local airspace restrictions, each pixel covers an area of $50\mathrm{cm}\times 48\mathrm{cm}$.

We consider ground activity extracted from images in the form of geographical coordinates. For example, in our case of thermal imaging, we extract the location of hot spots of a wildfire and monitor their distribution on the ground as time progresses. We refer to the locations of these objects of interest as targets or observations. We model the geographical distribution of the targets using a Gaussian mixture model (GMM), where each Gaussian component corresponds to a cluster of targets. The objective of this paper is two-fold: (1) to detect when the GMM needs to be updated due to changes on the geographical distribution of moving targets (i.e., the GMM is unfit) and (2) to update the GMM according to new observations (i.e., the GMM fits the new observations).

This paper is inspired by the work on anomaly detection in industrial processes [2]. Observations are extracted from a network of sensors distributed among different industrial process systems such as reactors, condensers, compressors, separators, and strippers [3], so the observations do not correspond to geographical locations in this case. The state of the industrial process is characterized by a GMM. For example, observations of temperature and pressure are expected to be within certain ranges for safe operations, and these ranges are quantified with GMMs. Their goal is to determine when a set of observations deviates from the GMM, indicating an anomaly that triggers an alarm. On the other hand, our goal is to determine when the set of observations of moving thermal targets deviate from the GMM, and when this deviation is detected, we then update the GMM to the new target locations. Therefore, the geographical distribution of the clusters of targets is characterized by a GMM that is updated when targets move.

This paper aims at distributed solutions to both the monitoring problem (i.e., determining when the GMM no longer fits the current distribution of targets) and the problem of updating the GMM (i.e., determining the new values of the parameters of the GMM to fit it to the current distribution of targets). Having distributed solutions makes the FANET resilient against a single point of failure by avoiding a central processing unit and commands, such as a ground station or mothership, commanding all UAVs and processing all data. In our solutions, UAVs exchange selected observations and local statistics with neighboring UAVs several times. We evaluate the performance of our solutions with the number of iterations of communications among UAVs. The reason is that the time required to determine the unfitness of the GMM and to calculate new GMM parameter values determines the maximum speed of targets on the ground that can be monitored (i.e., the Nyquist rate of observations).

The paper is organized as follows. The related work and contributions are discussed in Section 2. The system model and the problem statement are presented in Section 3. Section 4 and Section 5 cover distributed algorithms for monitoring and updating the values of the GMM parameters, respectively. The algorithms are evaluated in Section 6. Practical considerations on our open-source UAV network are discussed in Section 7. Conclusions and future work are discussed in Section 8.

2. Related Work

The use of GMMs for monitoring industrial and chemical processes includes centralized [4,5,6,7,8,9] and distributed [3,10] solutions.

In the seminal work in [4], the use of GMMs was introduced as an extension of the classic approach of principal component analysis. GMMs enable the monitoring of sensor data or observations that do not follow a normal distribution and of processes with multiple operating states. In [5], a Bayesian inference strategy is used to compute the posterior probability of observations belonging to each Gaussian component, and a probability index is used to detect process faults around different operating regions. The problem of dynamic processes (i.e., updates of GMM parameter values) is addressed in [6,7,8]. In [6], particle-filtered Bayesian inference statistics are used to detect anomalies. In [7], the problem is addressed by identifying the Gaussian component that needs to be updated and by updating its parameters with a moving window that selects the recent history of observations. In [8], a Chernoff bound is used to determine the number of unfit observations needed to determine when the GMM is considered unfit. The problem of monitoring online batch processes is addressed in [9]. In online monitoring, only observations up to the current time step are available, and they may not conform to the nominal distribution even if there are no anomalies.

The previous solutions require that all observations be processed in a single computing system, so these solutions are not distributed. This means that all observations need to be delivered to a single node if coming from sensors distributed over the industrial setting. Recent progress in monitoring with GMMs has transitioned to distributed solutions. In [10], the centralized solution presented in [5] is further developed to several local GMMs extracted from a global GMM and applied for distributed monitoring. This is achieved by grouping variables of the global GMM depending on the industrial unit they belong to (e.g., reactor, condenser, or workshop with coupled units) and deriving a GMM for each group. It is assumed that the process is in a faulty state if the observations in any local GMM are unfit. This distributed strategy is further developed in [3] by grouping variables using canonical correlation analysis. Principal component analysis is also performed on a global basis to determine the contribution of each group to the industrial process, enabling online monitoring.

Other related distributed algorithms are presented in [11,12], but these consist of a single Gaussian component, not a mixture as in GMMs, or extensions of other classic techniques, including principal component analysis, canonical correlation analysis, and partial least-squares.

There is another body of work outside the context of industrial/chemical processes that addresses the problem of monitoring in distributed computer systems [13,14,15,16,17,18,19]. Consider a function that depends on variables captured by sensors distributed in an area. The objective is to evaluate the function within a given accuracy level while minimizing data communication with a coordinator to reduce bandwidth and power consumption. The function in [13] is a binary indicator of when the frequency of a single type of event exceeds a threshold value. A heuristic algorithm is proposed that sets local thresholds at each sensor and initiates communication with the coordinator only when the local frequency exceeds the local threshold. The function in [14] is ${\sum }_i{m}_i^p$, where $m_i$ is the frequency of the ith type of event and p = 0, 1, or 2. Their contributions are upper and lower bounds on the communication complexity to evaluate the function within a given accuracy level. The function in [15] is a global property of the network graph (e.g., network diameter) that is decomposed into local conditions that nodes can evaluate with data collected from their local neighborhood. The function in [16] is arbitrary. Its evaluation is achieved with automatic differentiation and numerical optimization to derive local constraints, which are monitored with the geometric monitoring protocol, a proactive monitoring approach. The bandwidth consumption of geometric monitoring is addressed in [17], and an application of the previous monitoring technique is [18], where a coordinator is used to implement linear discriminant analysis on the data collected from the sensor network. On the other hand, a reactive monitoring protocol is proposed in [19], in which a node issues a query that is flooded to all other nodes to evaluate local constraints. The coordinator is then elected to assess the responses.

GMMs have not been considered under the previous monitoring framework (i.e., in [13,14,15,16,17,18,19]) to the best of our knowledge, and in the context of autonomous UAVs, the distributed approach considered in [10] does not apply because it is not guaranteed that each UAV is assigned to a subset of Gaussian components due to their limited coverage. In other words, individual Gaussian components (i.e., individual target clusters) can be spread over a geographical area larger than the area covered by individual UAVs. The distributed approach considered in [3] also does not apply because it assumes a large number of variables that correspond to individual sensors in the industrial plant. These variables are grouped according to the direction of transfer of energy throughout the industrial process, and methods are used to reduce dimensionality, given that the variables can be highly correlated. On the other hand, in the case of UAVs, only two variables are tracked: the x and y coordinates of the targets, and these variables do not correspond to the transfer of energy from x to y or vice versa.

It is also noted that, with the exception of [19], all previous distributed algorithms [3,10,11,12,13,14,15,16,17,18] rely on a star topology where all nodes connect to a coordinator directly, and in [19], a coordinator is elected dynamically to receive data from nodes via convergecast.

Table 1. Classification of monitoring algorithms.

Centralized	Distributed Under Star/Tree Topology
GMM	GMM	single Gaussian component	frequency of an event	arbitrary function
[4,5,6,7,8,9]	[3,10,20]	[11,12]	[13,14]	[15,16,17,18,19]

classifies all monitoring algorithms.

The first contribution of this paper is an algorithm to monitor a function of global data (i.e., the negative log-likelihood defined in Section 4). It compares the function with a threshold value to determine when the GMM is unfit. Our solution is inspired by the distributed algorithm presented in [20] that uses GMMs for monitoring in peer-to-peer computer networks, so there is no coordinator as in [3,10,11,12,13,14,15,16,17,18,19]. The concepts of knowledge, agreement, and withheld knowledge are borrowed from [20] to allow UAVs to communicate with neighboring UAVs iteratively until they can determine that the GMM is unfit. The intuition behind iterative data exchanges is to propagate knowledge that is local to each UAV across the FANET.

The second contribution of this paper is a distributed expectation maximization (EM) algorithm that updates the values of the GMM parameters when the GMM is found to be unfit by the first algorithm. The reason for adopting an EM algorithm different from the one implemented in [20] is that their algorithm depends on a tree-network topology that centralizes computations at the root of the tree (i.e., convergecast). On the other hand, our goal is to build a network that avoids single points of failure, so our distributed EM implementation is instead based on a token-ring protocol [21] in our FANET. It is an adaptation of the solution presented in [22], where nodes communicate sequentially over a token-ring network to complete the maximization step of the EM problem in a distributed way. In our algorithm, UAVs pass a token over the FANET, and when a UAV receives the token, it communicates with all of its one-hop neighbors, not just the next UAV in the ring, as in [22]. In this way, we implement distributed average consensus using Metropolis–Hastings (MH) weights to complete the maximization step of the EM problem faster. MH weights were adopted in [23] from the centralized MH sampling technique of Markov chain Monte Carlo methods [24,25,26]. The reason for our adoption of MH weights is that they guarantee the convergence of distributed average consensus in time-varying communication graphs [23,27,28]. This means that our UAV network can solve the EM problem when the sets of one-hop neighbors of UAVs change over time.

MH weights were also used in [29] for a diffusion-based algorithm originally proposed in [30], but convergence is faster on our token ring network, as demonstrated in our simulation results in Section 6. Other symmetric weights determined in [31] induce convergence faster than MH weights but are calculated by convex optimization, so they are not suitable for time-varying communication graphs, as the optimization problem needs to be solved when the sets of one-hop neighbors of UAVs change. Other distributed EM algorithms for estimating GMMs include [32,33,34,35,36,37,38], but they do not consider time-varying communication graphs. They consider networks of static nodes to the best of our knowledge.

Therefore, this paper contributes two distributed algorithms for the problems of (1) monitoring ground targets using GMMs with the goal of detecting the unfitness of the GMM when target locations change and (2) updating the GMM to the new target locations. The aim is to complete these two tasks while reducing the number of message exchanges among UAVs to increase the Nyquist rate of observations that can be monitored. To the best of our knowledge, this monitoring problem has not been addressed when UAVs have only partial coverage of target clusters under a communication graph that can change over time. The algorithms are evaluated through simulation for linear flight formations of 3 to 16 UAVs and grid formations of 9 to 121 UAVs as the number of target clusters increases from 2 to 16 and from 2 to 9 in linear and grid formations, respectively. The simulation results demonstrate performance superior to related algorithms to the best of our knowledge.

3. System Model

Let $\mathcal{U}=\{u_1,u_2,\dots ,u_n\}$ be a set of UAVs that communicate over a connected graph. The set of one-hop neighbors of $u_i$ is denoted as ${\mathcal{S}}_i$. Each UAV communicates only with its one-hop neighbors. There is a set of observations $\mathcal{O}=\{{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_m\}$ that, without loss of generality, are two-dimensional as they correspond to geolocations of moving targets on the ground, i.e., ${\mathit{x}}_a\in {\mathbb{R}}^2$ for $a=1,2,\dots ,m$. The target locations at any point in time follow the distribution of a GMM of k Gaussian components. 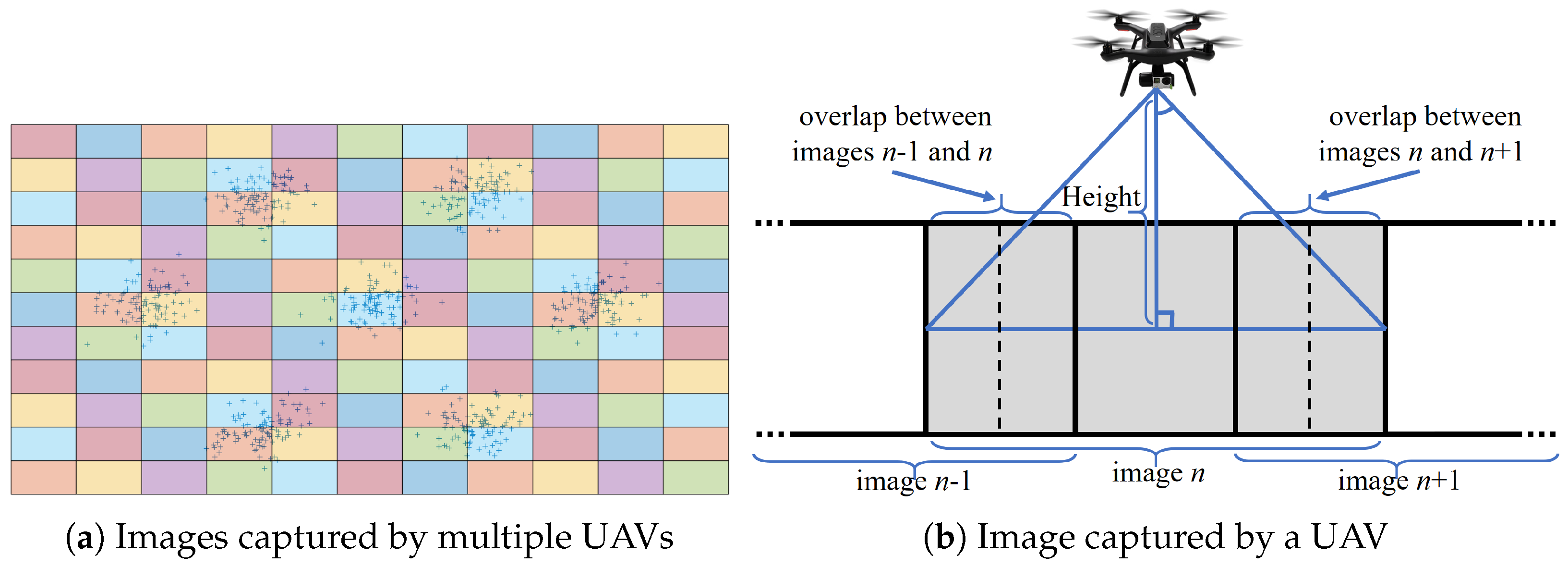Therefore, the probability density function (pdf) of ${\mathit{x}}_a$ is provided in (1), where $p\left({\mathit{x}}_a\right|s)$ and ${\varphi }_s$ are the pdf and weight of the sth Gaussian component; $p\left({\mathit{x}}_a\right|s)$ is provided in (2), where ${\mathit{\mu }}_s$ and ${\mathbf{\Sigma }}_s$ are the mean and covariance matrix of the sth component. Each UAV captures images, as shown in Figure 1b. Figure 1a shows observations from a GMM of 7 components.

$$p\left({\mathit{x}}_a\right)=\sum _{s=1}^k{\varphi }_{s}p\left({\mathit{x}}_a\right|s),$$

(1)

$$p\left({\mathit{x}}_a\right|s)={\displaystyle \frac{1}{2\pi \sqrt{\det {\mathbf{\Sigma }}_s}}}exp\left(-{\displaystyle \frac{{({\mathit{x}}_a-{\mathit{\mu }}_s)}^{\mathrm{T}}{{\mathbf{\Sigma }}_s}^{-1}({\mathit{x}}_a-{\mathit{\mu }}_s)}{2}}\right).$$

(2)

The area covered by UAVs is divided into a grid, as shown in Figure 1a. Each rectangle corresponds to the area that a UAV covers while hovering in the center of the rectangle, as shown in Figure 1b. We call this UAV location the waypoint of the corresponding rectangle. Figure 1b also shows that the adjacent images overlap. The UAV is capturing the nth image in Figure 1b. The images $n-1$ and $n+1$ are to the left and right of the nth image, and this sequence of images can continue depending on the flight path of the UAV. This path is indicated with the dotted lines on images $n-1$ and $n+1$. The overlap is purposely added to the flight paths due to errors in the location and orientation of the UAVs. Therefore, the images need to be realigned to form the grid in Figure 1a. The problem of aligning images and locating targets in overlapping areas is beyond the scope of this paper. We address this problem in our previous work in [39]. Each UAV is assigned a flight path that corresponds to a subset of waypoints on the grid and the order in which they are visited. UAVs fly through their sequence of waypoints periodically. We refer to a period as a tour. Tours from different UAVs are assumed to be disjoint, which means that each waypoint is assigned to one and only one UAV. The set of observations detected by $u_i$ during a tour is ${\mathcal{O}}_i=\{{\mathit{x}}_{i,1},{\mathit{x}}_{i,2},\dots ,{\mathit{x}}_{i,m_i}\}$.

It is assumed that UAVs cover all targets after the completion of all tours, i.e., $\mathcal{O}={\bigcup }_{i=1}^n{\mathcal{O}}_i$. The observation sets of UAVs are disjointed, i.e., ${\mathcal{O}}_i\cap {\mathcal{O}}_j=\varnothing$ for all $i\ne j$, because the tours are disjointed. It is also assumed that each UAV can communicate with one or more UAVs at one or more waypoints of the tour. The UAVs with which $u_i$ can communicate during a tour are $u_i$’s one-hop neighbors, i.e., ${\mathcal{S}}_i$.

UAVs are initialized with a priori values of ${\varphi }_s$, ${\mathit{\mu }}_s$, and ${\mathbf{\Sigma }}_s$. Therefore, it is assumed that the UAVs have already scanned the area in advance, as in [40,41], and the number of Gaussian components of the GMM has already been determined, as in [42,43]. Scanning unexplored areas is beyond the scope of this paper. The purpose of the periodic tours of this paper is to monitor the moving targets. It is also assumed that targets take more than one tour to move enough that the GMM parameters, ${\varphi }_s$, ${\mathit{\mu }}_s$, and ${\mathbf{\Sigma }}_s$, no longer correspond to the new target locations. The objective of this paper is two-fold. First, UAVs complete one or more tours to detect when the GMM parameters no longer correspond to the new target locations. We say that the GMM is unfit at this point. Second, UAVs calculate new parameter values to update the GMM.

It is also assumed that our algorithms are based on data-link protocols for wireless networks that detect packet losses and retransmit packets in response to the losses. Our monitoring algorithm then relies on data link acknowledgments to ensure that packets of each UAV are delivered to its one-hop neighbors. For example, our open-source UAV network [1] implements UAV-to-UAV communication over a Zigbee network, which is based on the IEEE 802.15.4 protocol architecture. Our algorithm for updating the values of the GMM parameters is based on the wireless token ring protocol [21], which we also implement over the Zigbee network.

4. Distributed Monitoring Algorithm

The objective of the monitoring algorithm is to determine whether ${\varphi }_s$, ${\mathit{\mu }}_s$, and ${\mathbf{\Sigma }}_s$ produce a GMM that does not fit the observations $\mathcal{O}$ of the last tour of the UAVs. Unfitness of the GMM is defined as follows.

Definition 1. 

Let Θ be the set of GMM parameters, i.e., $\mathsf{\Theta }=\left\{{\varphi }_s,{\mathit{\mu }}_s,{\mathbf{\Sigma }}_s:s=1,2,\dots ,k\right\}$. Consider the negative log-likelihood of Θ given ${\mathcal{O}}_i$ in (3), where $m_i$ is the number of observations in ${\mathcal{O}}_i$, i.e., $m_i=\left|{\mathcal{O}}_i\right|$. The average negative log-likelihood is defined as $\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)={\displaystyle \frac{{\sum }_{i=1}^n\mathcal{L}\left(\mathsf{\Theta }|{\mathcal{O}}_i\right)}{m}}$.

$$\mathcal{L}\left(\mathsf{\Theta }|{\mathcal{O}}_i\right)=-log\left(\prod _{a=1}^{m_i}p\left({\mathit{x}}_{i,a}|\mathsf{\Theta }\right)\right)=-\sum _{a=1}^{m_i}log\left(\sum _{s=1}^k{\varphi }_{s}p\left({\mathit{x}}_{i,a}|s\right)\right).$$

(3)

Definition 2. 

The GMM is classified as unfit when $\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)>ϵ$, where $\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)$ is provided in Definition 1, and ϵ is a threshold value defined by the user.

Let $u_j$ be one of $u_i$’s one-hop neighbors, i.e., $u_j\in {\mathcal{S}}_i$. When they communicate, the message sent by $u_i$ to $u_j$ is ${\mathcal{X}}_{i,j}$, and it is a subset of the target locations from ${\mathcal{O}}_i$. Definitions 3 to 5 and Theorem 1 are used to determine the unfitness of the GMM in a distributed manner.

Definition 3. 

The knowledge of $u_i$ is ${\mathcal{K}}_i=\bigcup _{u_j\in {\mathcal{S}}_i}{\mathcal{X}}_{j,i}\cup {\mathcal{O}}_i$.

Definition 4. 

The agreement of $u_i$ with $u_j$ is ${\mathcal{A}}_{i,j}={\mathcal{X}}_{i,j}\cup {\mathcal{X}}_{j,i}$.

Definition 5. 

The withheld knowledge of $u_i$ from $u_j$ is ${\mathcal{W}}_{i,j}={\mathcal{K}}_i\setminus {\mathcal{A}}_{i,j}$.

The union operations in Definitions 3 and 4 do not differentiate observations of the same value, i.e., if ${\mathit{x}}_i\in {\mathcal{O}}_i$, ${\mathit{x}}_j\in {\mathcal{X}}_{j,i}$, and ${\mathit{x}}_i={\mathit{x}}_j$, then $\left\{{\mathit{x}}_i\right\}\cup \left\{{\mathit{x}}_j\right\}=\left\{{\mathit{x}}_i\right\}$. Therefore, several observations of the same value are considered as one single observation. The reason is that two or more objects on the ground cannot occupy the same space, so target locations of the same value correspond to a single object on the ground.

The monitoring algorithm performs several message exchanges among UAVs. Therefore, the knowledge of a UAV propagates to other UAVs as the number of message exchanges increases. For example, consider three UAVs: $u_1$, $u_2$, and $u_3$. Let their initial knowledge be ${\mathcal{K}}_1={\mathcal{O}}_1=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_6\}$, ${\mathcal{K}}_2={\mathcal{O}}_2=\{{\mathbf{x}}_5,{\mathbf{x}}_6,\dots ,{\mathbf{x}}_{10}\}$, and ${\mathcal{K}}_3={\mathcal{O}}_3=\{{\mathbf{x}}_9,{\mathbf{x}}_{10},\dots ,{\mathbf{x}}_{14}\}$. Let $u_1$ and $u_2$ be within communication range of each other. Let $u_2$ and $u_3$ be within range of each other, too; $u_1$ and $u_3$ are not within range of each other. Their initial withheld knowledge is their full knowledge as they have not exchanged any messages yet, i.e., ${\mathcal{W}}_{1,2}={\mathcal{K}}_1$, ${\mathcal{W}}_{2,1}={\mathcal{W}}_{2,3}={\mathcal{K}}_2$, and ${\mathcal{W}}_{3,2}={\mathcal{K}}_3$. Now, let $u_1$ send a subset of observations from ${\mathcal{W}}_{1,2}$ to $u_2$. Let this subset be ${\mathcal{X}}_{1,2}=\{{\mathbf{x}}_4,{\mathbf{x}}_5\}$. Similarly, let the message from $u_2$ to $u_1$ be ${\mathcal{X}}_{2,1}=\{{\mathbf{x}}_6,{\mathbf{x}}_7\}$. Therefore, the agreement is ${\mathcal{A}}_{1,2}=\{{\mathbf{x}}_4,{\mathbf{x}}_5,{\mathbf{x}}_6,{\mathbf{x}}_7\}$. The knowledge and withheld knowledge of $u_1$ are updated after the messages are exchanged: ${\mathcal{K}}_1=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_6\}\cup \{{\mathbf{x}}_6,{\mathbf{x}}_7\}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_7\}$ and ${\mathcal{W}}_{1,2}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_6\}\setminus \{{\mathbf{x}}_4,{\mathbf{x}}_5,{\mathbf{x}}_6,{\mathbf{x}}_7\}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3\}$. The knowledge and withheld knowledge of $u_2$ are also updated: ${\mathcal{K}}_2=\{{\mathbf{x}}_5,{\mathbf{x}}_6,\dots ,{\mathbf{x}}_{10}\}\cup \{{\mathbf{x}}_4,{\mathbf{x}}_5\}=\{{\mathbf{x}}_4,{\mathbf{x}}_5,\dots ,{\mathbf{x}}_{10}\}$ and ${\mathcal{W}}_{2,1}=\{{\mathbf{x}}_5,{\mathbf{x}}_6,\dots ,{\mathbf{x}}_{10}\}\setminus \{{\mathbf{x}}_4,{\mathbf{x}}_5,{\mathbf{x}}_6,{\mathbf{x}}_7\}=\{{\mathbf{x}}_8,{\mathbf{x}}_9,{\mathbf{x}}_{10}\}$. Now, let $u_2$ and $u_3$ exchange the following messages: ${\mathcal{X}}_{2,3}=\{{\mathbf{x}}_4,{\mathbf{x}}_9\}$ and ${\mathcal{X}}_{3,2}=\{{\mathbf{x}}_{10},{\mathbf{x}}_{11}\}$. Their knowledge and withheld knowledge are updated to the following values: ${\mathcal{K}}_2=\{{\mathbf{x}}_4,{\mathbf{x}}_5,\dots ,{\mathbf{x}}_{11}\}$, ${\mathcal{W}}_{2,3}=\{{\mathbf{x}}_5,{\mathbf{x}}_6,{\mathbf{x}}_7,{\mathbf{x}}_8,{\mathbf{x}}_{10}\}$, ${\mathcal{K}}_3=\{{\mathbf{x}}_4,{\mathbf{x}}_9,{\mathbf{x}}_{10},\dots ,{\mathbf{x}}_{14}\}$, and ${\mathcal{W}}_{3,2}=\{{\mathbf{x}}_{12},{\mathbf{x}}_{13},{\mathbf{x}}_{14}\}$. Therefore, a subset of the knowledge of $u_1$ reaches $u_3$; $u_3$ now knows of ${\mathbf{x}}_4$.

The next theorem is used to determine the required number of message exchanges that allow individual UAVs to calculate the unfitness of the GMM.

Theorem 1. 

$\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)\le ϵ$ if for $i=1,2,\dots ,n$, (1) $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)\le ϵ$, (2) $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{A}}_{i,j}\right)\le ϵ$, and either $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{i,j}\right)\le ϵ$ or ${\mathcal{W}}_{i,j}=\varnothing$ for all $u_j\in {\mathcal{S}}_i$.

Proof. 

Without loss of generalization, consider UAVs selected in some sequence $u_1$, $u_2$, …, and $u_n$ such that $u_i$ and $u_{i+1}$ are one-hop neighbors. Let all UAVs meet both conditions (1) and (2). When $u_i$ is selected, it sends ${\mathcal{W}}_{i,i+1}$ to $u_{i+1}$. Therefore, when $u_1$ is selected first, the new knowledge of $u_2$ becomes ${\mathcal{K}}_2^{\prime }={\mathcal{K}}_2\cup {\mathcal{W}}_{1,2}$. Given that observations of the same value are considered as one single observation, the average negative log-likelihood of the new knowledge is $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_2^{\prime }\right)=\eta \overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_2\right)+\left(1-\eta \right)\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{1,2}\right)$, where $\eta \in [0,1]$. Therefore, $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_2^{\prime }\right)\le ϵ$ given that $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_2\right)\le ϵ$ and $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{1,2}\right)\le ϵ$. Continuing this process, the new knowledge of $u_n$ is ${\mathcal{K}}_n^{\prime }={\mathcal{K}}_n{\bigcup }_{i=1}^{n-1}{\mathcal{W}}_{i,i+1}=\mathcal{O}$, and $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_n^{\prime }\right)=\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)\le ϵ$. □

Monitoring is implemented with two algorithms, one for transmission (Algorithm 1) and one for reception (Algorithm 2). UAVs self-select to transmit to their one-hop neighbors when they are within range during their tours. Self-selection can be implemented via periodic transmission of hello packets that allow UAVs to detect each other. Algorithm 1 takes place in each self-selection of $u_i$. The outputs of the algorithm (line 2) are the messages ${\mathcal{X}}_{i,j}$ sent to each neighbor in ${\mathcal{S}}_i$ that is within range and a binary flag that signal the unfitness of the GMM parameters, i.e., $\mathsf{\Theta }$. The inputs of the algorithm (line 1) are $\mathsf{\Theta }$, the set of one-hop neighbors ${\mathcal{S}}_i$, $u_i$’s knowledge ${\mathcal{K}}_i$, its agreement with every neighbor ${\mathcal{A}}_{i,j}$, its knowledge withheld from every neighbor ${\mathcal{W}}_{i,j}$, and the number of transmissions T needed before testing unfitness of $\mathsf{\Theta }$. The first step is to apply an indicator function $I_{ϵ}(·)$ that determines whether its argument is greater than $ϵ$. For example, $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)\right)$ indicates whether the average negative log-likelihood of knowledge ${\mathcal{K}}_i$ is greater than $ϵ$ (line 6). The message ${\mathcal{X}}_{i,j}$ needs to be calculated and transmitted when ${\mathcal{A}}_{i,j}$ is empty (line 9). The message also needs to be calculated and transmitted when $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)\right)$ does not match either $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{A}}_{i,j}\right)\right)$ or $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{i,j}\right)\right)$ according to Theorem 1. These quantities are denoted by $I_{\mathcal{K}}$, $I_{\mathcal{A}}$, and $I_{\mathcal{W}}$ (lines 6 to 8). The reason ${\mathcal{X}}_{i,j}$ is calculated and transmitted when $I_{\mathcal{A}}\ne I_{\mathcal{K}}$ or $I_{\mathcal{W}}\ne I_{\mathcal{K}}$ is that these conditions indicate that $u_i$ and $u_j$ are not in agreement on the fitness of $\mathsf{\Theta }$. Under either of these two conditions, the UAVs need to exchange withheld knowledge to reach an agreement. ${\mathcal{X}}_{i,j}$ is assigned a subset of observations from ${\mathcal{W}}_{i,j}$ (line 10). This subset is determined by selecting observations from ${\mathcal{W}}_{i,j}$ until both $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{A}}_{i,j}\right)\right)$ and $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{i,j}\right)\right)$ match $I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)\right)$. After ${\mathcal{X}}_{i,j}$ is determined, the agreement ${\mathcal{A}}_{i,j}$ and withheld knowledge ${\mathcal{W}}_{i,j}$ are updated with ${\mathcal{X}}_{i,j}$ (lines 11 and 12) because the observations in ${\mathcal{X}}_{i,j}$ will now be known by $u_j$ after the transmission of ${\mathcal{X}}_{i,j}$ (line 13).

Algorithm 1 keeps count of the number of self-selections since initialization with variable t (line 16). If this number exceeds the threshold value T, the algorithm determines if $\mathsf{\Theta }$ is unfit (line 18). The value of T needs to be high enough to allow all UAV knowledge to reach other UAVs that are a number of hops away. In this way, when $t>T$, UAVs can reliably determine the fitness of $\mathsf{\Theta }$. This is carried out by evaluating conditions (1) and (2) of Theorem 1 (lines 20 and 24). The flag defaults to false (line 17), and if any of the conditions are not met, the flag becomes true (lines 21 and 25), indicating that $\mathsf{\Theta }$ is unfit. It should be noted that the event that any of conditions (1) and (2) is not met does not necessarily imply that $\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)>ϵ$. There can be false alarms declaring $\mathsf{\Theta }$ unfit. The false alarm rate can be decreased by increasing T; however, increasing T increases the time to determine unfitness of $\mathsf{\Theta }$. Section 6.1 evaluates the number of self-selections (i.e., T) that are needed to reliably determine the flag value. This value is highly dependent on the diameter of the FANET, as demonstrated by the simulation results in Section 6.1.

Algorithm 2 processes ${\mathcal{X}}_{j,i}$ when $u_i$ receives the message ${\mathcal{X}}_{j,i}$ from $u_j$. The inputs are the message ${\mathcal{X}}_{j,i}$, the knowledge ${\mathcal{K}}_i$, and the agreement ${\mathcal{A}}_{i,j}$ (line 1). There are no outputs. The sole purpose of the algorithm is to update $u_i$’s knowledge of ${\mathcal{K}}_i$ and its agreement ${\mathcal{A}}_{i,j}$ with $u_j$ (lines 5 and 6). The initialization is the same as the initialization of Algorithm 1.

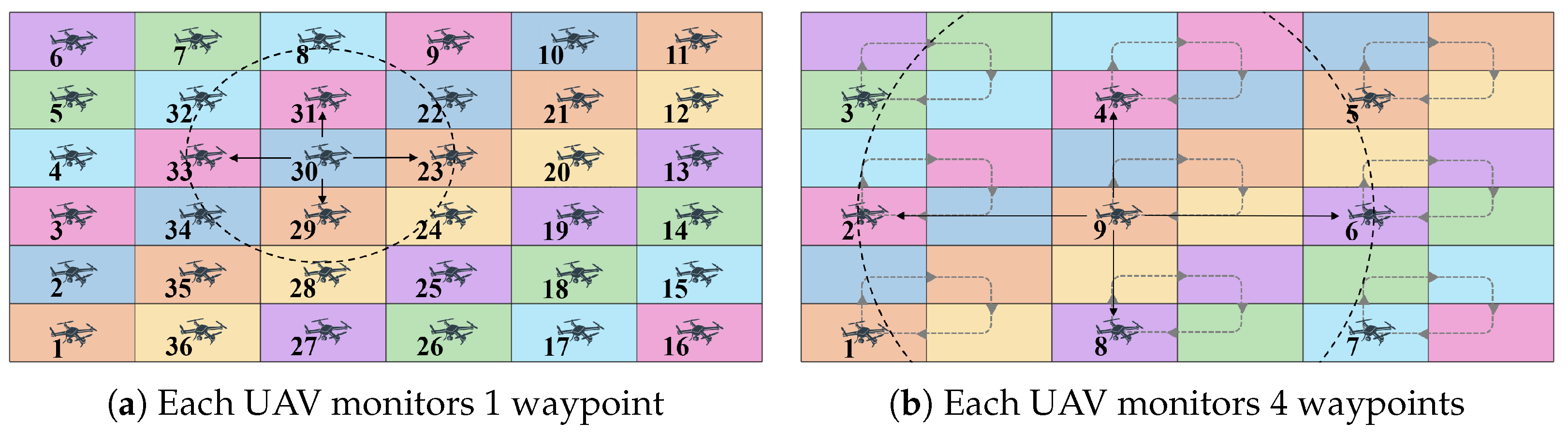
 Figure 2 shows an example of the transmission in line 13 of Algorithm 1. In Figure 2a, $u_{30}$ is self-selected and transmits ${\mathcal{X}}_{30,23}$, ${\mathcal{X}}_{30,29}$, ${\mathcal{X}}_{30,31}$, and ${\mathcal{X}}_{30,33}$ to its neighbors: $u_{23}$, $u_{29}$, $u_{31}$, and $u_{33}$. These transmissions take place one at a time. Each transmission corresponds to one loop of the for loops in lines 5 to 15 of Algorithm 1. Each neighbor executes Algorithm 2 when it receives its corresponding message ${\mathcal{X}}_{30,j}$. In Figure 2b, each UAV monitors four waypoints. In this case, $u_9$ has self-selected, and its transmission range is larger to reach its neighbors: $u_2$, $u_4$, $u_6$, and $u_8$.

Algorithm 1 Monitoring Algorithm (Transmission)

1:  Inputs: $\mathsf{\Theta },{\mathcal{S}}_i,{\mathcal{K}}_i,{\mathcal{A}}_{i,j},{\mathcal{W}}_{i,j},T$  2:  Outputs: ${\mathcal{X}}_{i,j}$, f  3:  Initialization: ${\mathcal{K}}_i\leftarrow {\mathcal{O}}_i$, ${\mathcal{A}}_{i,j}\leftarrow \varnothing$, ${\mathcal{W}}_{i,j}\leftarrow {\mathcal{O}}_i$, $t\leftarrow 0$  4:    5:  for all $\{u_j:u_j\in {\mathcal{S}}_i,u_j\mathrm{within}\mathrm{range}\}$ do  6:        $I_{\mathcal{K}}\leftarrow I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)\right)$  7:        $I_{\mathcal{A}}\leftarrow I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{A}}_{i,j}\right)\right)$  8:        $I_{\mathcal{W}}\leftarrow I_{ϵ}\left(\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{i,j}\right)\right)$  9:        if ${\mathcal{A}}_{i,j}=\varnothing$ or $I_{\mathcal{A}}\ne I_{\mathcal{K}}$ or $I_{\mathcal{W}}\ne I_{\mathcal{K}}$ do 10:              ${\mathcal{X}}_{i,j}\leftarrow \mathrm{S}\mathrm{E}\mathrm{L}\mathrm{E}\mathrm{T}\mathrm{O}\mathrm{B}\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{V}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}\mathrm{S}\left({\mathcal{W}}_{i,j}\right)$ 11:              ${\mathcal{A}}_{i,j}\leftarrow {\mathcal{A}}_{i,j}\cup {\mathcal{X}}_{i,j}$ 12:              ${\mathcal{W}}_{i,j}\leftarrow {\mathcal{K}}_i\setminus {\mathcal{A}}_{i,j}$ 13:              $\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{S}\mathrm{M}\mathrm{I}\mathrm{T}\left({\mathcal{X}}_{i,j}\right)$ 14:        end if 15:  end for 16:  $t\leftarrow t+1$ 17:  $f\leftarrow$ false 18:  if  $t>T$  do 19:        $t\leftarrow 0$ 20:        if $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)>ϵ$ do 21:              $f\leftarrow$ true 22:        end if 23:        for all $\{u_j:u_j\in {\mathcal{S}}_i,u_j\mathrm{within}\mathrm{range}\}$ do 24:              if $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{A}}_{i,j}\right)>ϵ$ or $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{i,j}\right)>ϵ$ do 25:                    $f\leftarrow$ true 26:           end if 27:        end for 28:  end if

Algorithm 2 Monitoring Algorithm (Reception).

1:  Inputs: ${\mathcal{X}}_{j,i},{\mathcal{K}}_i,{\mathcal{A}}_{i,j}$  2:  Outputs: none  3:  Initialization: same as Algorithm 1  4:    5:  ${\mathcal{K}}_i\leftarrow {\mathcal{K}}_i\cup {\mathcal{X}}_{j,i}$  6:  ${\mathcal{A}}_{i,j}\leftarrow {\mathcal{A}}_{i,j}\cup {\mathcal{X}}_{j,i}$

A UAV sends a message to each of its neighbors when it self-selects and executes Algorithm 1 (lines 5 to 15). It also evaluates its flag value after it has self-selected T times (lines 17 to 28). However, evaluating the flag value does not require any communication with neighbors. Therefore, the communication complexity of the algorithm is determined by the number of neighbors (lines 5 to 15), and this number depends on the network topology. For example, UAVs have a maximum of four neighbors in the topology of Figure 2. There are more topologies, with each having its own average and maximum number of neighbors. For example, when the topology is a random geometric graph (RGG), the average number of neighbors increases at a rate of $\mathsf{\Theta }\left(\log \left|\mathcal{U}\right|\right)$, where $\left|\mathcal{U}\right|$ is the number of UAVs, to ensure that the network is connected with high probability [44]. Therefore, the communication complexity of Algorithm 1 is $\mathsf{\Theta }\left(\log \left|\mathcal{U}\right|\right)$ in RGGs. The critical neighbor number of other topologies, including dense, sparse, and mobile networks, is the subject of [45].

5. Distributed GMM Estimation

When one or more UAVs determine that $\mathsf{\Theta }$ is unfit, the flag is true in Algorithm 1, and the UAVs begin to calculate new values for $\mathsf{\Theta }$. This can be accomplished by flooding the flag on the UAV network [46].

The calculation of the new values of $\mathsf{\Theta }$ is via expectation maximization [47]. The EM algorithm consists of the execution of two iterative steps. It determines a value of $\mathsf{\Theta }$ that decreases the average negative log-likelihood $\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)$ until a termination criterion is met. The criterion in this paper is $\overline{\mathcal{L}}\left(\mathsf{\Theta }|\mathcal{O}\right)\le ϵ$ because $\mathsf{\Theta }$ is considered unfit when the criterion is not met according to Definition 2. The steps are the following:

• Expectation Step: Estimate the contribution of each observation:

  $$q_{s,a}={\displaystyle \frac{{\varphi }_{s}p\left({\mathit{x}}_a|s\right)}{{\sum }_{r=1}^k{\varphi }_{r}p\left({\mathit{x}}_a|r\right)}}.$$

  (4)
• Maximization Step: Update the parameters

  $$\begin{array}{cc}\hfill {\varphi }_s& ={\displaystyle \frac{{\sum }_{a=1}^m{q}_{s,a}}{m}},\hfill \end{array}$$

  (5)

  $$\begin{array}{cc}\hfill {\mathit{\mu }}_s& ={\displaystyle \frac{{\sum }_{a=1}^m{q}_{s,a}{\mathit{x}}_a}{{\sum }_{a=1}^m{q}_{s,a}}},\hfill \end{array}$$

  (6)

  $$\begin{array}{cc}\hfill {\mathbf{\Sigma }}_s& ={\displaystyle \frac{{\sum }_{a=1}^m{q}_{s,a}\left({\mathit{x}}_a-{\mathit{\mu }}_s\right){\left({\mathit{x}}_a-{\mathit{\mu }}_s\right)}^{\mathrm{T}}}{{\sum }_{a=1}^m{q}_{s,a}}}.\hfill \end{array}$$

  (7)

The maximization step in (5)–(7) depends on the set of all observations in $\mathcal{O}=\left\{{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_m\right\}$. However, observations are distributed among ${\mathcal{O}}_1$, ${\mathcal{O}}_2$, …, and ${\mathcal{O}}_n$. Therefore, the EM algorithm can also be formulated as follows, where ${\mathit{x}}_{i,a}$ is $u_i$’s ath observation.

• Expectation Step:

  $$q_{i,s,a}={\displaystyle \frac{{\varphi }_{s}p\left({\mathit{x}}_{i,a}|s\right)}{{\sum }_{r=1}^k{\varphi }_{r}p\left({\mathit{x}}_{i,a}|r\right)}}.$$

  (8)
• Maximization Step:

  $$\begin{array}{cc}\hfill {\varphi }_s& ={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}{{\sum }_{i=1}^n{m}_i}},\hfill \end{array}$$

  (9)

  $$\begin{array}{cc}\hfill {\mathit{\mu }}_s& ={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}{\mathit{x}}_{i,a}}{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}},\hfill \end{array}$$

  (10)

  $$\begin{array}{cc}\hfill {\mathbf{\Sigma }}_s& ={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}\left({\mathit{x}}_{i,a}-{\mathit{\mu }}_s\right){\left({\mathit{x}}_{i,a}-{\mathit{\mu }}_s\right)}^{\mathrm{T}}}{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}}.\hfill \end{array}$$

  (11)

The expectation step in (8) is local to $u_i$. It only depends on its observations, i.e., ${\mathcal{O}}_i=\left\{{\mathit{x}}_{i,1},{\mathit{x}}_{i,2},\dots ,{\mathit{x}}_{i,m_i}\right\}$. However, the maximization step depends on observations of all drones, i.e., ${\mathcal{O}}_1$, ${\mathcal{O}}_2$, …, and ${\mathcal{O}}_n$. To allow a distributed implementation of this step, we first note that (9)–(11) correspond to averages across all UAVs of the following quantities: $q_{i,s,a}$ for (9), $q_{i,s,a}{\mathit{x}}_{i,a}$ for (10), and $q_{i,s,a}\left({\mathit{x}}_{i,a}-{\mathit{\mu }}_s\right){\left({\mathit{x}}_{i,a}-{\mathit{\mu }}_s\right)}^{\mathrm{T}}$ for (11). Therefore, we complete the maximization step via distributed average consensus (DAC) [31].

5.1. Distributed Average Consensus

Let $y_i\left(0\right)$ be $\mathbb{R}$ and assigned to $u_i$ at time $t=0$. The DAC problem is to compute the average $\overline{y_i\left(0\right)}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{y}_i\left(0\right)$ in every UAV using message exchanges with only one-hop neighbors. A well-known equation for this operation is in (12), where $w_{i,j}$, is the weight associated with the one-hop link between $u_i$ and $u_j$. Note that $w_{i,j}=0$ if $u_i$ and $u_j$ are not one-hop neighbors.

$$y_i(t+1)=y_i\left(t\right)+\sum _{u_j\in {\mathcal{S}}_i}{w}_{i,j}(y_j\left(t\right)-y_i\left(t\right)).$$

(12)

Since one-hop links are undirected, $w_{i,j}=w_{j,i}$, and $w_{i,i}=1-{\sum }_{u_j\in {\mathcal{S}}_i}{w}_{i,j}$. The weight matrix $\mathit{W}=\left[w_{i,j}\right]$ needs to satisfy the following properties where $\mathbf{1}$ is the all-ones vector:

$$\mathit{W}={\mathit{W}}^{\mathrm{T}}\mathrm{and}\mathit{W}\mathbf{1}=\mathbf{1}.$$

(13)

The calculation in (12) needs to converge to the average ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{y}_i\left(0\right)$ of the DAC problem for all UAVs (i.e., for $i=1,2,\dots ,n$) as follows:

$$\underset{t\to \infty }{lim}{y}_i\left(t\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{y}_i\left(0\right).$$

(14)

Weights that satisfy the constraints in (13) and the asymptotic average consensus in (14) always exist. In this paper, we use the Metropolis–Hastings (MH) weights [23]:

$$w_{i,j}=\left\{\begin{array}{ccc}\hfill & {\displaystyle \frac{1}{max\left(\right|{\mathcal{S}}_i|,|{\mathcal{S}}_j\left|\right)+1}}\hfill & \hfill i\ne j\\ \hfill & 1-\sum _{u_j\in {\mathcal{S}}_i}{\displaystyle \frac{1}{max\left(\right|{\mathcal{S}}_i|,|{\mathcal{S}}_j\left|\right)+1}}\hfill & \hfill i=j.\end{array}\right.$$

5.2. Distributed Maximization Step

The averages in (9)–(11) are computed using DAC. Let $y_i^m\left(0\right)=m_i$ and apply (12) to calculate the average number of local targets per UAV, i.e., $\overline{m_i}$. Therefore,

$$\underset{t\to \infty }{lim}{y}_i^m\left(t\right)=\overline{m_i}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{m}_i.$$

(15)

DAC is applied to calculate (9) by letting $y_{i,s}^{\varphi }\left(0\right)=q_{i,s}={\sum }_{a=1}^{m_i}{q}_{i,s,a}$. Therefore,

$${\varphi }_s={\displaystyle \frac{1}{\overline{m_i}}}\underset{t\to \infty }{lim}{y}_{i,s}^{\varphi }\left(t\right)={\displaystyle \frac{1}{\overline{m_i}}}{\displaystyle \frac{1}{n}}\sum _{i=1}^n{q}_{i,s}={\displaystyle \frac{1}{m}}\sum _{i=1}^n\sum _{a=1}^{m_i}{q}_{i,s,a}={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}{{\sum }_{i=1}^n{m}_i}}.$$

(16)

DAC is applied to calculate (10) by letting ${\mathit{y}}_{i,s}^{\mu }\left(0\right)={\sum }_{a=1}^{m_i}{q}_{i,s,a}{\mathit{x}}_{i,a}$. Therefore,

$$\begin{array}{cc}{\mathit{\mu }}_s={\displaystyle \frac{1}{{\varphi }_s\overline{m_i}}}\underset{t\to \infty }{lim}{\mathit{y}}_{i,s}^{\mu }\left(t\right)={\displaystyle \frac{1}{{\varphi }_s\overline{m_i}}}{\displaystyle \frac{1}{n}}\sum _{i=1}^n\sum _{a=1}^{m_i}{q}_{i,s,a}{\mathit{x}}_{i,a}& ={\displaystyle \frac{1}{m{\varphi }_s}}\sum _{i=1}^n\sum _{a=1}^{m_i}{q}_{i,s,a}{\mathit{x}}_{i,a}=\\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}{\mathit{x}}_{i,a}}{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}}.\end{array}$$

(17)

Similarly, let ${\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}\left(0\right)={\sum }_{a=1}^{m_i}{q}_{i,s,a}({\mathit{x}}_{i,a}-{\mathit{\mu }}_s){({\mathit{x}}_{i,a}-{\mathit{\mu }}_s)}^{\mathrm{T}}$, then

$$\begin{array}{cc}{\mathbf{\Sigma }}_s={\displaystyle \frac{1}{{\varphi }_s\overline{m_i}}}\underset{t\to \infty }{lim}{\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}\left(t\right)& ={\displaystyle \frac{1}{{\varphi }_s\overline{m_i}}}{\displaystyle \frac{1}{n}}\sum _{i=1}^n\sum _{a=1}^{m_i}{q}_{i,s,a}({\mathit{x}}_{i,a}-{\mathit{\mu }}_s){({\mathit{x}}_{i,a}-{\mathit{\mu }}_s)}^{\mathrm{T}}=\\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}\left({\mathit{x}}_{i,a}-{\mathit{\mu }}_s\right){\left({\mathit{x}}_{i,a}-{\mathit{\mu }}_s\right)}^{\mathrm{T}}}{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}}.\end{array}$$

(18)

5.3. Distributed EM Algorithm

Algorithm 3 performs a number of iterations (line 5) to evaluate the expectation step in (8) and the distributed maximization step in (16)–(18) until the termination criterion is met, i.e., $\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\le ϵ$ according to Definition 2. The inputs of the algorithm (line 1) are the current and unfit GMM parameters ${\mathsf{\Theta }}_{\mathrm{in}}$, the set of local observations ${\mathcal{O}}_i$, and the MH weights between $u_i$ and its one-hop neighbors, i.e., $\{w_{i,j}:u_j\in {\mathcal{S}}_i\}$. The output (line 2) is the new GMM parameters ${\mathsf{\Theta }}_{\mathrm{out}}$ that satisfy the termination criterion.

Algorithm 3 Distributed EM.

1:  Inputs: ${\mathsf{\Theta }}_{\mathrm{in}}$, ${\mathcal{O}}_i$, $\{w_{i,j}:u_j\in {\mathcal{S}}_i\}$  2:  Output: ${\mathsf{\Theta }}_{\mathrm{out}}$  3:  Initialization: $q_{i,s,a}$ for $s=1,2,\dots ,k$ and $a=1,2,\dots ,m_i$ according to (8), $y_i^m\left(0\right)$, $y_{i,s}^{\varphi }\left(0\right)$, ${\mathit{y}}_{i,s}^{\mu }\left(0\right)$, ${\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}\left(0\right)$  4:    5:  while termination is false do  6:        for all $u_i\in \mathcal{U}$ do  7:             evaluate $y_i^m(t+1)$ according to (12)  8:        end for  9:        for all $u_i\in \mathcal{U}$ do 10:             evaluate $y_{i,s}^{\varphi }(t+1)$ according to (12) 11:        end for 12:        for all $u_i\in \mathcal{U}$ do 13:             evaluate ${\mathit{y}}_{i,s}^{\mu }(t+1)$ according to (12) 14:        end for 15:        termination ← false 16:        for all $u_i\in \mathcal{U}$ do 17:             evaluate ${\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}(t+1)$ according to (12) 18:             ${\varphi }_s={\displaystyle \frac{y_{i,s}^{\varphi }(t+1)}{y_i^m(t+1)}}$ according to (16) 19:             ${\mathit{\mu }}_s={\displaystyle \frac{{\mathit{y}}_{i,s}^{\mu }(t+1)}{y_{i,s}^{\varphi }(t+1)}}$ according to (17) 20:             ${\mathbf{\Sigma }}_s={\displaystyle \frac{{\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}(t+1)}{y_{i,s}^{\varphi }(t+1)}}$ according to (18) 21:             ${\mathsf{\Theta }}_{\mathrm{out}}\leftarrow \{{\varphi }_s,{\mathit{\mu }}_s,{\mathbf{\Sigma }}_s:s=1,2,\dots ,n\}$ 22:             evaluate $q_{i,s,a}$ according to (8) for all s, a 23:             if termination is false do 24:                   termination $\leftarrow \mathrm{T}\mathrm{E}\mathrm{R}\mathrm{M}\mathrm{I}\mathrm{N}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}({\mathsf{\Theta }}_{\mathrm{out}},{\mathcal{O}}_i,m_i)$ 25:             end if 26:        end for 27:  end while

Algorithm 3 calculates ${\mathsf{\Theta }}_{\mathrm{out}}$ using DAC, as demonstrated in (16)–(18). Initialization (line 3) consists of calculating the initial average values $y_i^m\left(0\right)$, $y_{i,s}^{\varphi }\left(0\right)$, ${\mathit{y}}_{i,s}^{\mu }\left(0\right)$, and ${\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}\left(0\right)$. Given that these values depend on $q_{i,s,a}$ for $s=1,2,\dots ,k$ and $a=1,2,\dots ,m_i$, the evaluation of this quantity using (8) is the first step of the initialization.

Algorithm 3 operates on a token-ring protocol. The implementation of this protocol on wireless networks such as FANETs is well known [21]. For example, the ring in Figure 2a is the UAV sequence $u_1$, $u_2$, …, and $u_{36}$. The ring closes when $u_{36}$ transmits to $u_1$. The ring in Figure 2b is $u_1$, $u_2$, …, and $u_9$, and it closes when $u_2$ or $u_8$ relays the token from $u_9$ to $u_1$ because $u_1$ is not within $u_9$’s range.

In the first round of Algorithm 3 (line 6), each UAV updates the running average $y_i^m(t+1)$ that eventually converges to $\overline{m_i}$ according to (15). Similarly, in the following three rounds (lines 9, 12, and 16), each UAV updates the other running averages: $y_{i,s}^{\varphi }(t+1)$, ${\mathit{y}}_{i,s}^{\mu }(t+1)$, and ${\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}(t+1)$. The averages are updated by communicating with one-hope neighbors according to (12).

After all running averages are updated, the new values of the GMM parameters, i.e., ${\varphi }_s$, ${\mathit{\mu }}_s$, and ${\mathbf{\Sigma }}_s$, are calculated (lines 18, 19, and 20). The convergence of ${\displaystyle \frac{y_{i,s}^{\varphi }(t+1)}{y_i^m(t+1)}}$ to ${\varphi }_s$ (line 18) is demonstrated as follows:

$$\underset{t\to \infty }{lim}{\displaystyle \frac{y_{i,s}^{\varphi }(t+1)}{y_i^m(t+1)}}={\displaystyle \frac{{lim}_{t\to \infty }{y}_{i,s}^{\varphi }\left(t\right)}{{lim}_{t\to \infty }{y}_i^m\left(t\right)}}={\displaystyle \frac{\frac{1}{n}{\sum }_{i=1}^n{q}_{i,s}}{\frac{1}{n}{\sum }_{i=1}^n{m}_i}}={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{a=1}^{m_i}{q}_{i,s,a}}{{\sum }_{i=1}^n{m}_i}}={\varphi }_s.$$

The convergence of ${\displaystyle \frac{{\mathit{y}}_{i,s}^{\mu }(t+1)}{y_{i,s}^{\varphi }(t+1)}}$ to ${\mathit{\mu }}_s$ (line 19) and the convergence of ${\displaystyle \frac{{\mathit{Y}}_{i,s}^{\mathbf{\Sigma }}(t+1)}{y_{i,s}^{\varphi }(t+1)}}$ to ${\mathbf{\Sigma }}_s$ can be demonstrated in a similar way.

The last calculation in Algorithm 3 before evaluating the termination criteria is the expectation step in (8), i.e., the evaluation of $q_{i,s,a}$ for $s=1,2,\dots ,k$ and $a=1,2,\dots ,m_i$ using the updated values of the GMM parameters ${\varphi }_s$, ${\mathit{\mu }}_s$, and ${\mathbf{\Sigma }}_s$. This calculation depends on data local to $u_i$, so it does not require communication with $u_i$’s one-hop neighbors.

Evaluation of the termination criterion (line 24) requires the calculation of $\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})$, which is equivalent to ${\displaystyle \frac{{\sum }_{i=1}^n\mathcal{L}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|{\mathcal{O}}_i)}{{\sum }_{i=1}^n{m}_i}}$ according to Definition 1. Therefore, the criterion is evaluated by having the UAVs pass the values of $\mathcal{L}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|{\mathcal{O}}_i)$ and $m_i$ along the token ring network. The value of the criterion is defaulted to false (line 15) to iterate through the expectation and distributed maximization steps (lines 6 to 26) until all UAVs evaluate the criterion as true.

For each while loop of Algorithm 3 (lines 5 to 27), there are four rounds of communication over the token-ring network, which correspond to the for loops that begin on lines 6, 9, 12, and 16. Each UAV communicates with its neighbors according to (12). Given that the length of the ring is $\left|\mathcal{U}\right|$, the communication complexity of Algorithm 3 is then $\mathsf{\Theta }\left(\left|\mathcal{U}\right|\log \left|\mathcal{U}\right|\right)$ when the network topology is RGG.

6. Performance Evaluation

The monitoring algorithms (i.e., Algorithms 1 and 2) and the distributed EM algorithm (i.e., Algorithm 3) were implemented in MATLAB (v. R2024b), and their performance was evaluated by simulation for two flight formations, linear and grid.

The linear flight formation is shown in Figure 3. Without loss of generality, it is assumed that each rectangular area corresponds to a UAV hovering at the center of the rectangle, as shown in Figure 2a. Therefore, there are five UAVs in Figure 3a,b. This assumption is to consider the worst-case scenario with the highest number of UAVs to cover all rectangular areas. In this scenario, the global set of targets is distributed across the largest set of UAVs because no single UAV covers more than one rectangular area. The rectangular areas correspond to images captured with a camera with horizontal and vertical fields of view of 62° and 49°, respectively.

It is also assumed that only adjacent UAVs are within communication range of each other, as shown in Figure 2. Therefore, the left and right UAVs in Figure 3 each have one neighbor, and all other UAVs have two neighbors each. This is the worst-case scenario in terms of network connectivity, i.e., the number of one-hop neighbors of each UAV is the minimum that keeps the network graph connected. The number of communication exchanges among UAVs to propagate their withheld knowledge increases as the connectivity decreases.

Two different cluster configurations are considered, centered and uncentered. The cluster centroids are in the center of the rectangular areas in the centered configuration (Figure 3a), and they are at the border between adjacent areas in the uncentered configuration (Figure 3b). All clusters have 100 targets and covariance matrix $\left(\begin{array}{cc}5& 1\\ 1& 5\end{array}\right)$ unless otherwise specified.

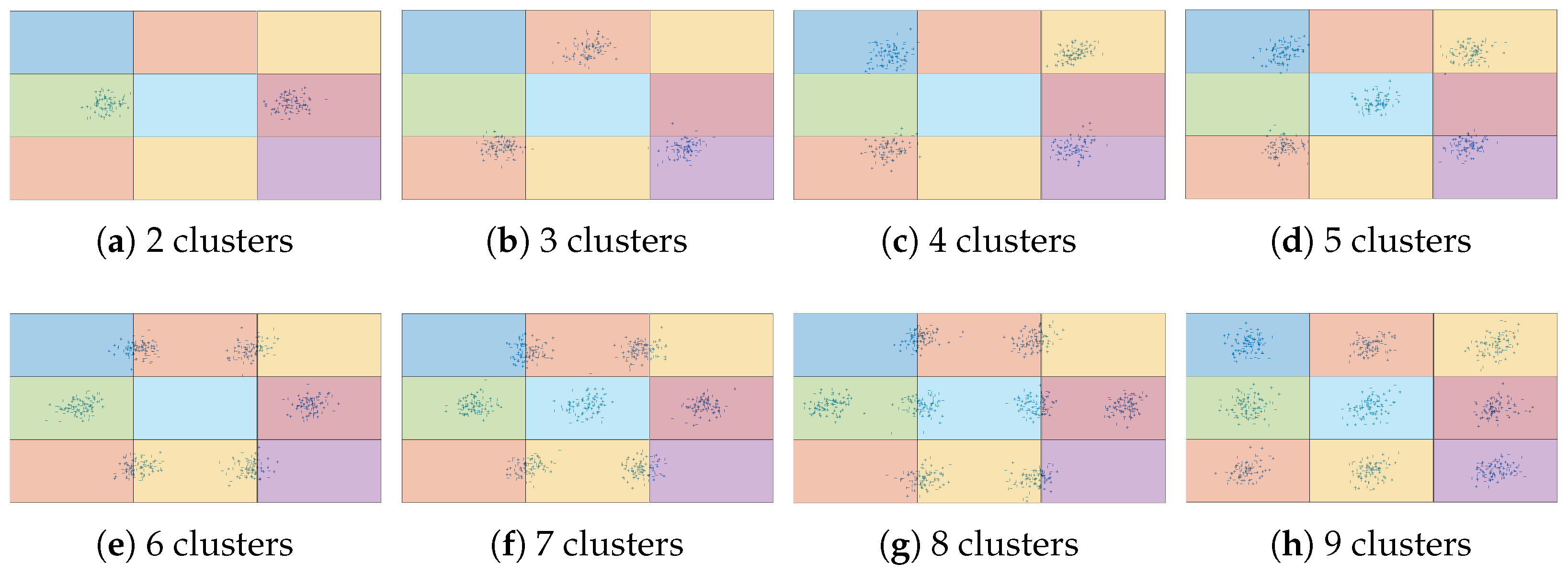
The grid flight formation is shown in Figure 4. It is also assumed that each rectangular area corresponds to a hovering UAV in the center of the rectangle and that only adjacent UAVs are within communication range of each other, including both vertical and horizontal directions. Therefore, each of the UAVs at the corners of the grid has two neighbors; each of the other UAVs at the boundary of the grid has three neighbors, and each of the UAVs in the interior of the grid has four neighbors. There are eight different cluster configurations with an increasing number of clusters, starting with two clusters, as shown in Figure 4a. Figure 4b–h show the cluster configurations with three to nine clusters, respectively. The grids in Figure 4 all have nine UAVs each, which is a grid of $3\times 3$. Larger grids are also included in our simulation results, from $4\times 4$ to $11\times 11$. In these cases, rectangular areas decrease in size, and cluster configurations remain the same. For example, Figure 1a shows the $11\times 11$ grid with seven clusters, which are the same seven clusters shown in the $3\times 3$ grid in Figure 4f. Increasing the dimensions of the grid implies that the rectangular areas decrease in size to cover the same overall area. This is equivalent to covering the same overall area with a higher number of UAVs hovering at lower altitudes.

6.1. Performance Evaluation: Monitoring Algorithm

The performance of the monitoring algorithm is evaluated with the number of monitoring instances that UAVs need to perform until they all have the same flag value. We define a monitoring instance as the self-selection of a UAV to execute the transmission monitoring algorithm (Algorithm 1) and the corresponding execution of the monitoring algorithm for reception (Algorithm 2) at all UAVs that are within range. The number of monitoring instances corresponds to T in Algorithm 1. Therefore, if $\mathsf{\Theta }$ is unfit, we count the number of monitoring instances (MI) until all UAVs have a flag value of true, and if $\mathsf{\Theta }$ is a good fit, we count the number of MIs until all UAVs have a flag value of false. The number of MIs for all UAVs to acquire full knowledge is also evaluated. We say that a UAV acquires full knowledge when its knowledge (i.e., ${\mathcal{K}}_i$) is equal to the global set of observations (i.e., $\mathcal{O}$). The reason is that the centralized solution to the monitoring problem (i.e., determining if $\mathsf{\Theta }$ is unfit) requires knowledge of $\mathcal{O}$, but this information is not initially available in any single UAV but distributed across all UAVs (i.e., ${\mathcal{O}}_1$, ${\mathcal{O}}_2$, …, ${\mathcal{O}}_n$).

The monitoring algorithm uses $ϵ$. The value of $ϵ$ determines the average value of the joint pdf of the observations (i.e., ${\prod }_{a=1}^{m_i}p\left({\mathit{x}}_{i,a}|\mathsf{\Theta }\right)$ for ${\mathit{x}}_{i,a}\in {\mathcal{O}}_i$) according to Definition 1. This means that the GMM is considered unfit when the average value of the joint pdf is less than ${10}^{-ϵ}$. We set its value at 3. Typical values for two-dimensional data range from 2 to 5. However, this value is application-dependent. It depends on the desired quality of the fit, variability of the data, and number of Gaussian components. The analysis of $ϵ$ is beyond the scope of this paper but is covered in depth in the GMM literature, including [48].

6.1.1. Linear Formation

Figure 5 shows the number of MIs needed for all UAVs to acquire full knowledge and for all UAVs to determine that the GMM does not fit the observations (i.e., all UAVs’ flags become true). The number of MIs is plotted as a function of the number of UAVs in both cases, centered (Figure 3a) and uncentered (Figure 3b).

The number of MIs increases with the number of UAVs in all cases. However, the rate of increase is lower for the case that all flags become true. At 3 UAVs, the number of MIs for all flags to become true is 4 in both cases, centered and uncentered, and for full knowledge, it is 10 for both cases. On the other hand, at 15 UAVs, the number of MIs for all flags to become true is 30 for both cases, and the number of MIs for full knowledge is 245 and 264 for the centered and uncentered cases, respectively.

The higher rate of increase for full knowledge demonstrates the effectiveness of the monitoring algorithm. It requires a lower number of MIs to detect the unfitness of the GMM as the number of UAVs increases. However, the location of clusters, centered versus uncentered, does not have a significant impact on the number of MIs. This result is a confirmation that the number of MIs is highly dependent on the FANET graph diameter (i.e., the number of hops of the shortest path between the two UAVs that are farthest apart). The reason is that a larger diameter is a larger distance that needs to be covered to propagate knowledge throughout the FANET.

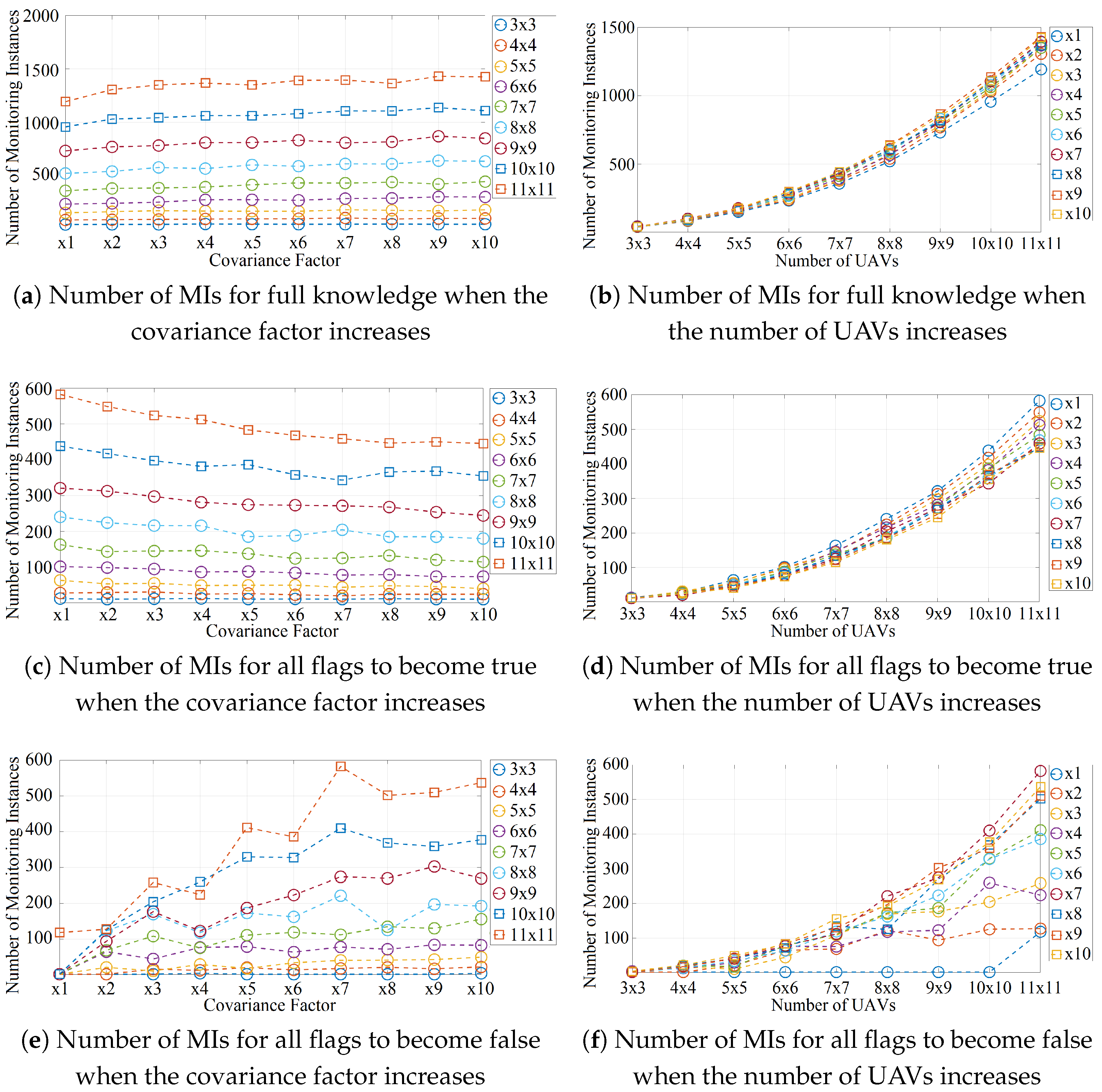
6.1.2. Grid Formation with an Increasing Covariance Factor

Figure 6 shows the number of MIs of the grid formation and when the clusters are more spread out. This is achieved by multiplying the diagonal of the covariance matrix by a scalar that we refer to as the covariance factor. It takes integer values that increase from 1 to 10. Different sizes of grid formation are included, from $3\times 3$ (Figure 4) to $11\times 11$ (Figure 1a). In addition, in this case, only two target clusters are considered. Their centroids are shown in Figure 4a. Their covariance matrices are $\left(\begin{array}{cc}5& 1\\ 1& 5\end{array}\right)$ and $\left(\begin{array}{cc}2& 1\\ 1& 2\end{array}\right)$ with 100 and 50 targets, respectively.

Figure 6a shows that the number of MIs for full knowledge increases slightly with the covariance factor, and the rate of increase is greater for larger grid sizes. When the grid size is $11\times 11$, the number of MIs increases from 1192 to 1425 as the covariance factor increases from 1 to 10. On the other hand, when the grid size is $3\times 3$, the number of MIs increases from 37 to 42. Figure 6b shows the same data points as Figure 6a but as a function of the grid size, not the covariance factor. The rate of increase is significant regardless of the covariance factor. The number of MIs increases from 37 to 1192 when the covariance factor is 1 and increases from 42 to 1425 when the covariance factor is 10.

Figure 6c shows that the number of MIs for all flags to become true decreases with the covariance factor and decreases faster when the size of the grid increases. At $11\times 11$, the number of MIs decreases from 583 to 445 as the covariance factor increases from 1 to 10. At $3\times 3$, the number of MIs decreases from 12 to 10. We attribute the decreasing trend to the larger area occupied by each cluster at larger factors. UAVs cover targets of multiple clusters at larger factors, facilitating the determination that the GMM parameters do not fit the target observations (i.e., all UAV flags becoming true). In other words, UAVs need to propagate knowledge further when clusters are covered by a small number of UAVs.

Figure 6d shows the same data points as Figure 6c but as a function of the grid size, not the covariance factor. The rate of increase is again significant regardless of the covariance factor. The number of MIs increases from 12 to 583 when the factor is 1 and from 10 to 445 when the factor is 10.

The results of the grid formation in Figure 6a–d are consistent with the results from the linear formation in Figure 5. In both cases, the number of MIs is highly dependent on the diameter of the FANET. In other words, the number of MIs increases with the number of hops that need to be covered to relay knowledge from every UAV to other UAVs.

Figure 6e,f corresponds to the case that the GMM fits the ground observations, so the UAV flag values are expected to all be false. Figure 6e shows that the number of MIs for all flags to become false increases with the covariance factor, and the rate of increase is greater for larger grid sizes. At $3\times 3$, the number of MIs increases from 0 to 3 when the covariance increases from 1 to 10. In fact, the number of MIs is 0 for all covariance factors less than 10, meaning that all UAVs start with the correct assumption that the GMM fits the observations (i.e., line 17 in Algorithm 1), and they do not override the initial assumption (lines 21 and 25). On the other hand, at $11\times 11$, the number of MIs increases from 118 to 536. Therefore, in this case, UAVs incorrectly override the initial assumption that the flag is false (line 17), changing its value to true (lines 21 and 25). However, after a number of MIs, all UAVs correctly determine that the flag is false.

Figure 6f shows the same data points as Figure 6e but as a function of the grid size, not the covariance factor. The number of MIs increases in all cases of covariance factor values, and the rate of increase is greater for larger covariance factors. The number of MIs increases from 0 to 118 when the factor is 1 and increases from 3 to 536 when the factor is 10. This result is consistent with previous results. The number of MIs increases with the diameter of the FANET.

6.1.3. Grid Formation with an Increasing Number of Target Clusters

Figure 7 shows the number of MIs of the grid formation and when the number of clusters increases from two to nine, as shown in Figure 4. Different sizes of grid formations are also included, from $3\times 3$ (Figure 4) to $11\times 11$ (Figure 1a).

Figure 7a,b shows the number of MIs for full knowledge. The differences between the subfigures in Figure 6a,b are negligible. This is confirmation that the acquisition of full knowledge by all UAVs is dependent on the diameter of the FANET, not on the number of clusters or the covariance factor.

Figure 7c,d shows the number of MIs for all flags to become true. The results show the same trends as Figure 6c,d with one difference. The number of MIs decreases faster with the number of clusters (Figure 7c) than with the covariance factor (Figure 6c). This means that the tests on lines 20 and 24 of Algorithm 1 are more sensitive to the number of clusters than the covariance factor. These tests compare $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{K}}_i\right)$, $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{A}}_{i,j}\right)$, and $\overline{\mathcal{L}}\left(\mathsf{\Theta }|{\mathcal{W}}_{i,j}\right)$ with $ϵ$, so the negative average log-likelihood given the UAV’s knowledge, agreement, or withheld knowledge is more sensitive to the number of clusters than the covariance factor.

It should also be noted that the faster decrease in the number of MIs in Figure 7c than in Figure 6c means that Algorithm 1 detects the unfitness of the GMM faster for larger numbers of clusters than for higher covariance factors. This observation is also valid for the number of MIs needed for all flags to become false. Figure 7e,f shows the same trends as Figure 6e,f with one difference. The number of MIs increases more slowly with the number of clusters (Figure 7e) than with the covariance factor (Figure 6e).

6.2. Performance Evaluation: Distributed EM Algorithm

The performance of the distributed EM algorithm is evaluated with the number of iterations of the while loop (i.e., line 5 of Algorithm 3) until the termination criterion is met. Given that one iteration consists of four for loops (i.e., lines 6, 9, 12, and 16), there are four rounds of communication on the wireless token-ring network per iteration.

In this case, we change our termination criterion to the same as the default criterion used in the centralized EM algorithm of the MATLAB Toolbox for Statistics and Machine Learning (i.e., fitgmdist in [49]). This criterion allows us to use fitgmdist to benchmark our distributed EM algorithm. The reason is that one EM step is completed per iteration of the while loop of our distributed EM algorithm (i.e., line 5 of Algorithm 3). Therefore, both algorithms perform one EM step per iteration, making the comparison of the number of iterations fair.

The termination criterion is as follows. Let $\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\left[i\right]$ be the average negative log-likelihood at the $i^{\mathrm{th}}$ iteration. The termination occurs when two conditions are met: (1) $|\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\left[i\right]-\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})[i-1]|<{\displaystyle \frac{\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\left[i\right]}{{10}^6}}$ and (2) $\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\left[i\right]-\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})[i-1]\ge 0$. This means that the new value of ${\mathsf{\Theta }}_{\mathrm{out}}$ no longer decreases significantly, $\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})$.

The distributed EM algorithm (i.e., Algorithm 3) and the MATLAB algorithm (i.e., fitgmdist [49]) are also given the same initial GMM parameter values (i.e., ${\mathsf{\Theta }}_{\mathrm{in}}$ in Algorithm 3) for a fair comparison. The values are calculated as follows. The weights ${\varphi }_s$ of ${\mathsf{\Theta }}_{\mathrm{in}}$ are uniform, i.e., ${\varphi }_s={\displaystyle \frac{1}{k}}\mathrm{for}s=1,2,\dots ,k$. The centroids ${\mathit{\mu }}_s$ of $\mathsf{\Theta }$ are calculated using the MATLAB implementation of k-means. The covariance matrices ${\mathbf{\Sigma }}_s$ of ${\mathsf{\Theta }}_{\mathrm{in}}$ are set to diagonal matrices with two diagonal elements. The values of the upper and lower elements are the variance of the x and y coordinates of the targets of the $s^{\mathrm{th}}$ cluster determined from k-means.

Figure 8 shows the number of iterations of the linear formation when the number of UAVs increases from 2 to 15. Both cluster locations, centered and uncentered, and both algorithms, distributed (Algorithm 3) and centralized (fitgmdist [49]), are evaluated in Figure 8. Each data point in Figure 8 is the average number of iterations of 20 simulations, with each simulation having a unique set of randomly generated targets. The number of iterations increases faster for the distributed EM algorithm than for the centralized EM algorithm as the number of UAVs increases. This result is expected because the centralized algorithm does not require DAC; all target observations are available to a single computing system, so the rounds of communication in Algorithm 3 are not needed in the centralized EM algorithm.

Figure 8 also shows that the location of clusters in the center of the image or in the boundaries of the image (i.e., centered vs. uncentered clusters shown in Figure 3) does not have a significant effect on the number of iterations. The number of iterations increases at similar rates in both cases, centered and uncentered, and for both algorithms, centralized and distributed.

Figure 9 shows the number of iterations of the grid formation. Each data point is the average number of iterations of 20 simulations, with each simulation having a unique set of randomly generated targets.

Figure 9a shows the number of iterations when the number of clusters increases from two to nine at grid sizes that increase from $3\times 3$ to $11\times 11$, including both distributed and centralized algorithms. The results are consistent with the linear configuration. The centralized EM algorithm converges with the lowest number of iterations in all cases. However, the trend of the centralized EM algorithm is to increase. On the other hand, the distributed EM algorithm tends to remain constant. There are exceptions, such as the $3\times 3$ and $9\times 9$ formations, which have decreasing and increasing trends, respectively, but the average trend when all grid sizes are considered is to remain constant.

Figure 9b shows the same data points as Figure 9a but rearranged. In this case, the number of iterations is shown as the grid size increases from 3 × 3 to 11 × 11 at numbers of clusters that increase from 2 to 9. The general trend is for the number of iterations to increase with the grid size. This is expected because completing DAC requires more iterations when the data being averaged is distributed across a higher number of UAVs. Figure 9b also shows exceptions to the general trend when the grid size increases from even to odd sizes (e.g., from 4 × 4 to 5 × 5). In other words, the number of iterations increases in both cases, even and odd, but grids of odd size converge faster. For example, the number of iterations is higher for a 10 × 10 grid than an 8 × 8 grid, and it is higher for an 11 × 11 grid than a 9 × 9 grid, but the 9 × 9 and 11 × 11 grids require fewer iterations than the 8 × 8 and 10 × 10 grids. We attribute this behavior to the effect that different network topologies have on DAC convergence [50].

6.3. Comparison of the Monitoring and Distributed EM Algorithms with Related Work

To the best of our knowledge, distributed monitoring algorithms are based on a coordinator that collects data from nodes of the network as in [3,10,11,12,13,14,15,16,17,18,19] covered in Section 2, and our monitoring algorithm is based on [20] to avoid the need for a coordinator. Therefore, the performance of our monitoring algorithm is not comparable to [3,10,11,12,13,14,15,16,17,18,19]. The performance evaluation in [20] did not cover the number of MIs needed for the nodes to propagate their local knowledge to determine the unfitness of the GMM. The framework closest to our monitoring algorithm is the gossip/consensus algorithm [51,52]. These algorithms also require a number of MIs to propagate local information across the network.

Table 2. Number of monitoring instances.

Nodes/UAVs	Algorithm 1	[51]	[52]
100	<600	>1000	N/A
7	16	N/A	12

compares the performance of Algorithm 1 [51,52].

Convergence in [51] requires at least 1000 MIs in a network of 100 temperature sensor nodes of higher connectivity (i.e., lower diameter) than our $10\times 10$ grid. Convergence in [52] requires 12 MIs in a network of 7 UAVs in linear formation that determine the location of a target UAV detected by all monitoring UAVs under Gaussian noise. In our monitoring algorithm, $10\times 10=100$ UAVs require no more than 600 MIs, according to Figure 6c and Figure 7c, and 7 UAVs in linear formation require 16 MIs, according to Figure 5.

Our distributed EM algorithm is compared to the algorithms in [22,29] because, as explained in Section 2, it is an adaptation of the algorithm in [22] that uses MH weights as in [29].

Table 3. Number of iterations for the EM termination criterion.

Nodes/UAVs, Clusters	Algorithm 3	[22]	[29]
100, 3	118	185	N/A
50, 2	N/A	N/A	100
49, 2	30	N/A	N/A

compares the performance of Algorithm 3 [22,29].

The algorithm in [22] was simulated for one scenario only: 100 nodes and 3 target clusters. The termination occurred when $|\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\left[i\right]-\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})[i-1]|<{\displaystyle \frac{\overline{\mathcal{L}}\left({\mathsf{\Theta }}_{\mathrm{out}}\right|\mathcal{O})\left[i\right]}{{10}^5}}$, which is 10 times less tight than the termination criterion used in our simulations in Section 6.2. The number of iterations until termination was 185. On the other hand, our distributed EM algorithm took 118 iterations for the same number of nodes and clusters (i.e., $10\times 10=100$ UAVs and 3 target clusters in Figure 9). The algorithm in [29] was also simulated for one scenario only: 50 nodes and 2 target clusters. The termination was at 100 iterations. Our algorithm ended with 30 iterations for $7\times 7=49$ UAVs and 2 target clusters, according to Figure 9.

7. Practical Considerations on a UAV Network

Our open-source network of autonomous UAVs is shown in Figure 10a and documented in [1]. Two adjacent thermal images captured with our UAVs are shown in Figure 10b.

UAV-to-UAV communication takes place over the Zigbee network, which is used for low-power and low-bandwidth industry applications. Each UAV is a WiFi router that connects to its controller, a Raspberry Pi, and a laptop computer. The controller is to override the autonomous operation of the UAV in the case of unsafe flight maneuvers due to unexpected events such as bugs in our code development or loss of GPS. The Raspberry Pi is used to interface the thermal camera with the operating system of the UAV. The laptop computer is used to program the UAVs for autonomous operation.

The thermal images in Figure 10b capture the same hotspot on the ground. The hotspot is partially covered on the left image and fully covered on the right image. In practice, adjacent images overlap due to geolocation errors and external factors such as wind. Hotspots are characterized by keypoints that are matched to each other to align the overlapping images. This operation is known as point-set registration [39]. All keypoints belong to the set of observations $\mathcal{O}=\{{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_m\}$ defined in Section 3, and their coordinates in meters with respect to a user-defined origin can be calculated from the UAVs’ telemetry (i.e., latitude, longitude, altitude, pitch, yaw, and roll) and the thermal camera’s fields of view and resolution.

Our preliminary work in [53] measured the maximum packet rate on a Zigbee wireless link at 65 packets per second.

Algorithm 1 transmits ${\mathcal{X}}_{i,j}$ from $u_i$ to each of its neighbors, one at a time (line 13 of Algorithm 1), and the maximum number of neighbors in our simulations is four. Therefore, Algorithm 1 spends ${\displaystyle \frac{4}{65}}=62$ ms to complete all transmissions. The $u_i$ and its neighbors are a total of 5 UAVs, and only one of them can transmit at a time not to interfere with each other. Therefore, five transmissions are $5\times 62=310$ ms long. Consider the $7\times 7$ grid flight formation. This is 49 UAVs. The number of MIs for all flags to become true is 140 on average, according to Figure 6d. This means that Algorithm 1 takes $140\times 0.31=43$ s at least to determine that all flag values are true when the flight formation is a $7\times 7$ grid of 49 UAVs.

Algorithm 3 requires passing the token along the ring network four times per iteration. These four rounds of communication correspond to the $for$ loops on lines 6, 9, 12, and 16 of the algorithm, and each UAV communicates with its neighbors in every round. Therefore, one iteration of Algorithm 3 in the $7\times 7$ grid is $7\times 7\times 4\times 62=$ 12,152 ms or 12 s long. Algorithm 3 converges after 30 iterations when there are 2 clusters of targets on the ground, according to Table 3. This is 360 s or 6 min. The same calculation can be completed for a higher number of UAVs. For example, for the case of 100 UAVs (i.e., $10\times 10$ grid), Algorithm 3 converges after 120 iterations when there are 3 clusters of targets on the ground, according to Figure 9a. Completing this number of iterations on a ring of 100 UAVs takes $10\times 10\times 4\times 0.062\times 120=2976$ s or 50 min, which is not practical. The Zigbee network would have to be replaced with a wireless network with higher data rates, such as WiFi, at the cost of higher power consumption.

The previous numerical analysis assumes ideal wireless links. It does not account for delays from lower layers of the protocol architecture: data-link and medium-access control layers. These delays can be significant when the number of neighbors increases (i.e., medium access control) and when packets are not received (i.e., data link). For example, one iteration of Algorithm 3 is 12 s long in the $7\times 7$ grid, so the convergence time increases by 12 s every time the token is lost due to a failed packet reception.

The analysis also neglects data processing time. Data processing is performed in Algorithm 1 to evaluate the average negative log-likelihood defined in (3) (lines 6, 7, 8, and 13). Data processing takes place on Algorithm 3 using the formulas in (3), (8), (12), (16)–(18). All formulas operate on observations in ${\mathcal{K}}_i$, and thermal images such as those in Figure 10b have a number of observations that do not exceed 350 in our data set. Each observation consists of two floating point numbers that correspond to the coordinates x and y. The evaluation of these formulas on this number of observations takes a fraction of a millisecond on our UAV platform. Therefore, data processing time is negligible with respect to UAV-to-UAV communication.

The power consumed for data processing and Zigbee radios [53] is also negligible with respect to other aspects of UAV operation (e.g., propellers, flight controller, image processing, and WiFi).

8. Conclusions

Distributed algorithms for a network of UAVs that monitor moving targets on the ground were proposed. The locations of the targets are assumed to follow a mixture of Gaussian distributions. The objective is to monitor the geographical distribution of the targets using a Gaussian mixture model (GMM). It is assumed that UAVs have a partial view of each target cluster due to limits on flight altitude and camera resolution. The UAVs monitor the clusters of targets with two algorithms that require data that are local to each UAV and data from UAVs that are one hop away in the communication graph. Therefore, monitoring is a distributed operation that does not rely on a single coordinator as in the related work. In the first algorithm, UAVs determine when the current GMM no longer represents the geographical distribution of the targets within a threshold accuracy. In the second algorithm, UAVs update the GMM to the new targets’ distribution. The performance of the algorithms was evaluated with the number of iterations the algorithms needed to converge. The reason is that a low number of iterations allows the algorithms to monitor target locations of a higher Nyquist rate (i.e., faster-moving targets). The simulation results confirmed superior performance to the best of our knowledge.

Future work will focus on the implementation and performance evaluation of the algorithms in our open-source UAV network [1] and the use of multimodal sensing using thermal and RGB images. We assumed that all UAVs have the same model and characteristics, so the algorithms do not take into account differences between UAVs. Future work will also consider a heterogeneous UAV network in which multimodal sensing is achieved with UAVs that have different instruments. Another important aspect that we plan to address is adding robustness against UAV failures. In the context of our algorithms, robustness can be achieved by recovering knowledge of a failed UAV from its neighbors, so a new UAV can replace the failed UAV.