LSTM-Enhanced Deep Reinforcement Learning for Robust Trajectory Tracking Control of Skid-Steer Mobile Robots Under Terra-Mechanical Constraints

Abstract

Autonomous navigation in mining environments is challenged by complex wheel–terrain interaction, traction losses caused by slip dynamics, and sensor limitations. This paper investigates the effectiveness of Deep Reinforcement Learning (DRL) techniques for the trajectory tracking control of skid-steer mobile robots operating under terra-mechanical constraints. Four state-of-the-art DRL algorithms, i.e., Proximal Policy Optimization (PPO), Deep Deterministic Policy Gradient (DDPG), Twin Delayed DDPG (TD3), and Soft Actor–Critic (SAC), are selected to evaluate their ability to generate stable and adaptive control policies under varying environmental conditions. To address the inherent partial observability in real-world navigation, this study presents an original approach that integrates Long Short-Term Memory (LSTM) networks into DRL-based controllers. This allows control agents to retain and leverage temporal dependencies to infer unobservable system states. The developed agents were trained and tested in simulations and then assessed in field experiments under uneven terrain and dynamic model parameter changes that lead to traction losses in mining environments, targeting various trajectory tracking tasks, including lemniscate and squared-type reference trajectories. This contribution strengthens the robustness and adaptability of DRL agents by enabling better generalization of learned policies compared with their baseline counterparts, while also significantly improving trajectory tracking performance. In particular, LSTM-based controllers achieved reductions in tracking errors of 10%, 74%, 21%, and 37% for DDPG-LSTM, PPO-LSTM, TD3-LSTM, and SAC-LSTM, respectively, compared with their non-recurrent counterparts. Furthermore, DDPG-LSTM and TD3-LSTM reduced their control effort through the total variation in control input by 15% and 20% compared with their respective baseline controllers, respectively. Findings from this work provide valuable insights into the role of memory-augmented reinforcement learning for robust motion control in unstructured and high-uncertainty environments.

1. Introduction

In the mining industry, the tracking control of autonomous vehicles presents significant challenges in off-road environments, where complex terra-mechanical interactions can lead to performance degradation. Autonomous driving can be affected by disturbances arising from the unpredictability of the operating environment, including uneven terrain, unpredictable frictional characteristics, and the presence of external aspects, such as airborne particulate matter. Specifically, the mining environment is characterized by complex topographical features on the soil, which reduces the soil’s traction properties, further complicating autonomous vehicle navigation [1]. These aspects not only impact the vehicle’s ability to maintain stable motion control but also introduce safety risks to both autonomous systems and human operators.

Terrain complexity exacerbates tire stress, particularly through the presence of turns and slopes that induce uneven load distribution, alongside the critical phenomena resulting from wheel–terrain interaction due to debris accumulation on the surface [2]. In particular, friction loss under these conditions leads to weakened traction forces, which can result in drifting and destabilization, thereby impairing the control of the vehicle [3]. These challenges can also affect the lifespan of tires [4], which leads to their necessitating frequent replacements and reduces the availability of the hauling fleet, which in turn impacts overall productivity. Due to the complex wheel–terrain interaction in mining mobile vehicles, there is a critical need to enhance the robustness of motion control systems to counteract terrain disturbances and mitigate the adverse effects of slip phenomena on traction and vehicle dynamics.

Traditional control methods, such as Model Predictive Control (MPC) [5,6] and Sliding Mode Control (SMC) [7,8], have been used to address such challenges in autonomous vehicle motion control and related dynamics. However, these approaches are inherently dependent on dynamic models of both the robot and its interaction with the environment. This reliance makes them vulnerable to the performance degradation caused by modeling mismatches, which may arise from inaccurate model assumptions or discrepancies between the assumed and actual vehicle dynamics. Such modeling errors can lead to suboptimal control performance, especially in highly dynamic and uncertain environments, such as those found in mining operations. Alternatively, Deep Reinforcement Learning (DRL) techniques offer a promising approach by learning control policies through continuous interaction with the environment, using real-time feedback to adapt to dynamic conditions [9,10]. This capability reduces reliance on an exact model, making DRL particularly advantageous in this study, as it enables the controller to operate based on the robot’s real-time dynamics rather than relying on precise and often complex terra-mechanical models. However, limitations in robot sensors during real-time data acquisition often result in partial observability, where the controller is unable to obtain information from a complete representation of the environment, potentially diminishing its effectiveness [11]. Although DRL-based navigation strategies have shown significant progress in mobile robots, current methods often face limitations in unstructured environments where simplified control structures are not adapted to varying motion conditions or terrain assumptions [12], highlighting the need for robust and adaptive control schemes capable of learning suitable dynamics under varying system conditions. The use of Recurrent Neural Networks (RNNs) has been studied to address this problem [11,13], leveraging historic observations to infer the current environment state. However, to the best of our knowledge, this integration has not been assessed on recent state-of-the-art DRL algorithms.

Work Contributions

The main contributions of this work are as follows:

• Integration of Long Short-Term Memory (LSTM) networks into DRL-based controllers, enabling control agents to recurrently retain and use temporal dependencies under partial observability of past dynamics. This enhancement improves the agents’ ability to infer unobservable system states caused by sensor limitations and complex terrain interactions, contributing to the generalization of learned policies and greater adaptability under challenging terrain conditions.
• A comprehensive evaluation of vanilla-based algorithms under policy gradient-based DRL algorithms that rely on fully observable state representations, such as PPO, DDPG, TD3, and SAC, for trajectory tracking control in skid-steer mobile robots operating under mining terra-mechanical constraints. This study analyzes the stability, adaptability, and effectiveness of the proposed algorithms while ensuring accurate trajectory tracking and regulation despite terrain disturbances and dynamic parameter variations.
• The application of DRL algorithms for autonomous motion control, focusing on tracking reference trajectories in numerical simulations and real-world mining environments subject to external disturbances and uncertainties. The findings provide insights into the role of memory-augmented reinforcement learning for robust motion control in unstructured and high-uncertainty environments, advancing in the enhanced performance of DRL approaches and their applicability for mobile robots in complex mining operations.

In summary, this work aims to develop a robust motion control strategy for the trajectory tracking of autonomous skid-steer robots operating in mining environments by integrating LSTM networks into policy gradient-based DRL methods. The proposed approach addresses the challenges of partial observability arising from vehicle dynamics and terrain-induced slip due to wheel–terrain interaction, enabling adaptive control without dependence on accurate terra-mechanical models.

The remainder of the paper is organized as follows: Section 2 provides a review of related works on reinforcement learning (RL) techniques applied to trajectory tracking control in autonomous motion. Section 3 outlines the theoretical background of Deep Reinforcement Learning (DRL), laying the foundation for the proposed methodologies. In Section 4, the DRL techniques used as the basis for the proposed motion controllers are detailed. Section 5 presents the vehicle dynamic model and terrain characterization used for training and evaluating the motion controllers. Section 6 covers the control design and parameter settings implemented in the trajectory tracking controllers. Section 7 describes the experimental setup and analyzes the results obtained from the experiments. Finally, the paper ends in Section 8 with concluding remarks on this work.

2. Related Works

Trajectory tracking remains a fundamental challenge in autonomous motion control, with traditional control methods often struggling to address complexities inherent to real-world environments. For instance, approaches such as Model Predictive Control (MPC) [5], Fuzzy Logic-based control [14], and Sliding Mode Control [7] have been extensively applied in trajectory tracking in autonomous motion tasks. However, these methods have been typically designed to be adaptive and have often relied on accurate models of the robot motion dynamics, which can be challenging or even infeasible to obtain in environments in the presence of uncertainties [15]. In contrast, reinforcement learning (RL) methods currently offer a compelling alternative by learning optimal control policies without necessarily requiring an explicit model formulation of the robot system dynamics. Instead, RL enables an agent to learn motion dynamics through direct interaction with the environment, iteratively refining its policy to maximize reward signals that guide the system toward prescribed trajectory tracking control and regulation objectives. This characteristic makes RL well suited for motion control in complex and uncertain environments, and it has been successfully applied to a wide variety of applications in structured and non-structured environments, including autonomous navigation of aerial [16,17,18] and marine vehicles [19], industrial process control [20], and even complex gameplay scenarios [21]. For instance, the work in [22] addressed a path tracking problem in autonomous ground vehicles using inverse RL under matched uncertainties. However, the approach assumed idealized system conditions and omitted accounting for external disturbances or environmental variability, which limited its applicability in real-world scenarios. In [23], a Q-Learning (QL) strategy was used in combination with a PID controller for obstacle avoidance in trajectory tracking tasks for simulated wheeled mobile robots. However, as Q-Learning relies on a tabular estimation of the state–action value function, it does not scale properly according to the continuous state and action spaces, which is often necessary for the effective trajectory tracking control of autonomous vehicles [21].

To address scalability limitations in Q-Learning and continuous control action constraints, Deep Q-Networks (DQNs) may be used instead by replacing tabular Q-value estimation with neural networks, enabling the handling of high-dimensional continuous state spaces [21]. Dual Deep Q-Network (DDQN) has been adopted as a variant of the DQN method to enhance stability and reduce overestimation biases in trajectory tracking controllers [24]. However, both DQN and DDQN inherently rely on discrete action spaces, as they approximate an optimal action value function by selecting actions from a finite set, limiting their ability to execute accurate and smooth control actions. Policy gradient methods address this limitation by directly optimizing a parameterized policy, enabling control in continuous action spaces. Offline learning techniques such as Conservative QL (CQL) [25] or Bayesian QL (BQL) [26] were not considered here since our objective focused on interaction-driven policy learning with real-time adaptability rather than leveraging a pre-collected or static dataset obtained from the robot dynamics. Similarly, while model-based RL approaches such as MBPO (Model-Based Policy Optimization) [27] and PETS (Probabilistic Ensembles with Trajectory Sampling) [28] have demonstrated data efficiency, they were not used here due to our focus being on model-free methods that avoid potential model bias and complexity in highly uncertain and partially observable environments.

A persistent challenge in autonomous driving arises when sensor limitations prevent the agent from fully observing the system state at any given time [11,13]. This issue is especially critical in mining and off-road environments, where observations from range sensors or positioning systems may be intermittent or unreliable due to environmental constraints such as occlusions, dust, or irregular terrain [29]. Moreover, complex terrain topography and variable soil conditions can constrain traversability and introduce uncertainties in planning and control, resulting from uneven friction conditions and dynamic weather effects on the soil’s physical properties [16]. For instance, in [30], RL methods based on convolutional neural networks and value iteration networks were used to address maneuverability tasks. However, the approach was limited to high-level planning under conditions of known terrain maps, with reward structures learned in a fully observable setting. Then, it did not consider partial observability introduced by sensor limitations or dynamic terrain changes, nor did it incorporate low-level control disturbances arising from wheel–terrain interaction.

Deep RL techniques have shown improved robust motion control and navigability on rough terrain [31,32]. Among policy gradient methods, Proximal Policy Optimization (PPO) has been applied to motion control tasks [13], where it has been integrated with Long Short-Term Memory (LSTM) networks in distributed architectures to address partial observability. LSTM networks have been used to process historical state information, which was used exclusively during random initializations of reference states in each learning episode. Such approach enhanced state inference and early exploration, aiding to mitigate the effects of unknown initial conditions on vehicle dynamics [11,13].

While PPO demonstrated effectiveness in continuous control, the on-policy nature of PPO limits its sample efficiency compared with off-policy approaches, making it less practical in scenarios with restricted data availability. Such concern has encouraged the development of Deep Reinforcement Learning (DRL) techniques that integrate the advantages of policy gradient methods, such as their capability to handle continuous action spaces, with the sample efficiency of off-policy algorithms such as Q-Learning. For instance, Deep Deterministic Policy Gradient (DDPG) strategies optimize deterministic policies by using the deterministic policy gradient approach [33]. This method uses an off-policy learning paradigm with an actor–critic architecture, enabling more efficient data reuse and improved convergence properties. In [10,34], DDPG-based trajectory tracking controllers were designed to enhance motion control in autonomous mobile robots with ground force interactions. Although extensive simulation tests demonstrated the effectiveness of DDPG in handling terrain disturbances, robust control performance was primarily assessed in the presence of external disturbances, while the system’s ability to adapt to dynamic and complex terrain conditions such as slip dynamics or terrain variations was not comprehensively evaluated. For instance, in [35], the authors developed a one-step RL strategy based on DDGP for simultaneous motion planning and tracking control in a simulated robot under ideal terrain conditions, which restricted the agent’s ability to model temporal dependencies and perform long-horizon multi-step learning. Then, this limitation could reduce control performance in the robot task since it requires sequence learning and complete adaptation over time. Similarly, the work in [11] proposed an extension of DDPG by integrating Long Short-Term Memory (LSTM) layers into the neural network architecture, improving control performance in partially observable environments. This approach uses a kinematic controller as a reference for two independent PI dynamic controllers for ideal conditions of motion without tractions losses, taking advantage of the LSTM’s ability to retain historical state information and explore control actions. Experimental results demonstrated that the hybrid DDPG-LSTM framework outperformed both conventional PI controllers and standard DDPG under dynamic uncertainty. However, its robustness across diverse trajectory configurations, particularly in scenarios involving sharp turns and terrain disturbances, was not assessed. To address some of DDPG’s limitations, such as value overestimation and training instability, the Twin Delayed DDPG (TD3) algorithm was developed [36]. In particular, the TD3 method incorporates mechanisms to stabilize learning, such as delayed target network updates and action smoothing [37]. This algorithm has been successfully applied to trajectory tracking for racing vehicles [38], particularly for drift control in high-speed racing scenarios. Alongside TD3, the Soft Actor–Critic (SAC) algorithm was introduced in [39]. SAC trains a stochastic policy in an off-policy manner by optimizing entropy as part of the learning objective. In such work, SAC has been shown to outperform DDPG and DQN in trajectory tracking for racing applications, particularly in drift control, by showcasing its adaptability to unseen environments [40]. Hybrid methods combining DDPG with deterministic algorithms [41] or modified SAC variants with heuristic integration [42] have shown improvements in trajectory smoothness and training efficiency under static or mildly dynamic conditions. Similarly, approaches such as HDRS-based DRL [43] and improved TD3 algorithms leveraging transfer learning and prioritized experience replay [44] focus primarily on reducing convergence time and optimizing path planning and control performance in structured environments. However, these methods largely operate under fully observable state assumptions and use feedforward architectures, limiting their ability to model temporally extended dependencies required for robust decision making in scenarios with incomplete state information and complex dynamic interactions. Alternatively to the previously discussed model-free RL algorithms, model-based RL techniques greatly improve sampling efficiency by learning a representation of the model dynamics. For instance, Model-Based Policy Optimization (MBPO) was applied to trajectory tracking in autonomous driving, outperforming SAC while requiring one-order-of-magnitude fewer training episodes [45]. Nevertheless, their reliance on a learned dynamic model may be unsuitable in mining environments due to a high degree of uncertainty. In particular, unpredictable terrain phenomena such as variable slip conditions, as well as operational hazards such as airborne materials, can degrade sensor reliability, introducing uncertainty into state estimation. These challenges could introduce significant modeling errors, which may lead the agent to exploit inaccuracies in the dynamic model and learn a suboptimal control policy. Moreover, while these RL-based methods have shown promise across various trajectory tracking tasks, selecting the most suitable algorithm for a given problem remains complex. Several factors, such as the agent’s observation space, the tuning of hyperparameters, and the design of the reward function, significantly impact the effectiveness of DRL-based controllers [46]. Therefore, this work also proposes a comparative study of DRL techniques, specifically for trajectory tracking in mobile robots subject to terra-mechanical constraints, to provide deeper insights into their performance and applicability.

3. Theoretical Background

In this section, the vehicle dynamics for trajectory tracking are formulated within the framework of a Markov Decision Process (MDP). Under this formulation, an agent selects an action $a_t$ from the action space $\mathcal{A}$ based on a policy $\pi \left(s_t\right)$, which maps observed system states $s_t$ to optimal control decisions. The selected action transitions the system to a new state within the state space $S$ and yields a reward $r_t$ from the reward set $\mathcal{R}$, which quantifies the quality of the chosen action in achieving the trajectory tracking objective. The goal of the proposed RL algorithms is to learn an optimal policy ${\pi }^{*}\left(s_t\right)$ so that the cumulative discounted reward $R_t$ is maximized, defined as

$$R_t=\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k+1},$$

(1)

where $r_t$ represents the immediate reward at each time step, and $\gamma \in [0,1]$ is the discount factor that determines the relative balance of immediate and future rewards. By optimizing ${\pi }^{*}\left(s\right)$, the agent learns to make decisions that not only maximize immediate rewards but also improve long-term performance. This optimization process requires balancing the trade-off between exploration, where the agent gathers new information about the environment, and exploitation, where it applies acquired knowledge to maximize rewards. Such a balance is crucial in complex and dynamic environments, where adaptability and continuous learning enable the agent to achieve robust control performance and efficient trajectory tracking.

To quantify the expected cumulative reward associated with specific actions and states, the action–state value function $Q^{\pi }(a_t,s_t)$, commonly referred to as the Q-function, is used. This function evaluates the long-term reward obtained by taking action $a_t$ in state $s_t$ and subsequently following policy $\pi \left(s_t\right)$. It is formally defined as follows:

$$Q^{\pi }(a_t,s_t)={\mathbb{E}}_{r_t,s_{t+1}\sim p(·|s_t,a_t)}\left[r_t+\gamma {\mathbb{E}}_{a_{t+1}\sim \pi }\left[Q^{\pi }(a_{t+1},s_{t+1})\right]\right],$$

(2)

where $a_t$ represents the control action taken at time step t, $s_t$ denotes the environment state at time step t, $p(s_{t+1},r_t\mid s_t,a_t)$ is the state transition probability distribution, $\gamma$ is the discount factor, and $\pi (a_{t+1}\mid s_{t+1})$ represents the probability of selecting action $a_{t+1}$ under policy $\pi$ given state $s_{t+1}$ [47].

4. Methodology

This study compares model-free DRL algorithms, including Proximal Policy Optimization (PPO), Deep Deterministic Policy Gradient (DDPG), Twin-Delayed Deep Deterministic Policy Gradient (TD3), and Soft Actor–Critic (SAC), all within the actor–critic framework, as presented in

Table 1. Overview of DRL algorithms compared in this work.

Algorithm	Training Strategy	Policy Type	Value Function	Parameters
				Actor	Critic	Total
PPO [48]	On-policy	Stochastic	State, $V\left(s\right)$	260	257	517
DDPG [33]	Off-policy	Deterministic	Action–state, $Q(s,a)$	$194\times 2$	$321\times 2$	1030
TD3 [37]	Off-policy	Deterministic	Action–state, $Q(s,a)$	$194\times 2$	$321\times 3$	1351
SAC [39]	Off-policy	Stochastic	Action–state, $Q(s,a)$	260	$321\times 3$	1223

. The focus of this work is on comparing on-policy and off-policy techniques, which enable the learning of both stochastic and deterministic policies through direct interaction with the robotic environment. A key aspect of this approach is the integration of Long Short-Term Memory (LSTM) networks into the DRL framework, as illustrated in the example in Figure 1, where LSTM networks are combined with a DDPG approach. This hybrid approach allows the agents to not only perform real-time trajectory tracking but also adapt to environmental uncertainties and terrain disturbances. Specifically, the integration of LSTM networks enables the agents to retain and process temporal dependencies, which is crucial when dealing with partial observability due to sensor limitations or rapidly changing environmental conditions. This capability allows the agents to infer unobservable system states, which is particularly beneficial in terrains where dynamic interactions between the robotic vehicle and the environment generate terra-mechanical constraints such as slip, which could lead to motion performance degradation. For completeness, the following subsections provide a detailed explanation of each DRL technique and their integration with the proposed LSTM networks.

4.1. Proximal Policy Optimization

Proximal Policy Optimization (PPO) is an on-policy reinforcement learning algorithm based on insights of Trust Region Policy Optimization (TRPO) [49]. PPO here optimizes a parameterized policy while constraining the step size of policy updates by limiting the deviation of a new policy’s probability distribution from an old policy. This approach mitigates the risk of policy collapse due to excessively large updates. Instead of explicitly enforcing a trust region constraint as in TRPO, the PPO strategy is aimed at achieving a similar effect by clipping the policy update step by using a probability ratio ${\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{{\pi }_{\theta }}_{old}\left(a_t\right|s_t)}}$. Consequently, the policy objective function becomes

$$\begin{array}{c}\hfill L^{PPO}\left(\theta \right)={\mathbb{E}}_t\left[min\left({\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{{\pi }_{\theta }}_{old}\left(a_t\right|s_t)}}{\widehat{A}}_t,\mathrm{clip}\left({\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{{\pi }_{\theta }}_{old}\left(a_t\right|s_t)}},1-ϵ,1+ϵ\right){\widehat{A}}_t\right)\right],\end{array}$$

(3)

where ${\widehat{A}}_t$ is an estimate of the advantage value for action $a_t$ on state $s_t$ and $ϵ$ is the clipping threshold that limits the policy deviation. By clipping the probability ratio within the interval $[1-ϵ,1+ϵ]$, the PPO approach prevents excessive policy updates and maintains training stability with reduced variance [48].

4.2. Deep Deterministic Policy Gradient

The Deep Deterministic Policy Gradient (DDPG) algorithm is an off-policy method designed to estimate an action value function $Q(s,a)$ by using neural networks, specifically tailored for environments with continuous action spaces [33]. Indeed, DDPG operates with an architecture composed by two primary components: the actor and the critic. The actor defines a policy function $\mu \left(s\right|{\theta }^{\mu })$, where ${\theta }^{\mu }$ represents the set of trainable parameters that are iteratively updated to optimize the learning objective $J={\mathbb{E}}_{r,s\sim E,a\sim \pi }\left[R_t\right]$, while the critic estimates an action value function $Q^{\mu }(s,a)$, which evaluates the quality of the actions a taken by the actor. The DDPG approach [50] is often used to update the actor, as it provides the gradient of the expected return with respect to deterministic policies, thus allowing for efficient updates in continuous action spaces. The learning objective focuses on optimizing the deterministic policy $\mu$ by estimating $Q^{\mu }$, as formulated in Equation (4). Thus, to provide a policy $\mu$, the Q-function can be formulated as the expected return as follows:

$$\begin{array}{c}\hfill Q^{\mu }(s_t,a_t)={\mathbb{E}}_{r_t,s_{t+1}\sim E}\left[r_t+\gamma Q^{\mu }(s_{t+1},\mu \left(s_{t+1}\right))\right],\end{array}$$

(4)

where $\gamma$ is a discount factor, and the expectation is removed from the policy $\mu$ to allow for off-policy learning. This deterministic policy removes randomness in action selection, making the critic’s learning more stable. The critic’s Q-function $Q^{\mu }$ is parameterized by neural network weights ${\theta }^Q$, and the objective is to minimize the loss function:

$$\begin{array}{c}\hfill \mathcal{L}\left({\theta }^Q\right)={\mathbb{E}}_{s_t\sim {\rho }^{\beta },a_t\sim \beta ,r_t\sim E}\left[{(Q(s_t,a_t|{\theta }^Q)-y_t)}^2\right],\end{array}$$

(5)

where ${\rho }^{\beta }$ is the state probability distribution under exploratory policy $\beta$[33] and $y_t$ is the target value for the Q-function, given by

$$\begin{array}{c}\hfill y_t=r(s_t,a_t)+(Q^{\prime }(s_{t+1},{\mu }^{\prime }(s_{t+1}|{\theta }^{{\mu }^{\prime }})|{\theta }^{Q^{\prime }}),\end{array}$$

(6)

where ${\mu }^{\prime }\left(s\right)$ and $Q^{\prime }(s,a)$ represent the target actor and target critic, respectively. To enable the control of continuous actions, the actor is defined as the parameterized function $\mu \left(s\right|{\theta }^{\mu })$, which is optimized by the gradient of J, as follows:

$$\begin{array}{ccc}\hfill & {\nabla }_{{\theta }^{\mu }}J\approx {\mathbb{E}}_{s_t\sim {\rho }^{\beta }}\left[{\nabla }_{{\theta }^{\mu }}Q(s_t,a_t|{\theta }^Q){|}_{s=s_t,a=\mu \left(s_t\right|{\theta }^{\mu })}\right]\hfill & \end{array}$$

(7)

$$\begin{array}{ccc}\hfill =& {\mathbb{E}}_{s_t\sim {\rho }^{\beta }}[{\nabla }_{a}Q(s_t,a|{\theta }^Q){|}_{s=s_t,a=\mu \left(s_t\right)}{\nabla }_{{\theta }^{\mu }}\mu \left(s\right|{\theta }^{\mu }){|}_{s=s_t}].\hfill & \hfill \end{array}$$

(8)

This optimized gradient provides the direction for improving the actor’s performance based on the critic’s evaluation. Incorporating ideas from [21], a replay buffer is used here to store transitions and random state and action samples. Such approach avoids temporal correlations among pieces of past information with the aim of maintaining independence and identically distributed conditions necessary for stable optimization. The target networks for both the actor and the critic are updated by using soft target updates, which ensures that the target networks slowly track the learned networks. This technique stabilizes training and improves convergence [33]. The exploratory policy used in DDPG to define the learning target incorporates noise to encourage exploration. The exploratory policy is then given by

$$\beta \left(s_t\right)=\mu \left(s_t\right|{\theta }^{\mu })+\mathcal{N},$$

(9)

where $\mathcal{N}$ represents noise added to the action, typically modeled as an Ornstein–Uhlenbeck process [33]. This process introduces temporally correlated noise to lead the agent to explore the environment more effectively, particularly in continuous action spaces.

4.3. Twin Delayed Deep Deterministic Policy Gradient

The DDPG technique may experience overestimation bias due to maximization of noisy Q-value estimates, which can lead to overly optimistic evaluations of suboptimal states [37]. To address this issue, clipped double Q-Learning is often introduced, accounting for two independently trained critic networks. Moreover, to address the overestimation bias inherent in Q-Learning, the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm introduces key modifications to account for stability and learning efficiency. By selecting the minimum Q-value estimate from two independently trained critics, TD3 effectively counteracts overestimations, resulting in more reliable value function approximations and stabilizing the learning process [37]. However, estimations of value functions can still introduce further variance, slowing down learning and degrading policy performance. To counteract this issue, TD3 implements two improvements. First, when the learned policy is suboptimal or constrains errors, the overestimation of the value function can lead to policy degradation, generating inaccurate value estimates and policy updates. While target networks facilitate the control of error accumulation by stabilizing value predictions, frequent policy updates can still cause divergence [37]. Then, an update delay is proposed to reduce critic estimation errors [37], ensuring that the critic maintains enough time to converge before modifying the policy. Further, deterministic policies may experience over-fitting when obtaining the Q-function, which can impact policy generalization. To address this issue, TD3 is aimed at smoothing target actions by adding clipped noise to the target action in the learning objective, ensuring that the disturbed action remains close to the original while preventing excessive variance. Such enhancements in TD3 are intended to achieve a more robust policy learning in continuous action spaces by reducing both overestimation bias and variance-related instability.

4.4. Soft Actor–Critic

The Soft Actor–Critic (SAC) algorithm is designed to enhance sampling efficiency and improve control robustness. It leverages a maximum entropy reinforcement learning framework, which optimizes both the expected reward and the entropy of the policy to encourage exploration and stability [39]. Entropy maximization encourages the policy to explore the environment more effectively by discouraging deterministic behavior and reducing reliance on suboptimal actions. To balance exploration and exploitation dynamically, SAC adapts the entropy coefficient term, weighting the importance of entropy maximization.

4.5. Long Short-Term Memory

In this study, Long Short-Term Memory (LSTM) networks are integrated into the baseline DRL strategies presented in Section 4.1–Section 4.4 to improve adaptability and robustness in motion control for skid-steer mobile robots navigating partially observable environments with uncertain terra-mechanical interactions. The primary motivation for integrating LSTM is to compensate for the agent’s incomplete perception of the system dynamics, which arises due to sensor limitations (e.g., slip detection sensors with restricted availability), terrain interactions (e.g., dynamic friction estimation), environmental occlusions (e.g., GPS signal loss in obstructed areas), and measurement noise in state estimation (e.g., inaccuracies in differential encoders mounted on the wheel axles). These constraints may impair the ability of conventional DRL approaches to infer accurate system dynamics, leading to suboptimal policy learning and degraded control performance in real-world settings.

The LSTM approach is aimed at overcoming the long-term dependency problem faced by traditional Recurrent Neural Networks (RNNs). When processing sequential data from mobile robots, RNNs usually struggle to effectively recover earlier information due to the vanishing gradient or exploding gradient problem [51]. Then, LSTM addresses such concern by introducing one cell state, one hidden state, and three gates (i.e., input gate, forget gate, and output gate) to regulate the flow of information across time steps, as shown in Figure 2. In particular, given the historical state observations for each DRL agent $z_t$, cell state $C_t$ stores information along the learning process and is updated at each time step, depending on the three gates. The forget gate $f_t$ decides the amount of previous memory that should be discarded. The input gate $i_t$ regulates how much new information should be stored in the cell state. Finally, the output gate $o_t$ controls the information that is passed by the next layer through the hidden state $h_t$.

By incorporating LSTM into the proposed DRL framework, the agent is complemented with an internal mechanism built upon an RNN architecture to store and use historical observations, effectively reconstructing a more complete representation of the underlying motion system dynamics. This is particularly critical in trajectory tracking, where instantaneous sensor readings are not always enough to obtain accurate control actions due to limited observability and partial accessibility of the system state. With the LSTM network’s ability to model temporal dependencies, the agent is able to account for past observations in order to predict and compensate for transient disturbances, dynamic variations in terrain conditions, and model uncertainties such as parameter variations. This improves the consistency of the learned policies of the proposed agent, leading to more stable and efficient motion control.

Table 2. DRL baseline algorithms and reference key parameters.

Algorithm	Policy Type	Architecture	Shared Actor/ Critic	Replay Buffer	Target Networks	Reference Key Hyperparameters
PPO	Stochastic	Shared MLP	Yes	Yes	No	clip $=0.2$, $\gamma =0.95$, $\lambda =0.95$
DDPG	Determi-nistic	Separate MLP	No	Yes	Yes	$\tau =0.0095$, buffer = 500, $\gamma =0.95$
TD3	Determi-nistic	Twin Critics and MLP	No	Yes	Yes	$\tau =0.0095$
SAC	Stochastic	Twin Critics and MLP	No	Yes	Yes	${\alpha }_{a,c}\approx \times {10}^{-4}$, $\tau =0.0095$, $\gamma =0.95$

provides a summary of the baseline approaches, detailing their key characteristics and associated parameters.

5. Environment Characterization: Skid-Steer Mobile Robot

A skid-steer mobile robot (SSMR) is used in this work as part of the environment to assess the proposed DRL approaches for trajectory tracking control. The robot incorporates a differential steering mechanism combined with a pair-driven four-wheel system to distribute the effects of lateral skidding and longitudinal slip experienced by each wheel, as illustrated in Figure 3. The SSMR model assumes a uniform load distribution across the vehicle to simplify the internal force balance. However, the SSMR is also prone to external forces induced by terrain unevenness, which may disrupt this balance and introduce additional disturbances. As shown in Figure 3, the SSMR model highlights key force interactions, including longitudinal traction forces $F_x$ and lateral resistance forces $F_y$ for each wheel. Unlike ideal unicycle models, this approach adopts the SSMR model presented in [5,52] as the environment for training and testing the proposed DRL algorithms. This model offers a more realistic representation of wheel–ground interactions, especially off-road or on uneven terrains commonly found in mining environments, where traction varies dynamically. To account for the nonholonomic restrictions inherent in skid-steer systems, the model explicitly incorporates lateral motion constraints, which are typically neglected in simplified models. This ensures a more accurate representation of the SSMR dynamics, particularly when navigating surfaces with different friction characteristics or when executing turns that may induce lateral skidding. However, model uncertainties still persist in the dynamics associated with the robot model due to the heterogeneous conditions of the navigation terrain. The motion model for the SSMR can be described as follows:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\psi }\\ \dot{v}\\ \dot{\omega }\end{array}\right]& =\left[\begin{array}{c}vcos\theta -\omega sin\theta \\ vsin\theta +\omega cos\theta \\ \omega \\ {\displaystyle \frac{{\beta }_3}{{\beta }_1}}{\omega }^2+{\displaystyle \frac{{\beta }_4}{{\beta }_1}}{v}^2\\ {\displaystyle \frac{{\beta }_5}{{\beta }_2}}v\omega +{\displaystyle \frac{{\beta }_6}{{\beta }_2}}\omega \end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ {\displaystyle \frac{1}{{\beta }_1}}& 0\\ 0& {\displaystyle \frac{1}{{\beta }_2}}\end{array}\right]\left[\begin{array}{c}{u}_v\\ u_{\omega }\end{array}\right],\hfill \\ \hfill & {+\left[{\delta }_x{\delta }_y{\delta }_{\psi }{\delta }_v{\delta }_{\omega }\right]}^T,\hfill \\ & -\dot{x}sin\psi +\dot{y}cos\psi -\left[2a+c-b\right]\dot{\psi }=0\hfill \end{array}$$

(10)

where x, y, and $\psi$ denote the robot’s pose, and v and $\omega$ are linear and angular speeds, respectively. Slippage and disturbances in skidding forces are accounted for in the vector $\delta ={\left[{\delta }_x{\delta }_y{\delta }_{\psi }{\delta }_v{\delta }_{\omega }\right]}^T$, which characterizes disturbances affecting the robot’s motion, including position, orientation, and speed errors. The vector of model parameters $\beta ={\left[{\beta }_1{\beta }_2{\beta }_3{\beta }_4{\beta }_5{\beta }_6\right]}^T$ is derived from the characteristics of the robot chassis, such as mass, inertia, and geometric specifications, obtained from [5]. Lastly, $u_v$ and $u_{\omega }$ represent the control actions applied to the SSMR, namely, traction and turning speeds, respectively. The reader is referred to [5] for further details of the SSMR model.

6. Reinforcement Learning-Based Tracking Control

In the proposed DRL framework, the agent learns an optimal control policy through continuous interaction with the robotic environment. At each time step, it receives state observations $o_t$ and a reward signal $r_t$, which guide the policy update process. The objective is to maximize the cumulative reward over time, ensuring accurate trajectory tracking. The policy is modeled as a neural network that maps observations to control actions, progressively improving its performance through exploration and exploitation. The following sections detail the state observations, reward function, and agent architecture for control.

6.1. State Observation

The environment states consist of the robot’s variables $s={[x,y,\varphi ,v,\omega ]}^T$ from Equation (10), which denote the robot pose and kinematic conditions. At each time step t, the reference trajectory is similarly composed by the coordinate position, orientation, and linear and angular speeds, which are used to compute trajectory errors and ensure coordinated tracking. The tracking errors are given by

$$\begin{array}{cc}\hfill e_t^x& =x_t^r-x_t,e_t^y=y_t^r-y_t,e_t^{\psi }={\psi }_t^r-{\psi }_t,\hfill \\ \hfill e_t^v& =v_t^r-v_t,e_t^{\omega }={\omega }_t^r-{\omega }_t\hfill \end{array}$$

(11)

where ${[x_t,y_t]}^T$ represents the robot’s current position in the global reference frame G and ${[x_t^r,y_t^r]}^T$ denotes the reference trajectory position. Similarly, ${\varphi }_t$ and ${\varphi }_t^r$ indicate the robot’s actual and reference orientation angles, respectively, whereas $v_t,{\omega }_t$ and $v_t^r,{\omega }_t^r$ denote the actual reference linear and angular speeds. To capture these dynamics effectively, the observation vector is defined as $o_t={[x_t,y_t,sin\left({\psi }_t\right),cos\left({\psi }_t\right),v,\omega ,e_t^x,e_t^y,e_t^{\psi },e_t^v,e_t^{\omega }]}^T$, where the error terms $(e_t^x,e_t^y,e_t^{\psi },e_t^v,e_t^{\omega })$ quantify the discrepancies between the robot’s actual and reference states. This formulation ensures that the agent has a comprehensive representation of the system’s state, enabling it to learn adaptive control policies for effective trajectory tracking.

All inputs for the DRL algorithms are normalized within the range $[-1,1]$ considering their maximum values. In particular, after setting the orientation angle of the robot in the range $[-\pi ,\pi ]$, the observations are decomposed into sine and cosine values to avoid angle discontinuities.

6.2. Reward Function Design

The reward function is designed to penalize position, orientation, and linear speed errors while simultaneously discouraging excessive control effort that may result in unstable motion. Specifically, a progressive decay function combined with linear penalization for each error component is proposed, assigning a maximum reward of 1 in the absence of trajectory tracking error and exponentially reducing the reward magnitude as such error increases. To prevent oscillatory motion and overly soft turns of the SSMR, a penalty function based on angular control actions is incorporated. Also, to guide and accelerate the agent’s learning process towards states that yield higher cumulative rewards, potential-based reward shaping is applied [53]. The potential function $\mathrm{\Phi }$ is assumed as the negative of the position error, ensuring that the reward shaping term leads the robot motion towards the reference position by preserving the control policy. Consequently, the total reward function $r_t$ is expressed as follows:

$$\begin{array}{cc}\hfill r_t^{shape}& =\mathrm{\Phi }\left(o_{t+1}\right)-\mathrm{\Phi }\left(o_t\right)\hfill \\ \hfill \mathrm{\Phi }\left(o_t\right)& =(-k_{shape} \times \parallel (e_t^x,e_t^y)\parallel )\hfill \\ \hfill r_t^p& =\exp [-k_x \times |e_t^x| - k_y \times |e_t^y\left|\right]-k_{x,y} \times \parallel (e_t^x,e_t^y)\parallel \hfill \\ \hfill r_t^{\psi }& =\exp [-k_{\psi } \times |e_t^{\psi }\left|\right]-k_{\psi } \times \left|e_t^{\psi }\right|\hfill \\ \hfill r_t^v& =\exp [-k_v \times |e_t^v\left|\right]-k_v \times \left|e_t^v\right|\hfill \\ \hfill r_t^{\omega }& =-k_{\omega } \times \left|u_{\omega }\right|\hfill \\ \hfill r_t^s& =-k_s\sum _{i=1}^4\left|{\displaystyle \frac{v_{x,i-\mathrm{wheel}}-v_{x,\mathrm{chassis}}}{max\left(\right|v_{x,i-\mathrm{wheel}}|,|v_{x,\mathrm{chassis}}\left|\right)+{ϵ}_s}}\right|-k_{\alpha }\sum _{i=1}^4\left|{\displaystyle \frac{v_{y,i-\mathrm{wheel}}}{max\left(\right|v_{x,i-\mathrm{wheel}}|,{ϵ}_{\alpha })}}\right|\hfill \\ \hfill r_t& =r_t^p+r_t^{\psi }+r_t^v+r_t^{\omega }+r_t^s+r_t^{shape}\hfill \end{array}$$

where $k_x,k_y,k_{x,y},k_{\psi },k_v,k_{\omega }$,$k_s$,$k_{\alpha }$, and $k_{shape}$ are scaling parameters that adjust the magnitude of penalties applied to each error component. Particularly, the parameters $k_x,k_y,k_{\psi },$ and $k_v$ are mainly used as exponential decay coefficients, regulating how fast the reward decreases while the tracking error increases. These parameters are heuristically selected to ensure that reward components $r_t^p,r_t^{\psi },$ and $r_t^v$ approach zero for relative small tracking errors. In addition, the parameters $k_{x,y},k_{\psi }$,$k_v$, and $k_{\omega }$ also adjust the linear penalization, ensuring that larger errors receive proportionally greater penalties, further encouraging precise control. The terms $k_s$ and $k_{\alpha }$ are specifically introduced to penalize speed differences between wheel and chassis speed as a way of longitudinal and lateral slip behavior during motion. The first term, associated with $k_s$, penalizes longitudinal slip by comparing the speed of each wheel $v_{x,i-\mathrm{wheel}}$ along the x-axis to the chassis velocity $v_{x,\mathrm{chassis}}$, discouraging significant discrepancies that could lead to inefficient or unstable traction losses. The second term, scaled by $k_{\alpha }$, penalizes lateral slip by evaluating the side speed components (y-axis) of each wheel relative to its forward motion, thus encouraging stable turning trajectories with minimized lateral drift. The penalization of each wheel slip is constrained within a defined range, with tolerances ${ϵ}_s$ and ${ϵ}_{\alpha }$ heuristically tuned to regulate the sensitivity to longitudinal and lateral slip deviations. These slip-related penalties not only aim at enhancing penalization over slippage phenomena but also contribute critically to maintaining traction and directional stability in SSMRs operating on loose or irregular terrains.

6.3. Agent Architecture for Tracking Control

Figure 4 presents the neural network architectures used for the actor and critic networks in the agents, implemented for the proposed DRL techniques. The DDPG technique was implemented by using a deterministic actor network that generates control actions normalized within the range $[-1,1]$ based on control policy $\mu$. Here, the critic network is also defined to assess Q as a function of the pair $(a,o)$. As shown in Figure 4a, the actor and critic work coordinately to approximate the optimal control policy and estimate the value function in DDPG. Similarly, the TD3 algorithm implements an actor-and-critic network scheme, as designed for DDPG. However, as TD3 uses two critic networks to mitigate overestimation bias, the second critic network is a replica of the first one, initialized with different parameters and updated by using a separate target network. On the other hand, the PPO agent learns a stochastic policy that is parametrized by a mean function $\overline{\pi }$ and standard deviation $\sigma \left(s\right)$ to represent a probability distribution over the control actions, as illustrated in Figure 4b. The PPO approach uses a state value function V as the critic network to estimate the expected return for a given observation and constrain possible large policy deviations. Likewise, the SAC algorithm learns a stochastic policy. The SAC actor network follows the same architecture as the PPO actor, while its critic network uses a Q-function approximator similar to the critic structure used in DDPG and TD3.

To address partial observability in the dynamic environment of the mobile robot, recurrent architectures incorporating LSTM networks are integrated into the agents. In particular, Figure 4c illustrates the recurrent deterministic policy network, where LSTM units are introduced into the deterministic actor and Q-function critic networks for DDPG and TD3, enabling temporal information processing. Meanwhile, Figure 4d depicts the recurrent stochastic policy network, where LSTM layers are embedded into the stochastic actor and state value function critic in PPO, along with the stochastic policy and Q-function critic used in SAC. Note that the LSTM layer configuration in the proposed architectures follows a structured criterion to effectively capture immediate sequential dependencies before processing them through dense layers responsible for generating deterministic or stochastic actions. Specifically, in deterministic policies (DDPG and TD3), the LSTM layer is positioned before the final dense layers to ensure that historical state information is incorporated into the control action, enhancing stability in the partially observable environment. For stochastic policies (PPO and SAC), the LSTM layer is placed before computing the probability distribution parameters over actions, allowing the agent to dynamically adapt its policy based on past observations while preserving exploration diversity. The integration of LSTM units at this stage, rather than earlier in the feature extraction process or after action selection, ensures the optimal utilization of sequential dependencies while preventing unnecessary computational complexity or instability. This structured incorporation of recurrent layers was aimed at enhancing the agent’s ability to cope with overall policy robustness in the dynamic robotic environment.

7. Experimental Setup and Results

To evaluate the performance of the proposed trajectory tracking controllers, both simulation and experimental trials were conducted by using the SSMR described in Section 5. The controllers were synthesized by using MATLAB V2024b (MathWorks^®, Natick, MA, USA), leveraging the Reinforcement Learning Toolbox and the Deep Learning Toolbox. The training of the DRL agents was executed on a laptop equipped with an AMD Ryzen 7 4800U processor (AMD^®, Santa Clara, CA, USA), 16 GB of RAM, and an NVIDIA GeForce RTX 3080 Ti graphics card (Nvidia^®, Santa Clara, CA, USA) to accelerate computations. Parallel processing was used through the Parallel Computing Toolbox to optimize efficiency by distributing tasks across multiple cores. While the implementation of the DRL algorithms was performed in MATLAB, the training, testing, and validation of the simulated agents were carried out within the Simulink environment (V24.2). The simulation setup featured a custom-built robotic environment in Simulink, which provides real-time feedback on position, orientation, and linear and angular speeds, with data sampled every 0.1 s. 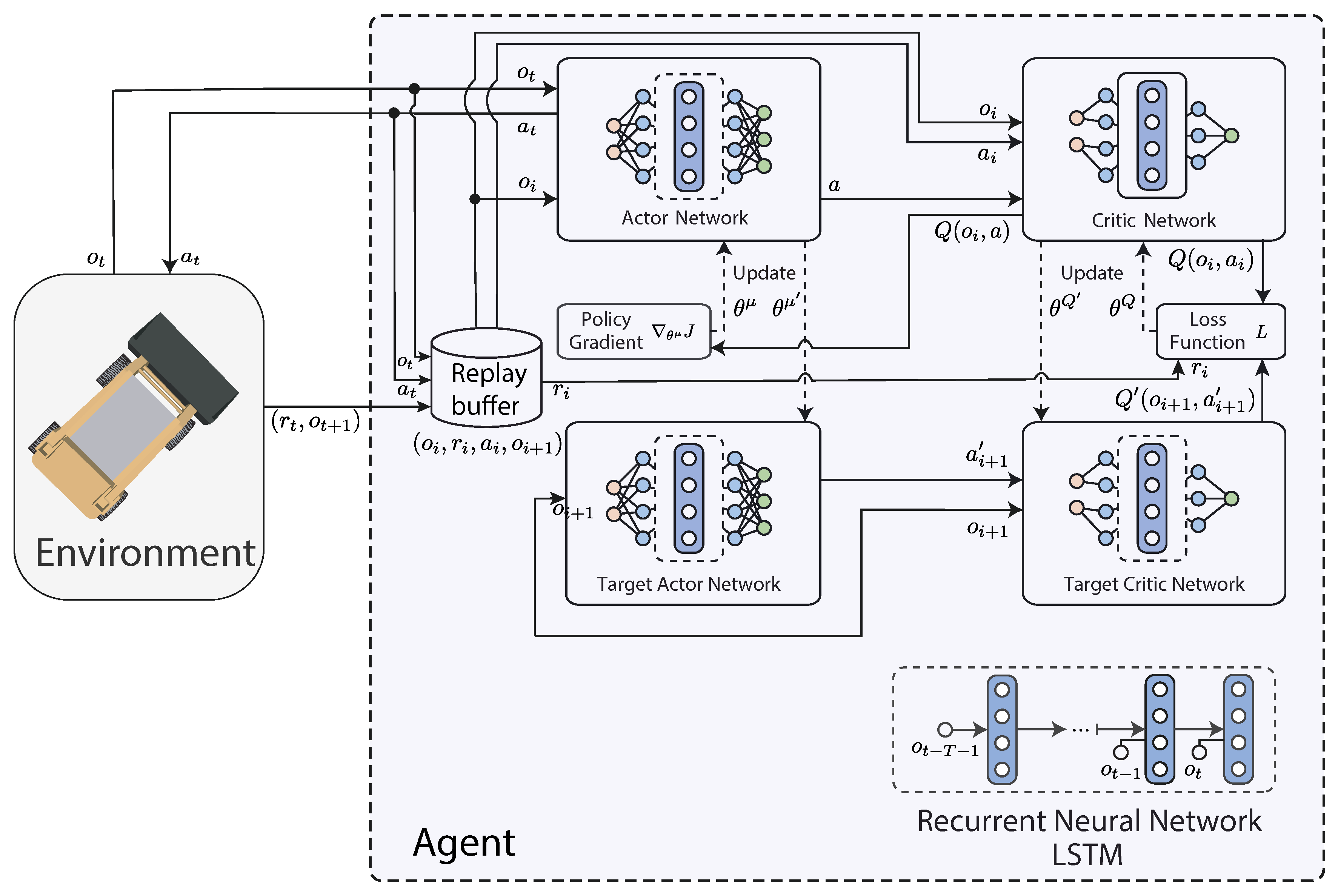Figure 5 presents the implementation diagram of an agent and the simulation environment.

For experimental validation, field trials were also conducted in a realistic mining environment. Specifically, a geographical model of an underground industrial mine was selected as a testbed [54]. The dataset was collected from a real-world mining environment within an active pit division, including a complex underground mine with over 4500 km of drifts, located in Chile’s Libertador General Bernardo O’Higgins Region [55]. The navigation terrain featured irregular surfaces, debris, and surface cavities partially covered by loose soil, generating conditions prone to slip phenomena due to the interaction with vehicle dynamics. Point-cloud maps of narrow tunnels and uneven surfaces with heterogeneous terrain conditions were first acquired by using 3D LiDAR (Riegl®, Horn, Austria), 2D radar (Acumine®, Eveligh, Australia), and stereo cameras (Point Grey Research®, Vancouver, BC, Canada) to define the test environment. The 3D LiDAR scans were manually aligned to estimate the robot pose throughout the traversed tunnels, obtaining a complete projection of the environment, from which a top-view 2D navigation map was extracted [54]. This top-view map was utilized as a testing environment, and a reference trajectory was generated by connecting pre-planned waypoints that fit on the navigation surface, ensuring alignment with spatial constraints. Only 2D point-cloud data were used to maintain a compact and control-relevant state representation suitable for low-level trajectory tracking under terra-mechanical constraints. The use of full 3D perception was intentionally avoided to reduce the state space dimensionality, minimize the computational burden, and ensure the feasibility of real-time policy deployment. This setup enabled a comprehensive evaluation of the proposed trajectory tracking controllers under realistic mining conditions. Figure 6 illustrates the tunnel section where the point-cloud dataset was collected, highlighting the segmented navigation map used to assess the performance of the proposed controllers under test.

7.1. Reference Trajectory Setup

To train the DRL-based controllers, two reference trajectories were considered: (i) a lemniscate-shaped trajectory and (ii) a square-shaped trajectory. First, the lemniscate-shaped trajectory was chosen for its ability to provide continuous and smooth turns, with varying angular and linear speeds throughout its path. This trajectory exposes the training agent to changing speeds to provide the agent a wide range of exploration references, which change dynamically over time. It also enables the agent to learn how to drive diverse turning and traction motion profiles. The lemniscate shape is relevant for mining environments as it simulates conditions of curved and narrow tunnels, which are common in underground mines. The continuous nature of the trajectory allows the agent to practice adapting to gradual changes in direction and speed, similar to the maneuvers required in mining tunnels, which often have irregular geometries and non-linear paths. The lemniscate-shaped trajectory is parameterized as follows:

$$\begin{array}{cc}\hfill x^{\mathrm{ref}}\left({\psi }^{\mathrm{ref}}\right)& =acos\left({\psi }^{\mathrm{ref}}\right)\hfill \\ \hfill y^{\mathrm{ref}}\left({\psi }^{\mathrm{ref}}\right)& =acos\left({\psi }^{\pi \mathrm{ref}}\right)sen\left({\psi }^{\mathrm{ref}}\right),\hfill \end{array}$$

where a is a scaling factor that defines the reference trajectory’s size and ${\psi }^{ref}=2\pi fT$ is the orientation angle for the SSMR, which varies according to a time vector $T\in [0,1]$ and frequency $f=0.075 rad/s$. Additionally, to evaluate the performance of the DRL agents under sharp-turning conditions, a square-shaped trajectory was also employed. The square trajectory, with a side length of $a=5$ m, was parameterized at a constant speed of 0.6 m/s, leading to a total simulation time of 333 s. This trajectory, characterized by abrupt directional changes at its corners, challenges the agent’s ability to respond to sudden orientation shifts, contrasting and complementing with the smoother transitions of the lemniscate trajectory.

7.2. Hyperparameter Configuration and Tuning

Commonly used hyperparameter configurations from related learning architectures for the control of motion dynamics were first selected [38,40]. Subsequently, a broader set of hyperparameters was initialized by using heuristic methods [10,11,13,34] during the exploration phase, ensuring functionality, bias reduction, and stable consistency of the cumulative rewards. Various parameter values were systematically evaluated to enhance training efficiency while maintaining stability in the learning process. Then, building upon these predefined values, the Whale Optimization Algorithm (WOA) [56] was applied to fine-tune the hyperparameters. This algorithm, inspired by the bubble-net feeding behavior of humpback whales, optimizes hyperparameters by iteratively refining candidate solutions based on cumulative training rewards [56]. In this context, each DRL agent is represented as a whale, the optimization objective corresponds to maximizing cumulative rewards, and the agent’s position is defined by the hyperparameter set. Following the approach in [57], eight PPO agents were trained under the same hardware conditions for ten iterations, resulting in a set of hyperparameters common to DDPG with similar values to the previously described heuristic method. This led to the selection of the final hyperparameter configurations for all the proposed DRL algorithms, which are summarized in

Table 3. Experimental hyperparameters used in proposed DRL approaches.

Hyperparameter	PPO	DDPG	TD3	SAC
Actor learning rate ${\alpha }_a$	$5.1\times {10}^{-4}$	$5.1\times {10}^{-4}$	$5.1\times {10}^{-4}$	$5.1\times {10}^{-4}$
Critic learning rate ${\alpha }_c$	$3.3\times {10}^{-4}$	$3.3\times {10}^{-4}$	$3.3\times {10}^{-4}$	$3.3\times {10}^{-4}$
Replay buffer size	${10}^6$	${10}^6$	${10}^6$	${10}^6$
Mini-batch size	-	500	500	500
Discount factor $\gamma$	0.95	0.95	0.95	0.95
Target critic update factor $\tau$	-	0.0095	0.0095	0.0095
Exploration noise standard deviation	-	0.1	0.1	-
Target noise standard deviation	-	-	0.1	-
Clip factor	0.2	-	-	-
GAE factor $\lambda$	0.95	-	-	-
Experience horizon	40	-	-	-
Target entropy $\overline{\mathcal{H}}$	-	-	-	−5
Maximum number of episodes (stop criterion)	3000	3000	3000	3000
Training episodes (Baseline controller)	1577	2255	806	1146
Training episodes (including LSTM)	2341	2269	2394	1843

. Table 3 also contains the number of episodes under which each algorithm required to approach convergence, as well as the maximum number of training episodes in which the algorithms were expected to stop at final stage. Based on the analysis of the slope of the mean cumulative reward, the TD3 and SAC agents exhibited the fastest policy convergence, as they reached convergence in 806 and 1146 episodes, respectively, which was expected due to their improved sample efficiency and stabilization characteristics. It is worth noting that due to computational constraints and the extensive training times required for hyperparameter tuning, the values used in this study may not represent globally optimal solutions but were selected based on the best trajectory tracking control performance within the given motion constraints.

7.3. Cumulative Reward Analysis

The DRL agents were first trained and evaluated on a lemniscate-shaped trajectory, designed to expose the controllers to a wide range of maneuverability conditions. This trajectory includes continuous turns with both positive and negative angular speeds, as well as straight segments with variable linear speeds, ensuring that the agents learn to adapt to different motion dynamics. The training phase focused exclusively on reference trajectory tracking, without external disturbances in order to isolate here their effects on the learned control policy. To reduce over-fitting and enhance generalization, reference trajectory randomization was applied at the beginning of each training episode. This was achieved by scaling and translating the lemniscate trajectory by a random amount of 25% over the predefined trajectory’s parameters while maintaining kinematic constraints. Additionally, initial condition randomization was implemented to improve the controller’s ability to realign with the reference trajectory. Specifically, an incremental value was added to the initial orientation of the SSMR at the start of each episode, with a randomly assigned sign to alter the direction of the offset. This value was progressively increased to prevent instability of learning, averaging ${\displaystyle \frac{\pi }{3600}}$ rads per episode, up to a maximum deviation of ${\displaystyle \frac{2\pi }{3}}$ rads over the training procedure. 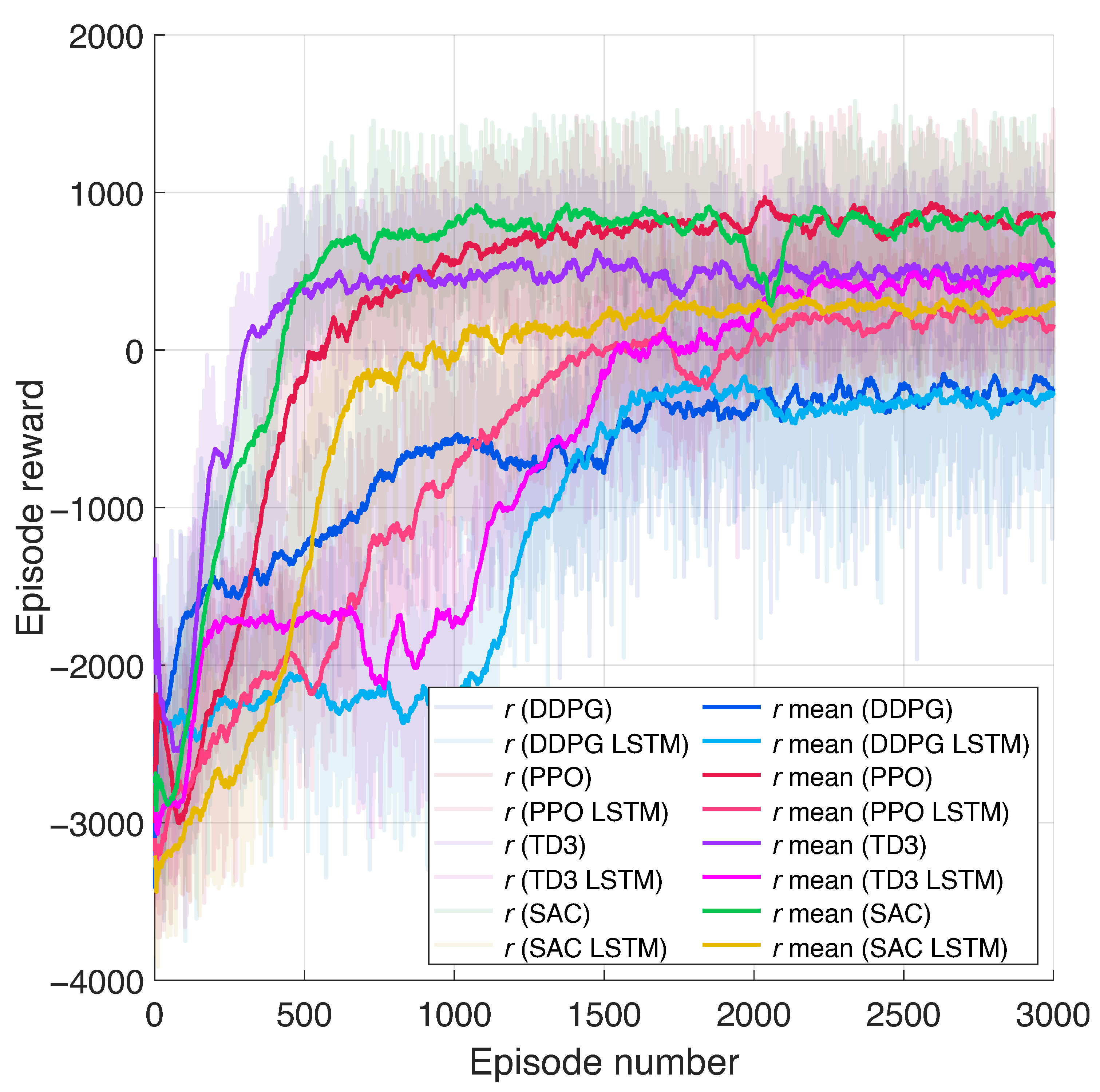Figure 7 depicts a comparison of cumulative rewards obtained after training DDPG, PPO, TD3, SAC, and their corresponding LSTM complementary models. The PPO agent achieved comparable convergence rate with respect to TD3 and SAC, which is explained by a grater exploration degree from its stochastic policy and the reduced dimensionality of the observation space that simplifies the optimal policy search space. Conversely, DDPG depicts the slowest mean reward growth compared with TD3, PPO, and SAC, which may be caused by the overestimation of the Q-function, leading to possible suboptimal local convergence. The LSTM-based approaches required more training episodes to converge on a policy compared with their base models (i.e., DDPG, PPO, TD3, and SAC). Specifically, PPO-LSTM and SAC-LSTM exhibit a lower final mean reward than PPO and SAC, respectively. For PPO-LSTM, the slower convergence could be attributed to the increased dimensionality introduced by historical sequence information, which expands the search space and thus reduces the sample efficiency. In SAC-LSTM, the performance drop may be explained by the increased complexity of entropy temperature optimization, leading to noisier control actions. Similarly, the DDPG-LSTM and TD3-LSTM approaches present comparable mean rewards to their respective base models but at a slower learning rate. The latter is expected, as the recurrent layer introduces additional parameters that require extended training to extract meaningful temporal dependencies from the historical observation sequence.

7.4. Tracking Test in Lemniscate-Type Trajectories

This test involved tracking a lemniscate reference trajectory to evaluate the control performance of the proposed agents using DDPG, PPO, TD3, SAC, and their respective LSTM-based approaches. The simulation results of this test are presented in Figure 8, and the performance metrics in terms of IAE, ISE, ITAE, ITSE, TVu, and cumulative control effort [58] are shown in

Table 4. Control performance assessment of simulated reinforcement learning-based controllers for the tracking of lemniscate-type reference trajectories in SSMRs.

	Position Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	81.78	56.46	97.40	242.09	71.50	70.51	71.60	75.65
ISE	238.10	194.97	258.83	432.64	217.13	207.31	225.60	220.95
ITAE	202,538.56	123,507.48	284,380.18	580,853.68	136,298.86	138,150.30	209,967.39	185,991.88
ITSE	10,377.11	8162.27	12,033.01	18,999.91	8526.07	10,163.42	10,435.81	8025.02
	Orientation Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	0.037	0.042	0.126	2.175	0.053	0.036	0.447	0.438
ISE	4.37	4.44	8.49	33.95	3.71	4.51	16.27	15.13
ITAE	142.88	87.88	314.58	2979.48	157.12	61.38	1621.39	1106.38
ITSE	228.99	176.80	369.31	1198.27	144.37	172.51	818.69	639.88
	Linear Speed Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	0.122	0.065	0.135	3.393	0.136	0.118	0.125	3.792
ISE	1.65	2.48	2.61	43.43	1.97	3.08	2.12	45.31
ITAE	8.09	13.22	22.26	7811.08	5.91	24.79	10.80	8360.84
ITSE	56.48	79.11	92.11	1807.02	55.31	98.97	67.35	1863.66
	Control Action Total Variation
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
v	2.46	1.74	11.42	279.87	2.51	1.91	5.77	180.65
$\omega$	2.08	2.06	63.66	444.78	2.37	1.96	25.96	423.83
TVu	3.38	2.84	66.82	574.02	3.62	2.90	27.64	494.89

. As illustrated in Figure 8, all DRL approaches presented similar trajectory tracking responses, except for PPO-LSTM and SAC-LSTM, under which the orientation and the lateral and longitudinal tracking errors were eventually deviated, as depicted in Figure 8c–f. Similarly, in Figure 8c,e, the lateral and longitudinal tracking errors were close to zero for most approaches, including DDPG, DDPG-LSTM, PPO, PPO-LSTM, TD3, and TD3-LSTM. However, among these, PPO was the only agent that achieved lower trajectory tracking errors compared with its LSTM-enhanced counterpart (i.e., PPO-LSTM), which can be attributed to its increased stochasticity relative to the other evaluated approaches. This result also suggests that the PPO agent prioritized minimizing orientation and linear speed errors over positional error, potentially favoring stability in trajectory tracking at the expense of accurate robot position. On the other hand, DDPG-LSTM achieved the lowest positional error across all agents, with reductions of 21% in the IAE and 10% in the ISE compared with TD3, which had the lowest positional error metrics among the base models. Such result in control performance can be attributed to the ability of LSTM-enhanced DDPG to retain past trajectory information, improving position tracking accuracy. In contrast, TD3-LSTM and SAC-LSTM provided only marginal improvements in tracking performance compared with their respective base models. Their IAE metrics showed minor differences, with TD3-LSTM improving by only 1.38% and SAC-LSTM increasing by 5.6% compared with SAC. Additionally, TD3-LSTM exhibited a 4.5% reduction in ISE relative to TD3, whereas SAC-LSTM had a slight 2.2% decrease in ISE compared with SAC.

Table 4 highlights differences in orientation and linear speed errors across the tested agents. For instance, PPO-LSTM exhibits the highest orientation and linear speed errors, with IAE values of 2.175 and 3.393, respectively, which are considerably higher than those of the other agents. In contrast, TD3-LSTM achieves the lowest orientation error, with an IAE of 0.036, while DDPG-LSTM demonstrates the best linear speed tracking performance, obtaining the lowest IAE of 0.065. Examining such error metrics, TD3-LSTM minimizes orientation error in terms of IAE and ITAE, whereas TD3 achieves lower ISE and ITSE values with respect to all test approaches. This behavior is also shown in Figure 8d, where TD3 maintains near-zero orientation error except for two brief deviations, whereas TD3-LSTM shows a more stable yet slightly less accurate response. Furthermore, the inclusion of LSTM layers in DDPG-LSTM and SAC-LSTM appears to contribute to lower ITAE and ITSE values for position and orientation error compared with their non-LSTM counterparts. A possible explanation for this is that LSTM’s memory mechanism aids to accumulate and mitigate orientation deviations over time, leading to corrective control actions that reduce long-term tracking errors. However, the reduced performance of PPO-LSTM may stem from the interaction between its policy update strategy and the LSTM memory dynamics, potentially leading to error accumulation rather than attenuation. The control effort exerted by each controller is also quantified in Table 4. Deterministic policy-based controllers exhibited lower control effort, with DDPG and TD3 attaining TVu values of 3.38 and 3.62, respectively. In contrast, stochastic policy-based controllers such as SAC and PPO showed significantly higher control variability, with TVu values of 27.64 and 66.82, respectively, indicating more abrupt control actions. The incorporation of LSTM into the deterministic controllers yielded further reductions in control effort. For instance, DDPG-LSTM and TD3-LSTM reduced TVu by approximately 16% and 20%, respectively, relative to their non-recurrent counterparts. This further supports that LSTM’s memory mechanism contributed to stable corrective actions. However, recurrent stochastic policies exerted a significantly higher control effort, as both PPO-LSTM and SAC-LSTM achieved TVu values of 574.02 and 494.89, respectively, indicating that the inclusion of LSTM may result in increased stochasticity. In general, these results suggest that LSTM layers store and integrate orientation error over time, enabling control actions that achieve lower tracking errors compared with those used by base controllers, as illustrated in the control actions depicted in Figure 8b.

7.5. Tracking Test in Square-Type Trajectory

This test assessed the control performance of DDPG, PPO, TD3, SAC, and their LSTM-based variants while tracking a square-type reference trajectory. The simulation results are depicted in Figure 9, whereas performance metrics (IAE, ISE, ITAE, ITSE, and TVu [58]) are summarized in

Table 5. The control performance assessment of simulated reinforcement learning-based controllers for the tracking of square-type reference trajectories in SSMRs.

	Position Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	202.41	202.49	287.94	73.64	191.47	150.46	192.34	120.87
ISE	230.87	233.17	250.57	130.26	224.44	206.78	222.60	184.81
ITAE	119,410.28	119,991.55	216,329.83	48,484.46	114,600.16	86,749.49	129,734.90	69,540.66
ITSE	4896.98	4910.52	5773.44	2624.34	4754.60	4222.31	4819.21	3784.80
	Orientation Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	76.66	80.13	83.22	69.34	76.15	81.99	79.78	77.70
ISE	74.89	78.89	91.93	88.13	75.63	81.00	84.34	80.36
ITAE	26,691.86	28,025.94	31,462.09	24,237.61	26,463.52	29,569.43	28,842.37	27,339.03
ITSE	1272.98	1394.08	1632.97	1475.18	1283.04	1445.09	1494.69	1398.08
	Linear Speed Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	0.48	0.58	0.79	1.99	0.56	0.73	0.76	1.58
ISE	3.70	5.61	9.70	18.56	5.82	9.62	10.47	15.16
ITAE	8.40	35.40	92.91	625.97	19.41	78.82	120.80	330.47
ITSE	40.50	73.63	132.13	297.92	68.25	135.32	160.46	226.01
	Control Action Total Variation
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
v [m/s]	0.73	0.61	3.76	72.37	0.95	0.70	1.87	42.72
$\omega$ [rad/s]	4.92	5.91	18.60	150.31	5.45	5.37	12.79	142.62
TVu	5.38	6.22	19.96	187.30	5.92	5.72	13.36	161.03

. Figure 9a depicts a significant error margin while tracking the reference trajectory with DDPG, PPO, TD3, and SAC, whereas the tracked trajectory for the LSTM-based strategies closely approach the reference with minimal positional drift. Except for the baseline DRL approaches, the LSTM-based strategies exhibit minimal lateral, orientation, and speed tracking errors along the trials, as shown in Figure 9c–f. This reinforces that the proposed LSTM-based agents prioritize maintaining orientation and linear speed accuracy beyond minimizing robot position deviations to effectively track the reference trajectory. Moreover, due to the controller’s limited turning capability, turns are not completed instantaneously, causing the agent to deviate from the trajectory once the turn is executed. Agents improved positional tracking based on the trade-off between positional errors and both linear speed and orientation accuracy. Actually, unlike baseline DRL approaches, the system response with LSTM-based methods can be attributed to the added LSTM layers that noticed and memorized changes for each observed orientation and position tracking error, influencing the learning process with improved rewards for each episode. Then, such rewards prioritized reducing trajectory tracking over orientation errors. For DDPG and DDPG-LSTM, the reduced positional tracking performance and the lack of LSTM improvement on this metric may stem from these agents overestimating the value of states with lower linear speed and orientation error, thereby prioritizing these variables over positional accuracy.

The PPO-LSTM agent demonstrated improved control performance of positional tracking against the other test controllers, achieving the lowest IAE, ISE, ITAE, and ITSE metrics, as shown in Table 5. Specifically, PPO-LSTM reduced the IAE by 74% compared with PPO, while TD3-LSTM and SAC-LSTM achieved reductions of 21% and 37%, respectively, relative to their non-LSTM counterparts. While DDPG and DDPG-LSTM exhibited similar performance in positional tracking, their tracking errors were higher than those of PPO-LSTM. For the orientation error, PPO-LSTM achieved the lowest IAE (69.34) and ITAE (24,237.61), exhibiting again its effectiveness in maintaining accurate orientation control. Despite each approach presenting a similar orientation error in terms of the ISE, DDPG performed the best among all proposed approaches, obtaining an ISE of around 74.89 and an ITSE of about 1272.98. This suggests that while PPO-LSTM minimized accumulated orientation errors over time, DDPG was more effective in reducing large deviations. In terms of linear speed error, DDPG consistently outperformed all other agents across all metrics, achieving the lowest IAE (0.48), ISE (3.70), ITAE (8.40), and ITSE (40.50). Moreover, the LSTM-enhanced versions of all models introduced higher linear speed errors in the trials, indicating that the added memory component may generate slower adaptation to speed changes. Lastly, regarding the control effort and its variation, DDPG achieved the lowest overall control effort, with a TVu of 5.38, followed closely by TD3 (5.92), suggesting that both deterministic controllers applied smoother control actions. The integration of LSTM slightly increased control effort for DDPG-LSTM (TVu = 6.22) but yielded a marginal reduction for TD3-LSTM (TVu = 5.72) compared with its base model. Conversely, PPO-LSTM and SAC-LSTM exhibited the highest TVu values, reaching 187.30 and 161.03, respectively, indicating high variations in control actions during control execution. These results show that while LSTM integration benefits stochastic policies in terms of tracking accuracy, it also significantly amplifies control action variability, potentially compromising smooth motion. Overall, PPO-LSTM emerged as the best control approach for position and orientation tracking, while DDPG excelled at minimizing linear speed errors and ensuring the smoothest control actions, especially at sharp corners in the square reference trajectory. The results highlight the effectiveness of integrating LSTM for stochastic policy agents, but its impact on deterministic agents led to an increase in errors in linear speed tracking and control action smoothness, suggesting that the added memory component may have hindered rapid adaptation to dynamic changes in the robot.

7.6. Tracking Test in Mining Environment

This test involves tracking a trajectory composed of pre-planned waypoints, designed to align with maneuverability constraints in a mining environment. The reference trajectory was obtained from the underground mine map presented in Section 7.1, with trials starting at waypoint A, passing by B, and concluding at waypoint C, as illustrated in Figure 10. The experimental results of tracking this trajectory within the underground mine are shown in Figure 10, while quantitative control performance metrics are detailed in

Table 6. Performance metrics for evaluating reinforcement learning-based controllers in tracking reference trajectories for SSMRs in underground mining scenarios.

	Position Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	$1.32\times {10}^5$	$1.65\times {10}^5$	$1.99\times {10}^5$	$2.05\times {10}^5$	$1.14\times {10}^5$	80,751.31	$3.68\times {10}^5$	$1.16\times {10}^5$
ISE	19,762.38	22,754.45	24,896.74	23,961.66	19,162.28	15,543.57	31,968.92	18,481.96
ITAE	$8.37\times {10}^9$	$7.85\times {10}^9$	$9.57\times {10}^9$	$1.23\times {10}^{10}$	$5.31\times {10}^9$	$\mathbf{4}.\mathbf{94}\times {\mathbf{10}}^{\mathbf{9}}$	$2.47\times {10}^{10}$	$7.35\times {10}^9$
ITSE	$4.30\times {10}^6$	$4.46\times {10}^6$	$3.68\times {10}^6$	$5.22\times {10}^6$	$3.69\times {10}^6$	$\mathbf{3}.\mathbf{32}\times {\mathbf{10}}^{\mathbf{6}}$	$7.17\times {10}^6$	$4.03\times {10}^6$
	Orientation Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	167.44	125.41	370.88	329.46	132.32	124.92	347.81	139.57
ISE	661.37	532.26	998.42	935.58	585.71	560.71	1007.60	587.43
ITAE	$1.25\times {10}^7$	$1.00\times {10}^7$	$2.54\times {10}^7$	$2.37\times {10}^7$	$9.53\times {10}^6$	$\mathbf{8}.\mathbf{55}\times {\mathbf{10}}^{\mathbf{6}}$	$2.09\times {10}^7$	$1.02\times {10}^7$
ITSE	$1.42\times {10}^5$	$\mathbf{1}.\mathbf{15}\times {\mathbf{10}}^{\mathbf{5}}$	$2.09\times {10}^5$	$2.02\times {10}^5$	$1.20\times {10}^5$	$1.18\times {10}^5$	$2.10\times {10}^5$	$1.23\times {10}^5$
	Linear Speed Error
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
IAE	1.15	15.40	1.38	18.39	2.22	5.90	1.17	18.74
ISE	53.52	206.93	61.16	212.38	67.46	125.47	52.24	209.45
ITAE	68,677.78	$1.03\times {10}^6$	66,502.34	$7.41\times {10}^5$	$1.80\times {10}^5$	$3.99\times {10}^5$	41,967.74	$8.69\times {10}^5$
ITSE	10,988.05	43,595.70	11,666.33	37,410.36	16,649.61	26,655.41	9040.31	38,351.87
	Control Action Total Variation
	DDPG	DDPG-LSTM	PPO	PPO-LSTM	TD3	TD3-LSTM	SAC	SAC-LSTM
v	0.38	0.48	59.02	1261.06	0.30	0.41	25.68	837.36
$\omega$	2.61	3.02	293.98	1983.14	2.74	2.26	126.79	1810.06
TVu	2.86	3.28	309.02	2550.60	2.87	2.57	133.57	2140.43

. Unlike previous tests, it is noticed in all test control approaches that the orientation error in Figure 10d initially increased at the very beginning of the trials at waypoint A due to changes in the initial pose conditions. However, as the agent began executing turning actions, the orientation error subsequently decreased. This degradation at the start of the trials may be attributed to over-fitting effects, as the trained agents tended to initiate their trajectories with a specific turning action learned during the training phase. This behavior suggests that the models developed a dependency on specific initial conditions, impacting their ability to generalize to initial conditions of new scenarios. Furthermore, during waypoint transitions, particularly at point B, abrupt turning maneuvers exposed significant differences in controller robustness. PPO- and SAC-based agents exhibited high instantaneous control inputs, leading to unstable angular responses and trajectory overshoots. These cases demonstrate limited generalization to tight angular transitions, a critical failure mode for underground navigation. Similarly, turning control actions in DDPG, PPO, PPO-LSTM, SAC, and SAC experienced abrupt compensation while turning at point B in Figure 10. Beyond the demanding turning actions, the new kinematic conditions for turning were not accurately met. Nonetheless, this issue was mitigated by improving the initial sampling strategy during the agent’s training process.

Table 6 provides a comprehensive comparison of tracking performance across the test DRL controllers. In terms of linear speed error, the lowest IAE was obtained by using the DDPG agent, achieving a value of 1.15, followed closely by SAC with 1.17, while PPO demonstrated slightly higher tracking errors, with an IAE of 1.38. Such results are consistent with the linear speed error trend, where SAC achieved the lowest ISE value (i.e., 52.24), outperforming the other test controllers. This suggests that SAC maintains stable speed control, reducing abrupt changes in the trajectory. Regarding position error metrics, TD3-LSTM achieved the lowest values across multiple metrics, including the IAE (i.e., 80,751.31) and ISE (i.e., 15,543.57), outperforming other LSTM-based models such as SAC-LSTM and DDPG-LSTM (see Table 6). This performance can be explained by TD3’s ability to mitigate overestimation bias, leading to more stable policy updates, while the LSTM layers enhance temporal information processing, allowing for better adaptation to the dynamic changes in the reference trajectory. Regarding the orientation error, TD3-LSTM also showed improved performance, attaining the lowest IAE (124.92) and ITAE ($8.55\times {10}^6$) and validating the advantage of memory-based architectures in handling trajectory deviations. In contrast, PPO exhibited the highest orientation error values, with an IAE of 370.88, indicating less stable heading control when navigating the underground mine environment.

In terms of deployment limitations, PPO-LSTM and SAC-LSTM exhibited inconsistent alignment in narrow corridors such as point B, where they occasionally triggered unexpected stops due to unsafe or overly conservative control commands. These issues were not anticipated during the simulation evaluations, underscoring the need to incorporate exteroceptive information into both the learning process and the reward scheme. These results also highlight the need to expose the agents to a broader range of environmental conditions during training, including the adoption of domain randomization strategies to improve policy generalization. Regarding control action smoothness, TD3 demonstrated the lowest variation in linear speed (i.e., 0.30), while TD3-LSTM minimized the variation in angular speed (i.e., 2.26). These results suggest that TD3 and its LSTM-enhanced counterpart generate smoother control actions compared with the other test controllers, reducing oscillations and improving trajectory adherence. TD3-LSTM showed the lowest TVu of 2.57, validating its ability to generate continuous control actions and mitigate oscillatory behavior in the physical actuators of the SSMR. Moreover, the results indicate that TD3-LSTM offers the best overall performance in terms of position and orientation tracking due to its ability to learn more stable policies while incorporating past observations. Conversely, while SAC and DDPG exhibit suitable control performance in linear speed control, they hardly generalize as effectively in position and orientation tracking, particularly in complex environments such as those found in underground mines.

7.7. Robustness Test Under Terrain Disturbances

The proposed controllers were tested for trajectory tracking on lemniscate and square reference trajectories under terrain disturbances to evaluate their robust control performance. The disturbances, unknown for the agents, involved transitioning from flat terrain (where no drifting occurs) to low-friction and uneven terrain, which leads to slip phenomena commonly encountered in mining environments. First, the disturbance conditions occurred across terrain transitions while tracking a lemniscate reference trajectory, specifically at time instants 100.6 [s] and 680.4 [s] of the trials. Figure 11 presents tracking results for the lemniscate trajectory, highlighting capabilities of tracking error regulation in the tested DRL controllers when rejecting external disturbances (see Figure 11c,e). At the first disturbance instant, the system response reincorporated each controller to the reference trajectory; thus, the linear speed, orientation, and lateral error reached near-zero values (see Figure 11d–f). Among the tested controllers, the proposed DDPG and TD3 approaches, along with their LSTM-enhanced variants, exhibited improved disturbance rejection against PPO and SAC, maintaining low tracking errors throughout terrain transition scenarios. In contrast, PPO-LSTM and SAC-LSTM showed increased tracking errors after the disturbance instants and exhibited slower convergence in reducing steady-state errors, leading to residual offsets throughout the trial. This suggests that while PPO combined with LSTM demonstrated adaptability by gradually reducing error offsets over time, its ability to reject disturbances was lower compared with that of the DRL baseline methods, which prioritize policy refinement through continuous value estimation. Moreover, despite all disturbance occurrences, all tested controllers successfully maintained low and close-to-zero orientation and speed errors (see Figure 11d,f), enabling the SSMR to align with the reference trajectory and recovering the reference speeds. Unlike DDPG-LSTM, TD3-LSTM, and PPO-LSTM, baseline DRL controllers such as PPO and SAC exhibited persistent lateral position errors after each disturbance event, primarily due to unobserved dynamics arising from unmodeled terra-mechanical variations, as shown in Figure 11e. Such disturbances, omitted during training, may have induced policy prioritization biases, leading the learned DRL controllers to favor orientation and linear speed corrections over accurate lateral position tracking. This highlights the need for a more comprehensive domain randomization strategy that accounts for the inherently random and heterogeneous terrain characteristics, ensuring further exploration across diverse terra-mechanical conditions.

The results of tracking for the square-type trajectory under terrain disturbances are presented in Figure 12, with disturbances occurring at approximately 12.6 [s] and 12.8 [s]. The agents show robust control performance, maintaining the trajectory orientation, as shown in Figure 12d, and reference speed, as depicted in Figure 12f. After the first disturbance, all DRL agents were capable of correcting for the external disturbances, thus showing orientation and linear speed errors close to the origin. However, the positional error was not fully corrected by the PPO agent, where the SSMR aimed to returning to the reference trajectory but maintained large steady-state tracking errors, as shown in Figure 12c,e. A similar transient response was observed after the second disturbance, where orientation and linear speed errors were again reduced to near-zero values. Longitudinal positional errors were effectively mitigated across all proposed controllers except for the one based on PPO, which initially counteracted disturbances but exhibited a continuous decline in robust control performance. Overall, these results indicate that while LSTM integration enhances trajectory tracking for most DRL agents, PPO demonstrated deficient robustness in the presence of disturbances.

It is worth noting that the training of the DRL controllers was conducted under transitory slip conditions, without incorporating prior physical information about the terrain type, such as grass, pavement, or gravel. Consequently, the learning process did not exploit any terrain classification cues but relied exclusively on observable states, including position, orientation, speed, and their respective tracking errors. Although the experimental validation was limited to a single robot configuration and a particular terrain disturbance scenario, the proposed methodology is not inherently constrained to this setup. The underlying control policy is observation-driven and model-free, allowing for potential transferability to other robotic platforms or unstructured environments exhibiting similar observation–action relationships. Nonetheless, such generalization should be approached under test conditions. Effective transfer would require that key aspects of the wheel–terrain interaction—such as friction and slip dynamics—be implicitly captured within the observation space and appropriately represented during training.

7.8. Test on Robustness Against Model Parameters

To assess the robustness of DRL agents under varying SSMR conditions, the proposed controllers were tested by using a different set of dynamic model parameters for varying robot dynamics. In this test, the parameters ${\beta }_1$ and ${\beta }_2$ were both gradually set to 5% increments, reaching a total variation of 25% from their original values, as defined in the SSMR model in Equation (10) and detailed in [3]. Such parameters were selected since they represent direct influence on traction and turning speeds. The results of this test for the maximum parameter variation of 25% on the lemniscate trajectory are presented in Figure 13. According to Figure 13a, the proposed DRL controllers successfully led the SSMR along the reference trajectory, maintaining reasonable tracking accuracy. However, lateral and longitudinal tracking errors progressively increased over the trial, indicating that the controllers struggled to generalize to entirely unobserved variations in system dynamics, as such variations were not explicitly included in the training process. While the control performance remained adaptable to moderate parameter variations, the tracking error increase became significant as the parameter variations approached their maximum tested value. In particular, the SSMR deviation from the reference position suggests that the proposed controllers could present potential over-fitting, even when the training process included varying robot dynamics. Comparing all tested DRL controllers, the LSTM-based DRL agents exhibited improved adaptability to dynamic variations by generating control actions that suitably accommodated model parameter changes over time. The integration of historical observations in LSTM-based controllers prevented abrupt policy changes, resulting in smoother and more stable trajectory tracking performance compared with the baseline DRL controllers. On the other hand, in Figure 13f, the DDPG and TD3 algorithms exhibited the lowest linear speed errors, followed by PPO and SAC, whereas DDPG-LSTM, TD3-LSTM, PPO-LSTM, and SAC-LSTM present higher orientation and linear speed errors with respect to the other controllers. By analyzing Figure 13d, it can also be observed that deterministic policy agents (i.e., DDPG and TD3) achieved lower orientation errors than their stochastic counterparts (i.e., PPO and SAC). This outcome aligns with the expectation that deterministic controllers can achieve more precise control in environments with parameter stability, whereas stochastic methods may introduce exploration noise that degrades orientation accuracy under dynamic variations. In the case of the on-policy recurrent agent (PPO-LSTM), an improvement in adaptability was observed compared with its base model, PPO. This behavior suggests that the use of the state value function as a critic prevents the over-fitting observed in off-policy recurrent cases. Since the critic network does not receive the agent’s action as an input, it is less likely to overlearn a linear relationship between linear speed error and traction speed control action, preserving adaptability to changing model parameters.

The control performance of the proposed DRL controllers under model parameter variations on a squared-type trajectory is presented in Figure 14. The turning response of the DRL agents remained qualitatively similar to that observed in trials without parameter variations. However, during cornering maneuvers, the agents exhibited overshoot in the turning response, leading to increased transient responses. The most significant deviations were observed in the SAC-LSTM and PPO-LSTM agents, as well as in PPO, TD3-LSTM, and DDPG-LSTM throughout the final turn of the trajectory. Figure 14f presents the linear speed error, where the TD3 agent achieved the lowest speed error values, followed by SAC and DDPG, PPO-LSTM, PPO, DDPG-LSTM, TD3-LSTM, and SAC-LSTM. Furthermore, the PPO-LSTM agent improved its positional speed error compared with the baseline PPO agent, as presented in Figure 14c,e. These results are consistent with the previous robustness test, reinforcing the observation that LSTM-based on-policy agents exhibit improved adaptability to model parameter variations by leveraging historical state information, further confirming the role of the policy architecture in adapting to system dynamics. Deterministic policy agents (DDPG and TD3) maintained better orientation stability than their stochastic counterparts (PPO and SAC), particularly in turns where rapid control adjustments were required. However, recurrent architectures (LSTM-based agents) demonstrated rougher control policies, as they presented increased control effort on turning maneuvers. While recurrent stochastic agents are expected to present a noisier response, as discussed on Section 7.3, the decrease observed in deterministic agents may be attributed to the over-fitting of the training conditions, as explained by the lemniscate-type trajectory test under model parameter variations. This suggest that LSTM-based agents’ performance on high-precision tasks such as corner turning maneuvers may require further optimization.

8. Conclusions

In this work, Deep Reinforcement Learning (DRL) techniques integrated with Long Short-Term Memory strategies were presented and validated for robust trajectory tracking control of skid-steer mobile robots (SSMRs) operating in mining environments with uncertain terrain conditions. Several DRL algorithms were assessed and compared each other, including Proximal Policy Optimization (PPO), Deep Deterministic Policy Gradient (DDPG), Twin Delayed DDPG (TD3), and Soft Actor–Critic (SAC), alongside their recurrent LSTM-enhanced counterparts, to address partial observability in real-world navigation scenarios. The proposed controllers were trained and tested on various reference trajectories, first in simulation scenarios and subsequently in a field experimental setup of mining environments. In general, performance metrics demonstrated that LSTM-based controllers significantly improved trajectory tracking accuracy, reducing the ISE by 10%, 74%, 21%, and 37% for DDPG-LSTM, PPO-LSTM, TD3-LSTM, and SAC-LSTM, respectively, compared with their non-recurrent counterparts. Furthermore, DDPG-LSTM and TD3-LSTM achieved the lowest orientation errors (in terms of the IAE, ISE and ITAE) and linear speed errors (in terms of the IAE and ITAE), outperforming baseline DRL controllers. These results highlight the effectiveness of integrating LSTM into DRL-based controllers, enabling them to leverage temporal dependencies and infer unobservable states, thereby enhancing robustness against terrain disturbances and model parameter variations. In addition, recurrent architectures improved their non-recurrent counterparts in generalizing to unobserved trajectories, suggesting that incorporating memory mechanisms enhances adaptability to dynamic and unstructured environments. However, further evaluation revealed limitations in the LSTM-based controllers, particularly within on-policy algorithms (PPO-LSTM), where a reduction in adaptability to varying model parameters and terrain disturbances was observed. This finding indicated the potential over-fitting of recurrent networks when subjected to significant model variations, emphasizing the need for improved regularization techniques or hybrid learning strategies to further enhance generalization capabilities. Future work will explore the integration of a more detailed terra-mechanical model with varying friction and slip conditions to enable a more realistic assessment of DRL controllers in adverse terrain scenarios. A formal robust control stability analysis of the proposed trajectory tracking controllers is also required in order to evaluate their practical feasibility for real-world deployment in autonomous mining operations. Furthermore, ongoing work aims to evaluate performance under heterogeneous terrain conditions and varying robot morphologies to assess the robustness and adaptability of the proposed control methodology across diverse operational scenarios.