Robotic Rehabilitation Through Multilateral Shared Control Architecture

Abstract

The shortage of therapists required for the rehabilitation of stroke patients, together with the patients’ lack of motivation in regular therapy, creates the need for a robotic rehabilitation platform. While studies on shared control architectures are present in the literature as a means of training, state-of-the-art training systems involve a complex architecture and, moreover, have notable performance limitations. In this paper, a simplified training architecture is proposed that is particularly targeted for rehabilitation and also adds missing features, such as complete force feedback, enhanced learning rate, and dynamic monitoring of the patient’s performance. In addition to the novel architecture, the design of controllers to ensure system stability is presented. These controllers are analytically shown to meet the performance objectives and maintain the system’s passivity. An experimental setup is built to test the architecture and the controllers. A comparison with the state-of-the-art methods is also performed to demonstrate the superiority of the proposed method. It is further demonstrated that the proposed architecture facilitates correcting the inaccurate frequencies at which the patient might operate. This was achieved by defining attribute-wise individual recovery factors for the patient.

1. Introduction

Neurological conditions such as stroke, multiple sclerosis, and Parkinson’s are a leading cause of long-term disability, with more than 795,000 Americans affected by stroke annually [1]. Upper extremity hemiparesis, weakness of one side of the body, is one of the most common impairments, found in approximately 70% of individuals after such neurological conditions [2,3]. The severity of paresis is the primary determinant of functional loss; therefore, rehabilitation is a necessary means to recover motor skills and associated functional skills [4]. Although high dosage, high intensity, and high repetitions of therapy are all recommended, many patients do not receive the recommended amount of rehabilitation for reasons such as shortage of therapists and lack of motivation levels [5].

To accommodate these limitations, a robotic rehabilitation platform is proposed in this paper. In a systematic review of the literature, robotic rehabilitation for motor and higher cortical deficits appears to be as effective as in-person therapies [6]. The outcomes of robotic rehabilitation in clinical studies with patients after stroke are detailed in [7,8]. A study on the cost-effectiveness of incorporating robotic platforms in rehabilitation can be seen in [9]. An overall systematic review, particularly focused on physical rehabilitation and its incorporation of robotic platforms, is presented in [10].

The proposed platform first calibrates the patient using a hand-writing simulator, since hand-writing exercise is a tool commonly used by therapists for recovering upper extremity motions. Based on the assessment of the patient’s initial performance in the hand-writing exercise, he/she is taken to a tele-training session in which there are virtual environments to perform daily tasks and in which the patient also receives assistance from the therapist precisely as per his/her need.

For the proposed robotic rehabilitation platform, a multilateral leader–follower architecture with multiple leaders and a single follower is adopted. In typical single leader–single follower systems, the leader robot is handled by a human who intends to manipulate objects in an environment. A follower robot, which replicates the motion of the leader robot, is placed in the environment, providing force feedback to the leader so that the human undergoes a “transparent” experience of touching the object [11,12].

Extending the leader–follower technology to dual-leader–single-follower (thus moving from bilateral to multilateral) is known for its ability to facilitate training [13,14], amongst other applications. In the context of rehabilitation, both the therapist and the patient are provided with one leader robot each, and a virtual follower robot is placed in a virtual environment. The therapist makes motions by which the patient’s motor skills will be enhanced, and the patient attempts to match the trajectory of the therapist while looking at the visual feedback on a screen. The virtual robot’s position is controlled on a shared basis by the two leader robots. This approach is technically called “Dual User Shared Control (DUSC)”. The virtual robot sends force feedback to both of the leader robots. Thus, both the therapist and the patient will be able to see the virtual robot interacting with the environment on screen and will also receive force feedback from the virtual environment.

Researchers provide DUSC signal flow architectures for similar training purposes, like an expert surgeon training a novice and training in car driving. The need for a novel architecture/controller and the specific objectives of this paper can be appreciated by studying the limitations in state-of-the-art DUSC architectures.

2. Problem Formulation and Literature Review

One of the first works that introduced realizing a haptic training system was by [15]. By controlling force in common mode and position in differential mode, it was possible to alter the trainer’s assistive forces according to the trainee’s recovery. However, a systematic architecture as well as standard performance objectives for DUSC came up only with [16]. In this work, a six-channel architecture was proposed, as shown in Figure 1.

Here, $V$ and $F$ refer to the velocity and force; suffixes $h1$, $h2,$ and $e$ correspond to Human 1 (trainer), Human 2 (trainee), and environment; and $\alpha$ is the dominance factor. The following are the limitations of this architecture:

(i)

Each human operator receives only partial force feedback, thus eclipsing her/his realistic experience.

(ii)

Transmitting both velocities and forces across all six channels makes it a complex implementation.

(iii)

The force exchange between the two leaders is not mandatory. Each human needs to feel the dynamics of the others in cooperative task performance but not necessarily for the training application.

To overcome some of these limitations, it was proposed in [17] that the follower is commanded based on the force inputs of the operators, while the feedback is experienced through the position itself. Although the architecture is now much simplified, it faces some major limitations, as mentioned below.

(i)

The transparent experience of the environment is obscured by the robot’s dynamics when its inertia is high.

(ii)

On a similar note, the follower may not reach the desired position when the inertia is high.

An extension of the above work is presented in [18], in which the follower is given a position-based command, and the operators are given full force feedback. Yet, it suffers from the following significant limitations:

(i)

The system loses its stability because of the additional energy accumulated by the follower while taking a position input, resulting in outputs that are double the equivalent force.

(ii)

This architecture does not send any signal from the trainer to the trainee. The only training is through force feedback from the follower. Thus, the presence of a therapist is not fully utilized.

Variations of the aforementioned architectures can also be found. It is proposed in [19] that the dominance factor could be time-varying in nature, and it is adapted as per the patient’s recovery. An architecture that introduces two independent dominance factors is presented in [20]. All possible signal transmissions in DUSC are shown in [21]. A review of the state of the art related to DUSC can be found in [22]. It is important to note that none of the architectures, except that of [16], provides feedback to the trainer on how well the trainee performs. This is practically important for the trainer to fine-tune their way of training. More importantly, in all these architectures, the trainee will not be able to be trained in the frequency at which they operate. This limitation is discussed in detail in Section 6 of this paper. The trainee might indeed make an error in various attributes such as amplitude of operation, adding some tremor, frequency mismatch, etc. The ideal architecture should be able to correct each of these erroneous attributes of the patient. Thus, there is a need to re-define the manner of computing trainee’s recovery in order to overcome such limitations.

While the controllers developed for DUSC are largely classified as pure position controllers [20] or pure force controllers [23], the training objective demands a hybrid controller and is presented in this work, along with the appropriate metrics. In particular, in the context of shared control, a review of the various metrics that can be used for evaluation is presented in [24].

Having analyzed the state of the art and its limitations, the objective of this paper is to propose improved architecture and controllers, specifically for rehabilitation. This involves

(i)

The development of simplified architecture and the mathematical notation of the desired objectives.

(ii)

Ensuring full force feedback to each human.

(iii)

Giving a measure of the patient’s performance to the therapist.

(iv)

Maintaining system stability despite full force feedback.

(v)

The development of hybrid controllers for the three robots satisfying both the position and force requirements.

(vi)

Defining a recovery factor for the patient to train them in various attributes, including operating frequency.

The following sections elaborate on these objectives. Section 3 shows Objectives (i)–(iii) being met using a novel architecture. Section 4 shows the development of gain independent, passivity-based controllers, which meet Objectives (iv) and (v), and Objective (vi) is shown to be met in Section 6 by using an attribute-based recovery factor.

3. Proposed Architecture

The proposed architecture is shown in Figure 2, which provides full feedback to users and allows the therapist to perceive the patient’s performance.

$x_t,x_p,$ and $x_v$ are the positions of the therapist’s robot, the patient’s robot, and the virtual robot, respectively. $F_e$ is the environmental force, $r$ is the recovery level, and $a$ is the assistance level to the patient.

The significance of each of the signals shown in Figure 2 is explained in the following sub-sections.

3.1. Virtual Robot’s Position Tracking

The training process’s ultimate objective is that the patient alone should operate the virtual robot accurately. Before the patient attains this recovery level, they are given only partial control over the virtual robot. The degree to which they can be trusted depends on the recovery they have acquired over time. $“r\left(t\right)”$ denotes the recovery level of the patient, which is graded on a scale of 0 to 1. For all practical purposes, the recovery level is computed in terms of the proportion of the error the patient makes to the worst possible error. The patient’s worst possible error is first identified for the given robot and task through a calibration session (the method is further detailed later in Section 5.1). The higher the patient’s position error is, the lesser their recovery level $r\left(t\right)$.

The proportion of position commands the virtual robot can accept from the patient is directly proportional to this recovery level. Thus, $r\left(t\right)x_p$ is fed to the virtual robot from the patient. The remaining proportion of $\left(1-r\left(t\right)\right)x_t$ comes from the therapist, compensating for the intended motion of the virtual robot.

$$x_{vd}=\left(1-r\left(t\right)\right)x_t+r\left(t\right)x_p$$

(1)

For brevity, the recovery level is expressed as $“r”$ from now.

When the patient is completely novice, the recovery level $r$ is set to zero, thus commanding the virtual robot to take the position of the therapist. As the patient begins to learn, they are assigned a higher recovery level until the recovery level reaches unity. In that scenario, the patient can independently manipulate the objects in the virtual environment.

3.2. Full Force Feedback to Users

Since the learning rate can become limited by providing only partial force feedback to each user (traditional architecture—Figure 1), the proposed architecture provides full force feedback to both the therapist and the patient. Mathematically, $F_{td}=F_{pd}=F_e$, where $F_{td}$ and $F_{pd}$ are the desired forces on the therapist’s robot and the patient’s robot. However, such liberal transmission of force feedback is not free from disadvantages. As explained in Section 2, giving excess net feedback tends to make the system unstable. The means of overcoming this instability is shown in Section 4.

3.3. Learning Experience for the Patient

The patient controlling the virtual robot and receiving force feedback does not necessarily ensure their learning from the therapist. To make full use of an expert therapist’s presence, it must be ensured that the patient also feels the motions the therapist makes through an “assistive signal”. A fraction of $x_t$ is thus required to be sent for the patient to obtain some help from the therapist without being completely forced by the therapist. The fraction is a function of the instantaneous recovery level of the patient, $\left(1-r\right)$, since a higher $“r”$ would necessitate lesser assistance. Thus, the patient’s robot is commanded an assistive signal of $\alpha \left(1-r\right)x_t$, where a handle of $\alpha <1$ is still available for the therapist in case fine-tuning is needed, depending on the specific patient and/or task.

3.4. Providing a Measure of Learning to the Therapist

The signals described in Section 3.1–Section 3.3 are self-sufficient to serve the training purpose, but careful introspection shows that the therapist is not given a measure (apart from visual feedback) of how well the patient adapts to the training offered. Thus, the therapist could be teaching any patient in the same manner without knowledge of the specific strengths and weaknesses of the patient. Hence, a function of the recovery factor, which can be provided as a measure of a patient’s performance, is identified here.

The patient’s lack of recovery is reflected in erroneous motion in the virtual robot. When the patient is completely recovered (ideal case), they make the same motion as the therapist, i.e., $x_p=x_t$, resulting in the virtual robot’s position of $x_v=x_t$. However, when $r<1$, the deviation in $x_p$ from $x_t$ results in the virtual robot’s position not being equal to $x_t$. The resulting error in the virtual robot position is shown in

Table 1. Analysis of learning and training phases.

	$\mathit{r}$	${\mathit{x}}_{\mathit{v}}$
Completely recovered case	=1	$x_t$
Recovering phase	$0<r<1$	$\left(1-r\right)x_t+r{x}_p$

.

Considering the ideal case as the completely recovered situation, the resulting error (say $e$) in the position of virtual robot can be calculated as

$$\begin{gathered} e=VirtualRobo{t}^{’}sIdealPosition\left(x_t\right)-VirtualRobo{t}^{’}sActualPosition\left(x_v\right) \\ e=x_t-\left[\left(1-r\right)x_t+r{x}_p\right]=r\left(x_t-x_p\right) \end{gathered}$$

(2)

Thus, the error term shown in (2), which is a function of the recovery factor, can be utilized to make the therapist realize the performance of the patient.

Since sending back $x_p$ and then computing the error would demand one more channel, it is proposed that the error be computed by sending $x_v$ back to the therapist’s robot. The error term can then be computed as the difference between the therapist’s position and the measured virtual robot’s position. This does not demand an additional channel since the force feedback signal is already being sent from the virtual robot to the therapist. Such minimization of the number of channels indeed reduces the complexity of the patient’s controller.

In summary, the following features were achieved through the proposed architecture shown in Figure 2:

(i)

Recovery-based authority for both operators on the virtual robot.

(ii)

Full force feedback to each operator.

(iii)

An effective learning experience for the patient through an appropriate assistive signal from the therapist.

(iv)

An estimate of the patient’s recovery that is passed to the therapist.

(v)

A simplified five-channel architecture, leading to the reduced complexity of the two leader controllers.

Based on the proposed architecture, the desired performance objectives can be mathematically expressed as below:

$$\begin{array}{c}{x}_{vd}=\left(1-r\right)x_t+r{x}_p\hfill \\ F_{h1d}=F_e\hfill \\ F_{h2d}=F_e\hfill \\ x_{td}=\left(x_t-x_s\right)\hfill \\ x_{pd}=c\left(1-r\right)x_t\hfill \end{array}$$

(3)

Here, $x_{vd}$ refers to the desired position of the virtual robot. $F_{h1d}$ and $F_{h2d}$ represent the desired forces to be experienced by Human 1 (therapist) and Human 2 (patient), respectively. $x_{td}$ and $x_{pd}$ are the desired position commands to be received by the therapist and the patient. Each of these vectors falls in the dimensional space of $R^{3\times 1}$.

Thus, the first three of the six goals, as mentioned toward the end of Section 2, are met using the proposed architecture.

4. Controller Design

In this section, controllers are developed for each of the three robots, which can meet the desired performance objectives and stabilize the system, as envisaged in Objectives (iv) and (v) of this paper. The system dynamics are first presented before presenting the controller design.

4.1. Dynamic Model of Tele-Rehabilitation System

The Lagrangian models of the therapist’s robot, patient’s robot, and virtual robot, respectively, are as follows [25]:

$$M_t\left(q_t\right){\ddot{q}}_t\left(t\right)+C_t\left(q_t,{\dot{q}}_t\right){\dot{q}}_t\left(t\right)+G_t\left(q_t\right)={\tau }_{h1}\left(t\right)-{\tau }_t\left(t\right)$$

(4)

$$M_p\left(q_p\right){\ddot{q}}_p\left(t\right)+C_p\left(q_p,{\dot{q}}_p\right){\dot{q}}_p\left(t\right)+G_p\left(q_p\right)={\tau }_{h2}\left(t\right)-{\tau }_p\left(t\right)$$

(5)

$$M_v\left(q_v\right){\ddot{q}}_v\left(t\right)+C_v\left(q_v,{\dot{q}}_v\right){\dot{q}}_v\left(t\right)+G_v\left(q_v\right)={\tau }_v\left(t\right)-{\tau }_e\left(t\right)$$

(6)

where $M\in R^{3\times 3}$ represents the mass matrix; $C\in R^{3\times 3}$ represents the Coriolis matrix; $G\in R^{3\times 1}$ represents the gravitational vector; $q\in R^{3\times 1}$ represents the joint variables of the robot; ${\tau }_{h1}\in R^{3\times 1}$ and ${\tau }_{h2}\in R^{3\times 1}$ represent the external torque applied by the therapist and patient, respectively; ${\tau }_e\in R^{3\times 1}$ represents the external torque from the environment; and ${\tau }_t$, ${\tau }_p$ and ${\tau }_v$ represent the joint torques $\left(\in R^{3\times 1}\right)$ of the therapist, patient, and virtual robots, respectively. The controllers are now developed using the nonlinear tool of passivity.

4.2. Concept of Passivity

Passivity is an appropriate tool for DUSC since the interconnection of multiple passive sub-systems confirms the passivity of the overall system. Passivity is attained here such that it retains stability irrespective of the controller gains, and the following facts [26] are utilized:

Lemma 1. 

A system can be proven to be output strictly passive from input $u$ to output $y$ by finding a positive semi-definite function  $S$ such that  $\dot{S}\le y^{T}u-{\delta }_y{y}^2$.

Lemma 1 ties in very closely with the traditional way of proving Lyapunov stability. The gap is bridged by making use of the zero-state observability of the system.

Definition 1. 

A system is zero-state observable if $x=0$ is the only set of states satisfying  $y=0$ as long as  $u=0$.

Finally, the relation between passivity and asymptotic stability is stated by the following theorem.

Theorem 1. 

For a system that is output-strictly passive and zero-state observable, if the storage function $S$ is radially unbounded, then the origin is also globally asymptotically stable.

Though not exactly the same, the underlying form of the controllers is derived for DUSC based on the prior work of robotic rehabilitation [26].

4.3. Virtual Robot’s Position Controller

As mentioned in Section 3.2, the stability of the virtual robot is at stake because of giving full force feedback to both operators. Thus, the crucial part of controller design is for the virtual robot. The controller shown in (7) is proposed as the virtual robot’s controller for the proposed architecture.

$${\tau }_v\left(t\right)=u+G_v-k_p\left(q_v\left(t\right)-\widetilde{q_l}\left(t\right)\right)+C_v\dot{\widetilde{q_l}}\left(t\right)+M_v\ddot{\widetilde{q_l}}\left(t\right)+{\tau }_e\left(t\right)-k\left(\dot{q_v}\left(t\right)-\dot{\widetilde{q_l}}\left(t\right)\right)$$

(7)

where $\widetilde{q_l}\left(t\right)=\left(1-r\right)q_t\left(t\right)+r{q}_p\left(t\right)$.

Here, $k_p$ and $k$ are the position and velocity controller gains, and $u$ is the new control input created as the handle to the system.

When the controller in (7) is incorporated into the virtual robot dynamics shown in (6), the modified dynamics of the virtual robot are given by

$$M_v\left({\ddot{q}}_v\left(t\right)-\ddot{\widetilde{q_l}}\left(t\right)\right)+\left(C_v+kI\right)\left({\dot{q}}_v\left(t\right)-\dot{\widetilde{q_l}}\left(t\right)\right)+k_p\left(q_v\left(t\right)-\widetilde{q_l}\left(t\right)\right)=u$$

(8)

where $I$ refers to the identity matrix. Let $e_v$ denote the position tracking error term of the virtual robot, $\left(q_v\left(t\right)-\widetilde{q_l}\left(t\right)\right)$.

$$\dot{e_v}\left(t\right)={\dot{q}}_v\left(t\right)-\dot{\widetilde{q_l}}\left(t\right);\ddot{e_v}\left(t\right)={\ddot{q}}_v\left(t\right)-\ddot{\widetilde{q_l}}\left(t\right)$$

(9)

Using (9), modified dynamics (8) can be re-written as,

$$M_v{\ddot{e}}_v+\left(C_v+kI\right){\dot{e}}_v+k_p{e}_v=u$$

(10)

Passivity analysis is carried out on (10) by choosing the positive semi-definite storage and radially unbounded $S$ as

$$S={\displaystyle \frac{1}{2}}{\dot{e_v}}^T{M}_v\dot{e_v}+{\displaystyle \frac{1}{2}}{e_v}^T{k}_p{e}_v$$

(11)

$$\dot{S}={\dot{e_v}}^T{M}_v\ddot{e_v}+{\displaystyle \frac{1}{2}}{\dot{e_v}}^T\dot{M_v}\dot{e_v}+{e_v}^T{k}_p\dot{e_v}$$

(12)

Extracting $M_v\ddot{e_v}$ from (10) into (12),

$$\begin{gathered} \dot{S}={\dot{e_v}}^T\left(u-C_v\dot{e_v}-K\dot{e_v}-K_p{e}_v\right)+{\displaystyle \frac{1}{2}}{\dot{e_v}}^T\dot{M_v}\dot{e_v}+{e_v}^T{k}_p\dot{e_v} \\ \dot{S}={\dot{e_v}}^{T}u+{\displaystyle \frac{1}{2}}{\dot{e_v}}^T\left(\dot{M_v}-2C_v\right)\dot{e_v}+k_p\left({e_v}^T\dot{e_v}-{\dot{e_v}}^T{e}_v\right)-k{\dot{e_v}}^T\dot{e_V} \end{gathered}$$

(13)

The robot’s property that $\left(\dot{M}-2C\right)$ is skew-symmetric ensures ${\dot{e_v}}^T\left(\dot{M_v}-2C_v\right)\dot{e_v}$ reduces to zero. In addition, any vector $e_v$ yielding $\left({e_v}^T\dot{e_v}-{\dot{e_v}}^T{e}_v\right)=0$ simplifies (13).

$$\dot{S}={\dot{e_v}}^{T}u-k{\Vert \dot{e_v}\Vert }^2$$

(14)

Viewing (14) in light of Lemma 1 proves output strictly passivity from input $u$ to output $\dot{e_v}$. To further confirm the zero-state observability of the system, these values are set to zero in the modified dynamics shown in (10). This leads to the important result of the state $e_v=0$, implying position tracking and zero-state observability of the follower. As the three criteria of Theorem 1 are satisfied, globally asymptotic stability is guaranteed.

4.4. Leader Robots’ Hybrid Controllers

As already mentioned, each of the leader robots has input commands of both position and force from the other robots. Thus, a hybrid controller that handles position references as well as force references is developed for each leader robot. This principle of simultaneous position and force control of robots is validated in [27] and has been implemented even in recent applications, as portrayed in [28]. The proposed controller takes the form shown in (15) for either of the leader robots.

$${\tau }_l\left(t\right)={\tau }_{lp}\left(t\right)+{\tau }_{lf}\left(t\right)$$

(15)

where ${\tau }_{lp}$ denotes the part of controller that ensures reaching the desired position and ${\tau }_{lf}$ denotes the part of controller that ensures attaining the desired force. Both these terms are expressed in (16).

$$\begin{gathered} {\tau }_{lp}=-u-G_l+k\dot{e_l}+k_p\left(q_l-q_d\right)-M_l\ddot{q_d}+{\tau }_h \\ {\tau }_{lf}={\displaystyle \frac{1}{2}}{\left({\tau }_h-{\tau }_d\right)}^T\left({\tau }_h-{\tau }_d\right)\dot{e_l}+\left({{\displaystyle \int }}_0^t{\left({\tau }_h-{\tau }_d\right)}^T\left({\tau }_h-{\tau }_d\right)dt\right){\ddot{e}}_l+\left(sgn\left(\dot{e_l}\right)+\epsilon \right){\left({\tau }_h-{\tau }_d\right)}^T\left({\tau }_h-{\tau }_d\right) \\ +{\left({\tau }_h-{\tau }_d\right)}^T\left({\tau }_h-{\tau }_d\right)\left({\dot{q}}_l-\dot{q_d}\right) \end{gathered}$$

(16)

where $M_l$, $C_l$, $G_l$, and $q_l$ denote the dynamic parameters (shown in (4) and (5)) of the corresponding leader robot (therapist/patient, as the case may be). $q_d$ denotes the reference position, and ${\tau }_d$ refers to the desired torque for the corresponding leader robot. $e_l$ refers to the position tracking error, i.e., $q_l\left(t\right)-q_d\left(t\right)$. All the torques and joint positions mentioned here are also functions of time, the indication of which is omitted in (16) to be concise. Though the controller given by (15) is common to both the leader robots, the difference lies in defining ${\tau }_d\left(t\right)$ and $q_d\left(t\right)$ for each robot.

The key point to note from the proposed architecture shown in Figure 2 is that for both leader robots, the goal of force tracking is the same, i.e., both users need to experience the environmental force.

$${\tau }_{td}\left(t\right)={\tau }_{pd}\left(t\right)={\tau }_e\left(t\right)$$

(17)

where ${\tau }_e$ refers to the environmental torque upon the virtual robot.

On the other hand, the reference position signal for both leader robots differs significantly, as can be seen from Figure 2. Thus, the term $q_d\left(t\right)$ can be expressed as $q_{td}\left(t\right)$ and $q_{pd}\left(t\right)$ for the therapist and the patient’s leader robots, respectively, as shown in (18).

$$q_{td}\left(t\right)=q_t\left(t\right)-q_s\left(t\right);q_{pd}\left(t\right)=\left(1-r\right)q_t\left(t\right)$$

(18)

Thus, the controllers for both leader robots, which satisfy the requirements of the proposed architecture, are completely described. To analytically verify the stability of the system with the incorporation of the proposed leader controllers, passivity analysis is performed as portrayed in Section 4.3. For brevity, the choice of storage function alone is shown here, and the proof of stability is similar to the detailed proof shown in the case of the virtual robot controller.

$$S={\displaystyle \frac{1}{2}}{\dot{e_l}}^T{M}_l\dot{e_l}+{\displaystyle \frac{1}{2}}{e_l}^T{k}_p{e}_l+{{\displaystyle \int }}_0^t{\dot{e_l}}^T{\left({\tau }_h-{\tau }_d\right)}^T\left({\tau }_h-{\tau }_d\right)\dot{e_l}dt$$

(19)

In summary, the following were achieved in this section:

(i)

A pure position controller for the virtual robot and a hybrid position-force controller for both leaders were developed.

(ii)

The system stability was maintained irrespective of the gains.

(iii)

The proposed architecture’s position and force-tracking requirements were met.

Thus, the first five of the six goals of this paper, as stated toward the end of Section 2, were met.

5. Experiments

The robots used for validating the proposed architecture and controllers are the Touch Devices (3D Systems^®, Rock Hill, CA, USA), which are particularly known for their force-feedback ability. The Touch device, a 6 Degrees of Freedom (DoF) robot, engages the proximal muscles of the upper extremity in addition to distal muscles as a result of the reaching movement required to handle the robot [29,30]. Other rehabilitation devices can be appreciated from a systematic review [31]. Furthermore, customized rehabilitation devices are also developed continuously, and noteworthy recent designs can be found in [32,33]. Interestingly, additional sensing methods are also continuously developed, and a method to utilize the magnetic actuation to provide smooth force transmission is one of the most recent advancements [34].

Since the current study involves only upper extremity movements, the Touch device provides sufficient dexterity. Movements of the hand are carried out by activation of muscles from the shoulder to the forearm and wrist. The device’s ability to render haptic feedback up to $3.3\mathrm{N}$ is a sufficient threshold during the rehabilitation tasks mentioned here. Each of these devices is provided to the therapist as well as the patient, both of whom can visualize their movements on a screen in front of them (Figure 3).

Each robot is connected to the computer through the Unity^© (Version 6000.0.30f1) Software Interface, which enables the users to perceive the real-time visualization of the robots. The rehabilitation is performed in two stages—the calibration session and the training session. The role of each session is briefly depicted in Figure 4 and is further detailed in the following sub-sections.

5.1. Calibration Session

The primary purpose of the calibration session is to analyze the patient’s abilities in a completely untrained condition. In this session, there are no obstacles placed in the environment, and no training features such as assistive force from the therapist are incorporated. 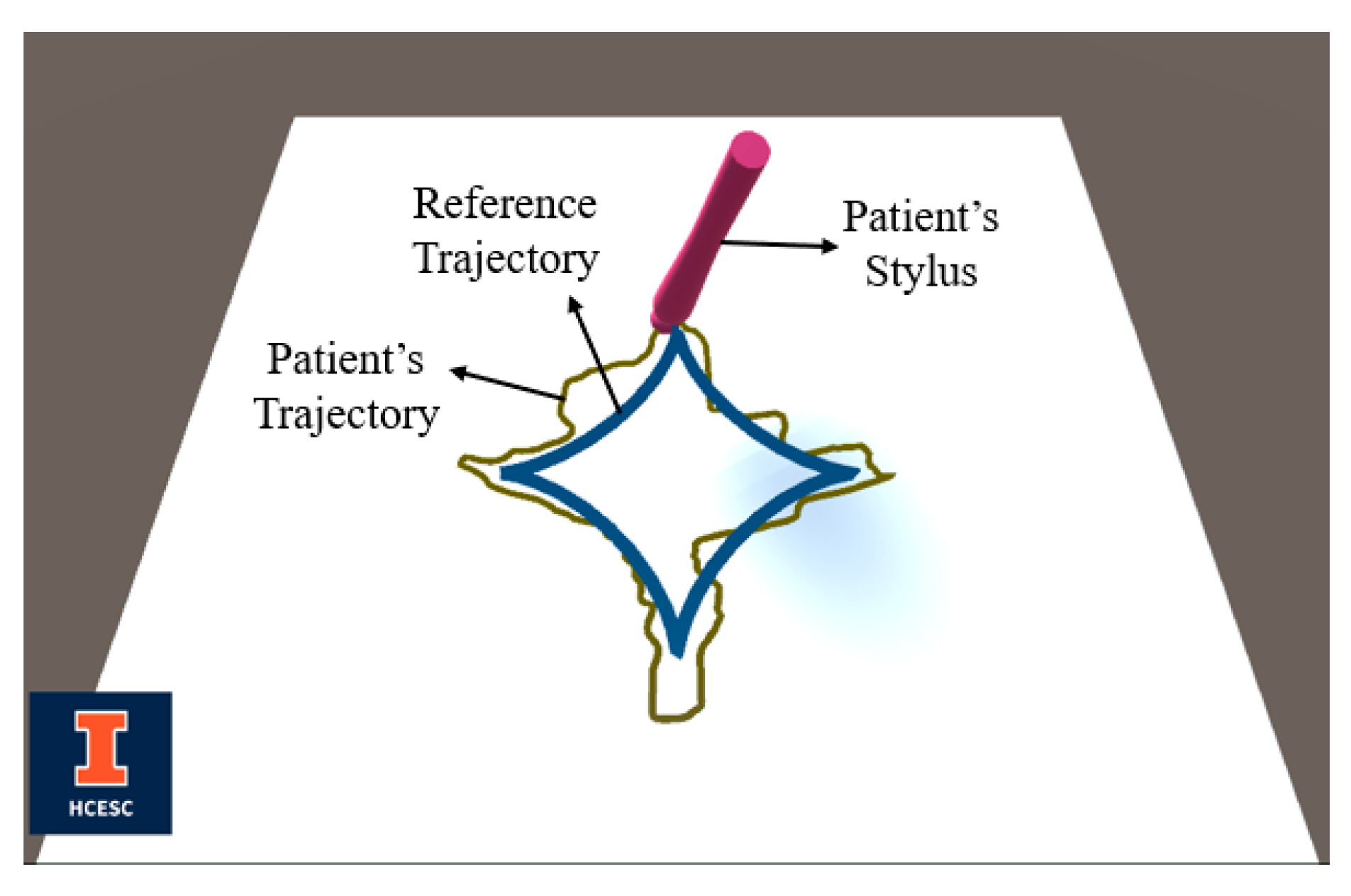Hand-writing exercises are recommended during the rehabilitation of the hemiparetic upper extremity in mildly impaired patients after a stroke to address their impacted dexterity skills [35]. Therefore, the calibration is performed through a hand-writing exercise, in which the patient attempts to follow a reference trajectory only through the visual feedback on the screen. The reference trajectory is either chosen by the therapist from a set of pre-defined symbols/letters or drawn by the therapist manually with their robot. In either case, the therapist ensures that the reference trajectory has a mixture of smooth curvatures as well as sharp corners. Such a trajectory enables researchers to accurately study the degree of a patient’s disabled motor skills. The patient attempting to follow a pre-defined reference trajectory, as seen in unity visualization, is shown in Figure 5.

The error that the patient makes depends on the nature of the reference trajectories, i.e., whether it has smooth curves (as in the letters “O”, “U”, etc.) or has sharp corners (as in the letters “A”, “M”, etc.). In order to obtain a complete perception of the patient’s motor skills, each pre-defined trajectory is typically a mixture of these two categories. The average error of the patient is recorded and stored as $e_0$, indicating the error they make at zero recovery level. If needed, the therapist may take the patient through multiple calibration sessions to obtain an average value for $e_0$. This might be necessary considering the scenario of the patient not becoming accustomed to the robotic platform. If in the calibration session, the patient is simply unable to move the robot or locate the stylus on the screen, the therapist typically chooses to guide them and then restart the calibration session. This value is used in the training session as a baseline to determine the recovery level of the patient. An error of $e_0$ or worse indicates that the patient is still in a completely untrained condition ($Recoverylevel\left(r\right)=0$), and an error of zero indicates a fully recovered condition $\left(r=1\right)$. Thus, any instantaneous error $e\left(t\right)$ between zero and $e_0$ is linearly mapped to a recovery level $r\left(t\right)$ on a scale of $\left(0–1\right)$ using the relation

$$r\left(t\right)=1-{\displaystyle \frac{e\left(t\right)}{e_0}}$$

(20)

The therapist is also given the flexibility to study the patient’s motor skills in 3D by generating real-time trajectories (by movement of their robot’s end-effector), which are closer to the patient’s daily activities. The calibration performed using a 3D trajectory is shown in Figure 6. The error made by the patient in this calibration $\left(e_0\right)$ is 29.27.

5.2. Training Session

Now that the patient’s abilities are quantitatively assessed through a metric, training is offered to help them recover from that condition. The virtual robot, which was not made use of in the calibration session, is introduced in the training session. The virtual robot takes a position based on the shared control of the therapist robot and the patient robot. The weightage depends on the instantaneous recovery level of the patient. In the proposed implementation protocol, the position error of the patient is continuously monitored, and so the recovery level of the patient is also dynamically updated according to the relation shown in (20). Thus, the proportion of the position command that the virtual robot takes from the patient’s robot also varies in real time.

The training session is carried out in a virtual environment, in which the patient has to learn to perform activities of daily living. Each virtual environment is modeled as a mass–spring–damper, and the corresponding dynamics are transmitted back to the robot’s dynamics (Equation (16)) so that the exact environmental forces are experienced by each user. As a preliminary step, a simple virtual environment is modeled, which has a wall rendering high-stiffness forces on the operators. A high-stiffness obstacle is purposely chosen here since stability proven in this case implies stability with lesser stiffness obstacles [36]. Whenever the virtual robot hits the wall, both operators feel the force feedback. The virtual environment and the virtual robot can be understood from Figure 7.

Throughout the session, the patient receives an assistive force from the therapist, the magnitude of which is inversely related to the recovery level. This assistive force $f\left(t\right)$ tends to prevent the patient from going away from the therapist, and its magnitude decreases as the patient approaches the therapist. The computation of the assistive force is performed through the following relation, using the Euclidean distance between the two robots $\left(d\right)$ and the recovery factor.

$$f\left(t\right)\propto \left(1-r\left(t\right)\right)d$$

(21)

The proportionality constant is chosen by the therapist to suit the needs of the patient (as discussed in Section 3). In the current experiment, the value of the proportionality constant ($a$) is chosen as 0.125. Thus, it leaves one layer of control completely in the hands of the therapist, allowing them to offer training on a patient-specific basis. A quantitative value of $“a”$ is nonetheless suggested to the therapist, based on the average errors of the patient obtained from each time frame. Recent studies on the dynamic levels of assistance during robotic rehabilitation can be seen [37]. The implementation protocol of the whole training session is depicted in Figure 8.

The therapist conducts a preliminary rehabilitation for a duration of 1 min, with the bandwidth of operation being approximately 5 cycles/min, which is typical for beginners’ rehabilitation. It is observed from subjective analysis that the patient demonstrates a higher level of motivation/enthusiasm in going through the “gamified” experience in robotic rehabilitation than in regular therapy. The subjective questionnaire for the patients is based on a very recent clinical study on stroke patients over robotic rehabilitation [38]. However, the subjective estimation can be translated to a more quantitative systematic measurement of the patient’s involvement through methods discussed in [39].

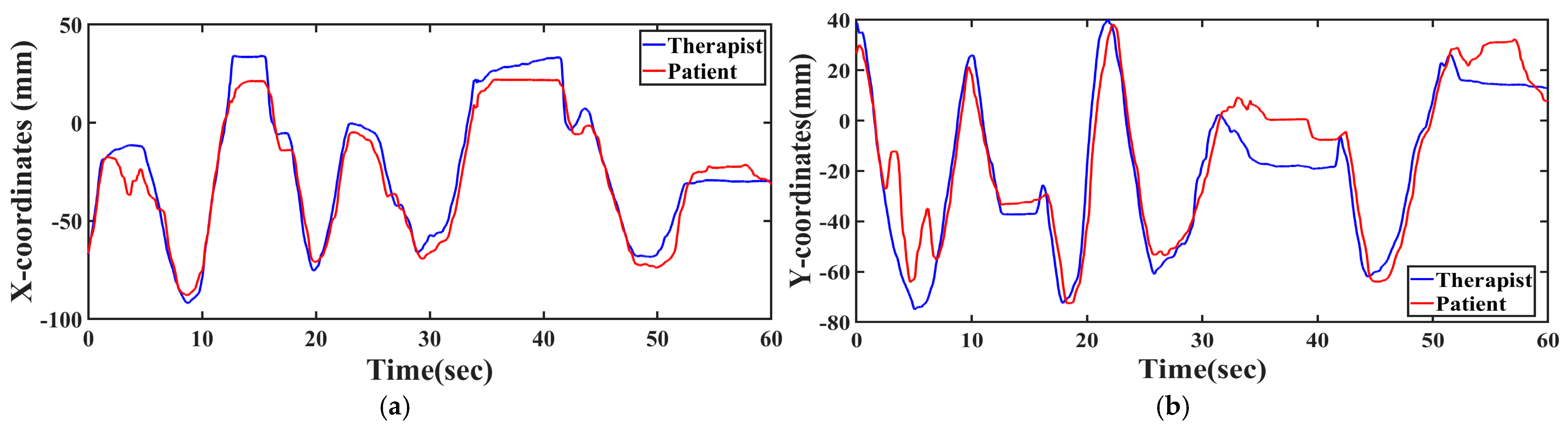
When the proposed architecture (Figure 2) and the proposed controllers (shown in (7) and (15)) are implemented in the system, the Cartesian coordinates of the end-effector (stylus) of both the therapist and the patient’s robots are recorded during the training session. These position values, along with the error in each dimension, are reported in Figure 9. Due to limitations in the current IRB approval, a healthy subject who behaves with patient characteristics was utilized to operate the robot.

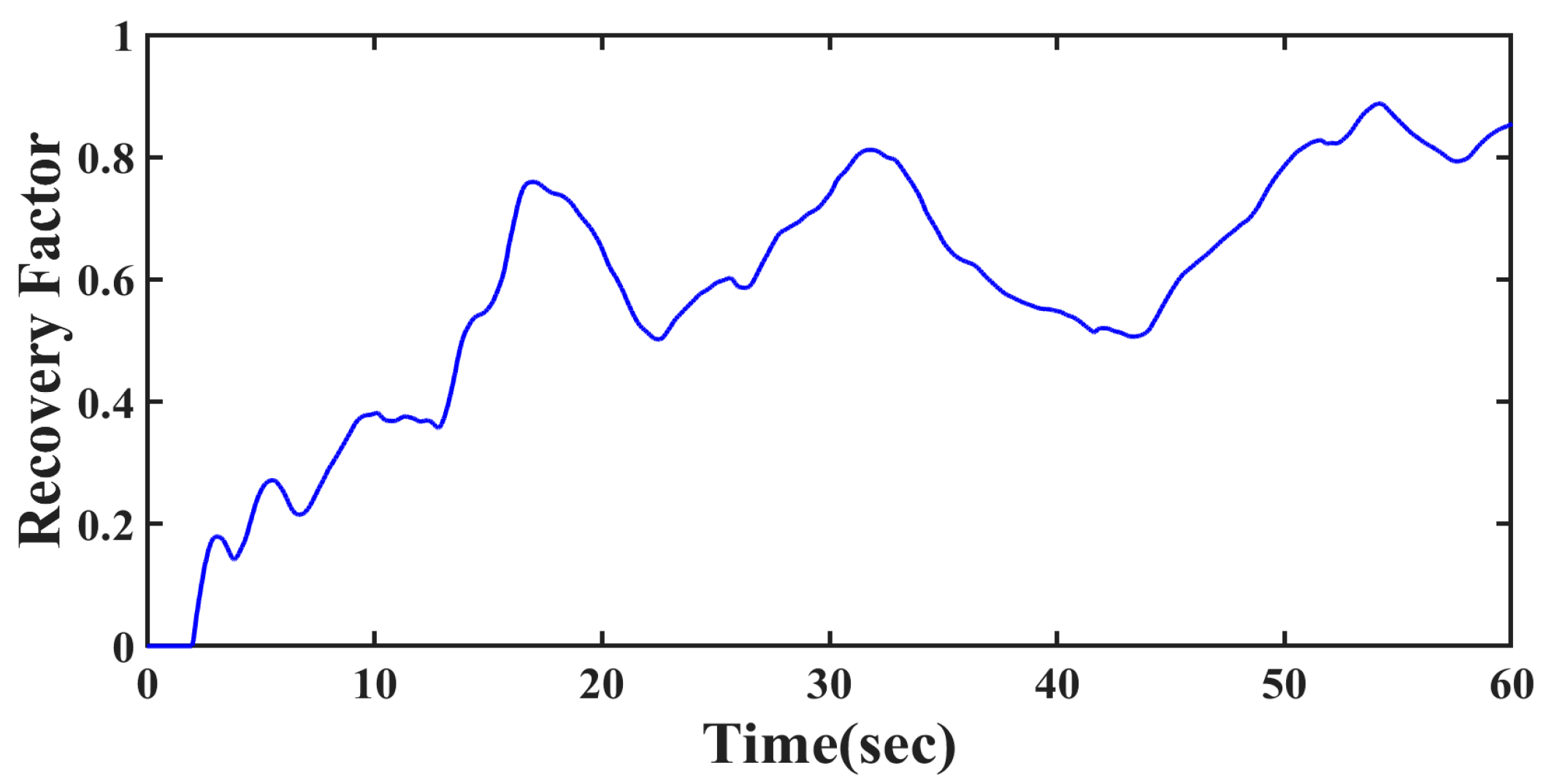
It is to be noted from Figure 9d that the positions converge over time. This is because the proposed architecture takes action to enhance the recovery rate of the patient while the therapy takes place. The actual learning rate is reflected through the varying recovery factor, which is reported in Figure 10.

5.3. Inferences from the Results

Growth in recovery: The patient who originally began with a recovery factor/level of zero was able to reach a recovery level of 0.84 during the 1 min session. In practice, the therapist actually takes the patient through several such training sessions, which can also eventually be performed for longer durations. This enables the patient to consistently perform their daily life activities with higher recovery levels than what they began with. The key observation here is the continuous growth in recovery, a characteristic that is seldom incorporated in the state of the art (see Section 2).

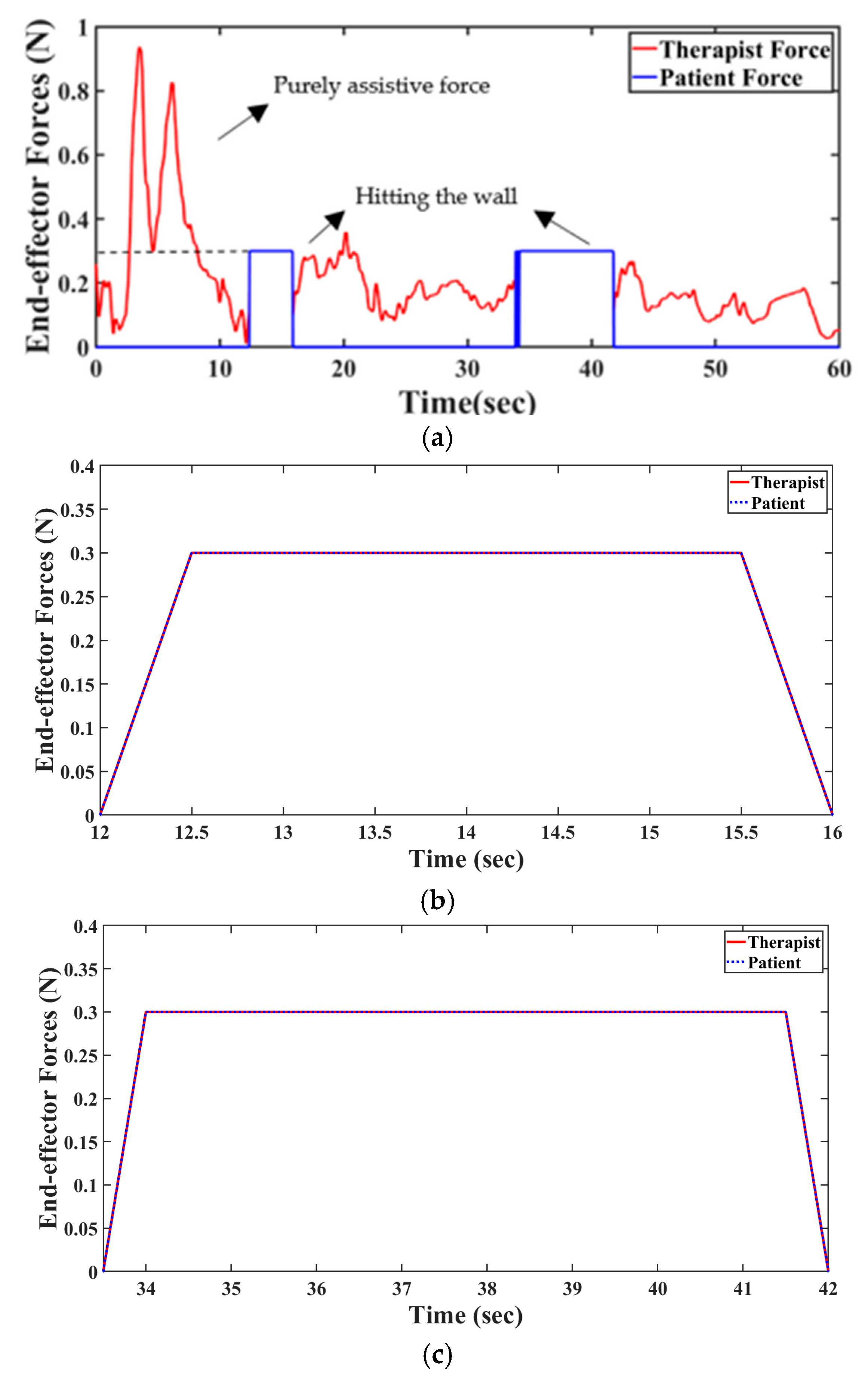
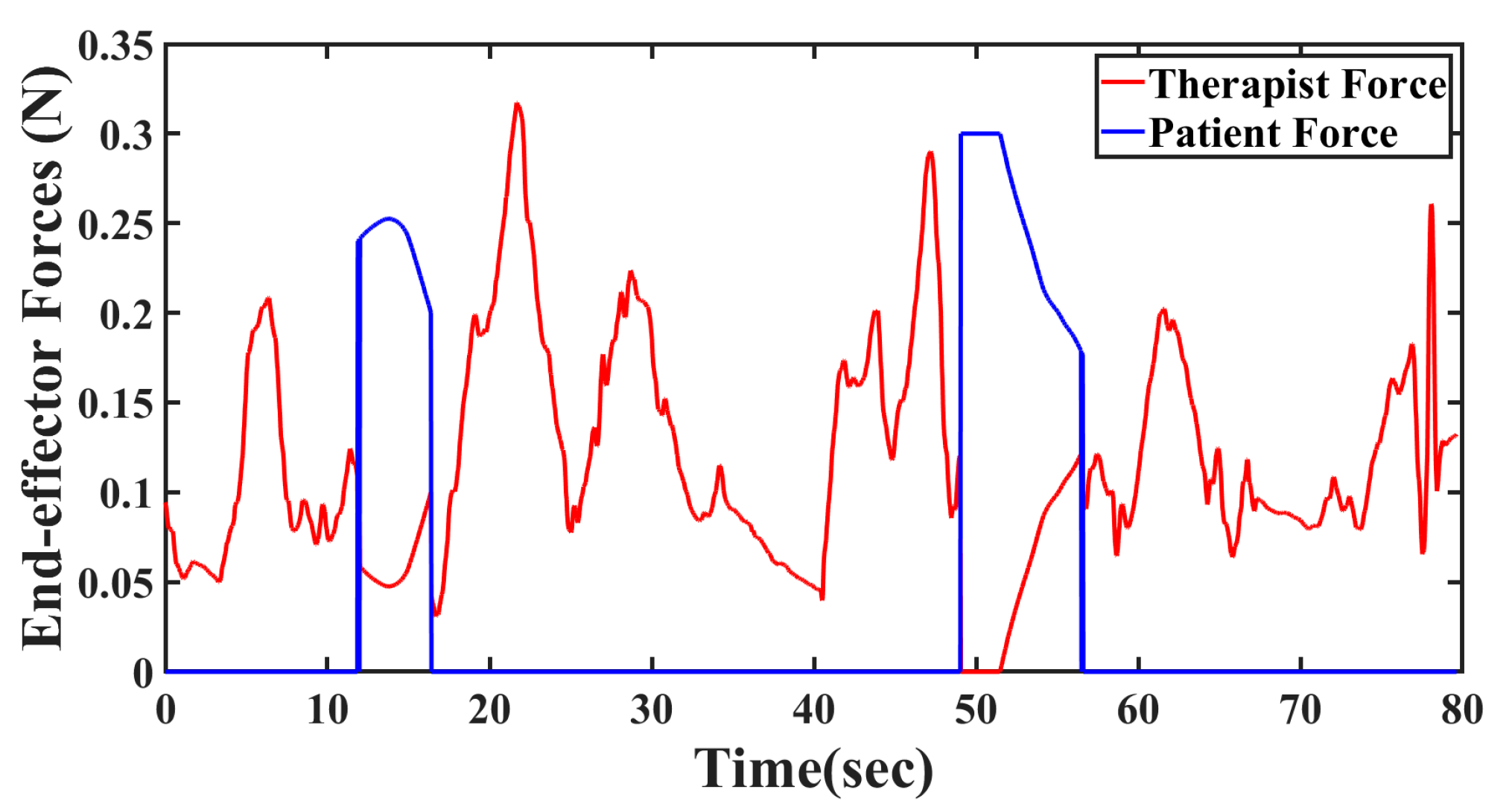
Full force feedback: Another significant improvement of the proposed method over the state-of-the-art method is the uncompromised full deliverance of feedback forces to both the therapist and patient. Force sensing plays a key role in medical applications, even up to the point of surgeries [40]. In most traditional architectures, the environmental force is fedback in proportion to the recovery factor, but here, the total environmental force is fedback to both users to enable complete and accurate perception of the environment. In order to evaluate this feature, the therapist intentionally hits the wall, which renders a constant force of $0.3\mathrm{N}$ at time intervals of $t=\left(11.8–16.4\right)\mathrm{s}$ and $t=\left(33.8–41.8\right)\mathrm{s}$. The forces that the end-effectors (stylus) experienced are shown in Figure 11a. For easy comprehension and to avoid the overlap, magnified views of the two forces while the robot is hitting the wall twice in the experiment are shown in Figure 11b,c.

Assistive forces: The forces portrayed here are the effective forces, which are a combination of the assistive force (in the case of the patient) and the environmental force. It can be seen from Figure 11 that during the environmental collision, both the therapist and the patient’s forces indeed overlap. And the magnitude of the force experienced is the same as the force that the virtual wall is modeled to render, irrespective of the recovery factor. At the instances when there is no collision, it can be observed from Figure 11 that the end-effector forces for the therapist are zero but for the patient are non-zero, indicating the assistive forces, which also decrease as the patient recovers.

Position tracking with respect to environment: A further observation can now be made from Figure 9a–c that, during the time interval of collisions, the positions of both these robots remain almost constant. During this collision period, the patient’s stopping position need not exactly be the wall position, since the therapists may prefer to give them full force feedback even if they have not yet reached perfection in position tracking.

Stability check: Under normal circumstances, providing full force feedback to both robots, as in Figure 11, should have led to instability [18]. In particular, handling very stiff environments, such as a wall, is shown to induce instability [36]. But the controllers proposed in (7) and (15) were able to maintain the stability of the system despite full force feedback and a high-stiffness environment. System stability is empirically confirmed by the positions not blowing up during collisions.

5.4. A Comparison with the State-of-the-Art Methods

A standard architecture, which is typically and widely used for DUSC applications [16], is also incorporated on the same experimental testbed, under the same experimental conditions. The time-varying nature of the recovery factor, which was actually missing in this reference, is added in order to make a fair comparison with the proposed method. The position errors obtained in this case are as shown in Figure 12.

It is evident that the errors in the case of the traditional architecture are unable to converge as significantly as in Figure 9d. The root mean square errors (RMSEs) in the positions tabulated for both the proposed and traditional architectures also show the superiority of the proposed method. The recovery factor and forces obtained are also reported in Figure 13 and Figure 14 for further analysis.

Although the recovery factor rises quickly even with the traditional architecture, it is unable to cross a threshold of $0.45$ even after multiple attempts by the therapist. It is because of the absence of the efficient assistive force (detailed in Section 3.3) that the recovery level is not improving beyond a limited extent.

As explained before, during the two collisions with the wall $(t=\left(11.8–16.4\right)\mathrm{s}\mathrm{and}t=\left(49.1–56.6\right)\mathrm{s})$ each of the humans experiences only partial force feedback, highly limiting the perception of the wall. During the first hit, the recovery factor of the patient is about $0.25$ (Figure 13), and thus, the force they experienced was only a quarter of $0.3\mathrm{N}$ (Figure 14). During the second hit, the patient’s recovery fell close to zero and, therefore, had almost no perception of the wall. Both users reported that such an experience severely inhibits the learning rate. This again demonstrates the superiority of the proposed method.

6. Additional Results with Attribute-Wise Recovery

Another salient feature that the proposed architecture is capable of achieving is the consideration of “attribute-wise recovery”. In the previous section, the computation of the recovery level is executed such that the error between the therapist and patient eventually reduces. In this section, it will be demonstrated that it is further possible to classify the error into specific attributes such as amplitude, frequency, and tremor. The advantage in classifying the error lies in the flexibility to train the patient in specific attributes in which they may need more training. A particular patient might be prone to making errors in their frequency of hand movements, while others may suffer primarily from adding tremors during their activities. Obtaining an individual recovery factor for each attribute enables them to receive focused training in the specific attribute(s).

6.1. Test Conditions

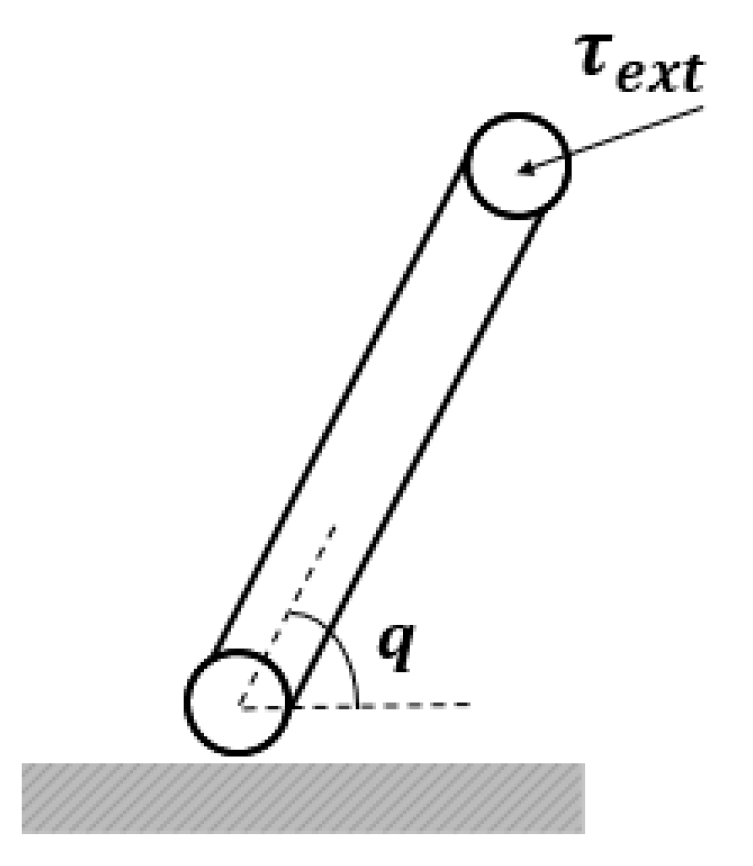
Although the proposed architecture facilitates such attribute-based recovery factors, as a preliminary step, simulations were performed to validate the claim. The simulation testbed consists of a simple 1-R manipulator (shown in Figure 15), assigned as the therapist’s robot, the patient’s robot, and the virtual robot.

A link with a mass of 100 g and a length of 10 cm is attached to a rotary joint along the axis perpendicular to the ground. The joint angle from the base is measured in the anti-clockwise direction as $q$. ${\tau }_{\mathrm{ext}}$ is the external torque applied by the therapist, the patient, or the environment, depending on the robot under consideration. This is denoted as ${\tau }_{h1}$, ${\tau }_{h2}$, and ${\tau }_e$ in (4)–(6). In practice, the external torque upon both leader robots is applied in the form of position inputs from the user, and for the virtual robot, it is directly applied in the form of torque from the environment. Thus, the position inputs from the therapist and patient are represented by $q_{m1}^{*}$ and $q_{m2}^{*}$, respectively. Throughout the simulations, it is assumed that the initial position of all three robots is $q=90°.$

6.2. Attribute-Wise Recovery Level

Let the therapist input a sinusoidal position of $q_{m1}^{*}\left(t\right)=A_{r}Sin\left({\omega }_{r}t\right)$. The therapist’s amplitude $A_r$ and frequency ${\omega }_r$ are the reference amplitude and frequency for the patient. Without any training, the patient tries to replicate this motion with some erroneous amplitude and frequency, possibly even adding some tremor into the system. Thus, the exogenous input of the patient is modeled as $q_{m2}^{*}\left(t\right)=ASin\left(\omega t\right)+dSin\left({\omega }_{t}t\right)$, where $A$ and $\omega$ correspond to the amplitude and frequency at which the patient is able to operate their leader robot. ${\omega }_t$ is the frequency of the tremor introduced by the patient. In practice, this can be measured by modeling the free-hand motion of the patient. For the sake of simulations, a choice of ${\omega }_t=20$, is made here since, typically, tremor frequency is about 10 times the actual operating frequency (${\omega }_r$ is chosen as 2 here). $d$ is the magnitude of the tremor added to the patient’s leader robot. The recovery attained by the patient with respect to the amplitude, $r_a$, can be defined as

$$r_a={\displaystyle \frac{A-A_0}{A_r-A_0}}$$

(22)

The relation shown in (22) effectively normalizes any given amplitude of the patient to a corresponding recovery value in the range of $0–1$. Similarly, the recovery level with respect to the frequency, $r_{\omega },$ and tremor, $r_t$, can be written as

$$r_{\omega }={\displaystyle \frac{\omega -{\omega }_0}{{\omega }_r-{\omega }_0}};r_t=1-{\displaystyle \frac{d}{d_0}}$$

(23)

Now that $q_{m1}^{*}\left(t\right)$, $q_{m2}^{*}\left(t\right)$, and the individual recovery factors of the patient are known, the position of the virtual robot $\left(q_s\right)$ can actually be computed as follows:

$$q_s\left(t\right)=A_{s}Sin\left({\omega }_{s}t\right)+d_{s}Sin\left(10{\omega }_{s}t\right)$$

(24)

where $A_s=r_{a}A+\left(1-r_a\right)A_r$; ${\omega }_s=r_{\omega }\omega +\left(1-r_{\omega }\right)A_{\omega }$; and $d_s=r_{t}d.$

Thus, by defining explicit recovery factors for each attribute, the position of the virtual robot can be accurately described. By following a similar definition as presented in (22), any number of attributes in which the patient needs to improve can be modeled. Each of these recovery levels falls within the range of $0–1$. The overall recovery of the patient $\left(r\right)$ can be expressed as an average of all the individual recovery factors.

$$r={\displaystyle \frac{r_a+r_{\omega }+r_t}{3}}$$

(25)

A weighted average can be used in (25) if the application demands. The procedure for computing the recovery level with consideration to multiple attributes is summarized in Figure 16.

6.3. Claims and Results

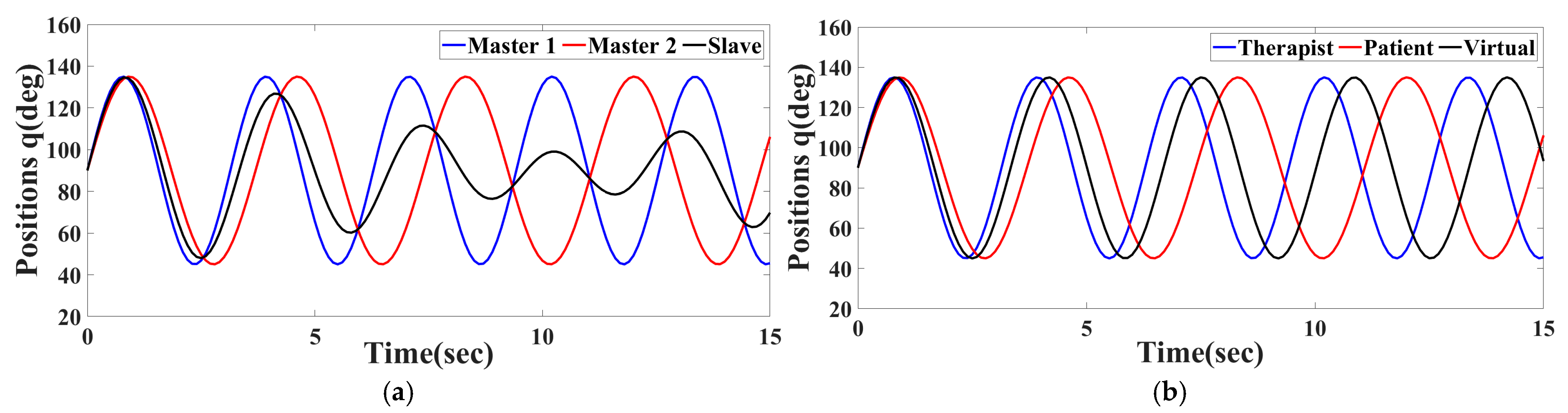
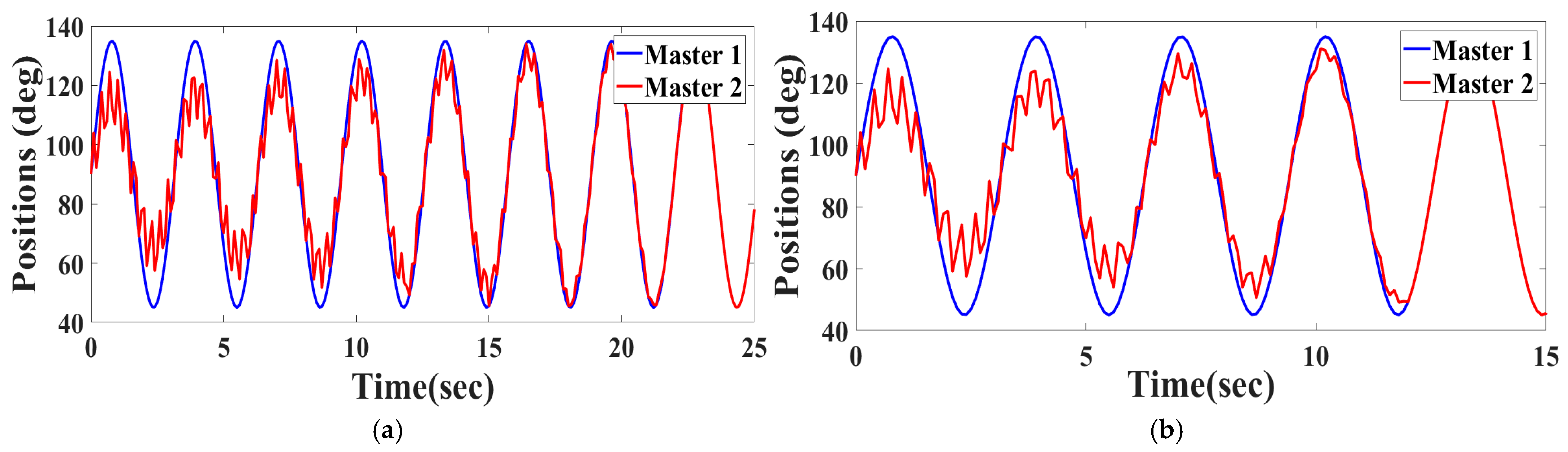
Claim 1: Using the attribute-wise recovery factor, the proposed architecture can even handle scenarios in which the patient operates with a different bandwidth (frequency), which leads to chaotic behavior in the traditional architecture.

To validate this claim, a therapist’s input of $45Sin\left(2t\right)$ and a patient’s initial input of $45Sin\left(1.75t\right)$ are considered. The resultant position of the virtual robot when implemented with the traditional architecture and proposed architecture are shown in Figure 17. The overall recovery level while taking these readings is 0.4.

It can be readily noted that even when the patient operates at the same amplitude as the therapist, and without any tremor, still, with a minor difference in the frequency of operation, the virtual robot’s (plotted in black) amplitude is also unpredictably affected in the case of the traditional architecture. But due to attribute-wise classification, the proposed architecture is able to maintain an averaged amplitude as well as frequency.

Claim 2: Using the attribute-wise recovery factor, the proposed architecture helps the patient to recover from errors much faster than the traditional architecture.

In order to validate this claim, a case study is considered in which the patient begins with a different amplitude than the therapist and also adds tremor. With the same therapist’s input of $45Sin\left(2t\right)$, the patient’s initial input is now taken as $25Sin\left(2t\right)+10Sin\left(20t\right)$. Since the effect of frequency mismatch is already demonstrated in Figure 17, this casestudy assumes that the patient operates at the same frequency as the therapist so that a fair comparison can be made between the two architectures. The recovery rates with the above-mentioned inputs are shown in Figure 18.

An observation can be made that with the same test conditions and the same initial conditions, the patient can match the therapist’s trajectory in about $12\mathrm{s}$ in the case of the proposed architecture, while it takes about $22\mathrm{s}$ to do the same with the traditional architecture. This again demonstrates the effect of the attribute-wise recovery factor.

7. Conclusions

The concept of dual-leader–single-follower is exploited in this paper to develop a platform for facilitating upper extremity rehabilitation in stroke patients. The proposed architecture allows the therapist and the patient to conjointly control a virtual robot in its environment while both humans perceive environmental forces. The recovery of the patient is continuously monitored, and they are provided with a corresponding assistive force from the therapist to enhance their performance. The controllers were developed to ensure that the system remains stable (irrespective of gains) and also that the performance objectives (such as position tracking and force perception) are accurately met. A therapist and a patient were allowed to operate on a 6 DoF robotic system, and it was subsequently found that the architecture and controllers were validated. Several features absent in the typical training architectures were incorporated in the proposed architecture and tested on the experimental setup.