An Arch-Shaped Electrostatic Actuator for Multi-Legged Locomotion
Abstract
1. Introduction
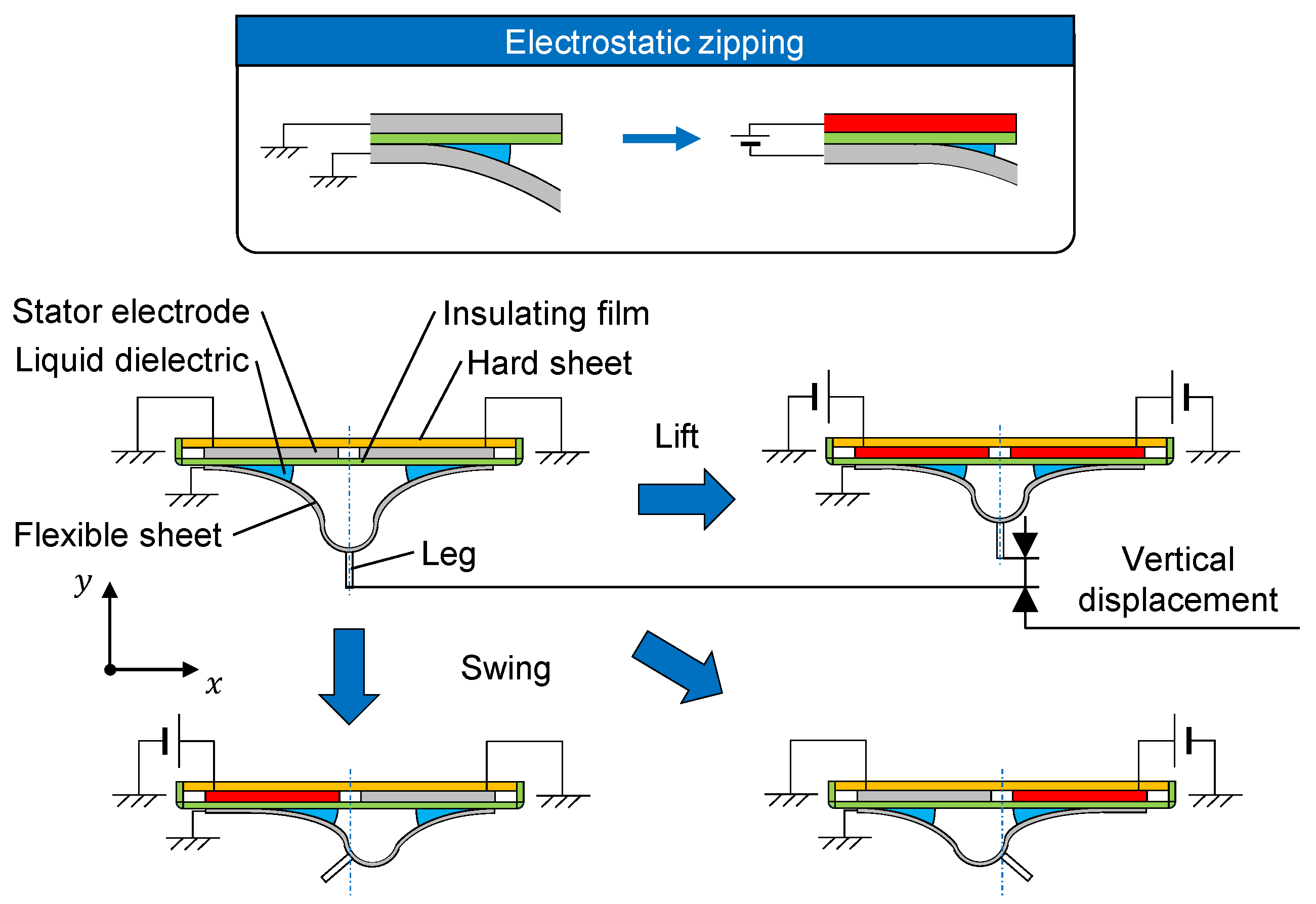
2. Arch-Shaped Electrostatic Actuator
2.1. Structure
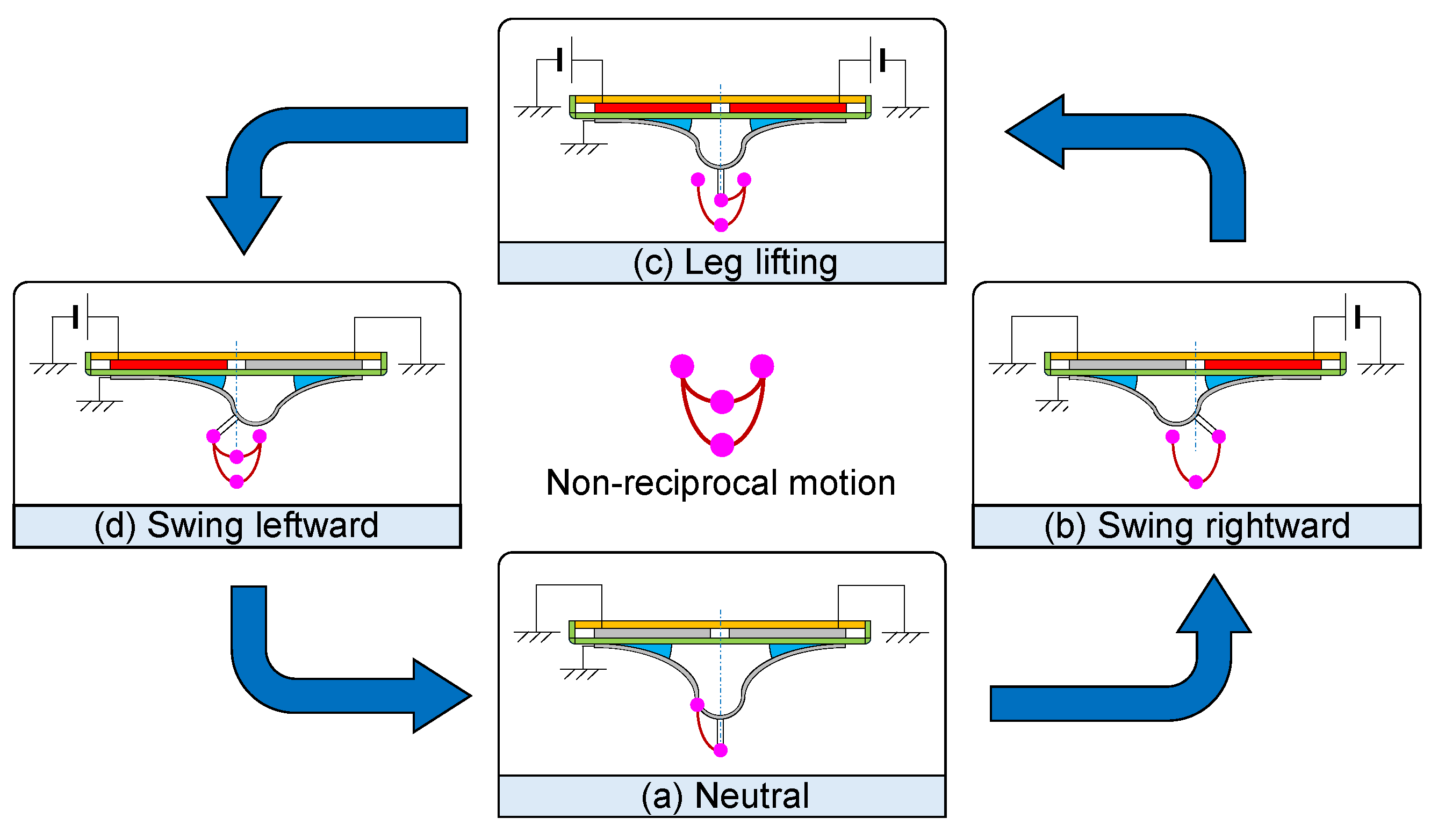
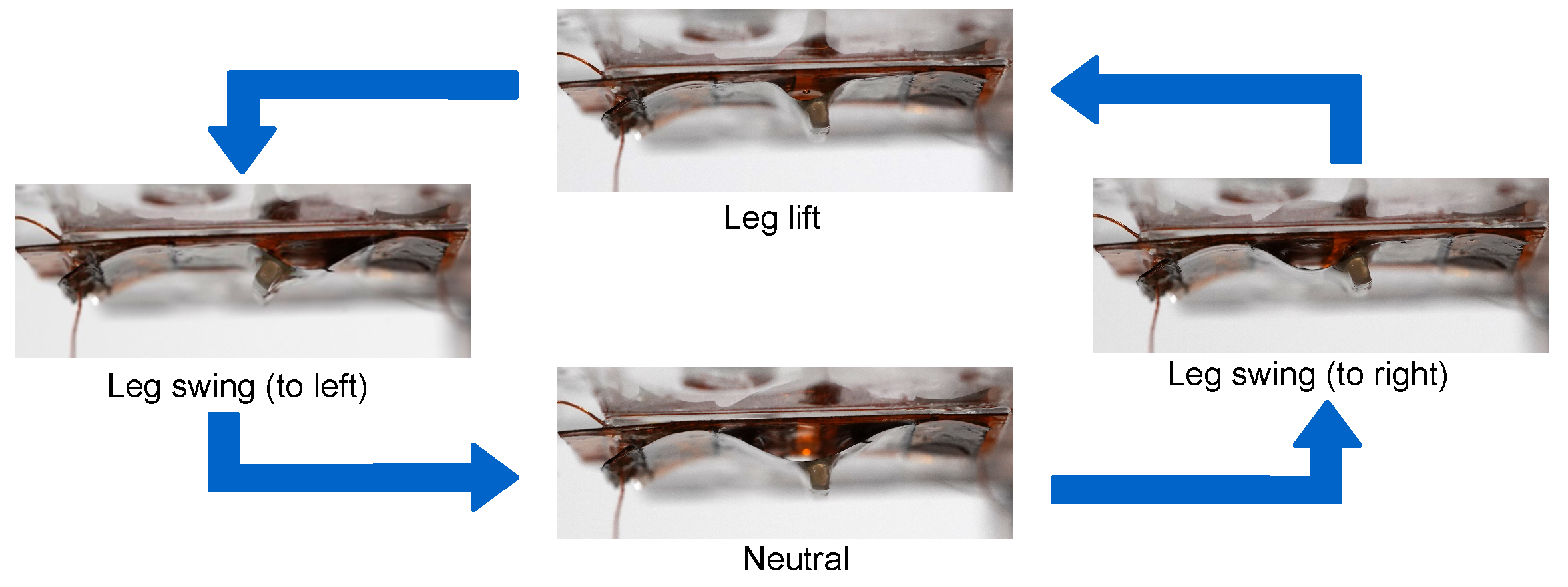
2.2. Operation Principle
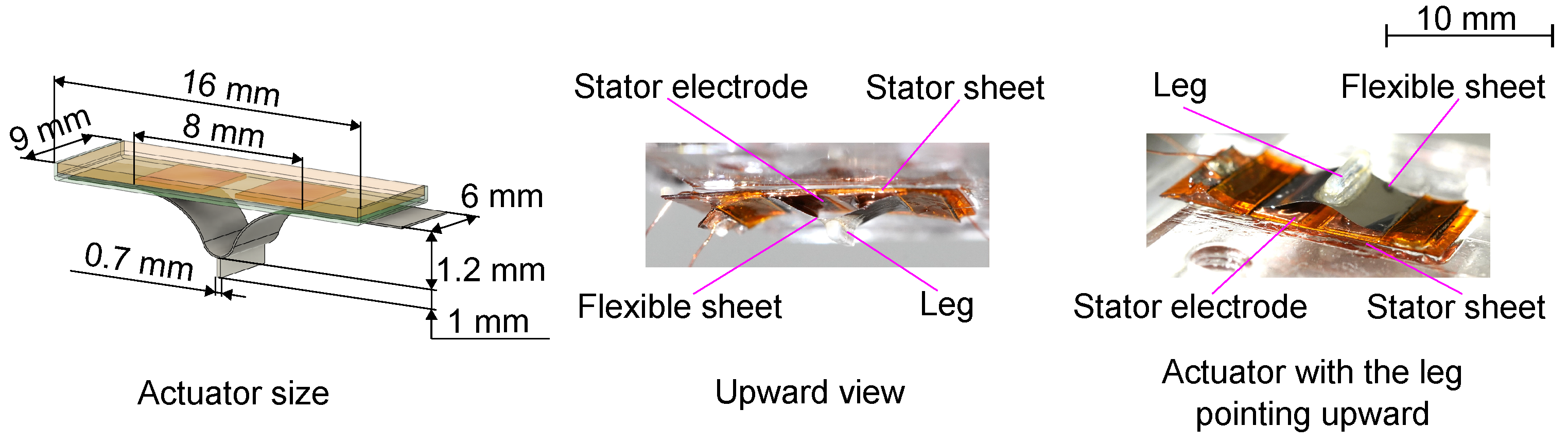
2.3. Prototype Fabrication
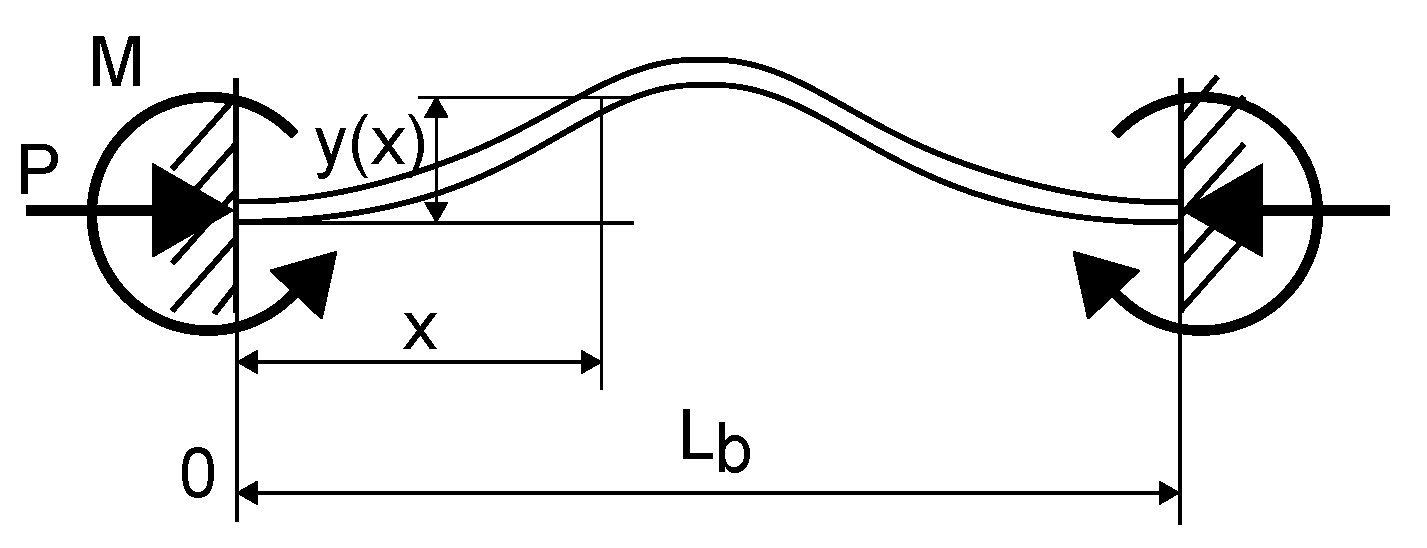
2.4. Modeling
3. Experiments
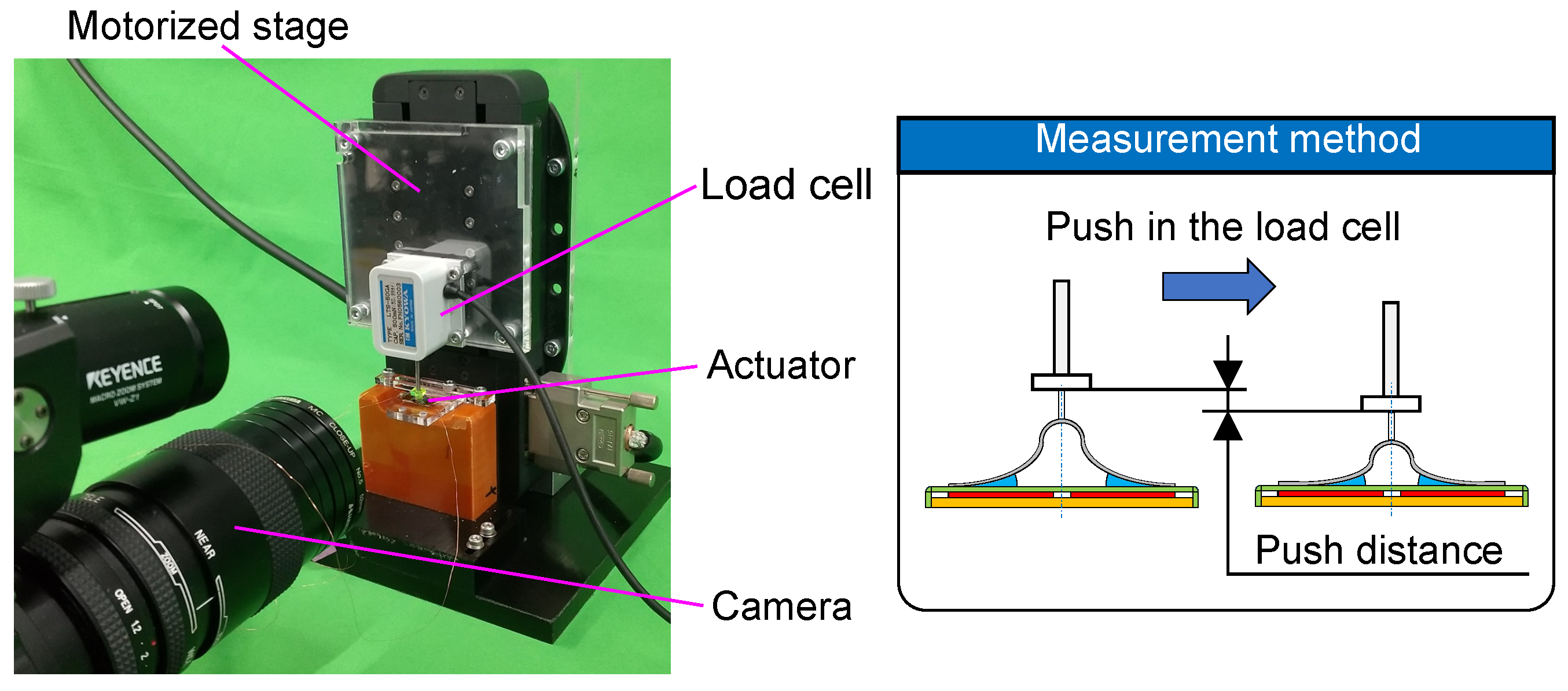
3.1. Experimental Setup
3.2. Leg Swing Characteristics
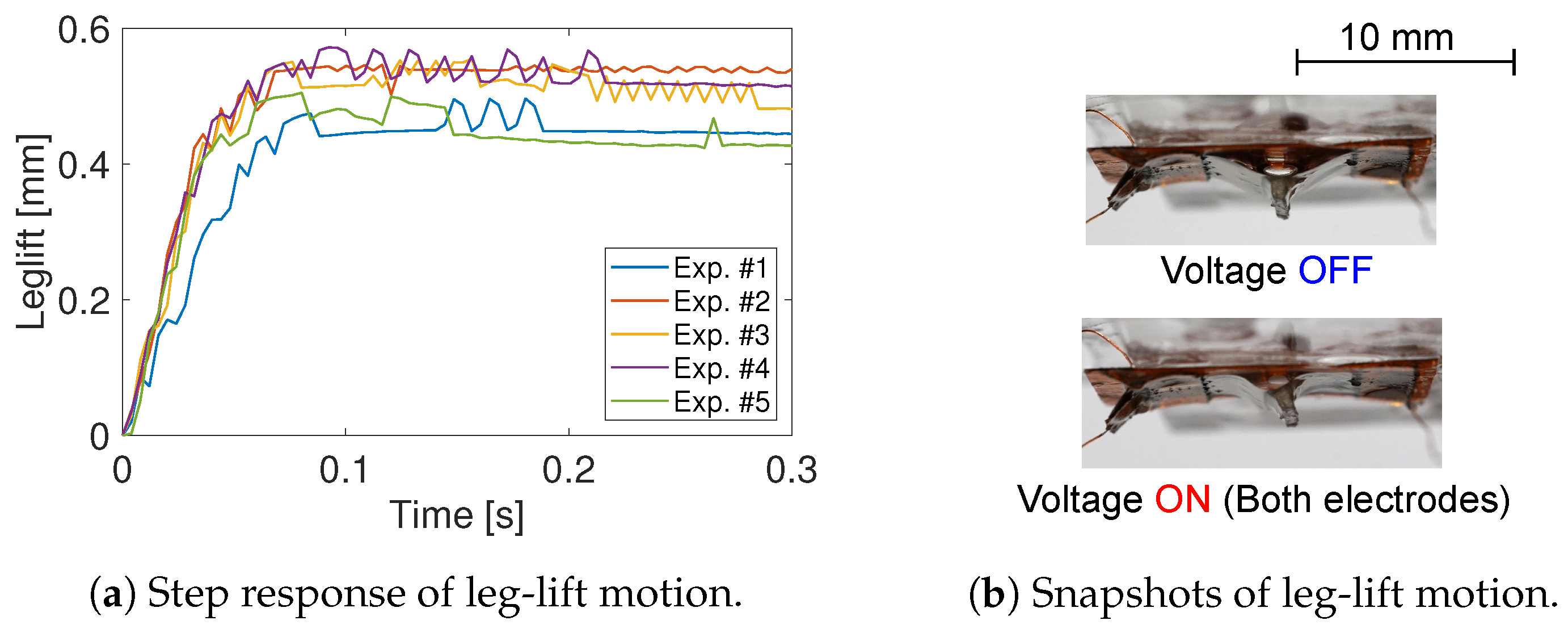
3.3. Leg Lifting Characteristics
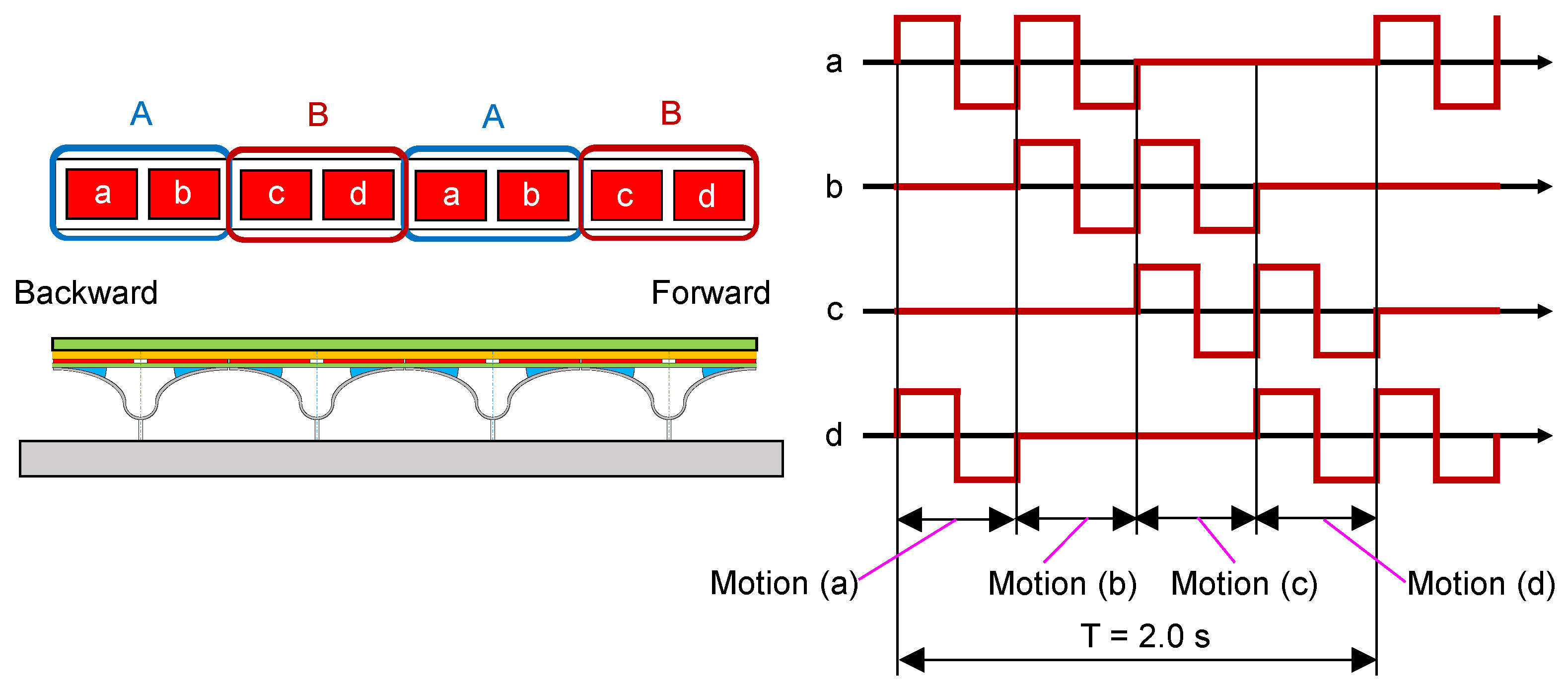
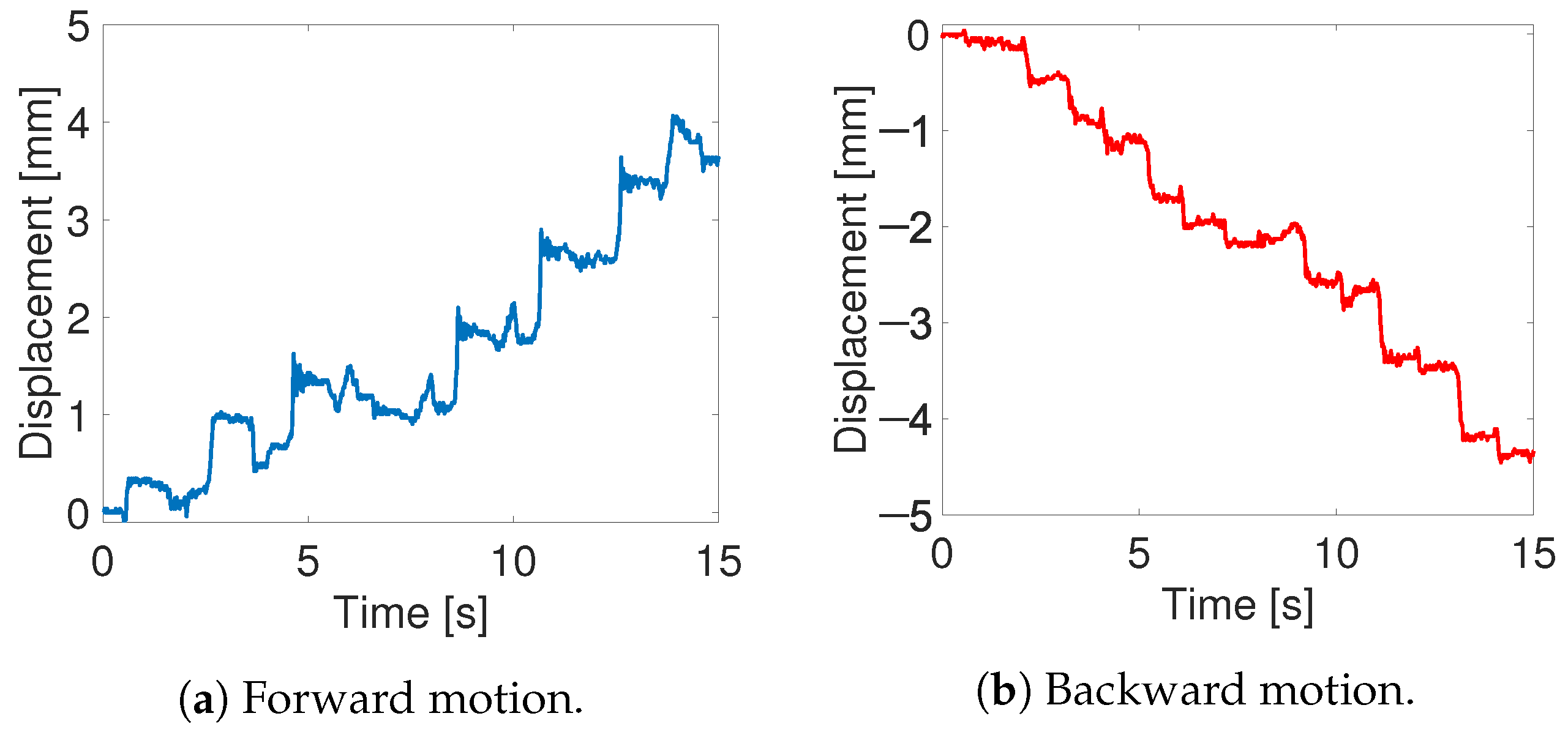
3.4. Non-Reciprocal Motion
3.5. Discussion
4. Multi-Legged Walking Mechanism
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Idogaki, T.; Kanayama, H.; Ohya, N.; Suzuki, H.; Hattori, T. Characteristics of piezoelectric locomotive mechanism for an in-pipe micro inspection machine. MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 193–198. [Google Scholar]
- Hong, C.; Wu, Y.; Wang, C.; Ren, Z.; Wang, C.; Liu, Z.; Hu, W.; Sitti, M. Wireless flow-powered miniature robot capable of traversing tubular structures. Sci. Robot. 2024, 9, eadi5155. [Google Scholar] [CrossRef] [PubMed]
- Xing, J.; Ning, C.; Zhi, Y.; Howard, I. Analysis of bifurcation and chaotic behavior of the micro piezoelectric pipe-line robot drive system with stick-slip mechanism. Commun. Nonlinear Sci. Numer. Simul. 2024, 134, 107998. [Google Scholar] [CrossRef]
- Misaki, D.; Murakami, Y. Development of a multi-leg type micro rescue robot for disaster victim search. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Phuket Island, Thailand, 7–11 December 2011; pp. 1801–1806. [Google Scholar]
- Baisch, A.T.; Wood, R.J. Design and fabrication of the Harvard ambulatory micro-robot. In Robotics Research: Proceedings of the 14th International Symposium ISRR, Lucern, Switzerland, 31 August–3 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1801–1806. [Google Scholar]
- Saab, W.; Racioppo, P.; Kumar, A.; Ben-Tzvi, P. Design of a miniature modular inchworm robot with an anisotropic friction skin. Robotica 2018, 37, 521–538. [Google Scholar] [CrossRef]
- Asamura, K.; Nagasawa, S. MEMS fabrication of compliant sheet for micro hexapod robots. Jpn. J. Appl. Phys. 2020, 59, SIIL03. [Google Scholar] [CrossRef]
- Supik, L.; Stránská, K.; Kulich, M.; Přeučil, L.; Somr, M.; Košnar, K. Magnetic Field-Driven Bristle-Bots. IEEE Robot. Autom. Lett. 2023, 12, 8098–8105. [Google Scholar] [CrossRef]
- Wang, D.; Sui, F.; Qiu, W.; Peng, Y.; Zhang, M.; Wang, X.; Lin, L. An Untethered Crawling and Jumping Micro-Robot. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Boston, America, 20–24 June 2021; pp. 353–356. [Google Scholar]
- Fath, A.; Liu, Y.; Xia, T.; Huston, D. MARSBot: A Bristle-Bot Microrobot with Augmented Reality Steering Control for Wireless Structural Health Monitoring. Micromachines 2024, 15, 202. [Google Scholar] [CrossRef]
- Jin, C.; Zhang, J.; Xu, Z.; Trase, I.; Huang, S.; Dong, L.; Liu, Z.; Usherwood, S.E.; Zhang, J.X.J.; Chen, Z. Tunable, Flexible, and Resilient Robots Driven by an Electrostatic Actuator. Adv. Intell. Syst. 2020, 2, 1900162. [Google Scholar] [CrossRef]
- Cao, J.; Qin, L.; Liu, J.; Ren, Q.; Foo, C.C.; Wang, H.; Lee, H.P.; Zhu, J. Untethered soft robot capable of stable locomotion using soft electrostatic actuators. Extrem. Mech. Lett. 2018, 21, 9–16. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, J.; Liu, L.; Liu, Y.; Leng, J. Bioinspired multimodal soft robot driven by a single dielectric elastomer actuator and two flexible electroadhesive feet. Extrem. Mech. Lett. 2022, 53, 101720. [Google Scholar] [CrossRef]
- Higuchi, T.; Furutani, K.; Yamagata, Y.; Kudoh, K.; Ogawa, M. Improvement of Velocity of Impact Drive Mechanism by Controlling Friction. J. Jpn. Soc. Precis. Eng. 1992, 58, 1327–1332. (In Japanese) [Google Scholar] [CrossRef]
- Ze, Q.; Wu, S.; Nishikawa, J.; Dai, J.; Sun, Y.; Leanza, S.; Zemelka, C.; Novelino, L.S.; Paulino, G.H.; Zhao, R.R. MARSBot: Soft robotic origami crawler. Sci. Adv. 2022, 8. [Google Scholar] [CrossRef] [PubMed]
- Ueno, S.; Takemura, K.; Yokota, S.; Edamura, K. Micro inchworm robot using electro-conjugate fluid. Sens. Actuators A: Phys. 2014, 216, 36–42. [Google Scholar] [CrossRef]
- Karakadioglu, C.; Askari, M.; Ozcan, O. Design and operation of MinIAQ: An untethered foldable miniature quadruped with individually actuated legs. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 247–252. [Google Scholar]
- Kawamura, S.; Tanaka, D.; Tanaka, T.; Noguchi, D.; Hayakawa, Y.; Kaneko, M.; Saito, K.; Uchikoba, F. Neural networks IC controlled multi-legged walking MEMS robot with independent leg mechanism. Artif. Life Robot. 2018, 23, 380–386. [Google Scholar] [CrossRef]
- Jayaram, K.; Shum, J.; Castellanos, S.; Helbling, E.F.; Wood, R.J. Scaling down an insect-size microrobot, HAMR-VI into HAMR-Jr. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10305–10311. [Google Scholar]
- Kaln, M.A.I.; Aygul, C.; Turkmen, A.; Kwiczak-Yigitbas, J.; Baytekin, B.; Ozcan, O. Design, Fabrication, and Locomotion Analysis of an Untethered Miniature Soft Quadruped, SQuad. IEEE Robot. Autom. Lett. 2020, 5, 3854–3860. [Google Scholar] [CrossRef]
- Askari, M.; Ozcan, O. Dynamic Modeling and Gait Analysis for Miniature Robots in the Absence of Foot Placement Control. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Paris, France, 20–24 May 2019; pp. 9754–9760. [Google Scholar]
- Karydis, K.; Liu, Y.; Poulakakis, I.; Tanner, H.G. A template candidate for miniature legged robots in quasi-static motion. Auton. Robot. 2014, 38, 193–209. [Google Scholar] [CrossRef]
- Mahkam, N.; Ugur, M.; Ozcan, O. Effect of Feet Failure and Control Uncertainties on the Locomotion of Multi-Legged Miniature Robots. IEEE Robot. Autom. Lett. 2022, 7, 5568–5574. [Google Scholar] [CrossRef]
- Asamura, K.; Nagasawa, S. A micro hexapod robot for swarm applications assembled from a single FPC sheet. Jpn. J. Appl. Phys. 2021, 60, SCCL03. [Google Scholar] [CrossRef]
- Bena, R.M.; Nguyen, X.-T.; Calderon, A.A.; Rigo, A.; Perez-Arancibia, N.O. SMARTI: A 60-mg Steerable Robot Driven by High-Frequency Shape-Memory Alloy Actuation. IEEE Robot. Autom. Lett. 2021, 6, 8173–8180. [Google Scholar] [CrossRef]
- de Rivaz, S.D.; Goldberg, B.; Doshi, N.; Jayaram, K.; Zhou, J.; Wood, R.J. Inverted and vertical climbing of a quadrupedal microrobot using electroadhesion. Sci. Robot. 2018, 3, eaau3038. [Google Scholar] [CrossRef]
- Fan, P.; Liu, H.; Zheng, L. Study on a new type of miniature piezo walking robot. Smart Mater. Struct. 2021, 30, 035023. [Google Scholar] [CrossRef]
- Kabutz, H.; Hedrick, A.; McDonnell, W.P.; Jayaram, K. mCLARI: A Shape-Morphing Insect-Scale Robot Capable of Omnidirectional Terrain-Adaptive Locomotion in Laterally Confined Spaces. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, America, 1 October–5 October 2023. [Google Scholar]
- Wang, W.; Deng, J.; Li, J.; Zhang, S.; Liu, Y. A Small and Agile Ring-Shaped Tripodal Piezoelectric Robot Driven by Standing and Traveling Mechanical Waves. Sci. Adv. 2024, 10, 2769–2778. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Deng, J.; Zhang, S.; Chen, W.; Xie, H.; Zhao, J. Arthropod-Metamerism-Inspired Resonant Piezoelectric Millirobot. Adv. Intell. Syst. 2021, 3, 2100015. [Google Scholar] [CrossRef]
- Li, J.; Deng, J.; Liu, Y.; Zhang, S.; Li, K. Development of a Planar Tripodal Piezoelectric Robot With a Compact Ring Structure. IEEE/ASME Trans. Mechatron. 2022, 27, 3908–3919. [Google Scholar] [CrossRef]
- Rios, S.A.; Fleming, A.J.; Yong, Y.K. Monolithic Piezoelectric Insect with Resonance Walking. IEEE/ASME Trans. Mechatron. 2018, 23, 524–530. [Google Scholar] [CrossRef]
- Seki, Y.; Yoshimoto, S.; Yamamoto, A. Performance Evaluation of a Miniaturized Leg-Swing Actuator Using Electrostatic Zipping. In Proceedings of the 16th IFToMM World Congress (IFToMM WC2023), Tokyo, Japan, 5–11 November 2023; Volume 2, pp. 399–407. [Google Scholar]
- Taghavi, M.; Helps, T.; Rossiter, J. Electro-ribbon actuators and electro-origami robots. Sci. Robot. 2018, 3, eaau9795. [Google Scholar] [CrossRef]
- Xu, Y.; Burdet, E.; Taghavi, M. Electromechanical model for electro-ribbon actuators. Int. J. Mech. Sci. 2024, 275, 109340. [Google Scholar] [CrossRef]
- Pashapour, M.; Pesteii, S.-M.; Rezazadeh, G.; Kouravand, S. Thermo-Mechanical behavior of a bilayer microbeam subjected to nonlinear electrostatic pressure. Sens. Transducers 2009, 103, 161–170. [Google Scholar]
- Yamamoto, A.; Nagasawa, S.; Yamamoto, H.; Higuchi, T. Electrostatic tactile display with thin film slider and its application to tactile telepresentation systems. IEEE Trans. Vis. Comput. Graph. 2006, 2, 168–177. [Google Scholar] [CrossRef] [PubMed]
- Giraud, F.; Amberg, M.; Lemaire-Semail, B. Merging two tactile stimulation principles: Electrovibration and squeeze film effect. In Proceedings of the 2013 World Haptics Conference (WHC), Daejeon, Republic of Korea, 14–17 April 2013; pp. 199–203. [Google Scholar]
- Vezzoli, E.; Amberg, M.; Giraud, F.; Lemaire-Semail, B. Electrovibration Modeling Analysis. In Haptics: Neuroscience, Devices, Modeling, and Applications; Auvray, M., Duriez., C., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 369–376. [Google Scholar]
- Chen, A.S.; Zhu, H.; Li, Y.; Hu, L.; Bergbreiter, S. A paper-based electrostatic zipper actuator for printable robots. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5038–5043. [Google Scholar]
- Felder, J.; Lee, E.; DeVoe, D.L.; Disarro, T.P.; Smith, J.A.; Felton, S.M. Large Vertical Displacement Electrostatic Zipper Microstage Actuators. IEEE Trans. Ind. Electron. 2024, 71, 2669–2778. [Google Scholar]
- Gravert, S.-D.; Varini, E.; Kazemipour, A.; Michelis, M.Y.; Buchner, T.; Hinchet, R.; Katzschmann, R.K. Low-voltage electrohydraulic actuators for untethered robotics. Sci. Adv. 2024, 10, 2669–2778. [Google Scholar] [CrossRef]














Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seki, Y.; Yamamoto, A. An Arch-Shaped Electrostatic Actuator for Multi-Legged Locomotion. Robotics 2024, 13, 131. https://doi.org/10.3390/robotics13090131
Seki Y, Yamamoto A. An Arch-Shaped Electrostatic Actuator for Multi-Legged Locomotion. Robotics. 2024; 13(9):131. https://doi.org/10.3390/robotics13090131
Chicago/Turabian StyleSeki, Yusuke, and Akio Yamamoto. 2024. "An Arch-Shaped Electrostatic Actuator for Multi-Legged Locomotion" Robotics 13, no. 9: 131. https://doi.org/10.3390/robotics13090131
APA StyleSeki, Y., & Yamamoto, A. (2024). An Arch-Shaped Electrostatic Actuator for Multi-Legged Locomotion. Robotics, 13(9), 131. https://doi.org/10.3390/robotics13090131






