Abstract
Recent advancements in quadrupedal robotics have explored the motor potential of these machines beyond simple walking, enabling highly dynamic skills such as jumping, backflips, and even bipedal locomotion. While reinforcement learning has demonstrated excellent performance in this domain, it often relies on complex reward function tuning and prolonged training times, and the interpretability is not satisfactory. Riemannian motion policies, a reactive control method, excel in handling highly dynamic systems but are generally limited to fully actuated systems, making their application to underactuated quadrupedal robots challenging. To address these limitations, we propose a novel framework that treats each leg of a quadrupedal robot as an intelligent agent and employs multi-agent reinforcement learning to coordinate the motion of all four legs. This decomposition satisfies the conditions for utilizing Riemannian motion policies and eliminates the need for complex reward functions, simplifying the learning process for high-level motion modalities. Our simulation experiments demonstrate that the proposed method enables quadrupedal robots to learn stable locomotion using three, two, or even a single leg, offering advantages in training speed, success rate, and stability compared to traditional approaches, and better interpretability. This research explores the possibility of developing more efficient and adaptable control policies for quadrupedal robots.
1. Introduction
1.1. Background
Quadrupedal robots have garnered significant attention in recent years due to their potential for navigating complex terrains and performing versatile tasks. Compared to wheeled or humanoid robots, quadrupedal robots combine more stability with flexible locomotion. Quadrupedal motion is a widespread structure in nature, and quadrupedal robots have a lot of potential to improve their locomotion. Recent advances in quadrupedal robotics have focused on improving locomotion control, enabling these robots to perform more dynamic and agile maneuvers. Traditional approaches to quadrupedal locomotion control often relied on hand-crafted algorithms and control strategies, such as the model predictive control (MPC) [1] or the zero-moment point (ZMP) methods [2]. These methods have been successful in achieving stable walking on flat surfaces and have been implemented on various quadrupedal platforms, such as the MIT Cheetah and the ANYmal robot. However, these approaches struggle to adapt to uneven terrains and lack the flexibility to perform more dynamic maneuvers, such as jumping or running. To address the limitations of traditional approaches, machine learning techniques have been increasingly applied to quadrupedal robot control. Supervised learning methods, such as neural networks, have been used to learn locomotion patterns from expert demonstrations. These methods have shown promising results in generating stable and efficient gaits for quadrupedal robots.
Reinforcement learning (RL) has emerged as a promising approach for enabling quadrupedal robots to learn adaptive and versatile locomotion skills [3]. By allowing the robot to learn through trial-and-error interactions with its environment, RL can discover optimal control policies without relying on explicit programming. Recent advancements in deep reinforcement learning (DRL) have further enhanced the capabilities of quadrupedal robots, enabling them to learn complex behaviors such as jumping, backflips, and even bipedal walking [4,5,6]. Enabling quadrupedal robots to walk on three or two legs has significant application value, as it allows the free legs of quadrupedal robots to perform manipulation tasks, combining the advantages of both quadrupedal and humanoid robots. This capability extends the functionality of quadrupedal robots, making them more versatile and adaptable to various scenarios, such as search and rescue operations, industrial inspection, and space exploration.
Despite the successes of DRL in quadrupedal locomotion, several challenges remain. One major issue is the need for carefully designed reward functions that guide the learning process toward desired behaviors. Crafting effective reward functions often requires extensive domain knowledge and trial-and-error tuning, which can be time consuming and limit the scalability of these methods. As the robot learns more complex skills, the design of the reward function becomes increasingly complex and task-specific, leading to less generalizable policies. This lack of generalizability hinders the robot’s ability to adapt to new tasks or environments without extensive retraining. Additionally, the learned policies often lack interpretability, making it difficult to understand and trust the robot’s decision-making process.
Riemannian motion policies (RMPs) have emerged as a promising approach for generating reactive and adaptive motions in highly dynamic environments. RMPs leverage the geometric structure of the robot’s configuration space to produce smooth and efficient motions that can quickly respond to changes in the environment [7]. The key principle behind RMPs is to define a Riemannian metric that encodes the desired behavior of the robot, such as obstacle avoidance or goal reaching, and then, use this metric to generate motion commands. One of the main advantages of RMPs is their ability to output reactive actions, which are crucial for robots operating in dynamic and uncertain environments. By continuously updating the robot’s motion based on the current state and the learned metric, RMPs can generate appropriate actions in real time without the need for extensive planning or optimization. This reactivity makes RMPs well suited for handling disturbances and adapting to changing conditions. However, the application of RMPs has primarily been limited to fully actuated systems [8], such as robotic arms [9]. In a fully actuated system, the number of actuators (motors or joints) is equal to the number of degrees of freedom, allowing the robot to independently control each degree of freedom. This property simplifies the application of RMPs, as the learned metric can directly map to the robot’s actuation commands.
On the other hand, many robotic systems, including quadrupedal robots, are underactuated, meaning they have fewer actuators than degrees of freedom. In these systems, the direct application of RMPs becomes more challenging, as the robot cannot independently control all its degrees of freedom. To address this issue, some studies have explored the use of kinematic decomposition to apply RMPs to underactuated systems, such as wheeled inverted pendulum robots [10]. By decomposing the robot’s motion into controllable and uncontrollable subspaces, these approaches can apply RMPs to the controllable subspace while handling the uncontrollable dynamics separately. Recent research has also investigated the application of RMPs to bipedal robots, which are inherently underactuated due to their floating base [11]. These studies have shown promising results in generating stable and adaptive walking motions by combining RMPs with other control techniques, such as whole-body control or model predictive control. However, the application of RMPs to quadrupedal robots, which exhibit more complex dynamics and require coordination between multiple legs, remains an open challenge.
1.2. Contributions
We propose a novel method for a quadrupedal robot to learn advanced motions, such as three-legged, two-legged, and one-legged locomotion (Figure 1). Our hierarchical architecture integrates multi-agent reinforcement learning (MARL) with Riemannian motion policies (RMPs) and a multi-head structure (Figure 2). The main contributions of our work are:

Figure 1.
Our proposed method enables quadrupedal robots to quickly learn advanced skills such as bipedal walking.
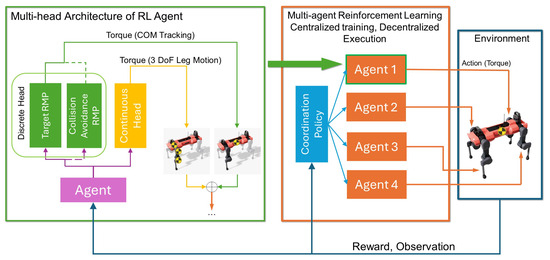
Figure 2.
Overview: The system consists of two main components: the multi-head architecture of the RL agent with RMPs, and the multi-agent reinforcement learning framework for centralized training and decentralized execution. The combination of the multi-head architecture and multi-agent reinforcement learning allows the system to learn complex and adaptive locomotion behaviors for the quadrupedal robot. The multi-head architecture enables the generation of appropriate torques for each leg, considering factors such as motion mode, self-collision avoidance, and center-of-mass tracking. The multi-agent reinforcement learning framework facilitates the coordination and synchronization of the four legs to achieve stable and efficient locomotion.
- Extending the applicability of RMPs to underactuated systems, such as quadrupedal robots, by leveraging the MARL framework for dynamic space decomposition.
- Learning diverse locomotion modes in a unified framework, such as three-legged, two-legged, and one-legged walking, within a single architecture, enabling the robot to maintain balance and stability in different motion policies by performing reactive center-of-mass tracking.
- Introduction of a multi-head structure agent to handle both discrete and continuous actions simultaneously.
- Demonstration of the method’s effectiveness through simulation experiments, showcasing advantages in learning efficiency, stability, and success rate, particularly in challenging tasks.
1.3. Layout
This paper is organized as follows. In Section 2, the fundamentals of the techniques used in our proposed framework are presented. This section includes the theory of Riemannian motion policies and the basic principles of reinforcement learning to control quadrupedal robots (Section 2.1, Section 2.2 and Section 2.3), and the working principle of distributed multi-agent reinforcement learning. In Section 3, how to build our proposed framework is presented, including the design of the RMPs, the design and implementation of agents with multi-head structure, and training using the distributed multi-agent RL framework (Section 3.1, Section 3.2, Section 3.3 and Section 3.4). In Section 4, experimental results training, simulation, and quantitative analysis are presented (Section 4.1, Section 4.2 and Section 4.3). Finally, we summarize the methodology and results in Section 5.1 and discuss the strengths and weaknesses and future work in Section 5.2.
2. Related Work
2.1. RMPs and RMPflow
Riemannian motion policies (RMPs), introduced by Ratliff and colleagues in [8], provide a novel perspective on motion planning and control by viewing task space as a manifold and describing motion using geodesics, which are the shortest paths on this manifold. In this framework, motion policies are considered generators of geodesics, and their behavior can be controlled by altering the Riemannian metric of the manifold. By choosing appropriate metrics, geodesics can form curved trajectories, exemplifying the application of RMPs.
Formally, RMPs are specified for a manifold with coordinate map x and defined acceleration , where a is the motion policy. An RMP is represented as , which combines the motion policy a with an importance weight M, a symmetric positive-definite matrix function that often represents the Riemannian metric of the manifold. The expression is known as the canonical form of an RMP, while is referred to as the natural form, with being the control force. One of the key advantages of RMPs is that motion policies can be transformed between manifolds using techniques from differential geometry, treating them as geometric objects. This allows for the seamless integration of multiple motion policies defined on different task manifolds. The configuration space of a robot is an n-dimensional manifold with a global chart , and task manifold motion policies can be mapped onto using techniques like the pullback operation. By leveraging the geometric structure of the task space and the configuration space, RMPs offer a powerful tool for motion planning and control in various applications, such as robotic manipulation and locomotion.
RMPflow [12] is a computational framework that embodies this concept, facilitating the consistent integration of task-space RMPs into a single motion policy on . It employs a tree-structured computational graph called an RMP-tree. Within an RMP-tree, each node represents an RMP and its corresponding state on a manifold, while the edges signify the operations that transform RMPs and states between nodes. The root node corresponds to the configuration space, and the leaf nodes correspond to the task spaces. The set of edge operations, collectively termed RMP-algebra, consists of three transformations: pushforward, pullback, and resolve.
2.2. Deep Reinforcement Learning for Quadrupedal Robots
Deep reinforcement learning (DRL) has emerged as a powerful approach for enabling quadruped robots to learn complex locomotion skills [13]. In DRL, an agent learns to make optimal decisions by interacting with its environment and receiving rewards or penalties based on its actions. The goal is to maximize the cumulative reward over time, which encourages the agent to discover effective control policies.
To apply DRL to quadruped robot control, the problem is typically modeled as a Markov decision process (MDP). An MDP is defined by a tuple , where represents the state space, denotes the action space, describes the transition probability between states, is the reward function, and is the discount factor that determines the importance of future rewards. In the context of quadruped robot control, the state space typically includes information such as the robot’s joint angles, velocities, and body orientation. The action space corresponds to the motor commands sent to the robot’s actuators, which can be continuous (e.g., joint torques) or discrete (e.g., predefined gait patterns). The transition probability represents the dynamics of the robot and its interaction with the environment, which can be either explicitly modeled or learned through experience.
The reward function plays a crucial role in guiding the learning process. It assigns a scalar value to each state–action pair, indicating the desirability of the action taken in that state. In quadruped locomotion tasks, the reward function often includes terms that encourage forward progress, stability, and energy efficiency, while penalizing falls and undesired behaviors [14].
A typical DRL training process for quadruped robot locomotion involves the following steps: The agent observes the current state of the robot and its environment. Based on the observed state, the agent selects an action according to its policy . The robot executes the chosen action and transitions to a new state according to the transition probability . The agent receives a reward based on the action taken and the resulting state. The agent updates its policy using a DRL algorithm, such as Q-learning [15], policy gradients [16], or actor–critic methods [17], to maximize the expected cumulative reward. The process repeats from step 1 until the agent converges to a satisfactory policy or a predefined termination criterion is met.
By iteratively exploring the state–action space and updating its policy, the DRL agent learns to make intelligent decisions that enable the quadruped robot to achieve stable and efficient locomotion. However, as the complexity of the task increases, the design of the reward function becomes more and more complex. For example, detailed objectives for the positions that need to be achieved by each joint of the robot.
2.3. Distributed Multi-Agent Reinforcement Learning Framework
Multi-agent reinforcement learning (MARL) is an extension of single-agent reinforcement learning (SARL) that deals with the challenges of learning in environments where multiple agents interact [18]. In MARL, each agent aims to learn an optimal policy that maximizes its individual or shared reward while considering the actions of other agents. The presence of multiple agents introduces additional complexities, such as coordination, communication, and potential conflicts among agents.
The key difference between MARL and SARL lies in the environment and the interactions among agents. In SARL, a single agent interacts with the environment and aims to maximize its cumulative reward. The agent’s actions directly influence the environment, and the environment’s state transitions depend solely on the agent’s actions. In contrast, MARL involves multiple agents acting simultaneously in the same environment. Each agent’s actions not only affect the environment but also influence the actions and rewards of other agents [19]. This interdependence among agents necessitates consideration of joint actions, joint observations, and potentially conflicting goals.
Diverging from the singular entity focus of traditional reinforcement learning and the decision-making framework of Markov decision processes, the domain of multi-agent reinforcement learning is encapsulated by the dynamics of a Markov game. This scenario unfolds with several agents independently and concurrently making decisions and taking actions, steered by the prevailing environmental state. The cumulative action choices determine the trajectory of environmental progression and its evolving state. The structure of this Markov game is encapsulated by the tuple , where S is the inventory of possible states, and are the respective sets of possible actions and rewards for agent i, and T embodies the state transition probabilities alongside the discount factor . The expected return for agent i, when employing policy , is quantified as
In multi-agent reinforcement learning pursuits, the quest is to achieve a Nash equilibrium among all agents involved. This conveys that in a collective scenario where agents cooperate, no single agent can improve its aggregate rewards by unilaterally altering its established policy. It is imperative to note that the Nash equilibrium is not synonymous with the absolute optimum; rather, it epitomizes the most expected stable condition and represents a convergence target during the learning phase.
Our previous work [20] has demonstrated that MARL can be effectively applied to train individual robots by treating the robot’s individual driving parts as separate agents. This approach offers several advantages. First, it compresses the action space, as each agent is responsible for controlling a specific part of the robot, rather than the entire robot. Second, it speeds up the training process, as the agents can learn their policies in parallel. Third, it provides each part of the robot with some degree of autonomy, allowing for more flexible and reactive behavior.
3. Methods
3.1. Overview
To realize our approach, we design a hierarchical architecture that integrates multi-agent reinforcement learning with RMPs. The top layer consists of collaborative policies that coordinate the movement of the four legs, while in the middle layer, we build an agent using a multi-head structure, which can output both discrete and continuous actions. In the bottom layer, multiple RMPs are deployed within the discrete head, which executes center-of-mass (COM) tracking actions based on the selected RMPs, the continuous head then outputs leg torque to ensure safety and stability during locomotion. In the following, we will detail how each layer is constructed.
3.2. RMPs for Leg Locomotion Control
In our analytical treatment of the quadruped robot’s dynamics, we initially partition the system into four discrete dynamical sectors. Each sector encompasses an individual leg in conjunction with the robot’s central trunk. Within each of these independent sectors, we identify three articulations corresponding to three degrees of freedom, thereby constituting a fully actuated subsystem, shown in Figure 3. This segmentation facilitates the direct application of RMPs to each leg–trunk pair.

Figure 3.
The area controlled by each agent includes a leg and trunk section.
It is critical to acknowledge that the trunk segment exhibits a state of superposition across the four delineated spaces. This characteristic is harmonious with the underlying architecture of our proposed model, wherein the collective operation of the quadruped’s limbs is synchronized to fortify the trunk’s stability. This synergy is a cornerstone of our approach, ensuring that the locomotive integrity of the robot is preserved through the coordinated mechanics of its constituent parts. The dynamics of legged robotic systems can be encapsulated by a set of fundamental equations that describe their motion:
In this equation, represents the generalized mass matrix, stands for the Coriolis force vector, and is the vector of gravitational forces. The matrix is used to select the actuated joints. The vectors and denote the torques at the joints and the augmented reaction forces, respectively, while is the contact Jacobian matrix that relates the forces at the points of contact to the joint torques. The term signifies the acceleration within the configuration space, with n being the count of actuated degrees of freedom in the robot’s structure. In this section, we will use two RMPs for control: the target RMP and the collision avoidance RMP.
3.2.1. Target RMP for Center-of-Mass Tracking
Center-of-mass tracking is an effective policy for keeping quadrupedal robots stable [21]. The function of the target RMP is to maintain the COM of the robot’s trunk at the desired position by outputting the leg’s locomotion. This function is similar to the target RMP in a robotic arm. However, there is a key difference: the robot’s foot contact with the ground is not fixed. This variability can be considered a kind of disturbing noise. This issue is addressed later on in reinforcement learning. In addition, it is almost impossible for one leg to maintain the center-of-mass stabilization on its own, but the four-legged agents can work together to solve this problem, and here, we only need to formulate a local RMP. The target RMP’s behavior is governed by the following equation:
The term represents the position gain, which plays a crucial role in the control of motion policies. The damping RMP, on the other hand, is given by , where is the damping gain. This damping term is essential because undamped Riemannian motion policies can lead to persistent oscillations when tracking a dynamic target. By incorporating damped RMPs, these oscillations can be significantly reduced, resulting in smoother and more stable motion. The parameter sets the transition scale from constant acceleration to linear behavior around the target. This parameter allows for a smooth transition between different motion regimes, ensuring that the robot’s movement remains continuous and well behaved.
Each motion policy in the RMP framework is associated with a specific Riemannian metric, denoted by M. The Riemannian metric plays a crucial role in determining the behavior of the motion policy, as it defines the notion of distance and curvature on the manifold. For a comprehensive understanding of how the Riemannian metric is derived, the reader is referred to [8], which provides a detailed explanation of the underlying mathematics. The Riemannian metric for the target RMP is constructed as follows:
The metric M, also known as the inertia matrix, lies within the range defined by the rank-deficient metric S and the identity matrix I. The metric S has a significant impact in areas far from the target, while the identity matrix I becomes dominant near the target, promoting faster convergence. The blending of these matrices is controlled by a radial basis function, specifically a Gaussian function, which smoothly transitions from a constant minimum value far from the target to a value close to 1 near the target.
In the above equations, the following definitions apply:
The parameters and are length scales, measured in meters, for the Gaussian functions used in the construction of the Riemannian metric for the target RMP. Specifically, is the length scale for the Gaussian function that blends the matrices S and I, which are used to define the metric’s behavior. On the other hand, is the length scale for the Gaussian function that enhances boosting near the target, allowing for more aggressive control when the robot is close to its goal. The parameter sets the minimum influence of on the overall Riemannian metric M. This ensures that the metric maintains a certain level of responsiveness even when the robot is far from the target. The priority weights and determine the relative influence of and on the overall metric M, respectively. These weights allow for a balance between the near and far target behaviors, enabling the robot to smoothly transition between different control regimes. Finally, the scaling factor b adjusts the intensity of the strengthening effect near the target. A higher value of b results in a more pronounced boosting effect, allowing for faster convergence to the target when the robot is in close proximity.
3.2.2. Collision Avoidance RMP for Leg Locomotion
The RMP framework includes a collision avoidance RMP designed to prevent collisions between the robot’s legs. To ensure computational efficiency, the geometric properties of the robot’s links are approximated using capsules, reducing the collision avoidance problem to avoiding collisions between witness points on these capsules. Only one collision RMP is required for each pair of link capsules, and the position of the witness points is determined using the algorithm proposed in the RMP framework. These collision avoidance RMPs are defined in a one-dimensional Euclidean distance space and are characterized by a repulsive acceleration policy and a corresponding metric. The repulsive acceleration policy ensures that the witness points on the capsules are pushed away from each other when they come too close, while the corresponding metric determines the strength and shape of the repulsive force, allowing for the desired balance between safety and efficiency.
where
The collision avoidance RMP is defined in terms of the Euclidean distance x between witness points on the capsules and its rate of change . The repulsion gain and damping gain determine the strength of the repulsive force and resistance to movement, respectively. The parameter sets the relative priority of the collision RMP, which is adjusted end-to-end by reinforcement learning (RL) in subsequent layers. The threshold distance determines the activation of the collision RMP, while scaling parameters , , and and offset parameters and enable fine-tuning of the collision avoidance behavior based on the specific requirements of the task and the robot’s environment.
3.3. Multi-Head Architecture of RL Agent
As discussed in the previous sections, we have decomposed the quadrupedal robot into four dynamic sections, each controlled by an agent with a multi-head structure [22]. This approach allows for more efficient and effective training of the robot, as each agent is responsible for controlling a specific part of the robot and can learn its policy.
The multi-head structure of the reinforcement learning agents enables them to output a mixture of actions, both discrete and continuous. The reason we introduce a multi-head structure is that we are not planning for gait and only need to satisfy the final reward maximization, so the movement of the legs is completely controlled end-to-end by the policy network. In this study, we employ two heads, a discrete head and a continuous head, and the two heads share an environment feature extractor. The discrete head is responsible for deciding whether to use the target RMP or the collision avoidance RMP. This decision is made within a short time frame of less than 2 ms, ensuring reactive action output. The moments generated by the selected RMP are then tracked against the COM position of the robot’s trunk, as the task requires a quick response to deviations.
Multi-head reinforcement learning (RL) and hierarchical RL are similar in structure, but they differ significantly in how they operate. Multi-head RL simultaneously generates multiple actions, whereas hierarchical RL chooses just one action from several options before executing it. This is a Markov decision process (MDP) characterized by a set of possible states , a repertoire of actions , a probability distribution for state transitions , and a function that assigns rewards . We refer to as a stochastic policy. The structure of the multi-head reinforcement learning agent can be described as follows:
where represents the overall policy of the agent, denotes the policy for the discrete head, and represents the policy for the continuous head. The discrete action is sampled from a categorical distribution, while the continuous action is sampled from a continuous distribution, such as a Gaussian distribution. The discrete head of the agent selects between the target RMP and the collision avoidance RMP based on the current state s. This selection is made by sampling from the categorical distribution output by the discrete policy . The chosen RMP then generates the appropriate moments to be tracked against the COM position of the trunk.
The discount factor , which lies between 0 and 1 (not inclusive), reduces the value of future rewards, and a trajectory represents a sequence of states and actions obtained from the system. The strategy of policy gradient techniques is to refine the policy in a direct manner. Typically, the policy is realized using a function that is defined by parameters . Moving forward, we will use to refer both to the specific parameters and the policy itself. In the domain of DRL, this policy is often encoded within a neural network known as the policy network, and we assume that it is smoothly differentiable with respect to the parameters .
On the other hand, the continuous head of the agent outputs moments for each joint of the leg with 3 degrees of freedom (DOF). These moments are used to control the leg motion and are sampled from the continuous distribution output by the continuous policy . The continuous actions are then applied to the corresponding joints of the leg, enabling smooth and coordinated locomotion.
The multi-head structure of the reinforcement learning agent allows for the simultaneous learning of discrete and continuous actions, which is particularly useful in tasks that require both high-level decision making and fine-grained control. By decomposing the control of the quadrupedal robot into separate agents with multi-head structures, we can effectively train the robot to perform complex tasks that involve both reactive decision making and precise leg motion control.
3.4. Updating Policies Using Distributed Multi-Agent RL Framework
Having constructed the agents using a multi-head structure, we proceed to train the four agents using distributed multi-agent reinforcement learning. We employ a centralized training, decentralized execution (CTDE) paradigm, specifically, the Multi-Agent Proximal Policy Optimization (MAPPO) method [23]. CTDE [24] is a popular approach in multi-agent reinforcement learning, where the training process is centralized, allowing agents to access additional information and learn coordinated policies, while the execution is decentralized, enabling each agent to make decisions based on its local observations. This paradigm strikes a balance between the benefits of centralized learning and the practicality of decentralized execution. MAPPO is an extension of the Proximal Policy Optimization (PPO) algorithm [25] to the multi-agent setting. In MAPPO, each agent maintains its policy and value function , while a central critic is used to estimate the total expected return of all agents. The central critic takes the joint state s and joint action as input, where n is the number of agents. During training, MAPPO updates the policies of all agents simultaneously using the following objective function:
where and are the parameters of the current and previous policies of agent i, respectively, and is the multi-agent advantage function, defined as
where r is the immediate reward, is the discount factor, and and are the next state and joint action, respectively.
In our task, the other legs are part of the environment for the leg being controlled, which provides a stable training environment for each individual agent. The central coordination policy helps to adjust the weights of each agent’s actions in different states, all agents can be in a state of dynamic equilibrium through collaboration. Specifically, for an agent, the action outputs of all other agents become environmental perturbations for this agent, who maintains the output action in the center-of-mass position. Similarly the action output of agent will also perturb the environment of all other agents, which in turn will allow all agents to make adjustments. The collaborative mechanism generated by the centralized training and reward function will help the multiple agents to enter a state of dynamic equilibrium. While a single agent cannot maintain a stable COM on its own, the coordination of all four agents can achieve this goal. Therefore, we do not need to pre-train individual agents and can proceed directly to full end-to-end training to obtain the desired result.
By utilizing the CTDE paradigm and the MAPPO algorithm, we can effectively train the multi-head agents to learn coordinated policies that enable the quadrupedal robot to maintain a stable COM and perform the desired tasks. The centralized training allows the agents to learn cooperative behaviors, while the decentralized execution ensures that each agent can make decisions based on its local observations during deployment.
3.5. Rewards
The reward function is a crucial component of reinforcement learning, as it guides the policy update process by providing feedback on the desirability of the agent’s actions. The complexity of the reward function often increases with the complexity of the task. For example, some previous studies have designed detailed reward terms to approximate the robot’s actions to teacher samples through adversarial and imitation learning [3,6]. For a standing task, the reward function needs to be designed as follows:
where
Here, the is the robot base-frame rotation. is the robot base-frame position. q is the joint DOF positions (excluding wheels). is the hind-Leg DOF position. is the robot axis, world axis). f is the feet on the ground (binary). s is the standing robots (binary). It is worth noting that the reward function applied by this method [3] is only applicable to the bipedal standing task and needs to be redesigned for other movements.
However, our proposed method relies less on the intricacies of the reward function design, making it more accessible and easier to implement. The reward function in our framework consists of three main components: First, a reward for minimizing the deviation of the COM from a set value in the x-, y-, and z-directions. Second, a reward for minimizing the angle between the horizontal direction of the robot’s coordinate system and the vertical direction of the world’s coordinate system, encouraging the robot to maintain an upright posture during the standing task. Third, a penalty term, our reward function needs little change for the different tasks, only the addition of a penalty term for when the leg makes contact with the ground. The reward function can be formally defined as follows:
denotes the reward for tracking COM, which increases when the agent outputs an action that reduces the deviation of the robot’s COM from the target position. For each agent, is the same. is the posture reward item, which increases when the angle between the robot’s trunk direction and the set target axis is reduced. For example, for the bipedal standing task, we set the Z-coordinate axis as the target, and when the agent outputs an action, the torso that remains vertical will receive a higher score, so this item can encourage the robot to maintain the standing posture. is the decay factor; the item is a hyperparameter, and the addition of the item and the value of the setting depends on experience and testing. After testing we found that adding a decay factor for the item was better, while was not suitable to add. t is the current time step, making the exponent decrease over time. By incorporating t in this way, the reward function can be dynamically adjusted, allowing the robot to focus on maintaining balance and stability initially, and then, gradually shifting attention to refining its movements and achieving more sophisticated locomotion patterns as the episode progresses. This temporal scaling helps in balancing the immediate and long-term objectives of the learning process. The is a penalty item with a negative reward that increases when the leg we set touches the ground, which in turn affects the global score, so this item makes the agent less likely to choose actions that we discourage. For example, in the bipedal standing task, we do not want the front left and front right legs to touch the ground, so we add penalties to both agents’ actions. Here, we define
where:
- , , and represent the current position of the COM in the x-, y-, and z-directions, respectively. , , and denote the target position of the COM in the x-, y-, and z-directions, respectively.
- is the angle between the orientation of the robot trunk and the vertical direction of the world’s coordinate system.
- is the decay factor for the leg contact penalty term. t represents the current time step.
- is a binary variable indicating whether the specified leg is in contact with the ground (1 for contact, 0 for no contact).
Our framework’s simplicity and flexibility allow for the learning of advanced skills, such as bipedal walking for the ANYmal C robot, with minimal modifications to the reward function. To achieve this, we set the target trajectory of the COM to a desired height (e.g., ) and specify the direction of motion (e.g., along the horizontal y-direction). By providing these straightforward guidelines, the robot can learn to walk in a bipedal manner without the need for a complex, task-specific reward function. Combining the multi-head agent structure, distributed multi-agent reinforcement learning, and the simplified reward function enables our framework to effectively learn complex behaviors while maintaining a high degree of generalization and adaptability to various tasks.
4. Experiments and Results
4.1. Experiment Setup
We used Isaac Gym, a simulation environment that allows large-scale parallel training using GPUs [26], and ANYmal C Robotics, developed by ANYRobotics [27], which is very powerful and has good support for RL-related algorithms, as our experimental platform. We incorporated accurate models of the robot’s kinematics, inertial properties, and actuator characteristics based on the specifications provided by the manufacturer. Based on these data, our simulation environment was carefully designed and validated to closely mimic the physical properties, dynamics, and constraints of the real robot. For specific simulation parameters, the stiffness is 85.0 Nm/rad, damping is 2.0 Nm/rad, action scale is set as 0.5, control frequency is 18 Hz, gravity is −9.81 N, number of position iterations is 4, number of velocity iterations is 1, bounce threshold velocity is 4, and maximum depenetration velocity is 100.
To bridge the gap between simulation and display, we use domain randomization techniques that allow agents to cope with environments that vary over a range rather than a single fixed environment. Specific parameters include, initial position range 0 s∼60 cm, initial orientation range 0∼2 rad, joint static ratio errors ±0.08, joint dynamic ratio errors ±0.05, friction coefficient ±0.05, joint damping range 0.5∼1.5 N, joint stiffness range 0.5∼1.5 N, mass errors ±1.5 g, and height of COM errors ±0.5 cm.
We ran 4096 parallel simulations on an Nvidia RTX4070 GPU, and we learned three tasks, namely, walking on three legs, walking upright on two legs, and jumping on one leg. We observed and recorded experimental data. The videos of the simulation results for all experiments can be found in the Supplementary Materials with download links.
4.2. Training
To evaluate the effectiveness of our proposed method, we compared its performance with the popular reinforcement learning algorithm Proximal Policy Optimization (PPO). The results of this comparison are presented in Figure 4. The x-axis of the graph represents the number of samples used during training, while the y-axis indicates the episode length, which serves as a measure of the learned policy’s effectiveness. Presenting the training results, particularly the rewards, in a unified graph is challenging due to the significant differences between single-agent reinforcement learning and the action space in our framework. These differences make it difficult to directly compare the reward values across different settings. However, to provide a meaningful comparison and insight into the effectiveness of the learned strategies, we analyzed the episode length during training. The episode length represents the duration for which the robot can successfully execute a learned strategy without failing and requiring a reset of the environment. A higher episode length indicates that the agent has learned a more robust and effective policy.
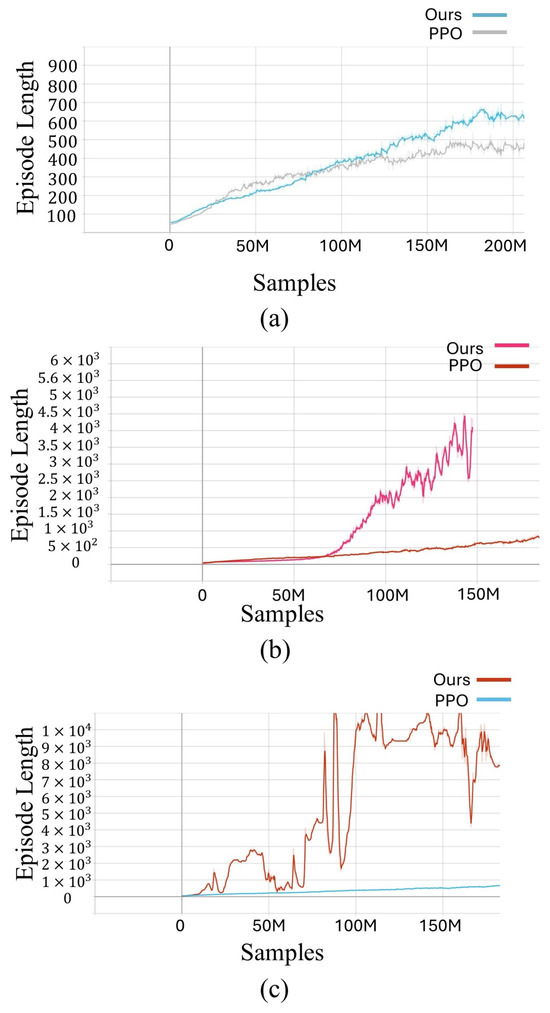
Figure 4.
Comparison of the proposed method with PPO on different tasks: (a) Three-legged walking, (b) two-legged upright walking, and (c) one-legged walking.
In experiments, the environment is reset whenever the robot falls. Consequently, a higher episode length on the y-axis indicates a more effective learned policy, as it demonstrates the robot’s ability to maintain stable walking for an extended period without falling. The steepness of the learning curve reflects the speed at which the policy is learned.
Our method achieved an advantage over PPO in each of the tasks investigated. Notably, we observed that the performance gap between the two methods widened as the difficulty of the task increased. In Figure 4a, the task involves walking using three legs. While PPO manages to learn a relatively effective policy, our method demonstrates a higher success rate and faster learning speed. Figure 4b presents the results for the task of walking upright using two legs, which poses a greater challenge. Initially, our method exhibits similar performance to PPO. However, after 70 M samples, the score of our method rapidly improves, eventually surpassing PPO in both training speed and final performance. Further observations revealed that PPO failed to learn an effective policy for walking upright on two legs. The most demanding task, one-legged walking, is depicted in Figure 4c. Maintaining an upright posture on a single leg is highly unstable due to the robot’s structural constraints, resulting in significant fluctuations in our method’s learning curve. Despite these challenges, our method ultimately learns an effective policy. In contrast, PPO once again fails to learn a successful policy for this task.
In terms of training results, our approach allows for the learning of highly dynamic locomotion or skills without complex reward design.
4.3. Simulation Results
In the simulation experiments, we observed the robot’s action posture under various conditions. We first conducted a three-legged walking experiment, and the results are presented in Figure 5. In this experiment, we added a penalty term for one leg being in contact with the ground, set the center-of-mass height position to , and specified the motion along the x-axis. The robot’s objective was to walk along the x-direction without falling. We observed that the robot could perform stable walking while lifting one leg. To investigate the effect of lifting different legs, we tested the robot’s performance when lifting the back leg (Figure 5a) and the left front leg (Figure 5b). In both cases, the robot maintained stable walking, suggesting that all four of our agents learned effective policies to help stabilize the tracking of the center-of-mass position.
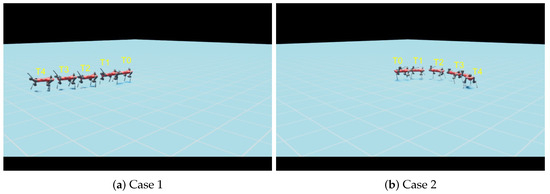
Figure 5.
Three-legged walking experiment: (a) Lifting the back leg and (b) lifting the left front leg. The robot demonstrates stable walking while lifting one leg, indicating that all four agents learned effective policies to stabilize the tracking of the center-of-mass position.
We proceeded to test the bipedal walking experiment, and the results are shown in Figure 6. In this experiment, we set a penalty term for the left front and right front legs being in contact with the ground, adjusted the center-of-mass height position to , and specified movement along the x-axis. The robot’s task was to walk along the x-direction without falling. We observed that the robot could perform stable walking using both legs. Interestingly, even though two legs were not actively involved in walking, their locomotion still contributed to stabilizing the position of the center of mass. The reduced weight of the locomotion of these two legs did not adversely affect the walking leg, thanks to the coordination achieved through MARL.

Figure 6.
Bipedal walking experiment: (a,b) show the robot demonstrates stable walking using two legs, with the locomotion of the non-walking legs contributing to the stabilization of the center-of-mass position. (c,d) show two failure cases of the comparison method PPO.
Finally, we conducted a single-leg walking experiment, which posed a significant challenge. The result is shown in Figure 7. In this experiment, we set a penalty term for three legs being in contact with the ground, adjusted the center-of-mass height position to , and specified movement along the x-axis. The robot’s objective was to run along the x-direction without falling. We found that the robot could stabilize its balance on one leg, but maintaining the direction of motion proved to be a struggle. The robot managed to jump as far as possible in the set direction of motion but with a large deviation in direction.

Figure 7.
Single-leg walking experiment: The robot stabilizes its balance on one leg but struggles to maintain the direction of motion. Positions where the legs are in contact with the ground are marked by red markers, and positions where they are not in contact are marked by green markers. Jumping as far as possible in the set direction with a large deviation in direction.
These simulation results demonstrate the effectiveness of our proposed method in enabling the robot to learn stable walking policies under various conditions, including three-legged, bipedal, and single-leg walking. The multi-head agent structure and distributed multi-agent reinforcement learning approach allow the robot to coordinate its locomotion and maintain stability, even when faced with challenging tasks such as single-leg walking.
We further performed a quantitative analysis to compare the stabilization of single-agent reinforcement learning with PPO, MAPPO, MPC. Our proposed framework combines RMP, a multi-head structure, and MARL. By including MAPPO, a state-of-the-art MARL algorithm, in our comparison, we aim to isolate and evaluate the effectiveness of the RMP and the multi-head structure components within our framework. Comparing our framework’s performance against MAPPO allows us to assess the extent to which RMP and the multi-head structure contribute to the overall effectiveness of our approach, beyond the benefits provided by MARL alone. Thus, the MAPPO method has the same parameter settings as our method except that it does not have the RMP and polytope structure.
The traditional approach in MPC was used; this approach learns the quadrupedal robot bipedal walking task by many repetitions [28]. By comparing our framework against MPC, we aim to demonstrate the advantages of our learning-based approach in terms of adaptability and robustness. The dynamic equations of motion for such a robot can be derived from the Lagrangian, which is the difference between the kinetic energy (T) and potential energy (V) of the system, , where T is the kinetic energy of the robot and V is the potential energy of the robot. Lagrange’s equations of motion are defined as , where is the generalized coordinates (positions of joints), is the derivatives of the generalized coordinates (velocities), and is the generalized forces acting on the joints. To ensure stability, the center of mass must remain within the support polygon defined by the contact points of the feet on the ground. For a bipedal stance using legs 1 and 2, the constraint can be represented as , where a, b, and c are coefficients calculated based on the positions of the feet and . Each joint angle and torque should respect the mechanical limits of the robot: , .
The cost function is designed to balance the objectives of tracking a desired stance, minimizing control effort, and penalizing deviations from constraints. It is defined as follows: . Where is the state vector at step k, including joint angles and velocities. is the reference state vector, representing the desired stance. is the control input (torques) at step k. is the penalty for constraint violations at step k, which could be based on balance and physical limits. , , and are the weights balancing the importance of pose tracking, control effort, and constraint adherence, respectively. The full results are shown in Table 1.

Table 1.
Comparison of stability and success rates of different methods under various tasks.
To evaluate the performance of our proposed method and compare it with other state-of-the-art approaches, we conducted a quantitative analysis of the experimental results. For each task, we measured the average range of deviation of the robot’s center of mass from the target in the x-, y-, and z-directions, which reflects the degree of stabilization of the movement. Additionally, we calculated the success rate of stabilized walking over 300 simulation experiments in non-rendering mode.
Although the focus of this work was not on the 4-leg walking task, it is still informative as basic locomotion for quadrupedal robots, so we present the results here. This is implemented by not adding any penalty term for leg–ground contact. It should be noted that our approach is more suitable for highly dynamic and unstable situations. Due to the structure of the quadruped robot, having four legs touching the ground is already a relatively stable configuration, so the 4-legged walking task does not show a significant advantage over other approaches. Taken together, all methods achieved very high success rates as well as COM tracking accuracy. Due to the lack of fine-tuning for the reward function, or the introduction of imitation learning, our motion, while ensuring stability, did not exhibit the same natural movement as seen in other outstanding works. Nonetheless, the advantage of scalability in our approach was still confirmed.
In the 3-legged walking task, all methods performed relatively well. Although there was a large deviation in the z-direction due to the walking ups and downs associated with the three legs, it was within normal limits. As the tasks became more challenging, the performance of the compared methods began to deteriorate.
In the 2-legged walking task, the unstable posture led to an increased deviation range for all methods. However, our proposed approach still maintained deviations within a controllable range and demonstrated a clear advantage over PPO and MAPPO. The success rate of PPO decreased significantly in this task, with many instances of unstable walking. In contrast, MPC maintained a very good result.
The 1-legged walking task posed the greatest challenge, as the robot’s posture became extremely unstable. Consequently, the deviations from all methods became very large, and it was difficult for the robot to maintain the direction of motion. Despite these challenges, our method showed promising results, with a relatively small deviation in the z-direction, indicating that it could still maintain the standing posture. The success rate also reflected that our method ensured the motion of the robot, while PPO and MAPPO were unable to control the robot in this stance. The success rate of MPC dropped drastically, revealing its inability to fully control the robot’s locomotion and maintain stability.
Our proposed method maintains stable and controlled movement across all tasks, particularly in the challenging 2-legged and 1-legged walking scenarios. The combination of multi-agent reinforcement learning and dynamic space decomposition enables our approach to effectively coordinate and adapt the robot’s locomotion, resulting in higher success rates and better stabilization compared to state-of-the-art methods.
5. Discussion
5.1. Conclusions
We proposed a method enabling quadrupedal robots to learn advanced and unstable motions, such as walking on one, two, or three legs. Traditional control methods struggle with such tasks due to instability and the need for precise leg coordination. Our proposed approach offers a promising solution for enabling quadrupedal robots to learn complex and adaptive locomotion behaviors. The combination of multi-agent reinforcement learning, RMPs, and dynamic space decomposition allows for the effective coordination and control of the robot’s legs and stable and efficient movement, even in highly dynamic and unstable situations, by tracking COM alone.
Our architecture uses a distributed multi-agent framework for training coordinated locomotion policies, a structural multi-head agent for generating RMPs for single-leg control and center-of-mass tracking, and a bottom layer for action execution to maintain safety and stability. By treating each leg as an independent agent with a fully actuated subsystem, we effectively apply RMPs to underactuated motion control. In contrast to traditional RL methods, our approach can be used for many different tasks with only penalty item changes to the reward function, making it highly generalizable.
The experimental results show our method outperforms state-of-the-art reinforcement learning algorithms like PPO and MAPPO, as well as traditional MPC, particularly in challenging bipedal and one-leg tasks. Our method learns useful policies very quickly, even if the rewards are sparse. Our approach resulted in lower COM deviations and higher success rates, demonstrating its ability to maintain stable, controlled movement across all tasks.
It is important to note that 4-legged walking is not discussed in this paper, because it has been extensively studied, with mature solutions available. Our primary objective in this work is to showcase the capabilities and advantages of our proposed control method in enabling advanced locomotion skills, include versatility, robustness, and ability to adapt to extreme and unconventional locomotion scenarios. Our method can also be easily used in conjunction with other quadrupedal walking methods if necessary. Therefore, it will not be further elaborated on.
5.2. Limitations and Future Work
Despite the promising results, our proposed method has several limitations. Currently, we are unable to experiment on real robots due to the simulation-to-reality gap and safety concerns that need to be verified. Additionally, the transformation process from quadrupedal to bipedal morphology is not yet possible with our method, which may require further training with the aid of imitative learning. Moreover, our experiments are limited to flat terrain, and we need to introduce more environments with terrain and obstacles to train the robot to operate in the real world.
Theoretically, our approach could be applied to various robotic platforms, such as humanoid robots, wheeled–legged robots, or other robots with multiple degrees of freedom. However, applying our approach to robots with different structures and control requirements may necessitate additional considerations and modifications. While our approach provides a general framework for controlling multi-degree-of-freedom robots, developing a unified framework that can seamlessly control different robot structures without secondary training remains a challenge.
Future work could focus on addressing these limitations by extending the approach to more diverse terrains and environments and investigating the application of transfer learning to accelerate the learning process for new tasks. Furthermore, combining the proposed method with advanced generative AI and learning from large amounts of video data could enable robots to learn more complex motor skills and interaction skills by using AI to plan more complex COM motion trajectories [29].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/robotics13060086/s1, Video S1: Simulation Experiment Results.
Author Contributions
Conceptualization, Y.W.; data curation, Y.W.; formal analysis, Y.W.; funding acquisition, Y.W., R.S. and Y.Y.; investigation, R.S. and Y.Y.; methodology, Y.W.; software, Y.W.; supervision, R.S. and Y.Y.; validation, Y.W.; writing—original draft, Y.W.; writing—review and editing, R.S. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JST SPRING, Grant Number JPMJSP2124 (Japan Science and Technology Agency Support for Pioneering Research Initiated by the Next Generation), JSPS JP22H00545, JP22H05002 (Japan Society for the Promotion of Science) and NEDO JPNP20006 (New Energy and Industrial Technology Development Organization) in Japan.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Bjelonic, M.; Grandia, R.; Harley, O.; Galliard, C.; Zimmermann, S.; Hutter, M. Whole-body MPC and online gait sequence generation for wheeled-legged robots. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8388–8395. [Google Scholar]
- Nagano, K.; Fujimoto, Y. Zero Moment Point Estimation Based on Resonant Frequencies of Wheel Joint for Wheel-Legged Mobile Robot. IEEJ J. Ind. Appl. 2022, 11, 408–418. [Google Scholar] [CrossRef]
- Smith, L.; Kew, J.C.; Li, T.; Luu, L.; Peng, X.B.; Ha, S.; Tan, J.; Levine, S. Learning and adapting agile locomotion skills by transferring experience. arXiv 2023, arXiv:2304.09834. [Google Scholar]
- Qi, J.; Gao, H.; Su, H.; Han, L.; Su, B.; Huo, M.; Yu, H.; Deng, Z. Reinforcement learning-based stable jump control method for asteroid-exploration quadruped robots. Aerosp. Sci. Technol. 2023, 142, 108689. [Google Scholar] [CrossRef]
- Tang, Z.; Kim, D.; Ha, S. Learning agile motor skills on quadrupedal robots using curriculum learning. In Proceedings of the 3rd International Conference on Robot Intelligence Technology and Applications; Springer: Singapore, 2021; Volume 3. [Google Scholar]
- Vollenweider, E.; Bjelonic, M.; Klemm, V.; Rudin, N.; Lee, J.; Hutter, M. Advanced skills through multiple adversarial motion priors in reinforcement learning. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Mattamala, M.; Chebrolu, N.; Fallon, M. An efficient locally reactive controller for safe navigation in visual teach and repeat missions. IEEE Robot. Autom. Lett. 2022, 7, 2353–2360. [Google Scholar] [CrossRef]
- Ratliff, N.D.; Issac, J. Riemannian motion policies. arXiv 2018, arXiv:1801.02854. [Google Scholar]
- Shaw, S.; Abbatematteo, B.; Konidaris, G. RMPs for safe impedance control in contact-rich manipulation. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 2707–2713. [Google Scholar]
- Wingo, B.; Cheng, C.A.; Murtaza, M.; Zafar, M.; Hutchinson, S. Extending Riemmanian motion policies to a class of underactuated wheeled-inverted-pendulum robots. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Marew, D.; Lvovsky, M.; Yu, S.; Sessions, S.; Kim, D. Integration of Riemannian Motion Policy with Whole-Body Control for Collision-Free Legged Locomotion. In Proceedings of the 2023 IEEE-RAS 22nd International Conference on Humanoid Robots (Humanoids), Austin, TX, USA, 12–14 December 2023. [Google Scholar]
- Cheng, C.-A.; Mukadam, M.; Issac, J.; Birchfield, S.; Fox, D.; Boots, B.; Ratliff, N. Rmpflow: A computational graph for automatic motion policy generation. In Algorithmic Foundations of Robotics XIII: Proceedings of the 13th Workshop on the Algorithmic Foundations of Robotics; Springer International Publishing: Cham, Switzerland, 2020; pp. 441–458. [Google Scholar]
- Bellegarda, G.; Chen, Y.; Liu, Z.; Nguyen, Q. Robust high-speed running for quadruped robots via deep reinforcement learning. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 10364–10370. [Google Scholar]
- Ladosz, P.; Weng, L.; Kim, M.; Oh, H. Exploration in deep reinforcement learning: A survey. Inf. Fusion 2022, 85, 1–22. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Tan, H. Reinforcement learning with deep deterministic policy gradient. In Proceedings of the 2021 International Conference on Artificial Intelligence, Big Data and Algorithms (CAIBDA), Sanya, China, 23–25 April 2021; pp. 82–85. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Canese, L.; Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Giardino, D.; Re, M.; Spanò, S. Multi-agent reinforcement learning: A review of challenges and applications. Appl. Sci. 2021, 11, 4948. [Google Scholar] [CrossRef]
- Wang, Y.; Sagawa, R.; Yoshiyasu, Y. A Hierarchical Robot Learning Framework for Manipulator Reactive Motion Generation via Multi-agent Reinforcement Learning and Riemannian Motion Policies. IEEE Access 2023, 1, 126979–126994. [Google Scholar] [CrossRef]
- Liu, M.; Qu, D.; Xu, F.; Zou, F.; Di, P.; Tang, C. Quadrupedal robots whole-body motion control based on centroidal momentum dynamics. Appl. Sci. 2019, 9, 1335. [Google Scholar] [CrossRef]
- Luo, J.; Li, C.; Fan, Q.; Liu, Y. A graph convolutional encoder and multi-head attention decoder network for TSP via reinforcement learning. Eng. Appl. Artif. Intell. 2022, 112, 104848. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of PPO in cooperative multi-agent games. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 24611–24624. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Advances in Neural Information Processing Systems 30; Curran Associates, Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Makoviychuk, V.; Wawrzyniak, L.; Guo, Y.; Lu, M.; Storey, K.; Macklin, M.; Hoeller, D.; Rudin, N.; Allshire, A.; Handa, A.; et al. Isaac Gym: High performance GPU-based physics simulation for robot learning. arXiv 2021, arXiv:2108.10470. [Google Scholar]
- ANYmal C—The Next Step in Robotic Industrial Inspection. Available online: https://www.anybotics.com/news/the-next-step-in-robotic-industrial-inspection (accessed on 20 August 2019).
- Corbères, T.; Flayols, T.; Léziart, P.A.; Budhiraja, R.; Souères, P.; Saurel, G.; Mansard, N. Comparison of predictive controllers for locomotion and balance recovery of quadruped robots. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 5021–5027. [Google Scholar]
- Brohan, A.; Brown, N.; Carbajal, J.; Chebotar, Y.; Chen, X.; Choromanski, K.; Ding, T.; Driess, D.; Dubey, A.; Finn, C.; et al. RT-2: Vision-Language-Action Models Transfer Web Knowledge to Robotic Control. arXiv 2023, arXiv:2307.15818. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).