Multiple-Object Grasping Using a Multiple-Suction-Cup Vacuum Gripper in Cluttered Scenes

Abstract

Multiple-suction-cup grasping can improve the efficiency of bin picking in cluttered scenes. In this paper, we propose a grasp planner for a vacuum gripper to use multiple suction cups to simultaneously grasp multiple objects or an object with a large surface. To take on the challenge of determining where to grasp and which cups to activate when grasping, we used 3D convolution to convolve the affordable areas inferred by a neural network with the gripper kernel in order to find graspable positions of sampled gripper orientations. The kernel used for 3D convolution in this work was encoded, including cup ID information, which helps to directly determine which cups to activate by decoding the convolution results. Furthermore, a sorting algorithm is proposed to determine the optimal grasp among the candidates. Our planner exhibited good generality and successfully found multiple-cup grasps in previous affordance map datasets. Our planner also exhibited improved picking efficiency using multiple suction cups in physical robot-picking experiments. Compared with single-object (single-cup) grasping, multiple-cup grasping contributed to $1.45\times$, $1.65\times$, and $1.16\times$ increases in efficiency for picking boxes, fruits, and daily necessities, respectively.

1. Introduction

With the growth of e-commerce, demand for the automation of bin picking by robots in warehouses has become high [1], particularly in Japan, since the country is faced with a labor shortage due to its aging society. COVID-19 has made the situation worse since picking tasks in warehouses is not amenable to telework. Most state-of-the-art robotic picking systems focus on single-object grasping. To further improve the efficiency of these systems, simultaneous grasping of multiple objects might reduce the number of pick attempts to improve the picking speed, as shown in Figure 1A. In addition, a robot can more stably grasp and hold objects that have a large surface using multiple suction cups to grasp the object, as demonstrated in Figure 1B.

Multiple-object grasp planning for jaw or multi-finger grippers has previously been proposed under various conditions, such as in well-organized scenes [2,3], rearranged scenes [4], and cluttered scenes [5,6,7,8]. These studies demonstrated that multiple-object grasping could improve picking speed. However, few studies have examined multiple-object grasping using a vacuum gripper with multiple suction cups. Most studies infer the single-object grasp point for a gripper with only a single suction cup using direct or indirect methods. Direct methods [9,10,11] use deep convolutional neural networks to directly infer the grasp point, while indirect methods [12,13,14] first infer the affordance map, which is a pixel-wise map indicating the graspability score for a single-cup vacuum gripper at each pixel, and then find the optimal grasp point in the map. Given that the affordance map contains all possible grasp points for a single suction cup, if all cups in a vacuum gripper have the same geometry (e.g., cup radius) and dynamics (e.g., suction force limit and friction coefficient), then we can search for a gripper pose where the center positions of at least two of the cups are located at non-zero pixels in the affordance map and satisfy the conditions described in Section 4 for grasping multiple objects or an object with a large surface area.

In this study, we propose an affordance-map-based grasp planner for a multiple-suction-cup vacuum gripper to grasp multiple objects or grasp an object with a large surface area. We propose a 3D convolution-based method, which takes advantage of the suction affordance map inferred by our prior work, suction graspability U-Net++ (SG-U-Net++) [14], to search for a gripper pose capable of grasping multiple objects or an object with a large surface area. Furthermore, unlike the control of a jaw gripper in which all fingers of the gripper are usually controlled to open or close simultaneously, the suction cups need to be controlled separately. Therefore, we design a kernel that includes an encoded cup ID to determine which suction cup to activate. Furthermore, as there might be many candidates for multiple-suction-cup grasping, we propose an evaluation metric for determining the optimal grasp among candidates. The proposed grasp planner is validated using previous affordance datasets and physical robot experiments.

In short, the contributions of this work include the following:

• A 3D-convolution-based grasp planner for a vacuum gripper with multiple cups to grasp multiple objects or an object with a large surface area.
• Control of suction cup activation by incorporating a convolution kernel, including the encoded cup ID.
• A robotic picking system with a hybrid planner that performs multiple-suction-cup grasp planning preferentially and switches to single-object grasp planning when there are no solutions.
• A sorting algorithm for determining the optimal grasp for multiple-cup grasping.
• Validation of the grasp planner on previous affordance datasets, including Suction FCN [12], SuctionNet-1Billion [13], and SG-U-Net++ [14].
• Experiments for picking boxes, fruits, and daily necessities with a vacuum gripper with two cups and a comparison of multiple- and single-cup grasping results.

2. Related Works

2.1. Single-Object Grasping Based on an Affordance Map

A pixel-wise affordance map contains grasp quality at each pixel when the robot grasps the object in the corresponding pose. Unlike end-to-end deep learning, which is used to directly predict grasp configurations such as a rotated bounding box [15,16,17] for a jaw gripper or a suction point for a vacuum gripper with only a single cup [9,10,11], affordance learning has the advantages that the neural network model can be anchor-free, and there is no need to sample candidate grasps as in [18]. Zeng et al. [12] were one of the first research groups to apply pixel-wise affordance learning to bin picking for four multiple-motion primitives of a hybrid robotic hand with both a jaw and a single suction cup. They used a manually annotated affordance dataset to train fully convolutional networks (FCNs). The precision and generalizability of the FCNs were then further improved by [19,20]. Another representative work is by Morrison et al. [21], who generated affordance and pose maps from the rotated bounding box and designed a generative grasp CNN (GG-CNN) to directly infer the pixel-wise grasp pose and quality. To learn the grasp of a jaw gripper, many researchers [17,22,23,24,25] later used similar methods to generate affordance map datasets from grasp configuration annotations represented by a rotated rectangle (e.g., the Cornell Grasp Dataset [15] and Jacquard Dataset [26]).

However, these studies required real images and an expert to perform pixel-wise grasp affordance annotation. To reduce dataset generation costs, datasets are generated in a physical simulator where affordance is evaluated using a designed contact model (e.g., the quasi-static spring model used in Dex-net [27]) on a previously synthesized image. Recently, a similar contact model was used by Cao et al. [13] to generate a larger suction pixel-wise affordance (seal score) dataset. However, these studies required that contact model parameters were determined properly and treated with a vacuum gripper with only a single cup.

In the present study, we used our previously proposed SG-U-Net++ [14] to infer the pixel-wise suction affordance map. SG-U-Net++ was trained on a synthesized dataset annotated by an analysis-based method and was competitive with the method trained on a dataset annotated by a contact model. We propose a grasp planner for multiple-suction-cup grasping that takes advantage of the predicted affordance map.

2.2. Multiple-Object Grasping

Most studies have focused on multiple-object grasping using a multi-finger gripper. Grasp conditions have been analyzed for a multi-finger gripper to stably grasp multiple cylinders [28,29], polyhedral objects [2], planar objects [3], and shaped spatial objects [30]. Recent studies have started to use data-driven methods to deal with the multiple-object grasping problem. Shenoy et al. [5] used a deep neural network to infer the number of objects for a three-finger gripper to grasp when digging into a pile of objects. They later proposed a Markov decision-based method to optimize pick-transfer routines when grasping multiple objects [6]. Sakamoto et al. [4] used mask-RCNN to detect objects and then searched for a gripper pose to push two boxes together in order to simultaneously grasp them. A similar push–grasp task was studied by Agboh et al. for grasping multiple arbitrary convex polygonal objects under frictional and frictionless contact conditions between objects [7,8]. They proposed MOG-Net to infer the maximum number of objects that a two-finger gripper could grasp by a sampled pose. However, the set of objects in these studies was still simple, and simultaneous grasping of objects with more complicated shapes (e.g., daily necessities) is required for more general applications (e.g., picking in warehouses). Mucchiani et al. [31] designed a novel end-effector to sequentially grasp multiple objects with complicated shapes. Similarly, Yao et al. [32] proposed a human-like grasp synthesis algorithm to achieve sequential multiple-object grasping. However, these studies grasped multiple objects sequentially rather than simultaneously.

For multiple-suction-cup grasping, most studies focus on grasping a single object rather than multiple objects using multiple cups. Mantriota [33] analyzed the suction force and friction coefficient to grasp and hold a large object with a four-cup vacuum gripper. Kozák [34] et al. used a deep neural network to estimate the pose of a round part and then used a six-cup vacuum gripper to grasp it. Tanaka et al. [35] designed a two-surface vacuum gripper in which each surface was equipped with multiple cups. They used a gripper to simultaneously suck two surfaces of a large box to improve the stability of grasping and holding. Leitner et al. [36] used a gripper with two different shaped cups to grasp an object on a shelf. These studies used a multiple-cup vacuum gripper to grasp a single object more stably. Kessens [37] et al. mounted a four-cup vacuum gripper on a drone to achieve sequential multiple-object grasping in the air, but found that simultaneous grasping was challenging. Islam et al. [38] proposed a planner for an unloading task in which the robot used a multiple-suction-cup vacuum gripper to simultaneously grasp and unload multiple cardboard boxes, but it was difficult to apply the planner to objects with complicated shapes in a cluttered scene. To our knowledge, the present study is the first to propose a grasp planner to simultaneously grasp multiple objects using a multiple-suction-cup vacuum gripper. The proposed planner can also determine gripper poses to stably grasp large objects with multiple cups.

3. Problem Statement

This study focuses on a bin-picking task in cluttered scenes. The robot is required to pick multiple objects or an object with a large surface area using multiple suction cups and then place them in a tote.

3.1. Assumption

We assume a suction vacuum gripper with multiple suction cups where all cups have the same specifications (e.g., the right side of Figure 2, in which both cups have the same shape, size, and suction force limits). In addition, the gripper tool center point (TCP) and all cups are in the same plane (e.g., the left side of Figure 2, in which the cup center points and TCP are in the same blue plane).

3.2. Vacuum Gripper State

The vacuum gripper state $\mathit{G}$ consists of gripper position $\mathit{P}$, orientation $\mathit{O}$, suction cup center position $\mathit{C}$, and cup activation mode $\mathit{A}$, as shown in Equation (1). $\mathit{P}$ is the position ($x_g,y_g,z_g$) of the TCP in world coordinates. $\mathit{O}$ is the orientation represented by a ZYZ rotation matrix $(R_z\left({\theta }_g\right)R_y^{\prime }\left({\varphi }_g\right)R_z^{\prime \prime }\left({\gamma }_g\right)$), where ${\theta }_g$ and ${\varphi }_g$ are the azimuthal angle and polar angle of the unit vector of gripper axis z, respectively, and ${\gamma }_g$ is the rotation angle around gripper axis z. Note that $sin$ and $cos$ are abbreviated to c and s in the matrix. $\mathit{C}$ consists of the center position ($x_{c_i},y_{c_i},z_{c_i}$) of each suction cup in world coordinates. ${\mathit{C}}^0$ is the center position ($x_{c_i}^0,y_{c_i}^0,z_{c_i}^0$) of each suction cup in local gripper coordinates (see the right side of Figure 2). $\mathit{A}$ is a one-hot vector representing the activation status ($a_{c_i}$) of each suction cup, where $a_{c_i}$ is 1 if the ith cup is activated, and 0 if it is disabled.

$$\begin{array}{cc}\hfill \mathit{G}& =[\mathit{P},\mathit{O},\mathit{C},\mathit{A}],\hfill \\ \hfill \mathit{P}& =[x_g,y_g,z_g],\hfill \\ \hfill \mathit{O}& =R_z\left({\theta }_g\right)R_y^{\prime }\left({\varphi }_g\right)R_z^{\prime \prime }\left({\gamma }_g\right),\hfill \\ \hfill & =\left[\begin{array}{ccc}{c}_{{\varphi }_g}{c}_{{\theta }_g}{c}_{{\gamma }_g}-s_{{\theta }_g}{c}_{{\gamma }_g}& -c_{{\varphi }_g}{c}_{{\theta }_g}{s}_{{\gamma }_g}-s_{{\theta }_g}{c}_{{\gamma }_g}& s_{{\varphi }_g}{c}_{{\theta }_g}\\ c_{{\varphi }_g}{s}_{{\theta }_g}{c}_{{\gamma }_g}+c_{{\theta }_g}{s}_{{\gamma }_g}& -c_{{\varphi }_g}{s}_{{\theta }_g}{s}_{{\gamma }_g}+c_{{\theta }_g}{c}_{{\gamma }_g}& s_{{\varphi }_g}{s}_{{\theta }_g}\\ -s_{{\varphi }_g}{c}_{{\gamma }_g}& s_{{\varphi }_g}{s}_{{\gamma }_g}& c_{{\varphi }_g}\end{array}\right],\hfill \\ \hfill \mathit{C}& =[[x_{c_1},y_{c_1},z_{c_1}],[x_{c_2},y_{c_2},z_{c_2}],...,[x_{c_i},y_{c_i},z_{c_i}]],\hfill \\ \hfill \mathit{A}& =[a_{c_1},a_{c_2},...,a_{c_i}].\hfill \end{array}$$

(1)

4. Conditions for Grasping Using Multiple Suction Cups

Since all suction cups installed in the gripper are assumed to be the same, the affordance map of each suction cup is the same. Hence, we can determine a gripper pose capable of grasping multiple objects or an object with a large surface area by multiple cups if the following conditions are satisfied (an example is shown in Figure 3).

Condition 1. 

At least two of the contact points are located in affordable areas on the object. If the contact points are located in affordable areas on different objects, the gripper can grasp multiple objects. If the contact points are located in the same affordable area, the gripper can grasp a large surface area using multiple cups.

Condition 2. 

The gripper TCP and all contact points located in affordable areas are in the same plane, which is perpendicular to the unit vector of the gripper’s z-axis (${\mathit{n}}_g$).

Condition 3. 

Normals of all contact points located in affordable areas (${\mathit{n}}_{{cp}_i}$) are in the same direction as the unit vector of the gripper’s z-axis (${\mathit{n}}_g$), as shown in Equation (2). Note that $af{f}_{c{p}_i}>0$ indicates that the ith contact point is located in an affordable area where its affordance score is non-zero.

$$\arccos ({\mathit{n}}_{{cp}_i}·{\mathit{n}}_g)<{\epsilon }_1\mathrm{where}af{f}_{c{p}_i}>0.$$

(2)

Condition 4. 

The distance from each contact point located in affordable areas to the TCP in world coordinates ($d_{c{p}_i}$) needs to be equal to the distance from the corresponding cup center to the TCP in local coordinates ($d_{c_i}^0$ in Figure 2).

$$|d_{c{p}_i}-d_{c_i}^0|<{\epsilon }_2\mathrm{where}af{f}_{c{p}_i}>0.$$

(3)

5. Multiple-Suction-Cup Grasp Planner

5.1. Overview of Architecture

Figure 4 and Algorithm 1 show the overall architecture and workflow of our multiple-suction-cup grasp planner. Given a depth image of $I_d$, our previous work SG-U-Net++ is used to infer the affordance map $I_{aff}$ for a single cup. The voxel grid generator then extracts the point cloud ($I_{pcd}$) affiliated with the affordable areas in the map and downsamples them to a voxel grid (V). The orientation generator uses the point normals ${\mathit{n}}_{pcd}$ of extracted points to efficiently generate the gripper orientation samples (${\mathit{S}}_O$). The gripper kernel generator generates 3D encoded gripper kernels ($\mathcal{K}$), including cup ID information. The decoder decodes the result ($ConvRes$) of 3D convolution (3D Conv.) of V over $\mathcal{K}$ and generates the gripper pose candidates (${\mathit{G}}_{cand}$). The normal direction checker removes candidates where the ${\mathit{n}}_g$ and contact point normals are not in the same direction. If ${\mathit{G}}_{cand}$ is successfully found, ${\mathit{G}}_{cand}$ is evaluated and ranked to obtain the optimal grasp (${\mathit{G}}_{opt}$). Otherwise, if no ${\mathit{G}}_{cand}$ is found, the planner is switched to our previous single-object grasp planner, where the position with the highest affordance score is set as the goal, and the cup that can reach the goal by the shortest trajectory is selected to grasp the object.

Algorithm 1 Multiple-suction-cup grasp planner

Input: Iaff: affordance map

Id: depth image

Ipcd: point cloud

l: voxel size

C0: local cup center positions (see the right side of Figure 2)

Output: $G_{opt}$: optimal grasp

1: $V\leftarrow \mathrm{GenerateVoxelGrid}(I_{pcl},I_{aff},l)$ 2: ${\mathit{n}}_{pcd}\leftarrow \mathrm{EstimateNormals}\left(I_{pcd}\right)$ 3: ${\mathit{S}}_O\leftarrow \mathrm{SampleGripperOrientation}({\mathit{n}}_{pcd},I_{aff})$ 4: $\mathcal{K}\leftarrow \mathrm{GenerateEncodedKernels}({\mathit{S}}_O,{\mathit{C}}^0,l)$ 5: $ConvRes\leftarrow \mathrm{Conv}3\mathrm{D}(V,\mathcal{K})$ 6: ${\mathit{G}}_{cand}\leftarrow \mathrm{Decode}\left(ConvRes\right)$ 7: ${\mathit{G}}_{cand}\leftarrow \mathrm{NormalDirectionCheck}\left(ConvRes\right)$ 8: if  $\mathrm{len}\left({\mathit{G}}_{cand}\right)>0$  then 9:     ${\mathit{G}}_{opt}\leftarrow \mathrm{Ranking}(I_{aff},{\mathit{G}}_{cand})$ 10: else 11:     $\#\mathrm{Single}-\mathrm{object}\mathrm{grasp}\mathrm{planning}$ 12:     ${\mathit{G}}_{opt}\leftarrow \mathrm{argmax}\left(I_{aff}\right)$ 13: end if 14: return  ${\mathit{G}}_{opt}$

5.2. Affordance Map Inference

We use SG-U-Net++ from our prior work to generate the affordance map. SG-U-Net++ has a nested U-Net structure and infers pixel-wise grasp quality and approachability based on a depth image. Refer to [14] for further details. Pixels with non-zero grasp quality scores are filtered out to generate an affordance map (the green area in the affordance map in Figure 4).

5.3. Voxel Grid Generation

We use voxel downsampling to generate the binary voxel grid (V) of the point cloud. Points located in the affordable areas are extracted and downsampled to a voxel grid with a defined grid size l. The voxel grid is further binarized such that if a grid in the voxel grid contained more than 10 points, the grid value would be 1 or 0. The voxel grid shape is $N_x\times N_y\times N_z$, where $N_x=\lfloor \frac{B_x^{max}-B_x^{min}}{l}\rfloor$, $N_y=\lfloor \frac{B_y^{max}-B_y^{min}}{l}\rfloor$, and $N_z=\lfloor \frac{B_z^{max}-B_z^{min}}{l}\rfloor$. $B^{max}$ and $B^{min}$ are the maximum and minimum bounds of the point cloud.

5.4. Grasp Orientation Candidate Generation

To satisfy Condition 3 in Section 4, Equation (2) must be computed for each point normal to sample the gripper orientations. If the size of the input point cloud is large, online sampling will result in high costs in terms of memory usage and computation time. We propose an efficient sampling method for a vacuum gripper by generating an offline normal to gripper orientation map. Since the Cartesian coordinates of a given vector $\mathit{vec}$ ($[ve{c}_x,ve{c}_y,ve{c}_z]$) can be represented by the azimuthal angle $\theta$ and polar angle $\varphi$ as in Equation (4), all possible normals of contact points can be sampled by an angle interval $\Delta \alpha$, as in Equation (5). Meanwhile, as in Equation (1), ${\mathit{n}}_g$ (the last column of $\mathit{O}$) depends on only ${\varphi }_g$ and ${\theta }_g$ and has the same representation as Equation (4), so ${\mathit{n}}_g$ can be sampled by the same angle interval as in Equation (6).

$$\begin{array}{cc}\hfill & \mathit{vec}=[ve{c}_x,ve{c}_y,ve{c}_z]=[c_{\theta }{s}_{\varphi },s_{\theta }{s}_{\varphi },c_{\varphi }],\hfill \\ \hfill & \theta =\arctan (ve{c}_y,ve{c}_x),\hfill \\ \hfill & \varphi =\arccos \left(ve{c}_z\right),\hfill \end{array}$$

(4)

where $\theta$ is the normal polar coordinate in the $x-o-y$ plane, and $\varphi$ is the angle between the vector and the z axis. Assuming the normal is always in the up direction, $\theta \in (-\pi ,\pi ]$ and $\varphi \in [0,\frac{\pi }{2}]$.

$$S_{\mathit{n}}(ii,jj)=[c_{ii\Delta \alpha -\pi }{s}_{jj\Delta \alpha },s_{ii\Delta \alpha -\pi }{s}_{jj·\Delta \alpha },c_{jj\Delta \alpha }],$$

(5)

$$S_{{\mathit{n}}_g}(i{i}^{\prime },j{j}^{\prime })=[c_{i{i}^{\prime }\Delta \alpha -\pi }{s}_{j{j}^{\prime }\Delta \alpha },s_{i{i}^{\prime }\Delta \alpha -\pi }{s}_{j{j}^{\prime }\Delta \alpha },c_{j{j}^{\prime }\Delta \alpha }],$$

(6)

where $ii,i{i}^{\prime }=0,1,\cdots ,\frac{\pi }{\Delta \alpha }$ and $jj,j{j}^{\prime }=0,1,\cdots ,\frac{\pi }{2\Delta \alpha }$.

For each $S_{{\mathit{n}}_{cp}}(ii,jj)$, we search for all $S_{{\mathit{n}}_g}(i{i}^{\prime },j{j}^{\prime })$ satisfying Equation (2) in order to create a map $\mathcal{M}:(ii,jj)\to (i{i}^{\prime },j{j}^{\prime })$, which maps a point normal entry to all ${\mathit{n}}_g$ in the same direction as the normal vector. This map could be generated offline, and this only needs to be carried out once, thus reducing the computation cost.

Based on $\mathcal{M}$, given the point normals, the feasible candidate ${\mathit{n}}_g$ could be rapidly obtained so that gripper orientation samples (${\mathit{S}}_O$) could be generated. Given ${\mathit{n}}_{pcd}$, normals of points located in affordable areas are extracted and azimuthal and polar angles are computed (lines 1–3 in Algorithm 2). The angles are then used to calculate the entry key $\mathit{ii},\mathit{jj}$ to query $\mathcal{M}$ to obtain the feasible ${\mathit{ii}}^{\prime },{\mathit{jj}}^{\prime }$, based on which samples (${\mathit{S}}_{{\theta }_g}$ and ${\mathit{S}}_{{\varphi }_g}$) of ${\theta }_g$ and ${\varphi }_g$ are obtained (lines 4–7 in Algorithm 2). Note that only unique $\mathit{ii},\mathit{jj}$ values with top-10% counts are used as entries. This helps to improve the sampling efficiency when the variation in ${\mathit{n}}_{pcd}$ is small. For example, if the input point cloud is a set of points in a plane, all ${\mathit{n}}_{pcd}$ and corresponding $\mathit{ii},\mathit{jj}$ are the same. Hence, using unique values, only one unique $\mathit{ii},\mathit{jj}$ rather than all $\mathit{ii},\mathit{jj}$ are used. As ${\mathit{n}}_g$ depends on only ${\theta }_g$ and ${\varphi }_g$, ${\gamma }_g$ could be any value if ${\theta }_g$ and ${\varphi }_g$ are feasible. Hence, ${\gamma }_g$ is sampled by the same interval $\Delta \alpha$ in the range $(-\pi ,\pi ]$ (lines 9–10 in Algorithm 2). The final ${\mathit{S}}_O$ is obtained by multiplying the rotation matrix of sampled ${\mathit{S}}_{{\theta }_g}$, ${\mathit{S}}_{{\varphi }_g}$, and ${\mathit{S}}_{{\gamma }_g}$.

Algorithm 2 Sample gripper orientation

Input: npcd: point normals

Iaff: affordance map

Δα: sampling interval

Output: SO: gripper orientation samples

1: $\mathit{n}\leftarrow {\mathit{n}}_{pcd}[I_{aff}>0]$ 2: $\mathit{\theta }\leftarrow \arctan ({\mathit{n}}_y,{\mathit{n}}_x)$ 3: $\mathit{\varphi }\leftarrow \arccos \left({\mathit{n}}_z\right)$ 4: $\mathit{ii}\leftarrow \frac{\mathit{\theta }+\pi }{\Delta \alpha }$ 5: $\mathit{jj}\leftarrow \frac{\mathit{\varphi }}{\Delta \alpha }$ 6: $\mathit{ii},\mathit{jj}\leftarrow \mathrm{Unique}(\mathit{ii},\mathit{jj})$ 7: ${\mathit{ii}}^{\prime },{\mathit{jj}}^{\prime }\leftarrow \mathcal{M}(\mathit{ii},\mathit{jj})$ 8: ${\mathit{S}}_{{\theta }_g}\leftarrow {\mathit{ii}}^{\prime }\Delta \alpha -\pi$ 9: ${\mathit{S}}_{{\varphi }_g}\leftarrow {\mathit{jj}}^{\prime }\Delta \alpha$ 10: ${\mathit{kk}}^{\prime }\leftarrow 0,1,\cdots ,\frac{\pi }{\Delta \alpha }$ 11: ${\mathit{S}}_{{\gamma }_g}\leftarrow {\mathit{kk}}^{\prime }\Delta \alpha -\pi$ 12: ${\mathit{S}}_O\leftarrow R_z\left({\mathit{S}}_{{\theta }_g}\right)R_y^{\prime }\left({\mathit{S}}_{{\varphi }_g}\right)R_z^{\prime \prime }\left({\mathit{S}}_{{\gamma }_g}\right)$ 13: return  ${\mathit{S}}_O$

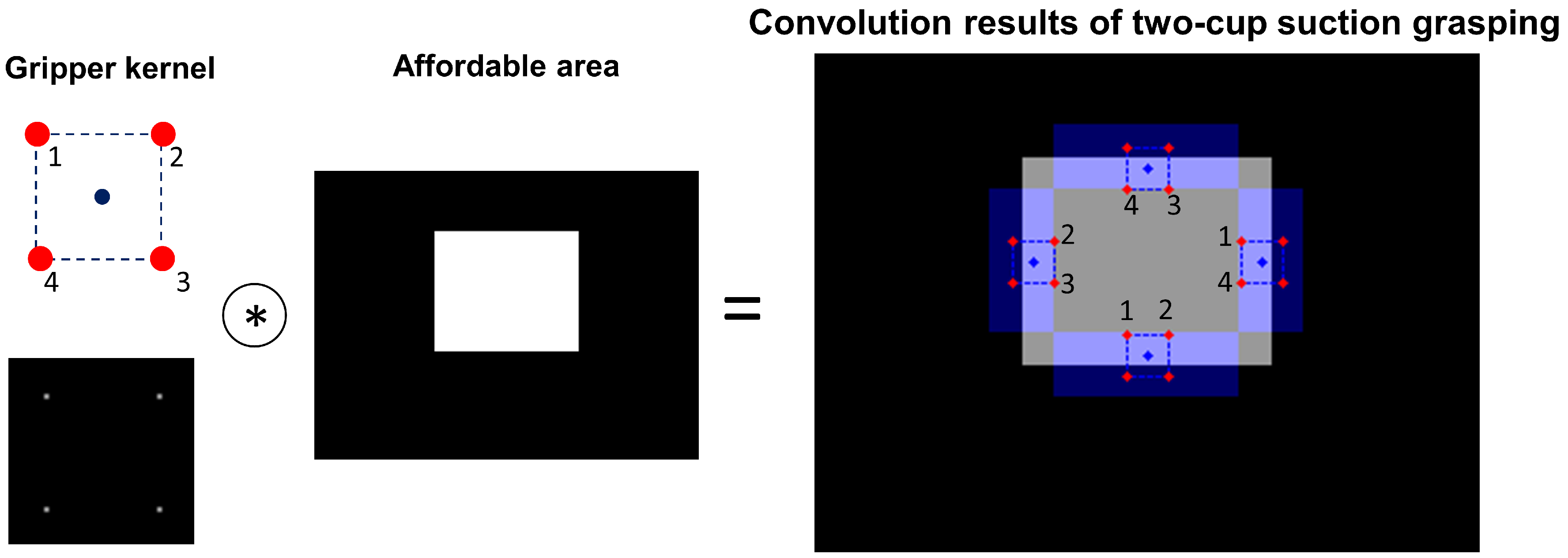
5.5. Gripper Orientation Kernel Generation and Suction Cup ID Encoding

The kernel representing each candidate gripper orientation generated in Section 5.4 is created using 3D convolution to determine the graspable position for each ${\mathit{S}}_{\mathit{O}}$, as in Algorithm 3. A binary kernel is used to represent gripper poses in previous studies using 2D convolution [39]. However, the convolution results can only determine the graspable position of the kernel and cannot directly determine which suction cup to activate. For example, as shown in Figure 5, although the convolution results for the four cases are the same, the suction cups chosen to be activated are different and cannot be directly determined from the convolution results. Hence, we design a 3D kernel that includes the suction cup ID information. Algorithm 3 is used to generate kernels ${\mathit{S}}_{\mathcal{K}}$ of ${\mathit{S}}_O$. The shape of one kernel $\mathcal{K}$ is $N_{{\mathcal{K}}_x}\times N_{{\mathcal{K}}_y}\times N_{{\mathcal{K}}_z}$, where $N_{{\mathcal{K}}_x}=N_{{\mathcal{K}}_y}=N_{{\mathcal{K}}_z}=\lfloor \frac{max\left(d_{C_i}^0\right)}{l}\rfloor$. $max\left(d_{C_i}^0\right)$ is the maximum distance of the suction cup center to the TCP in local gripper coordinates, and l is the grid size of the kernel, which is equal to that of the voxel grid. The kernel indices of cup centers are $\lfloor \frac{C}{l}\rfloor +\lfloor \frac{max\left(d_{C_i}^0\right)}{2l}\rfloor$, where C is the cup center position of ${\mathit{S}}_O$. The kernel grids at cup center kernel indices are filled with encoded vacuum ID information as in line 9 in Algorithm 3. Here, the ith suction cup ID information is encoded as ${10}^{-i}$, such that the cup ID is saved in the ith decimal place, and such encoding helps to directly obtain the target suction cups to activate from the decoding convolution results (see Section 5.7).

Algorithm 3 Generated encoded kernels

Input: SO: gripper orientation samples

C0: local cup center positions

(see the right side of Figure 2)

l: voxel size

Output: ${\mathit{S}}_{\mathcal{K}}$: kernels of SO

1: ${\mathrm{N}}_O\leftarrow \mathrm{len}\left({\mathit{S}}_O\right)$ 2: ${\mathit{S}}_{\mathcal{K}}\leftarrow \mathrm{Zeros}(N_O,N_{{\mathcal{K}}_x},N_{{\mathcal{K}}_y},N_{{\mathcal{K}}_z})$ 3: for $n\leftarrow 0$ to ${\mathrm{N}}_O$ do 4:     $\mathcal{K}\leftarrow \mathrm{Zeros}(N_{{\mathcal{K}}_x},N_{{\mathcal{K}}_y},N_{{\mathcal{K}}_z})$ 5:     for $i\leftarrow 0$ to ${\mathrm{N}}_c$ do 6:         $[C\left[i\right],1]\leftarrow \left[\begin{array}{cc}{\mathit{S}}_O\left[n\right]& \mathbf{0}\\ \mathbf{0}& 1\end{array}\right]\left[\begin{array}{c}{C}^0{\left[i\right]}^T\\ 1\end{array}\right]$ 7:         $C\left[i\right]\leftarrow C{\left[i\right]}^T$ 8:         $\#\mathrm{encoding}$ 9:         $\mathcal{K}[\lfloor \frac{C\left[i\right]}{l}\rfloor +\lfloor \frac{max\left(d_{C_i}^0\right)}{2l}\rfloor ]\leftarrow {10}^{-i}$ 10:     end for 11:     ${\mathit{S}}_{\mathcal{K}}\left[n\right]\leftarrow \mathcal{K}$ 12: end for 13: return  ${\mathit{S}}_{\mathcal{K}}$

5.6. Three-Dimensional Convolution

We perform 3D convolution to determine the indices in V, where the gripper can grasp using multiple suction cups. Because the kernel is generated from an oriented $C^0$ that is located in the same plane as the TCP, the corresponding kernel indices of cup centers and the TCP are in the same plane, which satisfies Condition 2 in Section 4. Furthermore, as the distances from cup centers to the TCP are represented in a kernel scale that is the same as the voxel grid scale, we can slide the kernel over the voxel grid to determine the voxel grid index where the TCP satisfies Conditions 2 and 4. Specifically, as in Equation (7), the kernel is set to each grid cell of the voxel grid to calculate the convolution sum. Note that $N_{\mathcal{K}}$ is the number of kernels, which is equal to $N_O$.

$$\begin{array}{cc}\hfill ConvRes=\sum _{n=0}^{N_{\mathcal{K}}}\sum _{m=0}^{N_{V_x}}& \sum _{t=0}^{N_{V_y}}\sum _{p=0}^{N_{V_z}}\sum _{i=-\frac{N_{{\mathcal{K}}_x}}{2}}^{\frac{N_{{\mathcal{K}}_x}}{2}}\sum _{j=-\frac{N_{{\mathcal{K}}_y}}{2}}^{\frac{N_{{\mathcal{K}}_y}}{2}}\sum _{k=-\frac{N_{{\mathcal{K}}_z}}{2}}^{\frac{N_{{\mathcal{K}}_z}}{2}}\hfill \\ \hfill & \mathcal{K}[i,j,k]·V[m+i,t+j,p+k].\hfill \end{array}$$

(7)

5.7. Convolution Results Decoding and Normal Direction Check

Algorithm 4 shows the decode function that decodes the 3D convolution results ($ConvRes$) to generate grasp candidates. As the 3D convolution of the kernel center is set to each grid cell of V and accumulates the kernel values where the corresponding voxel grid value is non-zero (Equation (7)), the cup to be activated can be determined by obtaining each digit of $ConvRes$. As in line 7 in Algorithm 4, $ConvRes$ is decoded to target ith suction cup activation $a_i$ in Equation (1) by scaling up $ConvRes$ by ${10}^i$ times and then calculating the value mod 10. If $a_i$ is 1, a contact point exists for the ith vacuum cup that should be activated. Otherwise, there is no contact point and the cup should be disabled. For example, for the gripper with two suction cups in Figure 2, there are four ($2^2$) possible values of convolution results: 0.00, 0.10, 0.01, and 0.11, and the decoding results are [0, 0], [1, 0], [0, 1], and [1, 1], indicating non-graspable, graspable for only the first cup, graspable for only the second cup, and graspable for both cups, respectively.

Algorithm 4 Decode

Input: ConvRes: 3D convolution results

Output: Gcand: grasp candidates for multiple-cup suction

1: ${\mathrm{N}}_{\mathcal{K}},{\mathrm{N}}_{V_x},{\mathrm{N}}_{V_y},{\mathrm{N}}_{V_z}\leftarrow convRes.\mathrm{shape}$ 2: $\mathit{A}\leftarrow \mathrm{Zeros}({\mathrm{N}}_{\mathcal{K}},{\mathrm{N}}_{V_x},{\mathrm{N}}_{V_y},{\mathrm{N}}_{V_z},{\mathrm{N}}_c)$ 3: for $Res$ in $ConvRes$ do 4:     for $i\leftarrow 0$ to ${\mathrm{N}}_c$ do 5:         $\#\mathrm{decoding}\mathrm{cup}\mathrm{ID}$ 6:         $\mathit{A}[...,i]\leftarrow \lfloor \frac{{10}^{N_{cup}}}{{10}^{N_{cup}-i}}Res\rfloor mod10$ 7:     end for 8: end for 9: $validInd\leftarrow \mathrm{sum}(A,\dim =-1)⩾2$ 10: ${\mathit{S}}_P\leftarrow validInd·l+{\mathit{B}}^{min}$ 11: ${\mathit{S}}_O\leftarrow {\mathit{S}}_O\left[validInd\right]$ 12: ${\mathit{S}}_C\leftarrow \left[\begin{array}{cc}{\mathit{S}}_O& {\mathit{S}}_P\\ \mathbf{0}& 1\end{array}\right]\left[\begin{array}{c}{C^0}^T\\ 1\end{array}\right]$ 13: ${\mathit{S}}_A\leftarrow \mathit{A}\left[validInd\right]$ 14: ${\mathit{G}}_{cand}\leftarrow [{\mathit{S}}_P,{\mathit{S}}_O,{\mathit{S}}_C,{\mathit{S}}_A]$ 15: return  ${\mathit{G}}_{cand}$

As A is a one-hot vector, the sum of A is the number of suction cups to be used. Therefore, we determine the indices ($validInd$) of V where the sum of A is greater than or equal to two ($sum(A,dim=-1)⩾2$) in order to find the voxel grid indices where multiple suction cups can be used to grasp multiple objects or an object with a large surface area. $validInd$ is further converted to TCP positions in world coordinates (${\mathit{S}}_P$ in Algorithm 4), and the corresponding orientation ${\mathit{S}}_P$, cup center positions ${\mathit{S}}_C$, and target activation status ${\mathit{S}}_A$ can be obtained to generate the grasp candidates (${\mathit{G}}_{cand}$), as in lines 12–15 in Algorithm 4.

The normal directions of all activated cups ($a_i$ = 1) of ${\mathit{G}}_{cand}$ are checked to satisfy Condition 3. Specifically, the closest point to the contact point of each activated cup is searched for in $I_{pcd}$, and then the normal of that point is checked for whether it is in the same direction as the gripper’s z-axis direction using Equation (2).

5.8. Ranking

Each ${\mathit{G}}_{cand}$ is evaluated and ranked to determine the optimal grasp ${\mathit{G}}_{opt}$. We first perform point clustering on the points with non-zero affordance values, which are extracted from $I_{pcd}$ to generate a label map $M_{label}$, distance map $M_{dist}$, and orientation map $M_{orient}$, as shown in Figure 6. $M_{label}$ contains the ID label of each cluster and is later used to calculate how many objects can be grasped. $M_{dist}$ contains the 3D distance from each point in the cluster to the cluster center. $M_{orient}$ contains the 3D orientation of each cluster. $M_{dist}$ and $M_{orient}$ are generated for later evaluation of the score (J) of ${\mathit{G}}_{opt}$. The height and width of the three maps are the same as those of $I_d$.

Lines 3–14 in Algorithm 5 evaluate the maximum number of objects that can be grasped $maxObj$ and the score J of each G in ${\mathit{G}}_{cand}$, saving the evaluation results to a dictionary ($rankingRes$). The image coordinates (${\mathit{u}}_c,{\mathit{v}}_c$) of cup center positions are calculated to obtain the contact point label for each cup in the $M_{label}$. Note that the contact labels might not be unique. If several cups have the same contact point label, it means that these cups can be used to grasp the same object, which has a large surface area. If all cups have different contact point labels, it means that each cup can grasp a unique object. Therefore, the number of unique contact labels is the maximum number of objects that can be grasped by G. J is the sum of $J_{center}$, $J_{var}$, and $J_{orient}$. 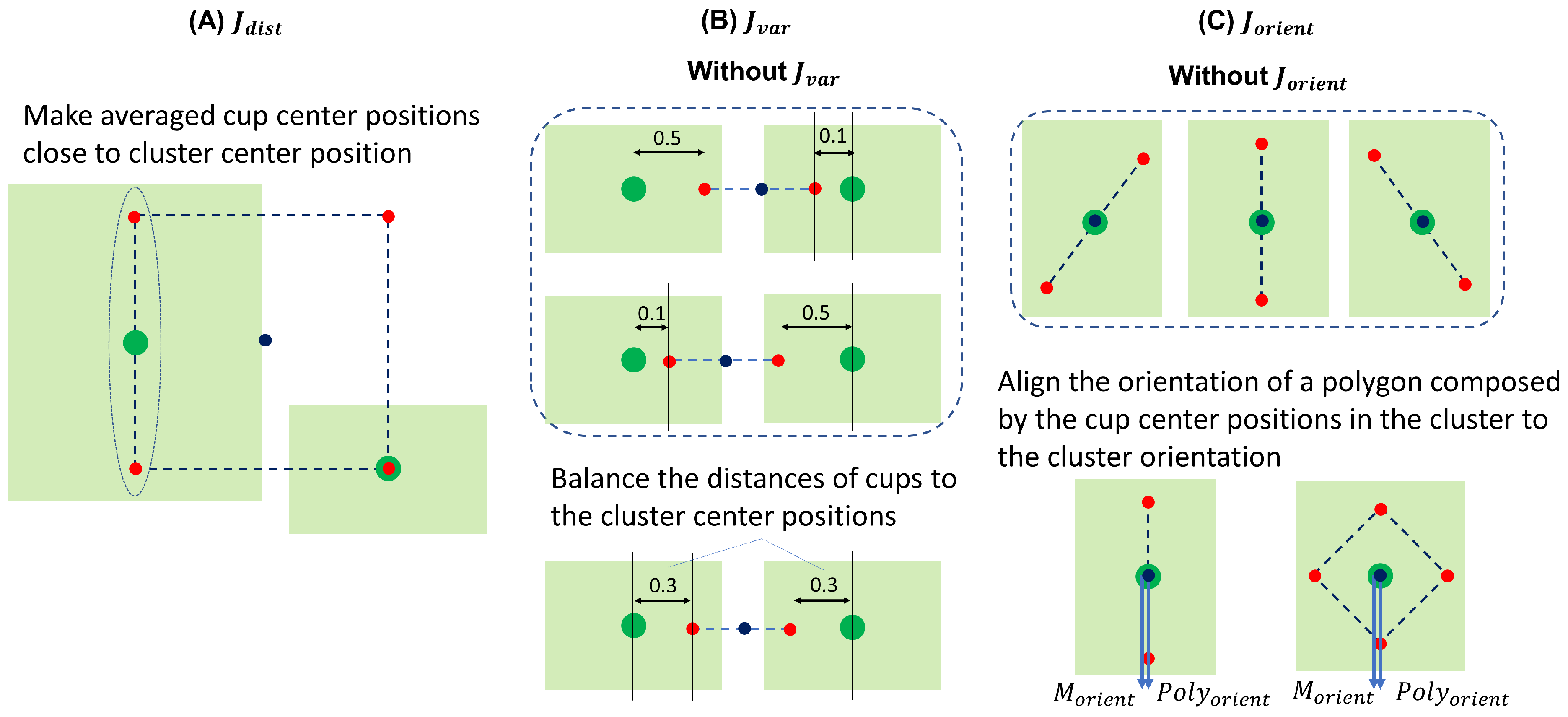$J_{center}$ evaluates the distance from the cup center or the average of cup centers to the cluster center because it is assumed to be more stable to hold the object at its center. As in Equation (8) and Figure 7A, $J_{dist}$ is evaluated as the average sum of distances from cups to the cluster center by obtaining the value of $M_{dist}$ at the position of the average cup center position ($\mathrm{avg}({\mathit{v}}_c,{\mathit{u}}_c,contactLabe{l}_i)]$) in each cluster.

$$J_{dist}=\frac{{\sum }_{i=0}^{N_{contactLabel}}{M}_{dist}\left[\mathrm{avg}({\mathit{v}}_c,{\mathit{u}}_c,contactLabe{l}_i)\right]}{maxObj}.$$

(8)

$J_{var}$ has been incorporated because there are cases where one cup is near, but another cup is far from the cluster center, and $J_{dist}$ cannot evaluate these cases. $J_{var}$ is used to balance the distances of cups to cluster center positions. Specifically, as in Equation (9) and Figure 7B, $J_{var}$ evaluates the variance of the $M_{dist}$ value at the position of average cup center positions.

$$J_{var}=\frac{{\sum }_{i=0}^{N_{contactLabel}}{(M_{dist}\left[\mathrm{avg}({\mathit{v}}_c,{\mathit{u}}_c,contactLabe{l}_i)\right]-J_{dist})}^2}{maxObj}.$$

(9)

Algorithm 5 Ranking

Input: Iaff: affordance map

Ipcd: point cloud

Gcand: grasp candidates

Output: Gopt: optimal grasp

1: ${\mathrm{M}}_{label},{\mathrm{M}}_{dist},{\mathrm{M}}_{orient}\leftarrow \mathrm{clustering}(I_{aff},I_{pcd})$ 2: $rankingRes\leftarrow \mathrm{Dict}\left(\right)$ 3: for $\mathit{G}$ in ${\mathit{G}}_{cand}$ do 4:     $\mathit{P},\mathit{O},\mathit{C},\mathit{A}\leftarrow \mathit{G}$ 5:     ${\mathit{u}}_{tcp},{\mathit{v}}_{tcp}\leftarrow \mathrm{getImgCoord}\left(\mathit{P}\right)$ 6:     ${\mathit{u}}_c,{\mathit{v}}_c\leftarrow \mathrm{getImgCoord}\left(\mathit{C}\right)$ 7:     $contactLabel\leftarrow \mathrm{unique}\left(M_{label}[{\mathit{v}}_c,{\mathit{u}}_c]\right)$ 8:     $maxObj\leftarrow \mathrm{len}\left(contactLabel\right)$ 9:     $J_{center}\leftarrow \mathrm{calcCenterScore}(M_{dist},{\mathit{u}}_c,{\mathit{v}}_c,contactLabel)$ 10:     $J_{var}\leftarrow \mathrm{calcVarScore}(M_{var},{\mathit{u}}_c,{\mathit{v}}_c,contactLabel)$ 11:     $J_{Orient}\leftarrow \mathrm{calcOrientScore}(M_{orient},{\mathit{u}}_c,{\mathit{v}}_c,contactLabel)$ 12:     $J\leftarrow J_{center}+J_{var}+J_{Orient}$ 13:     add $[maxObj,J]$ to $rankingRes\left[contactLabel\right]$ 14: end for 15: $rankingRes\leftarrow \mathrm{sort}\left(rankingRes\right)$ 16: for $Res$ in $rankingRes$ do 17:     if $maxObj$ in $Res>maxObj$ in ${\mathit{G}}_{opt}$ then 18:         ${\mathit{G}}_{opt}\leftarrow Res$ 19:     else if $maxObj$ in $Res=maxObj$ in ${\mathit{G}}_{opt}$ then 20:         if J in $Res>J$ in ${\mathit{G}}_{opt}$ then 21:            ${\mathit{G}}_{opt}\leftarrow Res$ 22:         end if 23:     end if 24: end for 25: return  ${\mathit{G}}_{opt},rankingRes$

$J_{orient}$ has been incorporated to align the orientation of a polygon composed of the cup center positions in the cluster to the cluster orientation. Specifically, we calculate the dot product between the cluster orientation (longer or short axis unit vector) and the polygon orientation, as shown in Equation (10) and Figure 7C.

$$J_{orient}=\frac{{\sum }_{i=0}^{N_{contactLabel}}{M}_{orient}[{\mathit{v}}_c,{\mathit{u}}_c]·Pol{y}_{orient}({\mathit{v}}_c,{\mathit{u}}_c,contactLabe{l}_i)}{maxObj}.$$

(10)

The $\mathit{G}$ and corresponding $maxObj$ and J are added to the dictionary using $contactLabel$ as a key. Key level (local level) sorting is first performed to sort stored J (line 15 in the algorithm). Next, dictionary-level (global level) sorting is performed to determine ${\mathit{G}}_{opt}$ with the highest $maxObj$ and J (lines 16–24 in the algorithm). Note that both ${\mathit{G}}_{opt}$ and sorted $rankingRes$ are returned because, if the motion planner fails to find a trajectory to ${\mathit{G}}_{opt}$, it would search for the trajectory to other goals with high $maxObj$ and J in $rankingRes$.

6. Experiments

The multiple-suction-cup planner was validated using previous affordance map datasets as well as real picking experiments. For both validations, thresholds ${\epsilon }_1$ in Equation (2) and ${\epsilon }_2$ in Equation (3) were set to $11.5^{\circ }$ and 0.01 m, respectively. The voxel grid size l was set to 0.005 m. The angle sampling interval $\Delta \alpha$ was set to $5^{\circ }$. Validations were performed on an Ubuntu 20.04 PC with an 11th Gen Intel Core^TM i7-11700K @ 3.60 GHz × 16 CPU and NVIDIA GeForce RTX 3060 GPU.

6.1. Validation Using a Previous Affordance Map Dataset

We used three datasets to validate the generality of the multiple-suction-cup grasp planner: Suction FCN [12], SuctionNet-1Billion [13], and SG-U-Net++ [14]. These datasets provide real RGB-D or synthesized depth images and the corresponding affordance maps. Point clouds converted from depth images and affordance maps in the dataset were used to determine the optimal multiple-cup graspable poses and the cups to activate two-cup and four-cup vacuum grippers. The accuracy of the position and orientation were evaluated by the average error of Equation (2) and Equation (3), respectively.

6.2. Validation Using the Picking Experiment

To evaluate the robot picking system and efficiency improvement using the multiple-suction-cup grasp planner, we conducted picking experiments and compared the results of single-cup (single-object) grasping and multiple-cup (multiple-object) grasping. The robot with a two-cup vacuum gripper was used to pick items from a bin and then place them into a tote (Figure 8A). Figure 8C shows the gripper architecture. The gripper was equipped with PISCO (PISCO CO., LTD., Nagano, Japan) standard suction cups. We used a cup with a 20 mm diameter because it can generate sufficient force to grasp and hold objects (weight less than 500 g) used in experiments under our vacuum pump setup. The cups were connected to vacuum ejector ports by tubes. Each ejector port controlled the on/off of the corresponding cup by supplying (on) or blocking (off) compressed air. A camera was installed in the center of the gripper, which captured the depth image at the robot’s home position. The affordance map was then inferred by SG-U-Net++ based on the depth image. For single-object grasping, the planner in our previous work [14] was used to find the position of maximum affordance value and selected the suction cup that can be used to reach the target grasp point by the shortest trajectory. For multiple-object grasping, a multiple-suction-cup grasp planner was first used to determine grasp poses capable of grasping multiple objects or an object with a large surface area using multiple cups. If there was no solution, the planner was switched to the planner for single-object grasping. Trajectories from the home position to grasp poses were generated by MoveIt. As shown in Figure 8B, the target object set included boxes, fruits, and daily necessities. The robot was required to pick 50 boxes, 50 fruits, and 51 daily necessities in a cluttered scene. The robot continued grasp attempts until the scene was cleared. A grasp attempt was considered to have failed if the robot could not pick up the item or the item was dropped during the movement of the manipulator. The results of single-object grasping and multiple-object grasping were evaluated and compared by success rate, picks per hour (PPH), and number of pick attempts. The success rate was defined as the number of successful attempts divided by the number of pick attempts. PPH was defined as the number of objects the robot could pick up in 1 h. The number of pick attempts was defined as a number of attempts for the robot to clear the cluttered scene.

7. Results and Discussion

To our knowledge, this study is the first to propose a grasp planner for multiple-suction-cup grippers to grasp multiple objects or an object with a large surface area. Most of the previous studies used a deep neural network to infer the affordance map for finding the optimal grasp for single-cup grasping. Our planner took advantage of the affordance map to determine the optimal grasp for multiple-cup grasping. The planner was validated on three previous affordance map datasets, and the results are shown in

Table 1. Position and orientation error of grasp pose.

Dataset	Two-Cup Gripper		Four-Cup Gripper
	Position Error	Orientation Error	Position Error	Orientation Error
	(Mean (SD) [m])	(Mean (SD) [deg.])	(Mean (SD) [m])	(Mean (SD) [deg.])
Suction FCN	6.28 $\times {10}^{-3}$ (0.80 $\times {10}^{-4}$)	4.50 (6.94)	5.94 $\times {10}^{-3}$ (0.23 $\times {10}^{-4}$)	5.04 (11.00)
suctionNet-1Billion	7.67 $\times {10}^{-3}$ (2.43 $\times {10}^{-4}$)	4.66 (6.30)	7.64 $\times {10}^{-3}$ (1.41$\times {10}^{-4}$)	4.59 (6.98)
SG-U-Net++	2.88 $\times {10}^{-3}$ (0.18 $\times {10}^{-4}$)	2.85 (10.2)	2.30 $\times {10}^{-3}$ (0.07 $\times {10}^{-4}$)	2.68 (8.07)

. Our planner successfully found multiple-suction-cup grasps from the affordance map from Suction FCN, SuctionNet-1Billion, and SG-U-Net++, indicating the high generality of the planner. There were no significant differences in position orientation error between the two-cup and four-cup gripper planning results. The error was the smallest when grasping was planned based on the affordance map from SG-U-Net++ because SG-U-Net++ used synthesized data (e.g., depth image and point cloud normals) without noise values. Figure 9 and Figure 10 show examples of grasp planning results for the two-cup and four-cup vacuum grippers. The planner successfully determined which of the cups to activate when grasping.

The physical experiment results show that multiple-cup suction grasping could improve the efficiency of picking tasks.

Table 2. Experimental results.

Object Set	Method	Total Attempts	Successful Attempts	Success Rate	PPH
Boxes	Single-object grasping	59	50	85%	468
	Multiple-object grasping	36	36	100%	677
Fruits	Single-object grasping	64	50	78%	472
	Multiple-object grasping	33	31	94%	779
Daily necessities	Single-object grasping	56	51	91%	502
	Multiple-object grasping	53	40	75%	583

shows a comparison of experimental results between single-cup (single-object) and multiple-cup (multiple-object) grasping. For single-object grasping, all three object sets could be cleared by the robot. Daily necessities had the highest success rate (91%) and highest PPH (502) among the three object sets. The success rate of picking fruits was the lowest because the objects had a ball-like shape and rolled and slipped when the gripper pushed them along the normal direction during grasping despite having the correct grasp pose. The success rate of picking boxes was lower than that of daily necessities because when two boxes were very close together, the planner treated them as a single box and grasped the center, which was actually the edge between two boxes. This problem did not occur in the case of multiple-suction-cup grasping because even when two boxes were treated as a single big box, the planner set the averaged cup center positions to the center of the affordable area, as shown in Figure 7, so that the cups did not suck the edge between boxes. For multiple-object grasping, all three object sets could also be cleared by the robot. The success rate for grasping boxes (100%) was the highest among the object sets. The robot picked fruits with the highest speed (PPH = 779). Multiple-object grasping improved the picking speed by $1.45\times$ for boxes (PPH: 467 vs. 677), $1.65\times$ for fruits (PPH: 472 vs. 779), and $1.16\times$ for daily necessities (PPH: 502 vs. 583). These results indicate that multiple-suction-cup grasping can improve picking speed. The improvement in picking daily necessities was minor because it was difficult to find multiple-cup graspable poses due to the complicated shapes of the items. Figure 11 shows one picking trial for multiple-suction-cup grasping of boxes, fruits, and daily necessities. More trials are shown in the Supplementary Materials Video S1 file.

In this study, the object sets are lightweight items. For the fruit object set, we used lightweight plastic fruit samples instead of real fruit to avoid crushing them. We mainly focused on the correct suction poses and assumed that the suction cup can generate enough force to hold the object if the MSC grasp pose is correct. Although we believe that the maximum load capacity of the selected suction cup is 500 g and that the cup can hold most of the common daily necessities, the influence of object weight on the planner result will be validated using objects with various weights (e.g., using real fruit with different weight) in the future. In addition, the objects in the experiments had rather large and flat surfaces, such that the formulated seals were circular shapes and all contact points between the cup and the surface were in the same plane. In this case, cups are assumed to be capable of fully generating the suction force. However, for a complicated object shape, the seal of a cup might be a polygon (see Figure 1 in [18]). In this case, a more precise contact force model should be used to evaluate the grasp quality (grasp success probability) of the cups, but this will also lead to an increase in planning time. Finding an efficient method to evaluate the contact force for MSC grasp candidates is one of our future works to improve the planner so it is applicable for grasping more complex shape objects in dense scenes.

The gripper dimensions will affect the planner in two ways. Firstly, the increase in dimensions will lead to an increase in the volume of the gripper kernels in Figure 4, which will further result in an increase in planning time. Therefore, proper kernel interval size should be determined based on gripper dimension. In this study, the gripper kernel interval size was determined empirically. Automatic determination of the size based on gripper dimension will be considered to make the planner applicable to grippers with different dimensions. Secondly, if the gripper is too large, it will easily collide with the neighboring objects or bins so it will be difficult for the planner to find solutions for MSC grasping.

The picking system is expected to be improved in future work aimed at further increasing the picking speed. Our current layout of cups is fixed, and the positions and orientations of cups are fixed in the gripper. However, the real-world scenario is complex in that the items may have complex shapes, and the poses of items are disorganized. Hence, a fixed cup configuration may lead to a low probability of finding MSC grasp poses in a very complex environment (e.g., a dense scene) because there are few candidates who satisfy the MSC grasp condition. Making the positions and poses of cups adjustable by a proper gripper mechanical design may increase the probability of finding MSC grasp poses, which could be one of the directions in our future work to further improve the picking efficiency. In addition, as described above, one common failure is that objects can move (e.g., roll) after being grasped. We intend to analyze the dynamics (e.g., object shape, friction, and contact force between items) after grasping to find a grasp that moves the object and neighboring objects such that grasp success is improved. Another area for improvement is depth filling because incomplete depth results in low accuracy in estimating the affordance map and normals and thus leads to low grasp success. Furthermore, we will consider the picking sequence to improve the possibility of picking multiple objects. Picking experiments using a gripper with more suction cups will be conducted to further validate the performance and application of the planner for MSC grasp in the future. Our system cannot detect whether or not the gripper has successfully grasped the object. There are no sensors to detect whether or not the seal has been successfully formulated. Using a force sensor to detect the grasp success will be conducted in the future. If the force load of the end-effector increases after grasping, the object will be considered to be successfully grasped by the gripper. Based on the success detection result, the robot will be required to re-grasp a certain object if grasp failure occurs without returning to its home position to improve the picking efficiency.

8. Conclusions

In this study, we proposed a grasp planner for a multiple-suction-cup vacuum gripper. The planner took advantage of an affordance map to determine grasp poses for multiple-cup grasping using a 3D convolution-based method. Thanks to the encoded cup ID kernel, the planner could directly determine which cups to activate by decoding the convolution results. The planner exhibited good generality on previous affordance map datasets. The planner also showed the ability to improve picking speed compared with single-cup grasping in physical experiments with a real robot. We will work on improving the planner in future work from several directions, including object state analysis after grasping, point cloud or depth image completion, and picking sequence planning.