Abstract
In recent years, tasks regarding autonomous mobility favoredthe use of legged robots rather than wheeled ones thanks to their higher mobility on rough and uneven terrains. This comes at the cost of more complex motion planners and controllers to ensure robot stability and balance. However, in the case of quadrupedal robots, balancing is simpler than it is for bipeds thanks to their larger support polygons. Until a few years ago, most scientists and engineers addressed the quadrupedal locomotion problem with model-based approaches, which require a great deal of modeling expertise. A new trend is the use of data-driven methods, which seem to be quite promising and have shown great results. These methods do not require any modeling effort, but they suffer from computational limitations dictated by the hardware resources used. However, only the design phase of these algorithms requires large computing resources (controller training); their execution in the operational phase (deployment), takes place in real time on common processors. Moreover, adaptive feet capable of sensing terrain profile information have been designed and have shown great performance. Still, no dynamic locomotion control method has been specifically designed to leverage the advantages and supplementary information provided by this type of adaptive feet. In this work, we investigate the use and evaluate the performance of different end-to-end control policies trained via reinforcement learning algorithms specifically designed and trained to work on quadrupedal robots equipped with passive adaptive feet for their dynamic locomotion control over a diverse set of terrains. We examine how the addition of the haptic perception of the terrain affects the locomotion performance.
1. Introduction
Legged robots have emerged as a fascinating field of study and innovation in the realm of robotics. The unique capabilities of legged robots stem from the natural motion patterns of animals, which have evolved over millions of years to be efficient and effective in various landscapes. Drawing inspiration from nature’s most agile creatures, quadrupedal robots aim to replicate the locomotion abilities of four-legged animals [1]. Their versatile and adaptive movement in unstructured environments has garnered significant interest across various industries, ranging from search-and-rescue operations [2] to the exploration of harsh terrains [3,4]. Legged locomotion holds a distinct advantage over wheeled or tracked locomotion as it allows robots to traverse challenging terrains, bypass obstacles, and maintain stability even in unpredictable environments [5]. Quadrupedal robots, in particular, have shown great promise due to their ability to distribute weight across four legs, ensuring better stability and load-bearing capacity.
Considerable effort and focus have gone into the design of robotic feet for stable interaction with the environment [6,7,8,9]. For instance, the authors in [10] developed passive mechanically adaptive feet for quadrupedal robots capable of adapting to different terrain surfaces, significantly reducing robot slippage with respect to flat and ball feet.
From the motion point of view, dynamic locomotion plays a pivotal role in achieving agile and efficient movements for legged robots [11]. Unlike static locomotion, dynamic locomotion emphasizes the agility of these machines. The exploration of dynamic locomotion control for quadrupedal robots has become a critical area of research, seeking to enhance their agility, stability, and overall performance. Through dynamic locomotion control, robots can adjust their gait, step frequency, and leg movements in response to varying terrains, slopes, or disturbances. This adaptability allows quadrupedal robots to quickly handle unexpected obstacles and maintain balance and stability while moving at different speeds. The development of effective dynamic locomotion control algorithms presents numerous challenges [12]. Engineers and researchers must face complex issues such as environment reconstruction, state estimation, motion planning, and feedback control. Furthermore, achieving seamless coordination between multiple legs and ensuring smooth transitions between different gaits demands sophisticated control strategies.
Recent works have demonstrated that by exploiting highly parallel GPU-accelerated simulators and deep reinforcement learning, end-to-end policies can be trained in minutes even for complex control tasks such as quadrupedal robot dynamic locomotion [13,14].
To the best of the authors’ knowledge, there is no previous research addressing the problem of designing dynamic locomotion control algorithms that work on quadrupedal robots equipped with the passive adaptive feet presented in [10] (Figure 1), which consistently differ from the well-known and extensively investigated ball and flat feet. Therefore, the motivation of this work is the lack of control approaches designed and thought to fully exploit and leverage the information provided by this type of adaptive feet.

Figure 1.
Quadrupedal robot dynamic locomotion with adaptive feet.
Given the kinematic and dynamic high complexity of these adaptive feet and considering the lack of good informative mathematical models regarding dynamic locomotion in harsh environments, as in the context of robotic environmental monitoring of natural habitats, we decided to address this problem by leveraging data-driven and learning-based methods over model-based approaches.
The contribution of this work is the design, training, and investigation of different learning-based end-to-end control policies enabling quadrupedal robots equipped with the passive adaptive feet presented in [10] to perform dynamic locomotion over a diverse set of terrains. For end-to-end policies, we mean that between the input and the output of the controller, there is only a single neural network without any additional model-based sub-module. The adaptive feet used in this work come from previous research [10]; thus, they are not a contribution of this work.
This paper is organized as follows: in Section 2, we present the state-of-the-art learning-based quadrupedal robot dynamic locomotion control approaches and other related works of the problem faced; in Section 3, we present the method used to solve the quadrupedal robot dynamic locomotion control problem with adaptive feet; in Section 4, the results obtained in simulation are shown; in Section 5, we compare the results of the different trained control policies, and we discuss them; and in Section 6, we conclude and present potential future work that could improve the performance of the system.
2. Related Work
State-of-the-art learning-based quadrupedal robot dynamic locomotion control approaches use hybrid methods like [15], where a policy is trained to provide a few parameters that modulate model-based foot trajectory generators. In [16], the authors train in simulation, using a hybrid simulator similar to the one in [17], a non-exteroceptive student policy to imitate the behavior of a teacher policy that has access to privileged information not available to the real robot, and using a temporal convolutional neural network-based policy [18]. In [19], the authors similarly train a LiDAR- and RGBD-based perceptive policy capable of distinguishing when to rely on proprioception rather than exteroception using a recurrent neural network-based belief-state encoder.
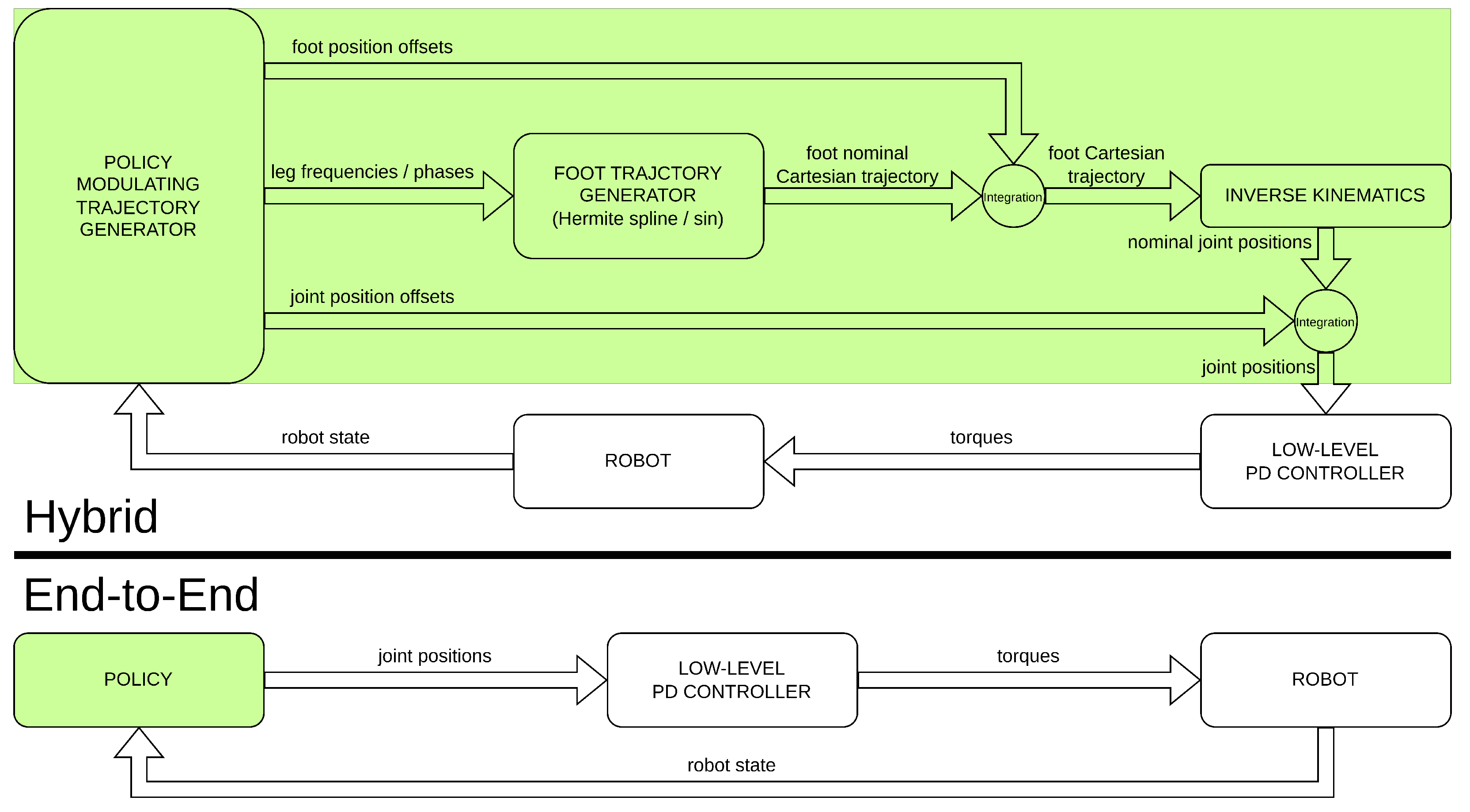
These methods are hybrid in the sense of [15], and they are not end-to-end in the sense that they do not rely on a purely learning-based approach. End-to-end pipelines have the freedom to learn behaviors that may not be possible to perform with an a priori fixed structure. On the other hand, hybrid approaches provide a better warm start in the learning phase, and they are more reliable because of their higher level of interpretability and robust in terms of stability because of their use of well-known first principles. However, certificated learning strategies [20] can be used to verify and satisfy safety and stability requirements directly during the training process. Figure 2 highlights the main differences in terms of different controller components of hybrid architectures versus end-to-end ones.
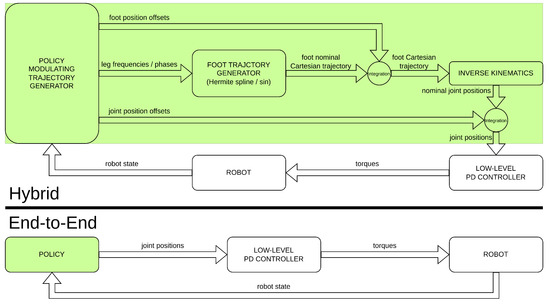
Figure 2.
Differences between hybrid [15] and end-to-end [14] approaches.
More recently, end-to-end methods [14] instead have been demonstrated to be able to successfully learn perceptive policies, whose performance is comparable to that of hybrid methods [19], without any model-based trajectory generator or other prior knowledge and without any privileged learning or teacher–student-based imitation learning. Other works [21,22,23,24,25] have been carried out to showcase how using end-to-end learning-based pipelines enables advanced motor skills for quadrupedal robot locomotion and navigation in unstructured and challenging environments. These methods, however, have all been designed to run on robots equipped with standard ball feet, with point-based contact dynamics assumptions.
Passive adaptive feet [10] have been designed to be able to adapt to the shape of any kind of obstacle, maximizing grip and avoiding slippage. Moreover, they are equipped with a sensing system capable of providing information about the environment and the foot interaction with the surroundings. The authors in [26] developed a foothold selection algorithm for quadrupedal robots equipped with SoftFoot-Q [10] mechanically adaptive soft feet. As in [27], on the baseline [28], a dataset of elevation maps of synthetically generated terrains is acquired and collected in simulation. Then a polynomial fitting algorithm is used, along with other computations, to compute the associated cost maps, which are then used for the foothold selection. Since the terrain assessment and constraint checking are computationally expensive, a convolutional neural network (CNN), more precisely an efficient residual factorized convolutional neural network (ERFNet) [29], is trained and used to predict a good approximation of the cost map, which is then used to compute the potential footholds on the elevation map.
Another interesting work addressing real-time dynamic locomotion on rough terrains that deals with dynamic footholds is presented in [30], but it is still designed to run on robots equipped with standard ball feet. In [31], the authors aim to improve dynamic quadrupedal locomotion robustness by employing a fast model-predictive foothold-planning algorithm and an LQR controller applied to projected inverse dynamic control for robust motion tracking. The method shows robustness by being able to achieve good dynamic locomotion performance also with unmodeled adaptive feet, but it does not make any use of the supplementary haptic information of the terrain provided by these feet and thus does not exploit the benefits of their passive adaptability.
Despite the good work performed on footstep planning with the adaptive feet presented in [10], there is no work on dynamic locomotion control explicitly designed for them. All the mentioned methods employ static walking gait patterns, such as crawling, where robot speed is limited. Moreover, all the works presented so far address the problem of dynamic locomotion but not with the use of the adaptive feet presented in [10].
3. Method
We model the quadrupedal robot dynamic locomotion control problem with adaptive feet as a Markov decision process (MDP). The latter is a mathematical framework to formulate discrete-time decision-making processes. The MDP is the standard mathematical formalism when dealing with reinforcement learning problems. An MDP is described by a tuple of five elements . defines the state space, defines the action space, is the reward function, is the transition probability density function, and is the starting state distribution.
At each time step t, the learning agent takes an action based on the environment state . The action is drawn from a parameterized policy , with being the set of policy parameters. This results in a reward value . In the case of policy optimization algorithms, among reinforcement learning methods, the goal is to find the optimal set of policy parameters , which maximizes the expected return , i.e., . This goal is achieved through interactions with the environment in a trial-and-error fashion, where are trajectories (sequences of states and actions) drawn from the policy, and is the infinite-horizon discounted return (the cumulative reward), with discount factor and being the reward at time step t.
A Gaussian distribution is used to model the policy , i.e., . We use a multi-layer perceptron (MLP) for the mean value and a state-independent standard deviation . The policy optimization is obtained through the proximal policy optimization (PPO) algorithm [32] from RL-Games [33].
We define our approach as end-to-end because it uses a single neural network as the only component of the controller.
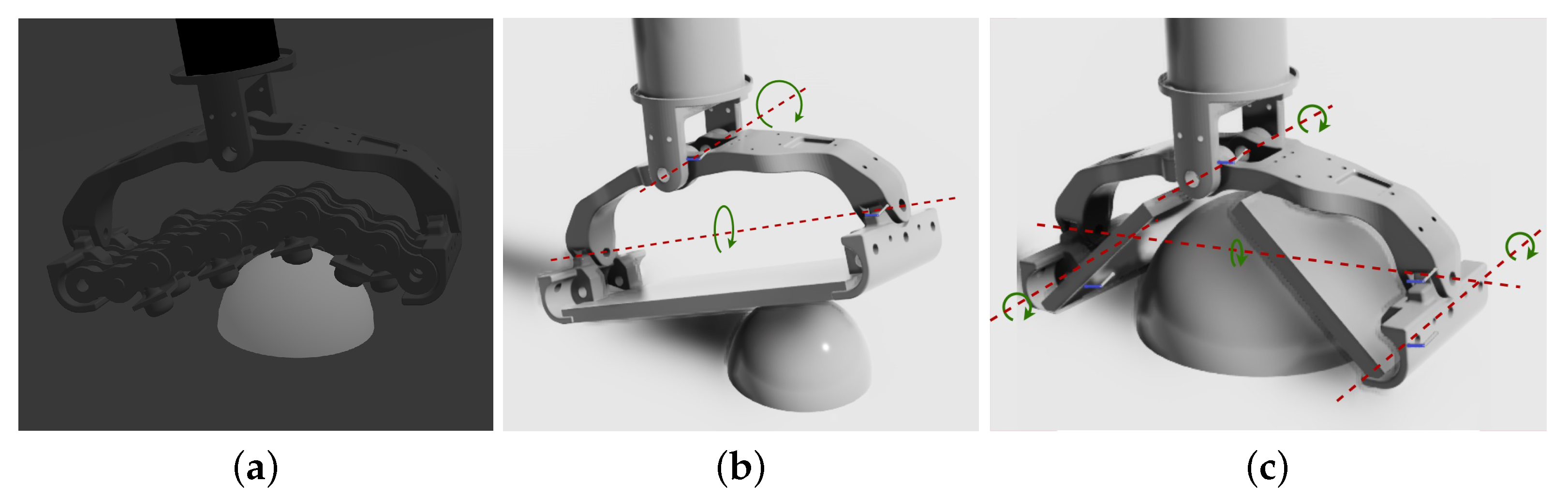
As the authors in [26] highlight, the simulation of the adaptive foot [10] is slow because of its mechanical complexity, since it counts a total of 34 joints, and a quadrupedal robot employs four of these feet. Even using a GPU-accelerated physics-based simulator such as Isaac Sim [34], the simulation remains slow, especially considering that to exploit its high level of parallelism, thousands of robots are simultaneously simulated, which is useful to find optimal policies for reinforcement learning problems in a short time [13]. Moreover, even if Isaac Sim supports closed kinematic chain simulation, given the high complexity of the adaptive feet, the simulation of the closed kinematic model of the foot is highly unstable and often leads to non-physical behaviors when high contact forces are involved. For these reasons, we decided to employ two simplified approximations of the adaptive foot model shown in Figure 3a, both of which have an open kinematic chain structure, preserving the major degrees of freedom of their adaptability.
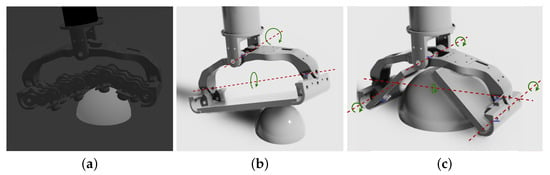
Figure 3.
Proposed approximations of the SoftFoot-Q [10] (a) model: (b) Adaptive Flat Foot (AFF) and (c) Adaptive Open Foot (AOF). The passive DoF rotation axes are highlighted in red.
These model approximations are shown in Figure 3. In particular, the two simplified models that were designed are the Adaptive Flat Foot (AFF) model and the Adaptive Open Foot (AOF) model, represented in Figure 3b,c, respectively. The Adaptive Flat Foot keeps the pitch and roll joints of the ankle of the SoftFoot-Q shown in Figure 3a, with the three chains being replaced by a single rigid flat body for the sole (2 passive degrees of freedom in total). The Adaptive Open Foot instead splits the single rigid flat body of the sole into two bodies, each one having an additional rotational degree of freedom with regard to the transversal axis of the foot roll link, allowing the foot to adapt to the shapes of different terrain obstacles and artifacts (4 passive degrees of freedom in total).
The reinforcement learning environments, shown in Figure 4, used for training the dynamic locomotion control policies are based on the baselines available in [35], a collection of reinforcement learning environments for common and complex continuous-time control problems, implemented to run on Isaac Sim. They are the flat terrain locomotion environment, shown in Figure 4a, and the rough terrain locomotion environment, shown in Figure 4b. Both of them use the ANYmal quadrupedal robot platform [36], equipped with a total of 12 actuated degrees of freedom, 3 per leg, namely, Hip Abduction–Adduction (HAA), Hip Flexion–Extension (HFE), and Knee Flexion–Extension (KFE).

Figure 4.
Reinforcement learning environments.
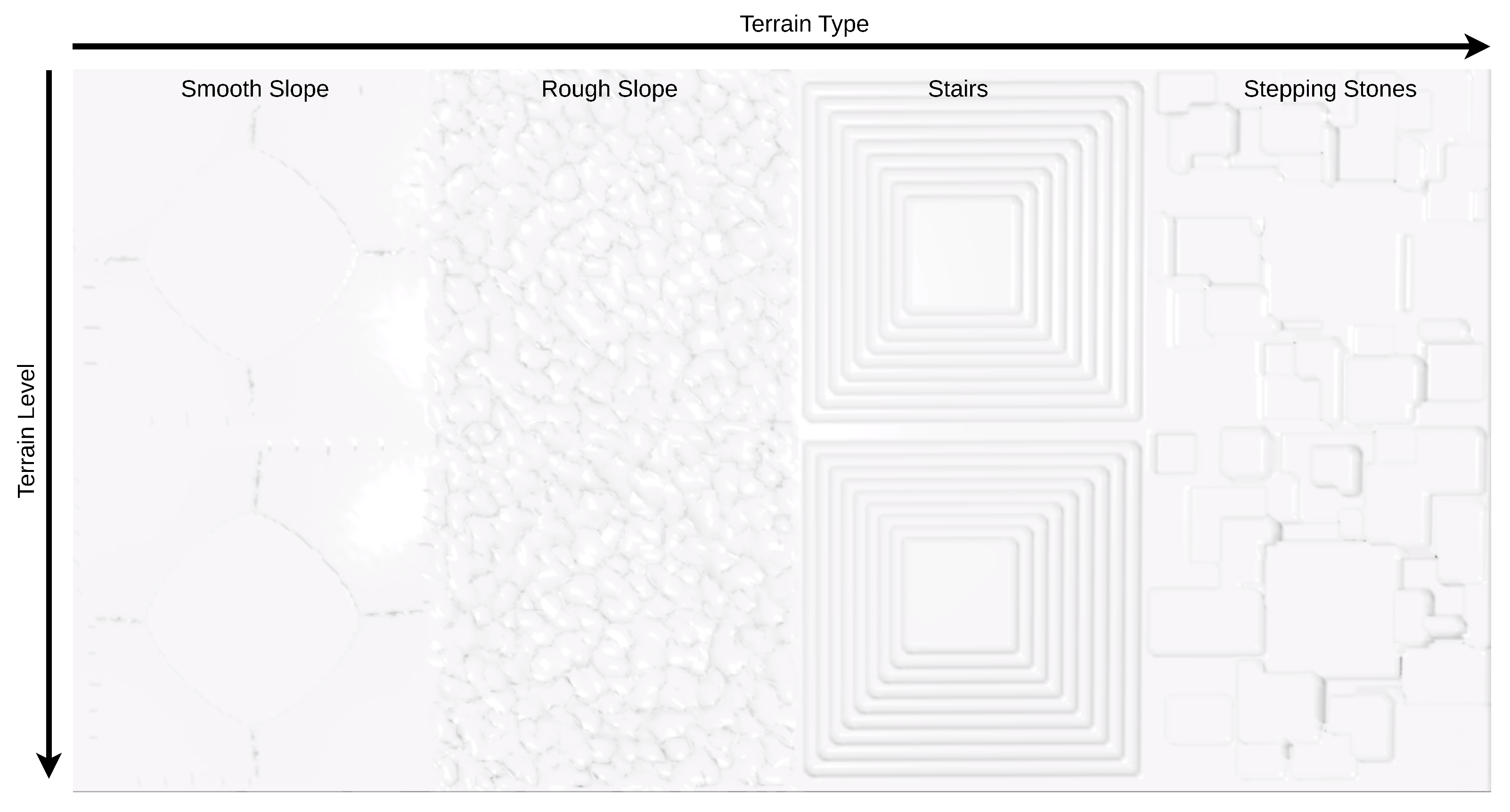
As in [14], the rough terrain policies were trained in a game-inspired automatic curriculum fashion [37], starting from simpler terrain samples and increasing in complexity once the control policies allow the robots to traverse them [38]. Therefore, the environment terrain is built as a single set of different terrains (smooth slope, rough slope, stairs, stepping stones) at different levels of difficulty, following the setup shown in Figure 5.
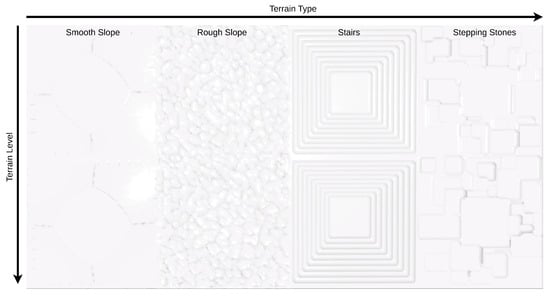
Figure 5.
Terrain setup for the rough terrain environment.
For the flat terrain locomotion environment, the policy MLP has three hidden layers, with 256, 128, and 64 units, respectively, and a 12-dimensional output layer representing the 12 desired joint velocities , which are then integrated with the current joint positions , to obtain the desired joint positions .
The rough terrain locomotion environment, instead, employs a policy MLP with three hidden layers with 512, 256, and 128 units, respectively, and a 12-dimensional output layer representing the 12 desired joint positions directly.
For both environments, a low-level PD controller is then used to compute the desired joint torques to apply to the robot actuated joints.
We considered different types of policy. In particular, the policy can either be perceptive, using a robot-centric elevation map of the surrounding terrain as shown in Figure 6 as part of the input, or blind, without considering it. Then, the policy can either exploit terrain haptic perception, taking as input also the joint positions and velocities of the feet, or not. Considering the combinations of these strategies, four types of locomotion policy have been defined: blind–non-haptic (B), perceptive–non-haptic (P), blind–haptic (BH), and perceptive–haptic (PH). The configuration of the policy observation space for each type of policy is given in Table 1. For the rough terrain locomotion task, all these types of policy were investigated, while for the flat terrain locomotion task, only the blind–non-haptic policy type (B) was considered.
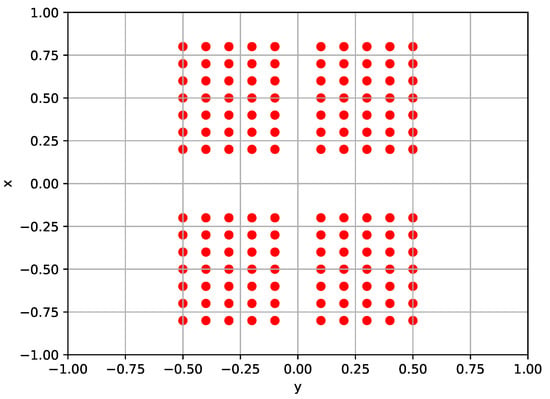
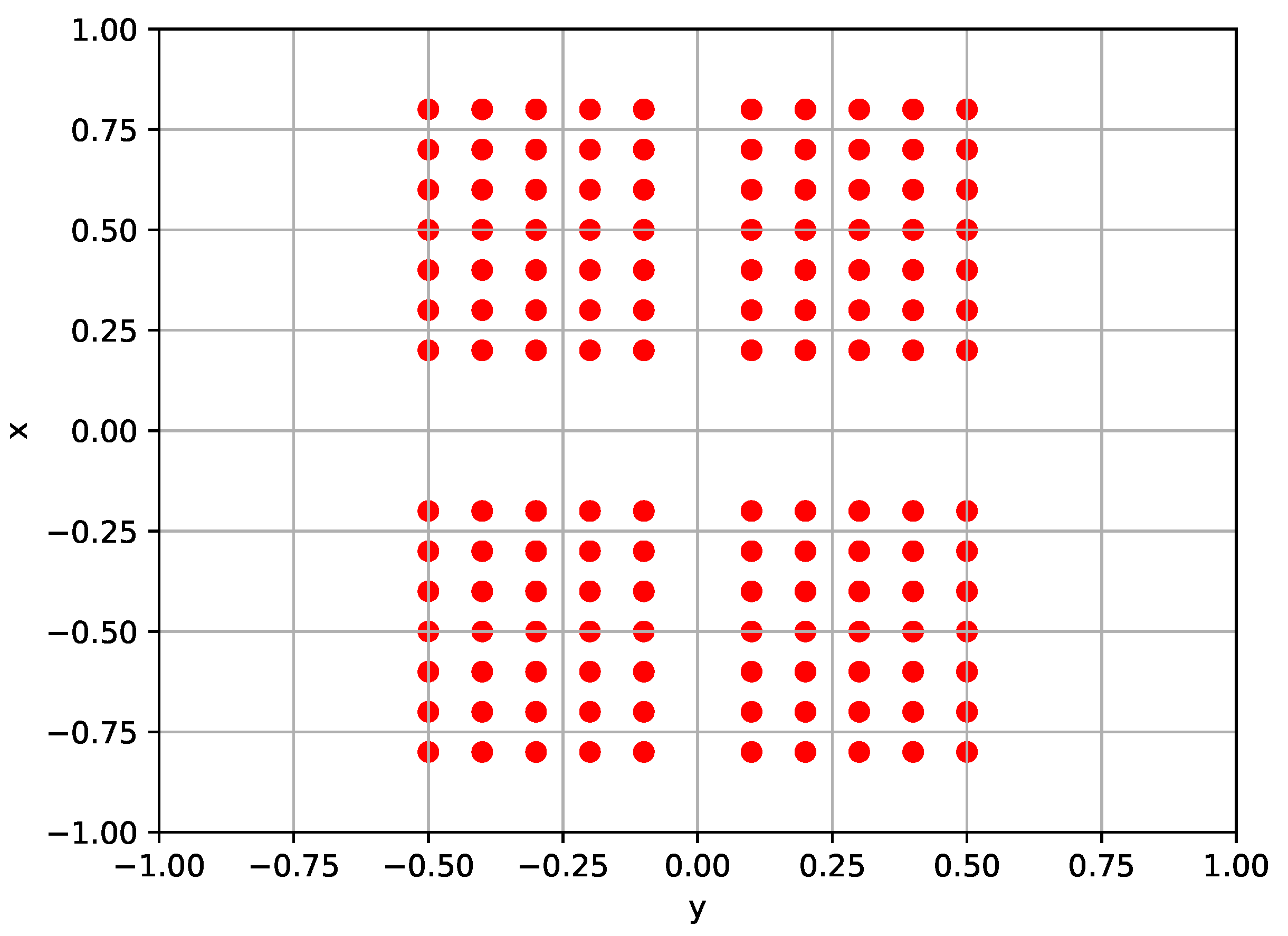
Figure 6.
Robot-centric elevation map with sampled point coordinates.

Table 1.
Policy observation space.
The contact conditions of the adaptive feet with the terrain are not contained in any of the policy inputs. The feet information that the different policies take as input comprises the feet joint positions and velocities, as described in Table 1. Even if the feet joint positions and velocities cannot be directly measured via joint encoders, they can be easily estimated from the four IMU measurements available on each foot [10].
The input components of these different types of policy can be all or some of the following: base twist , consisting of the 3 linear and angular velocities of the robot base; projected gravity , that is, the projection of the gravity vector on the base frame axes, which gives information about the robot base orientation with regard to the gravity direction; command , that is, the user-provided desired robot base twist reference, whose details are given in the next paragraphs; joint positions , namely, the positions of the actuated joint; joint velocities , namely, the velocities of the actuated joint; previous action , that is, the output of the policy at the previous time step; height map , i.e., the elevation map shown in Figure 6; feet joint positions , i.e., the positions of the feet passive joints; and feet joint velocities , i.e., the velocities of the feet passive joints.
The primary goal of the locomotion tasks is to track a user-provided commanded base twist reference without falling. The command is composed of three components: a linear velocity along the robot sagittal axis (), a linear velocity along the robot transversal axis (), and an angular velocity around the robot longitudinal axis ().
We also applied domain randomization [39], considering additive component-wise scaled random noise, generating randomized reference commands (the angular velocity command is generated starting from a randomized heading direction) and applying random disturbances to the robots through interspersed base random pushes.
The reward function is the sum of different conventional terms, and it aims to make the robot base twist:
to follow the commanded reference one
with , , and always equal to zero.
The linear velocity term aims at minimizing the velocity tracking errors in the forward and lateral linear directions:
The angular velocity term aims at minimizing the yaw angular velocity tracking error around the vertical axis of the robot base frame:
The longitudinal linear velocity penalty term keeps the robot base’s vertical velocity as small as possible to avoid jumping-like motions:
The angular velocity penalty term keeps the robot base’s roll and pitch angular velocities as small as possible to prevent the robot from rolling to the front or side:
The orientation penalty term penalizes all those robot base orientations that do not make the gravity vector perpendicular to the x–y plane of the robot base frame by keeping the x and y components of the projected gravity vector as close to zero as possible
The robot base height penalty term keeps the robot base height, with regard to the terrain beneath it, close to a predefined walking height h (0.52 m) to avoid the robot walking with a low base height (this penalty term is particularly helpful when training blind locomotion policies on rough terrains, as is shown in the results):
The joint torques penalty term aims at minimizing the robot actuated joint torques for energy-efficiency reasons:
The joint accelerations penalty term aims at minimizing the robot actuated joint accelerations to avoid abrupt motions of the robot joints:
The action rate penalty term smooths the policy output with regard to time steps, providing a certain continuity in the desired joint references regardless of whether they are joint positions or joint velocities:
The hip motion penalty term is used for aesthetic reasons, and it keeps the Hip Abduction–Adduction joint positions close to the default values, which makes the robot walk in a natural-looking manner:
where L, R, F, and H are the left, right, front, and hind sides of the robot, respectively, and are the default joint positions of the Hip Abduction–Adduction joints, which are 0.03 radians for the left-hand side joints and −0.03 radians for the right-hand side joints.
In Equations (5)–(12), are opportunely tuned constants, and n is the number of robot actuated joints. These reward and penalty terms do not impose any kind of specific walking pattern, gait, or behavior, neither static nor dynamic, since none of them uses any kind of information about feet contact timing. These terms only aim to impose a specific robot base motion, since they only involve robot base velocity, orientation, and height values, as well as joint velocities, accelerations, and torques. The dynamic locomotion gait is a self-emerging behavior during training. According to these terms, it is more convenient to employ a faster dynamic gait rather than a slower static one to track the required commanded base twists to obtain a higher reward.
The robots are reset and their rewards are penalized if their base or more than one knee gets in touch with the ground. Robots can also be reset if a timeout occurs when reaching the maximum episode length. Timeouts are correctly handled, as in [14], using the partial-episode bootstrapping method [40]. The values of the hyper-parameters of the policy optimization algorithm (PPO), used for the training of the locomotion policies, are the environment default ones as in [35].
The policies were all trained in simulation using Isaac Gym [13] in the Omniverse Isaac Sim [34] simulator, running thousands of robots in parallel, exploiting the power of GPU acceleration. The hardware setup for training the control policies employed an NVIDIA Tesla T4 GPU with 16 GB of VRAM.
4. Results
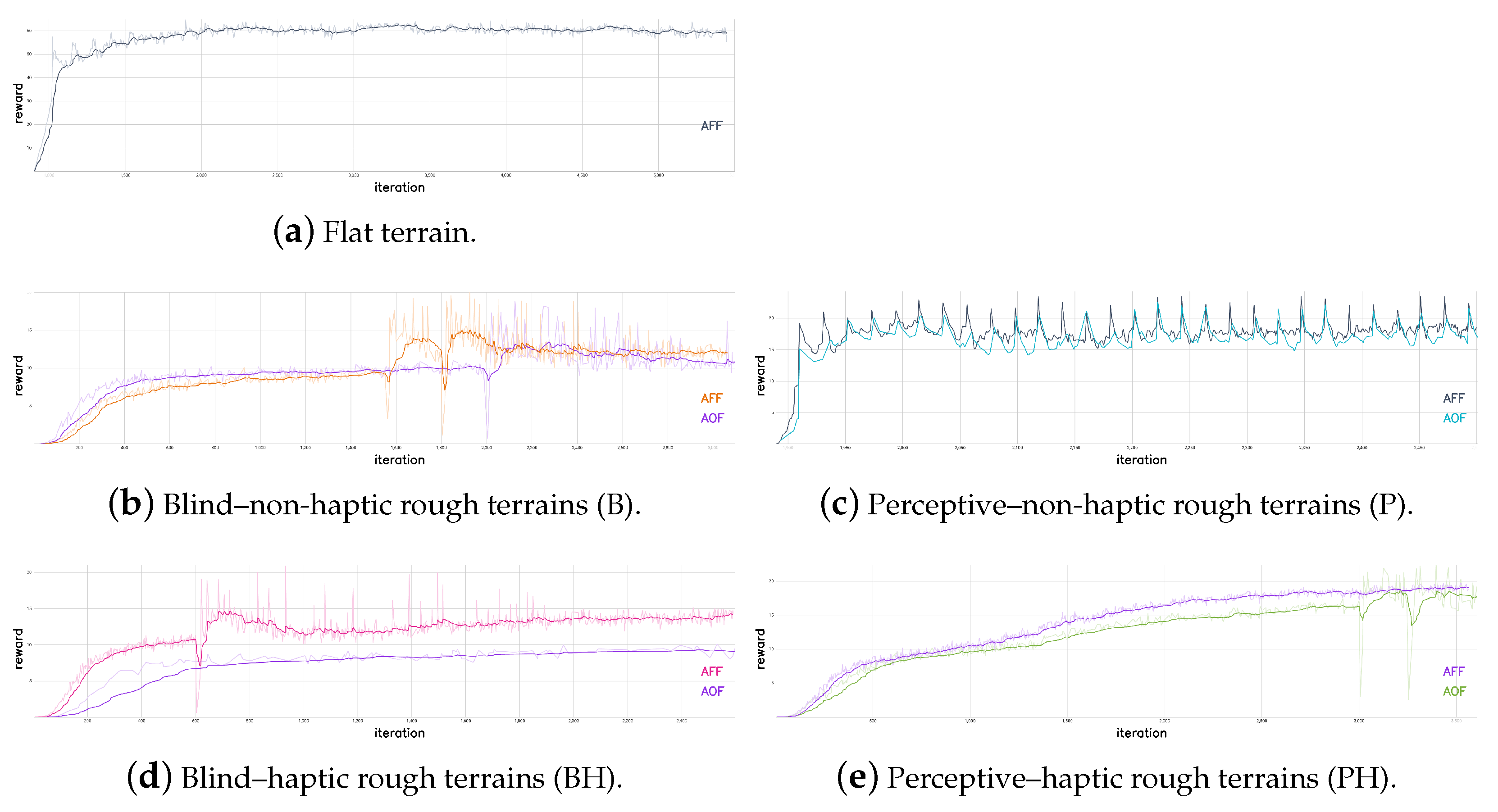
In Figure 7, the reward trends of the different training sessions are shown. The spikes in the trends are due to training restarts from checkpoints. The training was stopped when the reward did not significantly increase for more than a thousand iterations. The number of simultaneously simulated robots during the training process is 2048 for all the trained policies. A policy update iteration consists of 48 policy steps for each of these environments.
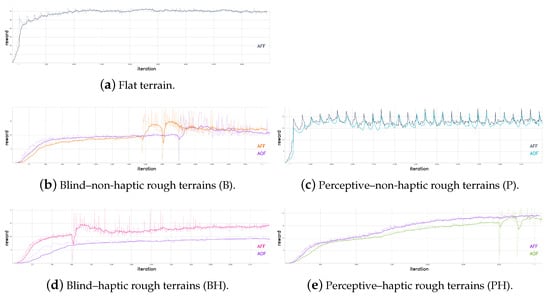
The performance indices evaluated are the following: the linear velocity tracking error in the forward and lateral directions; the yaw angular velocity tracking error around the vertical axis of the robot base frame; the desired joint positions rate, which is the difference between the previous policy output and the current one, to evaluate continuity; the actuated joint velocities rate, which is the difference between the previous actuated joint velocities and the current ones, to evaluate abrupt motions; actuated joint torques, to evaluate energy efficiency; and robot base height, to evaluate natural-looking walking style.
After the policies were trained, the performance indices were evaluated by simulating 1024 robots in parallel for a simulation time of 60 s for the flat terrain locomotion task and 17.5 s for the rough terrain policies. This is just for memory requirements and computational time reasons for computing these performance indices. Both the mean and standard deviation of the performance indices were computed over all these policy steps, and they are shown in the charts in terms of error bars.
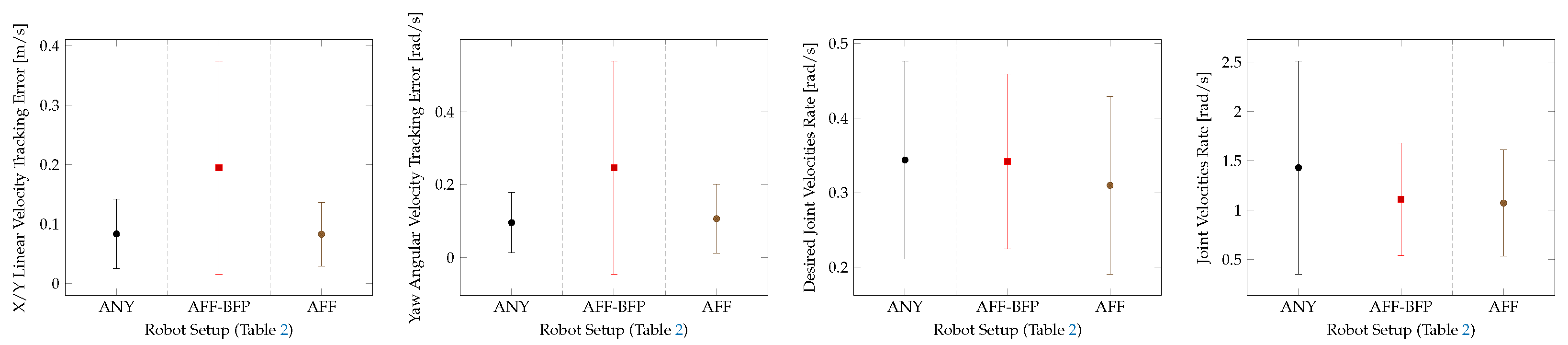
Figure 8 shows a performance evaluation and a comparison of the flat terrain locomotion policies. The performance of the baseline policy from [35], employed on the robot equipped with its own default ball feet, is compared with the performance of the same policy employed on the robot equipped with the Adaptive Flat Feet (AFF, Figure 3b). Then the performance of a third policy, opportunely trained using the robot equipped with the Adaptive Flat Feet, is also illustrated. A detailed description of the different policies tested on this task is given in Table 2.
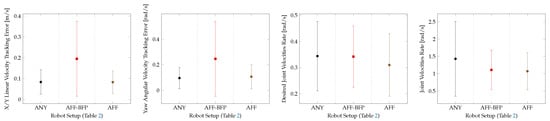
Figure 8.
Performance of the different robot setups tested for the flat terrain locomotion task.

Table 2.
Description of the different robot setups tested for the flat terrain locomotion task.
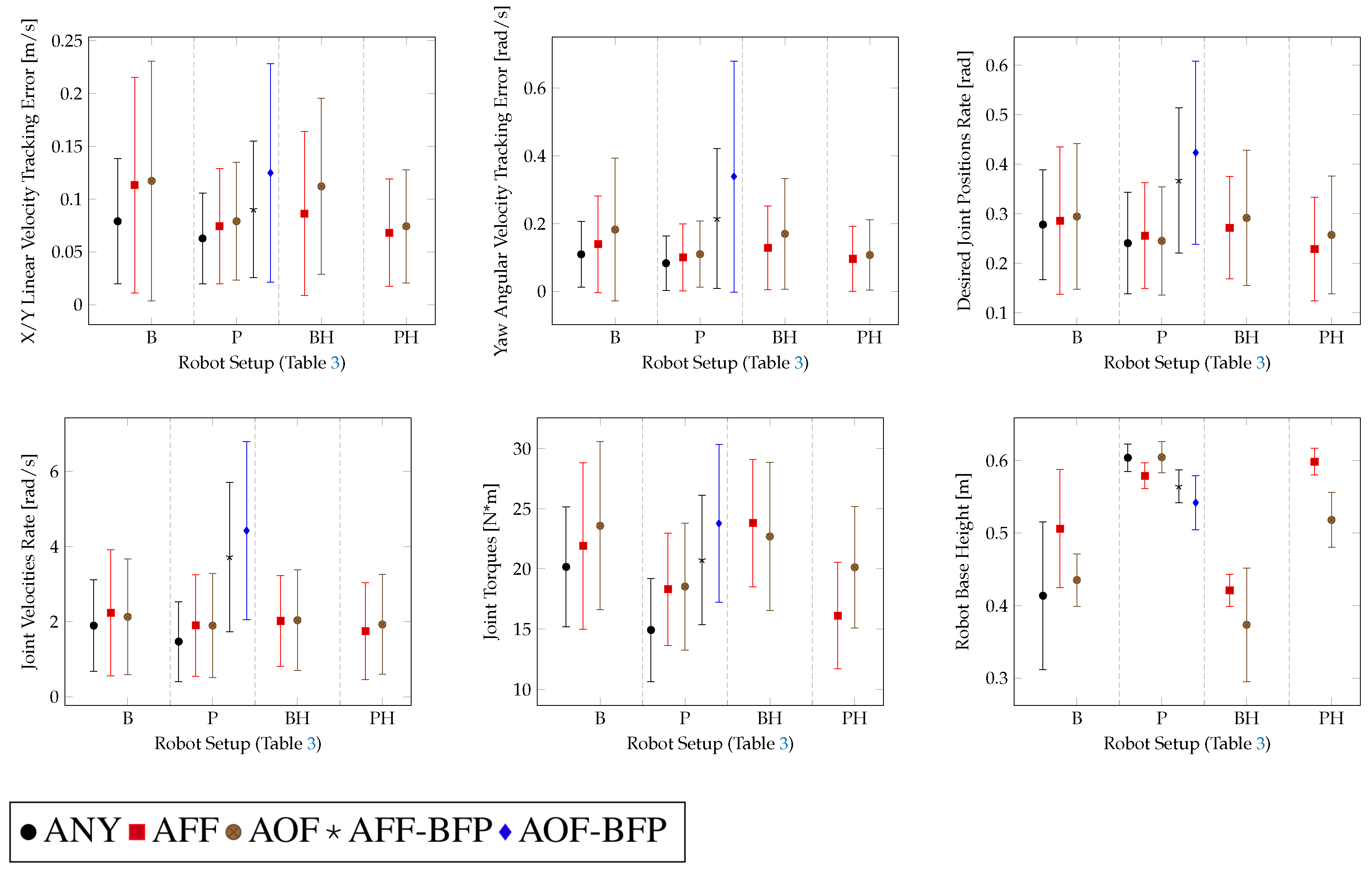
In Figure 9, a performance evaluation of the rough terrain locomotion policies and comparison with ball-feet baseline policies from [35] is presented. Furthermore, in this case, the baseline policy (perceptive–non-haptic with ball feet P-ANY) from [35], trained on the robot equipped with its own default ball feet, was tested on the robot equipped with both the approximations of the SoftFoot-Q. A detailed description of the different policies tested on this task is given in Table 3.
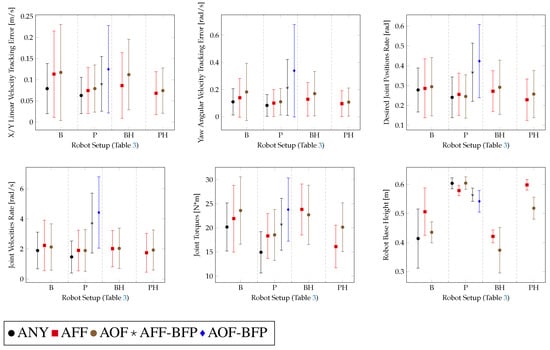
Figure 9.
Performance of the different robot setups tested for the rough terrain locomotion task.

Table 3.
Description of the different robot setups tested for the rough terrain locomotion task.
For the blind locomotion tasks, we noticed a common pattern: the robot learned to walk at a lower height of the base. As mentioned in Section 3, adding the base height penalty term partially helps to solve this problem at the expense of a worse base twist command tracking performance.
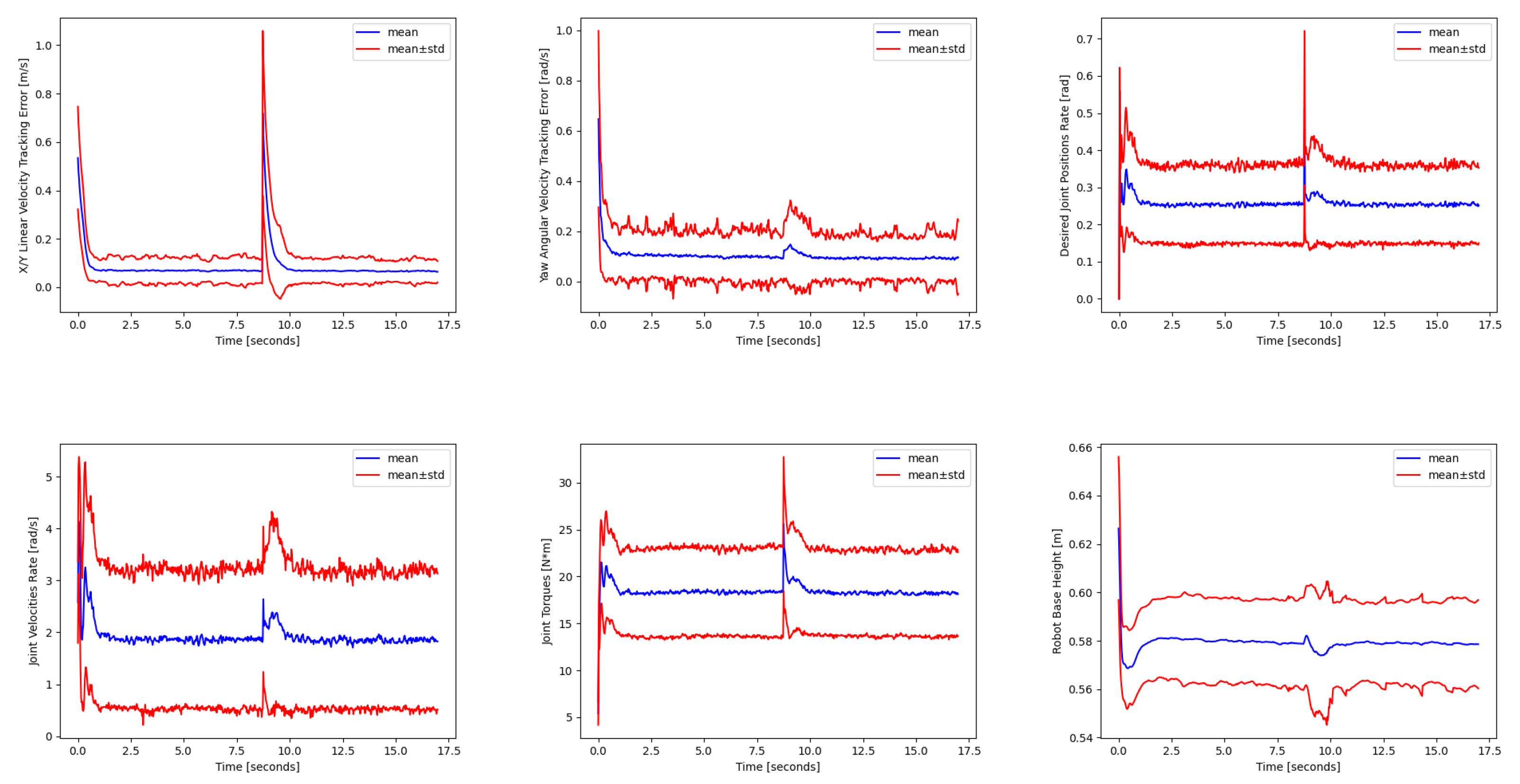
Since the policies were trained taking into account dynamics randomization, as discussed in Section 3, Figure 10 shows an example of the disturbance response to random pushes applied to the robot base for the perceptive–non-haptic rough terrain policy running on the robot equipped with the Adaptive Flat Feet (AFF).
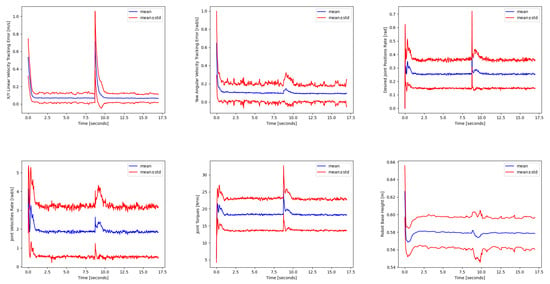
Figure 10.
Performance evaluation when random pushes are applied to the robot base. The disturbance is applied at 8.75 s. The mean and the standard deviation were computed by simulating 1024 robots in parallel, with each one following a random commanded base twist reference.
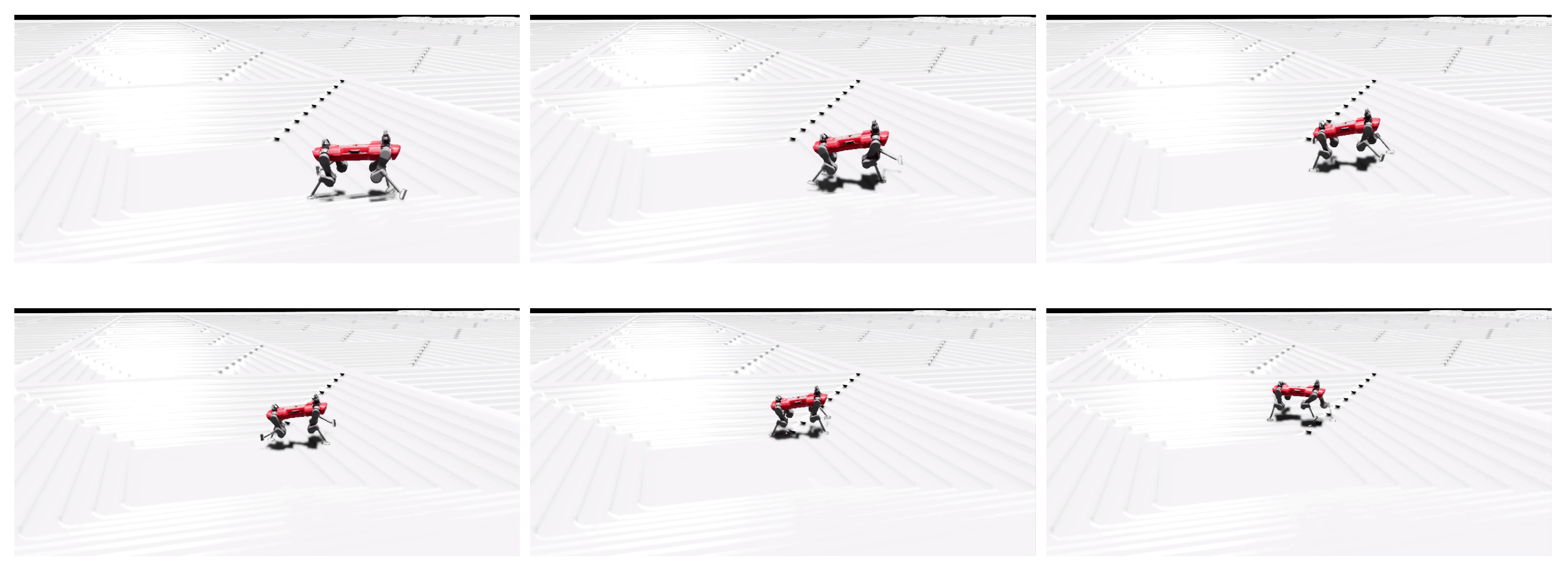
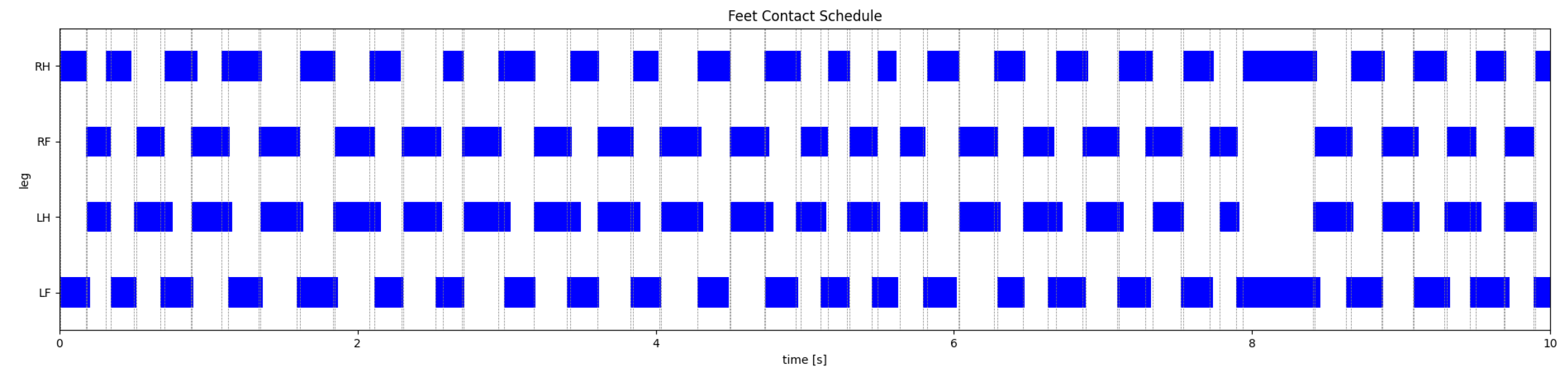
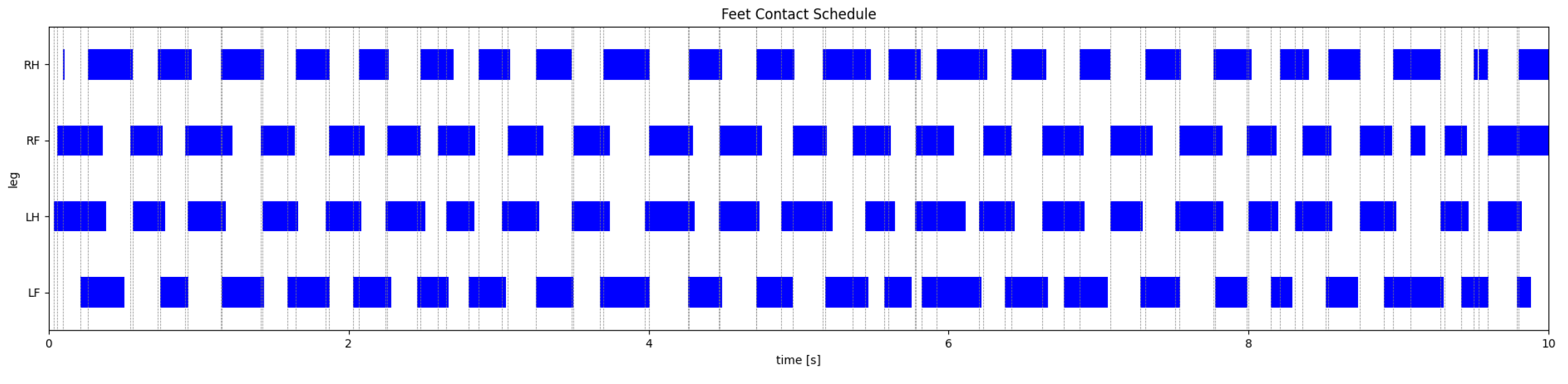
Figure 11, Figure 12, Figure 13 and Figure 14 show two motion captures of two different trained policies traversing two types of rough terrains among the considered ones and their corresponding feet contact schedules. Please refer also to the video attachment to visualize the full experiment. The feet contact schedules in Figure 12 and Figure 14 show that the learned locomotion gait follows a dynamic gait pattern, namely, the trotting gait.

Figure 11.
Photo sequence of the P-AFF policy on stairs.

Figure 12.
Feet contact schedule of the P-AFF policy on stairs.

Figure 13.
Photo sequence of the PH-AOF policy on a rough slope.

Figure 14.
Feet contact schedule of the PH-AOF policy on a rough slope.
5. Discussion
For the flat terrain locomotion task, only the Adaptive Flat Foot (AFF) approximation was considered, because on this type of terrain, the adaptability features of the SoftFoot-Q would not be exploited. In this case, we obtain similar results with regard to the robot equipped with ball feet. The performance of the flat terrain and perceptive–non-haptic rough terrain (P) baseline policies from [35], trained using the robot equipped with its own default ball feet (ANY), decreases when running on the robot equipped with either the Adaptive Flat Feet (AFF) or the Adaptive Open Feet (AOF) approximation. This shows that the same policy trained using ball feet cannot be employed with the adaptive feet. This proves that appropriate training is required to reach the same level of performance as in the ball feet case (ANY), as shown in Figure 8 and Figure 9. We can conclude that with adaptive feet, we reach a similar performance with regard to the flat terrain and perceptive–non-haptic rough terrain (P) baseline policies employing ball feet (ANY) [35].
In the cases of blind rough terrain locomotion (B, BH), the robot is led to walk with a lower height of the base, but it is still able to track the base twist reference command in a comparable manner to the perceptive-non-haptic (P) setup. This phenomenon is more evident in the case of ball feet (B-ANY). In Figure 9, we can see that with adaptive feet (B-AFF, B-AOF), the twist command tracking performance is similar to the ball feet case (B-ANY), but the robot base height is slightly higher and more stable given its lower variation. Therefore, in the blind settings, the walk is more resilient with adaptive feet [10].
We can also see that the Adaptive Open Foot (AOF) approximation, in the cases of blind locomotion on rough terrains, provides, in general, worse performance with regard to the Adaptive Flat Foot (AFF) approximation.
Finally, there are orientation problems with foot placement. On rough terrains, we experienced a lot of cases in which the feet assumed a configuration that would cause a break of the foot on the real robot, especially with blind locomotion, like walking while making contact with the ground either with the lateral sides of the feet or with the upper side of the front and back arch links. This problem can be seen in Figure 15.

Figure 15.
Foot orientation problem.
6. Conclusions & Future Works
In this work, we presented blind, perceptive, and haptic end-to-end learning-based policies for dynamic locomotion control of quadrupedal robots equipped with the adaptive soft feet in [10]. We presented the training setup and approach, with a detailed evaluation of the performance obtained and a comparison with existing baselines. We investigated the benefits and the faults.
Some of the future work that we aim to put our efforts into are experiments on the real robot, to better assess the goodness of the adaptive feet model approximations and validate them, and performing training using the foothold cost map instead of the elevation map. This second goal could be achieved through our previous work [26], in which we designed and developed a CNN-based foothold selection algorithm for static gaits that works with adaptive feet. Given the dynamic locomotion problem complexity, the selected footholds cannot be taken into account separately by planning static gaits, but the cost maps related to each foot need to be processed at the same time to guarantee convergence and good performance.
Moreover, model-based methods could also be used together with data-driven methods [41] to further improve the controller reliability and overall performance.
Author Contributions
Conceptualization, A.S., F.A. and M.G.; Methodology, A.S., F.A. and M.G.; Software, A.S.; Validation, A.S.; Formal analysis, A.S.; Investigation, A.S., F.A. and M.G.; Data curation, A.S.; Writing—original draft, A.S.; Writing—review and editing, F.A. and M.G.; Visualization, A.S.; Supervision, F.A. and M.G.; Project administration, M.G.; Funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement No. 101016970 (Natural Intelligence), in part by the Ministry of University and Research (MUR) as part of the PON 2014-2020 “Research and Innovation” resources—Green/Innovation Action—DM MUR 1061/2021 and DM MUR 1062/2021, and in part by the Italian Ministry of Education and Research (MIUR) in the framework of the FoReLab project (Departments of Excellence).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kim, S.; Wensing, P.M. Design of dynamic legged robots. Found. Trends Robot. 2017, 5, 117–190. [Google Scholar] [CrossRef]
- Fankhauser, P.; Hutter, M. Anymal: A unique quadruped robot conquering harsh environments. Res. Features 2018, 126, 54–57. [Google Scholar] [CrossRef]
- Wong, C.; Yang, E.; Yan, X.T.; Gu, D. Autonomous robots for harsh environments: A holistic overview of current solutions and ongoing challenges. Syst. Sci. Control. Eng. 2018, 6, 213–219. [Google Scholar] [CrossRef]
- Fahmi, S.; Mastalli, C.; Focchi, M.; Semini, C. Passive whole-body control for quadruped robots: Experimental validation over challenging terrain. IEEE Robot. Autom. Lett. 2019, 4, 2553–2560. [Google Scholar] [CrossRef]
- Liu, J.; Tan, M.; Zhao, X. Legged robots—An overview. Trans. Inst. Meas. Control 2007, 29, 185–202. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Zhang, M.; Zhang, S.; Qian, Z.; Chu, J. A novel metamorphic foot mechanism with toe joints based on spring-loaded linkages. IEEE Robot. Autom. Lett. 2022, 8, 97–104. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mo, A.; Kiss, B.; Gönen, E.C.; Badri-Spröwitz, A. Multi-segmented adaptive feet for versatile legged locomotion in natural terrain. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 1162–1169. [Google Scholar]
- Ranjan, A.; Angelini, F.; Nanayakkara, T.; Garabini, M. Design Guidelines for Bioinspired Adaptive Foot for Stable Interaction With the Environment. IEEE/ASME Trans. Mechatron. 2024, 29, 843–855. [Google Scholar] [CrossRef]
- Yao, C.; Shi, G.; Xu, P.; Lyu, S.; Qiang, Z.; Zhu, Z.; Ding, L.; Jia, Z. STAF: Interaction-based design and evaluation of sensorized terrain-adaptive foot for legged robot traversing on soft slopes. IEEE/ASME Trans. Mechatron. 2024, 1–12. [Google Scholar]
- Catalano, M.G.; Pollayil, M.J.; Grioli, G.; Valsecchi, G.; Kolvenbach, H.; Hutter, M.; Bicchi, A.; Garabini, M. Adaptive Feet for Quadrupedal Walkers. IEEE Trans. Robot. 2022, 38, 302–316. [Google Scholar] [CrossRef]
- Aoi, S.; Tanaka, T.; Fujiki, S.; Funato, T.; Senda, K.; Tsuchiya, K. Advantage of straight walk instability in turning maneuver of multilegged locomotion: A robotics approach. Sci. Rep. 2016, 6, 30199. [Google Scholar] [CrossRef]
- Holmes, P.; Full, R.J.; Koditschek, D.; Guckenheimer, J. The Dynamics of Legged Locomotion: Models, Analyses, and Challenges. SIAM Rev. 2006, 48, 207–304. [Google Scholar] [CrossRef]
- Makoviychuk, V.; Wawrzyniak, L.; Guo, Y.; Lu, M.; Storey, K.; Macklin, M.; Hoeller, D.; Rudin, N.; Allshire, A.; Handa, A.; et al. Isaac Gym: High Performance GPU Based Physics Simulation For Robot Learning. In Proceedings of the Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), Virtual-only Conference, 6–14 December; 2021. [Google Scholar]
- Rudin, N.; Hoeller, D.; Reist, P.; Hutter, M. Learning to Walk in Minutes Using Massively Parallel Deep Reinforcement Learning. In Proceedings of the 5th Conference on Robot Learning, PMLR, London, UK, 8–11 November 2022; In Proceedings of Machine Learning Research. Faust, A., Hsu, D., Neumann, G., Eds.; PMLR: London, UK, 2022; Volume 164, pp. 91–100. [Google Scholar]
- Iscen, A.; Caluwaerts, K.; Tan, J.; Zhang, T.; Coumans, E.; Sindhwani, V.; Vanhoucke, V. Policies modulating trajectory generators. In Proceedings of the 2nd Conference on Robot Learning, PMLR, Zürich, Switzerland, 29–31 October; 2018; pp. 916–926. [Google Scholar]
- Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning quadrupedal locomotion over challenging terrain. Sci. Robot. 2020, 5, eabc5986. [Google Scholar] [CrossRef] [PubMed]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, eaau5872. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Miki, T.; Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning robust perceptive locomotion for quadrupedal robots in the wild. Sci. Robot. 2022, 7, eabk2822. [Google Scholar] [CrossRef]
- Arena, P.; Li Noce, A.; Patanè, L. Stability and Safety Learning Methods for Legged Robots. Robotics 2024, 13, 17. [Google Scholar] [CrossRef]
- Rudin, N.; Hoeller, D.; Bjelonic, M.; Hutter, M. Advanced Skills by Learning Locomotion and Local Navigation End-to-End. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 2497–2503. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, M.; Hansen, N.; Xu, H.; Wang, X. Learning Vision-Guided Quadrupedal Locomotion End-to-End with Cross-Modal Transformers. arXiv 2022, arXiv:2107.03996. Available online: http://arxiv.org/abs/2107.03996 (accessed on 23 June 2024).
- Wu, J.; Xin, G.; Qi, C.; Xue, Y. Learning Robust and Agile Legged Locomotion Using Adversarial Motion Priors. IEEE Robot. Autom. Lett 2023, 8, 4975–4982. [Google Scholar] [CrossRef]
- Hoeller, D.; Rudin, N.; Sako, D.; Hutter, M. ANYmal parkour: Learning agile navigation for quadrupedal robots. Sci. Robot. 2024, 9, eadi7566. [Google Scholar] [CrossRef]
- Margolis, G.B.; Yang, G.; Paigwar, K.; Chen, T.; Agrawal, P. Rapid locomotion via reinforcement learning. Int. J. Robot. Res. 2024, 43, 572–587. [Google Scholar] [CrossRef]
- Bednarek, J.; Maalouf, N.; Pollayil, M.J.; Garabini, M.; Catalano, M.G.; Grioli, G.; Belter, D. CNN-based Foothold Selection for Mechanically Adaptive Soft Foot. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 10225–10232. [Google Scholar] [CrossRef]
- Belter, D.; Bednarek, J.; Lin, H.C.; Xin, G.; Mistry, M. Single-shot Foothold Selection and Constraint Evaluation for Quadruped Locomotion. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7441–7447. [Google Scholar] [CrossRef]
- Belter, D.; Skrzypczyński, P. Rough terrain mapping and classification for foothold selection in a walking robot. J. Field Robot. 2011, 28, 497–528. [Google Scholar] [CrossRef]
- Romera, E.; Álvarez, J.M.; Bergasa, L.M.; Arroyo, R. ERFNet: Efficient Residual Factorized ConvNet for Real-Time Semantic Segmentation. IEEE Trans. Intell. Transp. Syst. 2018, 19, 263–272. [Google Scholar] [CrossRef]
- Magaña, O.A.V.; Barasuol, V.; Camurri, M.; Franceschi, L.; Focchi, M.; Pontil, M.; Caldwell, D.G.; Semini, C. Fast and Continuous Foothold Adaptation for Dynamic Locomotion Through CNNs. IEEE Robot. Autom. Lett. 2019, 4, 2140–2147. [Google Scholar] [CrossRef]
- Xin, G.; Xin, S.; Cebe, O.; Pollayil, M.J.; Angelini, F.; Garabini, M.; Vijayakumar, S.; Mistry, M. Robust Footstep Planning and LQR Control for Dynamic Quadrupedal Locomotion. IEEE Robot. Autom. Lett. 2021, 6, 4488–4495. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. Available online: http://arxiv.org/abs/1707.06347 (accessed on 23 June 2024).
- Makoviichuk, D.; Makoviychuk, V. rl-games: A High-performance Framework for Reinforcement Learning. 2021. Available online: https://github.com/Denys88/rl_games (accessed on 23 June 2024).
- NVIDIA. Isaac Sim—Robotics Simulation and Synthetic Data Generation. 2022. Available online: https://developer.nvidia.com/isaac-sim (accessed on 23 June 2024).
- NVIDIA-Omniverse. Omniverse Isaac Gym Reinforcement Learning Environments for Isaac Sim. 2022. Available online: https://github.com/NVIDIA-Omniverse/OmniIsaacGymEnvs (accessed on 23 June 2024).
- Hutter, M.; Gehring, C.; Jud, D.; Lauber, A.; Bellicoso, C.D.; Tsounis, V.; Hwangbo, J.; Bodie, K.; Fankhauser, P.; Bloesch, M.; et al. ANYmal—A highly mobile and dynamic quadrupedal robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 38–44. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum Learning. In Proceedings of the 26th Annual International Conference on Machine Learning, ICML ’09, New York, NY, USA, 14–18 June 2009; pp. 41–48. [Google Scholar] [CrossRef]
- Wang, R.; Lehman, J.; Clune, J.; Stanley, K.O. Paired Open-Ended Trailblazer (POET): Endlessly Generating Increasingly Complex and Diverse Learning Environments and Their Solutions. arXiv 2019, arXiv:1901.01753. Available online: http://arxiv.org/abs/1901.01753 (accessed on 23 June 2024).
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-Real Transfer of Robotic Control with Dynamics Randomization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 3803–3810. [Google Scholar] [CrossRef]
- Pardo, F.; Tavakoli, A.; Levdik, V.; Kormushev, P. Time Limits in Reinforcement Learning. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Proceedings of Machine Learning Research. Dy, J., Krause, A., Eds.; PMLR: Stockholm, Sweden, 2018; Voume 80, pp. 4045–4054. [Google Scholar]
- Arena, P.; Patanè, L.; Taffara, S. A Data-Driven Model Predictive Control for Quadruped Robot Steering on Slippery Surfaces. Robotics 2023, 12, 67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).