6-DOFs Robot Placement Based on the Multi-Criteria Procedure for Industrial Applications
Abstract
1. Introduction
2. Integrated Multi-Criteria Procedure for Robot Base Location
- Task specification, workspace definition, and reachability measure;
- Robot inverse kinematic data-driven modeling for collision avoidance;
- Singularity and manipulability analyses;
- Energy consumption appraisal.
2.1. Task Specification, Workspace Definition, and Reachability Measure
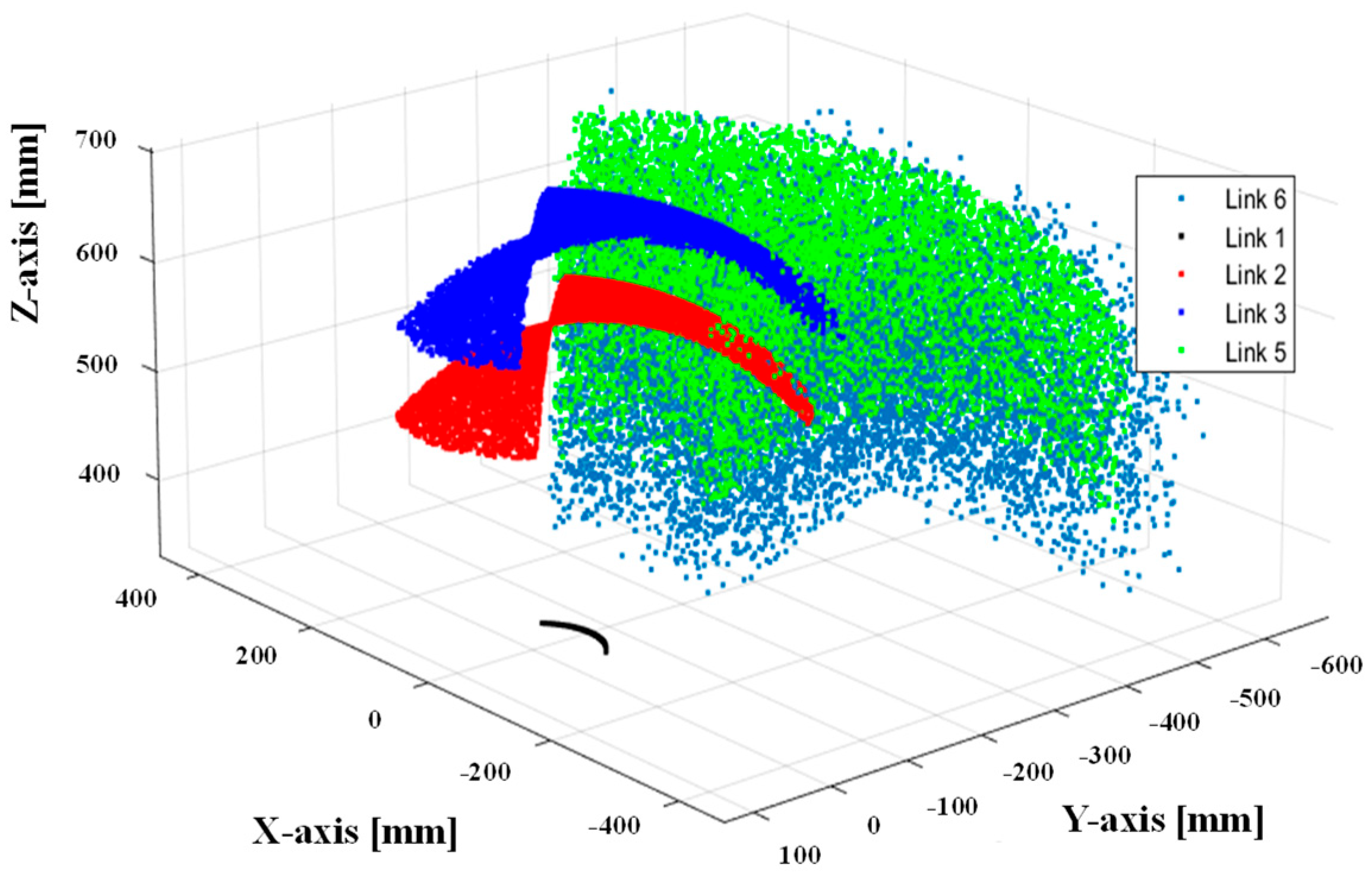
2.2. Robot Data-Driven Modeling for Collision Avoidance
2.3. Singularity and Manipulability Analyses
2.4. Energy Consumption Appraisal
3. Objective Function Formulation for Robot Positioning
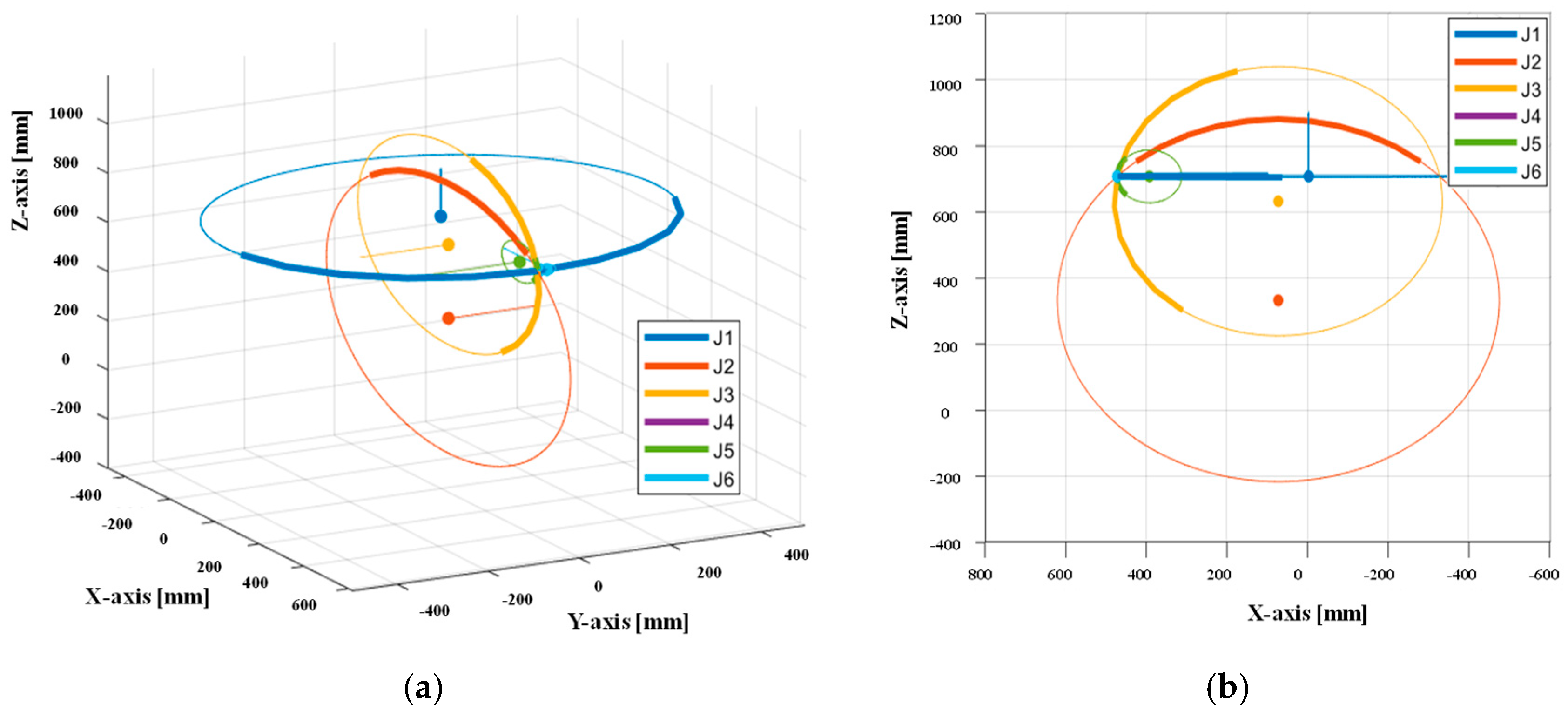
4. Simulation of Robot Base Placement and Case Studies
4.1. Robot-to-Workpiece Placement: Analytical Method
4.2. Robot-to-Workpiece Placement: Simulation Method
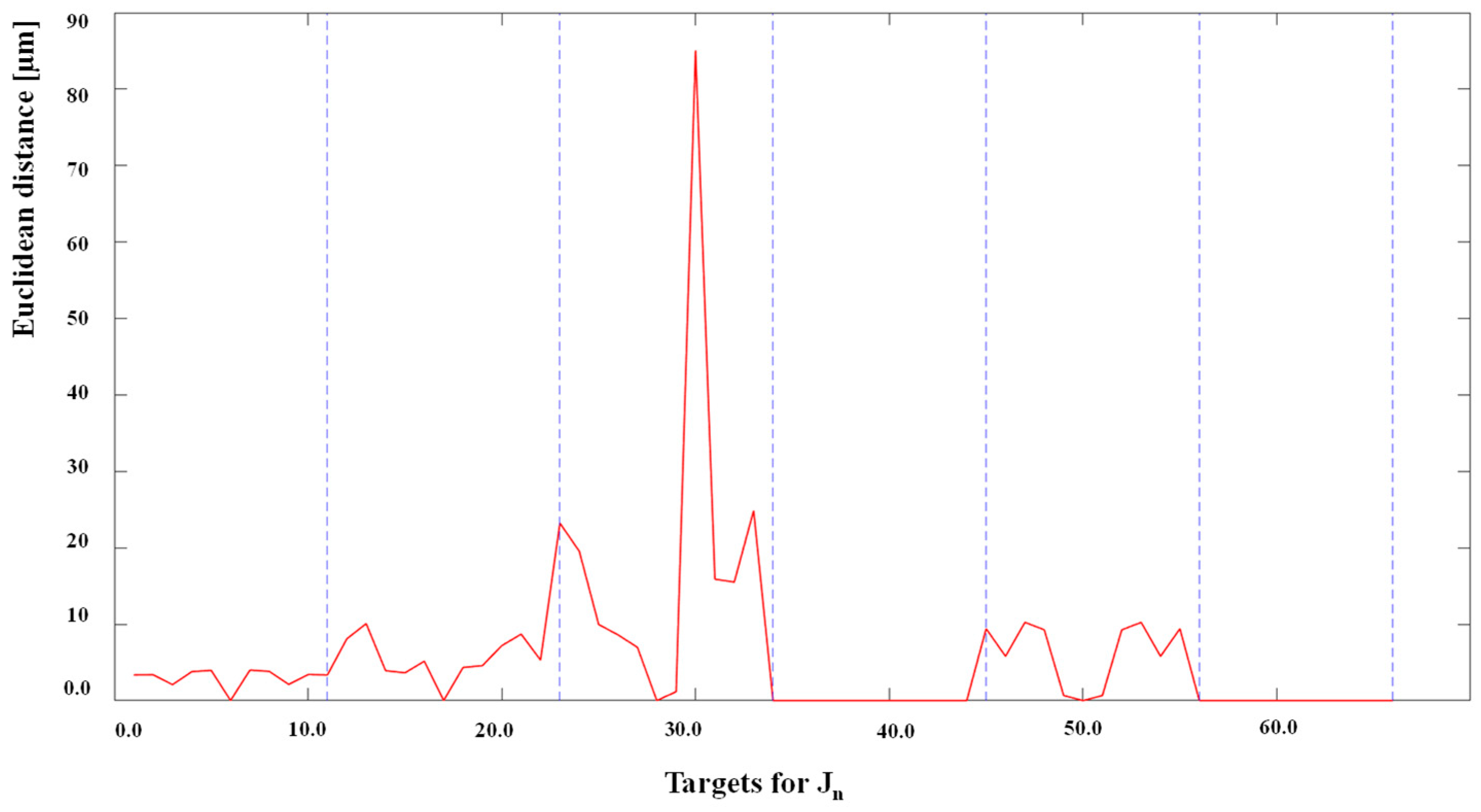
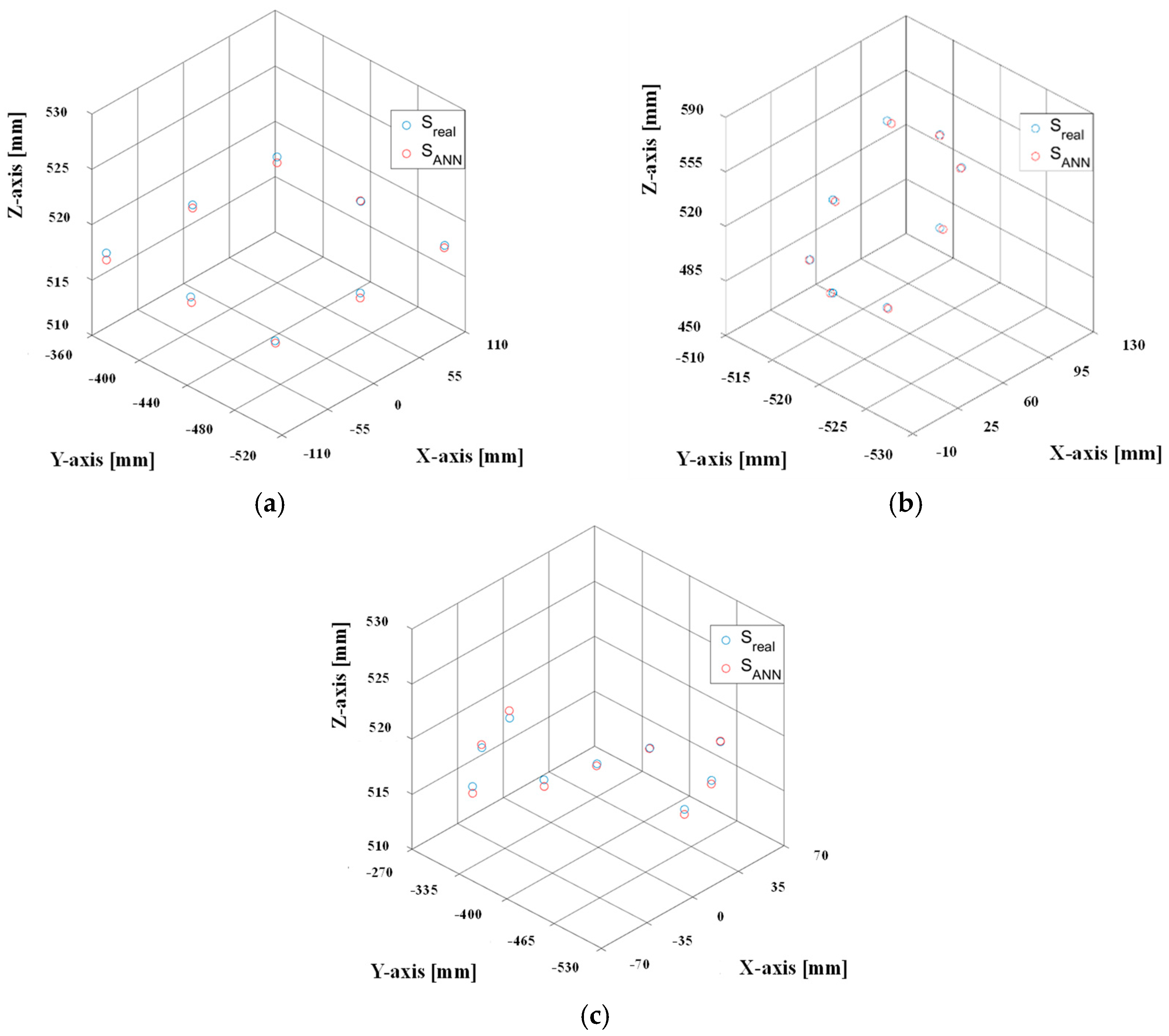
5. Experimental Validation: Results and Discussion
| Algorithm 1: Determining the base position to satisfy the multi-criteria boundaries |
| 1. Trajectories measured with the real LR-Mate 200ic robot are used. |
| 2. Let J be the joint’s vector and P be the Cartesian TCP vector of the trajectories. |
| 3. The direct kinematic model automatically acquired is applied to J, obtaining PDH. |
| 4. The resultant inverse kinematic model is established for PDH, obtaining JANN. |
| 5. The direct kinematic model is applied to JANN, obtaining PANN. |
| 6. The error is stated, comparing PDH and PANN. |
| 7. The JANN is adopted to verify the multicriteria boundaries. |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Zhu, W.; Dong, H.; Ke, Y. A method for robot placement optimization based on two-dimensional manifold in joint space. Robot. Comput. Integr. Manuf. 2021, 67, 102002. [Google Scholar] [CrossRef]
- Yang, J.; Wang, D.; Fan, B.; Dong, D.; Zhou, W. Online absolute pose compensation and steering control of industrial robot based on six degrees of freedom laser measurement. Opt. Eng. 2017, 56, 9. [Google Scholar] [CrossRef]
- Santolaria, J.; Yagüe, J.-A.; Jiménez, R.; Aguilar, J.-J. Calibration-based thermal error model for articulated arm coordinate measuring machines. Precis. Eng. 2009, 33, 476–485. [Google Scholar] [CrossRef]
- Wu, J.H.; Tao, Y.R. Review on Research Status of Positioning Accuracy Reliability of Industrial Robots. China Mech. Eng. 2020, 31, 2180–2188. [Google Scholar]
- Wang, X.W.; Zhou, X.; Xia, Z.L.; Gu, X.S. A survey of welding robot intelligent path optimization. J. Manuf. Process. 2021, 63, 14–23. [Google Scholar] [CrossRef]
- Votion, J.; Cao, Y.C. Diversity-Based Cooperative Multivehicle Path Planning for Risk Management in Costmap Environments. IEEE Trans. Ind. Electron. 2019, 66, 6117–6127. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Montiel, O.; Sepulveda, R. Pseudo-bacterial Potential Field Based Path Planner for Autonomous Mobile Robot Navigation. Int. J. Adv. Robot. Syst. 2015, 12, 81. [Google Scholar] [CrossRef]
- Wang, B.Y.; Liu, Z.; Li, Q.B.; Prorok, A. Mobile Robot Path Planning in Dynamic Environments Through Globally Guided Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 6932–6939. [Google Scholar] [CrossRef]
- Sartoretti, G.; Kerr, J.; Shi, Y.; Wagner, G.; Kumar, T.S.; Koenig, S.; Choset, H. Primal: Pathfinding via reinforcement and imitation multiagent learning. IEEE Robot. Autom. Lett. 2019, 4, 2378–2385. [Google Scholar] [CrossRef]
- Li, Q.; Gama, F.; Ribeiro, A.; Prorok, A. Graph neural networks for decentralized multi-robot path planning. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar]
- Kaczmarek, W.; Borys, S.; Panasiuk, J.; Siwek, M.; Prusaczyk, P. Experimental Study of the Vibrations of a Roller Shutter Gripper. Appl. Sci. 2022, 12, 9996. [Google Scholar] [CrossRef]
- Bucinskas, V.; Dzedzickis, A.; Sumanas, M.; Sutinys, E.; Petkevicius, S.; Butkiene, J.; Virzonis, D.; Morkvenaite-Vilkonciene, I. Improving Industrial Robot Positioning Accuracy to the Microscale Using Machine Learning Method. Machines 2022, 10, 940. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Pan, X.; Wang, W.; Zhang, X.; Li, B.; Yi, J.; Song, D. How you act tells a lot: Privacy-leaking attack on deep reinforcement learning. In Proceedings of the International Conference on Autonomous Agents and Multi-Agent Systems, Montreal, QC, Canada, 13–17 May 2019; pp. 368–376. [Google Scholar]
- Aspragathos, N.A.; Foussias, S. Optimal location of a robot path when considering velocity performance. Robotica 2002, 20, 139–147. [Google Scholar] [CrossRef]
- Li, G.; Zhu, W.D.; Dong, H.; Ke, Y. Error compensation based on surface reconstruction for industrial robot on two-dimensional manifold. Ind. Robot 2022, 49, 735–744. [Google Scholar] [CrossRef]
- Ur-Rehman, R.; Caro, S.; Chablat, D.; Wenger, P. Multi-objective path placement optimization of parallel kinematics machines based on energy consumption, shaking forces and maximum actuator torques: Application to the Orthoglide. Mech. Mach. Theory 2010, 45, 1125–1141. [Google Scholar] [CrossRef]
- Gürel, S.; Gultekin, H.; Emiroglu, N. Scheduling a dual gripper material handling robot with energy considerations. J. Manuf. Syst. 2023, 67, 265–280. [Google Scholar] [CrossRef]
- Ghungrad, S.; Mohammed, A.; Haghighi, A. Energy-efficient and quality-aware part placement in robotic additive manufacturing. J. Manuf. Syst. 2023, 68, 644–650. [Google Scholar] [CrossRef]
- Doan, N.C.N.; Lin, W. Optimal robot placement with consideration of redundancy problem for wrist-partitioned 6R articulated robots. Robot. Comput. Integr. Manuf. 2017, 48, 233–242. [Google Scholar] [CrossRef]
- Son, S.W.; Kwon, D.S. A convex programming approach to the base placement of a 6-DOF articulated robot with a spherical wrist. Int. J. Adv. Manuf. Technol. 2019, 102, 3135–3150. [Google Scholar] [CrossRef]
- Ren, S.; Xie, Y.; Yang, X.; Xu, J.; Wang, G.; Chen, K. A method for optimizing the base position of mobile painting manipulators. IEEE Trans. Autom. Sci. Eng. 2017, 14, 370–375. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, G.; Hua, X.; Zhang, S.; Song, L.; Zhang, J.; Chen, K. Base position optimization for mobile painting robot manipulators with multiple constraints. Robot Comput. Integr. Manuf. 2018, 54, 56–64. [Google Scholar] [CrossRef]
- Andulkar, M.V.; Chiddarwar, S.S.; Marathe, A.S. Novel integrated offline trajectory generation approach for robot assisted spray painting operation. J. Manuf. Syst. 2015, 37 Pt 1, 201–216. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Z.; Wu, C.; Hua, L.; Zhu, D. Towards region-based robotic machining system from perspective of intelligent manufacturing: A technology framework with case study. J. Manuf. Syst. 2023, 70, 451–463. [Google Scholar] [CrossRef]
- Spensieri, D.; Carlson, J.S.; Bohlin, R.; Kressin, J.; Shi, J. Optimal robot placement for tasks execution. Procedia CIRP 2016, 44, 395–400. [Google Scholar] [CrossRef]
- Malhan, R.K.; Kabir, A.M.; Shah, B.; Gupta, S.K. Identifying feasible workpiece placement with respect to redundant manipulator for complex manufacturing tasks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5585–5591. [Google Scholar]
- Available online: https://www.iso.org/committee/5915511.html (accessed on 10 October 2024).
- Available online: https://www.iso.org/standard/51330.html (accessed on 10 October 2024).
- Available online: https://www.iso.org/standard/41571.html (accessed on 10 October 2024).
- Available online: https://webstore.ansi.org/standards/ria/riatrr155062014 (accessed on 10 October 2024).
- Tagliani, F.L.; Pellegrini, N.; Aggogeri, F. Machine Learning Sequential Methodology for Robot Inverse Kinematic Modeling. Appl. Sci. 2022, 12, 9417. [Google Scholar] [CrossRef]
- Faria, C.; Vilaça, J.L.; Monteiro, S.; Erlhagen, W.; Bicho, E. Automatic Denavit-Hartenberg Parameter Identification for Serial Manipulators. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 610–617. [Google Scholar]
- Aggogeri, F.; Pellegrini, N.; Taesi, C.; Tagliani, F.L. Inverse kinematic solver based on machine learning sequential procedure for robotic applications. In Proceedings of the 2021 International Symposium on Intelligent Robotics and Systems (ISoIRS 2021), Online, 7–9 November 2022; Volume 2234. [Google Scholar]
- Zhu, Z.; Liu, Y.; He, Y.; Wu, W.; Wang, H.; Huang, C.; Ye, B. Fuzzy PID Control of the Three-Degree-of-Freedom Parallel Mechanism Based on Genetic Algorithm. Appl. Sci. 2022, 12, 11128. [Google Scholar] [CrossRef]
- Teodoro, I.-P. A Novel Optimization Robust Design of Artificial Neural Networks to Solve the Inverse Kinematics of a Manipulator of 6 DOF; IEEE: New York, NY, USA, 2021; pp. 838–843. [Google Scholar]
- Toquica, J.S.; Oliveira, P.S.; Souza, W.S.; Motta, J.M.S.; Borges, D.L. An analytical and a deep learning model for solving the inverse kinematic problem of an industrial parallel robot. Comput. Ind. Eng. 2020, 151, 106682. [Google Scholar] [CrossRef]
- Derya, S. A comparison of optimization algorithms for deep learning. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 51–65. [Google Scholar]
- Nektarios, A.; Aspragathos, N.A. Optimal location of a general position and orientation end-effector’s path relative to manipulator’s base, considering velocity performance, Robot. Comput.-Integr. Manuf. 2010, 26, 162–173. [Google Scholar] [CrossRef]
- Soylak, M.; Oktay, T.; Turkmen, İ. A simulation-based method using artificial neural networks for solving the inverse kinematic problem of articulated robots. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 470–479. [Google Scholar] [CrossRef]
- Azimirad, V.; Shorakaei, H. Dual hierarchical genetic-optimal control: A new global optimal path planning method for robots. J. Manuf. Syst. 2014, 33, 139–148. [Google Scholar] [CrossRef]
- Givehchi, M.; Ng, A.; Wang, L. Evolutionary optimization of robotic assembly operation sequencing with collision-free paths. J. Manuf. Syst. 2011, 30, 196–203. [Google Scholar] [CrossRef]



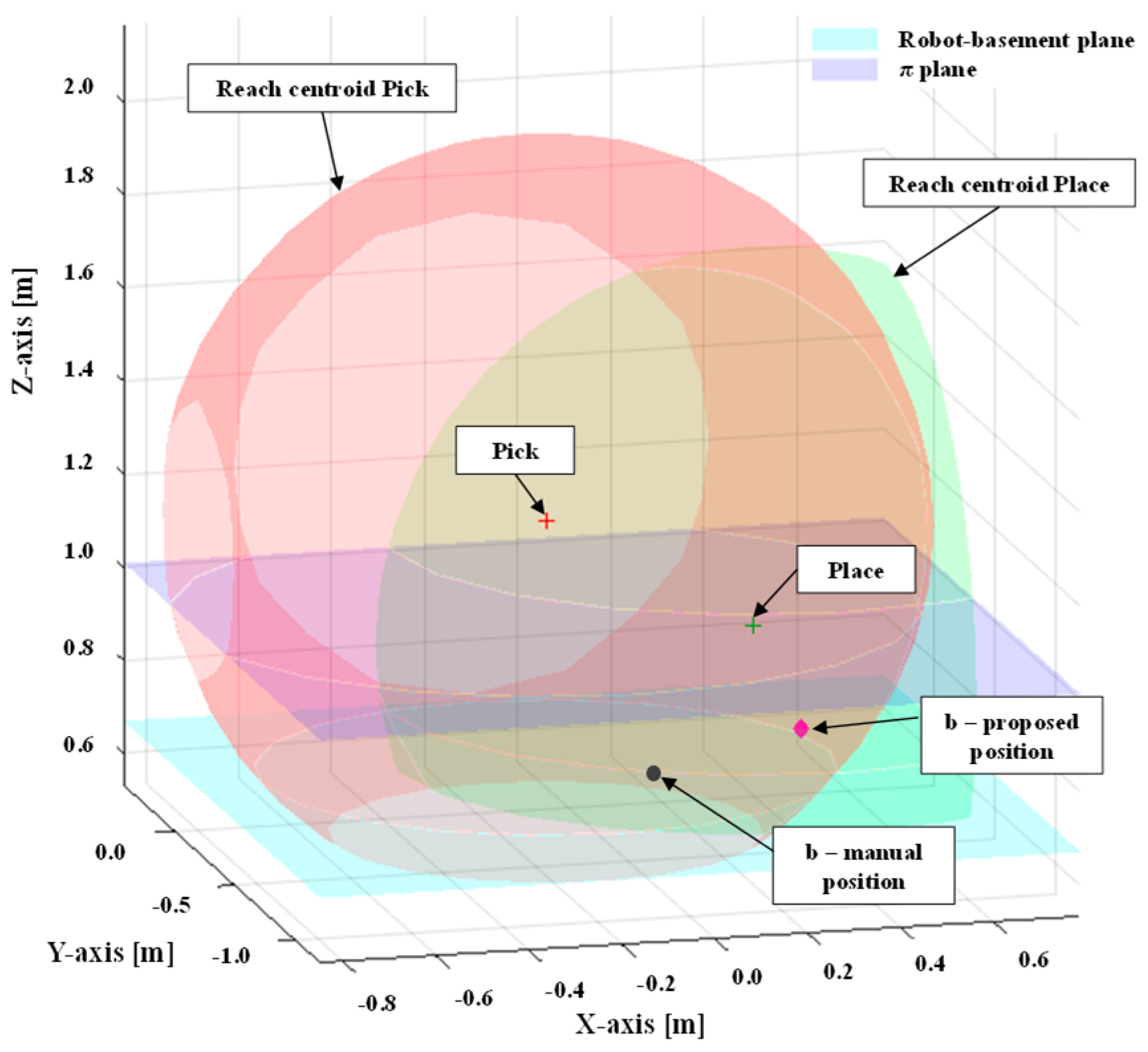


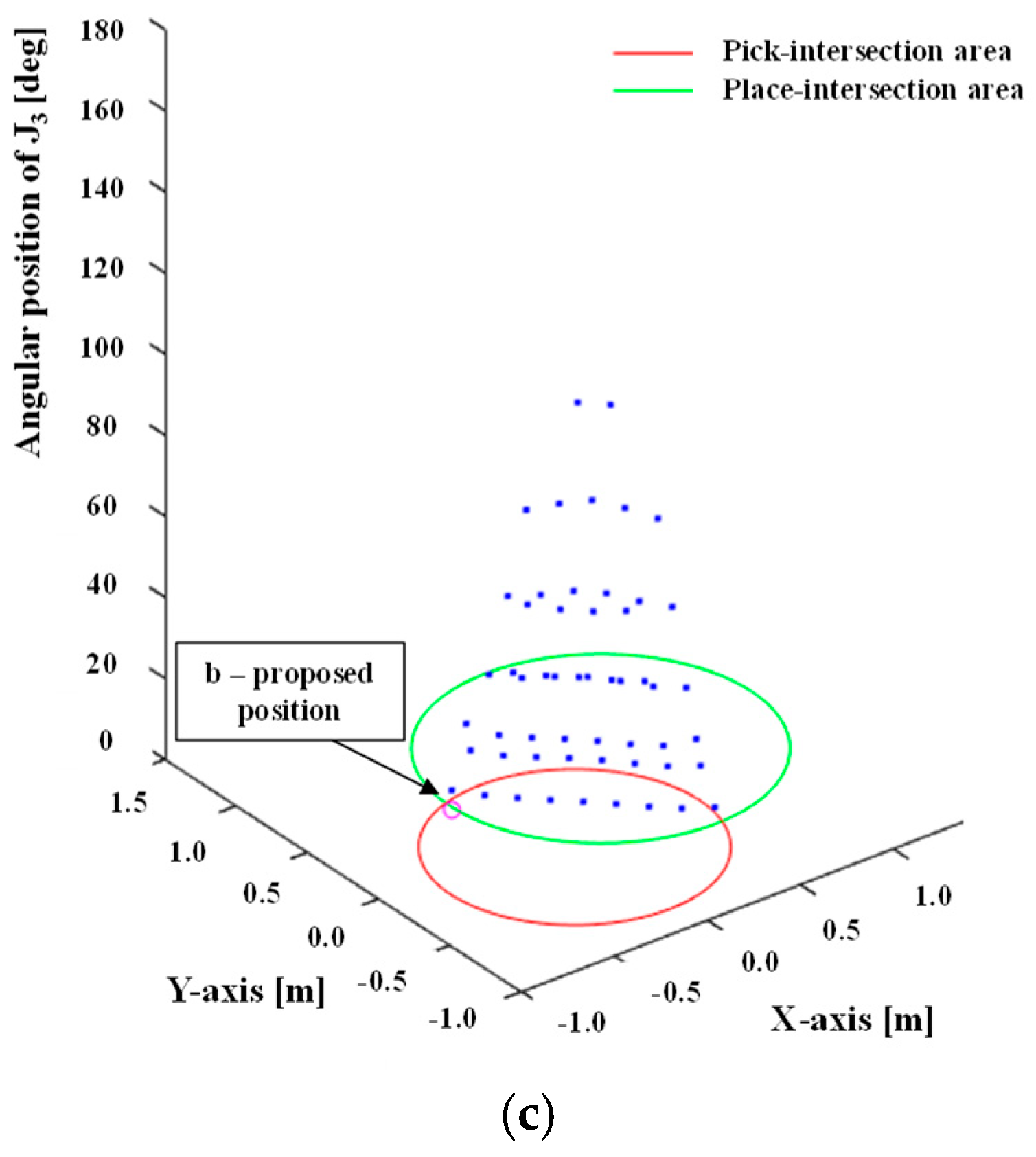
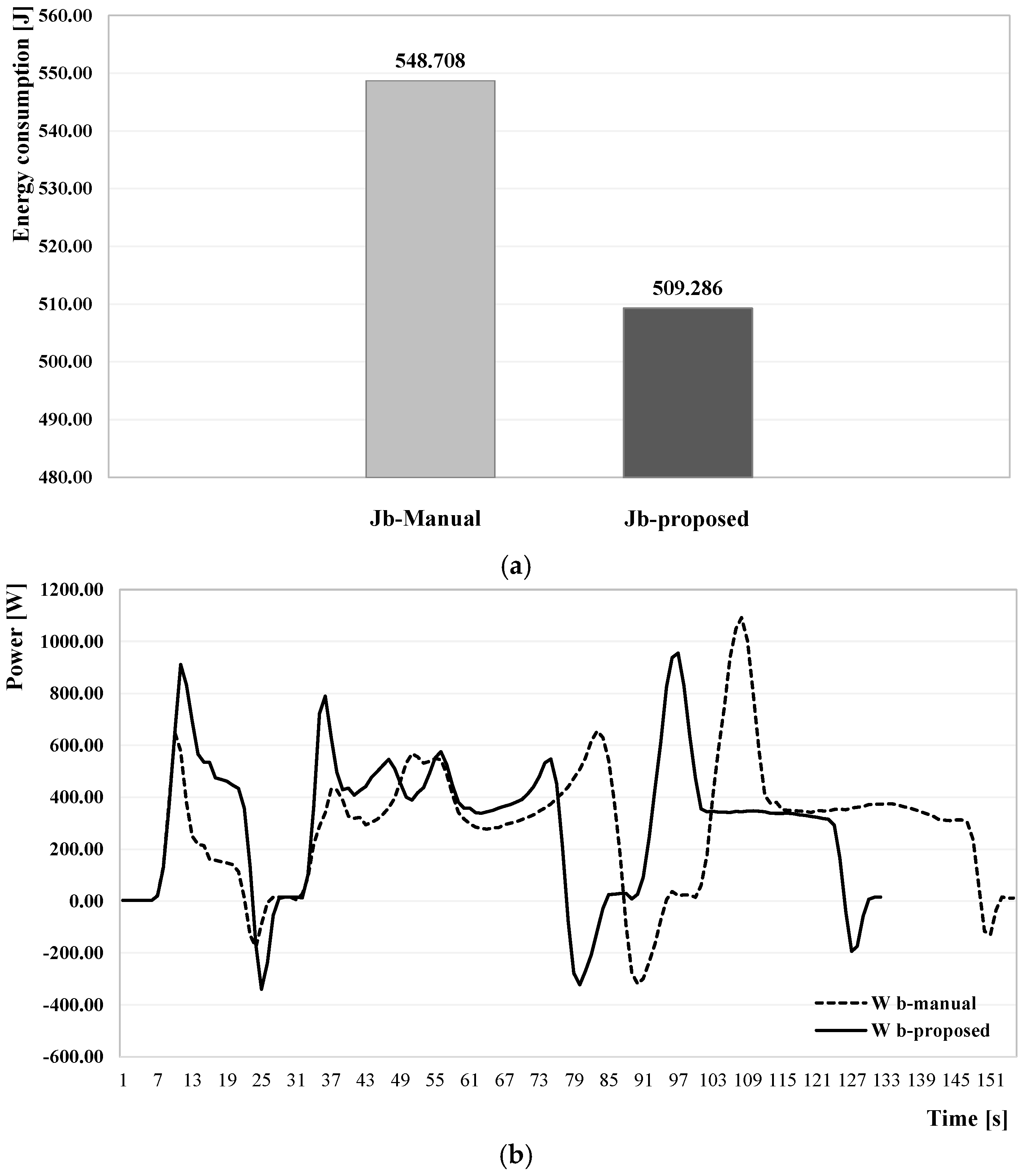
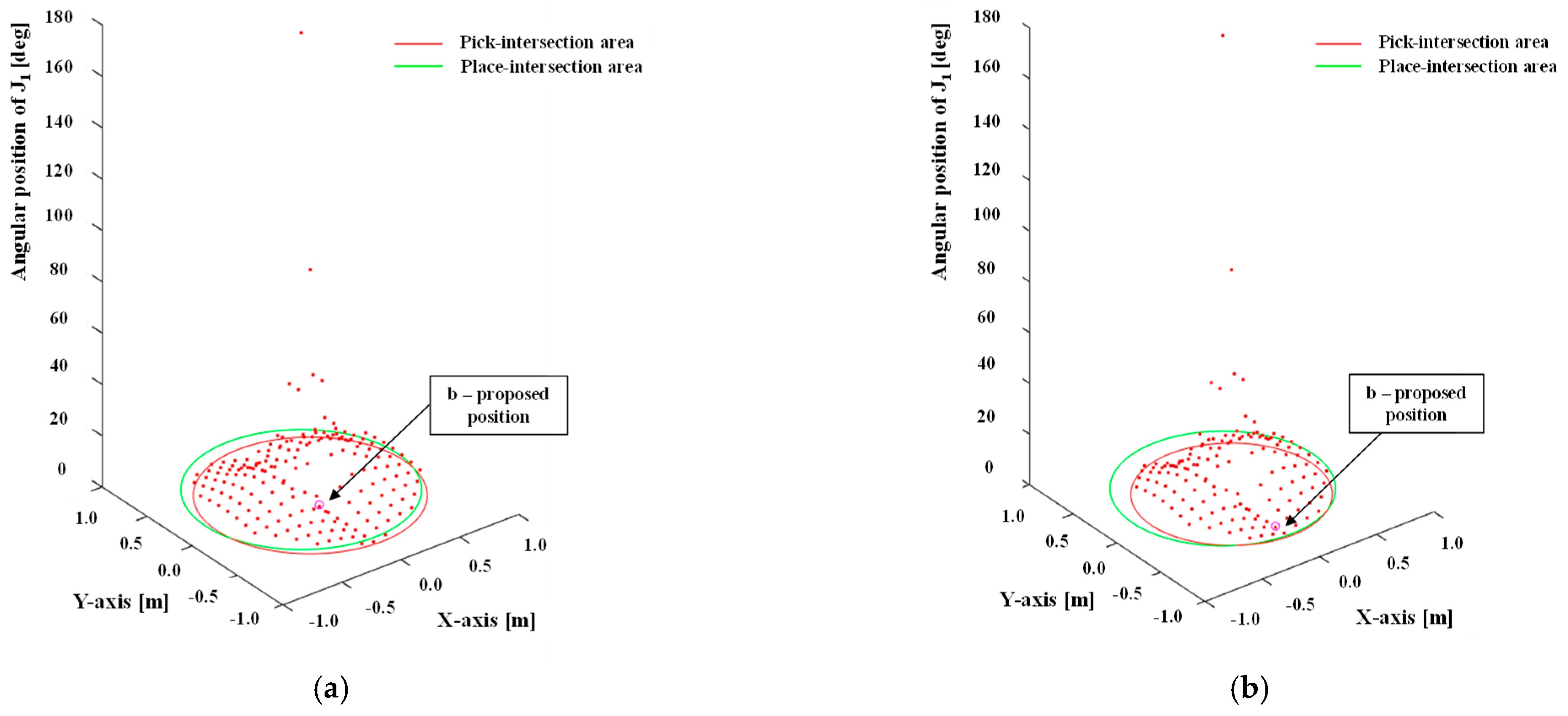
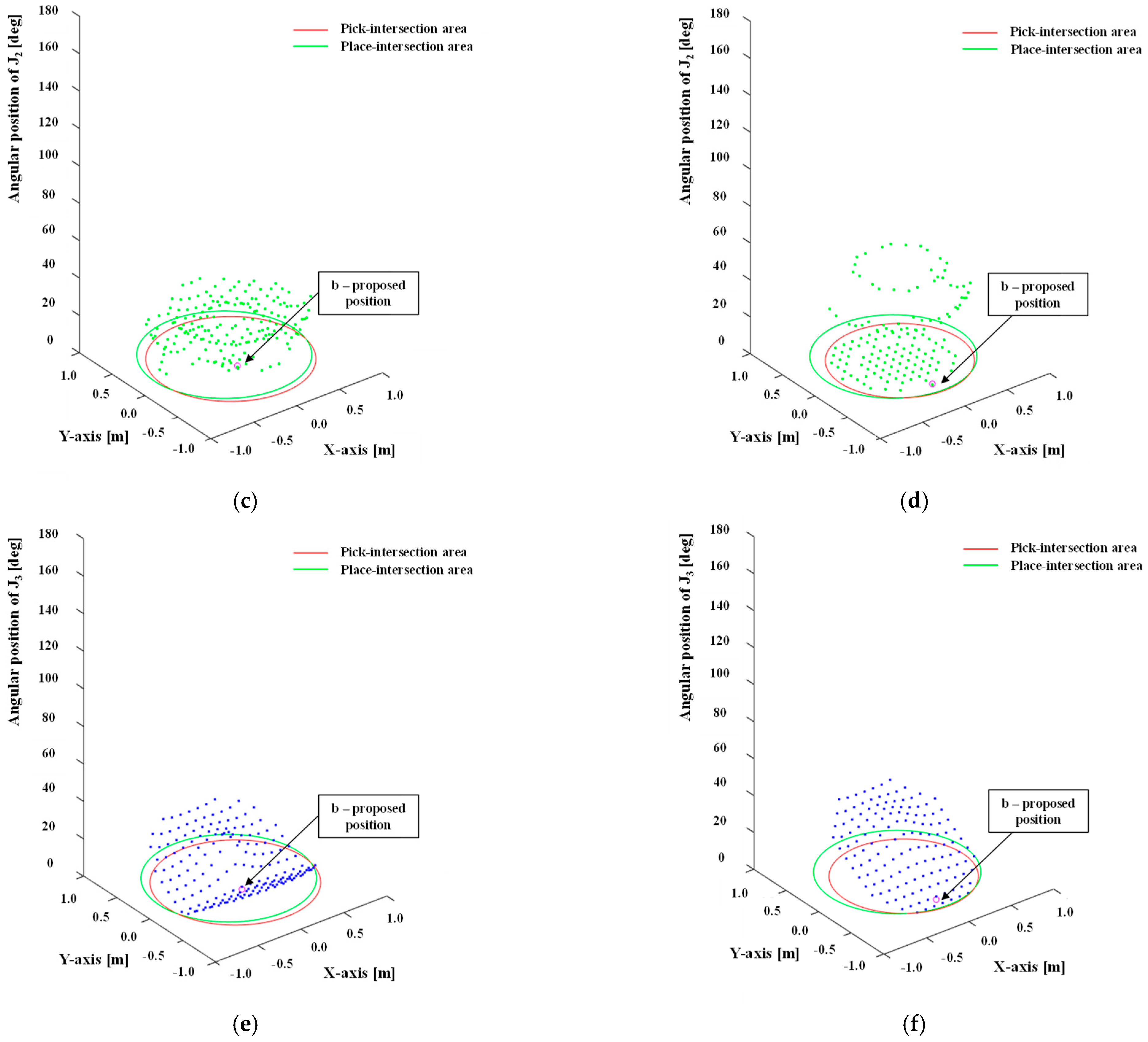





| Case 1 | ||||||
|---|---|---|---|---|---|---|
| Target TCP Position | Position [X, Y, Z] mm | Rotation [RX, RY, RZ] deg | Robot J1–J2 Link mm | Robot Base Height mm | z-Axis Robot Placement mm | b-Manual Position [X, Y] mm |
| TCP Pick | [−100, −200, 1200] | [0, 0, 0] | 448.0 | 339.1 | 670.0 | [200, 100] |
| TCP Place | [500, 400, 800] | [0, 0, 0] | ||||
| Case 1 | |||||
|---|---|---|---|---|---|
| Target | Position [X, Y, Z] mm | Rotation [RX, RY, RZ] deg | Robot Placement z-Axis mm | b-Manual Position [X, Y] mm | b-Proposed Position [X, Y] mm |
| TCP Pick | [−100, −200, 1200] | [0, 0, 0] | 670.0 | [200, 100] | [600, −300] |
| TCP Place | [500, 400, 800] | [0, 0, 0] | |||
| Case 2 | |||||
|---|---|---|---|---|---|
| Target | Position [X, Y, Z] mm | Rotation [RX, RY, RZ] deg | Robot Placement z-Axis mm | b-Manual Position [X, Y] mm | b-Proposed Position [X, Y] mm |
| T Pick | [−100, −200, 1200] | [0, 0, 0] | 400.0 | [200, 100] | [−300, 400] |
| T Place | [500, 400, 800] | [0, 0, 0] | |||
| Case 3—Input | ||||||||
| Target | Position [X, Y, Z] mm | Rotation [RX, RY, RZ] deg | Robot J1–J2 link mm | Robot Base Height mm | z-Axis Robot Placement mm | b-Manual Position [X, Y] mm | ||
| T Pick | [0, 0.1, 1200] | [0, 0, 0] | 448.0 | 339.1 | 670.0 | [500, 500] | ||
| T Place | [0, 0.1, 1000] | [0, 0, 0] | ||||||
| Case 3—Output | ||||||||
| Target | Position [X, Y, Z] mm | Rotation [RX, RY, RZ] deg | Robot Placement z-Axis mm | b-Manual Position [X, Y] mm | b-Proposed Position [X, Y] mm | |||
| T Pick | [0, 0.1, 1200] | [0, 0, 0] | 670.0 | [500, 500] | [0, −100] | |||
| T Place | [0, 0.1, 1000] | [0, 0, 0] | ||||||
| Case 4—Output | ||||||||
| Target | Position [X, Y, Z] mm | Rotation [RX, RY, RZ] deg | Robot Placement z-Axis mm | b-Manual Position [X, Y] mm | b-Proposed Position [X, Y] mm | |||
| T Pick | [0, 0.1, 1200] | [0, 0, 0] | 400.0 | [500, 500] | [0, −500] | |||
| T Place | [0, 0.1, 1000] | [0, 0, 0] | ||||||
| Layout Type | I/O System | Position [X mm, Y mm, Z mm] and Rotation [RX deg, RY deg, RZ deg] |
|---|---|---|
| Linear | Input system conveyor | [1830, 250, 630] [−90, 0, 90] |
| Output system conveyor | [4670, 250, 630] [−90, 0, −90] | |
| Workstation | Target 1 [3250, 1750, 620] [−90, 0, 0] Target 2 [2980, 1750, 750] [0, 90, 90] Target 3 [3250, 1750, 750] [0, −90, −90] | |
| U-type | Input system conveyor | [670, 250, 430] [−90, 0, 0] |
| Output system conveyor | [670, 750, 730] [−90, 0, 0] | |
| Workstation | Target 1 [250, 750, 620] [−90, 0, 90] Target 2 [−250, −1020, 750] [0, 90, −180] Target 3 [−250, −480, 750] [0, −90, 0] | |
| U-type | Input system conveyor | [670, 1100, 730][−90, 0, 0] |
| Output system pallet | Position 1 [370, 70, 270] [−90, 0, 0] Position 2 [370, 730, 270] [−90, 0, 0] Position 3 [1430, 70, 270] [−90, 0, 0] Position 4 [1430, 730, 270] [−90, 0, 0] | |
| Workstation | Target 1 [−250, −750, 620] [−90, 0, 90] Target 2 [−250, −1020, 750] [0, 90, −180] Target 3 [−250, −480, 750] [0, −90, 0] |
| Joint | Maximum Velocity [deg/s] | Range of Motion [deg] | Selected Range of Motion [deg] |
|---|---|---|---|
| 1 | 350 | ±340 | ±80 |
| 2 | 350 | ±200 | ±40 |
| 3 | 400 | ±388 | ±65 |
| 4 | 450 | ±380 | ±65 |
| 5 | 450 | ±240 | ±45 |
| 6 | 720 | ±720 | ±65 |
| Joint | θi [rad] | di [mm] | ai [mm] | αi [rad] |
|---|---|---|---|---|
| 1 | 0.0 | 3.30 × 10+02 | 7.50 × 10+01 | π/2 |
| 2 | π/2 | 0.00 | 3.00 × 10+02 | 0.0 |
| 3 | 0.0 | 0.00 | 7.50 × 10+01 | π/2 |
| 4 | 0.0 | 3.20 × 10+02 | 0.00 | −π/2 |
| 5 | 0.0 | 0.00 | 0.00 | π/2 |
| 6 | 0.0 | 1.40 × 10+02 | 0.00 | 0.0 |
| Trajectory | RMSE [mm] | Min–Max RMSE [mm] |
|---|---|---|
| Circle | 0.059 | 0.037–0.076 |
| S-shaped | 0.061 | 0.049–0.077 |
| Rectangle | 0.057 | 0.046–0.072 |
| Joint | Acquisition Range of Motion [deg] |
|---|---|
| 1 | −135; −45 |
| 2 | −45; +45 |
| 3 | −30; 0 |
| 4 | 0; 0 |
| 5 | −115; 0 |
| 6 | 0; 0 |
| ID | Input | Output |
|---|---|---|
| 1 | x, y, z, Rx, Ry, Rz | J1 |
| 2 | x, y, z, Rx, Ry, Rz, J1 | J2 |
| 3 | x, y, z, Rx, Ry, Rz, J1, J2 | J3 |
| 4 | x, y, z, Rx, Ry, Rz, J1, J2, J3 | J5 |
| ID | Output | Configuration |
|---|---|---|
| 1 | J1 |  |
| 2 | J2 |  |
| 3 | J3 |  |
| 4 | J5 |  |
| Requirements | Sequential |
|---|---|
| Number of joints | J1–J3 |
| Algorithm limitations | Mix |
| Activation functions | Tansig |
| Epochs | 1000 |
| Trajectory | RMSE [mm] | Min–Max RMSE [mm] |
|---|---|---|
| Circle | 0.567 | 0.338–0.701 |
| S-shaped | 0.702 | 0.358–1.060 |
| Rectangle | 0.546 | 0.288–0.803 |
| Task | Robot Basement Placement | Energy Consumption kW |
|---|---|---|
| Pick-and-place 50% Velocity—50% payload | Actual—measured | 0.480 |
| Actual—computed | 0.450 | |
| Proposed multi-criteria | 0.370 | |
| Pick-and-place 70% Velocity—20% payload | Actual—measured | 0.470 |
| Actual—computed | 0.420 | |
| Proposed multi-criteria | 0.410 | |
| Path tracking 35% Velocity—70% payload | Actual—measured | 0.350 |
| Actual—computed | 0.320 | |
| Proposed multi-criteria | 0.230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aggogeri, F.; Pellegrini, N. 6-DOFs Robot Placement Based on the Multi-Criteria Procedure for Industrial Applications. Robotics 2024, 13, 153. https://doi.org/10.3390/robotics13100153
Aggogeri F, Pellegrini N. 6-DOFs Robot Placement Based on the Multi-Criteria Procedure for Industrial Applications. Robotics. 2024; 13(10):153. https://doi.org/10.3390/robotics13100153
Chicago/Turabian StyleAggogeri, Francesco, and Nicola Pellegrini. 2024. "6-DOFs Robot Placement Based on the Multi-Criteria Procedure for Industrial Applications" Robotics 13, no. 10: 153. https://doi.org/10.3390/robotics13100153
APA StyleAggogeri, F., & Pellegrini, N. (2024). 6-DOFs Robot Placement Based on the Multi-Criteria Procedure for Industrial Applications. Robotics, 13(10), 153. https://doi.org/10.3390/robotics13100153






