Online Motion Planning for Safe Human–Robot Cooperation Using B-Splines and Hidden Markov Models
Abstract
:1. Introduction
1.1. Related Work
1.2. Methodology and Contributions
- Design an online controller that can fit generic tasks and smoothly avoid collisions with dynamic obstacles.
- Include the possibility to restore the original task whenever the robot is not prone to any collision.
- Exploit a probabilistic framework to gather information about the obstacle and modify the robot’s velocity accordingly.
- Combine trajectory and symbolic domains in a unified framework.
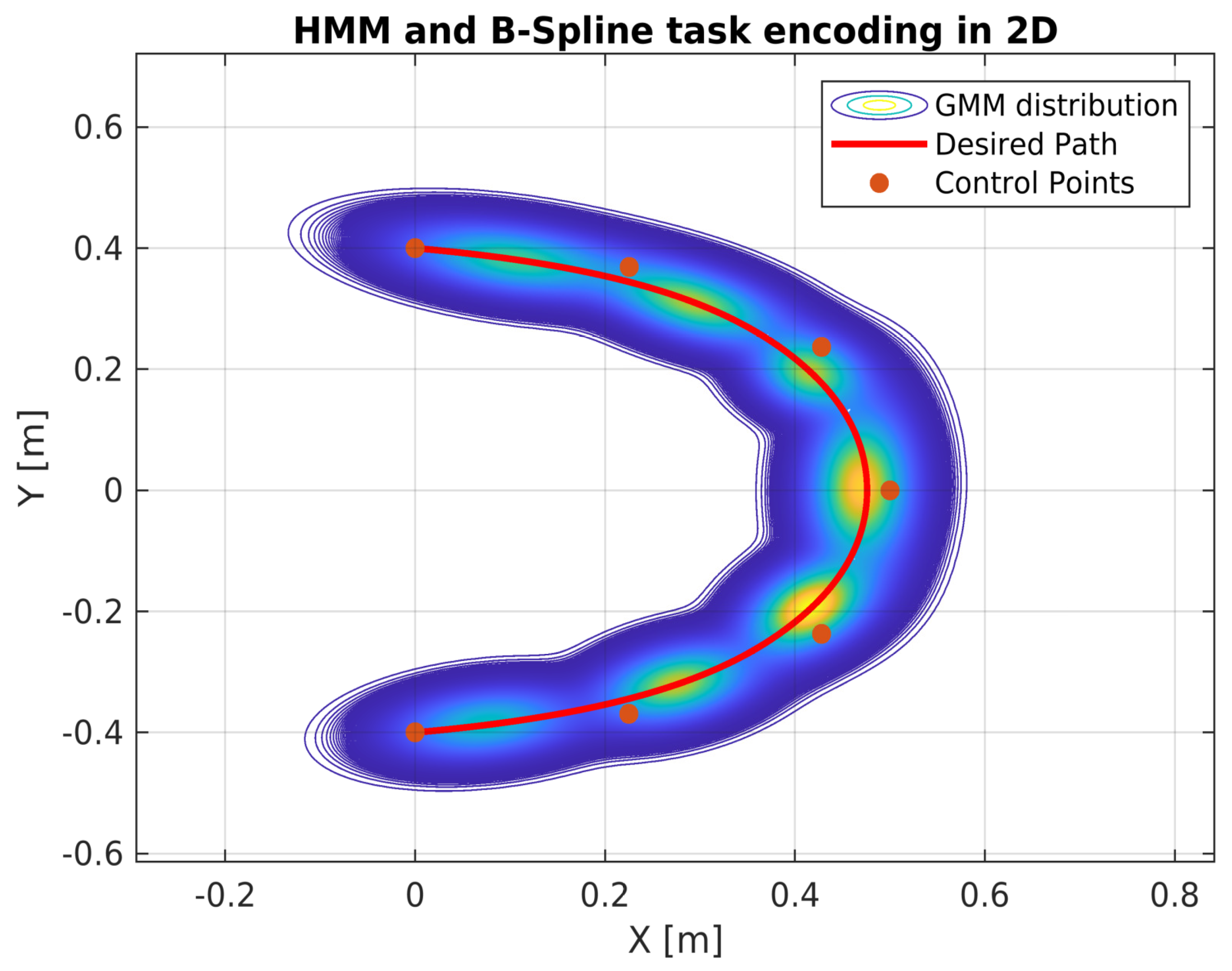
2. Task Encoding
2.1. Spatial Encoding Based on B-Splines
2.2. Temporal and Sequential Encoding Based on Hidden Markov Models
- is called the prior distribution, which tells us about the probability of starting a sequence in state ;
- is the transition probability matrix, where each element encodes the probability of moving from state i to state j;
- are the observation likelihoods, also called emission probabilities, where each element expresses the probability of an observation being generated from state i.
3. Proposed Method
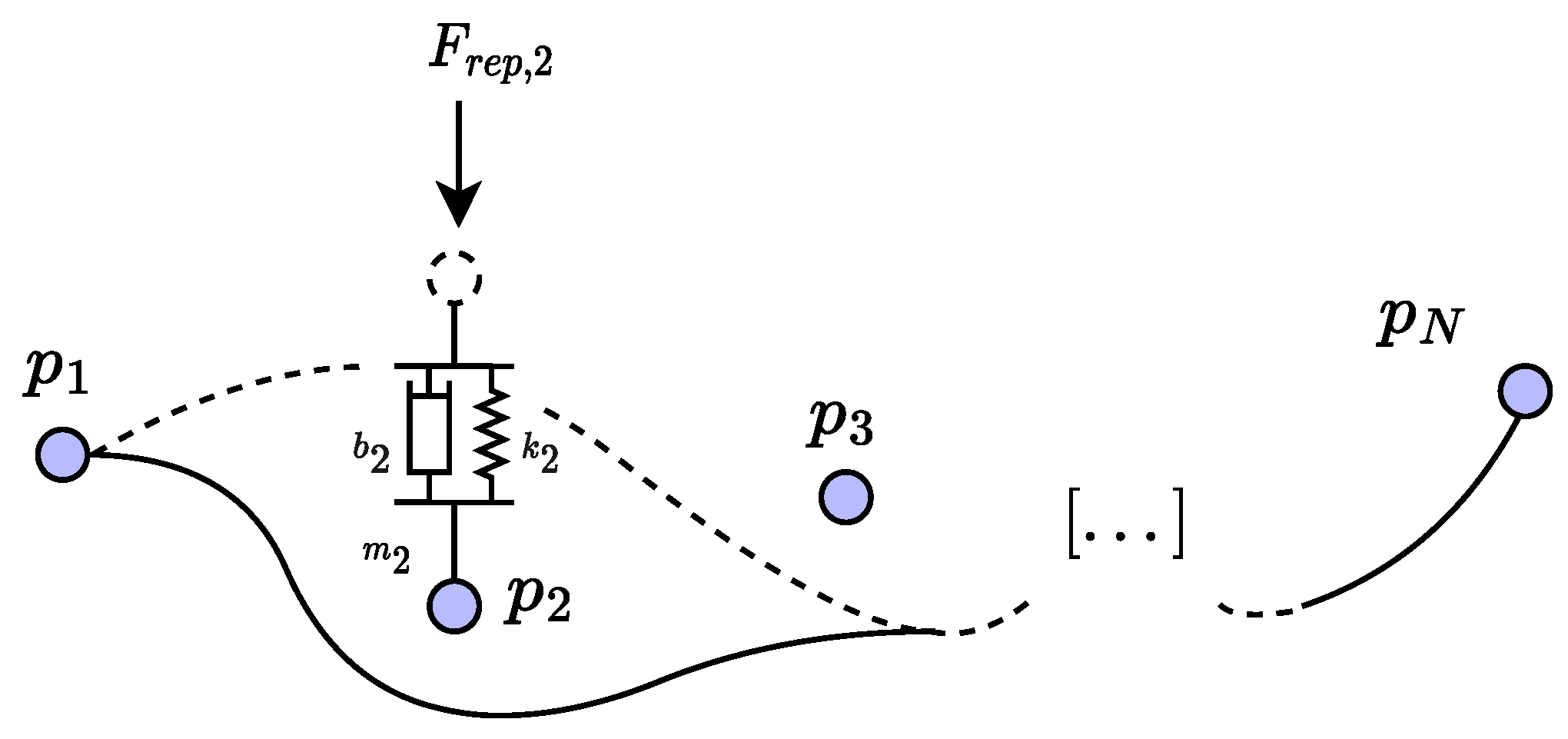
3.1. Spatial Modulation with Dynamical Control Points
3.2. Temporal Modulation with Varying Transition Probabilities in HMM
- If , the robot moves at nominal velocity.
- If , the robot slows down.
- If , the robot stops.
3.3. Switching between Trajectory and Symbolic Domains
- only the time-scaling mechanism based on HMM is active;
- B-spline and HMM cooperate with different proportions;
- only the B-spline modification algorithm is applied.
4. Experimental Validation
4.1. Experimental Setup and Methodology
- for ;
- for ;
- The average computation time for a single iteration .
- The normalized average path deviation , calculated as the mean deviation of the traveled distance normalized over the nominal path.
- The average stop time, , calculated as the average time taken for parameter in (9) to reach zero (i.e., stop the robot) once the hand collision was perceived.
- The success rate, , defined as the percentage of cases where the distance did not go below a given safety threshold (equal to 10 cm in our experiments) compared to the total number of situations where an incipient collision was detected.
4.2. Results
4.2.1. Controller at Trajectory Level Only ()
4.2.2. Controller at Symbolic Level Only ()
4.2.3. Controller at Both Trajectory and Symbolic Levels ()
4.2.4. Performance Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LbD | Learning by Demonstration |
| GMM | Gaussian Mixture Models |
| EE | End effector |
| HMM | Hidden Markov models |
| ROS | Robot Operative System |
References
- Khansari-Zadeh, S.M.; Khatib, O. Learning Potential Functions from Human Demonstrations with Encapsulated Dynamic and Compliant Behaviors. Auton. Robot. 2017, 41, 45–69. [Google Scholar] [CrossRef]
- Scalera, L.; Giusti, A.; Vidoni, R.; Gasparetto, A. Enhancing fluency and productivity in human-robot collaboration through online scaling of dynamic safety zones. Int. J. Adv. Manuf. Technol. 2022, 121, 6783–6798. [Google Scholar] [CrossRef]
- Liu, H.; Qu, D.; Xu, F.; Du, Z.; Jia, K.; Song, J.; Liu, M. Real-Time and Efficient Collision Avoidance Planning Approach for Safe Human-Robot Interaction. J. Intell. Robot. Syst. 2022, 105, 93. [Google Scholar] [CrossRef]
- Merckaert, K.; Convens, B.; Wu, C.-J.; Roncone, A.; Nicotra, M.M.; Vanderborght, B. Real-Time Motion Control of Robotic Manipulators for Safe Human-Robot Coexistence. Robotics 2022, 73, 102223. [Google Scholar] [CrossRef]
- Chiaravalli, D.; Califano, F.; Biagiotti, L.; De Gregorio, D.; Melchiorri, C. Physical-Consistent Behavior Embodied in B-Spline Curves for Robot Path Planning. IFAC-PapersOnLine 2018, 51, 306–311. [Google Scholar] [CrossRef]
- Kanazawa, A.; Kinugawa, J.; Kosuge, K. Adaptive Motion Planning for a Collaborative Robot Based on Prediction Uncertainty to Enhance Human Safety and Work Efficiency. IEEE Trans. Robot. 2019, 35, 817–832. [Google Scholar] [CrossRef]
- Zanchettin, A.M.; Ceriani, N.M.; Rocco, P.; Ding, H.; Matthias, B. Safety in Human-Robot Collaborative Manufacturing Environments: Metrics and Control. IEEE Trans. Autom. Sci. Eng. 2015, 13, 882–893. [Google Scholar] [CrossRef]
- Zucker, M.; Ratliff, N.; Dragan, A.D.; Pivtoraiko, M.; Klingensmith, M.; Dellin, C.M.; Bagnell, J.A.; Srinivasa, S.S. Chomp: Covariant Hamiltonian Optimization for Motion Planning. Int. J. Robot. Res. 2013, 32, 1164–1193. [Google Scholar] [CrossRef]
- Yang, C.; Sue, G.N.; Li, Z.; Yang, L.; Shen, H.; Chi, Y.; Rai, A.; Zeng, J.; Sreenath, K. Collaborative Navigation and Manipulation of a Cable-Towed Load by Multiple Quadrupedal Robots. IEEE Robot. Autom. Lett. 2022, 7, 10041–10048. [Google Scholar] [CrossRef]
- Mukadam, M.; Dong, J.; Yan, X.; Dellaert, F.; Boots, B. Continuous-Time Gaussian Process Motion Planning via Probabilistic Inference. Int. J. Robot. Res. 2018, 37, 1319–1340. [Google Scholar] [CrossRef]
- Toussaint, M.; Goerick, C. A Bayesian View on Motor Control and Planning. In From Motor Learning to Interaction Learning in Robots; Springer: Berlin/Heidelberg, Germany, 2010; pp. 227–252. [Google Scholar] [CrossRef]
- Fisac, J.F.; Bajcsy, A.; Herbert, S.L.; Fridovich-Keil, D.; Wang, S.; Tomlin, C.J.; Dragan, A.D. Probabilistically Safe Robot Planning with Confidence-Based Human Predictions. arXiv 2018, arXiv:1806.00109. [Google Scholar]
- Calinon, S.; Guenter, F.; Billard, A. On Learning, Representing, and Generalizing a Task in a Humanoid Robot. IEEE Trans. Syst. Man Cybern. Part Cybern. 2007, 37, 286–298. [Google Scholar] [CrossRef]
- Kavraki, L.E.; LaValle, S.M. Motion Planning. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 139–162. [Google Scholar] [CrossRef]
- Jankowski, J.; Brudermüller, L.; Hawes, N.; Calinon, S. VP-STO: Via-Point-Based Stochastic Trajectory Optimization for Reactive Robot Behavior. arXiv 2022, arXiv:2210.04067. [Google Scholar]
- Han, D.; Nie, H.; Chen, J.; Chen, M. Dynamic Obstacle Avoidance for Manipulators Using Distance Calculation and Discrete Detection. Robot. Comput.-Integr. Manuf. 2018, 49, 98–104. [Google Scholar] [CrossRef]
- Khatib, O. Real-time Obstacle Avoidance for Manipulators and Mobile Robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 500–505. [Google Scholar] [CrossRef]
- Quinlan, S.; Khatib, O. Elastic Bands: Connecting Path Planning and Control. In Proceedings of the [1993] Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; pp. 802–807. [Google Scholar] [CrossRef]
- Flacco, F.; Kröger, T.; Luca, A.D.; Khatib, O. A Depth Space Approach to Human-Robot Collision Avoidance. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 338–345. [Google Scholar] [CrossRef]
- Secil, S.; Ozkan, M. A collision-free path planning method for industrial robot manipulators considering safe human-robot interaction. Intell. Serv. Robot. 2023, 16, 323–359. [Google Scholar] [CrossRef]
- ISO/TS 15066; Robots and Robotic Devices—Collaborative Robots. International Organization for Standardization: Geneva, Switzerland, 2016.
- Rosenstrauch, M.J.; Pannen, T.J.; Krüger, J. Human Robot Collaboration—Using Kinect v2 for ISO/TS 15066 Speed and Separation Monitoring. Procedia CIRP 2018, 76, 183–186. [Google Scholar] [CrossRef]
- Lagomarsino, M.; Lorenzini, M.; Constable, M.D.; De Momi, E.; Becchio, C.; Ajoudani, A. Maximising Coefficiency of Human-Robot Handovers through Reinforcement Learning. IEEE Robot. Autom. Lett. 2023, 8, 4378–4385. [Google Scholar] [CrossRef]
- Calinon, S.; Billard, A.; Dillmann, R.; Schaal, S. Robot Programming by Demonstration. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Pentland, A.; Liu, A. Modeling and Prediction of Human Behavior. Neural Comput. 1999, 11, 229–242. [Google Scholar] [CrossRef]
- Hovland, G.E.; Sikka, P.; McCarragher, B.J. Skill Acquisition from Human Demonstration Using a Hidden Markov Model. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 3, pp. 2706–2711. [Google Scholar] [CrossRef]
- Roveda, L.; Magni, M.; Cantoni, M.; Piga, D.; Bucca, G. Human-Robot Collaboration in Sensorless Assembly Task Learning Enhanced by Uncertainties Adaptation via Bayesian Optimization. Robot. Auton. Syst. 2021, 136, 103711. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Online Trajectory Planning and Filtering for Robotic Applications via B-Spline Smoothing Filters. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 5668–5673. [Google Scholar] [CrossRef]
- Sayols, N.; Sozzi, A.; Piccinelli, N.; Hernansanz, A.; Casals, A.; Bonfè, M.; Muradore, R. Global/Local Motion Planning Based on Dynamic Trajectory Reconfiguration and Dynamical Systems for Autonomous Surgical Robots. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8483–8489. [Google Scholar] [CrossRef]
- Jurafsky, D.; Martin, J. Speech and Language Processing: An Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2008; Volume 2, Available online: https://dl.acm.org/doi/10.5555/555733 (accessed on 9 August 2023).
- Mongillo, G.; Deneve, S. Online Learning with Hidden Markov Models. Neural Comput. 2008, 20, 1706–1716. [Google Scholar] [CrossRef]
- Vasquez, D.; Fraichard, T.; Laugier, C. Incremental Learning of Statistical Motion Patterns with Growing Hidden Markov Models. IEEE Trans. Intell. Transp. Syst. 2009, 10, 403–416. [Google Scholar] [CrossRef]
- Walter, M.; Psarrou, A.; Psarrou, R.; Gong, S. Learning Prior and Observation Augmented Density Models for Behaviour Recognition. In Proceedings of the BMVC 1999—British Machine Vision Conference 1999, Nottingham, UK, 13–16 September 1999. [Google Scholar]
- Meuter, M.; Iurgel, U.; Park, S.-B.; Kummert, A. The Unscented Kalman Filter for Pedestrian Tracking from a Moving Host. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 37–42. [Google Scholar] [CrossRef]
- Wiest, J.; Höffken, M.; Kreßel, U.; Dietmayer, K. Probabilistic Trajectory Prediction with Gaussian Mixture Models. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; pp. 141–146. [Google Scholar] [CrossRef]
- Gaz, C.; Cognetti, M.; Oliva, A.; Robuffo Giordano, P.; De Luca, A. Dynamic Identification of the Franka Emika Panda Robot with Retrieval of Feasible Parameters Using Penalty-Based Optimization. IEEE Robot. Autom. Lett. 2019, 4, 4147–4154. [Google Scholar] [CrossRef]
- Quigley, M.; Gerkey, B.; Smart, W.D. Programming Robots with ROS: A Practical Introduction to the Robot Operating System; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic Generation and Detection of Highly Reliable Fiducial Markers Under Occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Kohler, M. Using the Kalman Filter to Track Human Interactive Motion: Modelling and Initialization of the Kalman Filter for Translational Motion; Citeseer: Pennsylvania, PA, USA, 1997. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–24 April 1997; Volume 3068, pp. 182–193. [Google Scholar] [CrossRef]





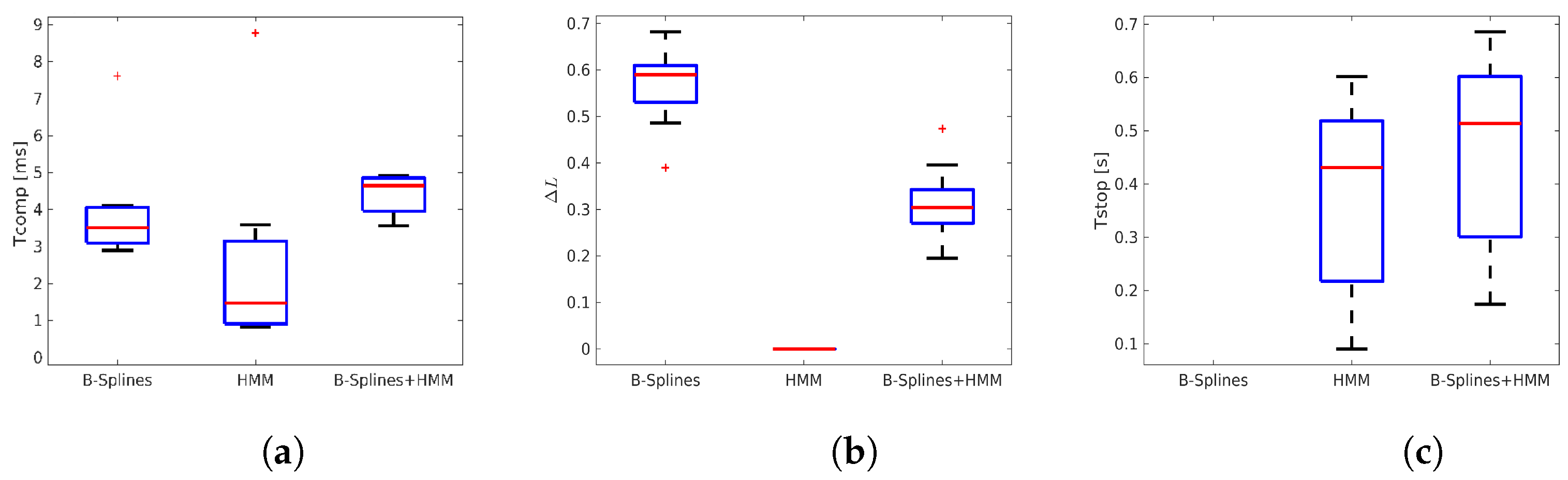

| (ms) | (s) | |||
|---|---|---|---|---|
| B-spline | 3.515 ± 1.53 | 0.590 ± 0.08 | / | 77.97% |
| HMM | 1.480 ± 2.70 | 0.000 ± 0.00 | 0.431 ± 0.01 | 89.66% |
| B-spline+HMM | 4.649 ± 0.55 | 0.304 ± 0.07 | 0.514 ± 0.01 | 94.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braglia, G.; Tagliavini, M.; Pini, F.; Biagiotti, L. Online Motion Planning for Safe Human–Robot Cooperation Using B-Splines and Hidden Markov Models. Robotics 2023, 12, 118. https://doi.org/10.3390/robotics12040118
Braglia G, Tagliavini M, Pini F, Biagiotti L. Online Motion Planning for Safe Human–Robot Cooperation Using B-Splines and Hidden Markov Models. Robotics. 2023; 12(4):118. https://doi.org/10.3390/robotics12040118
Chicago/Turabian StyleBraglia, Giovanni, Matteo Tagliavini, Fabio Pini, and Luigi Biagiotti. 2023. "Online Motion Planning for Safe Human–Robot Cooperation Using B-Splines and Hidden Markov Models" Robotics 12, no. 4: 118. https://doi.org/10.3390/robotics12040118
APA StyleBraglia, G., Tagliavini, M., Pini, F., & Biagiotti, L. (2023). Online Motion Planning for Safe Human–Robot Cooperation Using B-Splines and Hidden Markov Models. Robotics, 12(4), 118. https://doi.org/10.3390/robotics12040118









