MURM: Utilization of Multi-Views for Goal-Conditioned Reinforcement Learning in Robotic Manipulation
Abstract
:1. Introduction
- We propose a novel framework, MURM, for solving goal-conditioned RL by leveraging images from multiple viewpoints with two effective implementation methods called the dropout method and the separated Q-functions method.
- We empirically show the effectiveness of our framework MURM in complicated tasks compared to single-view baselines.
2. Related Works
3. Preliminaries
3.1. Variational Autoencoders (VAE)
3.2. Goal-Conditioned Reinforcement Learning
3.3. Offline Reinforcement Learning
4. Methods
4.1. Designing Demo Dataset for Offline RL
4.2. Representation Learning with VQVAE
4.3. Utilizing Multi-Views in Goal-Conditioned RL in Offline RL Settings
| Algorithm 1 MURM |
| Require: Dataset , policy , Q-function , RL algorithm , replay buffer , state , state 1: Collect demos of from noisy expert 2: Learn state-encoders for each i viewpoint 3: Change states with raw images to latent states 4: if = Separated Q-functions then 5: 6: end if 7: Initialize and Q by 8: for 1, …, do 9: Sample goals for used i views: 10: for do 11: sample 12: sample 13: end for 14: Store trajectory in replay buffer 15: if = Dropout then 16: with Bernoulli(p), = 17: end if 18: Update and Q with sampled batches using 19: end for |
5. Experimental Evaluation
5.1. Experimental Setups
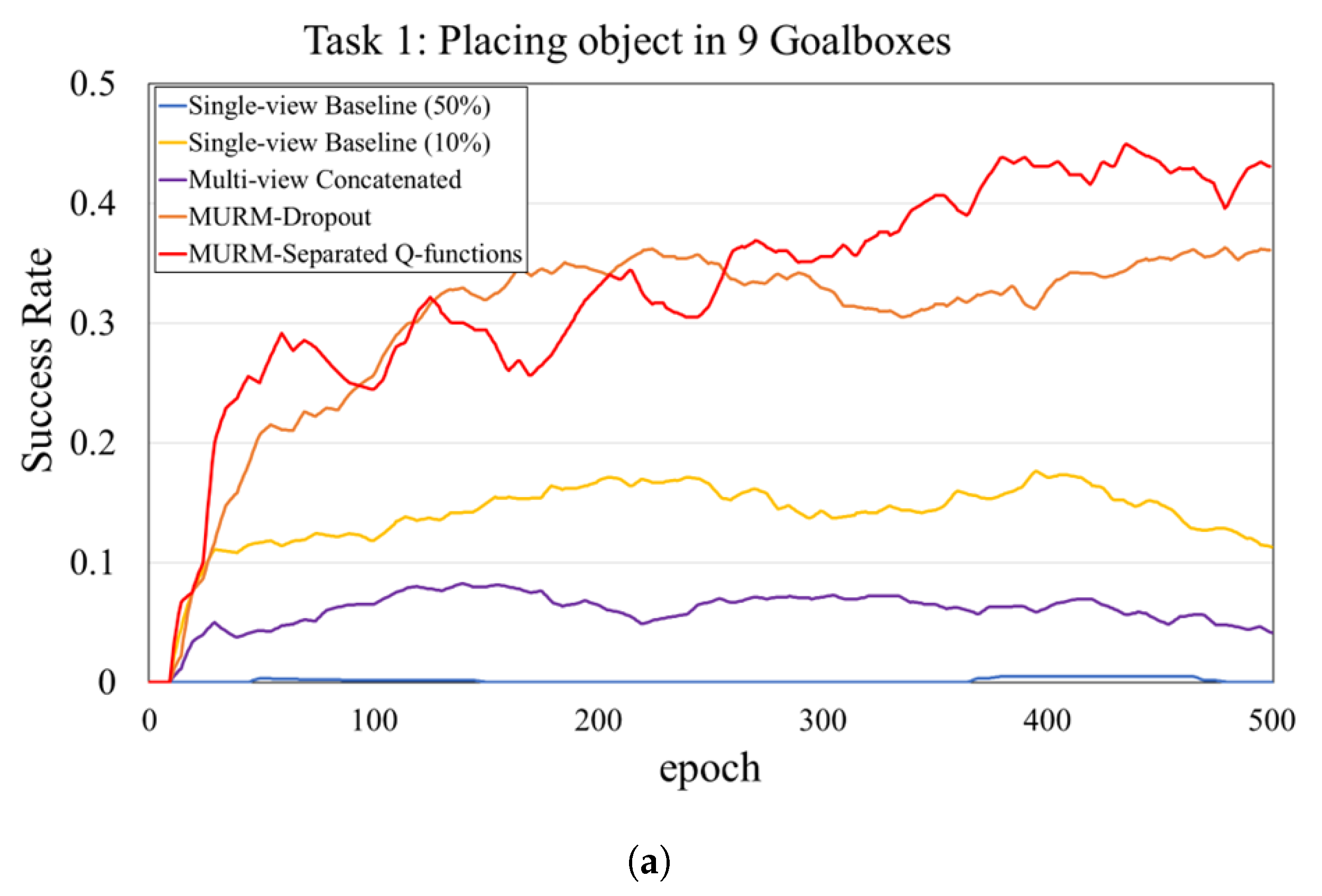
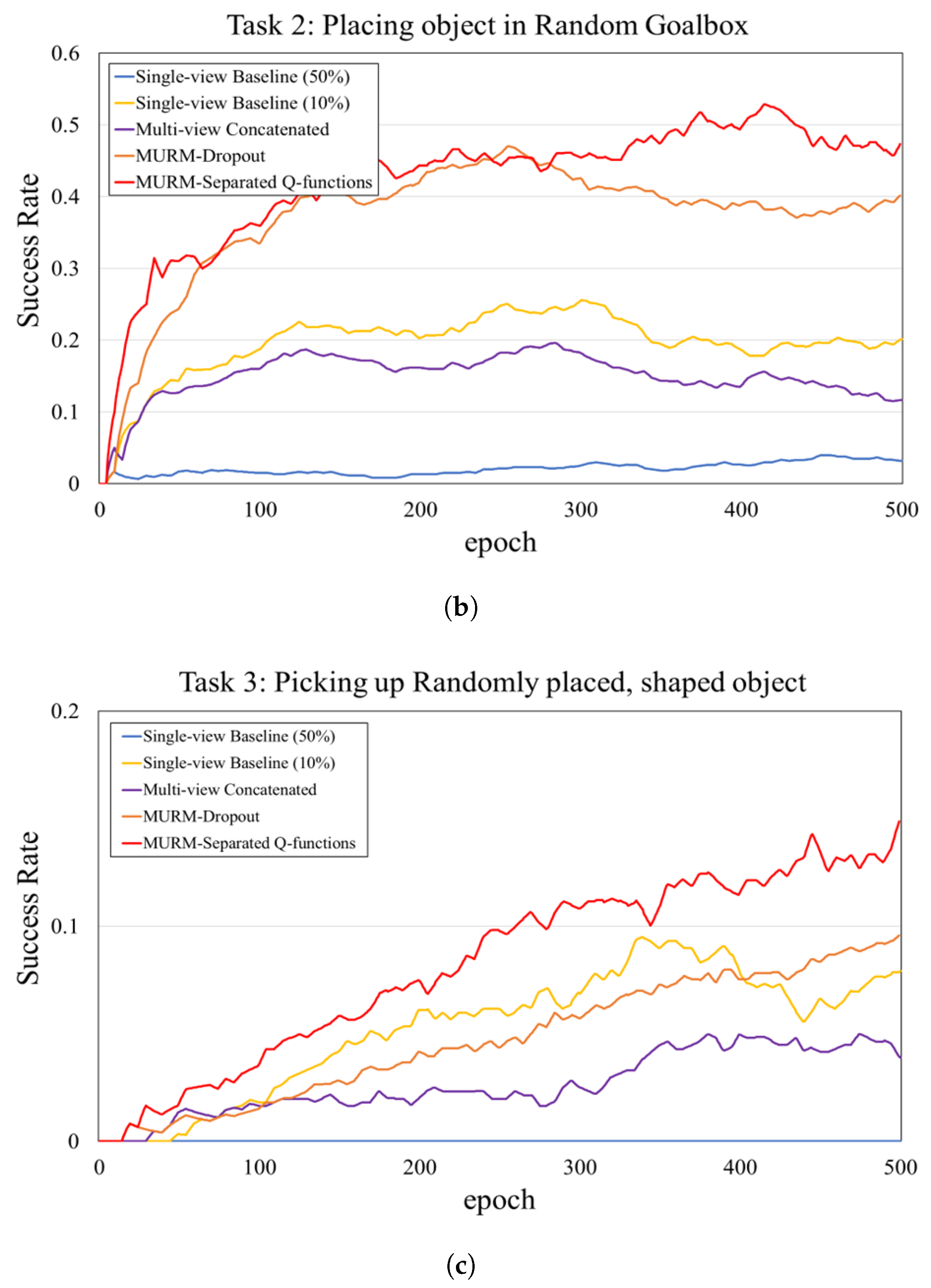
5.2. Results and Analysis
5.3. Ablation Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GCRL | Goal-Conditioned Reinforcement Learning |
| RL | Reinforcement Learning |
| VQVAE | Variational Autoencoders |
| MURM | Multi-view Unified Reinforcement Learning for Manipulation |
| MDP | Markov Decision Process |
| IQL | Implicit Q-Learning |
| HER | Hindsight Experience Replay |
| SOTA | State-of-the-art |
| MLP | Multi-Layer Perceptron |
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Lu, W. Deep reinforcement learning based moving object grasping. Inf. Sci. 2021, 565, 62–76. [Google Scholar] [CrossRef]
- Su, H.; Hu, Y.; Li, Z.; Knoll, A.; Ferrigno, G.; De Momi, E. Reinforcement learning based manipulation skill transferring for robot-assisted minimally invasive surgery. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2203–2208. [Google Scholar]
- Plappert, M.; Andrychowicz, M.; Ray, A.; McGrew, B.; Baker, B.; Powell, G.; Schneider, J.; Tobin, J.; Chociej, M.; Welinder, P.; et al. Multi-goal reinforcement learning: Challenging robotics environments and request for research. arXiv 2018, arXiv:1802.09464. [Google Scholar]
- Liu, M.; Zhu, M.; Zhang, W. Goal-conditioned reinforcement learning: Problems and solutions. arXiv 2022, arXiv:2201.08299. [Google Scholar]
- Hansen-Estruch, P.; Zhang, A.; Nair, A.; Yin, P.; Levine, S. Bisimulation Makes Analogies in Goal-Conditioned Reinforcement Learning. arXiv 2022, arXiv:2204.13060. [Google Scholar]
- Cong, L.; Liang, H.; Ruppel, P.; Shi, Y.; Görner, M.; Hendrich, N.; Zhang, J. Reinforcement Learning with Vision-Proprioception Model for Robot Planar Pushing. Front. Neurorobotics 2022, 16, 829437. [Google Scholar] [CrossRef]
- Qian, Z.; You, M.; Zhou, H.; He, B. Weakly Supervised Disentangled Representation for Goal-conditioned Reinforcement Learning. IEEE Robot. Autom. Lett. 2022, 7, 2202–2209. [Google Scholar] [CrossRef]
- Nair, A.V.; Pong, V.; Dalal, M.; Bahl, S.; Lin, S.; Levine, S. Visual reinforcement learning with imagined goals. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Nair, A.; Bahl, S.; Khazatsky, A.; Pong, V.; Berseth, G.; Levine, S. Contextual imagined goals for self-supervised robotic learning. In Proceedings of the Conference on Robot Learning, Cambridge, MA, USA, 16–18 November 2020; pp. 530–539. [Google Scholar]
- Khazatsky, A.; Nair, A.; Jing, D.; Levine, S. What can i do here? In learning new skills by imagining visual affordances. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14291–14297. [Google Scholar]
- Laskin, M.; Srinivas, A.; Abbeel, P. Curl: Contrastive unsupervised representations for reinforcement learning. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5639–5650. [Google Scholar]
- Fang, K.; Yin, P.; Nair, A.; Levine, S. Planning to practice: Efficient online fine-tuning by composing goals in latent space. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 4076–4083. [Google Scholar]
- Yang, R.; Zhang, M.; Hansen, N.; Xu, H.; Wang, X. Learning vision-guided quadrupedal locomotion end-to-end with cross-modal transformers. arXiv 2021, arXiv:2107.03996. [Google Scholar]
- Chen, B.; Abbeel, P.; Pathak, D. Unsupervised learning of visual 3d keypoints for control. In Proceedings of the International Conference on Machine Learning, Online, 18–24 July 2021; pp. 1539–1549. [Google Scholar]
- Hu, F. Mutual information-enhanced digital twin promotes vision-guided robotic grasping. Adv. Eng. Inform. 2022, 52, 101562. [Google Scholar] [CrossRef]
- Gupta, D.S.; Bahmer, A. Increase in mutual information during interaction with the environment contributes to perception. Entropy 2019, 21, 365. [Google Scholar] [CrossRef] [PubMed]
- Kroemer, O.; Niekum, S.; Konidaris, G. A review of robot learning for manipulation: Challenges, representations, and algorithms. J. Mach. Learn. Res. 2021, 22, 1395–1476. [Google Scholar]
- Jangir, R.; Hansen, N.; Ghosal, S.; Jain, M.; Wang, X. Look Closer: Bridging Egocentric and Third-Person Views With Transformers for Robotic Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 3046–3053. [Google Scholar] [CrossRef]
- James, S.; Wada, K.; Laidlow, T.; Davison, A.J. Coarse-to-fine q-attention: Efficient learning for visual robotic manipulation via discretisation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13739–13748. [Google Scholar]
- OpenAI, O.; Plappert, M.; Sampedro, R.; Xu, T.; Akkaya, I.; Kosaraju, V.; Welinder, P.; D’Sa, R.; Petron, A.; Pinto, H.P.d.O.; et al. Asymmetric self-play for automatic goal discovery in robotic manipulation. arXiv 2021, arXiv:2101.04882. [Google Scholar]
- Akinola, I.; Varley, J.; Kalashnikov, D. Learning precise 3d manipulation from multiple uncalibrated cameras. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4616–4622. [Google Scholar]
- James, S.; Davison, A.J. Q-attention: Enabling efficient learning for vision-based robotic manipulation. IEEE Robot. Autom. Lett. 2022, 7, 1612–1619. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, J.; James, S.; Lee, K.; Shin, J.; Abbeel, P. Multi-View Masked World Models for Visual Robotic Manipulation. arXiv 2023, arXiv:2302.02408. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. Beta-vae: Learning basic visual concepts with a constrained variational framework. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Van Den Oord, A.; Vinyals, O. Neural discrete representation learning. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1889–1897. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Kostrikov, I.; Nair, A.; Levine, S. Offline reinforcement learning with implicit q-learning. arXiv 2021, arXiv:2110.06169. [Google Scholar]
- Coumans, E.; Bai, Y. Pybullet, a Python Module for Physics Simulation for Games, Robotics and Machine Learning. 2016. Available online: https://scholar.google.com/citations?view_op=view_citation&hl=en&user=E_82W3EAAAAJ&citation_for_view=E_82W3EAAAAJ:hqOjcs7Dif8C (accessed on 16 August 2023).
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Andrychowicz, M.; Wolski, F.; Ray, A.; Schneider, J.; Fong, R.; Welinder, P.; McGrew, B.; Tobin, J.; Pieter Abbeel, O.; Zaremba, W. Hindsight experience replay. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]





| Neurons (MLP) | Success Rate (%) | Time Consumption |
|---|---|---|
| 32 | 0.52 | |
| 64 | 0.66 | |
| 128 | 33.14 ± 2.73 | 1.0 |
| 256 | 2.64 |
| Epsilon Values | 0.1 | 1.0 | 2.0 | 3.0 | 5.0 |
|---|---|---|---|---|---|
| Std () mean | ±5.64 | ±2.70 | ±2.97 | ±1.94 | ±2.86 |
| Success Rate (%) | 29.04 ± 0.89 | 29.97 ± 2.08 | 34.49 ± 3.08 | 33.14 ± 2.73 | 27.92 ± 3.43 |
| Viewpoints | Success Rate (%) | ||
|---|---|---|---|
| Task 1 | Task 2 | Task 3 | |
| Global-view | 34.49 | 46.63 | 15.74 |
| Adjacent-view | 33.76 | 39.50 | 14.65 |
| Top-view | 18.84 | 38.65 | 0.17 |
| Side-view | 17.99 | 33.86 | 12.74 |
| Active-view | 12.51 | 8.68 | 3.63 |
| Methods | Success Rate (%) | ||
|---|---|---|---|
| Task 1 | Task 2 | Task 3 | |
| Single-view Baseline (50%) | 0.0 | 3.17 | 0.0 |
| Single-view Baseline (10%) | 11.35 | 20.1 | 7.85 |
| Multi-view Concatenated | 4.22 | 11.65 | 3.93 |
| MURM-Dropout | 36.07 | 40.2 | 9.67 |
| MURM-Separated Q-functions | 38.35 | 43.96 | 14.88 |
| Methods | Time Consumption |
|---|---|
| (If Add a Viewpoint) | |
| Single-view Baselines | 1.0 |
| MURM-Dropout | 1.05 (+0.46) |
| MURM-Separated Q-functions | 1.55 (+0.5) |
| Viewpoint Added | Success Rate (%) |
|---|---|
| Top-view | 30.23 (−8.12) |
| Side-view | 32.87 (−5.48) |
| Active-view | 23.07 (−15.28) |
| Demo Episodes | 250 | 500 | 1000 | 2000 | 3000 |
| Success Rates (%) | 29.11 | 31.22 | 38.35 | 35.84 | 34.75 |
| Noisy Experts (k%) | 0% | 25% | 50% | 100% | |
| Success rates (%) | 26.57 | 31.85 | 33.73 | 38.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, S.; Jeong, H.; Yang, H. MURM: Utilization of Multi-Views for Goal-Conditioned Reinforcement Learning in Robotic Manipulation. Robotics 2023, 12, 119. https://doi.org/10.3390/robotics12040119
Jang S, Jeong H, Yang H. MURM: Utilization of Multi-Views for Goal-Conditioned Reinforcement Learning in Robotic Manipulation. Robotics. 2023; 12(4):119. https://doi.org/10.3390/robotics12040119
Chicago/Turabian StyleJang, Seongwon, Hyemi Jeong, and Hyunseok Yang. 2023. "MURM: Utilization of Multi-Views for Goal-Conditioned Reinforcement Learning in Robotic Manipulation" Robotics 12, no. 4: 119. https://doi.org/10.3390/robotics12040119
APA StyleJang, S., Jeong, H., & Yang, H. (2023). MURM: Utilization of Multi-Views for Goal-Conditioned Reinforcement Learning in Robotic Manipulation. Robotics, 12(4), 119. https://doi.org/10.3390/robotics12040119






