Modal Kinematic Analysis of a Parallel Kinematic Robot with Low-Stiffness Transmissions
Abstract
:1. Introduction
2. Materials and Methods
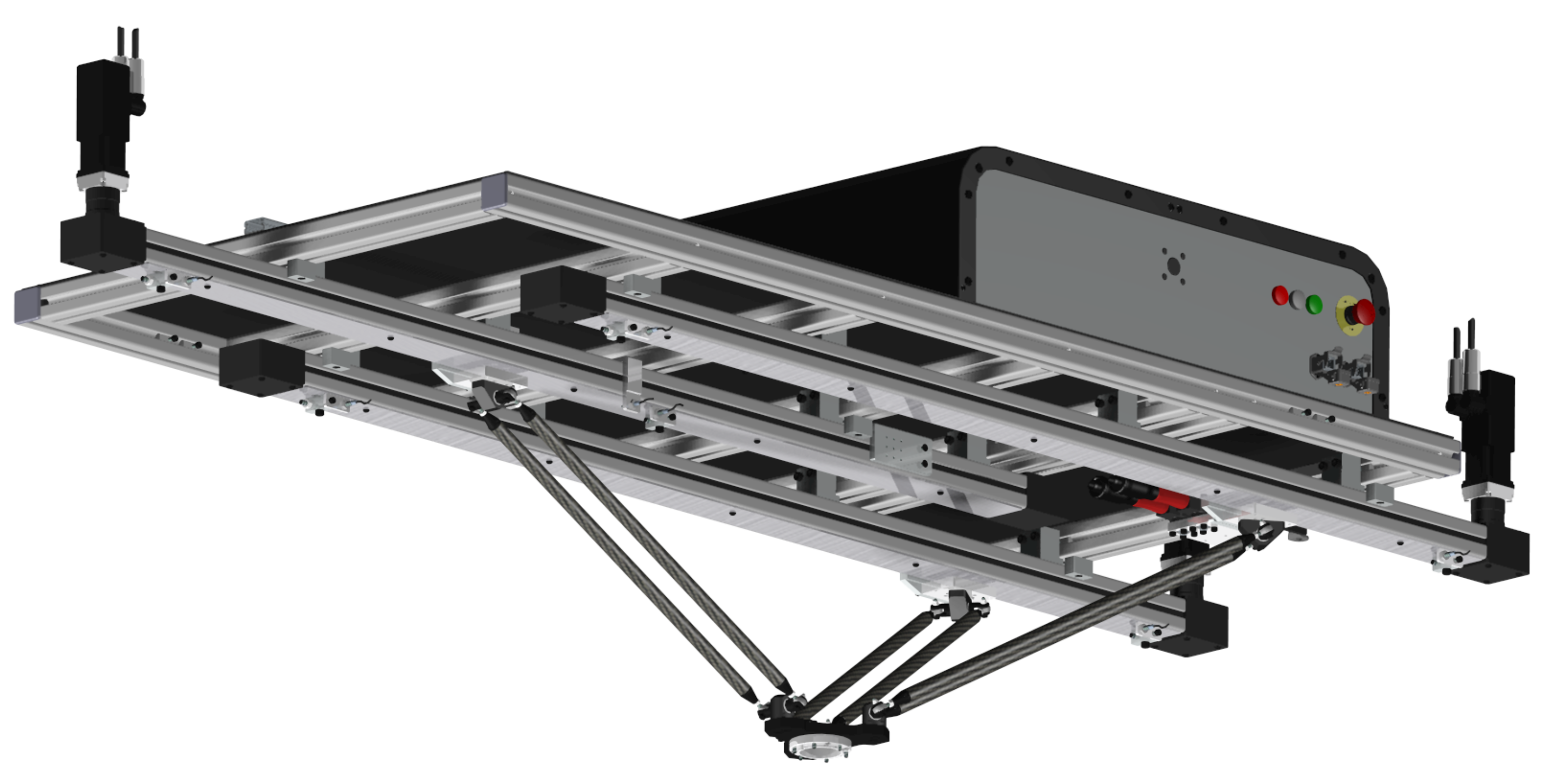
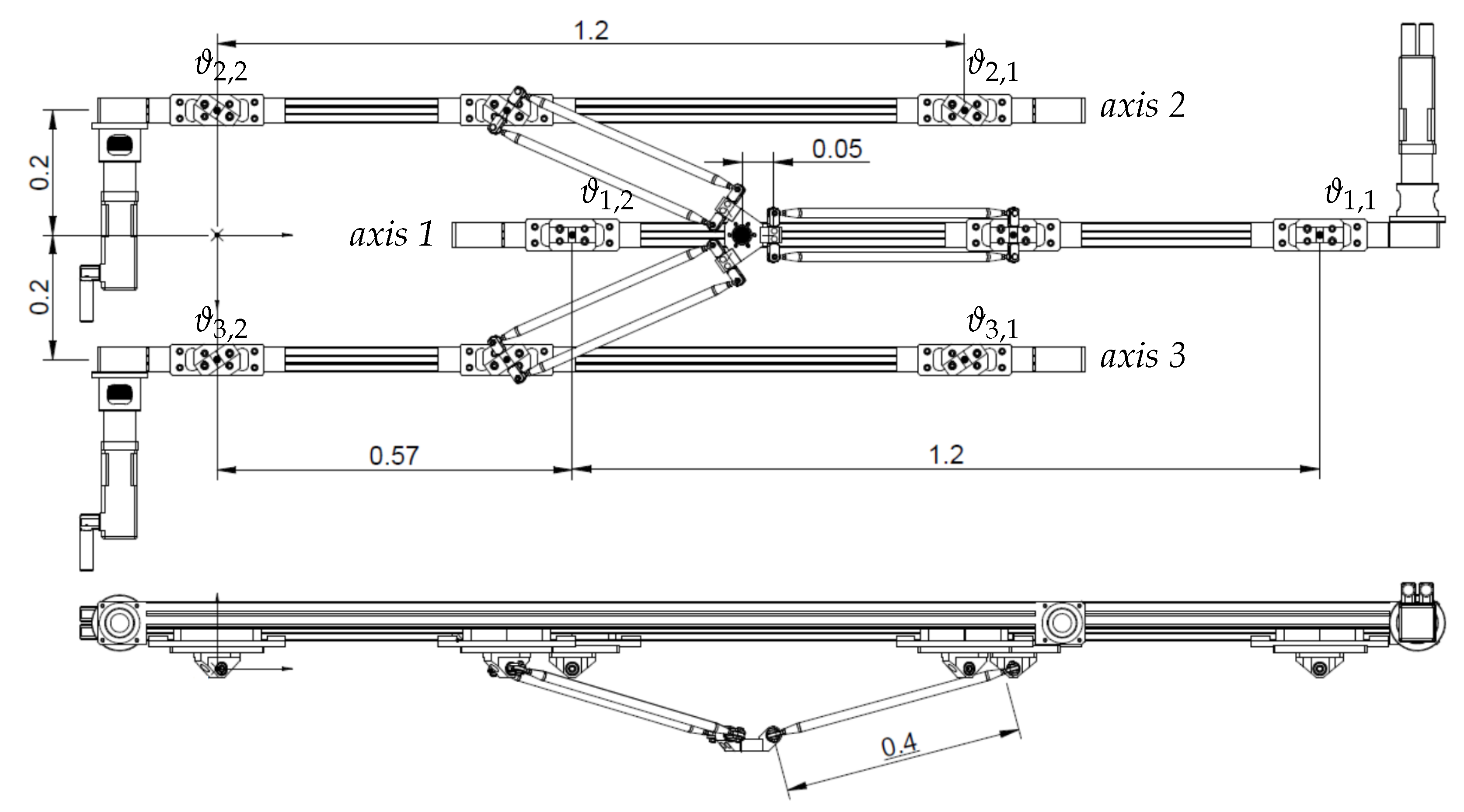
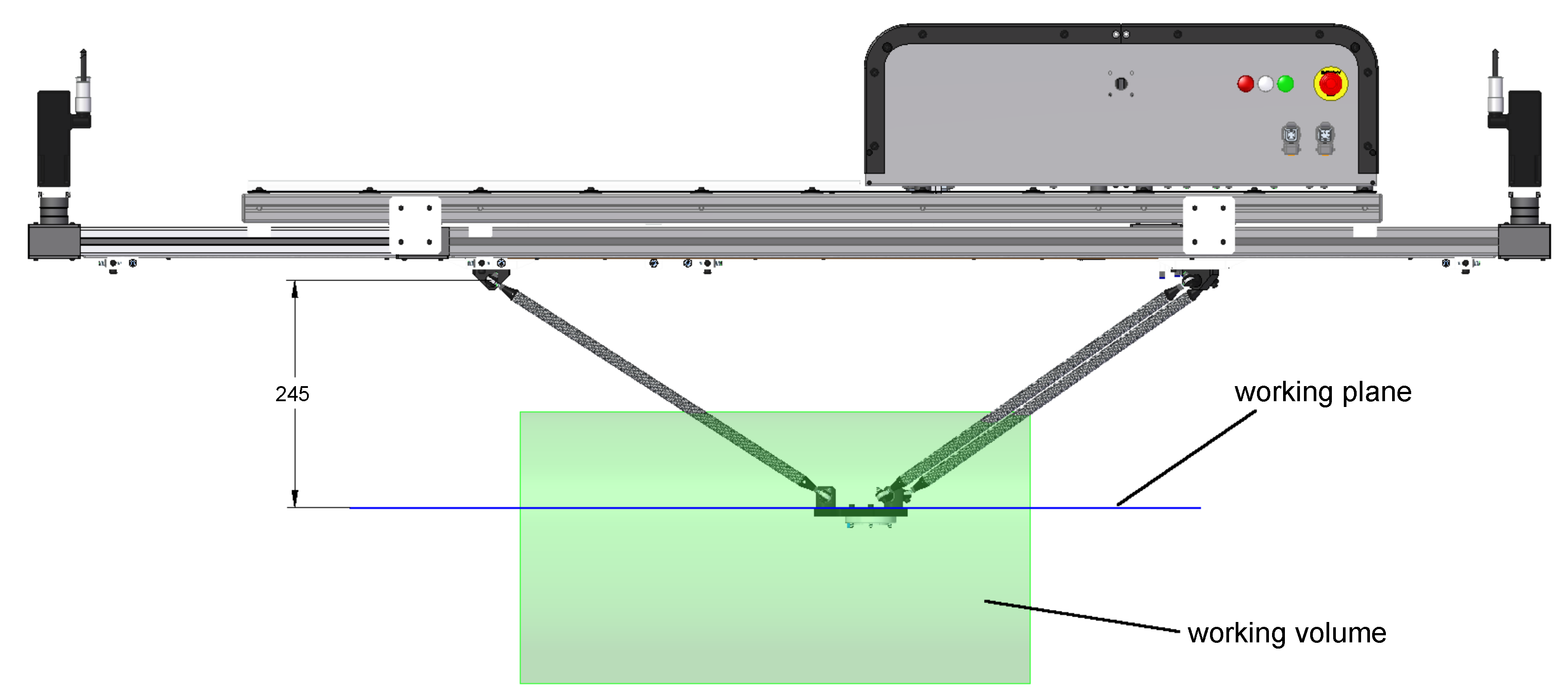
2.1. The Parallel Robot under Analysis
- The three linear axes are parallel.
- Each linear axis is composed of a linear belt transmission. The belt is a HTD-5 characterized by a 15 mm width and a specific stiffness (or stiffness per unit of length and unit of width) of = 2.42 × 106 N/m.
- The system is driven by means of brushless motors, characterized by a nominal torque of 0.7 Nm; a maximum velocity of 10,000 rpm; and a rotor inertia of 0.017 × 10−3 kg·m2.
- The motors are connected to the driven pulley of the linear belt transmission by means of a planetary gearbox characterized by a reduction ratio equal to 10.
- The maximum axis stroke is 1.2 m.
- The distance between axes is 200 mm.
- The length of the links connecting the carriages to the end-effector is 400 mm.
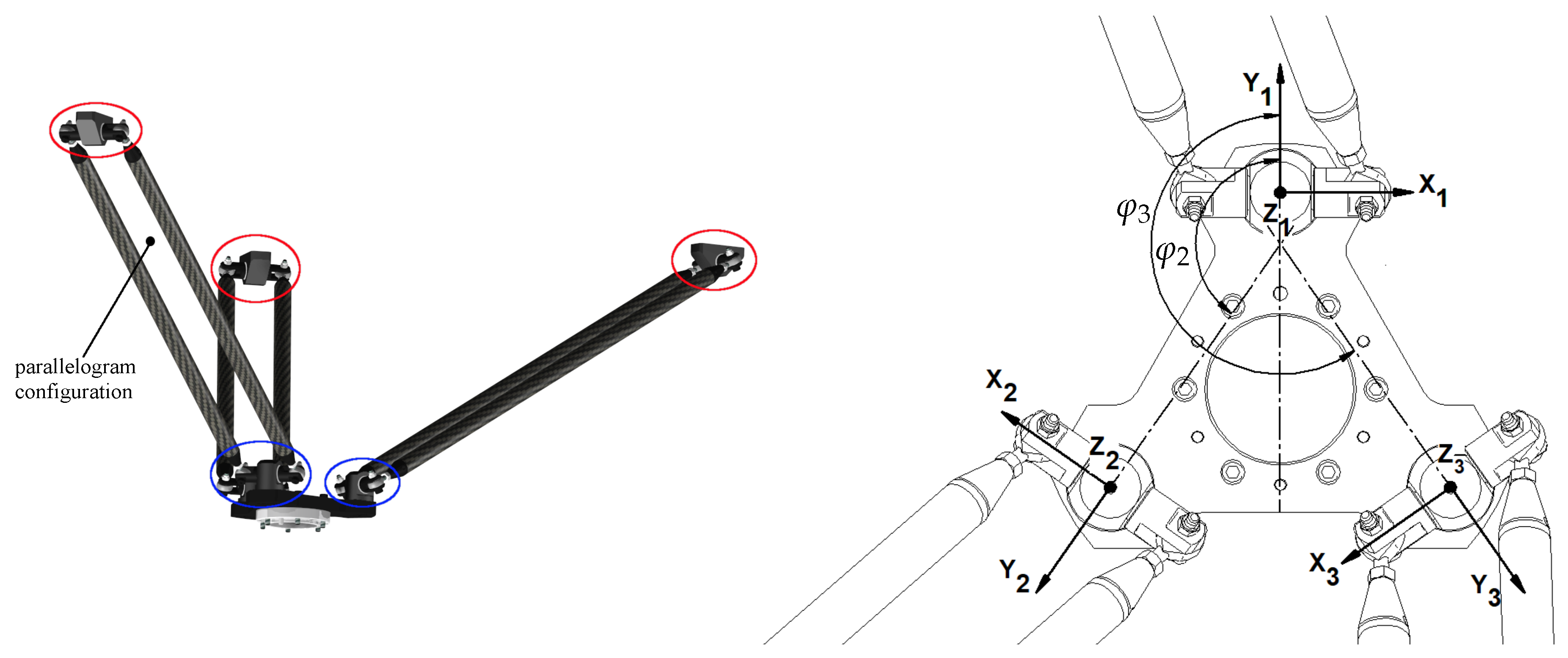
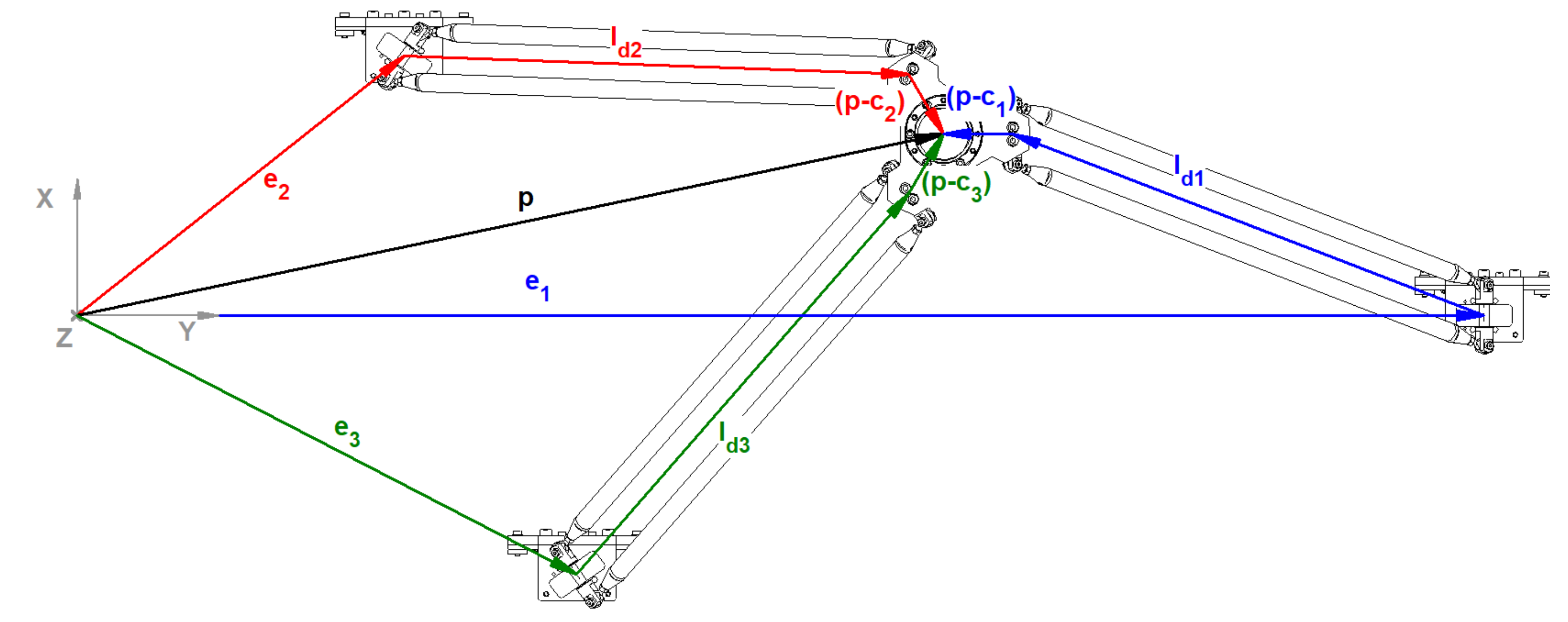
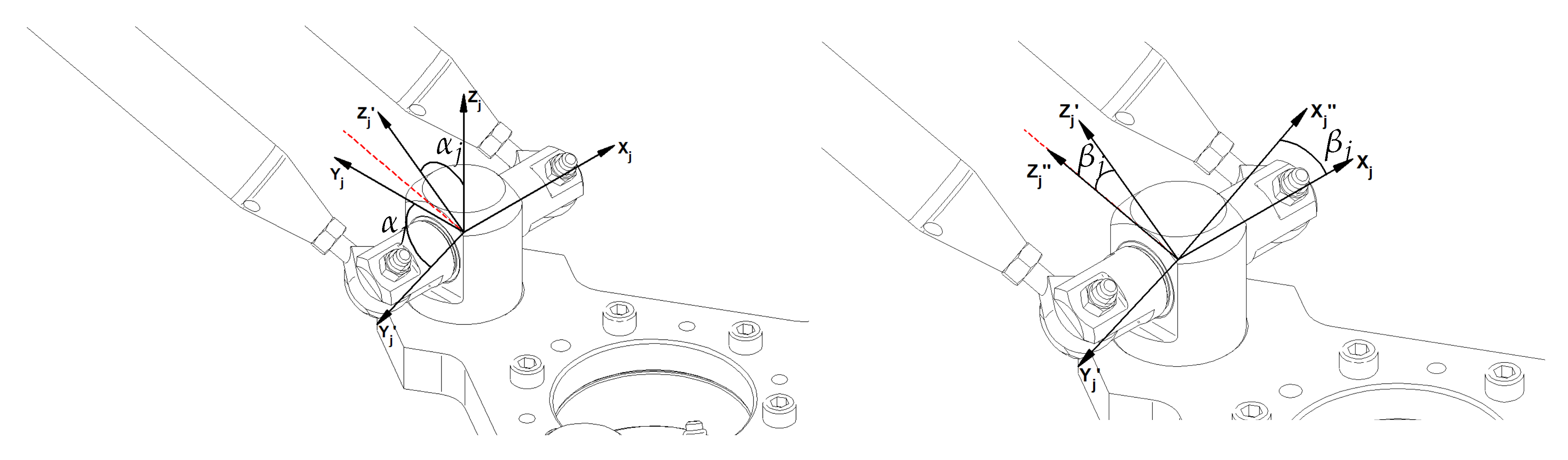
2.2. Kinematics and Dynamics of the Parallel Kinematic Part
- ,
- ,
- .
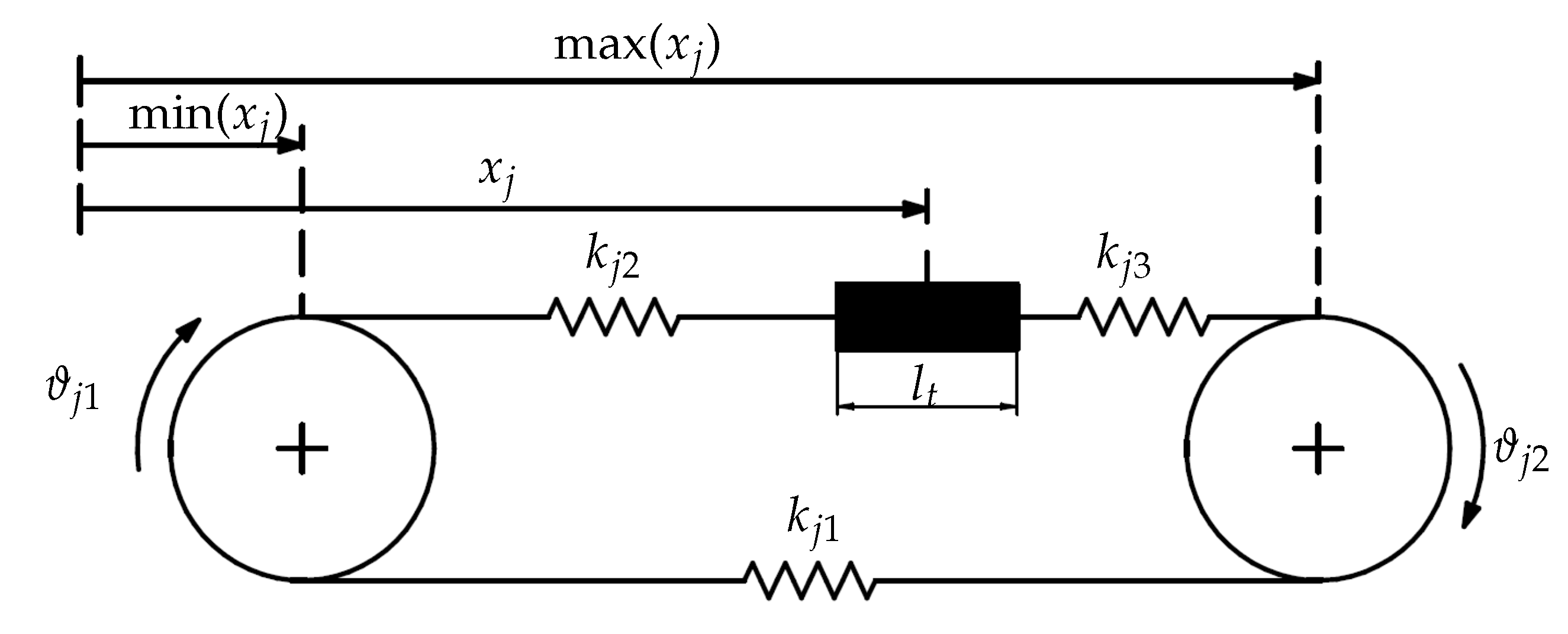
2.3. Belt Transmission Dynamics
- Radius mm,
- Inertia around the rotation axis kg · m2.
3. Overall Dynamics
4. Configuration-Dependent Modal Analysis
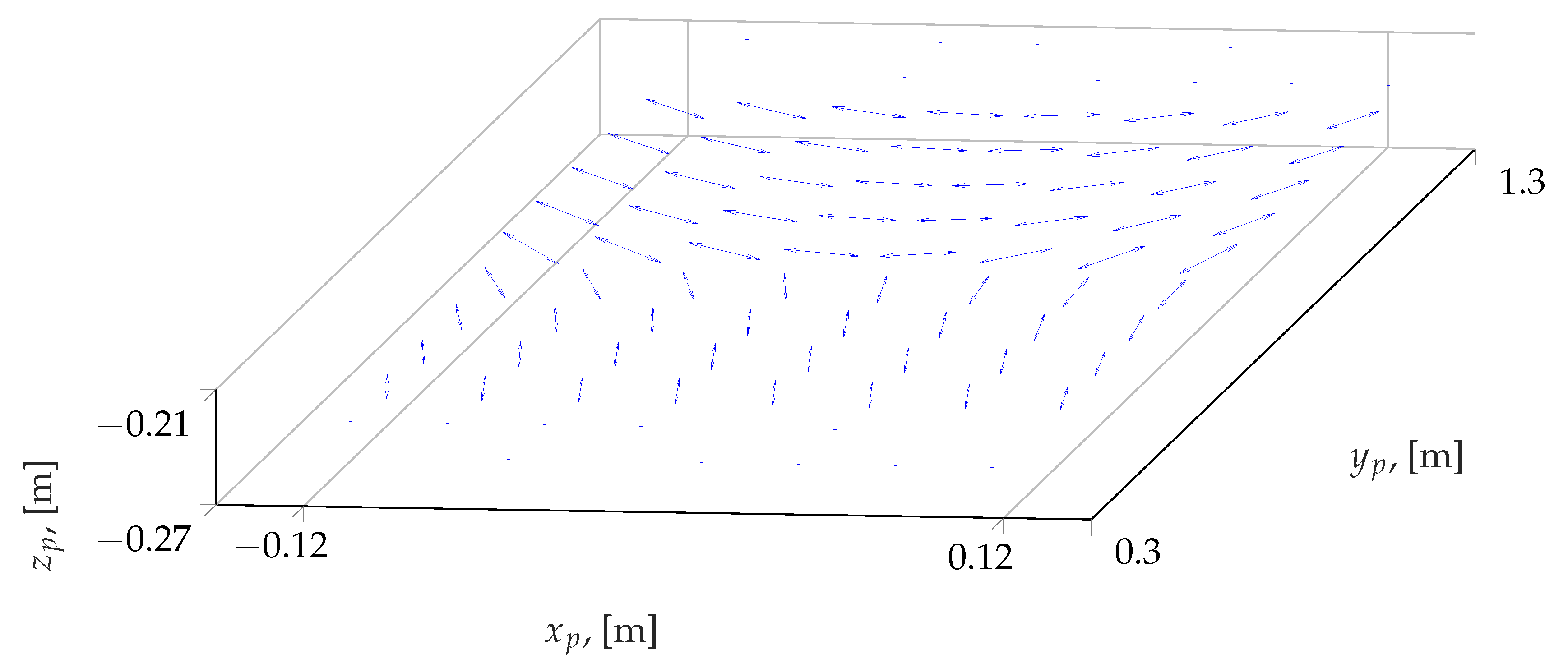
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clavel, R. DELTA: A fast robot with parallel geometry. Robotica 1988, 8, 105–109. [Google Scholar]
- Rey, L.; Clavel, R. The Delta Parallel Robot; Boër, C.R., Molinari-Tosatti, L., Smith, K.S., Eds.; Springer: London, UK, 1999. [Google Scholar]
- Bourim, M.; Clavel, R. The Linear Delta: Developments and Applications; Springer: Munich, Germany, 2010. [Google Scholar]
- Merlet, J. Parallel Robots; Kluwer Academic Publishers: Oxford, UK, 2000. [Google Scholar]
- Parallel Kinematic Machines: Theoretical Aspects and Industrial Requirements; Boër, C.R.; Molinari-Tosatti, L.; Smith, K.S. (Eds.) Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Righettini, P.; Lorenzi, V.; Zappa, B.; Ginammi, A.; Strada, R. Design and optimization of a PKM for micromanipulation. Appl. Mech. Mater. 2015, 799, 1088–1095. [Google Scholar] [CrossRef]
- Nevaranta, N.; Parkkinen, J.; Lindh, T.; Niemelä, M.; Pyrhönen, O.; Pyrhönen, J. Online Estimation of Linear Tooth Belt Drive System Parameters. IEEE Trans. Ind. Electron. 2015, 62, 7214–7223. [Google Scholar] [CrossRef]
- Poonia, S.; Singh, A.; Singh, J.; Sharma, S.; Kumar, N. Noise Problem Resolution and Sound Quality Improvement of Valve Timing Belt in 4 Cylinders PFI Gasoline Engine; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Belyaev, A.; Eliseev, V.; Irschik, H.; Oborin, E. Contact of two equal rigid pulleys with a belt modelled as Cosserat nonlinear elastic rod. Acta Mech. 2017, 228, 4425–4434. [Google Scholar] [CrossRef] [Green Version]
- Oborin, E.; Vetyukov, Y.; Steinbrecher, I. Eulerian description of non-stationary motion of an idealized belt-pulley system with dry friction. Int. J. Solids Struct. 2018, 147, 40–51. [Google Scholar] [CrossRef]
- Vetyukov, Y.; Oborin, E.; Krommer, M.; Eliseev, V. Transient modelling of flexible belt drive dynamics using the equations of a deformable string with discontinuities. Math. Comput. Model. Dyn. Syst. 2017, 23, 40–54. [Google Scholar] [CrossRef]
- Long, S.; Wang, W.; Yue, X.; Zhang, C. Dynamic Modeling of the Belt Drive System with an Equivalent Tensioner Model. J. Vib. Eng. Technol. 2021. [Google Scholar] [CrossRef]
- Long, S.; Zhao, X.; Shangguan, W.B.; Zhu, W. Modeling and validation of dynamic performances of timing belt driving systems. Mech. Syst. Signal Process. 2020, 144, 106910. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, W.; Hu, Y.; Wang, X. Periodic Response of a Timing Belt Drive System with an Oval Cogged Pulley and Optimal Design of the Pitch Profile for Vibration Reduction. J. Comput. Nonlinear Dyn. 2018, 13. [Google Scholar] [CrossRef]
- Passos, S.; Manin, L.; Remond, D.; Sauvage, O.; Rota, L.; Besnier, E. Investigation on the Rotational Dynamics of a Timing Belt Drive including an Oval Driving Pulley. J. Vib. Acoust. 2021, 143, 051014. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, W.; Fan, W. Dynamic modeling, simulation and experiment of power transmission belt drives: A systematic review. J. Sound Vib. 2021, 491, 115759. [Google Scholar] [CrossRef]
- Kulkarni, V.; Chandrashekara, C.; Sethuram, D. Modal Analysis of 3-RRR SPM Model. In Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022; pp. 673–678. [Google Scholar] [CrossRef]
- La Mura, F.; Giberti, H.; Pirovano, L.; Tarabini, M. Theoretical and experimental modal analysis of a 6 PUS PKM. ICINCO 2019, 2, 276–283. [Google Scholar] [CrossRef]
- Fiore, E.; Giberti, H. A montecarlo approach to test the modes of vibration of a 6-DoF parallel kinematic simulator. In Shock & Vibration, Aircraft/Aerospace, Energy Harvesting, Acoustics & Optics; Springer: Berlin/Heidelberg, Germany, 2017; pp. 315–323. [Google Scholar] [CrossRef]
- Palmieri, G.; Martarelli, M.; Palpacelli, M.; Carbonari, L. Configuration-dependent modal analysis of a Cartesian parallel kinematics manipulator: Numerical modeling and experimental validation. Meccanica 2014, 49, 961–972. [Google Scholar] [CrossRef]
- Ren, J.; Cao, Q. Dynamic modeling and frequency characteristic analysis of a novel 3-pss flexible parallel micro-manipulator. Micromachines 2021, 12, 678. [Google Scholar] [CrossRef] [PubMed]
- Sayahkarajy, M. Mode shape analysis, modal linearization, and control of an elastic two-link manipulator based on the normal modes. Appl. Math. Model. 2018, 59, 546–570. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.; Chen, Q. Natural frequency analysis of parallel manipulators using global independent generalized displacement coordinates. Mech. Mach. Theory 2021, 156, 104145. [Google Scholar] [CrossRef]
- Dong, C.; Liu, H.; Huang, T.; Chetwynd, D. A screw theory-based semi-analytical approach for elastodynamics of the tricept robot. J. Mech. Robot. 2019, 11, 031005. [Google Scholar] [CrossRef]
- Wu, L.; Dong, C.; Wang, G.; Liu, H.; Huang, T. An approach to predict lower-order dynamic behaviors of a 5-DOF hybrid robot using a minimum set of generalized coordinates. Robot. Comput. Integr. Manuf. 2021, 67, 102024. [Google Scholar] [CrossRef]
- Hasegawa, A.; Fujimoto, H.; Takahashi, T. Robot Joint Angle Control Based on Self Resonance Cancellation Using Double Encoders. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 460–465. [Google Scholar] [CrossRef]
- Oaki, J.; Chiba, Y. Simple Physically Parameterized Observer for Vibration Suppression Control of SCARA Robot with Elastic Joints. IFAC 2017, 50, 6085–6092. [Google Scholar] [CrossRef]
- Lee, T.; Choi, J.; Rhim, S. Dynamic analysis and parameter estimation of coupled three-link planar manipulator with flexible belt-drive system. J. Mech. Sci. Technol. 2015, 29, 981–988. [Google Scholar] [CrossRef]
- Negahbani, N.; Giberti, H.; Fiore, E. Error Analysis and Adaptive-Robust Control of a 6-DoF Parallel Robot with Ball-Screw Drive Actuators. J. Robot. 2016, 2016. [Google Scholar] [CrossRef]
- Negahbani, N.; Giberti, H.; Ferrari, D. A belt-driven 6-DoF parallel kinematic machine. In Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 1. [Google Scholar] [CrossRef]
- MDQUADRO srl | Advanced Mechatronic Solutions. Available online: https://www.mdquadro.com (accessed on 15 November 2021).
- Righettini, P.; Strada, R.; Zappa, B.; Lorenzi, V. Experimental set-up for the investigation of transmissions effects on the dynamic performances of a linear PKM. Mech. Mach. Sci. 2019, 73, 2511–2520. [Google Scholar] [CrossRef]


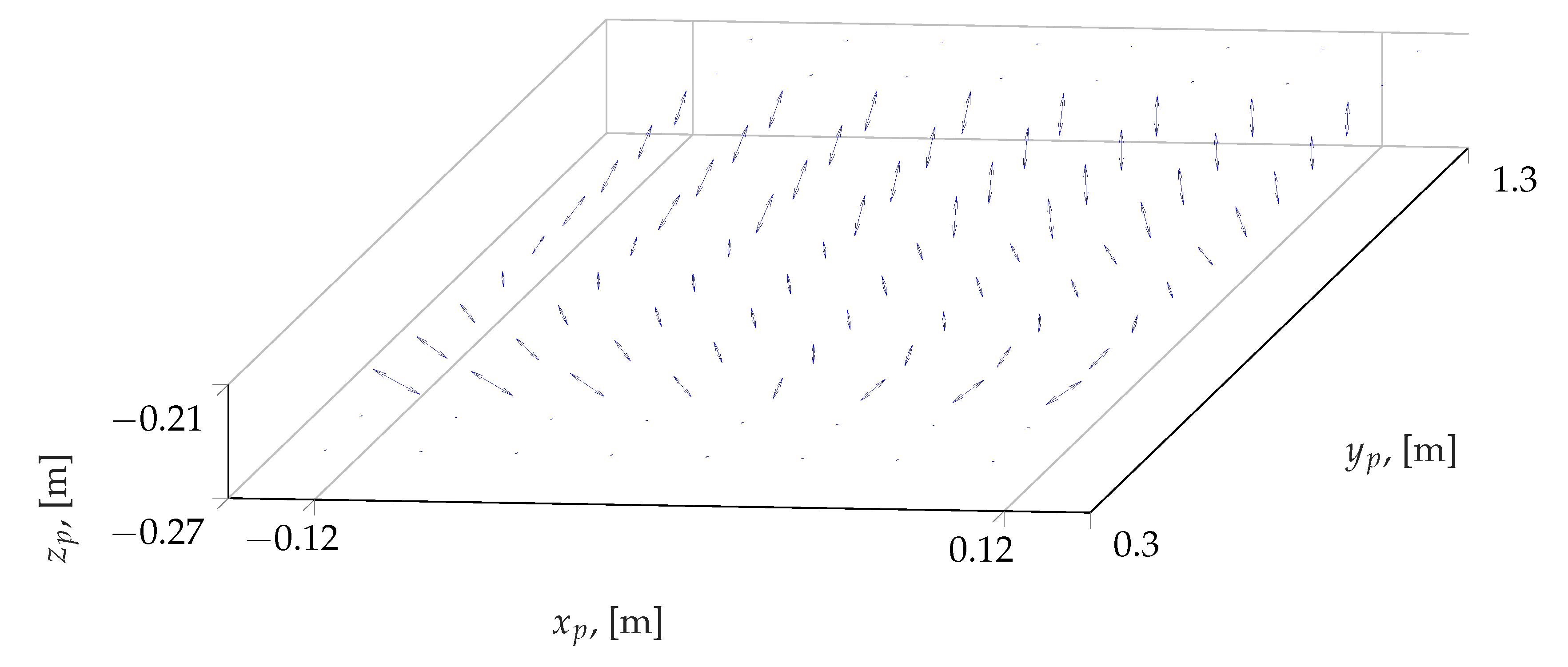

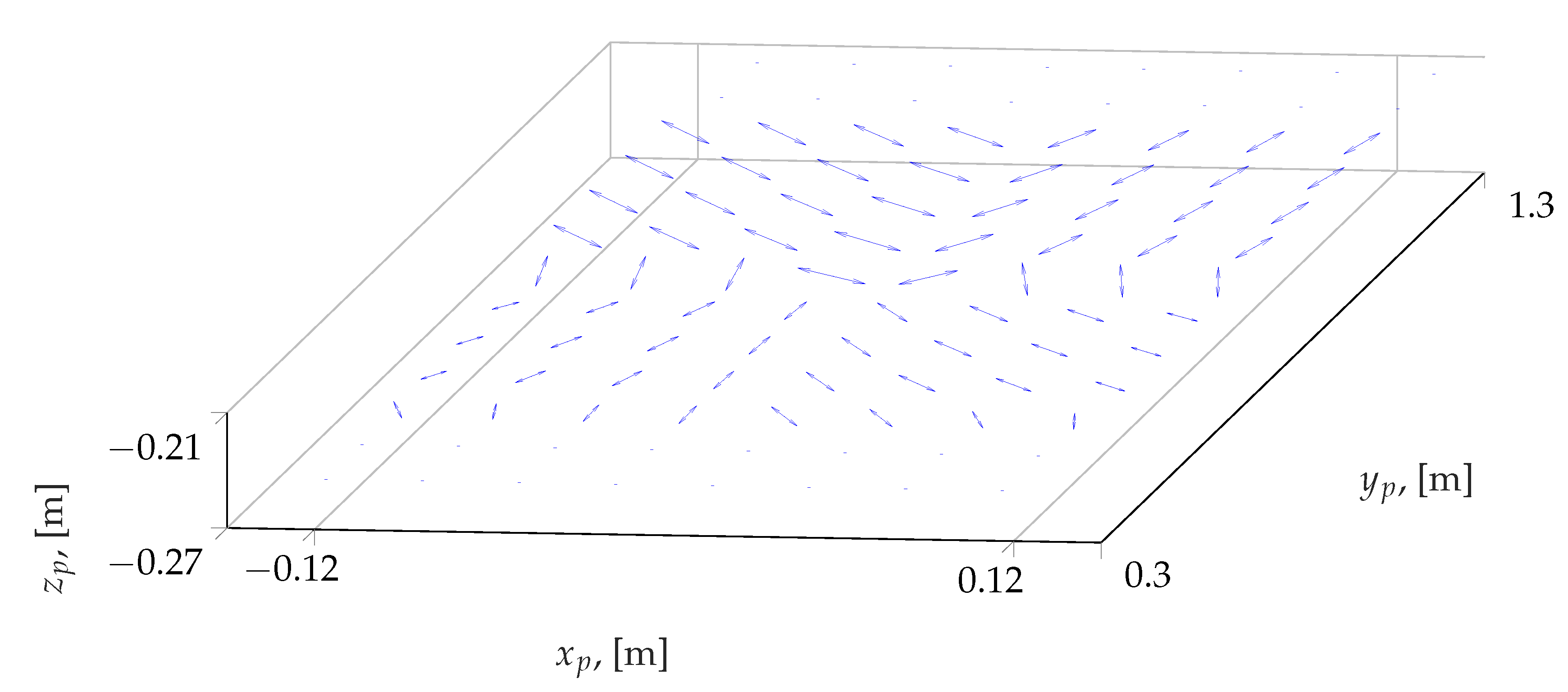

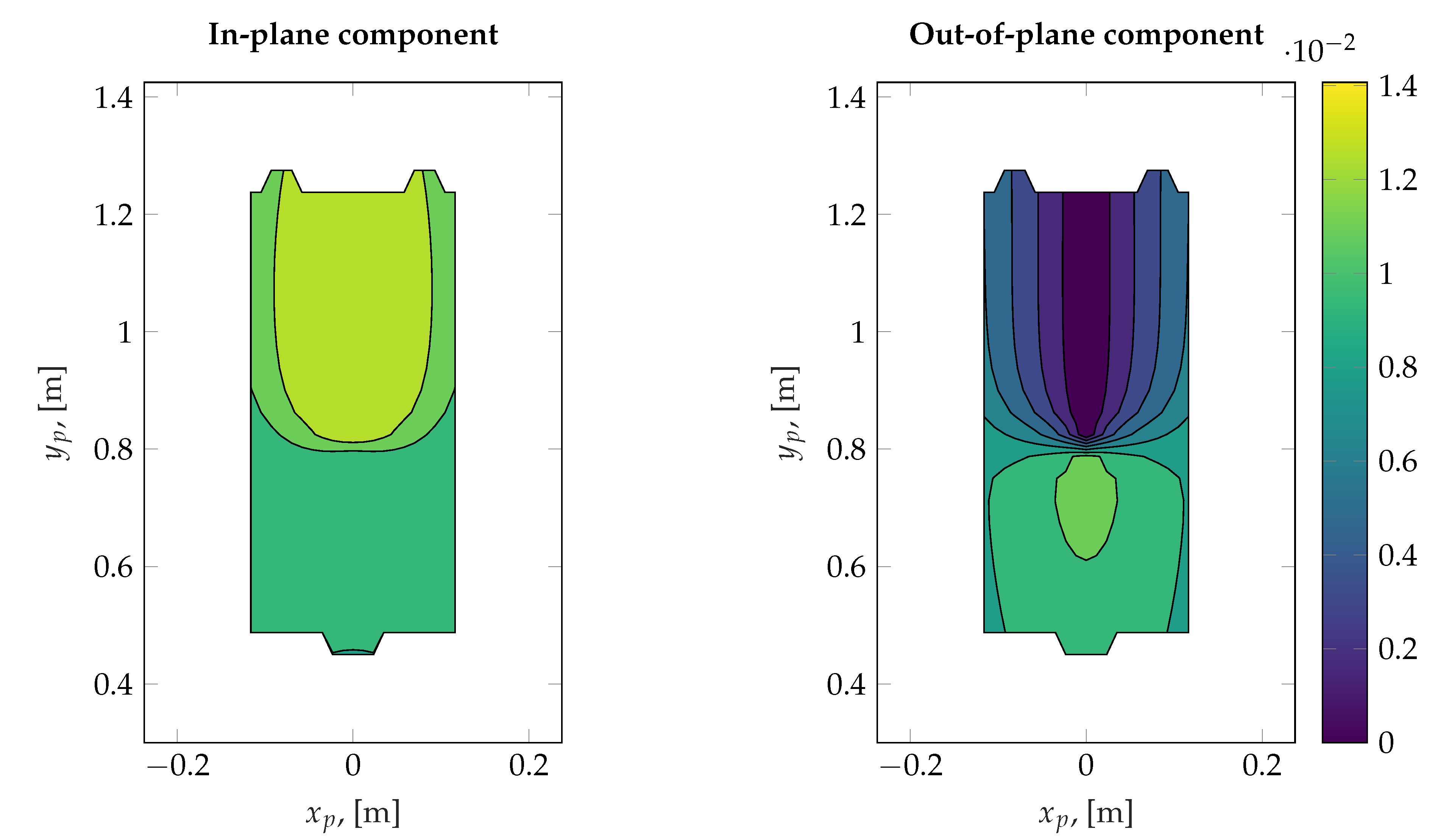




| Mode | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 40.873 | −6.77 × 10 | −3.19 × 10 | 3.19 × 10 | −9.69 × 10 | −1.37 × 10 | 1.37 × 10 | −8.31 × 10 | 1.00 | −1.00 |
| 2 | 46.854 | −4.04 × 10 | −2.54 × 10 | −2.54 × 10 | −1.50 × 10 | −5.02 × 10 | −5.02 × 10 | −1.50 × 10 | 1.00 | 1.00 |
| 3 | 54.286 | −1.89 × 10 | −6.88 × 10 | −6.88 × 10 | 1.00 | −5.35 × 10 | −5.35 × 10 | 3.94 × 10 | 2.50 × 10 | 2.50 × 10 |
| 4 | 136.237 | −4.90 × 10 | −9.67 × 10 | −9.67 × 10 | 7.36 × 10 | −3.35 × 10 | −3.35 × 10 | −1.00 | 2.37 × 10 | 2.37 × 10 |
| 5 | 136.835 | 2.17 × 10 | 7.78 × 10 | 7.78 × 10 | −5.46 × 10 | −1.00 | −1.00 | 7.79 × 10 | 4.15 × 10 | 4.15 × 10 |
| 6 | 159.823 | −5.25 × 10 | −1.23 × 10 | −1.23 × 10 | −4.13 × 10 | 1.00 | 1.00 | 1.92 × 10 | −2.40 × 10 | −2.40 × 10 |
| Mode | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 49.692 | 5.33 × 10 | −5.35 × 10 | −5.35 × 10 | −1.00 | 5.05 × 10 | 5.05 × 10 | 3.63 × 10 | 2.06 × 10 | 2.06 × 10 |
| 2 | 126.906 | −2.14 × 10 | 1.17 × 10 | −1.17 × 10 | 1.45 × 10 | −6.46 × 10 | 6.46 × 10 | −6.19 × 10 | −1.00 | 1.00 |
| 3 | 135.238 | −7.71 × 10 | −2.68 × 10 | −2.68 × 10 | 2.68 × 10 | 2.65 × 10 | 2.65 × 10 | −2.37 × 10 | 1.00 | 1.00 |
| 4 | 157.310 | 8.51 × 10 | 5.57 × 10 | 5.57 × 10 | 2.55 × 10 | 9.86 × 10 | 9.86 × 10 | −1.00 | −2.75 × 10 | −2.75 × 10 |
| 5 | 250.799 | 4.92 × 10 | 6.90 × 10 | −6.90 × 10 | −3.36 × 10 | −1.00 | 1.00 | −2.27 × 10 | 9.76 × 10 | −9.76 × 10 |
| 6 | 263.843 | 1.16 × 10 | 2.78 × 10 | 2.78 × 10 | 8.66 × 10 | −1.10 × 10 | −1.10 × 10 | −1.00 | −1.74 × 10 | −1.74 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Righettini, P.; Strada, R.; Cortinovis, F. Modal Kinematic Analysis of a Parallel Kinematic Robot with Low-Stiffness Transmissions. Robotics 2021, 10, 132. https://doi.org/10.3390/robotics10040132
Righettini P, Strada R, Cortinovis F. Modal Kinematic Analysis of a Parallel Kinematic Robot with Low-Stiffness Transmissions. Robotics. 2021; 10(4):132. https://doi.org/10.3390/robotics10040132
Chicago/Turabian StyleRighettini, Paolo, Roberto Strada, and Filippo Cortinovis. 2021. "Modal Kinematic Analysis of a Parallel Kinematic Robot with Low-Stiffness Transmissions" Robotics 10, no. 4: 132. https://doi.org/10.3390/robotics10040132
APA StyleRighettini, P., Strada, R., & Cortinovis, F. (2021). Modal Kinematic Analysis of a Parallel Kinematic Robot with Low-Stiffness Transmissions. Robotics, 10(4), 132. https://doi.org/10.3390/robotics10040132






