Mechanical Deformation and Electronic Structure of a Blue Copper Azurin in a Solid-State Junction
Abstract
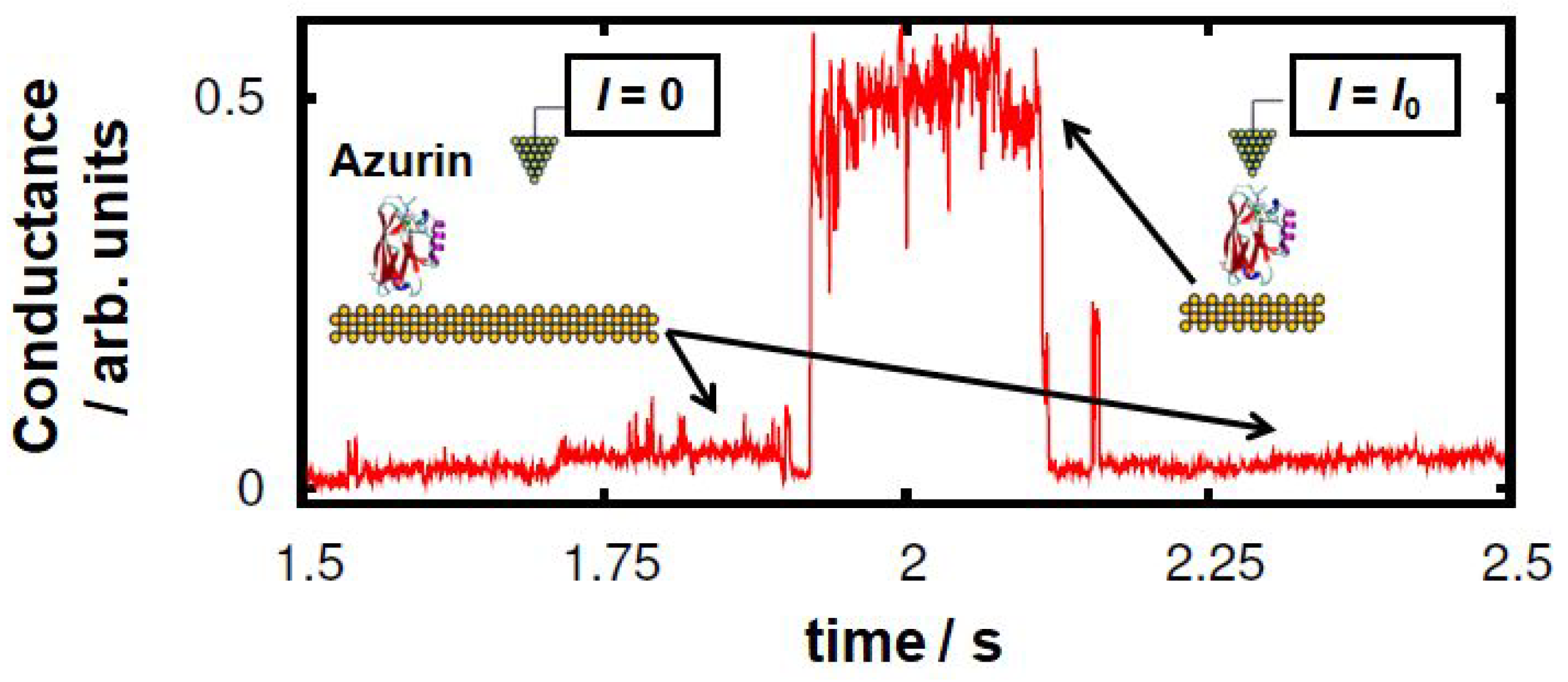
:1. Introduction
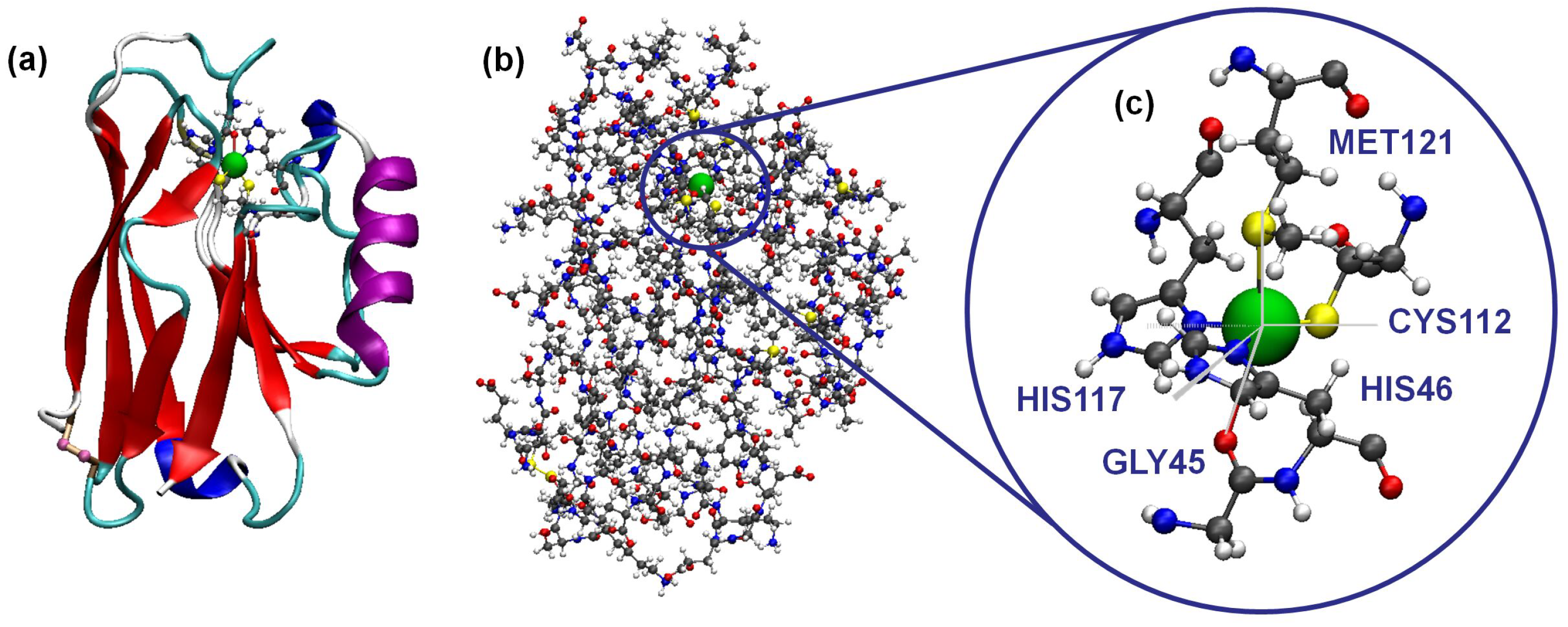
2. Methods
2.1. Molecular Dynamics
2.2. Density Functional Theory
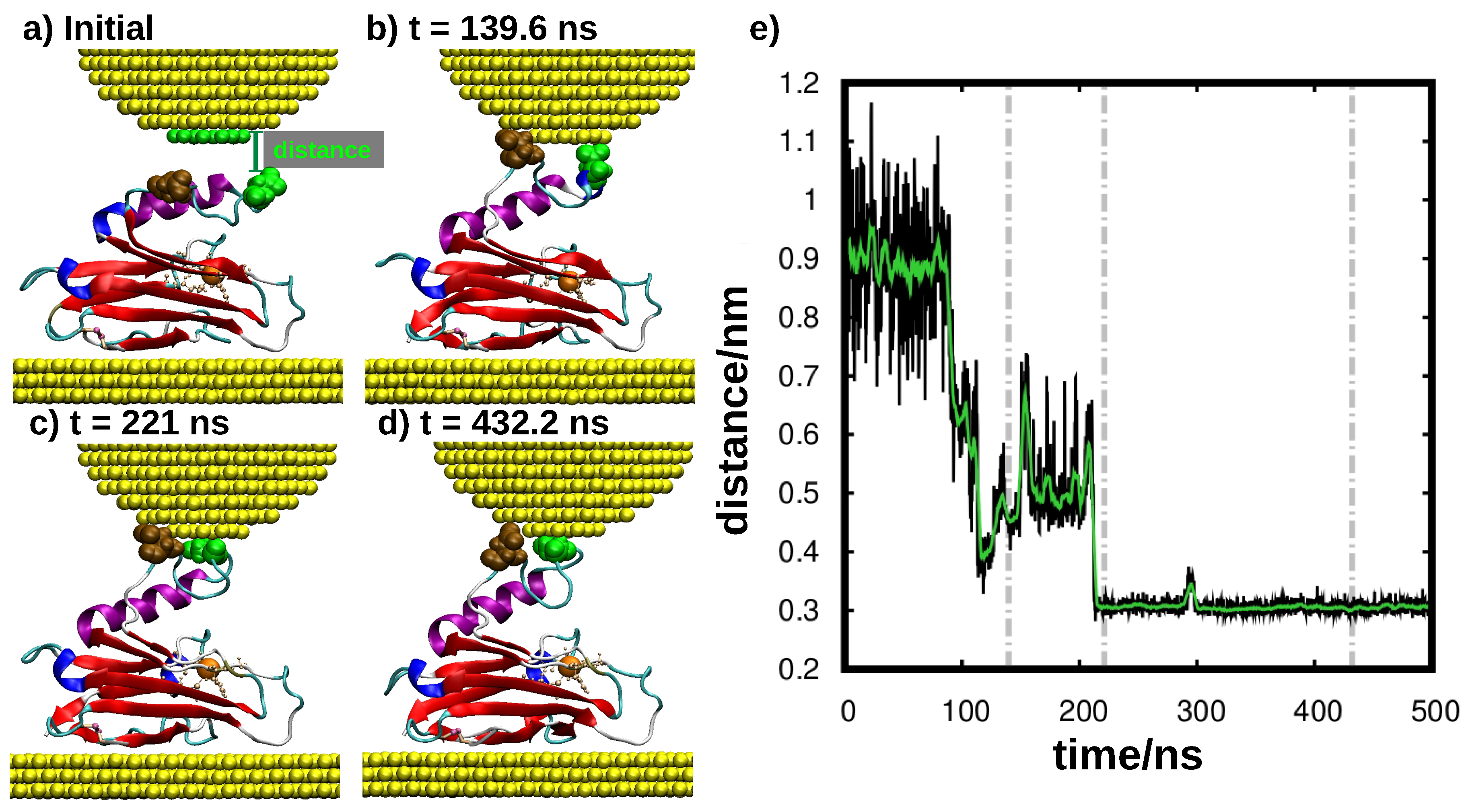
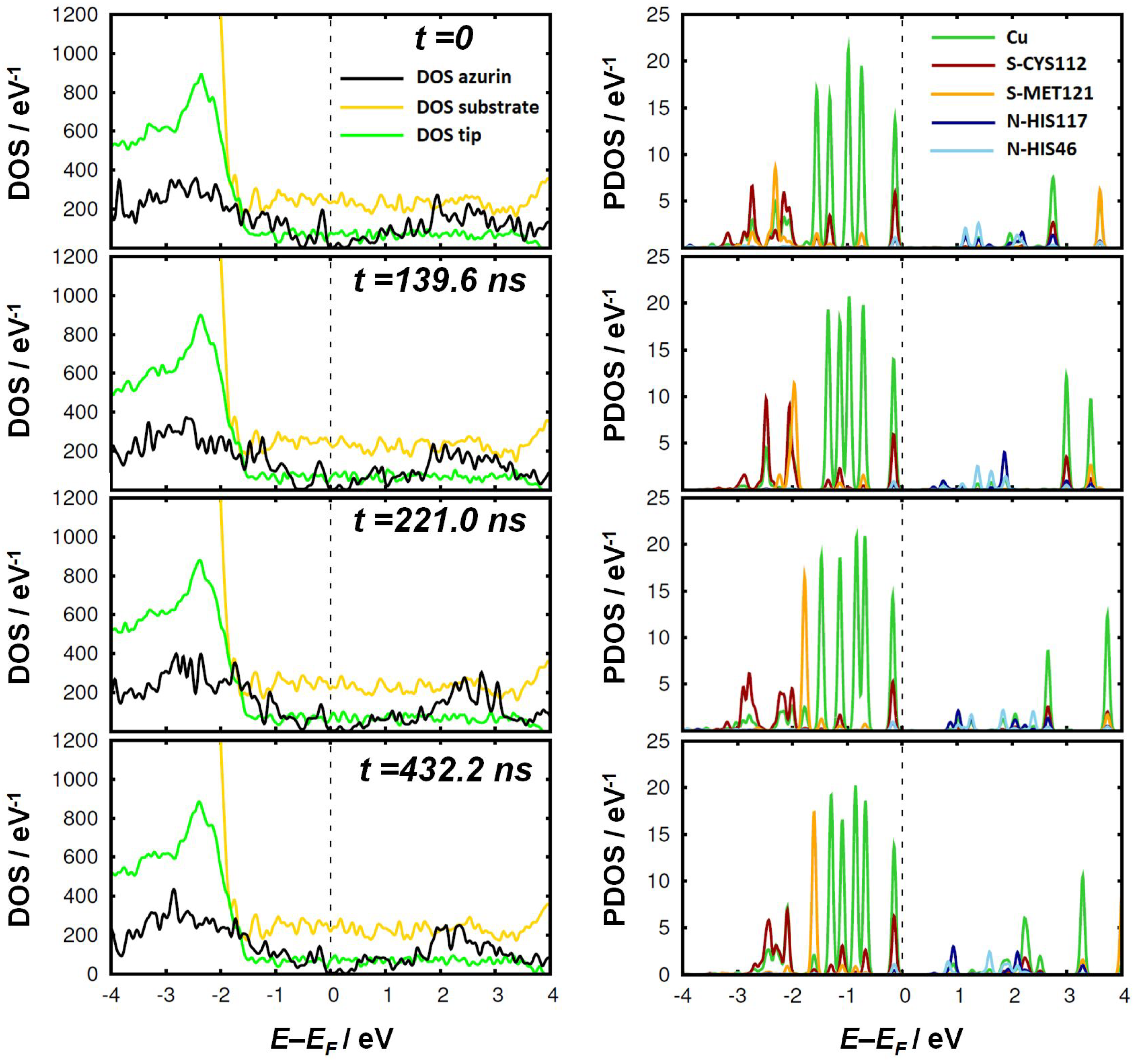
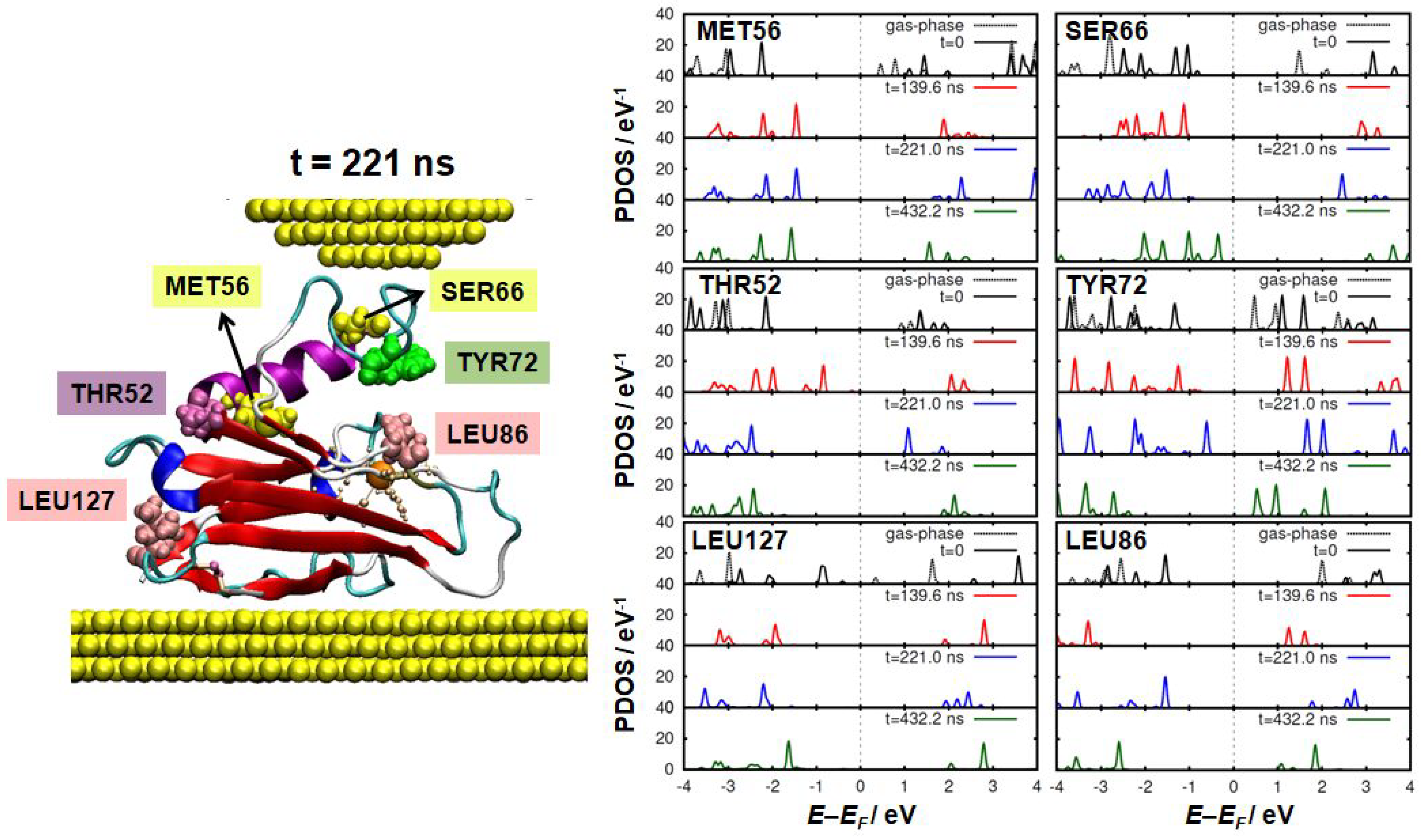
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| STM | Scanning Tunneling Microscopy |
| MD | Molecular Dynamics |
| DFT | Density Functional Theory |
References
- Bostick, C.D.; Mukhopadhyay, S.; Pecht, I.; Sheves, M.; Cahen, D.; Lederman, D. Protein bioelectronics: A review of what we do and do not know. Rep. Prog. Phys. 2018, 81, 026601. [Google Scholar] [CrossRef] [PubMed]
- Ing, N.L.; El-Naggar, M.Y.; Hochbaum, A.I. Going the distance: Long-range conductivity in protein and peptide bioelectronic materials. J. Phys. Chem. B 2018, 122, 10403–10423. [Google Scholar] [CrossRef]
- Amdursky, N.; Marchak, D.; Sepunaru, L.; Pecht, I.; Sheves, M.; Cahen, D. Electronic Transport via Proteins. Adv. Mater. 2014, 26, 7142–7161. [Google Scholar] [CrossRef] [PubMed]
- Artés, J.M.; López-Martínez, M.; Díez-Pérez, I.; Sanz, F.; Gorostiza, P. Conductance Switching in Single Wired Redox Proteins. Small 2014, 10, 2537–2541. [Google Scholar] [CrossRef] [PubMed]
- Solomon, E.I.; Szilagyi, R.K.; DeBeer George, S.; Basumallick, L. Electronic Structures of Metal Sites in Proteins and Models: Contributions to Function in Blue Copper Proteins. Chem. Rev. 2004, 104, 419–458. [Google Scholar] [CrossRef] [PubMed]
- Marshall, N.M.; Garner, D.K.; Wilson, T.D.; Gao, Y.G.; Robinson, H.; Nilges, M.J.; Lu, Y. Rationally tuning the reduction potential of a single cupredoxin beyond the natural range. Nature 2009, 462, 113. [Google Scholar] [CrossRef] [PubMed]
- Lancaster, K.M.; Farver, O.; Wherland, S.; Crane, E.J., III; Richards, J.H.; Pecht, I.; Gray, H.B. Electron Transfer Reactivity of Type Zero Pseudomonas aeruginosa Azurin. J. Am. Chem. Soc. 2011, 133, 4865–4873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lancaster, K.M.; Zaballa, M.E.; Sproules, S.; Sundararajan, M.; DeBeer, S.; Richards, J.H.; Vila, A.J.; Neese, F.; Gray, H.B. Outer-Sphere Contributions to the Electronic Structure of Type Zero Copper Proteins. J. Am. Chem. Soc. 2012, 134, 8241–8253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farver, O.; Marshall, N.M.; Wherland, S.; Lu, Y.; Pecht, I. Designed azurins show lower reorganization free energies for intraprotein electron transfer. Proc. Natl. Acad. Sci. USA 2013, 110, 10536–10540. [Google Scholar] [CrossRef] [Green Version]
- Baldacchini, C.; Bizzarri, A.R.; Cannistraro, S. Electron transfer, conduction and biorecognition properties of the redox metalloprotein Azurin assembled onto inorganic substrates. Eur. Polym. J. 2016, 83, 407–427. [Google Scholar] [CrossRef]
- Romero-Muñiz, C.; Ortega, M.; Vilhena, J.G.; Díez-Pérez, I.; Cuevas, J.C.; Pérez, R.; Zotti, L.A. Ab initio electronic structure calculations of entire blue copper azurins. Phys. Chem. Chem. Phys. 2018, 20, 30392–30402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corni, S.; Rienzo, F.D.; Felice, R.D.; Molinari, E. Role of the electronic properties of azurin active site in the electron-transfer process. Int. J. Quantum Chem. 2005, 102, 328–342. [Google Scholar] [CrossRef]
- Alessandrini, A.; Facci, P. Electron transfer in nanobiodevices. Eur. Polym. J. 2016, 83, 450–466. [Google Scholar] [CrossRef]
- Ruiz, M.P.; Aragonès, A.C.; Camarero, N.; Vilhena, J.G.; Ortega, M.; Zotti, L.A.; Pérez, R.; Cuevas, J.C.; Gorostiza, P.; Díez-Pérez, I. Bioengineering a Single-Protein Junction. J. Am. Chem. Soc. 2017, 139, 15337–15346. [Google Scholar] [CrossRef] [PubMed]
- Fereiro, J.A.; Yu, X.; Pecht, I.; Sheves, M.; Cuevas, J.C.; Cahen, D. Tunneling explains efficient electron transport via protein junctions. Proc. Natl. Acad. Sci. USA 2018, 115, E4577. [Google Scholar] [CrossRef] [PubMed]
- Valianti, S.; Cuevas, J.C.; Skourtis, S.S. Charge-Transport Mechanisms in Azurin-Based Monolayer Junctions. J. Phys. Chem. C 2019, 123, 5907–5922. [Google Scholar] [CrossRef]
- Panda, S.S.; Katz, H.E.; Tovar, J.D. Solid-state electrical applications of protein and peptide based nanomaterials. Chem. Soc. Rev. 2018, 47, 3640–3658. [Google Scholar] [CrossRef] [PubMed]
- Chi, Q.; Farver, O.; Ulstrup, J. Long-range protein electron transfer observed at the single-molecule level: In situ mapping of redox-gated tunneling resonance. Proc. Natl. Acad. Sci. USA 2005, 102, 16203–16208. [Google Scholar] [CrossRef] [PubMed]
- Chi, Q.; Zhang, J.; Andersen, J.E.T.; Ulstrup, J. Ordered Assembly and Controlled Electron Transfer of the Blue Copper Protein Azurin at Gold (111) Single-Crystal Substrates. J. Phys. Chem. B 2001, 105, 4669–4679. [Google Scholar] [CrossRef]
- Haiss, W.; Nichols, R.J.; van Zalinge, H.; Higgins, S.J.; Bethell, D.; Schiffrin, D.J. Measurement of single molecule conductivity using the spontaneous formation of molecular wires. Phys. Chem. Chem. Phys. 2004, 6, 4330–4337. [Google Scholar] [CrossRef]
- Haiss, W.; Wang, C.; Grace, I.; Batsanov, A.S.; Schiffrin, D.J.; Higgins, S.J.; Bryce, M.R.; Lambert, C.J.; Nichols, R.J. Precision control of single-molecule electrical junctions. Nat. Mater. 2006, 5, 995–1002. [Google Scholar] [CrossRef] [PubMed]
- Díez-Pérez, I.; Hihath, J.; Lee, Y.; Yu, L.; Adamska, L.; Kozhushner, M.A.; Oleynik, I.I.; Tao, N. Rectification and stability of a single molecular diode with controlled orientation. Nat. Chem. 2009, 1, 635. [Google Scholar] [CrossRef] [PubMed]
- Aragonès, A.C.; Darwish, N.; Ciampi, S.; Sanz, F.; Gooding, J.J.; Díez-Pérez, I. Single-molecule electrical contacts on silicon electrodes under ambient conditions. Nat. Commun. 2017, 8, 15056. [Google Scholar] [CrossRef] [PubMed]
- Leary, E.; González, M.T.; van der Pol, C.; Bryce, M.R.; Filippone, S.; Martín, N.; Rubio-Bollinger, G.; Agraït, N. Unambiguous One-Molecule Conductance Measurements under Ambient Conditions. Nano Lett. 2011, 11, 2236–2241. [Google Scholar] [CrossRef] [PubMed]
- Aragonès, A.C.; Darwish, N.; Saletra, W.J.; Pérez-García, L.; Sanz, F.; Puigmartí-Luis, J.; Amabilino, D.B.; Díez-Pérez, I. Highly Conductive Single-Molecule Wires with Controlled Orientation by Coordination of Metalloporphyrins. Nano Lett. 2014, 14, 4751–4756. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, J.C.; Scheer, E. Molecular Electronics: An Introduction to Theory and Experiment, 2nd ed.; World Scientific: Singapore, 2017. [Google Scholar]
- Evers, F.; Korytár, R.; Tewari, S.; van Ruitenbeek, J.M. Advances and challenges in single-molecule electron transport. arXiv 2019, arXiv:1906.10449. [Google Scholar]
- Leary, E.; Zotti, L.A.; Miguel, D.; Márquez, I.R.; Palomino-Ruiz, L.; Cuerva, J.M.; Rubio-Bollinger, G.; González, M.T.; Agrait, N. The Role of Oligomeric Gold–Thiolate Units in Single-Molecule Junctions of Thiol-Anchored Molecules. J. Phys. Chem. C 2018, 122, 3211–3218. [Google Scholar] [CrossRef]
- AMBER14. 2014. Available online: http://ambermd.org/ (accessed on 25 August 2019).
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef]
- Grand, S.L.; Götz, A.W.; Walker, R.C. SPFP: Speed without compromise A mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013, 184, 374–380. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van den Bosch, M.; Swart, M.; Snijders, J.G.; Berendsen, H.J.C.; Mark, A.E.; Oostenbrink, C.; van Gunsteren, W.F.; Canters, G.W. Calculation of the Redox Potential of the Protein Azurin and Some Mutants. ChemBioChem 2005, 6, 738–746. [Google Scholar] [CrossRef] [PubMed]
- Paltrinieri, L.; Borsari, M.; Ranieri, A.; Battistuzzi, G.; Corni, S.; Bortolotti, C.A. The Active Site Loop Modulates the Reorganization Energy of Blue Copper Proteins by Controlling the Dynamic Interplay with Solvent. J. Phys. Chem. Lett. 2013, 4, 710–715. [Google Scholar] [CrossRef] [PubMed]
- Beedle, A.E.M.; Lezamiz, A.; Stirnemann, G.; Garcia-Manyes, S. The mechanochemistry of copper reports on the directionality of unfolding in model cupredoxin proteins. Nat. Commun. 2015, 6, 7894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanetti-Polzi, L.; Bortolotti, C.A.; Daidone, I.; Aschi, M.; Amadei, A.; Corni, S. A few key residues determine the high redox potential shift in azurin mutants. Org. Biomol. Chem. 2015, 13, 11003–11013. [Google Scholar] [CrossRef] [PubMed]
- Zanetti-Polzi, L.; Corni, S.; Daidone, I.; Amadei, A. Extending the essential dynamics analysis to investigate molecular properties: Application to the redox potential of proteins. Phys. Chem. Chem. Phys. 2016, 18, 18450–18459. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Nar, H.; Messerschmidt, A.; Huber, R.; van de Kamp, M.; Canters, G.W. Crystal structure analysis of oxidized Pseudomonas aeruginosa azurin at pH 5.5 and pH 9.0: A pH-induced conformational transition involves a peptide bond flip. J. Mol. Biol. 1991, 221, 765–772. [Google Scholar] [CrossRef]
- Gordon, J.C.; Myers, J.B.; Folta, T.; Shoja, V.; Heath, L.S.; Onufriev, A. H++: A server for estimating pKas and adding missing hydrogens to macromolecules. Nucleic Acids Res. 2005, 33, W368–W371. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Heinz, H.; Lin, T.J.; Kishore Mishra, R.; Emami, F.S. Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The INTERFACE Force Field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef]
- Heinz, H.; Ramezani-Dakhel, H. Simulations of inorganic–bioorganic interfaces to discover new materials: Insights, comparisons to experiment, challenges, and opportunities. Chem. Soc. Rev. 2016, 45, 412–448. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Fereiro, J.A.; Kayser, B.; Romero-Muñiz, C.; Vilan, A.; Dolgikh, D.A.; Chertkova, R.V.; Cuevas, J.C.; Zotti, L.A.; Pecht, I.; Sheves, M.; et al. A Solid-State Protein Junction Serves as a Bias-Induced Current Switch. Angew. Chem. Int. Ed. 2019, 58, 11852–11859. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Morrison, I.; Bylander, D.M.; Kleinman, L. Nonlocal Hermitian norm-conserving Vanderbilt pseudopotential. Phys. Rev. B 1993, 47, 6728. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kerker, G.P. Efficient iteration scheme for self-consistent pseudopotential calculations. Phys. Rev. B 1981, 23, 3082–3084. [Google Scholar] [CrossRef]
- Xie, Z.; Bâldea, I.; Frisbie, C.D. Determination of Energy-Level Alignment in Molecular Tunnel Junctions by Transport and Spectroscopy: Self-Consistency for the Case of Oligophenylene Thiols and Dithiols on Ag, Au, and Pt Electrodes. J. Am. Chem. Soc. 2019, 141, 3670–3681. [Google Scholar] [CrossRef]
- Brooke, C.; Vezzoli, A.; Higgins, S.J.; Zotti, L.A.; Palacios, J.J.; Nichols, R.J. Resonant transport and electrostatic effects in single-molecule electrical junctions. Phys. Rev. B 2015, 91, 195438. [Google Scholar] [CrossRef]
- Xie, Z.; Bâldea, I.; Haugstad, G.; Daniel Frisbie, C. Mechanical Deformation Distinguishes Tunneling Pathways in Molecular Junctions. J. Am. Chem. Soc. 2019, 141, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Zotti, L.A.; Kirchner, T.; Cuevas, J.C.; Pauly, F.; Huhn, T.; Scheer, E.; Erbe, A. Revealing the Role of Anchoring Groups in the Electrical Conduction Through Single-Molecule Junctions. Small 2010, 6, 1529–1535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero-Muñiz, C.; Ortega, M.; Vilhena, J.G.; Diéz-Pérez, I.; Cuevas, J.C.; Pérez, R.; Zotti, L.A. Mechanical Deformation and Electronic Structure of a Blue Copper Azurin in a Solid-State Junction. Biomolecules 2019, 9, 506. https://doi.org/10.3390/biom9090506
Romero-Muñiz C, Ortega M, Vilhena JG, Diéz-Pérez I, Cuevas JC, Pérez R, Zotti LA. Mechanical Deformation and Electronic Structure of a Blue Copper Azurin in a Solid-State Junction. Biomolecules. 2019; 9(9):506. https://doi.org/10.3390/biom9090506
Chicago/Turabian StyleRomero-Muñiz, Carlos, María Ortega, J. G. Vilhena, Ismael Diéz-Pérez, Juan Carlos Cuevas, Rubén Pérez, and Linda A. Zotti. 2019. "Mechanical Deformation and Electronic Structure of a Blue Copper Azurin in a Solid-State Junction" Biomolecules 9, no. 9: 506. https://doi.org/10.3390/biom9090506







