Can One Define the Conductance of Amino Acids?
Abstract
1. Introduction
2. Materials and Methods
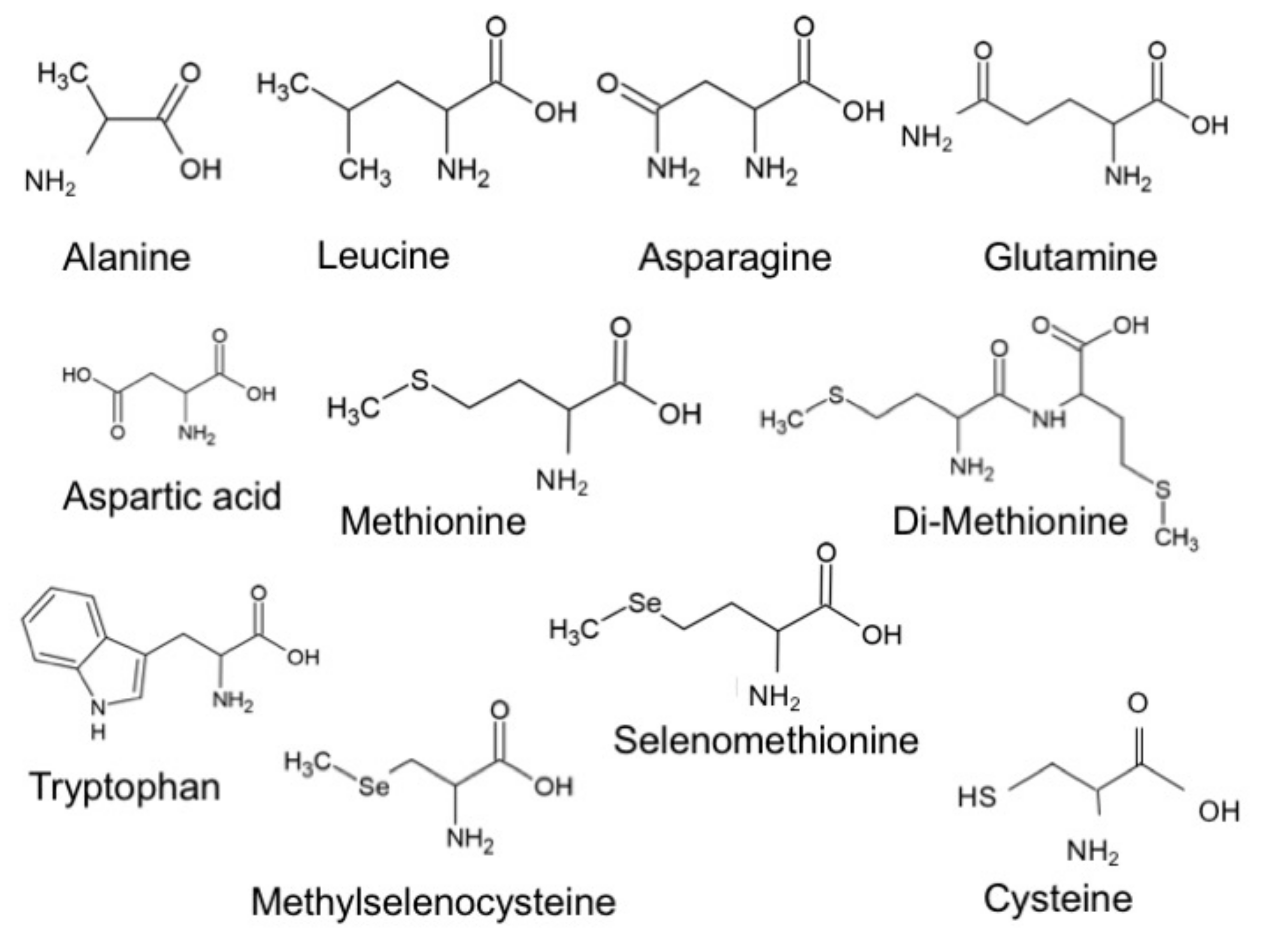
2.1. Experiments

2.2. Theoretical Calculations
3. Results and Discussion
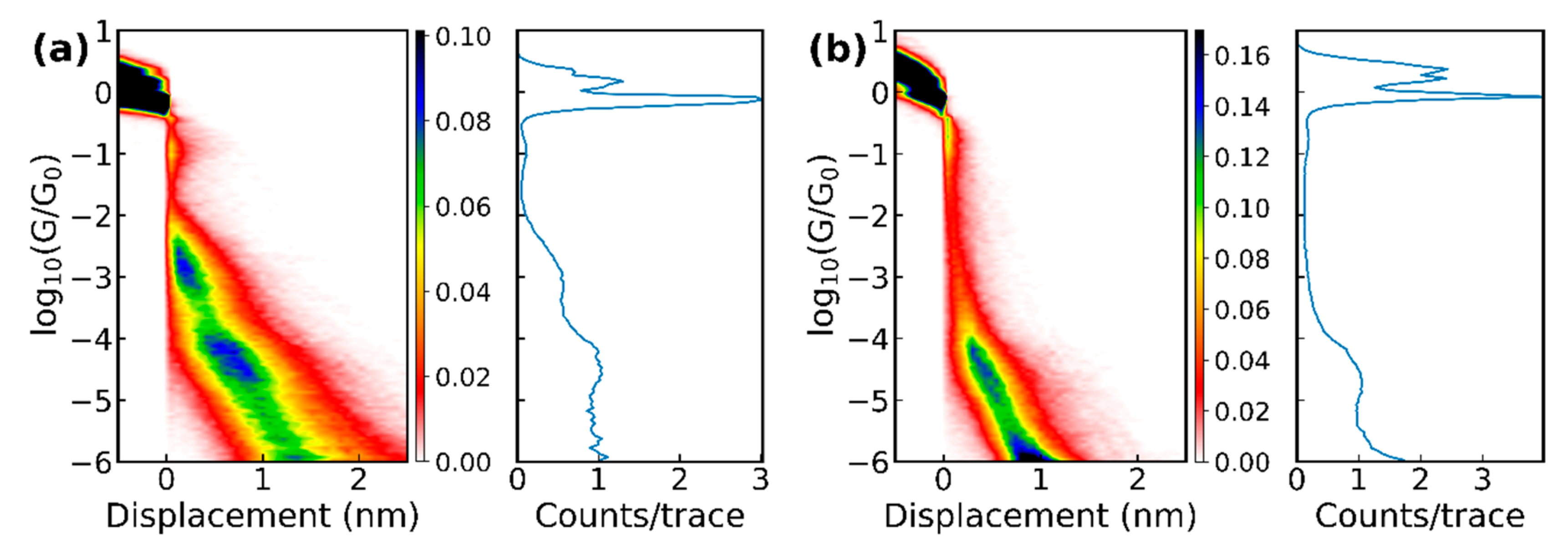
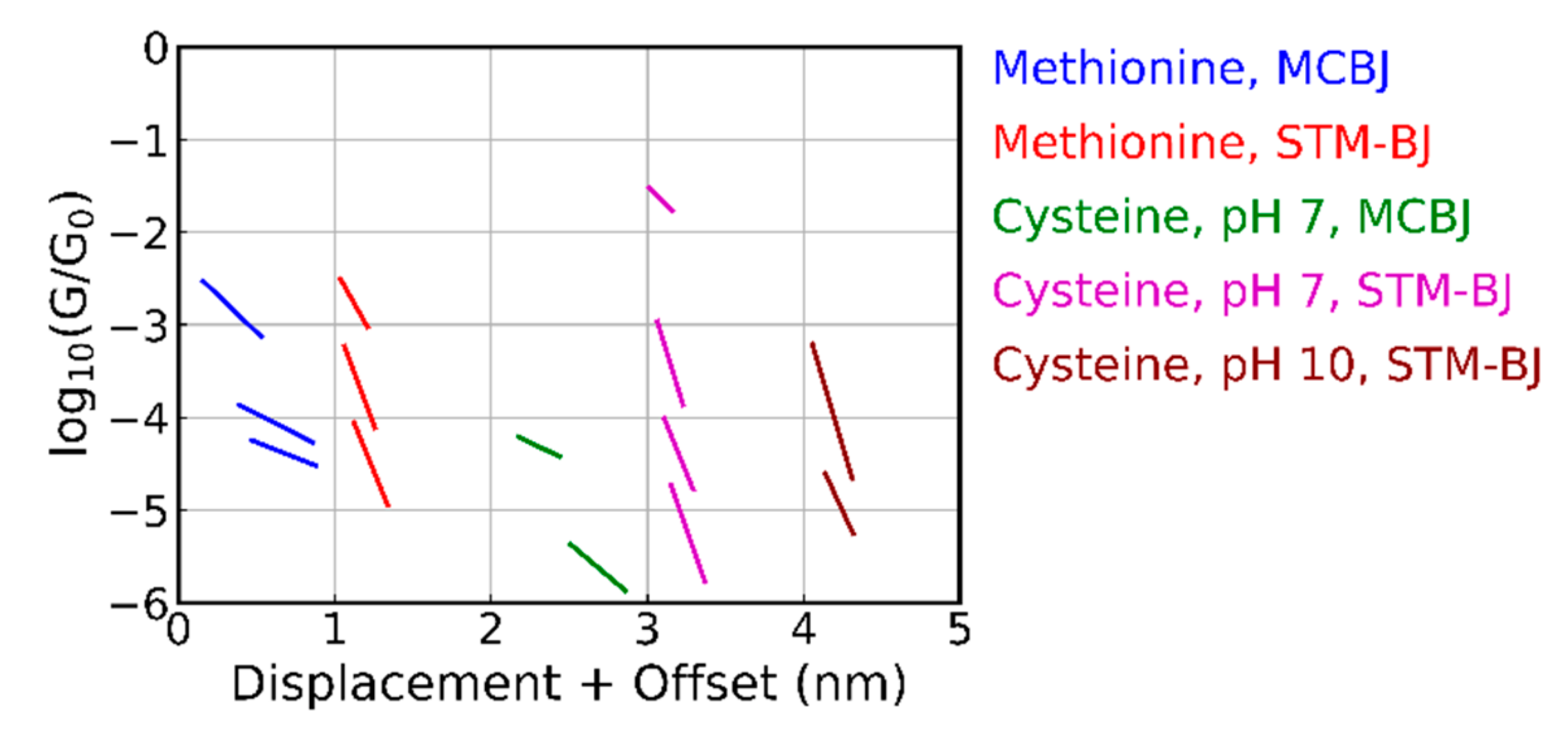
3.1. Experiments
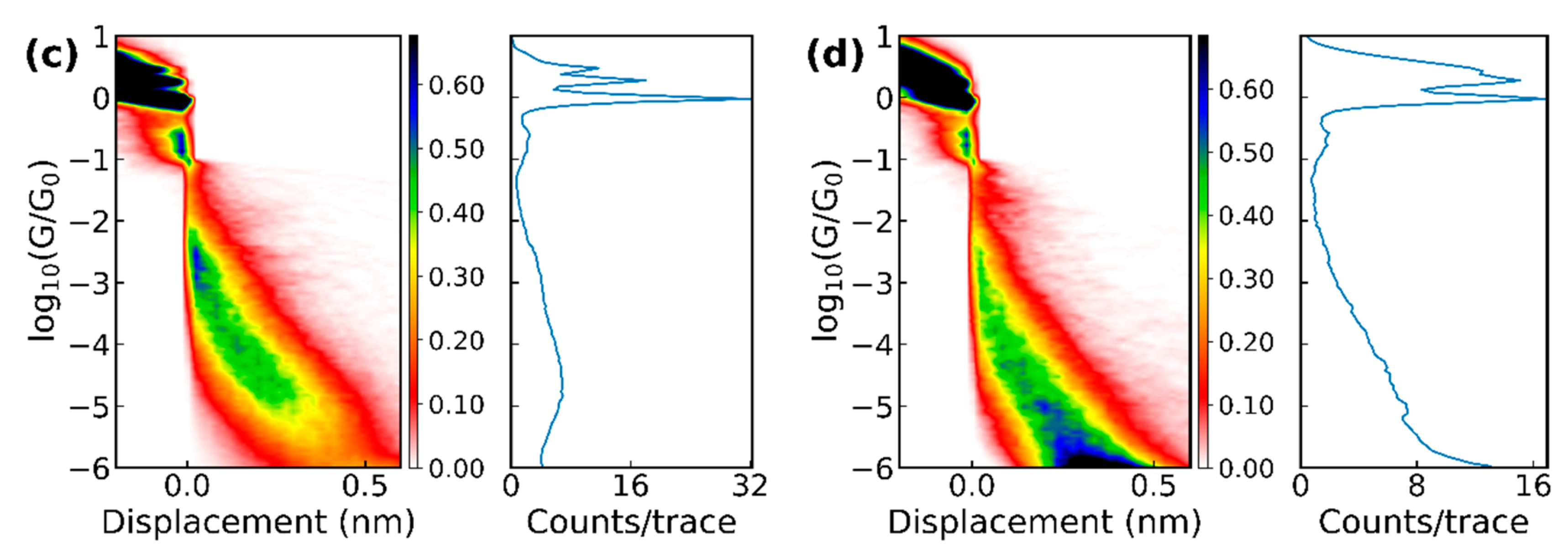
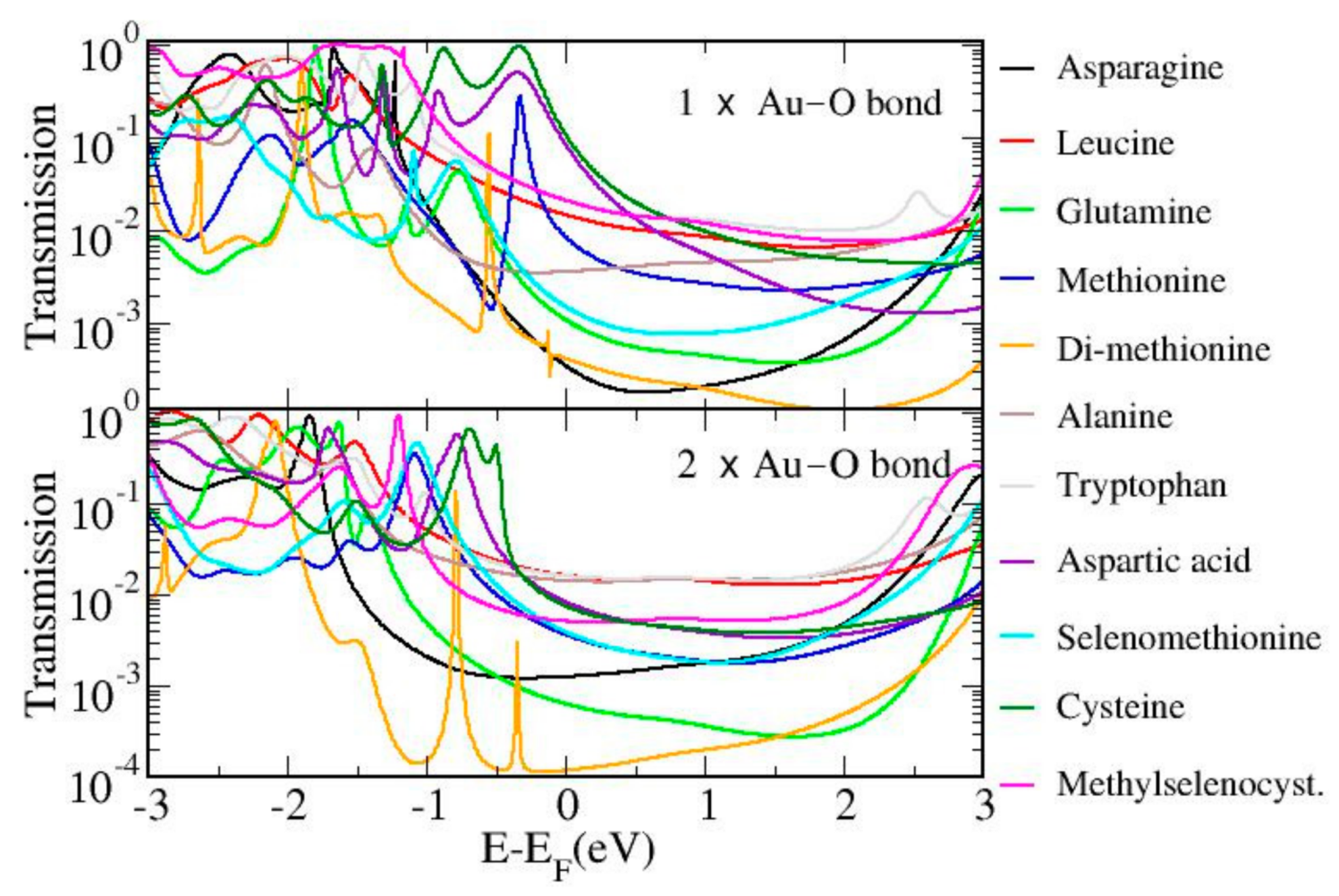
3.2. Theoretical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bostick, C.D.; Mukhopadhyay, S.; Pecht, I.; Sheves, M.; Cahen, D.; Lederman, D. Protein bioelectronics: A review of what we do and do not know. Rep. Prog. Phys. 2018, 81, 026601. [Google Scholar] [CrossRef] [PubMed]
- Ing, N.L.; El-Naggar, M.Y.; Hochbaum, A.I. Going the distance: Long-range conductivity in protein and peptide bioelectronic materials. J. Phys. Chem. B 2018, 122, 10403–10423. [Google Scholar] [CrossRef] [PubMed]
- Beratan, D.N. Why are DNA and protein electron transfer so different? Annu. Rev. Phys. Chem. 2019, 70, 71–97. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, M.P.; Aragones, A.C.; Camarero, N.; Vilhena, J.; Ortega, M.; Zotti, L.A.; Perez, R.; Cuevas, J.C.; Gorostiza, P.; Díez-Pérez, I. Bioengineering a Single-Protein Junction. J. Am. Chem. Soc. 2017, 139, 15337–15346. [Google Scholar] [CrossRef]
- Fereiro, J.A.; Yu, X.; Pecht, I.; Sheves, M.; Cuevas, J.C.; Cahen, D. Tunneling explains efficient electron transport via protein junctions. Proc. Natl. Acad. Sci. USA 2018, 115, E4577–E4583. [Google Scholar] [CrossRef]
- Romero-Muñiz, C.; Ortega, M.; Vilhena, J.; Díez-Pérez, I.; Cuevas, J.C.; Pérez, R.; Zotti, L.A. Ab initio electronic structure calculations of entire blue copper azurins. Phys. Chem. Chem. Phys. 2018, 20, 30392–30402. [Google Scholar] [CrossRef]
- Sepunaru, L.; Refaely-Abramson, S.; Lovrinčić, R.; Gavrilov, Y.; Agrawal, P.; Levy, Y.; Kronik, L.; Pecht, I.; Sheves, M.; Cahen, D. Electronic transport via homopeptides: The role of side chains and secondary structure. J. Am. Chem. Soc. 2015, 137, 9617–9626. [Google Scholar] [CrossRef]
- Zotti, L.A.; Cuevas, J.C. Electron transport through homopeptides: Are they really good conductors? ACS Omega 2018, 3, 3778–3785. [Google Scholar] [CrossRef]
- Schosser, W.M.; Zotti, L.A.; Cuevas, J.C.; Pauly, F. Doping hepta-alanine with tryptophan: A theoretical study of its effect on the electrical conductance of peptide-based single-molecule junctions. J. Chem. Phys. 2019, 150, 174705. [Google Scholar] [CrossRef]
- Hihath, J.; Tao, N. Rapid measurement of single-molecule conductance. Nanotechnology 2008, 19, 265204. [Google Scholar] [CrossRef]
- Li, W.Q.; Huang, B.; Huang, M.L.; Peng, L.L.; Hong, Z.W.; Zheng, J.F.; Chen, W.B.; Li, J.F.; Zhou, X.S. Detecting electron transport of amino acids by using conductance measurement. Sensors 2017, 17, 811. [Google Scholar] [CrossRef]
- Zhao, Y.; Ashcroft, B.; Zhang, P.; Liu, H.; Sen, S.; Song, W.; Im, J.; Gyarfas, B.; Manna, S.; Biswas, S.; et al. Single-molecule spectroscopy of amino acids and peptides by recognition tunnelling. Nat. Nanotechnol. 2014, 9, 466. [Google Scholar] [CrossRef] [PubMed]
- Farimani, A.B.; Heiranian, M.; Aluru, N.R. Identification of amino acids with sensitive nanoporous MoS2: Towards machine learning-based prediction. npj 2D Mater. Appl. 2018, 2, 14. [Google Scholar] [CrossRef]
- Buimaga-Iarinca, L.; Floare, C.G.; Calborean, A.; Turcu, I. DFT study on cysteine adsorption mechanism on Au (111) and Au (110). In AIP Conference Proceedings; AIP: University Park, MD, USA, 2013; Volume 1565, pp. 29–33. [Google Scholar]
- Ganji, M. Density functional theory based treatment of amino acids adsorption on single-walled carbon nanotubes. Diam. Relat. Mater. 2009, 18, 662–668. [Google Scholar] [CrossRef]
- Frau, J.; Glossman-Mitnik, D. Conceptual DFT descriptors of amino acids with potential corrosion inhibition properties calculated with the latest minnesota density functionals. Front. Chem. 2017, 5, 16. [Google Scholar] [CrossRef] [PubMed]
- Ganji, M.D.; Aghaie, H.; Gholami, M.R. Theoretical Study of the Electron Transport through the Cysteine Amino Acid Nanomolecular Wire. Int. J. Nanosci. 2008, 07, 95–102. [Google Scholar] [CrossRef]
- Gehring, P.; Thijssen, J.M.; van der Zant, H.S. Single-molecule quantum-transport phenomena in break junctions. Nat. Rev. Phys. 2019, 1, 381–396. [Google Scholar] [CrossRef]
- Xu, B.; Tao, N.J. Measurement of single-molecule resistance by repeated formation of molecular junctions. Science 2003, 301, 1221–1223. [Google Scholar] [CrossRef]
- Gonzalez, M.T.; Leary, E.; García, R.; Verma, P.; Herranz, M.A.; Rubio-Bollinger, G.; Martín, N.; Agraït, N. Break-junction experiments on acetyl-protected conjugated dithiols under different environmental conditions. J. Phys. Chem. C 2011, 115, 17973–17978. [Google Scholar] [CrossRef]
- Frisenda, R.; Stefani, D.; van der Zant, H.S. Quantum transport through a single conjugated rigid molecule, a mechanical break junction study. Acc. Chem. Res. 2018, 51, 1359–1367. [Google Scholar] [CrossRef]
- Cabosart, D.; El Abbassi, M.; Stefani, D.; Frisenda, R.; Calame, M.; van der Zant, H.S.; Perrin, M.L. A reference-free clustering method for the analysis of molecular break-junction measurements. Appl. Phys. Lett. 2019, 114, 143102. [Google Scholar] [CrossRef]
- Risenda, R. OPE3: A Model System for Single-Molecule Transport. Ph.D. Thesis, TU Delft, Delft, The Netherland, 2016. [Google Scholar]
- Pauly, F.; Viljas, J.K.; Huniar, U.; Häfner, M.; Wohlthat, S.; Bürkle, M.; Cuevas, J.C.; Schön, G. Cluster-based density-functional approach to quantum transport through molecular and atomic contacts. New J. Phys. 2008, 10, 125019. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic structure calculations on workstation computers: The program system turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Zotti, L.A.; Bürkle, M.; Pauly, F.; Lee, W.; Kim, K.; Jeong, W.; Asai, Y.; Reddy, P.; Cuevas, J.C. Heat dissipation and its relation to thermopower in single-molecule junctions. New J. Phys. 2014, 16, 015004. [Google Scholar] [CrossRef]
- Lee, W.; Kim, K.; Jeong, W.; Zotti, L.A.; Pauly, F.; Cuevas, J.C.; Reddy, P. Heat dissipation in atomic-scale junctions. Nature 2013, 498, 209. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Kamenetska, M.; Koentopp, M.; Whalley, A.; Park, Y.; Steigerwald, M.; Nuckolls, C.; Hybertsen, M.; Venkataraman, L. Formation and evolution of single-molecule junctions. Phys. Rev. Lett. 2009, 102, 126803. [Google Scholar] [CrossRef]
- Leary, E.; Zotti, L.A.; Miguel, D.; Márquez, I.R.; Palomino-Ruiz, L.; Cuerva, J.M.; Rubio-Bollinger, G.; González, M.T.; Agrait, N. The Role of Oligomeric Gold–Thiolate Units in Single-Molecule Junctions of Thiol-Anchored Molecules. J. Phys. Chem. C 2018, 122, 3211–3218. [Google Scholar] [CrossRef]
- Martín, S.; Haiss, W.; Higgins, S.; Cea, P.; Lopez, M.C.; Nichols, R.J. A comprehensive study of the single molecule conductance of α, $ømega$-dicarboxylic acid-terminated alkanes. J. Phys. Chem. C 2008, 112, 3941–3948. [Google Scholar] [CrossRef]
- Provorse, M.R.; Aikens, C.M. Binding of carboxylates to gold nanoparticles: A theoretical study of the adsorption of formate on Au 20. Comput. Theor. Chem. 2012, 987, 16–21. [Google Scholar] [CrossRef]
- Han, S.W.; Joo, S.W.; Ha, T.H.; Kim, Y.; Kim, K. Adsorption characteristics of anthraquinone-2-carboxylic acid on gold. J. Phys. Chem. B 2000, 104, 11987–11995. [Google Scholar] [CrossRef]
- Bao, D.L.; Liu, R.; Leng, J.C.; Zuo, X.; Jiao, Y.; Li, Z.L.; Wang, C.K. Theoretical study on mechanical and electron-transport properties of conjugated molecular junctions with carboxylic or methyl sulfide links. Phys. Lett. A 2014, 378, 1290–1295. [Google Scholar] [CrossRef]
- Ahn, S.; Aradhya, S.V.; Klausen, R.S.; Capozzi, B.; Roy, X.; Steigerwald, M.L.; Nuckolls, C.; Venkataraman, L. Electronic transport and mechanical stability of carboxyl linked single-molecule junctions. Phys. Chem. Chem. Phys. 2012, 14, 13841–13845. [Google Scholar] [CrossRef] [PubMed]
- Paik, W.; Han, S.; Shin, W.; Kim, Y. Adsorption of carboxylic acids on gold by anodic reaction. Langmuir 2003, 19, 4211–4216. [Google Scholar] [CrossRef]
- Chen, F.; Li, X.; Hihath, J.; Huang, Z.; Tao, N. Effect of anchoring groups on single-molecule conductance: Comparative study of thiol-, amine-, and carboxylic-acid-terminated molecules. J. Am. Chem. Soc. 2006, 128, 15874–15881. [Google Scholar] [CrossRef]
- Zotti, L.A.; Kirchner, T.; Cuevas, J.C.; Pauly, F.; Huhn, T.; Scheer, E.; Erbe, A. Revealing the role of anchoring groups in the electrical conduction through single-molecule junctions. Small 2010, 6, 1529–1535. [Google Scholar] [CrossRef]
- Kühnle, A.; Linderoth, T.R.; Hammer, B.; Besenbacher, F. Chiral recognition in dimerization of adsorbed cysteine observed by scanning tunnelling microscopy. Nature 2002, 415, 891. [Google Scholar] [CrossRef]
- Strange, M.; Lopez-Acevedo, O.; Häkkinen, H. Oligomeric gold- thiolate units define the properties of the molecular junction between gold and benzene dithiols. J. Phys. Chem. Lett. 2010, 1, 1528–1532. [Google Scholar] [CrossRef]
- Migliore, A. Full-electron calculation of effective electronic couplings and excitation energies of charge transfer states: Application to hole transfer in DNA π-stacks. J. Chem. Phys. 2009, 131, 114113. [Google Scholar] [CrossRef]
- Migliore, A.; Corni, S.; Varsano, D.; Klein, M.L.; di Felice, R. First Principles Effective Electronic Couplings for Hole Transfer in Natural and Size-Expanded DNA. J. Phys. Chem. B 2009, 113, 9402–9415. [Google Scholar] [CrossRef] [PubMed]
- Sit, P.H.L.; Migliore, A.; Ho, M.H.; Klein, M.L. Quantum Mechanical and Quantum Mechanical/Molecular Mechanical Studies of the Iron−Dioxygen Intermediates and Proton Transfer in Superoxide Reductase. J. Chem. Theory Comput. 2010, 6, 2896–2909. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.L.; Gagliardi, L.; Truhlar, D.G. Self-Interaction Error in Density Functional Theory: An Appraisal. J. Phys. Chem. Lett. 2018, 9, 2353–2358. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Pobelov, I.; Wandlowski, T.; Bagrets, A.; Arnold, A.; Evers, F. Charge transport in single Au| alkanedithiol| Au junctions: Coordination geometries and conformational degrees of freedom. J. Am. Chem. Soc. 2008, 130, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, S.; He, J.; Sankey, O.; Hapala, P.; Jelinek, P.; Zhang, P.; Chang, S.; Huang, S. Recognition tunneling. Nanotechnology 2010, 21, 262001. [Google Scholar] [CrossRef] [PubMed]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zotti, L.A.; Bednarz, B.; Hurtado-Gallego, J.; Cabosart, D.; Rubio-Bollinger, G.; Agrait, N.; van der Zant, H.S.J. Can One Define the Conductance of Amino Acids? Biomolecules 2019, 9, 580. https://doi.org/10.3390/biom9100580
Zotti LA, Bednarz B, Hurtado-Gallego J, Cabosart D, Rubio-Bollinger G, Agrait N, van der Zant HSJ. Can One Define the Conductance of Amino Acids? Biomolecules. 2019; 9(10):580. https://doi.org/10.3390/biom9100580
Chicago/Turabian StyleZotti, Linda A., Beatrice Bednarz, Juan Hurtado-Gallego, Damien Cabosart, Gabino Rubio-Bollinger, Nicolas Agrait, and Herre S.J. van der Zant. 2019. "Can One Define the Conductance of Amino Acids?" Biomolecules 9, no. 10: 580. https://doi.org/10.3390/biom9100580
APA StyleZotti, L. A., Bednarz, B., Hurtado-Gallego, J., Cabosart, D., Rubio-Bollinger, G., Agrait, N., & van der Zant, H. S. J. (2019). Can One Define the Conductance of Amino Acids? Biomolecules, 9(10), 580. https://doi.org/10.3390/biom9100580





