Life in Phases: Intra- and Inter- Molecular Phase Transitions in Protein Solutions
Abstract
1. Introduction
2. Intramolecular Phase Transitions of Ordered Proteins
2.1. Brief Description of Major Partially-Folded States of Globular Proteins
2.1.1. Molten Globule
2.1.2. Premolten Globule
2.2. Thermodynamics of the Protein Denaturation. “Wet” and “Dry” Molten Globules
2.3. Kinetics of the “Unfolded Chain ↔ Native State” Transitions
3. Intramolecular Phase Transitions in Disordered Proteins Induced by Interactions with Binding Partners
4. Nucleation in Bulk, on the Interface and on the Impurities
- (1)
- At , and , which, according to conventional transition state theory, means that the time of the first order phase transition (exponentially dependent on the value) is infinitely high near the point of thermodynamic equilibrium of the “new” and “old” macroscopic phases. This is a kinetic origin of hysteresis, overcooled liquids, etc., and, by the way, of the enormous time required for the formation of β-sheets in long polypeptides [144,145]. It is worth mentioning that extremely slow nucleation leads to the formation of single and extremely large compact pieces of the erasing phase.
- (2)
- There is a kind of competition between in bulk and on-surface nucleation of the new phase. At , turns to infinity in proportion to , while turns to infinity in proportion to only , i.e., much more slowly. This means that close to the conditions of phase equilibrium, 3-dimensional (“in bulk”) nucleation becomes kinetically impossible due to the very large value, while the 2-dimensional (“on surface”) nucleation can still avoid kinetic problems, and occurs until also becomes too large.
- (3)
- In contrast, when the phases are far from the equilibrium, that is increases and starts to approach and (or and are small and approach ), the nucleation in bulk should become fast and overcome the on-surface nucleation, because the surface layer is several orders of magnitude smaller than the bulk. It is worth mentioning that fast nucleation leads to the formation of many pieces of the erasing phase that can glue together, forming noncompact, amorphous, or branched aggregates.
- (4)
- If an all-or-none transition occurs in a microscopic body that includes L particles only, the “new” phase can be stable only if the seed of the arising phase is smaller than L, i.e., . This means that the new phase can arise only when its stability exceeds some threshold, i.e., . At the mid-transition point, where both phases have equal stability, and thus , the transition state free energy is , and it includes particles. This means that the time of transition to the new phase (which is as stable as that of old one) scales with L in the way given by Equation (1) for formation of the “native phase” of a protein (a microscopic body!), and that the folding nucleus of the new phase includes nearly 1/3 of the body, i.e., it is not small.
- (5)
- If the new phase is a little more stable than the old one, that is , where , the free energy of the completely formed new phase is < 0, and the transition state free energy of nucleation of this stable phase by is lower than the transition state free energy at the mid-transition point. Such an estimate has been used in [176] to describe the decrease in the protein folding time with the increase in protein stability.
- (6)
- If the new phase is formed around some local “impurity” and interacts with it with the free energy , the free energy of the emerging phase obtains the form (and ), instead of that given by Equations (3) and (4). This correspondingly (by ) decreases the nucleation free energy (as well as ) of the new phase as compared to that given by Equation (5), and does not change the size (as well as ) of the critical nucleus given by Equation (6), but decreases the size (as well as ) of the “seed” relatively to that given by Equation (7).
5. Protein Crystallization, Amorphous Aggregation, and Fibrillation as Intermolecular Phase Transitions
5.1. Protein Crystallization as a Peculiar Case of Phase Separation of Supersaturated Protein Solutions
5.2. Protein Amorphous Aggregation
5.3. Protein Fibrillation
5.3.1. Conformational Prerequisites for Amyloidogenesis
5.3.2. Fibrillogenesis of Globular Proteins Depends on Partial Unfolding
5.3.3. Fibrillogenesis of Extended IDPs Is Driven by Partial Folding
5.3.4. Premolten Globule as a Universal Amyloidogenic Intermediate
5.3.5. Sequential Mechanism of Fibril Formation and Morphological Heterogeneity of Amyloid Fibrils
6. Reincarnation of Liquid–Liquid and Liquid–Gel Phase Transitions: Drivers of the Biogenesis of Membraneless Organelles
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Finkelstein, A.V.; Ptitsyn, O.B. Protein Physics: A Course of Lectures, 2nd ed.; Academic Press, An Imprint of Elsevier Science: Amsterdam, The Netherlands; Boston, MA, USA; Heidelberg, Germany; London, UK; New York, NY, USA; Oxford, UK; Paris, France; San Diego, CA, USA; San Francisco, CA, USA; Singapore; Sydney, Australia; Tokyo, Japan, 2016; p. 354. [Google Scholar]
- Anson, M.L.; Mirsky, A.E. The effect of denaturation on the viscosity of protein systems. J. Gen. Physiol. 1932, 15, 341–350. [Google Scholar] [CrossRef]
- Mirsky, A.E.; Pauling, L. On the structure of native, denatured, and coagulated proteins. Proc. Natl. Acad. Sci. USA 1936, 22, 439–447. [Google Scholar] [CrossRef] [PubMed]
- Neurath, H.; Greenstein, J.P.; Putnam, F.W.; Erickson, J.O. The chemistry of protein denaturation. Chem. Rev. 1944, 34, 157–265. [Google Scholar] [CrossRef]
- Tanford, C. Protein denaturation. Adv. Protein Chem. 1968, 23, 121–282. [Google Scholar] [PubMed]
- Anfinsen, C.B.; Haber, E.; Sela, M.; White, F.H., Jr. The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain. Proc. Natl. Acad. Sci. USA 1961, 47, 1309–1314. [Google Scholar] [CrossRef]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Anfinsen, C.B.; Scheraga, H.A. Experimental and theoretical aspects of protein folding. Adv. Protein Chem. 1975, 29, 205–300. [Google Scholar] [CrossRef]
- Ptitsyn, O.B.; Pain, R.H.; Semisotnov, G.V.; Zerovnik, E.; Razgulyaev, O.I. Evidence for a Molten Globule State as a General Intermediate in Protein Folding. FEBS Lett. 1990, 262, 20–24. [Google Scholar] [CrossRef]
- Ptitsyn, O.B.; Uversky, V.N. The molten globule is a third thermodynamical state of protein molecules. FEBS Lett. 1994, 341, 15–18. [Google Scholar] [CrossRef]
- Uversky, V.N.; Ptitsyn, O.B. “Partly folded” state, a new equilibrium state of protein molecules: Four-state guanidinium chloride-induced unfolding of beta-lactamase at low temperature. Biochemistry 1994, 33, 2782–2791. [Google Scholar] [CrossRef]
- Ptitsyn, O.B.; Bychkova, V.E.; Uversky, V.N. Kinetic and equilibrium folding intermediates. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1995, 348, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Ptitsyn, O.B. Molten globule and protein folding. Adv. Protein Chem. 1995, 47, 83–229. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N.; Ptitsyn, O.B. Further evidence on the equilibrium “pre-molten globule state”: Four-state guanidinium chloride-induced unfolding of carbonic anhydrase B at low temperature. J. Mol. Biol. 1996, 255, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Diversity of equilibrium compact forms of denatured globular proteins. Protein Pept. Lett. 1997, 4, 355–367. [Google Scholar]
- Turoverov, K.K.; Kuznetsova, I.M.; Uversky, V.N. The protein kingdom extended: Ordered and intrinsically disordered proteins, their folding, supramolecular complex formation, and aggregation. Prog. Biophys. Mol. Biol. 2010, 102, 73–84. [Google Scholar] [CrossRef]
- Uversky, V.N. Protein folding revisited. A polypeptide chain at the folding-misfolding-nonfolding cross-roads: Which way to go? Cell. Mol. Life Sci. 2003, 60, 1852–1871. [Google Scholar] [CrossRef]
- Tcherkasskaya, O.; Uversky, V.N. Polymeric aspects of protein folding: A brief overview. Protein Pept. Lett. 2003, 10, 239–245. [Google Scholar] [CrossRef]
- Uversky, V.N. Natively unfolded proteins: A point where biology waits for physics. Protein Sci. 2002, 11, 739–756. [Google Scholar] [CrossRef]
- Uversky, V.N. What does it mean to be natively unfolded? Eur. J. Biochem. 2002, 269, 2–12. [Google Scholar] [CrossRef]
- Tcherkasskaya, O.; Uversky, V.N. Denatured collapsed states in protein folding: Example of apomyoglobin. Proteins 2001, 44, 244–254. [Google Scholar] [CrossRef]
- Ptitsyn, O.B. Stages in the mechanism of self-organization of protein molecules. Dokl. Akad. Nauk SSSR 1973, 210, 1213–1215. [Google Scholar] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.; Henrick, K.; Nakamura, H. Announcing the worldwide Protein Data Bank. Nat. Struct. Biol. 2003, 10, 980. [Google Scholar] [CrossRef] [PubMed]
- DeForte, S.; Uversky, V.N. Resolving the ambiguity: Making sense of intrinsic disorder when PDB structures disagree. Protein Sci. 2016, 25, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Ringe, D.; Petsko, G.A. Study of protein dynamics by X-ray diffraction. Methods Enzymol. 1986, 131, 389–433. [Google Scholar] [CrossRef] [PubMed]
- Radivojac, P.; Obradovic, Z.; Smith, D.K.; Zhu, G.; Vucetic, S.; Brown, C.J.; Lawson, J.D.; Dunker, A.K. Protein flexibility and intrinsic disorder. Protein Sci. 2004, 13, 71–80. [Google Scholar] [CrossRef]
- Le Gall, T.; Romero, P.R.; Cortese, M.S.; Uversky, V.N.; Dunker, A.K. Intrinsic disorder in the Protein Data Bank. J. Biomol. Struct. Dyn. 2007, 24, 325–342. [Google Scholar] [CrossRef]
- Carugo, O.; Djinovic-Carugo, K. Criteria to Extract High-Quality Protein Data Bank Subsets for Structure Users. Methods Mol. Biol. 2016, 1415, 139–152. [Google Scholar] [CrossRef]
- Dunker, A.K.; Obradovic, Z.; Romero, P.; Garner, E.C.; Brown, C.J. Intrinsic protein disorder in complete genomes. Genome Inform. Ser. Workshop Genome Inform. 2000, 11, 161–171. [Google Scholar]
- Uversky, V.N. The mysterious unfoldome: Structureless, underappreciated, yet vital part of any given proteome. J. Biomed. Biotechnol. 2010, 2010, 568068. [Google Scholar] [CrossRef]
- Ward, J.J.; Sodhi, J.S.; McGuffin, L.J.; Buxton, B.F.; Jones, D.T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004, 337, 635–645. [Google Scholar] [CrossRef] [PubMed]
- Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef]
- Uversky, V.N.; Dunker, A.K. Understanding protein non-folding. Biochim. Biophys. Acta 2010, 1804, 1231–1264. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Dunker, A.K.; Uversky, V.N. Orderly order in protein intrinsic disorder distribution: Disorder in 3500 proteomes from viruses and the three domains of life. J. Biomol. Struct. Dyn. 2012, 30, 137–149. [Google Scholar] [CrossRef]
- Peng, Z.; Yan, J.; Fan, X.; Mizianty, M.J.; Xue, B.; Wang, K.; Hu, G.; Uversky, V.N.; Kurgan, L. Exceptionally abundant exceptions: Comprehensive characterization of intrinsic disorder in all domains of life. Cell. Mol. Life Sci. 2015, 72, 137–151. [Google Scholar] [CrossRef]
- Tokuriki, N.; Oldfield, C.J.; Uversky, V.N.; Berezovsky, I.N.; Tawfik, D.S. Do viral proteins possess unique biophysical features? Trends Biochem. Sci. 2009, 34, 53–59. [Google Scholar] [CrossRef]
- Xue, B.; Williams, R.W.; Oldfield, C.J.; Dunker, A.K.; Uversky, V.N. Archaic chaos: Intrinsically disordered proteins in Archaea. BMC Syst. Biol. 2010, 4 (Suppl. 1), S1. [Google Scholar] [CrossRef]
- Tompa, P.; Dosztanyi, Z.; Simon, I. Prevalent structural disorder in E. coli and S. cerevisiae proteomes. J. Proteome Res. 2006, 5, 1996–2000. [Google Scholar] [CrossRef]
- Krasowski, M.D.; Reschly, E.J.; Ekins, S. Intrinsic disorder in nuclear hormone receptors. J. Proteome Res. 2008, 7, 4359–4372. [Google Scholar] [CrossRef]
- Shimizu, K.; Toh, H. Interaction between intrinsically disordered proteins frequently occurs in a human protein-protein interaction network. J. Mol. Biol. 2009, 392, 1253–1265. [Google Scholar] [CrossRef]
- Pentony, M.M.; Jones, D.T. Modularity of intrinsic disorder in the human proteome. Proteins 2010, 78, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P.; Kalmar, L. Power law distribution defines structural disorder as a structural element directly linked with function. J. Mol. Biol. 2010, 403, 346–350. [Google Scholar] [CrossRef] [PubMed]
- Schad, E.; Tompa, P.; Hegyi, H. The relationship between proteome size, structural disorder and organism complexity. Genome Biol. 2011, 12, R120. [Google Scholar] [CrossRef] [PubMed]
- Dyson, H.J. Expanding the proteome: Disordered and alternatively folded proteins. Q. Rev. Biophys. 2011, 44, 467–518. [Google Scholar] [CrossRef] [PubMed]
- Pancsa, R.; Tompa, P. Structural disorder in eukaryotes. PLoS ONE 2012, 7, e34687. [Google Scholar] [CrossRef] [PubMed]
- Midic, U.; Obradovic, Z. Intrinsic disorder in putative protein sequences. Proteome Sci. 2012, 10 (Suppl. 1), S19. [Google Scholar] [CrossRef]
- Hegyi, H.; Tompa, P. Increased structural disorder of proteins encoded on human sex chromosomes. Mol. Biosyst. 2012, 8, 229–236. [Google Scholar] [CrossRef]
- Korneta, I.; Bujnicki, J.M. Intrinsic disorder in the human spliceosomal proteome. PLoS Comput. Biol. 2012, 8, e1002641. [Google Scholar] [CrossRef]
- Kahali, B.; Ghosh, T.C. Disorderness in Escherichia coli proteome: Perception of folding fidelity and protein-protein interactions. J. Biomol. Struct. Dyn. 2013, 31, 472–476. [Google Scholar] [CrossRef]
- Di Domenico, T.; Walsh, I.; Tosatto, S.C. Analysis and consensus of currently available intrinsic protein disorder annotation sources in the MobiDB database. BMC Bioinform. 2013, 14 (Suppl. 7), S3. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Cheng, Y.; Cortese, M.S.; Brown, C.J.; Uversky, V.N.; Dunker, A.K. Comparing and combining predictors of mostly disordered proteins. Biochemistry 2005, 44, 1989–2000. [Google Scholar] [CrossRef] [PubMed]
- Na, I.; Redmon, D.; Kopa, M.; Qin, Y.; Xue, B.; Uversky, V.N. Ordered disorder of the astrocytic dystrophin-associated protein complex in the norm and pathology. PLoS ONE 2013, 8, e73476. [Google Scholar] [CrossRef] [PubMed]
- Wright, P.E.; Dyson, H.J. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar] [CrossRef]
- Dunker, A.K.; Brown, C.J.; Obradovic, Z. Identification and functions of usefully disordered proteins. Adv. Protein Chem. 2002, 62, 25–49. [Google Scholar]
- Dunker, A.K.; Brown, C.J.; Lawson, J.D.; Iakoucheva, L.M.; Obradovic, Z. Intrinsic disorder and protein function. Biochemistry 2002, 41, 6573–6582. [Google Scholar] [CrossRef]
- Dunker, A.K.; Obradovic, Z. The protein trinity--linking function and disorder. Nat. Biotechnol. 2001, 19, 805–806. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Coupling of folding and binding for unstructured proteins. Curr. Opin. Struct. Biol. 2002, 12, 54–60. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005, 6, 197–208. [Google Scholar] [CrossRef]
- Tompa, P. The interplay between structure and function in intrinsically unstructured proteins. FEBS Lett. 2005, 579, 3346–3354. [Google Scholar] [CrossRef]
- Obradovic, Z.; Peng, K.; Vucetic, S.; Radivojac, P.; Brown, C.J.; Dunker, A.K. Predicting intrinsic disorder from amino acid sequence. Proteins 2003, 53, 566–572. [Google Scholar] [CrossRef]
- Uversky, V.N.; Oldfield, C.J.; Dunker, A.K. Showing your ID: Intrinsic disorder as an ID for recognition, regulation and cell signaling. J. Mol. Recognit. 2005, 18, 343–384. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Romero, P.R.; Noutsou, M.; Maurice, M.M.; Rudiger, S.G.; William, A.M., Jr.; Mizianty, M.J.; Kurgan, L.; Uversky, V.N.; Dunker, A.K. Stochastic machines as a colocalization mechanism for scaffold protein function. FEBS Lett. 2013, 587, 1587–1591. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Qiu, W.J.; Chan, S.C.; Han, J.; He, X.; Lin, S.C. Casein kinase I and casein kinase II differentially regulate axin function in Wnt and JNK pathways. J. Biol. Chem. 2002, 277, 17706–17712. [Google Scholar] [CrossRef] [PubMed]
- Dajani, R.; Fraser, E.; Roe, S.M.; Yeo, M.; Good, V.M.; Thompson, V.; Dale, T.C.; Pearl, L.H. Structural basis for recruitment of glycogen synthase kinase 3beta to the axin-APC scaffold complex. Embo J. 2003, 22, 494–501. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Takemaru, K.; Liu, J.; Berndt, J.D.; Zheng, J.J.; Moon, R.T.; Xu, W. Crystal structure of a full-length beta-catenin. Structure 2008, 16, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Wright, P.E.; Dyson, H.J. Linking folding and binding. Curr. Opin. Struct. Biol. 2009, 19, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Multitude of binding modes attainable by intrinsically disordered proteins: A portrait gallery of disorder-based complexes. Chem. Soc. Rev. 2011, 40, 1623–1634. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsic disorder-based protein interactions and their modulators. Curr. Pharm. Des. 2013, 19, 4191–4213. [Google Scholar] [CrossRef]
- Janin, J.; Sternberg, M.J. Protein flexibility, not disorder, is intrinsic to molecular recognition. F1000 Biol. Rep. 2013, 5, 2. [Google Scholar] [CrossRef]
- Jakob, U.; Kriwacki, R.; Uversky, V.N. Conditionally and transiently disordered proteins: Awakening cryptic disorder to regulate protein function. Chem. Rev. 2014, 114, 6779–6805. [Google Scholar] [CrossRef]
- Mitrea, D.M.; Kriwacki, R.W. Regulated unfolding of proteins in signaling. FEBS Lett. 2013, 587, 1081–1088. [Google Scholar] [CrossRef] [PubMed]
- Bardwell, J.C.; Jakob, U. Conditional disorder in chaperone action. Trends Biochem. Sci. 2012, 37, 517–525. [Google Scholar] [CrossRef] [PubMed]
- Creamer, T.P. Transien disorder: Calcineurin as an example. Intrinsically Disord. Proteins 2013, 1, e26412. [Google Scholar] [CrossRef]
- Merrill, A.R.; Cohen, F.S.; Cramer, W.A. On the nature of the structural change of the colicin E1 channel peptide necessary for its translocation-competent state. Biochemistry 1990, 29, 5829–5836. [Google Scholar] [CrossRef]
- Polverino de Laureto, P.; De Filippis, V.; Di Bello, M.; Zambonin, M.; Fontana, A. Probing the molten globule state of alpha-lactalbumin by limited proteolysis. Biochemistry 1995, 34, 12596–12604. [Google Scholar] [CrossRef]
- De Filippis, V.; de Laureto, P.P.; Toniutti, N.; Fontana, A. Acid-induced molten globule state of a fully active mutant of human interleukin-6. Biochemistry 1996, 35, 11503–11511. [Google Scholar] [CrossRef]
- Polverino de Laureto, P.; Frare, E.; Gottardo, R.; Van Dael, H.; Fontana, A. Partly folded states of members of the lysozyme/lactalbumin superfamily: A comparative study by circular dichroism spectroscopy and limited proteolysis. Protein Sci. 2002, 11, 2932–2946. [Google Scholar] [CrossRef]
- Fontana, A.; de Laureto, P.P.; Spolaore, B.; Frare, E.; Picotti, P.; Zambonin, M. Probing protein structure by limited proteolysis. Acta Biochim. Pol. 2004, 51, 299–321. [Google Scholar] [CrossRef]
- Campioni, S.; Mossuto, M.F.; Torrassa, S.; Calloni, G.; de Laureto, P.P.; Relini, A.; Fontana, A.; Chiti, F. Conformational properties of the aggregation precursor state of HypF-N. J. Mol. Biol. 2008, 379, 554–567. [Google Scholar] [CrossRef]
- Hegyi, H.; Tompa, P. Intrinsically disordered proteins display no preference for chaperone binding in vivo. PLoS Comput. Biol. 2008, 4, e1000017. [Google Scholar] [CrossRef]
- Galea, C.A.; Pagala, V.R.; Obenauer, J.C.; Park, C.G.; Slaughter, C.A.; Kriwacki, R.W. Proteomic studies of the intrinsically unstructured mammalian proteome. J. Proteome Res. 2006, 5, 2839–2848. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P. Intrinsically unstructured proteins. Trends Biochem. Sci. 2002, 27, 527–533. [Google Scholar] [CrossRef]
- Uversky, V.N. Biophysical Methods to Investigate Intrinsically Disordered Proteins: Avoiding an “Elephant and Blind Men” Situation. Adv. Exp. Med. Biol. 2015, 870, 215–260. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N.; Dunker, A.K. Multiparametric analysis of intrinsically disordered proteins: Looking at intrinsic disorder through compound eyes. Anal. Chem. 2012, 84, 2096–2104. [Google Scholar] [CrossRef] [PubMed]
- Receveur-Brechot, V.; Bourhis, J.M.; Uversky, V.N.; Canard, B.; Longhi, S. Assessing protein disorder and induced folding. Proteins 2006, 62, 24–45. [Google Scholar] [CrossRef] [PubMed]
- Dunker, A.K.; Cortese, M.S.; Romero, P.; Iakoucheva, L.M.; Uversky, V.N. Flexible nets: The roles of intrinsic disorder in protein interaction networks. FEBS J. 2005, 272, 5129–5148. [Google Scholar] [CrossRef]
- Dunker, A.K.; Silman, I.; Uversky, V.N.; Sussman, J.L. Function and structure of inherently disordered proteins. Curr. Opin. Struct. Biol. 2008, 18, 756–764. [Google Scholar] [CrossRef]
- Cortese, M.S.; Uversky, V.N.; Dunker, A.K. Intrinsic disorder in scaffold proteins: Getting more from less. Prog. Biophys. Mol. Biol. 2008, 98, 85–106. [Google Scholar] [CrossRef]
- Tompa, P.; Prilusky, J.; Silman, I.; Sussman, J.L. Structural disorder serves as a weak signal for intracellular protein degradation. Proteins 2008, 71, 903–909. [Google Scholar] [CrossRef]
- Suskiewicz, M.J.; Sussman, J.L.; Silman, I.; Shaul, Y. Context-dependent resistance to proteolysis of intrinsically disordered proteins. Protein Sci. 2011, 20, 1285–1297. [Google Scholar] [CrossRef]
- Gsponer, J.; Futschik, M.E.; Teichmann, S.A.; Babu, M.M. Tight regulation of unstructured proteins: From transcript synthesis to protein degradation. Science 2008, 322, 1365–1368. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N.; Dunker, A.K. Biochemistry. Controlled chaos. Science 2008, 322, 1340–1341. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Vucetic, S.; Iakoucheva, L.M.; Oldfield, C.J.; Dunker, A.K.; Obradovic, Z.; Uversky, V.N. Functional anthology of intrinsic disorder. 3. Ligands, post-translational modifications, and diseases associated with intrinsically disordered proteins. J. Proteome Res. 2007; 6, 1917–1932. [Google Scholar] [CrossRef]
- Iakoucheva, L.M.; Radivojac, P.; Brown, C.J.; O’Connor, T.R.; Sikes, J.G.; Obradovic, Z.; Dunker, A.K. The importance of intrinsic disorder for protein phosphorylation. Nucleic Acids Res. 2004, 32, 1037–1049. [Google Scholar] [CrossRef]
- Daily, K.M.; Radivojac, P.; Dunker, A.K. Intrinsic disorder and protein modifications: Building an SVM predictor for methylation. In Proceedings of the IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology, La Jolla, CA, USA, 15 November 2005. [Google Scholar] [CrossRef]
- Radivojac, P.; Vacic, V.; Haynes, C.; Cocklin, R.R.; Mohan, A.; Heyen, J.W.; Goebl, M.G.; Iakoucheva, L.M. Identification, analysis, and prediction of protein ubiquitination sites. Proteins 2010, 78, 365–380. [Google Scholar] [CrossRef]
- Reddy, K.D.; Malipeddi, J.; DeForte, S.; Pejaver, V.; Radivojac, P.; Uversky, V.N.; Deschenes, R.J. Physicochemical sequence characteristics that influence S-palmitoylation propensity. J. Biomol. Struct. Dyn. 2017, 35, 2337–2350. [Google Scholar] [CrossRef]
- Pejaver, V.; Hsu, W.L.; Xin, F.; Dunker, A.K.; Uversky, V.N.; Radivojac, P. The structural and functional signatures of proteins that undergo multiple events of post-translational modification. Protein Sci. 2014, 23, 1077–1093. [Google Scholar] [CrossRef]
- Ge, X.; Conley, A.J.; Brandle, J.E.; Truant, R.; Filipe, C.D. In vivo formation of protein based aqueous microcompartments. J. Am. Chem. Soc. 2009, 131, 9094–9099. [Google Scholar] [CrossRef]
- Privalov, P.L.; Khechinashvili, N.N. A thermodynamic approach to the problem of stabilization of globular protein structure: A calorimetric study. J. Mol. Biol. 1974, 86, 665–684. [Google Scholar] [CrossRef]
- Privalov, P.L. Stability of proteins: Small globular proteins. Adv. Protein Chem. 1979, 33, 167–241. [Google Scholar] [CrossRef]
- Ohgushi, M.; Wada, A. Liquid-like state of side chains at the intermediate stage of protein denaturation. Adv. Biophys. 1984, 18, 75–90. [Google Scholar] [CrossRef]
- Kuwajima, K. The molten globule state as a clue for understanding the folding and cooperativity of globular-protein structure. Proteins 1989, 6, 87–103. [Google Scholar] [CrossRef] [PubMed]
- Goto, Y.; Calciano, L.J.; Fink, A.L. Acid-induced folding of proteins. Proc. Natl. Acad. Sci. USA 1990, 87, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Christensen, H.; Pain, R.H. Molten globule intermediates and protein folding. Eur. Biophys. J. 1991, 19, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Haynie, D.T.; Freire, E. Structural energetics of the molten globule state. Proteins 1993, 16, 115–140. [Google Scholar] [CrossRef] [PubMed]
- Dobson, C.M. Protein folding. Solid evidence for molten globules. Curr. Biol. 1994, 4, 636–640. [Google Scholar] [CrossRef]
- Fink, A.L.; Calciano, L.J.; Goto, Y.; Kurotsu, T.; Palleros, D.R. Classification of acid denaturation of proteins: Intermediates and unfolded states. Biochemistry 1994, 33, 12504–12511. [Google Scholar] [CrossRef]
- Ptitsyn, O.B. Structures of folding intermediates. Curr. Opin. Struct. Biol. 1995, 5, 74–78. [Google Scholar] [CrossRef]
- Creighton, T.E. How important is the molten globule for correct protein folding? Trends Biochem. Sci. 1997, 22, 6–10. [Google Scholar] [CrossRef]
- Arai, M.; Kuwajima, K. Role of the molten globule state in protein folding. Adv. Protein Chem. 2000, 53, 209–282. [Google Scholar]
- Englander, S.W. Protein folding intermediates and pathways studied by hydrogen exchange. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 213–238. [Google Scholar] [CrossRef]
- Redfield, C. Using nuclear magnetic resonance spectroscopy to study molten globule states of proteins. Methods 2004, 34, 121–132. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, R.L.; Rose, G.D. Molten globules, entropy-driven conformational change and protein folding. Curr. Opin. Struct. Biol. 2013, 23, 4–10. [Google Scholar] [CrossRef] [PubMed]
- Bychkova, V.E.; Semisotnov, G.V.; Balobanov, V.A.; Finkelstein, A.V. The Molten Globule Concept: 45 Years Later. Biochemistry 2018, 83, S33–S47. [Google Scholar] [CrossRef] [PubMed]
- Judy, E.; Kishore, N. A look back at the molten globule state of proteins: Thermodynamic aspects. Biophys. Rev. 2019, 11, 365–375. [Google Scholar] [CrossRef]
- Vassilenko, K.S.; Uversky, V.N. Native-like secondary structure of molten globules. Biochim. Biophys. Acta 2002, 1594, 168–177. [Google Scholar] [CrossRef]
- Uversky, V.N. Use of fast protein size-exclusion liquid chromatography to study the unfolding of proteins which denature through the molten globule. Biochemistry 1993, 32, 13288–13298. [Google Scholar] [CrossRef]
- Eliezer, D.; Chiba, K.; Tsuruta, H.; Doniach, S.; Hodgson, K.O.; Kihara, H. Evidence of an Associative Intermediate on the Myoglobin Refolding Pathway. Biophys. J. 1993, 65, 912–917. [Google Scholar] [CrossRef][Green Version]
- Kataoka, M.; Hagihara, Y.; Mihara, K.; Goto, Y. Molten Globule of Cytochrome-C Studied by Small-Angle X-Ray-Scattering. J. Mol. Biol. 1993, 229, 591–596. [Google Scholar] [CrossRef]
- Semisotnov, G.V.; Kihara, H.; Kotova, N.V.; Kimura, K.; Amemiya, Y.; Wakabayashi, K.; Serdyuk, I.N.; Timchenko, A.A.; Chiba, K.; Nikaido, K.; et al. Protein globularization during folding. A study by synchrotron small-angle X-ray scattering. J. Mol. Biol. 1996, 262, 559–574. [Google Scholar] [CrossRef]
- Kataoka, M.; Kuwajima, K.; Tokunaga, F.; Goto, Y. Structural characterization of the molten globule of alpha-lactalbumin by solution X-ray scattering. Protein Sci. 1997, 6, 422–430. [Google Scholar] [CrossRef]
- Uversky, V.N.; Karnoup, A.S.; Segel, D.J.; Seshadri, S.; Doniach, S.; Fink, A.L. Anion-induced folding of Staphylococcal nuclease: Characterization of multiple equilibrium partially folded intermediates. J. Mol. Biol. 1998, 278, 879–894. [Google Scholar] [CrossRef] [PubMed]
- Baum, J.; Dobson, C.M.; Evans, P.A.; Hanley, C. Characterization of a Partly Folded Protein by Nmr Methods-Studies on the Molten Globule State of Guinea-Pig Alpha-Lactalbumin. Biochemistry 1989, 28, 7–13. [Google Scholar] [CrossRef] [PubMed]
- Bushnell, G.W.; Louie, G.V.; Brayer, G.D. High-resolution three-dimensional structure of horse heart cytochrome c. J. Mol. Biol. 1990, 214, 585–595. [Google Scholar] [CrossRef]
- Jeng, M.F.; Englander, S.W.; Elove, G.A.; Wand, A.J.; Roder, H. Structural description of acid-denatured cytochrome c by hydrogen exchange and 2D NMR. Biochemistry 1990, 29, 10433–10437. [Google Scholar] [CrossRef] [PubMed]
- Chyan, C.L.; Wormald, C.; Dobson, C.M.; Evans, P.A.; Baum, J. Structure and stability of the molten globule state of guinea-pig alpha-lactalbumin: A hydrogen exchange study. Biochemistry 1993, 32, 5681–5691. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.C.; Laub, P.B.; Elove, G.A.; Carey, J.; Roder, H. A noncovalent peptide complex as a model for an early folding intermediate of cytochrome c. Biochemistry 1993, 32, 10271–10276. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, J.R.; Shortle, D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. II. Distance restraints from paramagnetic relaxation and calculation of an ensemble of structures. J. Mol. Biol. 1997, 268, 170–184. [Google Scholar] [CrossRef]
- Gillespie, J.R.; Shortle, D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. I. Paramagnetic relaxation enhancement by nitroxide spin labels. J. Mol. Biol. 1997, 268, 158–169. [Google Scholar] [CrossRef]
- Eliezer, D.; Yao, J.; Dyson, H.J.; Wright, P.E. Structural and dynamic characterization of partially folded states of apomyoglobin and implications for protein folding. Nat. Struct. Biol. 1998, 5, 148–155. [Google Scholar] [CrossRef]
- Bose, H.S.; Whittal, R.M.; Baldwin, M.A.; Miller, W.L. The active form of the steroidogenic acute regulatory protein, StAR, appears to be a molten globule. Proc. Natl. Acad. Sci. USA 1999, 96, 7250–7255. [Google Scholar] [CrossRef]
- van Mierlo, C.P.; Steensma, E. Protein folding and stability investigated by fluorescence, circular dichroism (CD), and nuclear magnetic resonance (NMR) spectroscopy: The flavodoxin story. J. Biotechnol. 2000, 79, 281–298. [Google Scholar] [CrossRef]
- Bracken, C. NMR spin relaxation methods for characterization of disorder and folding in proteins. J. Mol. Graph. Model. 2001, 19, 3–12. [Google Scholar] [CrossRef]
- Ikeguchi, M. Transient non-native helix formation during the folding of beta-lactoglobulin. Biomolecules 2014, 4, 202–216. [Google Scholar] [CrossRef] [PubMed]
- Ray, S.S.; Singh, S.K.; Balaram, P. An electrospray ionization mass spectrometry investigation of 1-anilino-8-naphthalene-sulfonate (ANS) binding to proteins. J. Am. Soc. Mass Spectrom. 2001, 12, 428–438. [Google Scholar] [CrossRef]
- Uversky, V.N.; Winter, S.; Lober, G. Use of fluorescence decay times of 8-ANS-protein complexes to study the conformational transitions in proteins which unfold through the molten globule state. Biophys. Chem. 1996, 60, 79–88. [Google Scholar] [CrossRef]
- Shi, L.; Palleros, D.R.; Fink, A.L. Protein conformational changes induced by 1,1’-bis(4-anilino-5-naphthalenesulfonic acid): Preferential binding to the molten globule of DnaK. Biochemistry 1994, 33, 7536–7546. [Google Scholar] [CrossRef]
- Semisotnov, G.V.; Rodionova, N.A.; Razgulyaev, O.I.; Uversky, V.N.; Gripas, A.F.; Gilmanshin, R.I. Study of the “molten globule” intermediate state in protein folding by a hydrophobic fluorescent probe. Biopolymers 1991, 31, 119–128. [Google Scholar] [CrossRef]
- Uversky, V.N.; Ptitsyn, O.B. All-or-none solvent-induced transitions between native, molten globule and unfolded states in globular proteins. Fold. Des. 1996, 1, 117–122. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Collapse and intramolecular phase layering in a polymer in which each unit may be in two states. Biophysics 1984, 29, 621–626. [Google Scholar]
- Adonts, V.G.; Birshtein, T.M.; Elyashevich, A.M.; Skvortsov, A.M. Intramolecular conformational transitions “random coil-helix-folded structure” in polypeptides. Biopolymers 1976, 15, 1037–1059. [Google Scholar] [CrossRef]
- Finkelstein, A.V. Kinetics of antiparallel beta-structure formation. Bioorganicheskaya Khimiya 1978, 4, 340–344. [Google Scholar]
- Finkelstein, A.V. Rate of beta-structure formation in polypeptides. Proteins 1991, 9, 23–27. [Google Scholar] [CrossRef] [PubMed]
- Gil’manshin, R.I.; Dolgikh, D.A.; Ptitsyn, O.B.; Finkel’shtein, A.V.; Shakhnovich, E.I. Protein globule without the unique three-dimensional structure: Experimental data for alpha-lactalbumins and general model. Biofizika 1982, 27, 1005–1016. [Google Scholar] [PubMed]
- Dolgikh, D.A.; Gilmanshin, R.I.; Brazhnikov, E.V.; Bychkova, V.E.; Semisotnov, G.V.; Venyaminov, S.; Ptitsyn, O.B. Alpha-Lactalbumin: Compact state with fluctuating tertiary structure? FEBS Lett. 1981, 136, 311–315. [Google Scholar] [CrossRef]
- Kayaman, N.; Guerel, E.E.; Baysal, B.M.; ve Karasz, F. Kinetics of coil-globule collapse in poly(methyl methacrylate) in dilute solutions below theta temperatures. Macromolecules 1999, 32, 8399–8403. [Google Scholar] [CrossRef]
- Podewitz, M.; Wang, Y.; Quoika, P.K.; Loeffler, J.R.; Schauperl, M.; Liedl, K.R. Coil-Globule Transition Thermodynamics of Poly(N-isopropylacrylamide). J. Phys. Chem. B 2019, 123, 8838–8847. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; American Institute of Physics: New York, NY, USA, 1994. [Google Scholar]
- Shakhnovich, E.I.; Finkel’shtein, A.V. The theory of cooperative transitions in protein globules. Dokl. Akad. Nauk SSSR 1982, 267, 1247–1250. [Google Scholar]
- Finkelstein, A.V.; Shakhnovich, E.I. Theory of cooperative transitions in protein molecules. II. Phase diagram for a protein molecule in solution. Biopolymers 1989, 28, 1681–1694. [Google Scholar] [CrossRef]
- Shakhnovich, E.I.; Finkelstein, A.V. Theory of cooperative transitions in protein molecules. I. Why denaturation of globular protein is a first-order phase transition. Biopolymers 1989, 28, 1667–1680. [Google Scholar] [CrossRef]
- Schulz, G.E.; Schirmer, R.H. Principles of Protein Structure, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kharakoz, D.P.; Bychkova, V.E. Molten globule of human alpha-lactalbumin: Hydration, density, and compressibility of the interior. Biochemistry 1997, 36, 1882–1890. [Google Scholar] [CrossRef]
- Jha, S.K.; Udgaonkar, J.B. Direct evidence for a dry molten globule intermediate during the unfolding of a small protein. Proc. Natl. Acad. Sci. USA 2009, 106, 12289–12294. [Google Scholar] [CrossRef] [PubMed]
- Jennings, P.A.; Wright, P.E. Formation of a molten globule intermediate early in the kinetic folding pathway of apomyoglobin. Science 1993, 262, 892–896. [Google Scholar] [CrossRef] [PubMed]
- Samatova, E.N.; Katina, N.S.; Balobanov, V.A.; Melnik, B.S.; Dolgikh, D.A.; Bychkova, V.E.; Finkelstein, A.V. How strong are side chain interactions in the folding intermediate? Protein Sci. 2009, 18, 2152–2159. [Google Scholar] [CrossRef] [PubMed]
- Eichmann, C.; Preissler, S.; Riek, R.; Deuerling, E. Cotranslational structure acquisition of nascent polypeptides monitored by NMR spectroscopy. Proc. Natl. Acad. Sci. USA 2010, 107, 9111–9116. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; David, A.; Liu, B.; Magadan, J.G.; Bennink, J.R.; Yewdell, J.W.; Qian, S.B. Monitoring cotranslational protein folding in mammalian cells at codon resolution. Proc. Natl. Acad. Sci. USA 2012, 109, 12467–12472. [Google Scholar] [CrossRef]
- Holtkamp, W.; Kokic, G.; Jager, M.; Mittelstaet, J.; Komar, A.A.; Rodnina, M.V. Cotranslational protein folding on the ribosome monitored in real time. Science 2015, 350, 1104–1107. [Google Scholar] [CrossRef]
- Flanagan, J.M.; Kataoka, M.; Shortle, D.; Engelman, D.M. Truncated staphylococcal nuclease is compact but disordered. Proc. Natl. Acad. Sci. USA 1992, 89, 748–752. [Google Scholar] [CrossRef]
- Levinthal, C. Are there pathways for protein folding? J. Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Levinthal, C. How to fold graciously. In Proceedings of the Mössbauer Spectroscopy in Biological Systems, Monticello, IL, USA, 17–18 March 1969; pp. 22–24. [Google Scholar]
- Go, N.; Abe, H. Noninteracting local-structure model of folding and unfolding transition in globular proteins. I. Formulation. Biopolymers 1981, 20, 991–1011. [Google Scholar] [CrossRef]
- Leopold, P.E.; Montal, M.; Onuchic, J.N. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA 1992, 89, 8721–8725. [Google Scholar] [CrossRef]
- Wolynes, P.G.; Onuchic, J.N.; Thirumalai, D. Navigating the folding routes. Science 1995, 267, 1619–1620. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R.; Szabo, A.; Bagchi, B. Levinthal’s paradox. Proc. Natl. Acad. Sci. USA 1992, 89, 20–22. [Google Scholar] [CrossRef] [PubMed]
- Abkevich, V.I.; Gutin, A.M.; Shakhnovich, E.I. Specific nucleus as the transition state for protein folding: Evidence from the lattice model. Biochemistry 1994, 33, 10026–10036. [Google Scholar] [CrossRef] [PubMed]
- Sali, A.; Shakhnovich, E.; Karplus, M. Kinetics of protein folding. A lattice model study of the requirements for folding to the native state. J. Mol. Biol. 1994, 235, 1614–1636. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Badretdinov, A.Y. Physical reason for fast folding of the stable spatial structure of proteins: A solution of the Levinthal paradox. Mol. Biol. 1997, 31, 391–398. [Google Scholar]
- Finkelstein, A.V.; Badretdinov, A. Rate of protein folding near the point of thermodynamic equilibrium between the coil and the most stable chain fold. Fold. Des. 1997, 2, 115–121. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Badretdinov, A.Y. Influence of chain knotting on the rate of folding. ADDENDUM to rate of protein folding near the point of thermodynamic equilibrium between the coil and the most stable chain fold. Fold. Des. 1998, 3, 67–68. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Badretdinov, A.; Gutin, A.M. Why do protein architectures have Boltzmann-like statistics? Proteins 1995, 23, 142–150. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Gutin, A.M.; Badretdinov, A. Boltzmann-like statistics of protein architectures. Origins and consequences. Subcell. Biochem. 1995, 24, 1–26. [Google Scholar] [CrossRef]
- Garbuzynskiy, S.O.; Ivankov, D.N.; Bogatyreva, N.S.; Finkelstein, A.V. Golden triangle for folding rates of globular proteins. Proc. Natl. Acad. Sci. USA 2013, 110, 147–150. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Pauling, L. General Chemistry; W.H. Freeman & Co.: New York, NY, USA, 1970. [Google Scholar]
- Emanuel, N.M.; Knorre, D.G. The Course in Chemical Kinetics, 4th ed.; Vysshaja Shkola: Moscow, Russia, 1984. [Google Scholar]
- Zana, R. On the rate determining step for helix propagation in the helix–coil transition of polypeptides in solution. Biopolymers 1975, 14, 2425–2428. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Badretdin, A.J.; Galzitskaya, O.V.; Ivankov, D.N.; Bogatyreva, N.S.; Garbuzynskiy, S.O. There and back again: Two views on the protein folding puzzle. Phys. Life Rev. 2017, 21, 56–71. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A.R. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding; W. H. Freeman & Co: New York, NY, USA, 1999. [Google Scholar]
- Takada, S. Go-ing for the prediction of protein folding mechanisms. Proc. Natl. Acad. Sci. USA 1999, 96, 11698–11700. [Google Scholar] [CrossRef]
- Alm, E.; Baker, D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11305–11310. [Google Scholar] [CrossRef]
- Galzitskaya, O.V.; Finkelstein, A.V. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11299–11304. [Google Scholar] [CrossRef]
- Munoz, V.; Eaton, W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11311–11316. [Google Scholar] [CrossRef]
- Galzitskaya, O.V.; Ivankov, D.N.; Finkelstein, A.V. Folding nuclei in proteins. FEBS Lett. 2001, 489, 113–118. [Google Scholar] [CrossRef]
- Garbuzynskiy, S.O.; Finkelstein, A.V.; Galzitskaya, O.V. Outlining folding nuclei in globular proteins. J. Mol. Biol. 2004, 336, 509–525. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Ivankov, D.N.; Garbuzynskiy, S.O.; Galzitskaya, O.V. Understanding the folding rates and folding nuclei of globular proteins. Curr. Protein Pept. Sci. 2007, 8, 521–536. [Google Scholar] [CrossRef]
- Garbuzynskiy, S.O.; Kondratova, M.S. Structural features of protein folding nuclei. FEBS Lett. 2008, 582, 768–772. [Google Scholar] [CrossRef] [PubMed]
- Ivankov, D.N.; Finkelstein, A.V. Protein folding as flow across a network of folding-unfolding pathways. 2. The “in-water” case. J. Phys. Chem. B 2010, 114, 7930–7934. [Google Scholar] [CrossRef]
- Ivankov, D.N.; Finkelstein, A.V. Protein folding as flow across a network of folding-unfolding pathways. 1. The mid-transition case. J. Phys. Chem. B 2010, 114, 7920–7929. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, A.V.; Galzitskaya, O.V. Physics of protein folding. Phys. Life Rev. 2004, 1, 23–56. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Bogatyreva, N.S.; Garbuzynskiy, S.O. Restrictions to protein folding determined by the protein size. FEBS Lett. 2013, 587, 1884–1890. [Google Scholar] [CrossRef] [PubMed]
- Ivankov, D.N.; Finkelstein, A.V. Prediction of protein folding rates from the amino acid sequence-predicted secondary structure. Proc. Natl. Acad. Sci. USA 2004, 101, 8942–8944. [Google Scholar] [CrossRef]
- Ivankov, D.N.; Garbuzynskiy, S.O.; Alm, E.; Plaxco, K.W.; Baker, D.; Finkelstein, A.V. Contact order revisited: Influence of protein size on the folding rate. Protein Sci. 2003, 12, 2057–2062. [Google Scholar] [CrossRef] [PubMed]
- Galzitskaya, O.V.; Garbuzynskiy, S.O.; Ivankov, D.N.; Finkelstein, A.V. Chain length is the main determinant of the folding rate for proteins with three-state folding kinetics. Proteins 2003, 51, 162–166. [Google Scholar] [CrossRef]
- Ivankov, D.N.; Finkelstein, A.V. Solution of the Levinthal’s paradox and a physical theory of protein folding rates. Biophysics 2016, 61, 1–5. [Google Scholar]
- Finkelstein, A.V.; Garbuzynskiy, S.O. Reduction of the Search Space for the Folding of Proteins at the Level of Formation and Assembly of Secondary Structures: A New View on the Solution of Levinthal’s Paradox. Chemphyschem 2015, 16, 3375–3378. [Google Scholar] [CrossRef]
- Finkelstein, A.V. Some additional remarks to the solution of the protein folding puzzle: Reply to comments on “There and back again: Two views on the protein folding puzzle”. Phys. Life Rev. 2017, 21, 77–79. [Google Scholar] [CrossRef]
- Fink, A.L. Compact intermediate states in protein folding. Annu. Rev. Biophys. Biomol. Struct. 1995, 24, 495–522. [Google Scholar] [CrossRef] [PubMed]
- Daughdrill, G.W.; Pielak, G.J.; Uversky, V.N.; Cortese, M.S.; Dunker, A.K. Natively disordered proteins. In Handbook of Protein Folding; Buchner, J., Kiefhaber, T., Eds.; Wiley-VCH, Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005; pp. 271–353. [Google Scholar]
- Maity, H.; Maity, M.; Krishna, M.M.; Mayne, L.; Englander, S.W. Protein folding: The stepwise assembly of foldon units. Proc. Natl. Acad. Sci. USA 2005, 102, 4741–4746. [Google Scholar] [CrossRef] [PubMed]
- Englander, S.W.; Mayne, L.; Krishna, M.M. Protein folding and misfolding: Mechanism and principles. Q. Rev. Biophys. 2007, 40, 287–326. [Google Scholar] [CrossRef] [PubMed]
- Bedard, S.; Krishna, M.M.; Mayne, L.; Englander, S.W. Protein folding: Independent unrelated pathways or predetermined pathway with optional errors. Proc. Natl. Acad. Sci. USA 2008, 105, 7182–7187. [Google Scholar] [CrossRef]
- Krishna, M.M.; Englander, S.W. A unified mechanism for protein folding: Predetermined pathways with optional errors. Protein Sci. 2007, 16, 449–464. [Google Scholar] [CrossRef]
- Lindberg, M.O.; Oliveberg, M. Malleability of protein folding pathways: A simple reason for complex behaviour. Curr. Opin. Struct. Biol. 2007, 17, 21–29. [Google Scholar] [CrossRef]
- Maity, H.; Maity, M.; Englander, S.W. How cytochrome c folds, and why: Submolecular foldon units and their stepwise sequential stabilization. J. Mol. Biol. 2004, 343, 223–233. [Google Scholar] [CrossRef]
- Bedard, S.; Mayne, L.C.; Peterson, R.W.; Wand, A.J.; Englander, S.W. The foldon substructure of staphylococcal nuclease. J. Mol. Biol. 2008, 376, 1142–1154. [Google Scholar] [CrossRef][Green Version]
- Uversky, V.N. Unusual biophysics of intrinsically disordered proteins. Biochim. Biophys. Acta 2013, 1834, 932–951. [Google Scholar] [CrossRef]
- Uversky, V.N. p53 Proteoforms and Intrinsic Disorder: An Illustration of the Protein Structure-Function Continuum Concept. Int. J. Mol. Sci. 2016, 17, 1874. [Google Scholar] [CrossRef]
- Uversky, V.N. Protein intrinsic disorder and structure-function continuum. Prog. Mol. Biol. Transl. Sci. 2019, 166, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Intrinsically disordered proteins and their “mysterious” (meta)physics. Front. Phys. 2019, 7, 10. [Google Scholar] [CrossRef]
- Uversky, V.N. Dancing Protein Clouds: The Strange Biology and Chaotic Physics of Intrinsically Disordered Proteins. J. Biol. Chem. 2016, 291, 6681–6688. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.M.; Kelleher, N.L.; Consortium for Top Down Proteomics. Proteoform: A single term describing protein complexity. Nat. Methods 2013, 10, 186–187. [Google Scholar] [CrossRef]
- Fonin, A.V.; Darling, A.L.; Kuznetsova, I.M.; Turoverov, K.K.; Uversky, V.N. Multi-functionality of proteins involved in GPCR and G protein signaling: Making sense of structure-function continuum with intrinsic disorder-based proteoforms. Cell. Mol. Life Sci. 2019, 76, 4461–4492. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Paradoxes and wonders of intrinsic disorder: Complexity of simplicity. Intrinsically Disord. Proteins 2016, 4, e1135015. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N.; Oldfield, C.J.; Dunker, A.K. Intrinsically disordered proteins in human diseases: Introducing the D2 concept. Annu. Rev. Biophys. 2008, 37, 215–246. [Google Scholar] [CrossRef]
- Fisher, C.K.; Stultz, C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011, 21, 426–431. [Google Scholar] [CrossRef]
- Hemmings, H.C., Jr.; Nairn, A.C.; Aswad, D.W.; Greengard, P. DARPP-32, a dopamine- and adenosine 3’:5’-monophosphate-regulated phosphoprotein enriched in dopamine-innervated brain regions. II. Purification and characterization of the phosphoprotein from bovine caudate nucleus. J. Neurosci. 1984, 4, 99–110. [Google Scholar] [CrossRef]
- Gast, K.; Damaschun, H.; Eckert, K.; Schulze-Forster, K.; Maurer, H.R.; Muller-Frohne, M.; Zirwer, D.; Czarnecki, J.; Damaschun, G. Prothymosin alpha: A biologically active protein with random coil conformation. Biochemistry 1995, 34, 13211–13218. [Google Scholar] [CrossRef]
- Weinreb, P.H.; Zhen, W.; Poon, A.W.; Conway, K.A.; Lansbury, P.T., Jr. NACP, a protein implicated in Alzheimer’s disease and learning, is natively unfolded. Biochemistry 1996, 35, 13709–13715. [Google Scholar] [CrossRef] [PubMed]
- Romero, P.; Obradovic, Z.; Kissinger, C.R.; Villafranca, J.E.; Garner, E.; Guilliot, S.; Dunker, A.K. Thousands of proteins likely to have long disordered regions. Pac. Symp. Biocomput. 1998, 3, 437–448. [Google Scholar]
- Garner, E.; Cannon, P.; Romero, P.; Obradovic, Z.; Dunker, A.K. Predicting Disordered Regions from Amino Acid Sequence: Common Themes Despite Differing Structural Characterization. Genome Inform. Ser. Workshop Genome Inform. 1998, 9, 201–213. [Google Scholar] [PubMed]
- Williams, R.M.; Obradovi, Z.; Mathura, V.; Braun, W.; Garner, E.C.; Young, J.; Takayama, S.; Brown, C.J.; Dunker, A.K. The protein non-folding problem: Amino acid determinants of intrinsic order and disorder. Pac. Symp. Biocomput. 2001, 89–100. [Google Scholar] [CrossRef]
- Romero, P.; Obradovic, Z.; Li, X.; Garner, E.C.; Brown, C.J.; Dunker, A.K. Sequence complexity of disordered protein. Proteins 2001, 42, 38–48. [Google Scholar] [CrossRef]
- Radivojac, P.; Iakoucheva, L.M.; Oldfield, C.J.; Obradovic, Z.; Uversky, V.N.; Dunker, A.K. Intrinsic disorder and functional proteomics. Biophys. J. 2007, 92, 1439–1456. [Google Scholar] [CrossRef] [PubMed]
- Vacic, V.; Uversky, V.N.; Dunker, A.K.; Lonardi, S. Composition Profiler: A tool for discovery and visualization of amino acid composition differences. BMC Bioinform. 2007, 8, 211. [Google Scholar] [CrossRef]
- Ban, N.; Nissen, P.; Hansen, J.; Moore, P.B.; Steitz, T.A. The complete atomic structure of the large ribosomal subunit at 2.4 A resolution. Science 2000, 289, 905–920. [Google Scholar] [CrossRef]
- Teschke, C.M.; King, J. Folding and assembly of oligomeric proteins in Escherichia coli. Curr. Opin. Biotechnol. 1992, 3, 468–473. [Google Scholar] [CrossRef]
- Xu, D.; Tsai, C.J.; Nussinov, R. Mechanism and evolution of protein dimerization. Protein Sci. 1998, 7, 533–544. [Google Scholar] [CrossRef]
- Gunasekaran, K.; Tsai, C.J.; Nussinov, R. Analysis of ordered and disordered protein complexes reveals structural features discriminating between stable and unstable monomers. J. Mol. Biol. 2004, 341, 1327–1341. [Google Scholar] [CrossRef] [PubMed]
- Schulz, G.E. Nucleotide Binding Proteins. In Molecular Mechanism of Biological Recognition; Balaban, M., Ed.; Elsevier/North-Holland Biomedical Press: New York, NY, USA, 1979; pp. 79–94. [Google Scholar]
- Iakoucheva, L.M.; Brown, C.J.; Lawson, J.D.; Obradovic, Z.; Dunker, A.K. Intrinsic disorder in cell-signaling and cancer-associated proteins. J. Mol. Biol. 2002, 323, 573–584. [Google Scholar] [CrossRef]
- Meador, W.E.; Means, A.R.; Quiocho, F.A. Modulation of calmodulin plasticity in molecular recognition on the basis of x-ray structures. Science 1993, 262, 1718–1721. [Google Scholar] [CrossRef] [PubMed]
- Kriwacki, R.W.; Hengst, L.; Tennant, L.; Reed, S.I.; Wright, P.E. Structural studies of p21Waf1/Cip1/Sdi1 in the free and Cdk2-bound state: Conformational disorder mediates binding diversity. Proc. Natl. Acad. Sci. USA 1996, 93, 11504–11509. [Google Scholar] [CrossRef]
- Dunker, A.K.; Garner, E.; Guilliot, S.; Romero, P.; Albrecht, K.; Hart, J.; Obradovic, Z.; Kissinger, C.; Villafranca, J.E. Protein disorder and the evolution of molecular recognition: Theory, predictions and observations. Pac. Symp. Biocomput. 1998, 3, 473–484. [Google Scholar]
- Hsu, W.L.; Oldfield, C.J.; Xue, B.; Meng, J.; Huang, F.; Romero, P.; Uversky, V.N.; Dunker, A.K. Exploring the binding diversity of intrinsically disordered proteins involved in one-to-many binding. Protein Sci. 2013, 22, 258–273. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Dunker, A.K. Intrinsically disordered proteins and intrinsically disordered protein regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Meng, J.; Yang, J.Y.; Yang, M.Q.; Uversky, V.N.; Dunker, A.K. Flexible nets: Disorder and induced fit in the associations of p53 and 14-3-3 with their partners. BMC Genom. 2008, 9 (Suppl. 1), S1. [Google Scholar] [CrossRef]
- Lattman, E.E.; Rose, G.D. Protein folding--what’s the question? Proc. Natl. Acad. Sci. USA 1993, 90, 439–441. [Google Scholar] [CrossRef]
- Rackovsky, S. On the nature of the protein folding code. Proc. Natl. Acad. Sci. USA 1993, 90, 644–648. [Google Scholar] [CrossRef]
- Alexander, P.A.; Rozak, D.A.; Orban, J.; Bryan, P.N. Directed evolution of highly homologous proteins with different folds by phage display: Implications for the protein folding code. Biochemistry 2005, 44, 14045–14054. [Google Scholar] [CrossRef] [PubMed]
- Tasayco, M.L.; Carey, J. Ordered self-assembly of polypeptide fragments to form nativelike dimeric trp repressor. Science 1992, 255, 594–597. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.P.; Shoelson, S.E. Cooperative self-assembly of SH2 domain fragments restores phosphopeptide binding. Biochemistry 1993, 32, 11279–11284. [Google Scholar] [CrossRef] [PubMed]
- Betton, J.M.; Hofnung, M. In vivo assembly of active maltose binding protein from independently exported protein fragments. Embo J. 1994, 13, 1226–1234. [Google Scholar] [CrossRef]
- Kaur, P.; Rosen, B.P. In vitro assembly of an anion-stimulated ATPase from peptide fragments. J. Biol. Chem. 1994, 269, 9698–9704. [Google Scholar]
- Kippen, A.D.; Fersht, A.R. Analysis of the mechanism of assembly of cleaved barnase from two peptide fragments and its relevance to the folding pathway of uncleaved barnase. Biochemistry 1995, 34, 1464–1468. [Google Scholar] [CrossRef]
- Ridge, K.D.; Lee, S.S.; Yao, L.L. In vivo assembly of rhodopsin from expressed polypeptide fragments. Proc. Natl. Acad. Sci. USA 1995, 92, 3204–3208. [Google Scholar] [CrossRef]
- Ridge, K.D.; Abdulaev, N.G. Folding and assembly of rhodopsin from expressed fragments. Methods Enzymol. 2000, 315, 59–70. [Google Scholar] [CrossRef]
- Kobayashi, N.; Honda, S.; Yoshii, H.; Uedaira, H.; Munekata, E. Complement assembly of two fragments of the streptococcal protein G B1 domain in aqueous solution. FEBS Lett. 1995, 366, 99–103. [Google Scholar] [CrossRef]
- Rochet, J.C.; Oikawa, K.; Hicks, L.D.; Kay, C.M.; Bridger, W.A.; Wolodko, W.T. Productive interactions between the two domains of pig heart CoA transferase during folding and assembly. Biochemistry 1997, 36, 8807–8820. [Google Scholar] [CrossRef]
- Chaffotte, A.F.; Li, J.H.; Georgescu, R.E.; Goldberg, M.E.; Tasayco, M.L. Recognition between disordered states: Kinetics of the self-assembly of thioredoxin fragments. Biochemistry 1997, 36, 16040–16048. [Google Scholar] [CrossRef] [PubMed]
- Marti, T. Refolding of bacteriorhodopsin from expressed polypeptide fragments. J. Biol. Chem. 1998, 273, 9312–9322. [Google Scholar] [CrossRef] [PubMed]
- Martin, N.P.; Leavitt, L.M.; Sommers, C.M.; Dumont, M.E. Assembly of G protein-coupled receptors from fragments: Identification of functional receptors with discontinuities in each of the loops connecting transmembrane segments. Biochemistry 1999, 38, 682–695. [Google Scholar] [CrossRef] [PubMed]
- Jourdan, M.; Searle, M.S. Cooperative assembly of a nativelike ubiquitin structure through peptide fragment complexation: Energetics of peptide association and folding. Biochemistry 2000, 39, 12355–12364. [Google Scholar] [CrossRef]
- Ni, X.; Schachman, H.K. In vivo assembly of aspartate transcarbamoylase from fragmented and circularly permuted catalytic polypeptide chains. Protein Sci. 2001, 10, 519–527. [Google Scholar] [CrossRef]
- Johnsson, N.; Varshavsky, A. Split ubiquitin as a sensor of protein interactions in vivo. Proc. Natl. Acad. Sci. USA 1994, 91, 10340–10344. [Google Scholar] [CrossRef]
- Ozawa, T. Designing split reporter proteins for analytical tools. Anal. Chim. Acta 2006, 556, 58–68. [Google Scholar] [CrossRef]
- Remy, I.; Michnick, S.W. Clonal selection and in vivo quantitation of protein interactions with protein-fragment complementation assays. Proc. Natl. Acad. Sci. USA 1999, 96, 5394–5399. [Google Scholar] [CrossRef]
- Blakely, B.T.; Rossi, F.M.; Tillotson, B.; Palmer, M.; Estelles, A.; Blau, H.M. Epidermal growth factor receptor dimerization monitored in live cells. Nat. Biotechnol. 2000, 18, 218–222. [Google Scholar] [CrossRef]
- Magliery, T.J.; Wilson, C.G.; Pan, W.; Mishler, D.; Ghosh, I.; Hamilton, A.D.; Regan, L. Detecting protein-protein interactions with a green fluorescent protein fragment reassembly trap: Scope and mechanism. J. Am. Chem. Soc. 2005, 127, 146–157. [Google Scholar] [CrossRef]
- Kaihara, A.; Kawai, Y.; Sato, M.; Ozawa, T.; Umezawa, Y. Locating a protein-protein interaction in living cells via split Renilla luciferase complementation. Anal. Chem. 2003, 75, 4176–4181. [Google Scholar] [CrossRef] [PubMed]
- Galarneau, A.; Primeau, M.; Trudeau, L.E.; Michnick, S.W. Beta-lactamase protein fragment complementation assays as in vivo and in vitro sensors of protein protein interactions. Nat. Biotechnol. 2002, 20, 619–622. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics (v. 5 of A Course of Theoretical Physics), 3rd ed.; Elsevier: London, UK, 1980. [Google Scholar]
- Ubbelohde, A.R. Melting and Crystal Structure; Clarendon Press: Oxford, UK, 1965. [Google Scholar]
- Bagdasarov, K.S.; Givargizov, E.I.; Kuznetsov, V.A.; Demianets, L.N.; Lobachev, A.N.; Chernov, A.A. Modern Crystallography; Crystal Growth: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1984; Volume 3. [Google Scholar]
- Frenkel, J.D. Kinetic Theory of Liquids, Reissue ed.; Dover Publications: Mineola, NY, USA, 1955. [Google Scholar]
- Wang, R.; Yang, X.; Cui, L.; Yin, H.; Xu, S. Gels of Amyloid Fibers. Biomolecules 2019, 9, 210. [Google Scholar] [CrossRef] [PubMed]
- Stahnke, J. Hemoglobin crystals from Reichert to Hoppe-Seyler. Sudhoffs Arch. 1979, 63, 154–189. [Google Scholar]
- Matthews, B.W. Solvent content of protein crystals. J. Mol. Biol. 1968, 33, 491–497. [Google Scholar] [CrossRef]
- Chruszcz, M.; Potrzebowski, W.; Zimmerman, M.D.; Grabowski, M.; Zheng, H.; Lasota, P.; Minor, W. Analysis of solvent content and oligomeric states in protein crystals—Does symmetry matter? Protein Sci. 2008, 17, 623–632. [Google Scholar] [CrossRef]
- Muschol, M.; Rosenberger, F. Liquid-liquid phase separation in supersaturated lysozyme solutions and associated precipitate formation/crystallization. J. Chem. Phys. 1997, 107, 1953–1962. [Google Scholar] [CrossRef]
- Dumetz, A.C.; Chockla, A.M.; Kaler, E.W.; Lenhoff, A.M. Protein phase behavior in aqueous solutions: Crystallization, liquid-liquid phase separation, gels, and aggregates. Biophys. J. 2008, 94, 570–583. [Google Scholar] [CrossRef]
- Neal, B.L.; Asthagiri, D.; Lenhoff, A.M. Molecular origins of osmotic second virial coefficients of proteins. Biophys. J. 1998, 75, 2469–2477. [Google Scholar] [CrossRef]
- George, A.; Wilson, W.W. Predicting protein crystallization from a dilute solution property. Acta Crystallogr. D Biol. Crystallogr. 1994, 50, 361–365. [Google Scholar] [CrossRef]
- Neal, B.L.; Asthagiri, D.; Velev, O.D.; Lenhoff, A.M.; Kaler, E.W. Why is the osmotic second virial coefficient related to protein crystallization? J. Cryst. Growth 1999, 196, 377–387. [Google Scholar] [CrossRef]
- Pullara, F.; Emanuele, A.; Palma-Vittorelli, M.B.; Palma, M.U. Lysozyme crystallization rates controlled by anomalous fluctuations. J. Cryst. Growth 2005, 58, 426–438. [Google Scholar] [CrossRef]
- Pullara, F.; Emanuele, A.; Palma-Vittorelli, M.B.; Palma, M.U. Protein aggregation/crystallization and minor structural changes: Universal versus specific aspects. Biophys. J. 2007, 93, 3271–3278. [Google Scholar] [CrossRef] [PubMed]
- Debenedetti, P.G. Metastable Liquids. Concepts and Principles; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
- Scholte, T.G. Thermodynamic parameters of polymer-solvent systems from light-scattering measurements below the theta temperature. J. Polym. Sci. B 1971, 9, 1553–1577. [Google Scholar] [CrossRef]
- Fink, A.L. Protein aggregation: Folding aggregates, inclusion bodies and amyloid. Fold. Des. 1998, 3, R9–R23. [Google Scholar] [CrossRef]
- Mitraki, A.; King, J. Protein folding intermediates and inclusion body formation. Biotechnology 1989, 7, 690–697. [Google Scholar] [CrossRef]
- Wetzel, R. Mutations and off-pathway aggregation of proteins. Trends Biotechnol. 1994, 12, 193–198. [Google Scholar] [CrossRef]
- Jaenicke, R. Folding and association versus misfolding and aggregation of proteins. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1995, 348, 97–105. [Google Scholar] [CrossRef]
- Wetzel, R. For protein misassembly, it’s the “I” decade. Cell 1996, 86, 699–702. [Google Scholar] [CrossRef]
- Speed, M.A.; Morshead, T.; Wang, D.I.; King, J. Conformation of P22 tailspike folding and aggregation intermediates probed by monoclonal antibodies. Protein Sci. 1997, 6, 99–108. [Google Scholar] [CrossRef]
- Speed, M.A.; Wang, D.I.; King, J. Specific aggregation of partially folded polypeptide chains: The molecular basis of inclusion body composition. Nat. Biotechnol. 1996, 14, 1283–1287. [Google Scholar] [CrossRef] [PubMed]
- Wetzel, R.; Chrunyk, B.A. Inclusion body formation by interleukin-1 beta depends on the thermal sensitivity of a folding intermediate. FEBS Lett. 1994, 350, 245–248. [Google Scholar] [CrossRef]
- Haase-Pettingell, C.A.; King, J. Formation of aggregates from a thermolabile in vivo folding intermediate in P22 tailspike maturation. A model for inclusion body formation. J. Biol. Chem. 1988, 263, 4977–4983. [Google Scholar] [PubMed]
- Yoshimura, Y.; Lin, Y.X.; Yagi, H.; Lee, Y.H.; Kitayama, H.; Sakurai, K.; So, M.; Ogi, H.; Naiki, H.; Goto, Y. Distinguishing crystal-like amyloid fibrils and glass-like amorphous aggregates from their kinetics of formation. Proc. Natl. Acad. Sci. USA 2012, 109, 14446–14451. [Google Scholar] [CrossRef]
- Dovidchenko, N.V.; Finkelstein, A.V.; Galzitskaya, O.V. How to determine the size of folding nuclei of protofibrils from the concentration dependence of the rate and lag-time of aggregation. I. Modeling the amyloid protofibril formation. J. Phys. Chem. B 2014, 118, 1189–1197. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Dovidchenko, N.V.; Galzitskaya, O.V. What is Responsible for Atypical Dependence of the Rate of Amyloid Formation on Protein Concentration: Fibril-Catalyzed Initiation of New Fibrils or Competition with Oligomers? J. Phys. Chem. Lett. 2018, 9, 1002–1006. [Google Scholar] [CrossRef]
- Come, J.H.; Fraser, P.E.; Lansbury, P.T., Jr. A kinetic model for amyloid formation in the prion diseases: Importance of seeding. Proc. Natl. Acad. Sci. USA 1993, 90, 5959–5963. [Google Scholar] [CrossRef]
- Jarrett, J.T.; Lansbury, P.T., Jr. Seeding “one-dimensional crystallization” of amyloid: A pathogenic mechanism in Alzheimer’s disease and scrapie? Cell 1993, 73, 1055–1058. [Google Scholar] [CrossRef]
- Crespo, R.; Rocha, F.A.; Damas, A.M.; Martins, P.M. A generic crystallization-like model that describes the kinetics of amyloid fibril formation. J. Biol. Chem. 2012, 287, 30585–30594. [Google Scholar] [CrossRef]
- Jarrett, J.T.; Lansbury, P.T., Jr. Amyloid fibril formation requires a chemically discriminating nucleation event: Studies of an amyloidogenic sequence from the bacterial protein OsmB. Biochemistry 1992, 31, 12345–12352. [Google Scholar] [CrossRef]
- Bergfors, T. Seeds to crystals. J. Struct. Biol. 2003, 142, 66–76. [Google Scholar] [CrossRef]
- Dima, R.I.; Thirumalai, D. Exploring protein aggregation and self-propagation using lattice models: Phase diagram and kinetics. Protein Sci. 2002, 11, 1036–1049. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, Y. Biophysical studies of protein solubility and amorphous aggregation by systematic mutational analysis and a helical polymerization model. Biophys. Rev. 2018, 10, 473–480. [Google Scholar] [CrossRef] [PubMed]
- Boatz, J.C.; Whitley, M.J.; Li, M.; Gronenborn, A.M.; van der Wel, P.C.A. Cataract-associated P23T gammaD-crystallin retains a native-like fold in amorphous-looking aggregates formed at physiological pH. Nat. Commun. 2017, 8, 15137. [Google Scholar] [CrossRef]
- Kato, A.; Maki, K.; Ebina, T.; Kuwajima, K.; Soda, K.; Kuroda, Y. Mutational analysis of protein solubility enhancement using short peptide tags. Biopolymers 2007, 85, 12–18. [Google Scholar] [CrossRef]
- Hirota, N.; Edskes, H.; Hall, D. Unified theoretical description of the kinetics of protein aggregation. Biophys. Rev. 2019, 11, 191–208. [Google Scholar] [CrossRef]
- Hirota, N.; Hall, D. Protein Aggregation Kinetics: A Unified Theoretical Description. In Protein Solubility and Amorphous Aggregation: From Academic Research to Applications in Drug Discovery and Bioindustry; Kuroda, Y., Arisaka, F., Eds.; CMC Publishing Co., Ltd.: Tokyo, Japan, 2019. [Google Scholar]
- Kelly, J.W. Amyloid fibril formation and protein misassembly: A structural quest for insights into amyloid and prion diseases. Structure 1997, 5, 595–600. [Google Scholar] [CrossRef]
- Kelly, J.W. The alternative conformations of amyloidogenic proteins and their multi-step assembly pathways. Curr. Opin. Struct. Biol. 1998, 8, 101–106. [Google Scholar] [CrossRef]
- Dobson, C.M. Protein misfolding, evolution and disease. Trends Biochem. Sci. 1999, 24, 329–332. [Google Scholar] [CrossRef]
- Bellotti, V.; Mangione, P.; Stoppini, M. Biological activity and pathological implications of misfolded proteins. Cell. Mol. Life Sci. 1999, 55, 977–991. [Google Scholar] [CrossRef]
- Uversky, V.N.; Talapatra, A.; Gillespie, J.R.; Fink, A.L. Protein deposits as the molecular basis of amyloidosis. I. Systemic amyloidoses. Med. Sci. Monit. 1999, 5, 1001–1012. [Google Scholar]
- Uversky, V.N.; Talapatra, A.; Gillespie, J.R.; Fink, A.L. Protein deposits as the molecular basis of amyloidosis. II. Localized amyloidosis and neurodegenerative disordres. Med. Sci. Monit. 1999, 5, 1238–1254. [Google Scholar]
- Uversky, V.N.; Fink, A.L. Conformational constraints for amyloid fibrillation: The importance of being unfolded. Biochim. Biophys. Acta 2004, 1698, 131–153. [Google Scholar] [CrossRef]
- Rochet, J.C.; Lansbury, P.T., Jr. Amyloid fibrillogenesis: Themes and variations. Curr. Opin. Struct. Biol. 2000, 10, 60–68. [Google Scholar] [CrossRef]
- Sunde, M.; Serpell, L.C.; Bartlam, M.; Fraser, P.E.; Pepys, M.B.; Blake, C.C. Common core structure of amyloid fibrils by synchrotron X-ray diffraction. J. Mol. Biol. 1997, 273, 729–739. [Google Scholar] [CrossRef]
- Chiti, F.; Dobson, C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006, 75, 333–366. [Google Scholar] [CrossRef] [PubMed]
- Fandrich, M.; Fletcher, M.A.; Dobson, C.M. Amyloid fibrils from muscle myoglobin. Nature 2001, 410, 165–166. [Google Scholar] [CrossRef]
- Dobson, C.M. Protein folding and its links with human disease. Biochem. Soc. Symp. 2001, 68, 1–26. [Google Scholar]
- Uversky, V.N.; Li, J.; Fink, A.L. Evidence for a partially folded intermediate in alpha-synuclein fibril formation. J. Biol. Chem. 2001, 276, 10737–10744. [Google Scholar] [CrossRef]
- Goers, J.; Permyakov, S.E.; Permyakov, E.A.; Uversky, V.N.; Fink, A.L. Conformational prerequisites for alpha-lactalbumin fibrillation. Biochemistry 2002, 41, 12546–12551. [Google Scholar] [CrossRef]
- Munishkina, L.A.; Fink, A.L.; Uversky, V.N. Conformational prerequisites for formation of amyloid fibrils from histones. J. Mol. Biol. 2004, 342, 1305–1324. [Google Scholar] [CrossRef] [PubMed]
- Dobson, C.M. Getting out of shape. Nature 2002, 418, 729–730. [Google Scholar] [CrossRef] [PubMed]
- Dobson, C.M. Protein folding and misfolding. Nature 2003, 426, 884–890. [Google Scholar] [CrossRef] [PubMed]
- Dobson, C.M. Protein aggregation and its consequences for human disease. Protein Pept. Lett. 2006, 13, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.S.; Richardson, D.C. Natural beta-sheet proteins use negative design to avoid edge-to-edge aggregation. Proc. Natl. Acad. Sci. USA 2002, 99, 2754–2759. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J.W. Alternative conformations of amyloidogenic proteins govern their behavior. Curr. Opin. Struct. Biol. 1996, 6, 11–17. [Google Scholar] [CrossRef]
- Lansbury, P.T., Jr. Evolution of amyloid: What normal protein folding may tell us about fibrillogenesis and disease. Proc. Natl. Acad. Sci. USA 1999, 96, 3342–3344. [Google Scholar] [CrossRef]
- Canet, D.; Sunde, M.; Last, A.M.; Miranker, A.; Spencer, A.; Robinson, C.V.; Dobson, C.M. Mechanistic studies of the folding of human lysozyme and the origin of amyloidogenic behavior in its disease-related variants. Biochemistry 1999, 38, 6419–6427. [Google Scholar] [CrossRef]
- Zerovnik, E. Amyloid-fibril formation. Proposed mechanisms and relevance to conformational disease. Eur. J. Biochem. 2002, 269, 3362–3371. [Google Scholar]
- Teplow, D.B. Structural and kinetic features of amyloid beta-protein fibrillogenesis. Amyloid Int. J. Exp. Clin. Investig. Off. J. Int. Soc. Amyloidosis 1998, 5, 121–142. [Google Scholar] [CrossRef]
- Schweers, O.; Schonbrunn-Hanebeck, E.; Marx, A.; Mandelkow, E. Structural studies of tau protein and Alzheimer paired helical filaments show no evidence for beta-structure. J. Biol. Chem. 1994, 269, 24290–24297. [Google Scholar] [PubMed]
- Kayed, R.; Bernhagen, J.; Greenfield, N.; Sweimeh, K.; Brunner, H.; Voelter, W.; Kapurniotu, A. Conformational transitions of islet amyloid polypeptide (IAPP) in amyloid formation in vitro. J. Mol. Biol. 1999, 287, 781–796. [Google Scholar] [CrossRef] [PubMed]
- Englander, S.W.; Kallenbach, N.R. Hydrogen exchange and structural dynamics of proteins and nucleic acids. Q. Rev. Biophys. 1983, 16, 521–655. [Google Scholar] [CrossRef] [PubMed]
- Chamberlain, A.K.; Handel, T.M.; Marqusee, S. Detection of rare partially folded molecules in equilibrium with the native conformation of RNaseH. Nat. Struct. Biol. 1996, 3, 782–787. [Google Scholar] [CrossRef]
- Lashuel, H.A.; Wurth, C.; Woo, L.; Kelly, J.W. The most pathogenic transthyretin variant, L55P, forms amyloid fibrils under acidic conditions and protofilaments under physiological conditions. Biochemistry 1999, 38, 13560–13573. [Google Scholar] [CrossRef]
- Wetzel, R. Domain stability in immunoglobulin light chain deposition disorders. Adv. Protein Chem. 1997, 50, 183–242. [Google Scholar]
- Saraiva, M.J. Transthyretin amyloidosis: A tale of weak interactions. FEBS Lett. 2001, 498, 201–203. [Google Scholar] [CrossRef]
- Nielsen, L.; Frokjaer, S.; Brange, J.; Uversky, V.N.; Fink, A.L. Probing the mechanism of insulin fibril formation with insulin mutants. Biochemistry 2001, 40, 8397–8409. [Google Scholar] [CrossRef]
- Heegaard, N.H.; Sen, J.W.; Kaarsholm, N.C.; Nissen, M.H. Conformational intermediate of the amyloidogenic protein beta 2-microglobulin at neutral pH. J. Biol. Chem. 2001, 276, 32657–32662. [Google Scholar] [CrossRef]
- Nielsen, L.; Khurana, R.; Coats, A.; Frokjaer, S.; Brange, J.; Vyas, S.; Uversky, V.N.; Fink, A.L. Effect of environmental factors on the kinetics of insulin fibril formation: Elucidation of the molecular mechanism. Biochemistry 2001, 40, 6036–6046. [Google Scholar] [CrossRef]
- Peterson, S.A.; Klabunde, T.; Lashuel, H.A.; Purkey, H.; Sacchettini, J.C.; Kelly, J.W. Inhibiting transthyretin conformational changes that lead to amyloid fibril formation. Proc. Natl. Acad. Sci. USA 1998, 95, 12956–12960. [Google Scholar] [CrossRef]
- Baures, P.W.; Peterson, S.A.; Kelly, J.W. Discovering transthyretin amyloid fibril inhibitors by limited screening. Bioorgan. Med. Chem. 1998, 6, 1389–1401. [Google Scholar] [CrossRef]
- Oza, V.B.; Petrassi, H.M.; Purkey, H.E.; Kelly, J.W. Synthesis and evaluation of anthranilic acid-based transthyretin amyloid fibril inhibitors. Bioorgan. Med. Chem. Lett. 1999, 9, 1–6. [Google Scholar] [CrossRef]
- Klabunde, T.; Petrassi, H.M.; Oza, V.B.; Raman, P.; Kelly, J.W.; Sacchettini, J.C. Rational design of potent human transthyretin amyloid disease inhibitors. Nat. Struct. Biol. 2000, 7, 312–321. [Google Scholar] [CrossRef]
- Chiti, F.; Taddei, N.; Stefani, M.; Dobson, C.M.; Ramponi, G. Reduction of the amyloidogenicity of a protein by specific binding of ligands to the native conformation. Protein Sci. 2001, 10, 879–886. [Google Scholar] [CrossRef]
- McCammon, M.G.; Scott, D.J.; Keetch, C.A.; Greene, L.H.; Purkey, H.E.; Petrassi, H.M.; Kelly, J.W.; Robinson, C.V. Screening transthyretin amyloid fibril inhibitors: Characterization of novel multiprotein, multiligand complexes by mass spectrometry. Structure 2002, 10, 851–863. [Google Scholar] [CrossRef]
- Oza, V.B.; Smith, C.; Raman, P.; Koepf, E.K.; Lashuel, H.A.; Petrassi, H.M.; Chiang, K.P.; Powers, E.T.; Sachettinni, J.; Kelly, J.W. Synthesis, structure, and activity of diclofenac analogues as transthyretin amyloid fibril formation inhibitors. J. Med. Chem. 2002, 45, 321–332. [Google Scholar] [CrossRef]
- Raghu, P.; Reddy, G.B.; Sivakumar, B. Inhibition of transthyretin amyloid fibril formation by 2,4-dinitrophenol through tetramer stabilization. Arch. Biochem. Biophys. 2002, 400, 43–47. [Google Scholar] [CrossRef]
- Uversky, V.N. Under-folded proteins: Conformational ensembles and their roles in protein folding, function, and pathogenesis. Biopolymers 2013, 99, 870–887. [Google Scholar] [CrossRef]
- Chirita, C.N.; Congdon, E.E.; Yin, H.; Kuret, J. Triggers of full-length tau aggregation: A role for partially folded intermediates. Biochemistry 2005, 44, 5862–5872. [Google Scholar] [CrossRef]
- Yamin, G.; Munishkina, L.A.; Karymov, M.A.; Lyubchenko, Y.L.; Uversky, V.N.; Fink, A.L. Forcing nonamyloidogenic beta-synuclein to fibrillate. Biochemistry 2005, 44, 9096–9107. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N.; Li, J.; Souillac, P.; Millett, I.S.; Doniach, S.; Jakes, R.; Goedert, M.; Fink, A.L. Biophysical properties of the synucleins and their propensities to fibrillate: Inhibition of alpha-synuclein assembly by beta- and gamma-synucleins. J. Biol. Chem. 2002, 277, 11970–11978. [Google Scholar] [CrossRef]
- Goldsbury, C.; Goldie, K.; Pellaud, J.; Seelig, J.; Frey, P.; Muller, S.A.; Kistler, J.; Cooper, G.J.; Aebi, U. Amyloid fibril formation from full-length and fragments of amylin. J. Struct. Biol. 2000, 130, 352–362. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, N.A.; Cherny, D.I.; Heim, G.; Jovin, T.M.; Subramaniam, V. Amyloid fibrils from the mammalian protein prothymosin alpha. FEBS Lett. 2002, 517, 37–40. [Google Scholar] [CrossRef]
- Uversky, V.N. Mysterious oligomerization of the amyloidogenic proteins. FEBS J. 2010, 277, 2940–2953. [Google Scholar] [CrossRef]
- Merlini, G.; Bellotti, V. Molecular mechanisms of amyloidosis. N. Engl. J. Med. 2003, 349, 583–596. [Google Scholar] [CrossRef]
- Smith, D.P.; Jones, S.; Serpell, L.C.; Sunde, M.; Radford, S.E. A systematic investigation into the effect of protein destabilisation on beta 2-microglobulin amyloid formation. J. Mol. Biol. 2003, 330, 943–954. [Google Scholar] [CrossRef]
- Wagner, R. Einige Bemerkungen und Fragen über das Keimbläschen (vesicular germinativa). Müllers Arch. Anat. Physiol. Wiss. Med. 1835, 268, 373–377. [Google Scholar]
- Valentin, G.G. Repertorium für Anatomie und Physiologie; Verlag von Veit und Comp.: Berlin, Germany, 1836. [Google Scholar]
- Toretsky, J.A.; Wright, P.E. Assemblages: Functional units formed by cellular phase separation. J. Cell Biol. 2014, 206, 579–588. [Google Scholar] [CrossRef]
- Hyman, A.A.; Weber, C.A.; Julicher, F. Liquid-liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 2014, 30, 39–58. [Google Scholar] [CrossRef]
- Forman-Kay, J.D.; Kriwacki, R.W.; Seydoux, G. Phase Separation in Biology and Disease. J. Mol. Biol. 2018, 430, 4603–4606. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Brangwynne, C.P. Liquid phase condensation in cell physiology and disease. Science 2017, 357, eaaf4382. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Dormann, D. Liquid-Liquid Phase Separation in Disease. Annu. Rev. Genet. 2019, 53, 171–194. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Gladfelter, A.; Mittag, T. Considerations and Challenges in Studying Liquid-Liquid Phase Separation and Biomolecular Condensates. Cell 2019, 176, 419–434. [Google Scholar] [CrossRef]
- Gomes, E.; Shorter, J. The molecular language of membraneless organelles. J. Biol. Chem. 2019, 294, 7115–7127. [Google Scholar] [CrossRef] [PubMed]
- Hnisz, D.; Shrinivas, K.; Young, R.A.; Chakraborty, A.K.; Sharp, P.A. A Phase Separation Model for Transcriptional Control. Cell 2017, 169, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Banani, S.F.; Lee, H.O.; Hyman, A.A.; Rosen, M.K. Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef]
- Alberti, S. The wisdom of crowds: Regulating cell function through condensed states of living matter. J. Cell. Sci. 2017, 130, 2789–2796. [Google Scholar] [CrossRef]
- Saha, S.; Weber, C.A.; Nousch, M.; Adame-Arana, O.; Hoege, C.; Hein, M.Y.; Osborne-Nishimura, E.; Mahamid, J.; Jahnel, M.; Jawerth, L.; et al. Polar Positioning of Phase-Separated Liquid Compartments in Cells Regulated by an mRNA Competition Mechanism. Cell 2016, 166, 1572–1584. [Google Scholar] [CrossRef]
- Courchaine, E.M.; Lu, A.; Neugebauer, K.M. Droplet organelles? Embo J. 2016, 35, 1603–1612. [Google Scholar] [CrossRef]
- Chong, P.A.; Forman-Kay, J.D. Liquid-liquid phase separation in cellular signaling systems. Curr. Opin. Struct. Biol. 2016, 41, 180–186. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Hyman, A.A. Are aberrant phase transitions a driver of cellular aging? Bioessays 2016, 38, 959–968. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Supramolecular fuzziness of intracellular liquid droplets: Liquid-liquid phase transitions, membrane-less organelles, and intrinsic disorder. Molecules 2019, 24, 3265. [Google Scholar] [CrossRef] [PubMed]
- Zaslavsky, B.Y.; Uversky, V.N. In Aqua Veritas: The Indispensable yet Mostly Ignored Role of Water in Phase Separation and Membrane-less Organelles. Biochemistry 2018, 57, 2437–2451. [Google Scholar] [CrossRef]
- Uversky, V.N. Protein intrinsic disorder-based liquid-liquid phase transitions in biological systems: Complex coacervates and membrane-less organelles. Adv. Colloid Interface Sci. 2017, 239, 97–114. [Google Scholar] [CrossRef]
- Handwerger, K.E.; Cordero, J.A.; Gall, J.G. Cajal bodies, nucleoli, and speckles in the Xenopus oocyte nucleus have a low-density, sponge-like structure. Mol. Biol. Cell 2005, 16, 202–211. [Google Scholar] [CrossRef]
- Brangwynne, C.P. Phase transitions and size scaling of membrane-less organelles. J. Cell Biol. 2013, 203, 875–881. [Google Scholar] [CrossRef]
- Sokolova, E.; Spruijt, E.; Hansen, M.M.; Dubuc, E.; Groen, J.; Chokkalingam, V.; Piruska, A.; Heus, H.A.; Huck, W.T. Enhanced transcription rates in membrane-free protocells formed by coacervation of cell lysate. Proc. Natl. Acad. Sci. USA 2013, 110, 11692–11697. [Google Scholar] [CrossRef]
- Strulson, C.A.; Molden, R.C.; Keating, C.D.; Bevilacqua, P.C. RNA catalysis through compartmentalization. Nat. Chem. 2012, 4, 941–946. [Google Scholar] [CrossRef]
- Nikolic, J.; Lagaudriere-Gesbert, C.; Scrima, N.; Blondel, D.; Gaudin, Y. Structure and Function of Negri Bodies. Adv. Exp. Med. Biol. 2019, 1140, 111–127. [Google Scholar] [CrossRef]
- Formicola, N.; Vijayakumar, J.; Besse, F. Neuronal ribonucleoprotein granules: Dynamic sensors of localized signals. Traffic 2019, 20, 639–649. [Google Scholar] [CrossRef] [PubMed]
- Dundr, M.; Misteli, T. Biogenesis of nuclear bodies. Cold Spring Harb. Perspect. Biol. 2010, 2, a000711. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.S.; Zhang, B.; Spector, D.L. Biogenesis and function of nuclear bodies. Trends Genet. 2011, 27, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Phair, R.D.; Misteli, T. High mobility of proteins in the mammalian cell nucleus. Nature 2000, 404, 604–609. [Google Scholar] [CrossRef]
- Pederson, T. Protein mobility within the nucleus—What are the right moves? Cell 2001, 104, 635–638. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Eckmann, C.R.; Courson, D.S.; Rybarska, A.; Hoege, C.; Gharakhani, J.; Julicher, F.; Hyman, A.A. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 2009, 324, 1729–1732. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Mitchison, T.J.; Hyman, A.A. Active liquid-like behavior of nucleoli determines their size and shape in Xenopus laevis oocytes. Proc. Natl. Acad. Sci. USA 2011, 108, 4334–4339. [Google Scholar] [CrossRef]
- Feric, M.; Brangwynne, C.P. A nuclear F-actin scaffold stabilizes ribonucleoprotein droplets against gravity in large cells. Nat. Cell Biol. 2013, 15, 1253–1259. [Google Scholar] [CrossRef]
- Wippich, F.; Bodenmiller, B.; Trajkovska, M.G.; Wanka, S.; Aebersold, R.; Pelkmans, L. Dual specificity kinase DYRK3 couples stress granule condensation/dissolution to mTORC1 signaling. Cell 2013, 152, 791–805. [Google Scholar] [CrossRef]
- Uversky, V.N.; Kuznetsova, I.M.; Turoverov, K.K.; Zaslavsky, B. Intrinsically disordered proteins as crucial constituents of cellular aqueous two phase systems and coacervates. FEBS Lett. 2015, 589, 15–22. [Google Scholar] [CrossRef]
- Zhu, L.; Brangwynne, C.P. Nuclear bodies: The emerging biophysics of nucleoplasmic phases. Curr. Opin. Cell Biol. 2015, 34, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Holehouse, A.S.; Pappu, R.V. Functional Implications of Intracellular Phase Transitions. Biochemistry 2018, 57, 2415–2423. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Intrinsically disordered proteins in overcrowded milieu: Membrane-less organelles, phase separation, and intrinsic disorder. Curr. Opin. Struct. Biol. 2017, 44, 18–30. [Google Scholar] [CrossRef] [PubMed]
- Darling, A.L.; Liu, Y.; Oldfield, C.J.; Uversky, V.N. Intrinsically Disordered Proteome of Human Membrane-Less Organelles. Proteomics 2018, 18, e1700193. [Google Scholar] [CrossRef] [PubMed]
- Nott, T.J.; Petsalaki, E.; Farber, P.; Jervis, D.; Fussner, E.; Plochowietz, A.; Craggs, T.D.; Bazett-Jones, D.P.; Pawson, T.; Forman-Kay, J.D.; et al. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell 2015, 57, 936–947. [Google Scholar] [CrossRef] [PubMed]
- Darling, A.L.; Zaslavsky, B.Y.; Uversky, V.N. Intrinsic Disorder-Based Emergence in Cellular Biology: Physiological and Pathological Liquid-Liquid Phase Transitions in Cells. Polymers 2019, 11, 990. [Google Scholar] [CrossRef]
- Turoverov, K.K.; Kuznetsova, I.M.; Fonin, A.V.; Darling, A.L.; Zaslavsky, B.Y.; Uversky, V.N. Stochasticity of Biological Soft Matter: Emerging Concepts in Intrinsically Disordered Proteins and Biological Phase Separation. Trends Biochem. Sci. 2019, 44, 716–728. [Google Scholar] [CrossRef]
- Ambadipudi, S.; Biernat, J.; Riedel, D.; Mandelkow, E.; Zweckstetter, M. Liquid-liquid phase separation of the microtubule-binding repeats of the Alzheimer-related protein Tau. Nat. Commun. 2017, 8, 275. [Google Scholar] [CrossRef]
- Ambadipudi, S.; Reddy, J.G.; Biernat, J.; Mandelkow, E.; Zweckstetter, M. Residue-specific identification of phase separation hot spots of Alzheimer’s-related protein tau. Chem. Sci. 2019, 10, 6503–6507. [Google Scholar] [CrossRef]
- Reichheld, S.E.; Muiznieks, L.D.; Keeley, F.W.; Sharpe, S. Direct observation of structure and dynamics during phase separation of an elastomeric protein. Proc. Natl. Acad. Sci. USA 2017, 114, E4408–E4415. [Google Scholar] [CrossRef] [PubMed]
- Murthy, A.C.; Dignon, G.L.; Kan, Y.; Zerze, G.H.; Parekh, S.H.; Mittal, J.; Fawzi, N.L. Molecular interactions underlying liquid-liquid phase separation of the FUS low-complexity domain. Nat. Struct. Mol. Biol. 2019, 26, 637–648. [Google Scholar] [CrossRef] [PubMed]
- Ryan, V.H.; Dignon, G.L.; Zerze, G.H.; Chabata, C.V.; Silva, R.; Conicella, A.E.; Amaya, J.; Burke, K.A.; Mittal, J.; Fawzi, N.L. Mechanistic View of hnRNPA2 Low-Complexity Domain Structure, Interactions, and Phase Separation Altered by Mutation and Arginine Methylation. Mol. Cell 2018, 69, 465–479. [Google Scholar] [CrossRef] [PubMed]
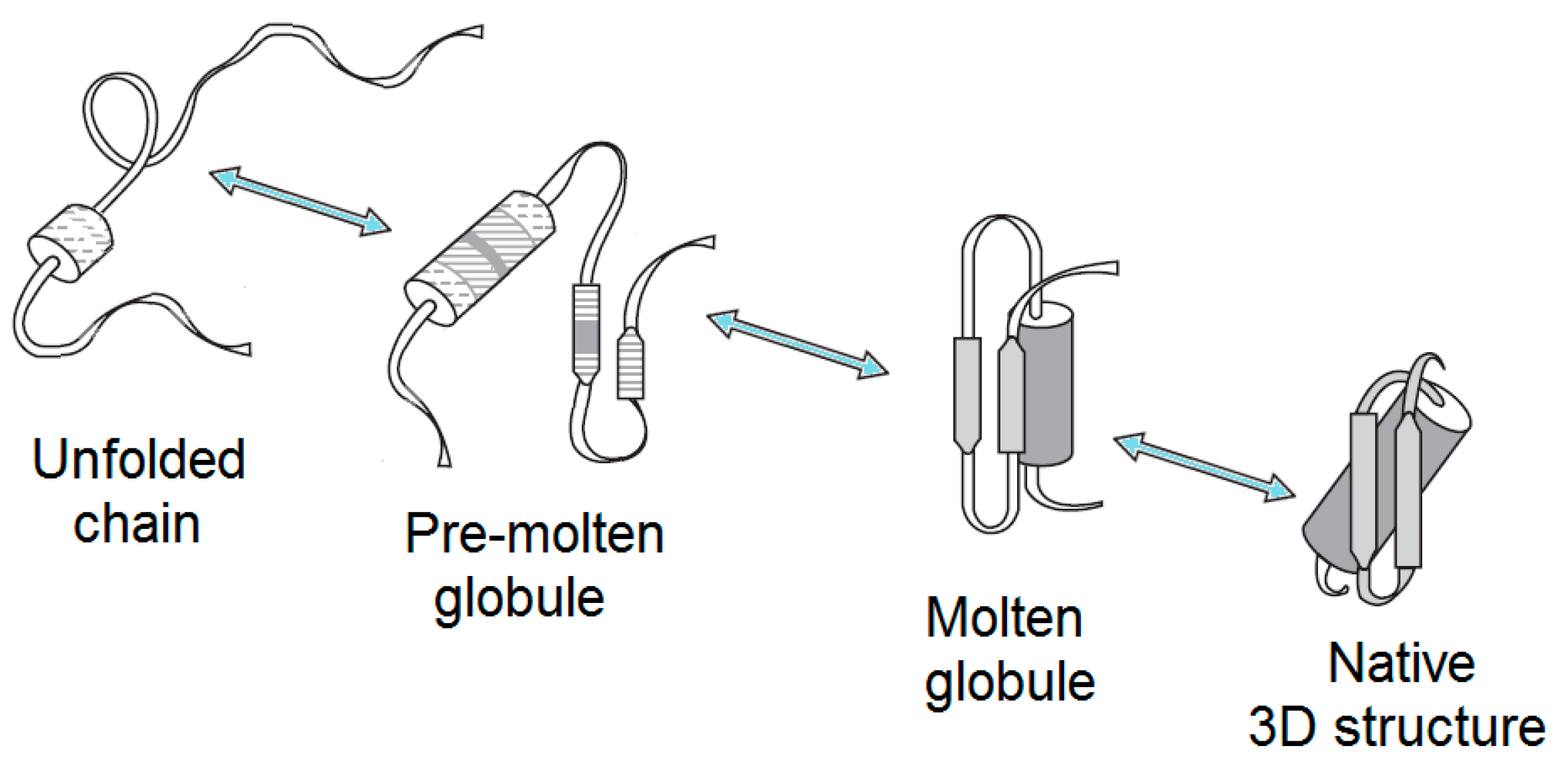
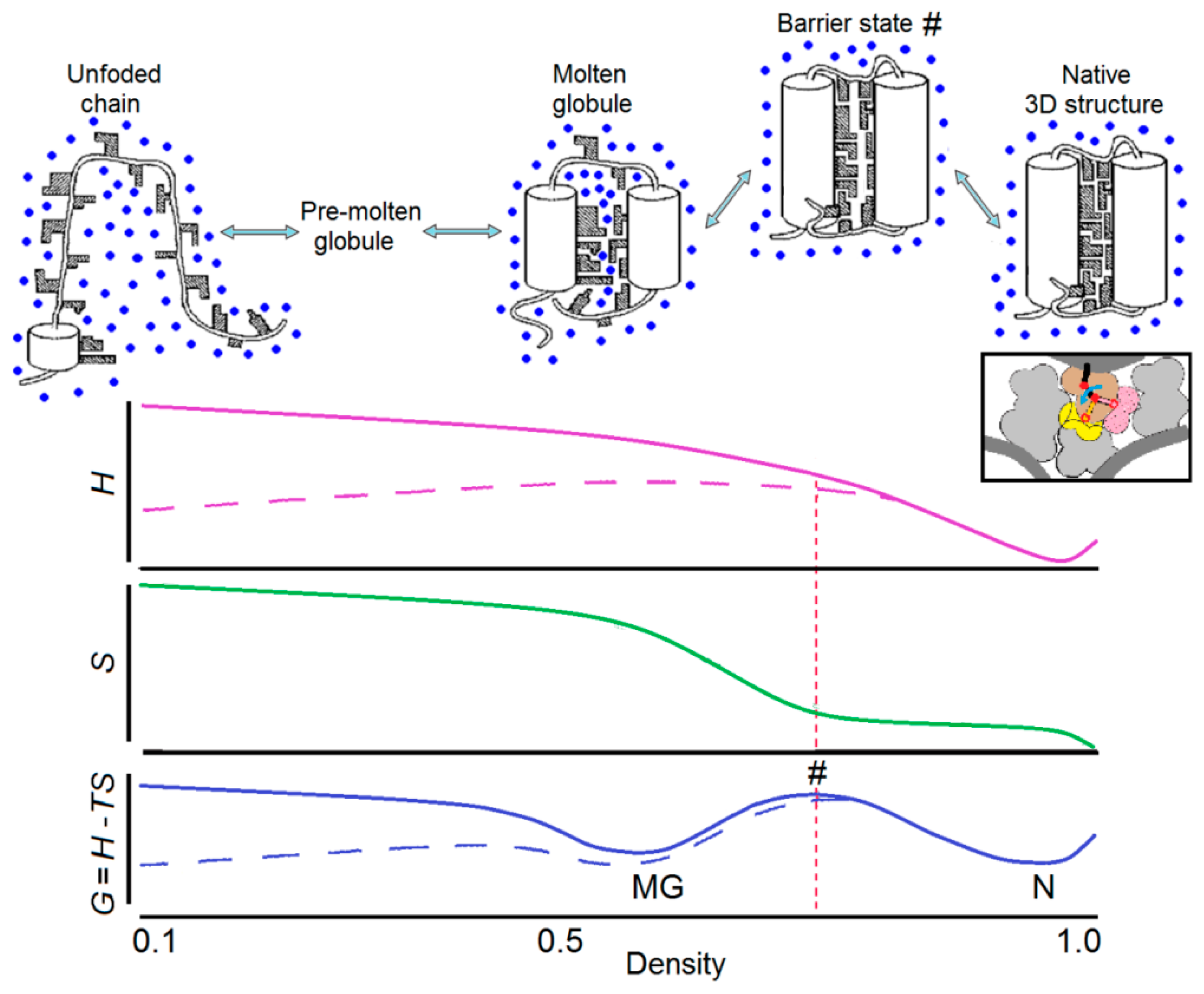
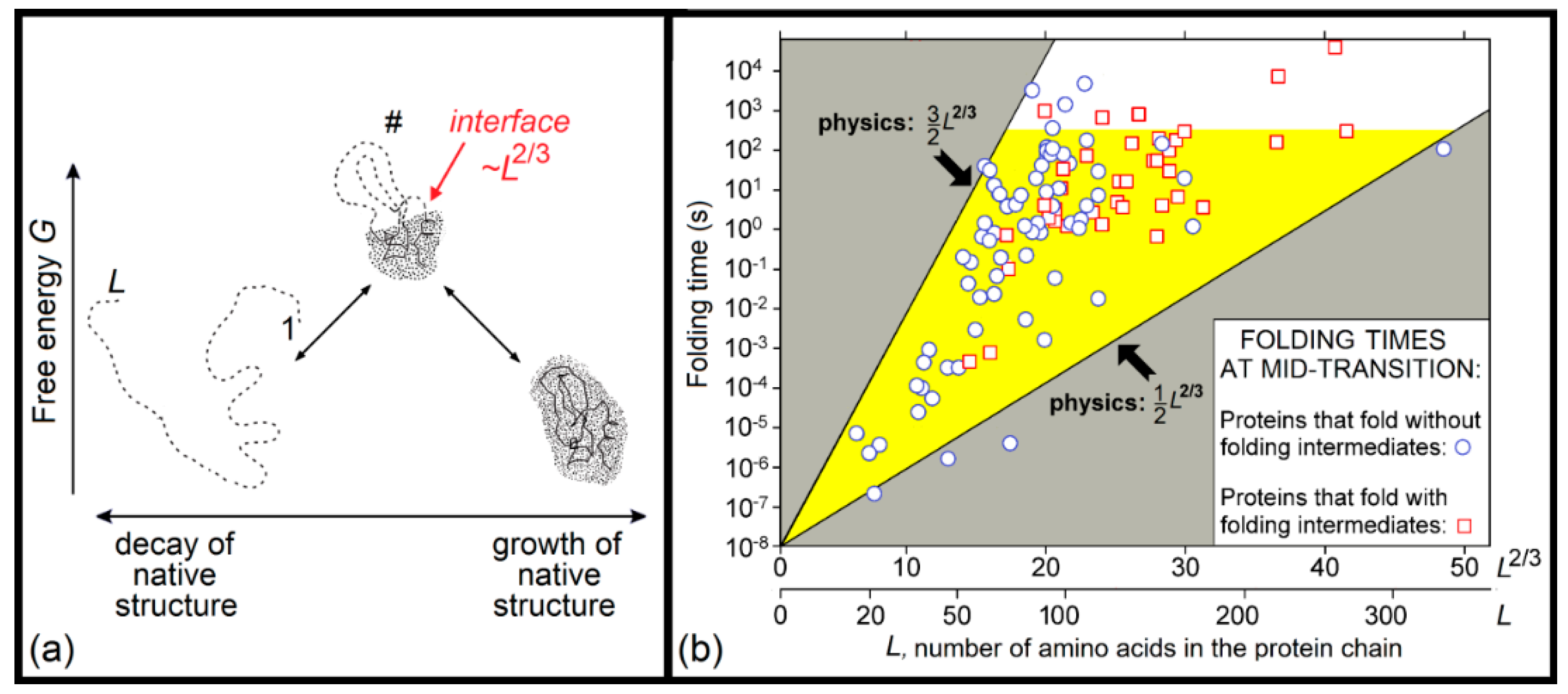
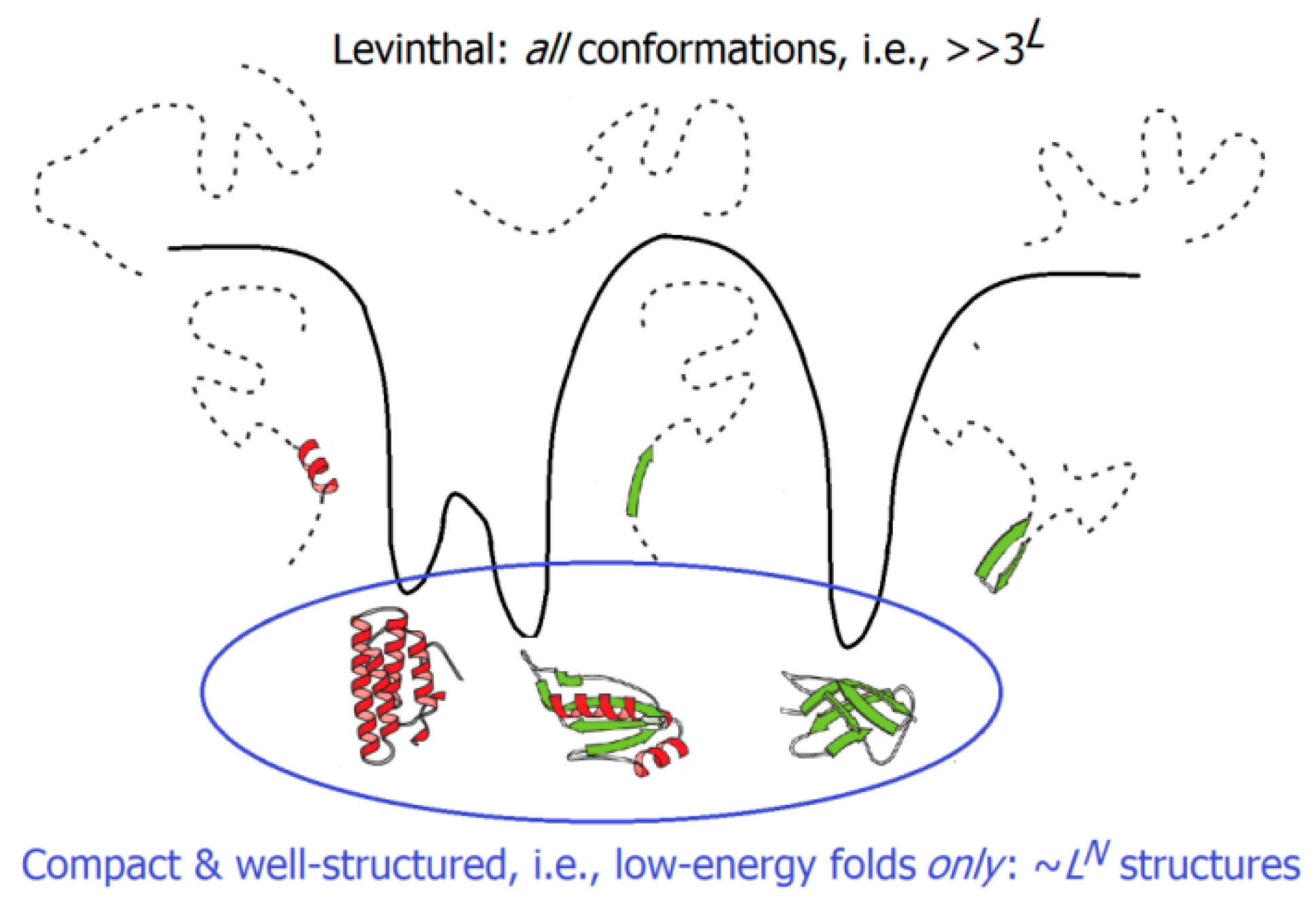
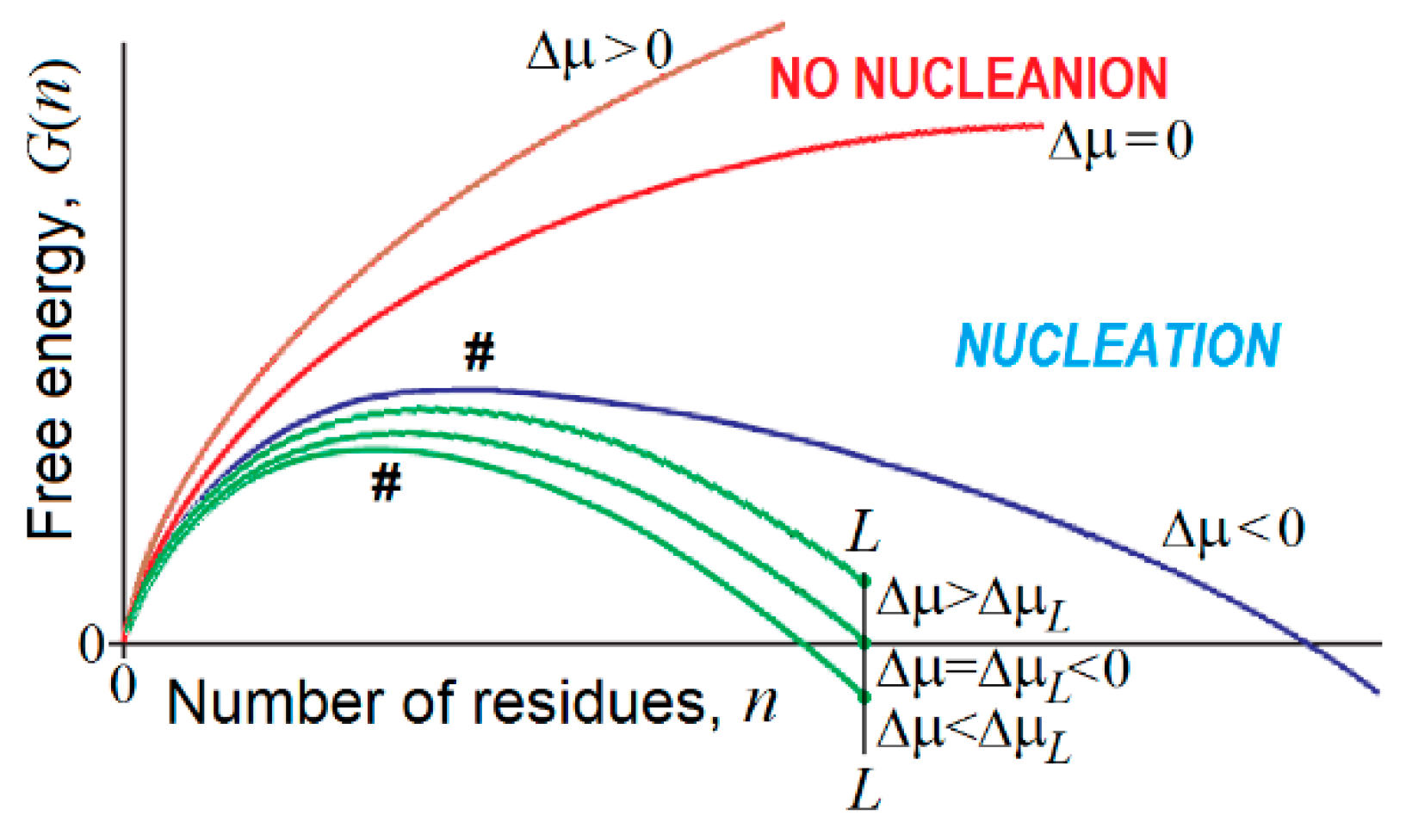
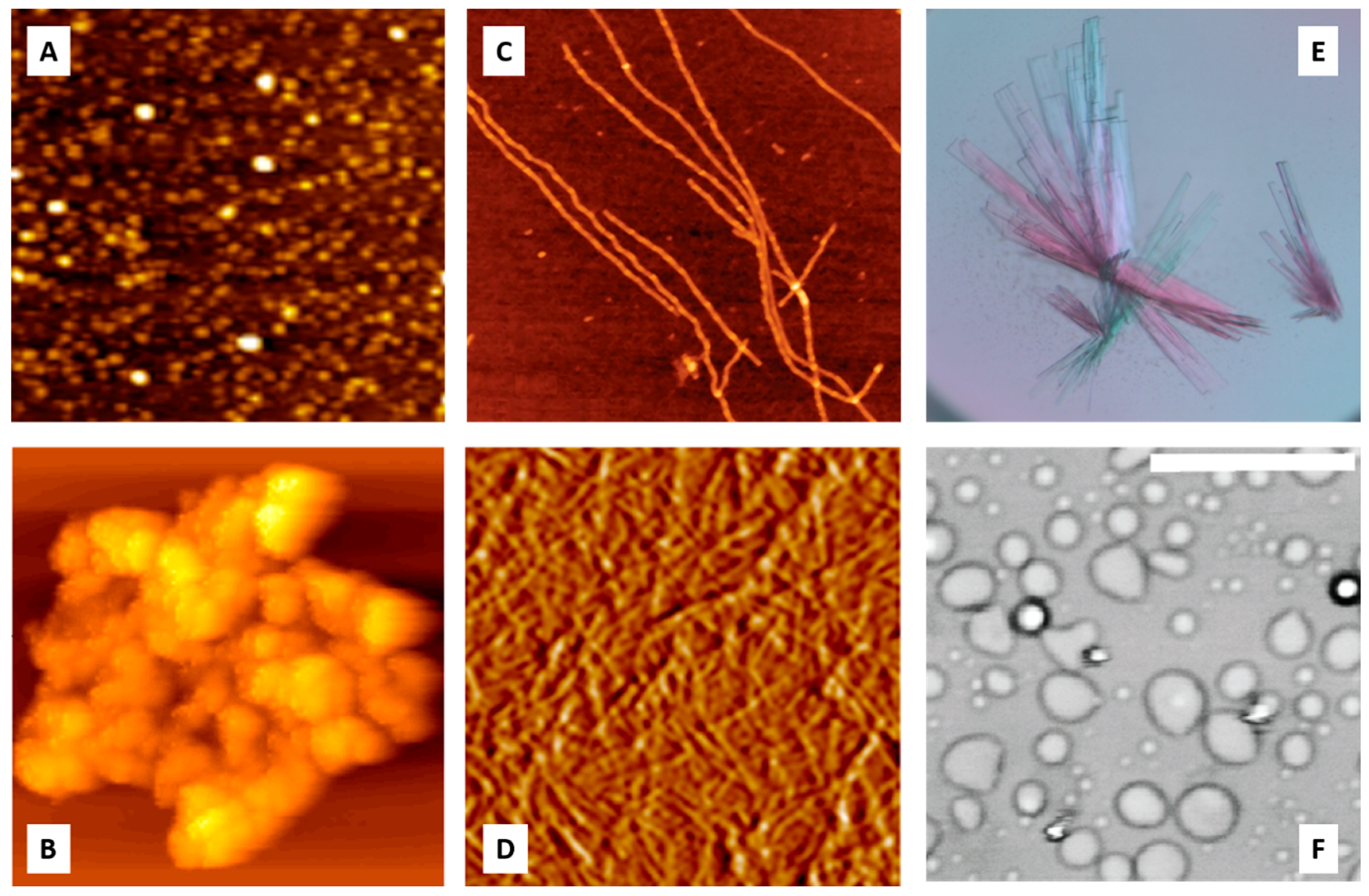


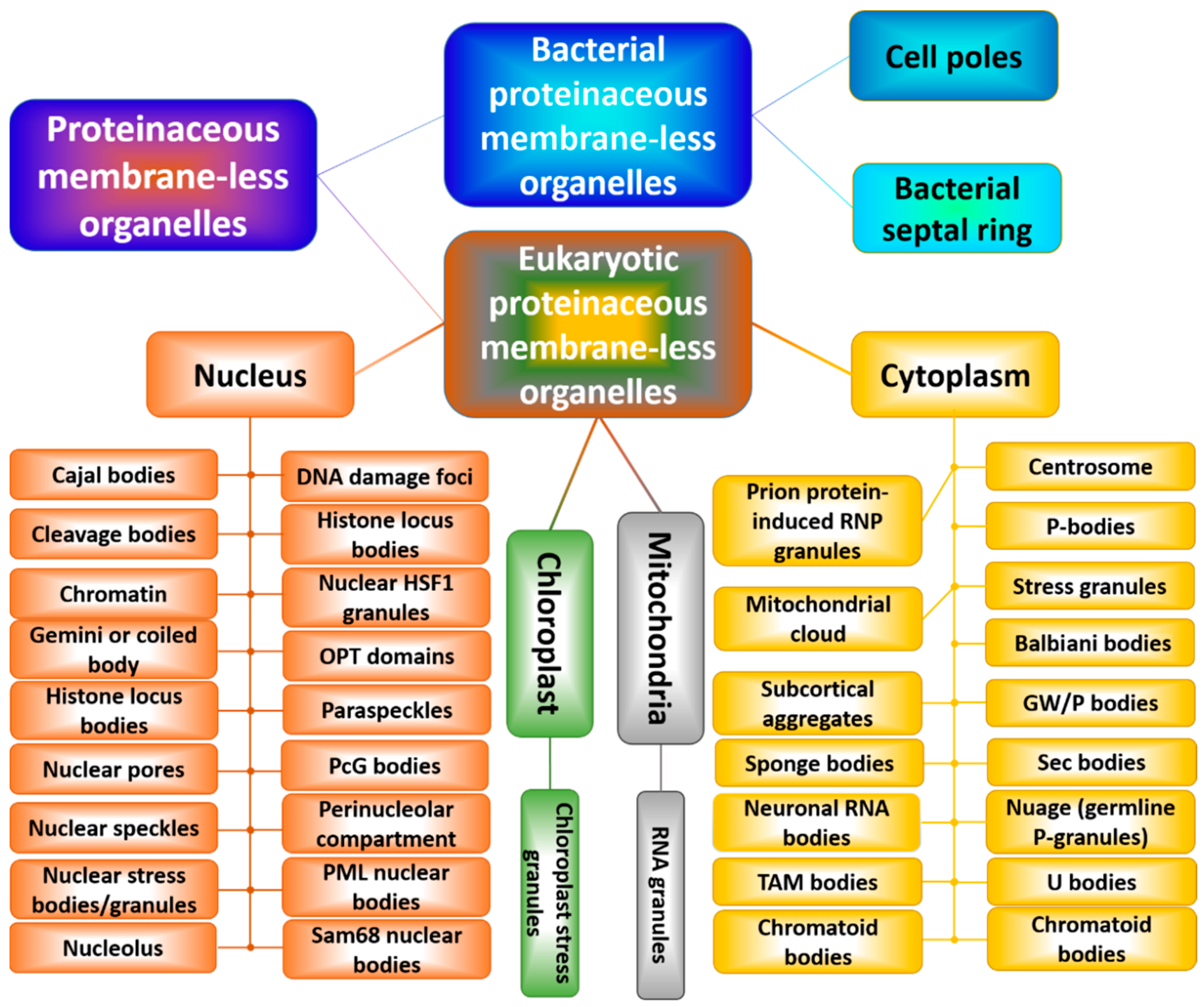
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uversky, V.N.; Finkelstein, A.V. Life in Phases: Intra- and Inter- Molecular Phase Transitions in Protein Solutions. Biomolecules 2019, 9, 842. https://doi.org/10.3390/biom9120842
Uversky VN, Finkelstein AV. Life in Phases: Intra- and Inter- Molecular Phase Transitions in Protein Solutions. Biomolecules. 2019; 9(12):842. https://doi.org/10.3390/biom9120842
Chicago/Turabian StyleUversky, Vladimir N., and Alexei V. Finkelstein. 2019. "Life in Phases: Intra- and Inter- Molecular Phase Transitions in Protein Solutions" Biomolecules 9, no. 12: 842. https://doi.org/10.3390/biom9120842
APA StyleUversky, V. N., & Finkelstein, A. V. (2019). Life in Phases: Intra- and Inter- Molecular Phase Transitions in Protein Solutions. Biomolecules, 9(12), 842. https://doi.org/10.3390/biom9120842





