Modeling Membrane Curvature Generation due to Membrane–Protein Interactions
Abstract
1. Introduction
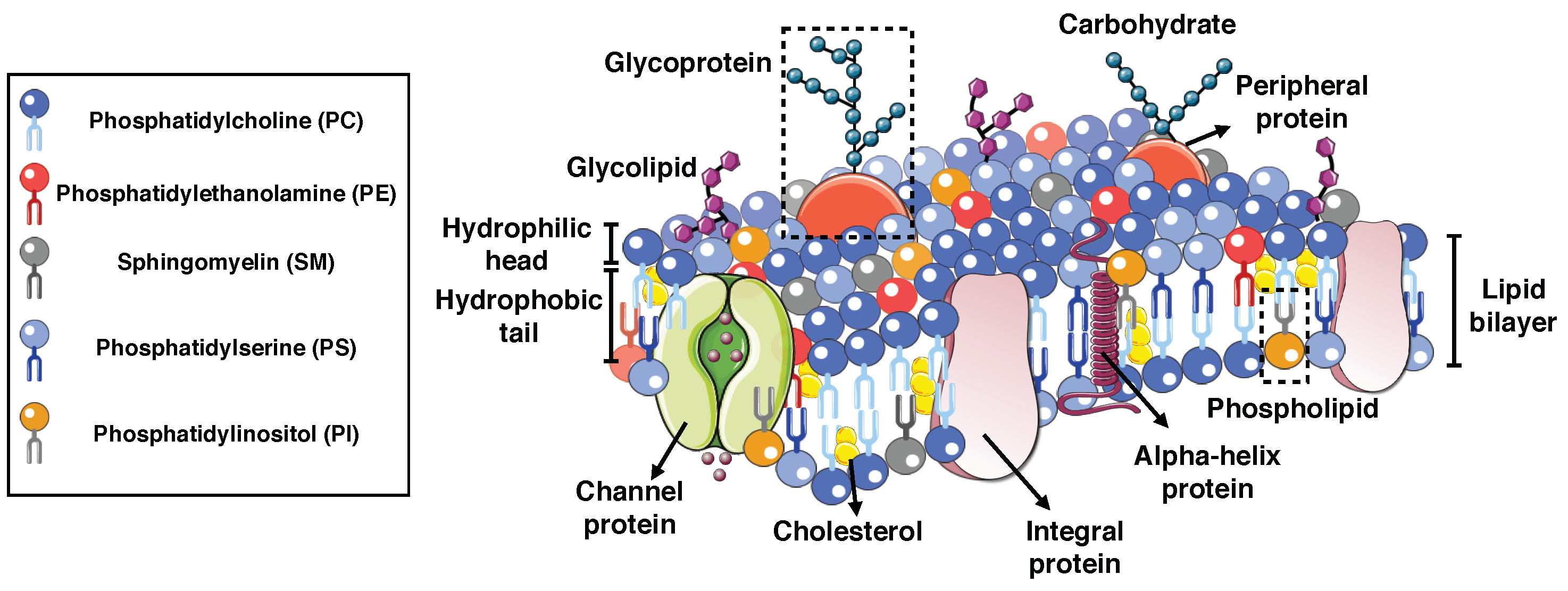
2. Composition of Biological Membranes
2.1. Integral Proteins
2.2. Peripheral Proteins
3. Membrane Curvature Generation due to Proteins
3.1. Conical and Inverted Conical-Shaped Proteins
3.2. BIN-Amphiphysin-Rvs Domain Proteins
3.3. Coat Proteins
4. Theoretical Models of Biological Membranes
4.1. Mechanical Viewpoint
4.2. Simulation Techniques
5. Continuum Elastic Energy Models of Membrane–Protein Interactions
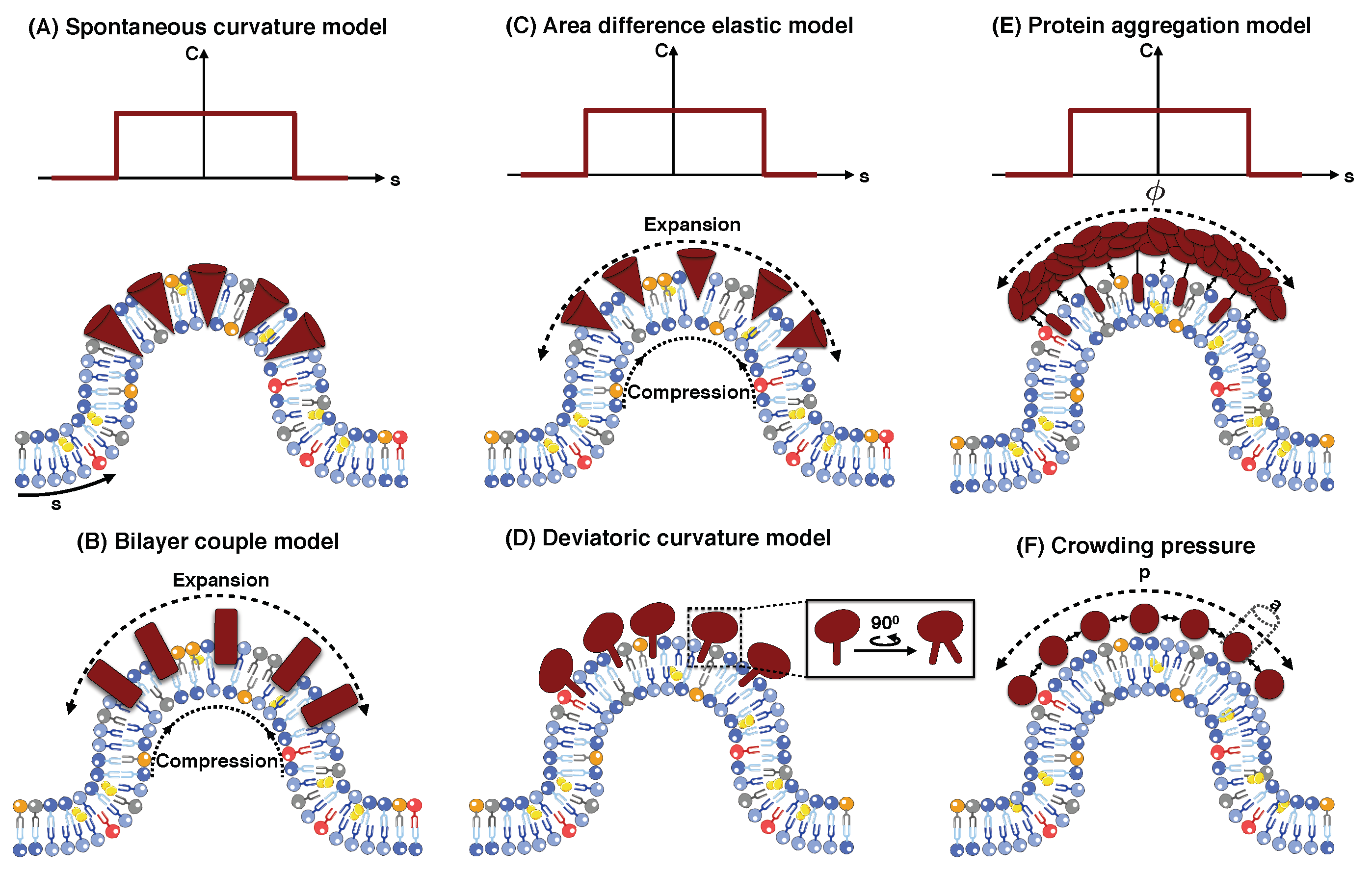
5.1. Spontaneous Curvature Model
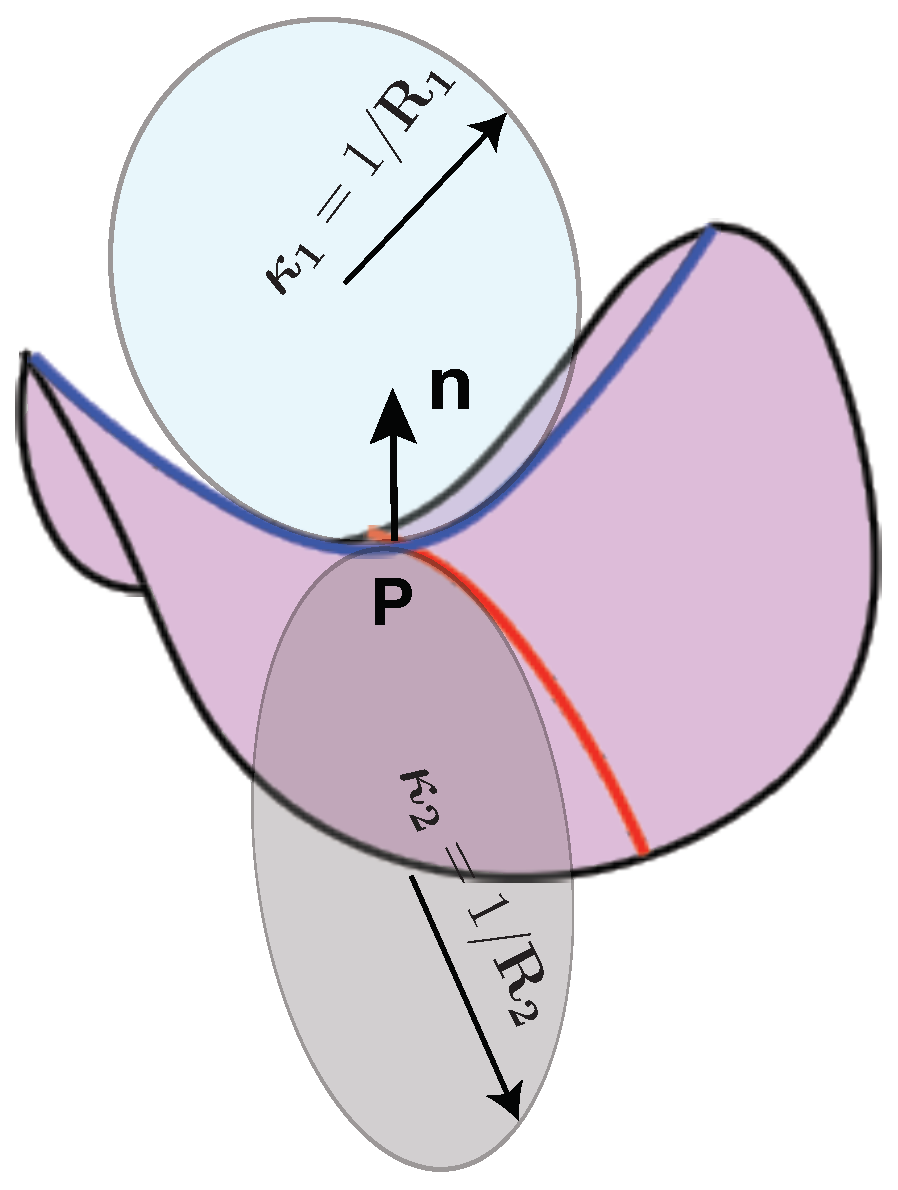
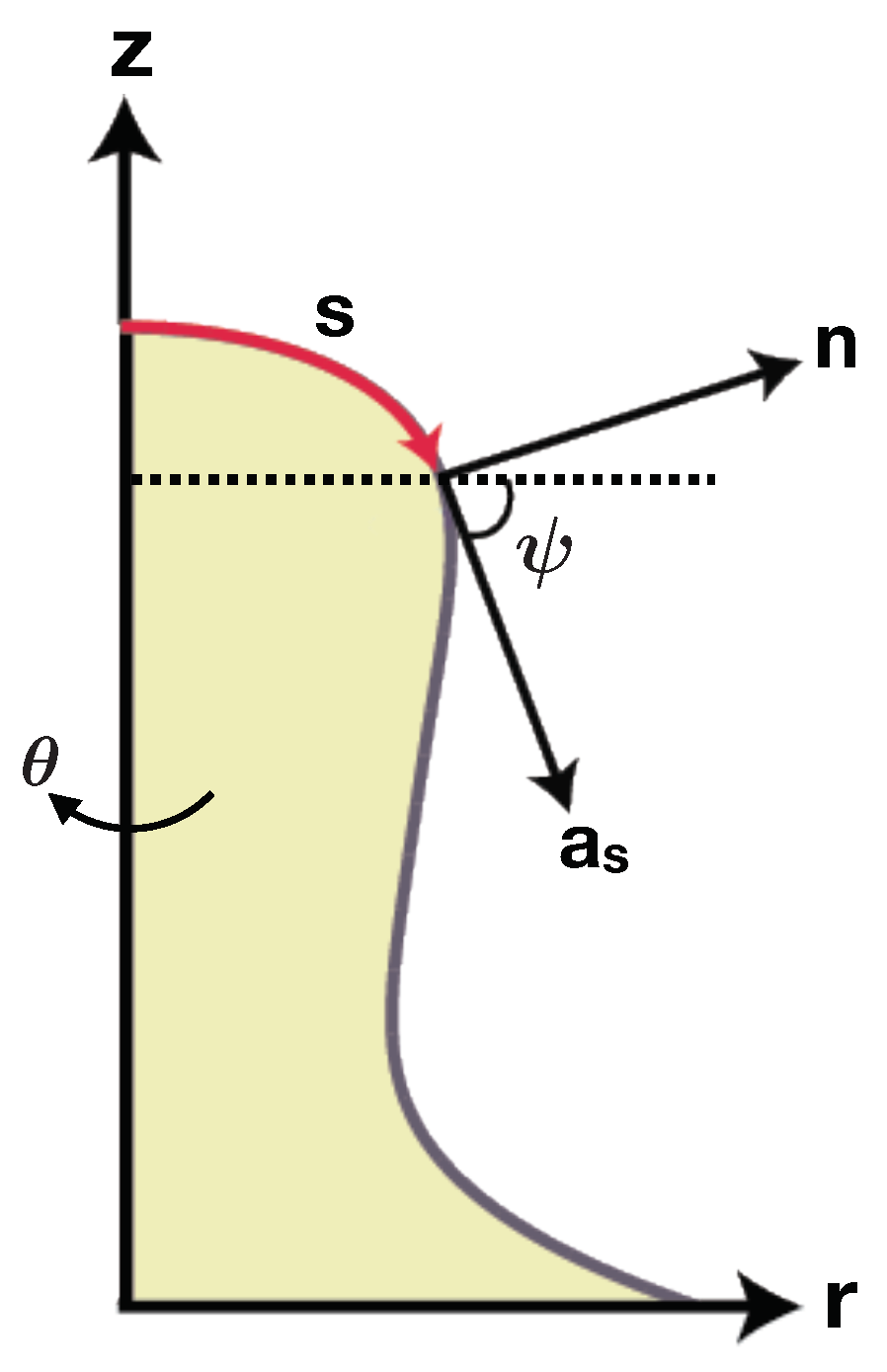
5.2. Bilayer Couple Model
5.3. Area Difference Elasticity Model
5.4. Deviatoric Curvature Model
5.5. Protein Aggregation Model
5.6. Protein Crowding
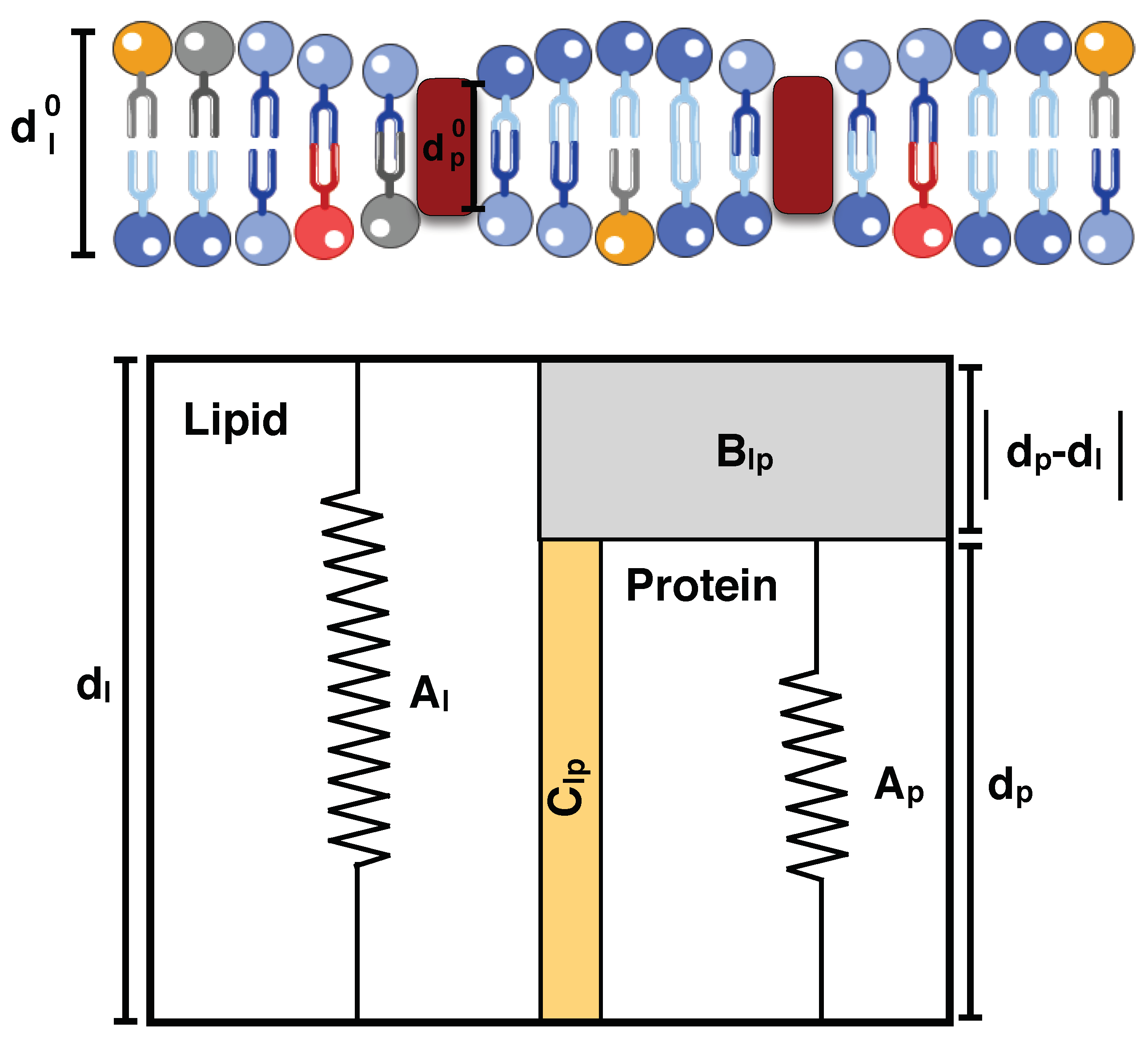
5.7. Hydrophobic Mismatch
6. Future Perspective and Challenges
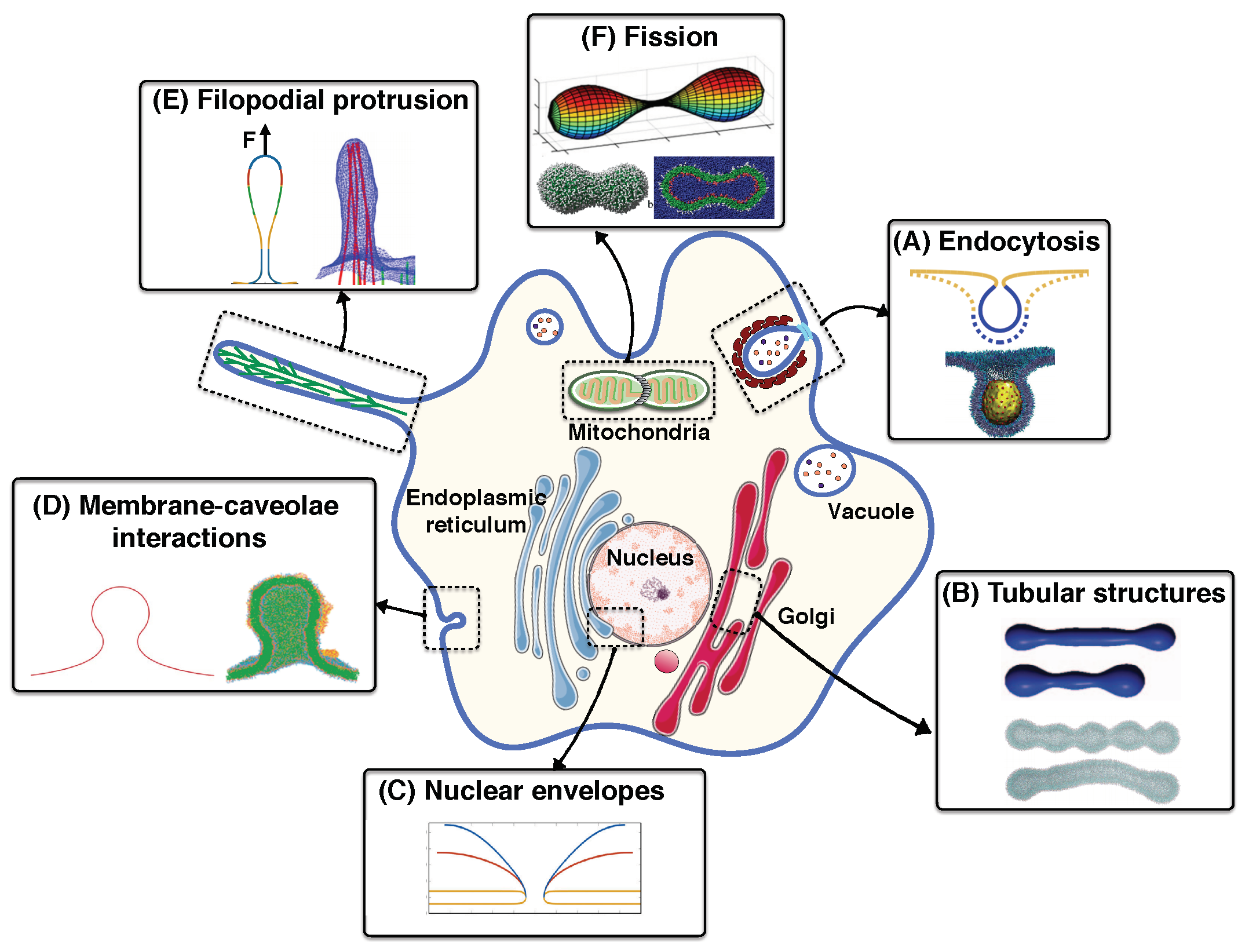
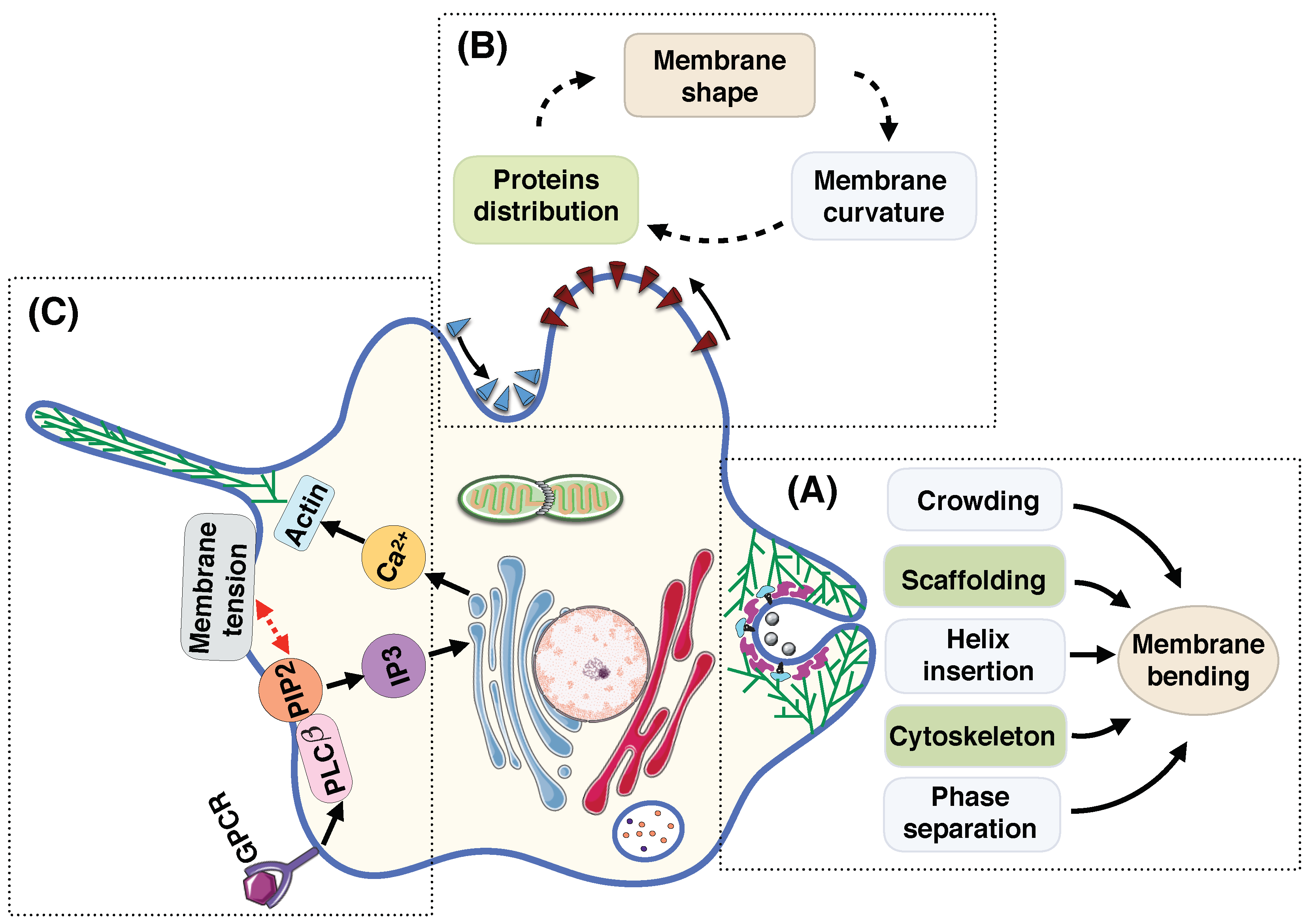
- Membrane deformation is a dynamic process; surrounding fluid flow, thermal fluctuation, and diffusion of proteins actively regulate the shape of the membrane at each instance [11,188,225,226,227,228,229]. Currently, the models for membranes at mechanical equilibrium are well-developed but the models for dynamic processes have not been as well-developed and the community must invest some effort in this aspect.
- In vivo, multiple mechanisms coupling membrane deformation and cytoskeletal remodeling are commonplace (Figure 5A). Therefore, the models should be extended to include the dynamic effects and the rearrangement of the actin cytoskeleton layer underneath of the membrane.
- Membrane deformation and protein absorption/rearrangement are often considered as two separate processes with little to no impact on each other. However, recent studies show that proteins can sense the membrane curvature (Figure 5B). Therefore, there is a feedback loop between the protein distribution and the membrane configuration. While some models have considered this feedback loop [176,230,231,232,233], we still need more quantitative agreements between theory and experiment.
- Cell shape can control signal transduction at the plasma membrane, while intracellular signaling changes the membrane tension [234] (Figure 5C). This coupling between the cell shape and the signaling network inside the cell should be further understood in terms of both quantitative experimental and theoretical biology.
- As discussed above, membrane deformation is a multiscale phenomena that results from the reorientation of lipids to large-scale change in the membrane curvature. This suggests the extension of available models toward multiscale models that could represent each biological process over multiple length scales [117,235].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mukherjee, S.; Maxfield, F.R. Role of membrane organization and membrane domains in endocytic lipid trafficking. Traffic 2000, 1, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Gruenberg, J. The endocytic pathway: A mosaic of domains. Nat. Rev. Mol. Cell Biol. 2001, 2, 721. [Google Scholar] [CrossRef] [PubMed]
- Westermann, B. Mitochondrial fusion and fission in cell life and death. Nat. Rev. Mol. Cell Biol. 2010, 11, 872. [Google Scholar] [CrossRef] [PubMed]
- Van der Bliek, A.M.; Shen, Q.; Kawajiri, S. Mechanisms of mitochondrial fission and fusion. Cold Spring Harb. Perspect. Biol. 2013, 5, a011072. [Google Scholar] [CrossRef] [PubMed]
- Grafmuller, A.; Shillcock, J.; Lipowsky, R. The fusion of membranes and vesicles: Pathway and energy barriers from dissipative particle dynamics. Biophys. J. 2009, 96, 2658–2675. [Google Scholar] [CrossRef] [PubMed]
- Jahn, R.; Fasshauer, D. Molecular machines governing exocytosis of synaptic vesicles. Nature 2012, 490, 201. [Google Scholar] [CrossRef] [PubMed]
- Reilly, G.C.; Engler, A.J. Intrinsic extracellular matrix properties regulate stem cell differentiation. J. Biomech. 2010, 43, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Rangamani, P.; Fardin, M.A.; Lipshtat, A.; Dubin-Thaler, B.; Rossier, O.; Sheetz, M.P.; Iyengar, R. Mechanisms controlling cell size and shape during isotropic cell spreading. Biophys. J. 2010, 98, 2136–2146. [Google Scholar] [CrossRef] [PubMed]
- Rangamani, P.; Fardin, M.A.; Xiong, Y.; Lipshtat, A.; Rossier, O.; Sheetz, M.P.; Iyengar, R. Signaling network triggers and membrane physical properties control the actin cytoskeleton-driven isotropic phase of cell spreading. Biophys. J. 2011, 100, 845–857. [Google Scholar] [CrossRef] [PubMed]
- Neves, S.R.; Tsokas, P.; Sarkar, A.; Grace, E.A.; Rangamani, P.; Taubenfeld, S.M.; Alberini, C.M.; Schaff, J.C.; Blitzer, R.D.; Moraru, I.I.; et al. Cell shape and negative links in regulatory motifs together control spatial information flow in signaling networks. Cell 2008, 133, 666–680. [Google Scholar] [CrossRef] [PubMed]
- Rangamani, P.; Lipshtat, A.; Azeloglu, E.U.; Calizo, R.C.; Hu, M.; Ghassemi, S.; Hone, J.; Scarlata, S.; Neves, S.R.; Iyengar, R. Decoding information in cell shape. Cell 2013, 154, 1356–1369. [Google Scholar] [CrossRef] [PubMed]
- Bell, M.; Bartol, T.; Sejnowski, T.; Rangamani, P. Dendritic spine geometry and spine apparatus organization govern the spatiotemporal dynamics of calcium. bioRxiv 2018, 386367. [Google Scholar] [CrossRef]
- Cowling, B.S.; Toussaint, A.; Muller, J.; Laporte, J. Defective membrane remodeling in neuromuscular diseases: insights from animal models. PLoS Genet. 2012, 8, e1002595. [Google Scholar] [CrossRef] [PubMed]
- De Matteis, M.A.; Luini, A. Mendelian disorders of membrane trafficking. N. Engl. J. Med. 2011, 365, 927–938. [Google Scholar] [CrossRef] [PubMed]
- Ward, K.E.; Ropa, J.P.; Adu-Gyamfi, E.; Stahelin, R.V. C2 domain membrane penetration by group IVA cytosolic phospholipase A2 induces membrane curvature changes. J. Lipid Res. 2012. [Google Scholar] [CrossRef] [PubMed]
- Hewson, C.A.; Patel, S.; Calzetta, L.; Campwala, H.; Havard, S.; Luscombe, E.; Clarke, P.A.; Peachell, P.T.; Matera, M.G.; Cazzola, M.; et al. Preclinical evaluation of an inhibitor of cytosolic phospholipase A2α for the treatment of asthma. J. Pharmacol. Exp. Ther. 2012, 340, 656–665. [Google Scholar] [CrossRef] [PubMed]
- Tai, N.; Kuwabara, K.; Kobayashi, M.; Yamada, K.; Ono, T.; Seno, K.; Gahara, Y.; Ishizaki, J.; Hori, Y. Cytosolic phospholipase A2 alpha inhibitor, pyrroxyphene, displays anti-arthritic and anti-bone destructive action in a murine arthritis model. Inflamm. Res. 2010, 59, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Kishimoto, K.; Li, R.C.; Zhang, J.; Klaus, J.A.; Kibler, K.K.; Dore, S.; Koehler, R.C.; Sapirstein, A. Cytosolic phospholipase A2 alpha amplifies early cyclooxygenase-2 expression, oxidative stress and MAP kinase phosphorylation after cerebral ischemia in mice. J. Neuroinflamm. 2010, 7, 42. [Google Scholar]
- Kerkela, R.; Boucher, M.; Zaka, R.; Gao, E.; Harris, D.; Piuhola, J.; Song, J.; Serpi, R.; Woulfe, K.C.; Cheung, J.Y.; et al. Cytosolic phospholipase A2α protects against ischemia/reperfusion injury in the heart. Clin. Transl. Sci. 2011, 4, 236–242. [Google Scholar] [CrossRef] [PubMed]
- Sundarraj, S.; Kannan, S.; Thangam, R.; Gunasekaran, P. Effects of the inhibition of cytosolic phospholipase A2α in non-small cell lung cancer cells. J. Cancer Res. Clin. Oncol. 2012, 138, 827–835. [Google Scholar] [CrossRef] [PubMed]
- Toussaint, A.; Cowling, B.S.; Hnia, K.; Mohr, M.; Oldfors, A.; Schwab, Y.; Yis, U.; Maisonobe, T.; Stojkovic, T.; Wallgren-Pettersson, C.; et al. Defects in amphiphysin 2 (BIN1) and triads in several forms of centronuclear myopathies. Acta Neuropathol. 2011, 121, 253–266. [Google Scholar] [CrossRef] [PubMed]
- McMahon, H.T.; Gallop, J.L. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 2005, 438, 590. [Google Scholar] [CrossRef] [PubMed]
- Jarsch, I.K.; Daste, F.; Gallop, J.L. Membrane curvature in cell biology: An integration of molecular mechanisms. J. Cell Biol. 2016, 214, 375–387. [Google Scholar] [CrossRef] [PubMed]
- Hochmuth, R.; Waugh, R. Erythrocyte membrane elasticity and viscosity. Annu. Rev. Physiol. 1987, 49, 209–219. [Google Scholar] [CrossRef] [PubMed]
- Giardini, P.A.; Fletcher, D.A.; Theriot, J.A. Compression forces generated by actin comet tails on lipid vesicles. Proc. Natl. Acad. Sci. USA 2003, 100, 6493–6498. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, A.E. Membrane bending by actin polymerization. Curr. Opin. Cell Biol. 2018, 50, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kaksonen, M.; Toret, C.P.; Drubin, D.G. Harnessing actin dynamics for clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2006, 7, 404. [Google Scholar] [CrossRef] [PubMed]
- Zimmerberg, J.; Kozlov, M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006, 7, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Argudo, D.; Bethel, N.P.; Marcoline, F.V.; Grabe, M. Continuum descriptions of membranes and their interaction with proteins: Towards chemically accurate models. Biochim. Biophys. Acta 2016, 1858, 1619–1634. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, M.M.; Campelo, F.; Liska, N.; Chernomordik, L.V.; Marrink, S.J.; McMahon, H.T. Mechanisms shaping cell membranes. Curr. Opin. Cell Biol. 2014, 29, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, J. Static equilibrium configurations of a model red blood cell. J. Math. Biol. 1977, 4, 149–169. [Google Scholar] [CrossRef] [PubMed]
- Alimohamadi, H.; Vasan, R.; Hassinger, J.; Stachowiak, J.C.; Rangamani, P. The role of traction in membrane curvature generation. Mol. Biol. Cell 2018, 29, 2024–2035. [Google Scholar] [CrossRef] [PubMed]
- Alimohamadi, H.; Vasan, R.; Hassinger, J.; Stachowiak, J.; Rangamani, P. The role of traction in membrane curvature generation. Biophys. J. 2018, 114, 600a. [Google Scholar] [CrossRef]
- Guven, J. Membrane geometry with auxiliary variables and quadratic constraints. J. Phys. A 2004, 37, L313. [Google Scholar] [CrossRef]
- Aridor, M.; Bannykh, S.I.; Rowe, T.; Balch, W.E. Sequential coupling between COPII and COPI vesicle coats in endoplasmic reticulum to Golgi transport. J. Cell Biol. 1995, 131, 875–893. [Google Scholar] [CrossRef] [PubMed]
- Davies, K.M.; Anselmi, C.; Wittig, I.; Faraldo-Gomez, J.D.; Kuhlbrandt, W. Structure of the yeast F1Fo-ATP synthase dimer and its role in shaping the mitochondrial cristae. Proc. Natl. Acad. Sci. USA 2012, 109, 13602–13607. [Google Scholar] [CrossRef] [PubMed]
- Landau, E.M.; Rosenbusch, J.P. Lipidic cubic phases: A novel concept for the crystallization of membrane proteins. Proc. Natl. Acad. Sci. USA 1996, 93, 14532–14535. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, N.W.; Mishra, A.; Wang, J.; DeGrado, W.F.; Wong, G.C. Influenza virus A M2 protein generates negative Gaussian membrane curvature necessary for budding and scission. J. Am. Chem. Soc. 2013, 135, 13710–13719. [Google Scholar] [CrossRef] [PubMed]
- Gallop, J.L.; Jao, C.C.; Kent, H.M.; Butler, P.J.G.; Evans, P.R.; Langen, R.; McMahon, H.T. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006, 25, 2898–2910. [Google Scholar] [CrossRef] [PubMed]
- Pucadyil, T.J.; Schmid, S.L. Conserved functions of membrane active GTPases in coated vesicle formation. Science 2009, 325, 1217–1220. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.C.; Orci, L.; Hamamoto, S.; Futai, E.; Ravazzola, M.; Schekman, R. Sar1p N-terminal helix initiates membrane curvature and completes the fission of a COPII vesicle. Cell 2005, 122, 605–617. [Google Scholar] [CrossRef] [PubMed]
- Campelo, F.; McMahon, H.T.; Kozlov, M.M. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 2008, 95, 2325–2339. [Google Scholar] [CrossRef] [PubMed]
- Karotki, L.; Huiskonen, J.T.; Stefan, C.J.; Ziolkowska, N.E.; Roth, R.; Surma, M.A.; Krogan, N.J.; Emr, S.D.; Heuser, J.; Grunewald, K.; et al. Eisosome proteins assemble into a membrane scaffold. J. Cell Biol. 2011, 195, 889–902. [Google Scholar] [CrossRef] [PubMed]
- Daumke, O.; Roux, A.; Haucke, V. BAR domain scaffolds in dynamin-mediated membrane fission. Cell 2014, 156, 882–892. [Google Scholar] [CrossRef] [PubMed]
- Snead, W.T.; Hayden, C.C.; Gadok, A.K.; Zhao, C.; Lafer, E.M.; Rangamani, P.; Stachowiak, J.C. Membrane fission by protein crowding. Proc. Natl. Acad. Sci. USA 2017, 114, E3258–E3267. [Google Scholar] [CrossRef] [PubMed]
- Stachowiak, J.C.; Schmid, E.M.; Ryan, C.J.; Ann, H.S.; Sasaki, D.Y.; Sherman, M.B.; Geissler, P.L.; Fletcher, D.A.; Hayden, C.C. Membrane bending by protein–protein crowding. Nat. Cell Biol. 2012, 14, 944–949. [Google Scholar] [CrossRef] [PubMed]
- Busch, D.J.; Houser, J.R.; Hayden, C.C.; Sherman, M.B.; Lafer, E.M.; Stachowiak, J.C. Intrinsically disordered proteins drive membrane curvature. Nat. Commun. 2015, 6, 7875. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y. A glimpse of structural biology through X-ray crystallography. Cell 2014, 159, 995–1014. [Google Scholar] [CrossRef] [PubMed]
- Hsia, C.Y.; Richards, M.J.; Daniel, S. A review of traditional and emerging methods to characterize lipid–protein interactions in biological membranes. Anal. Methods 2015, 7, 7076–7094. [Google Scholar] [CrossRef]
- Marion, D. An introduction to biological NMR spectroscopy. Mol. Cell. Proteom. 2013. [Google Scholar] [CrossRef] [PubMed]
- Emsley, J.W.; Feeney, J.; Sutcliffe, L.H. High Resolution Nuclear Magnetic Resonance Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2. [Google Scholar]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Shao, L.; Higgins, C.D.; Poulton, J.S.; Peifer, M.; Davidson, M.W.; Wu, X.; Goldstein, B.; Betzig, E. Noninvasive imaging beyond the diffraction limit of 3D dynamics in thickly fluorescent specimens. Cell 2012, 151, 1370–1385. [Google Scholar] [CrossRef] [PubMed]
- Bozzola, J.J.; Russell, L.D. Electron Microscopy: Principles and Techniques for Biologists; Jones and Bartlett Learning: Burlington, MA, USA, 1999. [Google Scholar]
- Stephens, D.J.; Allan, V.J. Light microscopy techniques for live cell imaging. Science 2003, 300, 82–86. [Google Scholar] [CrossRef] [PubMed]
- De Vries, A.H.; Mark, A.E.; Marrink, S.J. Molecular dynamics simulation of the spontaneous formation of a small DPPC vesicle in water in atomistic detail. J. Am. Chem. Soc. 2004, 126, 4488–4489. [Google Scholar] [CrossRef] [PubMed]
- Marcoline, F.V.; Bethel, N.; Guerriero, C.J.; Brodsky, J.L.; Grabe, M. Membrane protein properties revealed through data-rich electrostatics calculations. Structure 2015, 23, 1526–1537. [Google Scholar] [CrossRef] [PubMed]
- MacCallum, J.L.; Bennett, W.D.; Tieleman, D.P. Partitioning of amino acid side chains into lipid bilayers: results from computer simulations and comparison to experiment. J. Gen. Physiol. 2007, 129, 371–377. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Liu, C.; Wang, X. Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions. J. Comput. Phys. 2006, 212, 757–777. [Google Scholar] [CrossRef]
- Chabanon, M.; Rangamani, P. Gaussian curvature directs the distribution of spontaneous curvature on bilayer membrane necks. Soft Matter 2018, 14, 2281–2294. [Google Scholar] [CrossRef] [PubMed]
- Muller, M.; Katsov, K.; Schick, M. Biological and synthetic membranes: What can be learned from a coarse-grained description? Phys. Rep. 2006, 434, 113–176. [Google Scholar] [CrossRef]
- Noid, W.; Chu, J.W.; Ayton, G.S.; Krishna, V.; Izvekov, S.; Voth, G.A.; Das, A.; Andersen, H.C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 244114. [Google Scholar] [CrossRef] [PubMed]
- Alimohamadi, H.; Ovryn, B.; Rangamani, P. Protein-Mediated Beads-on-a-String Structure Formation Along Membrane Nanotubes in Live Cells. Biophys. J. 2018, 114, 392a. [Google Scholar] [CrossRef]
- Cuvelier, D.; Derenyi, I.; Bassereau, P.; Nassoy, P. Coalescence of membrane tethers: Experiments, theory, and applications. Biophys. J. 2005, 88, 2714–2726. [Google Scholar] [CrossRef] [PubMed]
- Vasan, R.; Hassinger, J.; Alimohamadi, H.; Drubin, D.; Rangamani, P. Energetics and Stability of Neck Formation in Yeast and Mammalian Endocytosis. Biophys. J. 2018, 114, 281a. [Google Scholar] [CrossRef]
- Hassinger, J.E.; Oster, G.; Drubin, D.G.; Rangamani, P. Design principles for robust vesiculation in clathrin-mediated endocytosis. Proc. Natl. Acad. Sci. USA 2017, 114, E1118–E1127. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Ye, H.; Li, Y. Understanding receptor-mediated endocytosis of elastic nanoparticles through coarse grained molecular dynamic simulation. Phys. Chem. Chem. Phys. 2018, 20, 16372–16385. [Google Scholar] [CrossRef] [PubMed]
- Bobrovska, N.; Gozdz, W.; Kralj-Iglic, V.; Iglic, A. On the role of anisotropy of membrane components in formation and stabilization of tubular structures in multicomponent membranes. PLoS ONE 2013, 8, e73941. [Google Scholar] [CrossRef] [PubMed]
- Bahrami, A.H.; Hummer, G. Formation and stability of lipid membrane nanotubes. ACS Nano 2017, 11, 9558–9565. [Google Scholar] [CrossRef] [PubMed]
- Torbati, M.; Lele, T.P.; Agrawal, A. Ultradonut topology of the nuclear envelope. Proc. Natl. Acad. Sci. USA 2016, 113, 11094–11099. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Zu, Y.; Cao, Y.P.; Yang, C. A dual-scale model for the caveolin-mediated vesiculation. Soft Matter 2013, 9, 7981–7987. [Google Scholar] [CrossRef]
- Woo, H.J.; Wallqvist, A. Spontaneous buckling of lipid bilayer and vesicle budding induced by antimicrobial peptide magainin 2: A coarse-grained simulation study. J. Phys. Chem. B 2011, 115, 8122–8129. [Google Scholar] [CrossRef] [PubMed]
- Walani, N.; Torres, J.; Agrawal, A. Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc. Natl. Acad. Sci. USA 2015. [Google Scholar] [CrossRef] [PubMed]
- Weichsel, J.; Geissler, P.L. The more the tubular: Dynamic bundling of actin filaments for membrane tube formation. PLoS Comput. Biol. 2016, 12, e1004982. [Google Scholar] [CrossRef] [PubMed]
- Beltran-Heredia, E.; Almendro-Vedia, V.G.; Monroy, F.; Cao, F.J. Modeling the Mechanics of Cell Division: Influence of Spontaneous Membrane Curvature, Surface Tension, and Osmotic Pressure. Front. Psychol. 2017, 8, 312. [Google Scholar] [CrossRef] [PubMed]
- Markvoort, A.J.; Smeijers, A.; Pieterse, K.; van Santen, R.; Hilbers, P. Lipid-based mechanisms for vesicle fission. J. Phys. Chem. B 2007, 111, 5719–5725. [Google Scholar] [CrossRef] [PubMed]
- Cevc, G.; Marsh, D. Phospholipid Bilayers: Physical Principles and Models; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Stillwell, W. An Introduction to Biological Membranes: From Bilayers to Rafts; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Terzi, M.M.; Deserno, M. Lipid Membranes: From Self-assembly to Elasticity. In The Role of Mechanics in the Study of Lipid Bilayers; Springer: Berlin, Germany, 2018; pp. 105–166. [Google Scholar]
- Guidotti, G. The composition of biological membranes. J. Intern. Med. 1972, 129, 194–201. [Google Scholar]
- Yeagle, P.L. The Structure of Biological Membranes; CRC press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Watson, H. Biological membranes. Essays Biochem. 2015, 59, 43–69. [Google Scholar] [CrossRef] [PubMed]
- Schulz, G.E.; Schirmer, R.H. Principles of protein structure; Springer Science and Business Media: Berlin, Germany, 2013. [Google Scholar]
- Albersheim, P.; Anderson-Prouty, A.J. Carbohydrates, proteins, cell surfaces, and the biochemistry of pathogenesis. Annu. Rev. Plant Biol. 1975, 26, 31–52. [Google Scholar] [CrossRef]
- Jain, M.K.; Wagner, R.C. Introduction to Biological Membranes; Technical Report; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Singer, S.J.; Nicolson, G.L. The fluid mosaic model of the structure of cell membranes. Science 1972, 175, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Lodish, H.; Berk, A.; Zipursky, S.L.; Matsudaira, P.; Baltimore, D.; Darnell, J. Molecular Cell Biology; WH Freeman: New York, NY, USA, 1995; Volume 3. [Google Scholar]
- Darnell, J.E.; Lodish, H.F.; Baltimore, D. Molecular Cell Biology; Scientific American Books: New York, NY, USA, 1990; Volume 2. [Google Scholar]
- Seaton, B.A.; Roberts, M.F. Peripheral membrane proteins. In Biological Membranes; Springer: Berlin, Germany, 1996; pp. 355–403. [Google Scholar]
- Singer, S. The molecular organization of membranes. Annu. Rev. Biochem. 1974, 43, 805–833. [Google Scholar] [CrossRef] [PubMed]
- MacKinnon, R. Potassium channels. FEBS Lett. 2003, 555, 62–65. [Google Scholar] [CrossRef]
- Unwin, N. Refined structure of the nicotinic acetylcholine receptor at 4 Å resolution. J. Mol. Biol. 2005, 346, 967–989. [Google Scholar] [CrossRef] [PubMed]
- Silverman, B.D. Hydrophobicity of transmembrane proteins: Spatially profiling the distribution. Protein Sci. 2003, 12, 586–599. [Google Scholar] [CrossRef] [PubMed]
- Auth, T.; Gompper, G. Budding and vesiculation induced by conical membrane inclusions. Phys. Rev. E 2009, 80, 031901. [Google Scholar] [CrossRef] [PubMed]
- McMahon, H.T.; Boucrot, E. Membrane curvature at a glance. J. Cell Sci. 2015, 128, 1065–1070. [Google Scholar] [CrossRef] [PubMed]
- Weikl, T.R. Membrane-Mediated Cooperativity of Proteins. Annu. Rev. Phys. Chem. 2018, 69, 521–539. [Google Scholar] [CrossRef] [PubMed]
- Reynwar, B.J.; Deserno, M. Membrane-mediated interactions between circular particles in the strongly curved regime. Soft Matter 2011, 7, 8567–8575. [Google Scholar] [CrossRef]
- Chou, T.; Kim, K.S.; Oster, G. Statistical thermodynamics of membrane bending-mediated protein–protein attractions. Biophys. J. 2001, 80, 1075–1087. [Google Scholar] [CrossRef]
- Peter, B.J.; Kent, H.M.; Mills, I.G.; Vallis, Y.; Butler, P.J.G.; Evans, P.R.; McMahon, H.T. BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science 2004, 303, 495–499. [Google Scholar] [CrossRef] [PubMed]
- Gallop, J.L.; McMahon, H.T. BAR domains and membrane curvature: Bringing your curves to the BAR. Biochem. Soc. Symp. 2005, 72, 223–231. [Google Scholar] [CrossRef]
- Ren, G.; Vajjhala, P.; Lee, J.S.; Winsor, B.; Munn, A.L. The BAR domain proteins: Molding membranes in fission, fusion, and phagy. Microbiol. Mol. Biol. Rev. 2006, 70, 37–120. [Google Scholar] [CrossRef] [PubMed]
- Dawson, J.C.; Legg, J.A.; Machesky, L.M. Bar domain proteins: A role in tubulation, scission and actin assembly in clathrin-mediated endocytosis. Trends Cell Biol. 2006, 16, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, V.K.; Madsen, K.L.; Bolinger, P.Y.; Kunding, A.; Hedegaard, P.; Gether, U.; Stamou, D. Amphipathic motifs in BAR domains are essential for membrane curvature sensing. EMBO J. 2009, 28, 3303–3314. [Google Scholar] [CrossRef] [PubMed]
- Mim, C.; Unger, V.M. Membrane curvature and its generation by BAR proteins. Trends Biochem. Sci. 2012, 37, 526–533. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Mukhopadhyay, A.; Craig, A.W. Transducer of Cdc42-dependent actin assembly promotes epidermal growth factor-induced cell motility and invasiveness. J. Biol. Chem. 2011, 286, 2261–2272. [Google Scholar] [CrossRef] [PubMed]
- Pichot, C.S.; Arvanitis, C.; Hartig, S.M.; Jensen, S.A.; Bechill, J.; Marzouk, S.; Yu, J.; Frost, J.A.; Corey, S.J. Cdc42-interacting protein 4 promotes breast cancer cell invasion and formation of invadopodia through activation of N-WASp. Cancer Res. 2010, 70, 8347–8356. [Google Scholar] [CrossRef] [PubMed]
- Scales, S.J.; Gomez, M.; Kreis, T.E. Coat proteins regulating membrane traffic. In International Review of Cytology; Elsevier: Amsterdam, The Netherlands, 1999; Volume 195, pp. 67–144. [Google Scholar]
- McMahon, H.T.; Boucrot, E. Molecular mechanism and physiological functions of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2011, 12, 517–533. [Google Scholar] [CrossRef] [PubMed]
- Bonifacino, J.S.; Lippincott-Schwartz, J. Coat proteins: shaping membrane transport. Nat. Rev. Mol. Cell Biol. 2003, 4, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Agudo-Canalejo, J.; Lipowsky, R. Domes and cones: Adhesion-induced fission of membranes by ESCRT proteins. PLoS Comput. Biol. 2018, 14, e1006422. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, N.; Kumar, P.S.; Radhakrishnan, R. Mesoscale computational studies of membrane bilayer remodeling by curvature-inducing proteins. Phys. Rep. 2014, 543, 1–60. [Google Scholar] [CrossRef] [PubMed]
- Canham, P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970, 26, 61–81. [Google Scholar] [CrossRef]
- Safran, S. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Tobias, D.J.; Tu, K.; Klein, M.L. Atomic-scale molecular dynamics simulations of lipid membranes. Curr. Opin. Colloid Interface Sci. 1997, 2, 15–26. [Google Scholar] [CrossRef]
- Tieleman, D.P.; Marrink, S.J.; Berendsen, H.J. A computer perspective of membranes: Molecular dynamics studies of lipid bilayer systems. Biochim. Biophys. Acta 1997, 1331, 235–270. [Google Scholar] [CrossRef]
- Lindahl, E.; Sansom, M.S. Membrane proteins: Molecular dynamics simulations. Curr. Opin. Struct. Biol. 2008, 18, 425–431. [Google Scholar] [CrossRef] [PubMed]
- Chabanon, M.; Stachowiak, J.C.; Rangamani, P. Systems biology of cellular membranes: A convergence with biophysics. Wiley Interdiscip. Rev. Syst. Biol. Med. 2017, 9, e1386. [Google Scholar] [CrossRef] [PubMed]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 1973, 28, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Sauer, R.A. On the computational modeling of lipid bilayers using thin-shell theory. In The Role of Mechanics in the Study of Lipid Bilayers; Springer: Berlin, Germany, 2018; pp. 221–286. [Google Scholar]
- Alimohamadi, H.; Ovryn, B.; Rangamani, P. Protein aggregation and membrane bending govern nanotube morphology. bioRxiv 2018. [Google Scholar] [CrossRef]
- Agrawal, A.; Steigmann, D.J. Boundary-value problems in the theory of lipid membranes. Contin. Mech. Thermodyn. 2009, 21, 57–82. [Google Scholar] [CrossRef]
- Laadhari, A.; Saramito, P.; Misbah, C. An adaptive finite element method for the modeling of the equilibrium of red blood cells. Int. J. Numer. Methods Fluids 2016, 80, 397–428. [Google Scholar] [CrossRef]
- Sauer, R.A.; Duong, T.X.; Mandadapu, K.K.; Steigmann, D.J. A stabilized finite element formulation for liquid shells and its application to lipid bilayers. J. Comput. Phys. 2017, 330, 436–466. [Google Scholar] [CrossRef]
- Duong, T.X.; Roohbakhshan, F.; Sauer, R.A. A new rotation-free isogeometric thin shell formulation and a corresponding continuity constraint for patch boundaries. Comput. Methods Appl. Mech. Eng. 2017, 316, 43–83. [Google Scholar] [CrossRef]
- Ramakrishnan, N.; Kumar, P.S.; Ipsen, J.H. Monte Carlo simulations of fluid vesicles with in-plane orientational ordering. Phys. Rev. E 2010, 81, 041922. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Ma, M.; Gan, Z.; Xu, Z.; Li, B. Hybrid Monte Carlo and continuum modeling of electrolytes with concentration-induced dielectric variations. Phys. Rev. E 2016, 94, 053312. [Google Scholar] [CrossRef] [PubMed]
- Sreeja, K.; Ipsen, J.H.; Kumar, P.S. Monte Carlo simulations of fluid vesicles. J. Phys. Condens. Matter 2015, 27, 273104. [Google Scholar] [CrossRef] [PubMed]
- Lau, C.; Brownell, W.E.; Spector, A.A. Internal forces, tension and energy density in tethered cellular membranes. J. Biomech. 2012, 45, 1328–1331. [Google Scholar] [CrossRef] [PubMed]
- Gu, R.; Wang, X.; Gunzburger, M. Simulating vesicle–substrate adhesion using two phase field functions. J. Comput. Phys. 2014, 275, 626–641. [Google Scholar] [CrossRef]
- Banham, T.; Li, B.; Zhao, Y. Pattern formation by phase-field relaxation of bending energy with fixed surface area and volume. Phys. Rev. E 2014, 90, 033308. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Wang, X. Convergence of numerical approximations to a phase field bending elasticity model of membrane deformations. Int. J. Numer. Anal. Model 2006, 1, 1–18. [Google Scholar]
- Zhang, J.; Das, S.; Du, Q. A phase field model for vesicle–substrate adhesion. J. Comput. Phys. 2009, 228, 7837–7849. [Google Scholar] [CrossRef]
- Arkhipov, A.; Yin, Y.; Schulten, K. Four-scale description of membrane sculpting by BAR domains. Biophys. J. 2008, 95, 2806–2821. [Google Scholar] [CrossRef] [PubMed]
- Steigmann, D. Fluid films with curvature elasticity. Arch. Ration. Mech. Anal. 1999, 150, 127–152. [Google Scholar] [CrossRef]
- Kishimoto, T.; Sun, Y.; Buser, C.; Liu, J.; Michelot, A.; Drubin, D.G. Determinants of endocytic membrane geometry, stability, and scission. Proc. Natl. Acad. Sci. USA 2011. [Google Scholar] [CrossRef] [PubMed]
- Rangamani, P.; Mandadap, K.K.; Oster, G. Protein-induced membrane curvature alters local membrane tension. Biophys. J. 2014, 107, 751–762. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Steigmann, D.J. Modeling protein-mediated morphology in biomembranes. Biomech. Model. Mechanobiol. 2009, 8, 371. [Google Scholar] [CrossRef] [PubMed]
- Spivak, M.D. A Comprehensive Introduction to Differential Geometry; Publish or Perish: Houston, TX, USA, 1970. [Google Scholar]
- Deserno, M. Fluid lipid membranes: From differential geometry to curvature stresses. Chem. Phys. Lipids 2015, 185, 11–45. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R. Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature. Faraday Discuss. 2013, 161, 305–331. [Google Scholar] [CrossRef] [PubMed]
- Sens, P.; Turner, M.S. Theoretical model for the formation of caveolae and similar membrane invaginations. Biophys. J. 2004, 86, 2049–2057. [Google Scholar] [CrossRef]
- Rozycki, B.; Boura, E.; Hurley, J.H.; Hummer, G. Membrane-elasticity model of Coatless vesicle budding induced by ESCRT complexes. PLoS Comput. Biol. 2012, 8, e1002736. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shibata, Y.; Voss, C.; Shemesh, T.; Li, Z.; Coughlin, M.; Kozlov, M.M.; Rapoport, T.A.; Prinz, W.A. Membrane proteins of the endoplasmic reticulum induce high-curvature tubules. Science 2008, 319, 1247–1250. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Sun, Y.; Drubin, D.G.; Oster, G.F. The mechanochemistry of endocytosis. PLoS Biol. 2009, 7, e1000204. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Kaksonen, M.; Drubin, D.G.; Oster, G. Endocytic vesicle scission by lipid phase boundary forces. Proc. Natl. Acad. Sci. USA 2006, 103, 10277–10282. [Google Scholar] [CrossRef] [PubMed]
- Faris, M.E.A.; Lacoste, D.; Pecreaux, J.; Joanny, J.F.; Prost, J.; Bassereau, P. Membrane tension lowering induced by protein activity. Phys. Rev. Lett. 2009, 102, 038102. [Google Scholar] [CrossRef] [PubMed]
- Manneville, J.B.; Bassereau, P.; Ramaswamy, S.; Prost, J. Active membrane fluctuations studied by micropipet aspiration. Phys. Rev. E 2001, 64, 021908. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Graber, Z.T.; Baumgart, T.; Stone, H.A.; Cohen, A.E. Cell membranes resist flow. bioRxiv 2018. [Google Scholar] [CrossRef]
- Sheetz, M.P.; Singer, S. Biological membranes as bilayer couples. A molecular mechanism of drug-erythrocyte interactions. Proc. Natl. Acad. Sci. USA 1974, 71, 4457–4461. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.; Seifert, U.; Wortis, M.; Dobereiner, H.G. Budding transitions of fluid-bilayer vesicles: The effect of area-difference elasticity. Phys. Rev. E 1994, 49, 5389. [Google Scholar] [CrossRef]
- Svetina, S.; Brumen, M.; Zeks, B. Lipid bilayer elasticity and the bilayer couple interpretation of red-cell shape transformations and lysis. Stud. Biophys. 1985, 110, 177–184. [Google Scholar]
- Svetina, S.; Zeks, B. Membrane bending energy and shape determination of phospholipid vesicles and red blood cells. Eur. Biophys. J. 1989, 17, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Dobereiner, H.G.; Evans, E.; Kraus, M.; Seifert, U.; Wortis, M. Mapping vesicle shapes into the phase diagram: A comparison of experiment and theory. Phys. Rev. E 1997, 55, 4458. [Google Scholar] [CrossRef]
- Bozic, B.; Svetina, S.; Zeks, B.; Waugh, R. Role of lamellar membrane structure in tether formation from bilayer vesicles. Biophys. J. 1992, 61, 963–973. [Google Scholar] [CrossRef]
- Waugh, R.E. Elastic energy of curvature-driven bump formation on red blood cell membrane. Biophys. J. 1996, 70, 1027–1035. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; Lim, H.G.; Wortis, M. Echinocyte shapes: bending, stretching, and shear determine spicule shape and spacing. Biophys. J. 2002, 82, 1756–1772. [Google Scholar] [CrossRef]
- Hw, G.L.; Wortis, M.; Mukhopadhyay, R. Stomatocyte–discocyte–echinocyte sequence of the human red blood cell: Evidence for the bilayer–couple hypothesis from membrane mechanics. Proc. Natl. Acad. Sci. USA 2002, 99, 16766–16769. [Google Scholar]
- Svetina, S.; Kuzman, D.; Waugh, R.E.; Ziherl, P.; Zeks, B. The cooperative role of membrane skeleton and bilayer in the mechanical behaviour of red blood cells. Bioelectrochemistry 2004, 62, 107–113. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer, Y.; Kozlov, M.M. Membrane-mediated interaction between strongly anisotropic protein scaffolds. PLoS Comput. Biol. 2015, 11, e1004054. [Google Scholar] [CrossRef] [PubMed]
- Simunovic, M.; Prevost, C.; Callan-Jones, A.; Bassereau, P. Physical basis of some membrane shaping mechanisms. Phil. Trans. R. Soc. A 2016, 374, 20160034. [Google Scholar] [CrossRef] [PubMed]
- Frost, A.; Perera, R.; Roux, A.; Spasov, K.; Destaing, O.; Egelman, E.H.; De Camilli, P.; Unger, V.M. Structural basis of membrane invagination by F-BAR domains. Cell 2008, 132, 807–817. [Google Scholar] [CrossRef] [PubMed]
- Shimada, A.; Niwa, H.; Tsujita, K.; Suetsugu, S.; Nitta, K.; Hanawa-Suetsugu, K.; Akasaka, R.; Nishino, Y.; Toyama, M.; Chen, L.; et al. Curved EFC/F-BAR-domain dimers are joined end to end into a filament for membrane invagination in endocytosis. Cell 2007, 129, 761–772. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglic, V.; Svetina, S.; Zekz, B. Shapes of bilayer vesicles with membrane embedded molecules. Eur. Biophys. J. 1996, 24, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Fournier, J. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett. 1996, 76, 4436. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglic, V.; Heinrich, V.; Svetina, S.; Zeks, B. Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B 1999, 10, 5–8. [Google Scholar] [CrossRef]
- Kralj-Iglic, V.; Remskar, M.; Vidmar, G.; Fosnaric, M.; Iglic, A. Deviatoric elasticity as a possible physical mechanism explaining collapse of inorganic micro and nanotubes. Phys. Lett. A 2002, 296, 151–155. [Google Scholar] [CrossRef]
- Iglic, A.; Hagerstrand, H.; Veranic, P.; Plemenitas, A.; Kralj-Iglic, V. Curvature-induced accumulation of anisotropic membrane components and raft formation in cylindrical membrane protrusions. J. Theor. Biol. 2006, 240, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Bobrovska, N.; Gozdz, W.; Gov, N.; Kralj-Iglic, V.; Veranic, P.; Iglic, A. On the role of membrane anisotropy and BAR proteins in the stability of tubular membrane structures. J. Biomech. 2012, 45, 231–238. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Gongadze, E.; Elter, P.; Van Rienen, U.; Gimsa, J.; Kralj-Iglic, V.; Iglic, A. Attachment of rod-like (BAR) proteins and membrane shape. Mini-Rev. Med. Chem. 2011, 11, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Walani, N.; Torres, J.; Agrawal, A. Anisotropic spontaneous curvatures in lipid membranes. Phys. Rev. E 2014, 89, 062715. [Google Scholar] [CrossRef] [PubMed]
- Reynwar, B.J.; Illya, G.; Harmandaris, V.A.; Müller, M.M.; Kremer, K.; Deserno, M. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature 2007, 447, 461. [Google Scholar] [CrossRef] [PubMed]
- Tourdot, R.W.; Ramakrishnan, N.; Radhakrishnan, R. Defining the free-energy landscape of curvature-inducing proteins on membrane bilayers. Phys. Rev. E 2014, 90, 022717. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Baumgart, T. Dynamics and instabilities of lipid bilayer membrane shapes. Adv. Colloid Interface Sci. 2014, 208, 76–88. [Google Scholar] [CrossRef] [PubMed]
- Shnyrova, A.V.; Frolov, V.A.; Zimmerberg, J. Domain-driven morphogenesis of cellular membranes. Curr. Biol. 2009, 19, R772–R780. [Google Scholar] [CrossRef] [PubMed]
- Veksler, A.; Gov, N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J. 2007, 93, 3798–3810. [Google Scholar] [CrossRef] [PubMed]
- Gov, N. Guided by curvature: shaping cells by coupling curved membrane proteins and cytoskeletal forces. Phil. Trans. R. Soc. B 2018, 373, 20170115. [Google Scholar] [CrossRef] [PubMed]
- Gil, T.; Ipsen, J.H.; Mouritsen, O.G.; Sabra, M.C.; Sperotto, M.M.; Zuckermann, M.J. Theoretical analysis of protein organization in lipid membranes. Biochim. Biophys. Acta 1998, 1376, 245–266. [Google Scholar] [CrossRef]
- Givli, S.; Giang, H.; Bhattacharya, K. Stability of multicomponent biological membranes. SIAM J. Appl. Math. 2012, 72, 489–511. [Google Scholar] [CrossRef]
- Katz, S.; Givli, S. Curvature-Induced Spatial Ordering of Composition in Lipid Membranes. Comput. Math. Methods Med. 2017, 2017, 7275131. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Shlomovitz, R.; Schloen, K.; Stradal, T.; Gov, N.S. Theoretical model for cellular shapes driven by protrusive and adhesive forces. PLoS Comput. Biol. 2011, 7, e1001127. [Google Scholar] [CrossRef] [PubMed]
- Shlomovitz, R.; Gov, N. Exciting cytoskeleton-membrane waves. Phys. Rev. E 2008, 78, 041911. [Google Scholar] [CrossRef] [PubMed]
- Orly, G.; Naoz, M.; Gov, N. Physical model for the geometry of actin-based cellular protrusions. Biophys. J. 2014, 107, 576–587. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Gongadze, E.; Jorgacevski, J.; Kreft, M.; Rienen, U.; Zorec, R.; Iglic, A. Exploring the binding dynamics of BAR proteins. Cell. Mol. Biol. Lett. 2011, 16, 398. [Google Scholar] [CrossRef] [PubMed]
- Phillips, R.; Ursell, T.; Wiggins, P.; Sens, P. Emerging roles for lipids in shaping membrane–protein function. Nature 2009, 459, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Weikl, T.R.; Asfaw, M.; Krobath, H.; Rozycki, B.; Lipowsky, R. Adhesion of membranes via receptor–ligand complexes: Domain formation, binding cooperativity, and active processes. Soft Matter 2009, 5, 3213–3224. [Google Scholar] [CrossRef]
- Daum, B.; Auerswald, A.; Gruber, T.; Hause, G.; Balbach, J.; Kuhlbrandt, W.; Meister, A. Supramolecular organization of the human N-BAR domain in shaping the sarcolemma membrane. J. Struct. Biol. 2016, 194, 375–382. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, H. Membrane tubule formation by banana-shaped proteins with or without transient network structure. Sci. Rep. 2016, 6, 20935. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Steigmann, D.J. A model for surface diffusion of trans-membrane proteins on lipid bilayers. Z. Angew. Math. Phys. 2011, 62, 549. [Google Scholar] [CrossRef]
- Kirchhausen, T. Bending membranes. Nat. Cell Biol. 2012, 14, 906–908. [Google Scholar] [CrossRef] [PubMed]
- Guigas, G.; Weiss, M. Effects of protein crowding on membrane systems. Biochim. Biophys. Acta 2016, 1858, 2441–2450. [Google Scholar] [CrossRef] [PubMed]
- Stachowiak, J.C.; Brodsky, F.M.; Miller, E.A. A cost–benefit analysis of the physical mechanisms of membrane curvature. Nat. Cell Biol. 2013, 15, 1019–1027. [Google Scholar] [CrossRef] [PubMed]
- Derganc, J.; Copic, A. Membrane bending by protein crowding is affected by protein lateral confinement. Biochim. Biophys. Acta 2016, 1858, 1152–1159. [Google Scholar] [CrossRef] [PubMed]
- Linden, M.; Sens, P.; Phillips, R. Entropic tension in crowded membranes. PLoS Comput. Biol. 2012, 8, e1002431. [Google Scholar] [CrossRef] [PubMed]
- Van Wylen, G.J.; Sonntag, R.E. Fundamentals of Classical Thermodynamics; Technical Report; John Wiley and Sons, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Luding, S. Global equation of state of two-dimensional hard sphere systems. Phys. Rev. E 2001, 63, 042201. [Google Scholar] [CrossRef] [PubMed]
- Carnahan, N.F.; Starling, K.E. Equation of state for nonattracting rigid spheres. J. Chem. Phys. 1969, 51, 635–636. [Google Scholar] [CrossRef]
- Stachowiak, J.C.; Hayden, C.C.; Sasaki, D.Y. Steric confinement of proteins on lipid membranes can drive curvature and tubulation. Proc. Natl. Acad. Sci. USA 2010, 107, 7781–7786. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Atefi, E.; Baumgart, T. Membrane shape instability induced by protein crowding. Biophys. J. 2016, 111, 1823–1826. [Google Scholar] [CrossRef] [PubMed]
- Callan-Jones, A.; Bassereau, P. Curvature-driven membrane lipid and protein distribution. Curr. Opin. Solid State Mater. Sci. 2013, 17, 143–150. [Google Scholar] [CrossRef]
- Snead, W.; Zeno, W.; Kago, G.; Perkins, R.; Richter, J.B.; Lafer, E.; Stachowiak, J. BAR scaffolds drive membrane fission by crowding disordered domains. bioRxiv 2018. [Google Scholar] [CrossRef]
- Dalbey, R.E. Leader peptidase. Mol. Microbiol. 1991, 5, 2855–2860. [Google Scholar] [CrossRef] [PubMed]
- Kaback, H.R.; Frillingos, S.; Jung, H.; Jung, K.; Prive, G.G.; Ujwal, M.; Weitzman, C.; Wu, J.; Zen, K. The lactose permease meets Frankenstein. J. Exp. Biol. 1994, 196, 183–195. [Google Scholar] [PubMed]
- Killian, J.A. Hydrophobic mismatch between proteins and lipids in membranes. Biochim. Biophys. Acta 1998, 1376, 401–416. [Google Scholar] [CrossRef]
- Thurmond, R.L.; Niemi, A.R.; Lindblom, G.; Wieslander, A.; Rilfors, L. Membrane thickness and molecular ordering in Acholeplasma laidlawii strain A studied by 2H NMR spectroscopy. Biochemistry 1994, 33, 13178–13188. [Google Scholar] [CrossRef] [PubMed]
- Duque, D.; Li, X.j.; Katsov, K.; Schick, M. Molecular theory of hydrophobic mismatch between lipids and peptides. J. Chem. Phys. 2002, 116, 10478–10484. [Google Scholar] [CrossRef]
- Fattal, D.R.; Ben-Shaul, A. Mean-field calculations of chain packing and conformational statistics in lipid bilayers: Comparison with experiments and molecular dynamics studies. Biophys. J. 1994, 67, 983–995. [Google Scholar]
- Argudo, D.; Bethel, N.P.; Marcoline, F.V.; Wolgemuth, C.W.; Grabe, M. New Continuum Approaches for Determining Protein-Induced Membrane Deformations. Biophys. J. 2017, 112, 2159–2172. [Google Scholar] [CrossRef] [PubMed]
- Mouritsen, O.; Bloom, M. Mattress model of lipid-protein interactions in membranes. Biophys. J. 1984, 46, 141–153. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Mixtures: The Theory of the Equilibrium Properties of Some Simple Classes of Mixtures, Solutions and Alloys; Clarendon Press: Oxford, UK, 1952. [Google Scholar]
- Andersen, O.S.; Koeppe, R.E. Bilayer thickness and membrane protein function: An energetic perspective. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 107–130. [Google Scholar] [CrossRef] [PubMed]
- Marcelja, S. Lipid-mediated protein interaction in membranes. Biochim. Biophys. Acta 1976, 455, 1–7. [Google Scholar] [CrossRef]
- Owicki, J.C.; McConnell, H.M. Theory of protein-lipid and protein-protein interactions in bilayer membranes. Proc. Natl. Acad. Sci. USA 1979, 76, 4750–4754. [Google Scholar] [CrossRef] [PubMed]
- Lewis, B.A.; Engelman, D.M. Lipid bilayer thickness varies linearly with acyl chain length in fluid phosphatidylcholine vesicles. J. Mol. Biol. 1983, 166, 211–217. [Google Scholar] [CrossRef]
- Ryba, N.J.; Marsh, D. Protein rotational diffusion and lipid/protein interactions in recombinants of bovine rhodopsin with saturated diacylphosphatidylcholines of different chain lengths studied by conventional and saturation-transfer electron spin resonance. Biochemistry 1992, 31, 7511–7518. [Google Scholar] [CrossRef] [PubMed]
- Vonck, J. A three-dimensional difference map of the N intermediate in the bacteriorhodopsin photocycle: Part of the F helix tilts in the M to N transition. Biochemistry 1996, 35, 5870–5878. [Google Scholar] [CrossRef] [PubMed]
- Rangamani, P.; Benjamini, A.; Agrawal, A.; Smit, B.; Steigmann, D.J.; Oster, G. Small scale membrane mechanics. Biomech. Model. Mechanobiol. 2014, 13, 697–711. [Google Scholar] [CrossRef] [PubMed]
- Fournier, J.; Galatola, P. Tubular vesicles and effective fourth-order membrane elastic theories. EPL 1997, 39, 225–230. [Google Scholar] [CrossRef]
- Siegel, D.P. Fourth-Order Curvature Energy Model for the Stability of Bicontinuous Inverted Cubic Phases in Amphiphile—Water Systems. Langmuir 2010, 26, 8673–8683. [Google Scholar] [CrossRef] [PubMed]
- Brannigan, G.; Brown, F.L. Contributions of Gaussian curvature and nonconstant lipid volume to protein deformation of lipid bilayers. Biophys. J. 2007, 92, 864–876. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Neu, J.; Oster, G. Effect of protein shape on multibody interactions between membrane inclusions. Phys. Rev. E 2000, 61, 4281. [Google Scholar] [CrossRef]
- Latorraca, N.R.; Callenberg, K.M.; Boyle, J.P.; Grabe, M. Continuum approaches to understanding ion and peptide interactions with the membrane. J. Membr. Biol. 2014, 247, 395–408. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: New York, NY, USA, 2011. [Google Scholar]
- Zhou, Y.; Lu, B.; Gorfe, A.A. Continuum electromechanical modeling of protein-membrane interactions. Phys. Rev. E 2010, 82, 041923. [Google Scholar] [CrossRef] [PubMed]
- Steigmann, D.; Agrawal, A. Electromechanics of polarized lipid bilayers. Math. Mech. Complex Syst. 2016, 4, 31–54. [Google Scholar] [CrossRef]
- Steigmann, D.J. The Role of Mechanics in the Study of Lipid Bilayers; Springer: Berlin, Germany, 2017; Volume 577. [Google Scholar]
- Monzel, C.; Sengupta, K. Measuring shape fluctuations in biological membranes. J. Phys. D 2016, 49, 243002. [Google Scholar] [CrossRef]
- Shlomovitz, R.; Gov, N.; Roux, A. Membrane-mediated interactions and the dynamics of dynamin oligomers on membrane tubes. New J. Phys. 2011, 13, 065008. [Google Scholar] [CrossRef]
- Peng, Z.; Asaro, R.J.; Zhu, Q. Multiscale simulation of erythrocyte membranes. Phys. Rev. E 2010, 81, 031904. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, H.; Gompper, G. Fluid vesicles with viscous membranes in shear flow. Phys. Rev. Lett. 2004, 93, 258102. [Google Scholar] [CrossRef] [PubMed]
- Prevost, C.; Zhao, H.; Manzi, J.; Lemichez, E.; Lappalainen, P.; Callan-Jones, A.; Bassereau, P. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat. Commun. 2015, 6, 8529. [Google Scholar] [CrossRef] [PubMed]
- Wedlich-Soldner, R.; Betz, T. Self-organization: the fundament of cell biology. Philos. Trans. R. Soc. B 2018, 373, 20170103. [Google Scholar] [CrossRef] [PubMed]
- Ramaswamy, S.; Toner, J.; Prost, J. Nonequilibrium fluctuations, traveling waves, and instabilities in active membranes. Phys. Rev. Lett. 2000, 84, 3494. [Google Scholar] [CrossRef] [PubMed]
- Madsen, K.L.; Bhatia, V.; Gether, U.; Stamou, D. BAR domains, amphipathic helices and membrane-anchored proteins use the same mechanism to sense membrane curvature. FEBS Lett. 2010, 584, 1848–1855. [Google Scholar] [CrossRef] [PubMed]
- Raucher, D.; Stauffer, T.; Chen, W.; Shen, K.; Guo, S.; York, J.D.; Sheetz, M.P.; Meyer, T. Phosphatidylinositol 4,5-bisphosphate functions as a second messenger that regulates cytoskeleton-plasma membrane adhesion. Cell 2000, 100, 221–228. [Google Scholar] [CrossRef]
- Ayton, G.S.; McWhirter, J.L.; Voth, G.A. A second generation mesoscopic lipid bilayer model: Connections to field-theory descriptions of membranes and nonlocal hydrodynamics. J. Chem. Phys. 2006, 124, 064906. [Google Scholar] [CrossRef] [PubMed]
- Kirchhausen, T.; Owen, D.; Harrison, S.C. Molecular structure, function, and dynamics of clathrin-mediated membrane traffic. Cold Spring Harb. Perspect. Biol. 2014, 6, a016725. [Google Scholar] [CrossRef] [PubMed]
- Ford, M.G.; Mills, I.G.; Peter, B.J.; Vallis, Y.; Praefcke, G.J.; Evans, P.R.; McMahon, H.T. Curvature of clathrin-coated pits driven by epsin. Nature 2002, 419, 361–366. [Google Scholar] [CrossRef] [PubMed]
- Calizo, R.C.; Ron, A.; Hu, M.; Bhattacharya, S.; Janssen, W.G.; Hone, J.; Scarlata, S.; Rangamani, P.; Iyengar, R. Curvature regulates subcellular organelle location to control intracellular signal propagation. bioRxiv 2017. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimohamadi, H.; Rangamani, P. Modeling Membrane Curvature Generation due to Membrane–Protein Interactions. Biomolecules 2018, 8, 120. https://doi.org/10.3390/biom8040120
Alimohamadi H, Rangamani P. Modeling Membrane Curvature Generation due to Membrane–Protein Interactions. Biomolecules. 2018; 8(4):120. https://doi.org/10.3390/biom8040120
Chicago/Turabian StyleAlimohamadi, Haleh, and Padmini Rangamani. 2018. "Modeling Membrane Curvature Generation due to Membrane–Protein Interactions" Biomolecules 8, no. 4: 120. https://doi.org/10.3390/biom8040120
APA StyleAlimohamadi, H., & Rangamani, P. (2018). Modeling Membrane Curvature Generation due to Membrane–Protein Interactions. Biomolecules, 8(4), 120. https://doi.org/10.3390/biom8040120




