A Rationale for Mesoscopic Domain Formation in Biomembranes
Abstract
1. Introduction
2. In Thermodynamic Equilibrium
2.1. Weak-Segregation Limit in the Vicinity of a Critical Point
2.1.1. Curvature-Composition Coupling in Planar Membranes
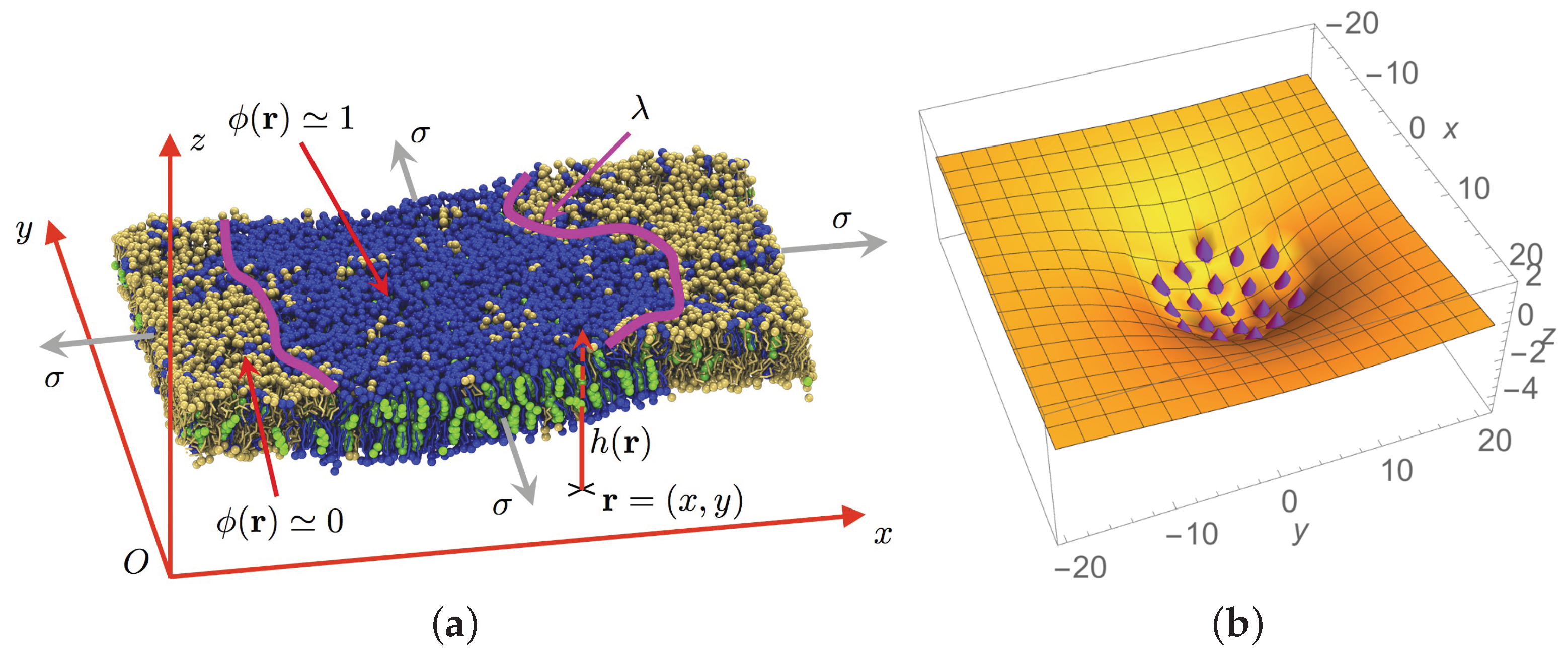
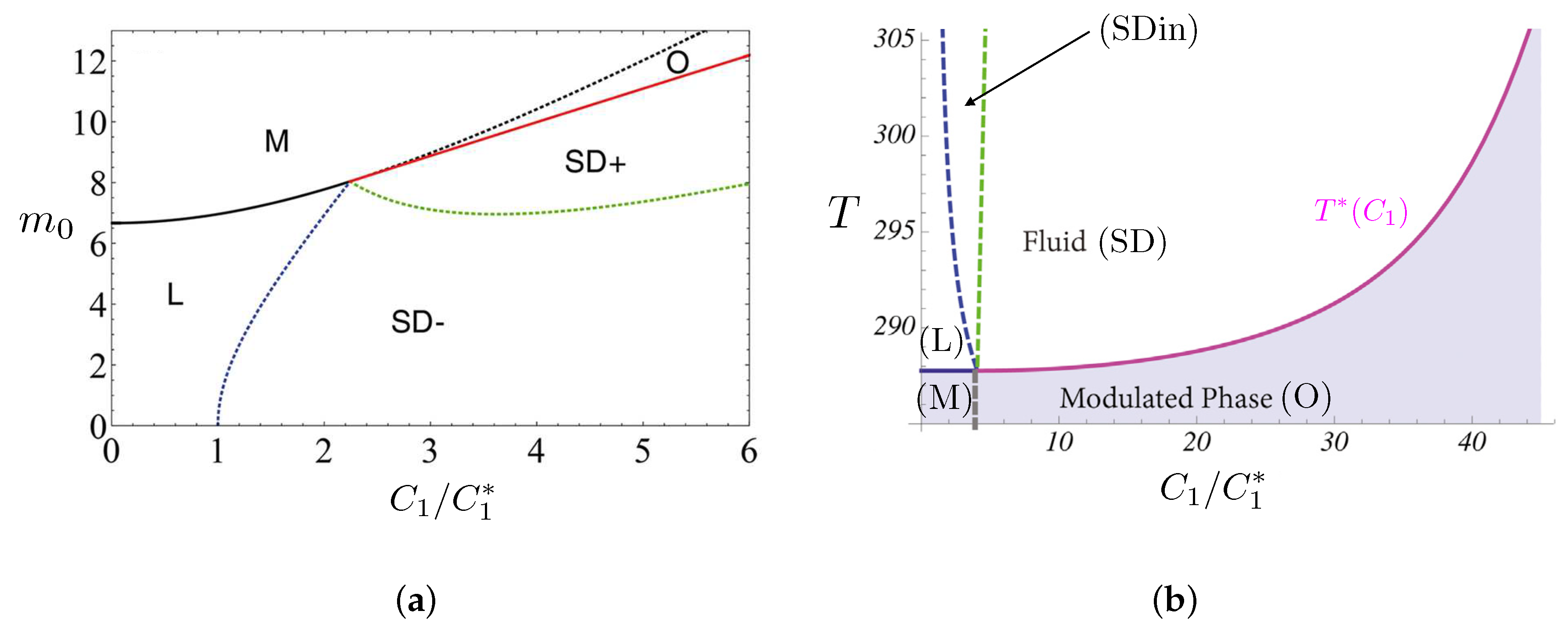
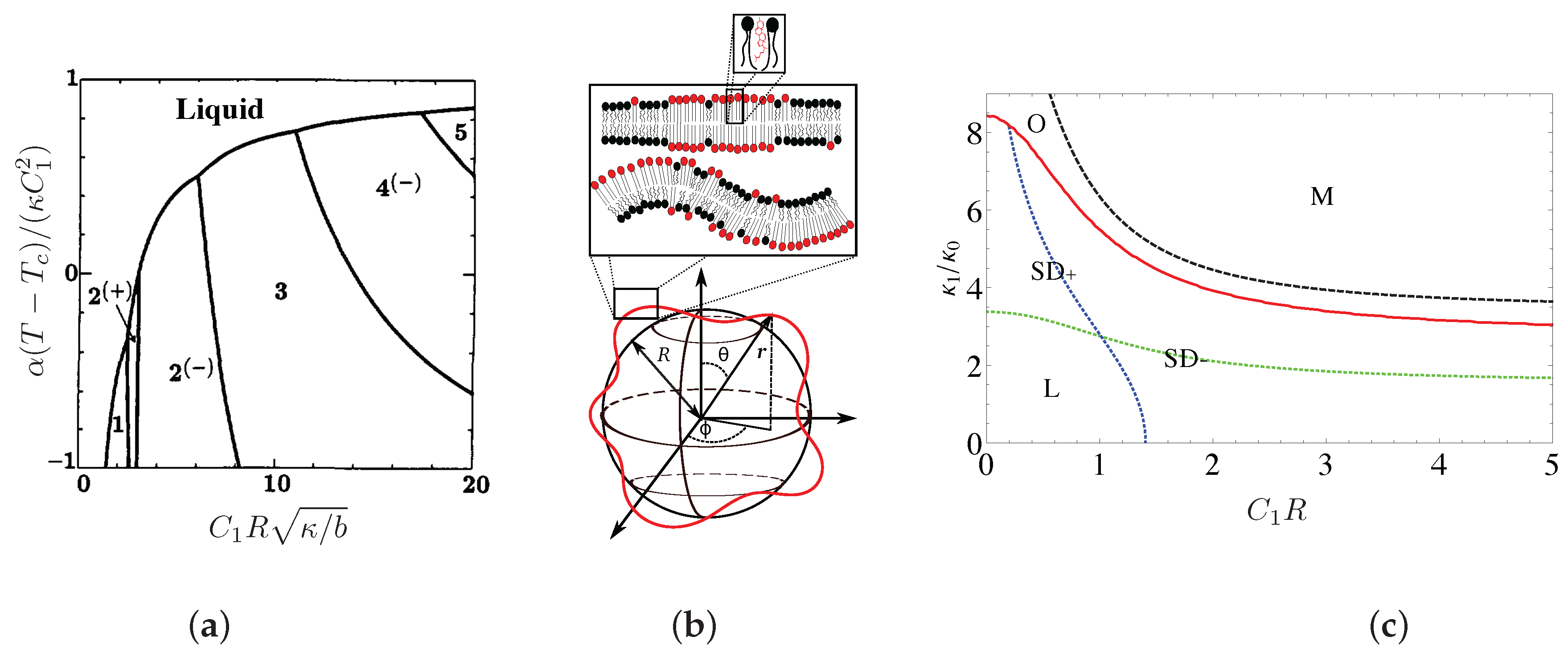
- (a)
- The difference in lipid composition between both leaflets is important in cellular membranes, and it is maintained by the active cell metabolism. It can lead to bilayer spontaneous curvature if both leaflets conspire in this direction, because the bilayer curvature results form the difference in the spontaneous curvature of the monolayers [12]. The spontaneous curvatures of the main lipids found in plasma membranes are listed in [71] and they can be as large as nm for cholesterol or 1,2-Dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE). This is global on the whole membrane, but it can be accentuated locally due to the membrane lateral heterogeneity. For example, it has been shown on the basis of coarse-grained molecular dynamics simulations that mean curvatures of about nm can be attained in asymmetric membranes containing separated Lo and Ld phases on one leaflet and pure unsaturated lipid on the other leaflet [72].
- (b)
- The difference in the aqueous solution composition on the two sides of the membrane is maintained by the cell [1]. As explained by Lipowsky in 2013, a difference of solute concentrations, including ions and small molecules, generically leads to spontaneous curvature when they adsorb onto the membrane surface, for purely entropic causes [73]. The membrane “bends away from the exterior compartment if the concentration in this compartment exceeds the concentration in the interior compartment”. For a single solute with different concentrations across the membrane, the spontaneous curvature is given bywhere ℓ is the membrane thickness, is the maximal surface density by adsorption and is the equilibrium constant of adsorption. Putting realistic numbers in this relation (in particular and nm [74]), one gets nm. The membrane itself is supposed to be up-down symmetric here. The adsorption of biopolymers is also examined in this work [73]. However, it is demonstrated to lead to smaller spontaneous curvature in realistic regimes of parameters.
- (c)
- The area difference between both leaflets can also lead to global spontaneous curvature. For instance, an area difference of % leads a to spontaneous curvature nm [71]. This is the keystone of the area-difference-elasticity (ADE) model that has been developed to explain the rich shape variability of homogeneous lipid vesicles, in particular in function of their reduced volume v [12,75].
2.1.2. Bending Modulus-Composition Coupling in Planar Membranes
2.1.3. Vesicles
2.2. Strong Segregation Limit
2.2.1. Domain Buckling Induced by Line Tension—Spontaneous Symmetry Breaking
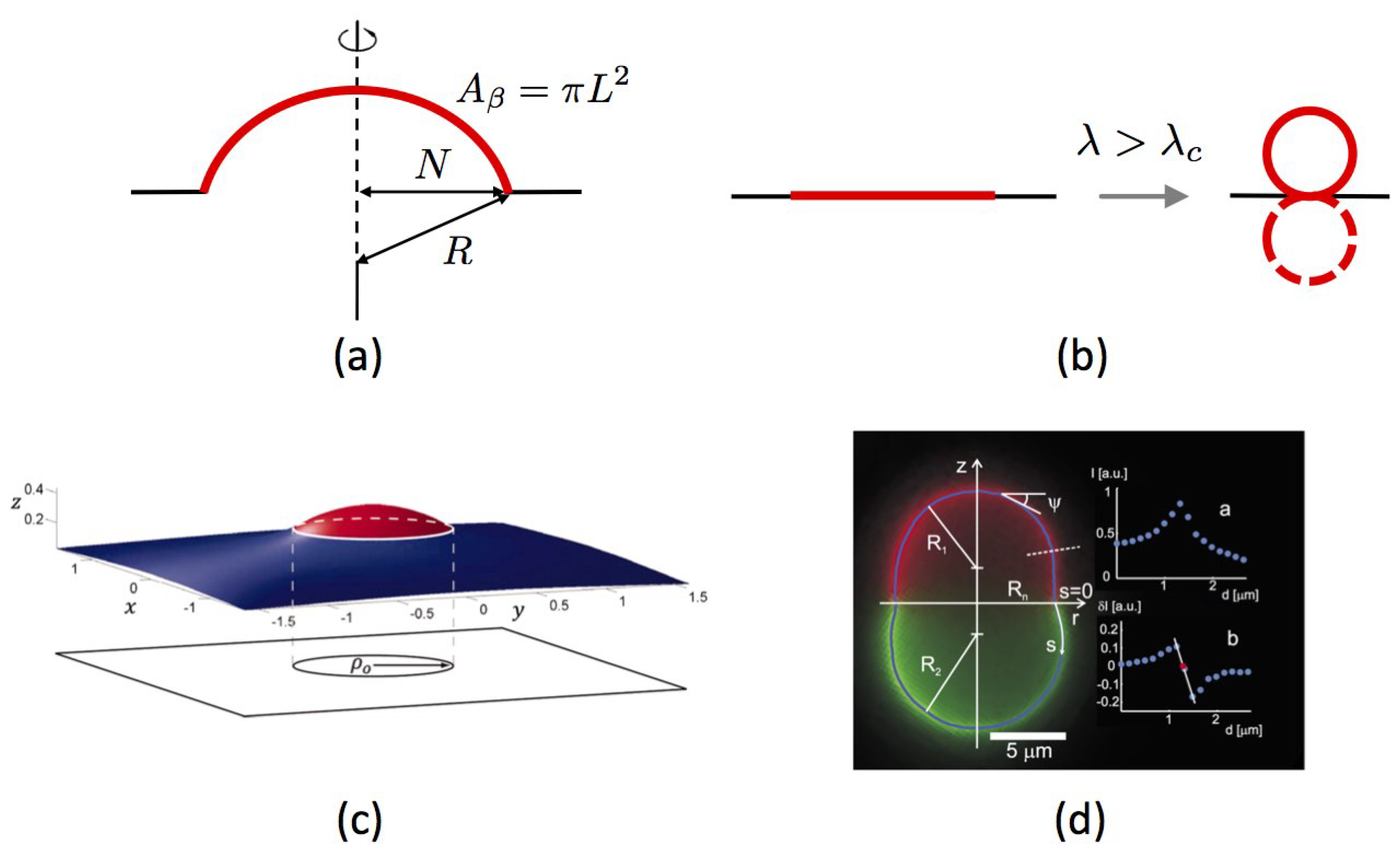
- Planar membranes—We begin with the simplest form of this mechanism, as proposed in planar geometry by Lipowsky in 1992 [110]. We consider a single membrane Lo domain (denoted -phase in this work) in a large planar Ld membrane (-phase). Well below the demixing temperature, the boundary shape is close to a circle to minimize the interfacial energy. The total domain area is denoted by (L is its radius in the membrane plane). Lipowsky first assumes that the surface tension is vanishingly small (). If it buds in the third dimension, the domain adopts the shape of a spherical cap supported by a sphere of radius R, while the surrounding membrane remains flat (Figure 4a). The interface is now a circle of radius . Adopting a mechanical approach where fluctuations are ignored, the total elastic energy of the domain is given by the sum of two antagonist contributions: the boundary line-energy that is proportional to the domain boundary length and tends to minimize it (by protruding in the third dimension); and the elastic Helfrich energy which disfavors bending. For a fixed domain area the value of the cap radius R is obtained by minimizing . A natural length-scale can be introduced, called the “invagination length”. If for the Lo phase [106] and pN far from the critical point, then nm. When getting closer to the critical point, decreases as with a universal critical exponent equal to 1 in 2D biphasic systems in the 2D Ising universality class [15,110] and grows. We shall come back to these values later in the Discussion Section.Lipowsky shows that if , then the optimal geometry is a flat domain (); conversely, if , it is a complete sphere (), protruding upward or downward with equal probability. Differently said, this simple model without surface tension proposes that above a critical line tensionspontaneously breaking the up-down symmetry is energetically favorable because it reduces to zero the interfacial energy cost in spite of the increased bending energy (Figure 4b). The transition is first order. When , the symmetry between the two sides of the membrane is explicitly broken. If the value of is sufficiently small, the minimization of energy predicts intermediate equilibrium values of N, between 0 and L. This situation for which the bending energy and the interfacial energy balance each other is called incomplete budding, or “dimpling”.
- Additional role of surface tension—The case where the surface tension is finite, , has been explored in detail in [107]. As bending stiffness, membrane tension applied in the membrane plane favors flat domains and comes in opposition to interfacial energy minimization. In this case also, and without necessarily appealing to spontaneous curvature, incomplete budding occurs above a critical line tension, through the spontaneous symmetry breaking principle (Figure 4c). The transition from flat to dimpled domains is now continuous whereas it was discontinuous without tension. More quantitatively, it is proven in this work that the critical line tension is given by in the limiting case where the domain area . Here is the domain stiffness, which can be different from the surrounding membrane one, . Coming back to the notations used in the paragraph just above, this condition reads at the critical point, which is twice the transition value found when . This means that in the interval , budding is energetically favored when , but becomes less stable than the flat geometry as soon as is positive, even if small.Furthermore, just above this critical value, the contact angle at the domain boundary scales as . The Lo domain continuously but rapidly deviates from the flat state. By up-down symmetry, the domain is equally likely to bud upward () or downward (). When , this symmetry is again explicitly broken, and phase diagrams can also be inferred [107].
- Vesicles—Jülicher and Lipowsky addressed the same question in the case of biphasic vesicles with spherical topology [111]. As above, different situations exist, but the up-down symmetry (more precisely the exterior/interior symmetry in this case) is explicitly broken on a vesicle. As stressed in the field-theoretic approaches presented in Section 2.1.3, a new ingredient can come into play here, namely the conservation of the volume V enclosed by the vesicle, or equivalently the pressure jump across the membrane, , which can be controlled through the osmotic pressure difference. The control parameter is, e.g., the reduced volume , measuring the deviation to a sphere (for which ). If two domains coexist as above, describing the membrane through an elastic continuum theory, the minimization of the total energy provides the so-called “shape equations”, from which the equilibrium vesicle shape under the relevant constraints is derived. In particular, it depends on the relative area fractions and on the different parameters (bending moduli , saddle-splay moduli , spontaneous curvature ), which can in principle be different in the two phases. Indeed, even though it is not a pre-requisite, the difference between the bending moduli of the two phases now likely plays a role, contrary to the planar case, because both phases are bent in this geometry.A rich phase diagram can be computed by minimizing the membrane energy, still neglecting thermal fluctuations. In this case as well, budding can be incomplete or complete, a closed vesicle then being connected to the main vesicle through an infinitesimal “neck”. However, a strong volume constraint (or equivalently large ), where the shape is quasi-spherical, can act against the budding process but does not, in general, suppress it. The reader can refer to [111] for further details. These results have been confirmed by numerical coarse-grained modeling (4-bead lipids and explicit solvent) based on dissipative particle dynamics, where both area and volume are conserved [112].
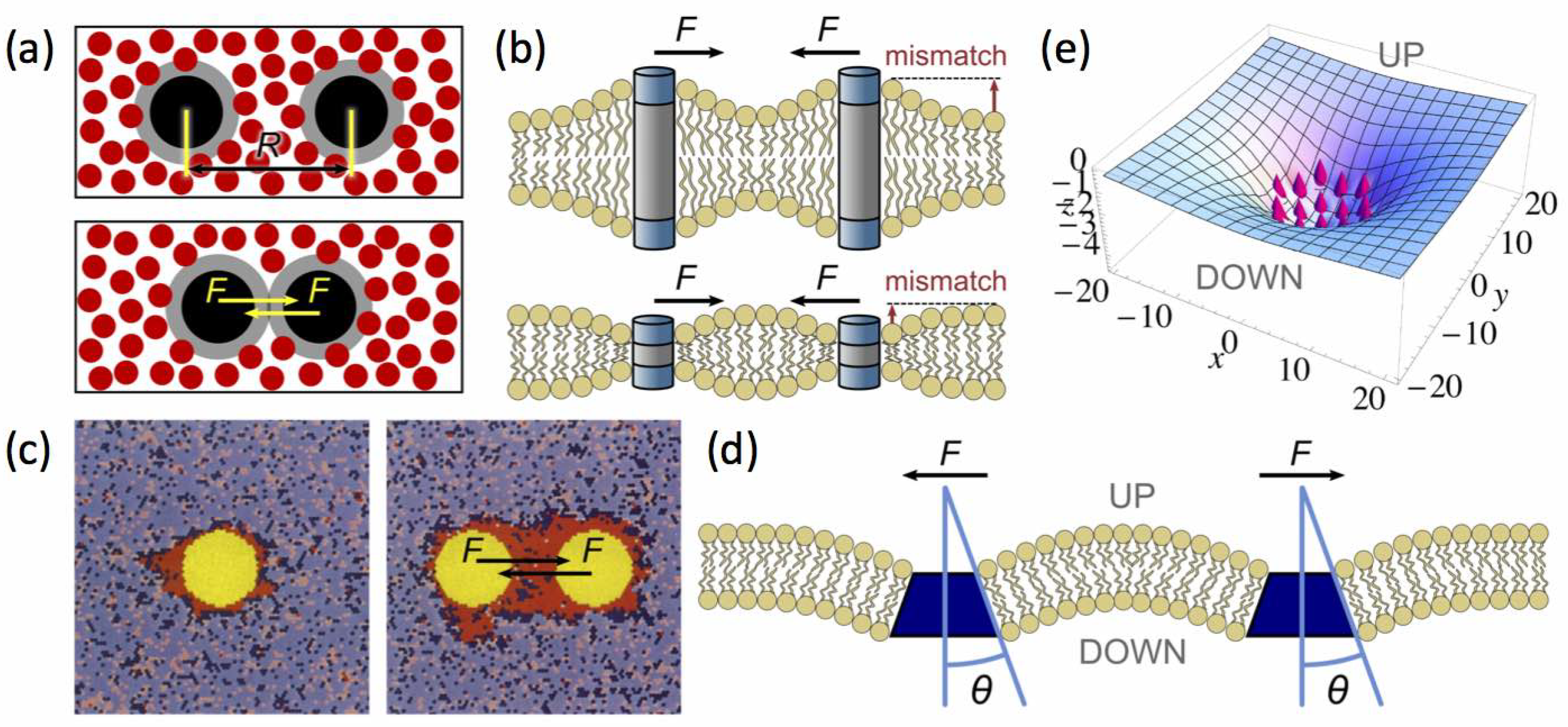
- Experiments—Fluorescence microscopy experiments [105,106,113] have later validated this theoretical approach on free-floating giant unilamellar vesicles (GUV) made of ternary mixtures of saturated lipids, unsaturated lipids and cholesterol, well below the demixing temperature, which display separated Lo and Ld phases (Figure 4d). In reference [114], the reduced volume v of GUVs made of a DPPC/DOPC/cholesterol mixture is controlled by varying the osmotic pressure. If one starts from a spherical vesicle, domains bud (inward or outward according to the experimental conditions) when the enclosed volume decreases. Following these original studies, a series of papers studied the experimental counterpart of these theoretically predicted circular, budded Lo domains and established phase diagrams [63,107,115]. When the cholesterol concentration was increased above %, a reversal phenomenon was observed, now with Ld domains in a Lo continuous background. The domain sizes were typically observed to be in the micron scale. We have previously explained that if [105], then the critical radius L above which domains buckles is few m with the above value of nm. Experiments and theory are compatible. Even though in a less evident manner, AFM experiments also suggest that budding exists in planar geometry [25], as predicted by theoretical approaches in the relevant regimes of parameters.
- Elastic interaction between budded domains—In these experiments, it is also observed that domains sometimes coalesce [105,115] but that this process is very slow and does not follow the usual laws of coarsening [116]. The reason is that budded domains repel each other when they come in close proximity because they deform the elastic membrane, in an enhanced way if they are very close. This repulsion has even be very well quantified experimentally [63,107,115] and shown to be compatible with theoretical predictions. A supposedly metastable configuration is then observed with long but finite lifetime. After several hours, all Lo domains eventually coalesce and one ends with a complete macro-phase separation. Note also that coarsening is not always trapped and that the existence of normal coarsening has been correlated to a vesicle reduced volume v very close to 1 [115]. Indeed, budding requires excess area that is only available if the vesicle is at least slightly deflated.As a matter of fact, the complete proposed scenario is as follows: after quenching below the demixing temperature and once domain have nucleated, normal coarsening is initiated, with small but growing nanoscopic domains. Being small, these domains are flat as demonstrated above [63]. When their size reaches the critical value, all these domains suddenly buckle and coarsening is then trapped in the metastable state [107,115]. The lateral organization of domains observed on phase-separated Sphingomyelin(SM)/DOPC/cholesterol vesicles in [117] has been attributed to this inter-domain repulsion, and the force between domain measured. Strong slowing-down of domain coarsening observed in DPPC/DOPC/cholesterol GUVs [118] was also attributed to budding, even though the inter-bud repulsion was not explicitly appealed to in this work. In contrast, when budding is avoided on sufficiently taut vesicles, no slowing-down is observed with respect to the expected dynamical exponent [119].
2.2.2. Competing Interactions: Phase-Dependent Bending Modulus
2.3. Competing Interactions: Spontaneous Curvature Induced by Membrane Inclusions
2.3.1. Inter-Protein Short-Range Forces
- Electrostatic, van der Waals and hydrogen-bond interactions—Polar and charged amino acids at their surface can interact when two proteins come in close proximity. The Debye length nm in water at physiological salt condition [2] sets the typical range above which these interactions are screened. Inside the apolar hydrophobic membrane region where the dielectric constant is weaker, the range can be somewhat larger, of a few nanometers [133,134]. The range of van der Waals and hydrogen-bond interactions is also nanometric.
- Hydrophobic mismatch—Integral proteins have transmembrane domains consisting of alpha helices with hydrophobic amino-acid side chains, buried inside the hydrophobic core of the lipid membrane. Protein and membrane hydrophobic core thicknesses do not necessarily match. Since exposure of hydrophobic residues to the aqueous solvent is energetically unfavorable, the membrane must be deformed in the case of significant mismatch [12,135]. If two (or more) proteins are in proximity, the overall energy penalty depends on their distance d. As above, an effective force ensues (Figure 7b). It is attractive when both mismatches have the same sign and repulsive in the converse case. The energies at play go from a fraction of to several , depending on the degree of hydrophobic mismatch, and the range of these forces is few nanometers [136,137,138,139]. It has been suggested that hydrophobic mismatch forces are not pairwise additive [140].
- Casimir interaction—This attractive interaction, of entropic origin, is named by extension of the Casimir interaction in quantum physics (the attraction between conducting plates mediated by quantum fluctuations in the electromagnetic field). Here it results from the transverse thermal fluctuations of the elastic membrane. The number of vibrational degrees of liberty of a membrane in which two (or more) inclusions are embedded depends on their mutual distance d. The potential of mean force thus depends on d, and has been shown to behave as in the case of vanishing membrane tension [131,141]. The calculation can be extended to the case , where the interaction energy decays much faster with d, as when , and as when [142,143].
- Depletion (or excluded-volume) forces—Attractive depletion forces (Figure 7a) are well characterized in soft condensed matter when large particles evolve among smaller ones, and play a role in physical biology (see [2] for example). In the present case, they are due to the 2D osmotic pressure laterally exerted by the surrounding lipids on large transmembrane proteins (larger than lipids). It should be far less pronounced for peptides. Roughly speaking, when two proteins are far away, the lateral osmotic pressure is isotropic and no net force ensues. When the relative distance becomes on the order of the lipid lateral size (<1 nm), the interval between the two inclusions tends to be depleted in lipids, and the pressure is not isotropic anymore. This tends to bring proteins closer when they are about a nanometer away [144,145]. The ensuing binding energy is on the range, even though the actual value depends on the model details.
- Lipid wetting—Some lipids are known to have a preferential affinity for given proteins species [39,146,147,148], in particular but not exclusively because they better match their hydrophobic length. Even above the phase-transition temperature, the protein can nucleates a small “halo” of such lipids, the range of which is on the order of magnitude of the composition correlation length (see Section 2). This mechanism known as “wetting” [132,149,150] is reminiscent of the “lipid annulus” or “lipid shell” concepts that have become popular in the biophysical literature a dozen of years ago [40]. When two proteins approach close enough for their halos to overlap, they tend to assemble because it reduces the net interfacial energy. An effective attractive force ensues (Figure 7c). This nucleation mechanism can also promote the formation of a lipid halo of a thermodynamic phase that would be unstable in absence of the inclusion. A similar mechanism has been demonstrated to emerge in a very illustrative way [151]. In all cases, the range is set by the correlation length .This force is enhanced near a miscibility critical point because the composition correlation length grows significantly. Exactly at the critical point, a long-range, power-law decrease of the potential of mean force at large inter-inclusion distance d has been predicted by a conformal field theory approach, with exponent , and confirmed by Monte Carlo simulations of the Ising model [152]. Coarse-grained molecular dynamics simulations on a model membrane and a phenomenological Ginzburg-Landau theory have explored the same mechanism in the case of peripheral proteins adsorbed onto the bilayer and interacting preferentially with one lipid species (among two). They drawn similar conclusions [147]. The binding energy at close range for two identical particles is also found in the range.Note that this mechanism is specific to the protein species and the lipids with which it preferentially interacts because the halos must be miscible if the interaction is attractive. In the case where they are immiscible, the force can even become repulsive instead [147,152]. Small alterations in lipid chemical structure can thus lead to dramatic changes in the membrane organization. This mechanism has been evidenced in model membranes [146].
2.3.2. The Cluster Phase Scenario
2.3.3. Spontaneous Curvature Can Play the Same Role as a Long-Range Repulsion
2.3.4. Sources of (Local) Spontaneous Curvature
- The transmembrane part of an integral protein has no reason to be up-down symmetric, not least because the cytosolic and extracellular protein regions do not have the same biological function. This is either apparent in the molecular shape of transmembrane proteins or can be inferred from their behavior in biophysical experiments [71,163,169,170,171,172,173,174]. However, it seems difficult to infer the spontaneous curvature from the sole molecular shape displaying up-down symmetry breaking, for the reasons that we discuss now.
- Peripheral proteins naturally break the up-down symmetry [70,175,176], to a degree that depends in particular on the depth of penetration of the hydrophobic domain of the protein into the bilayer [71]. Numerical evidence can be found for example in Ref. [147], where the small shoulder on the interaction potential at intermediate range indicates a weak repulsion. More generally, anchored molecules can play the same role, as it was non-ambigously demonstrated in reference [86] on experimental proofs.
- The coupling between lipid composition and protein wetting by lipids is also a potential source of local curvature if a protein recruits different lipids in the two leaflets, themselves promoting markedly differential local curvature of the two leaflets.
2.3.5. Diversity of Membrane Proteins and Biological Specialization of Clusters
2.4. A Unifying Rationale: Up-Down Symmetry Breaking
3. Active and Out-of-Equilibrium Processes
3.1. Models
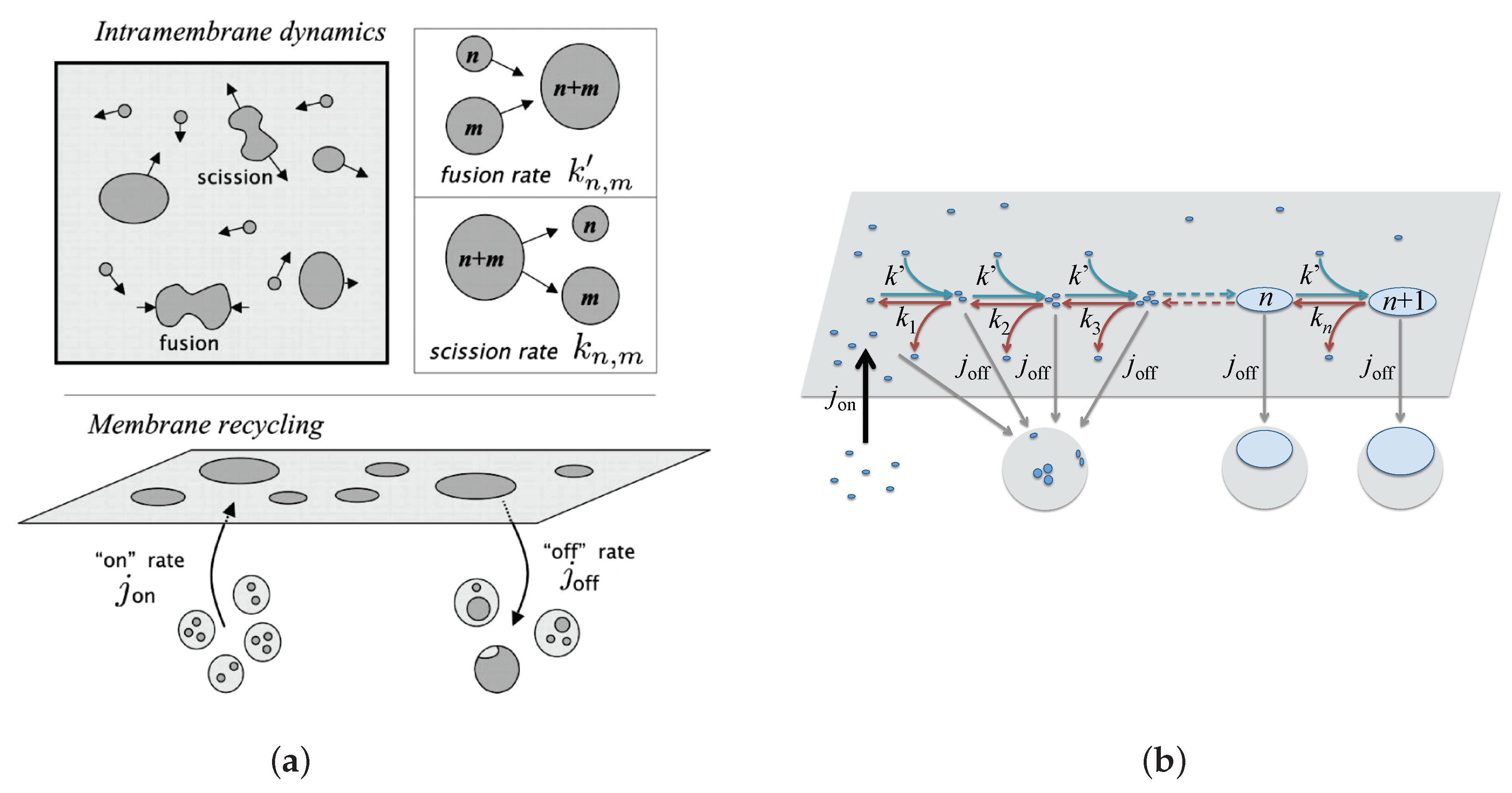
- (i)
- Master Smoluchowski’s coagulation equation [57,196,199,201]. For example, Turner et al. [57] studied the coagulation equationwhere is the area fraction of domains or clusters containing n monomers and the constants and are scission and fusion rates, respectively. Finally, controls recycling. Both cases in Figure 8a,b correspond to because only monomers are injected in the membrane with a rate while domains are recycled to the cytosol with a rate independent of their size n.
- (ii)
- Non-linear reaction-diffusion equations [56,197,198,200,202], which can also be seen as Cahn-Hilliard equations [15,116] suitably modified to take recycling into effect. For instance, in Ref [56], the Cahn-Hilliard equationis used. The order parameter again measures the local concentration of one phase (say the Lo phase), is its equilibrium value, is the recycling rate as discussed above, and A is a kinetic constant proportional to the lipid diffusion coefficient. The function is the Landau-Ginzburg expansion of a membrane patch free-energy, at the relevant order in powers of the order parameter , as already evoked in Section 2. Recycling is embedded in the first term of the r.h.s, while the second term describes the diffusive transport of the conserved order parameter .
- The off-rates (from the membrane to the cytosol) can be size-dependent [190] or not [57,199]. In the former case, it means for example that endocytosis is able to extract patches from the membrane with a limited size set by the endocytosed vesicle typical size [201]. A “recycling correlation length” can also be introduced in the modified Cahn-Hilliard equations, mimicking the spatial range of recycling processes, i.e., the typical size of membrane patches recycled through vesicle traffic [197,202]. In the models of Refs. [56,57,196,198,200], only monomers are locally extracted from the membrane.
- The on-rates (from the cytosol to the membrane) are also size-dependent. Several models only inject monomers or tiny domains in the membrane [56,57,190,196,198,199,200,201] because they do not assume any pre-order in the exocytosed patches or because they assume direct exchange of monomers from the cytosol to the membrane, e.g., for peripheral proteins. Indeed, Foret argues that the traffic should be modeled differently for peripheral and transmembrane proteins [196], because the former are preferentially exchanged as monomers between the cytosol and the membrane, while the latter preferentially escape and join the membrane by endo- and exocytosis, respectively. Another approach assumes that domains with a characteristic size are directly injected in the membrane [197,202].
- Inside the membrane, two mechanisms control the domain dynamics: either the domains principally exchange matter through Ostwald ripening (exchange of monomers via the surrounding dilute “gas” phase [116,193], as illustrated in Figure 8b), see references [56,196,197,198,199,200,202], or through domain scission or fusion events, for all sizes [57,190] (Figure 8a).
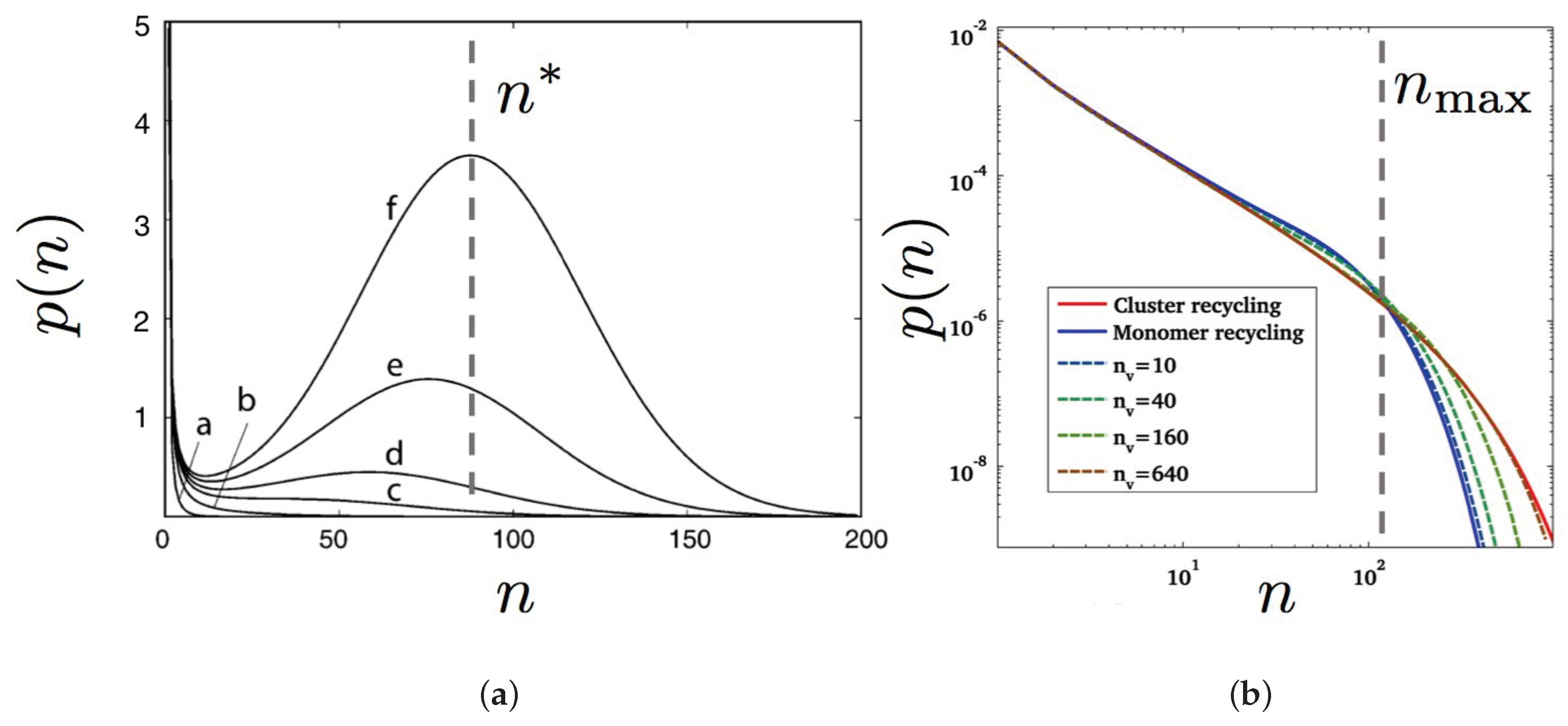
3.2. Results and Prospects
4. General Discussion and Conclusions
4.1. A Variety of Mechanisms in Equilibrium in the Strong Segregation Limit
4.2. Nanodomains and Critical Density Fluctuations
4.3. Needed Theoretical Clarifications
4.4. Needed New Experiments
4.5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alberts, B.; Johnson, A.; Lewis, J.; Ra, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Phillips, R.; Kondev, J.; Thierot, J.; Orme, N. Physical Biology of the Cell; Garland Science: New York, NY, USA, 2009. [Google Scholar]
- Singer, S.J.; Nicolson, G.L. The fluid mosaic model of the structure of cell membranes. Science 1972, 175, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Edidin, M. The state of lipid rafts: From model membranes to cells. Annu. Rev. Biochem. Biomol. Struct. 2003, 32, 257–283. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, K.; Mouritsen, O.G.; Anderson, R.G.W. Lipid rafts: At a crossroad between cell biology and physics. Nat. Cell Biol. 2007, 9, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Lenne, P.-F.; Nicolas, A. Physics puzzles on membrane domains posed by cell biology. Soft Matter 2009, 5, 2841–2848. [Google Scholar] [CrossRef]
- Komura, S.; Andelman, D. Physical aspects of heterogeneities in multi-component lipid membranes. Adv. Coll. Interf. Sci. 2014, 208, 34–46. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, K.; Liu, P. Complexity revealed: A hierarchy of clustered membrane proteins. Biophys. J. 2016, 111, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Destainville, N.; Schmidt, T.H.; Lang, T. Where biology meets physics—A converging view on membrane microdomain dynamics. Curr. Top. Membr. 2016, 77, 27–65. [Google Scholar] [PubMed]
- Sezgin, E.; Levental, I.; Mayor, S.; Eggeling, C. The mystery of membrane organization: Composition, regulation and physiological relevance of lipid rafts. Nat. Rev. Mol. Cell Biol. 2017, 18, 361–374. [Google Scholar] [CrossRef] [PubMed]
- Safran, S.A. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. Frontiers in Physic; Westview Press: Boulder, CO, USA, 2003. [Google Scholar]
- Mouritsen, O.G. Life—As a Matter of Fat; Springer: Berlin, Germany, 2005. [Google Scholar]
- Marsh, D. Cholesterol-induced fluid membrane domains: A compendium of lipid-raft ternary phase diagrams. Biochim. Biophys. Acta Biomembr. 2009, 1788, 2114–2123. [Google Scholar] [CrossRef] [PubMed]
- Schmid, F. Physical mechanisms of micro- and nanodomain formation in multicomponent lipid membranes. Biochim. Biophys. Acta 2017, 1859, 509–528. [Google Scholar] [CrossRef] [PubMed]
- Chaikin, P.M.; Lubensky, T.C. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Onuki, A. Phase Transition Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Veatch, S.L.; Keller, S.L. Seeing spots: Complex phase behavior in simple membranes. Biochim. Biophys. Acta 2005, 1746, 172–185. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp-Smith, A.R.; Veatch, S.L.; Keller, S.L. An introduction to critical points for biophysicists; observations of compositional heterogeneity in lipid membranes. Biochim. Biophys. Acta 2009, 1788, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Ipsen, J.H.; Karlstrom, G.; Mouritsen, O.G.; Wennerstrom, H.; Zuckermann, M.J. Phase equilibria in the phosphatidylcholine-cholesterol system. Biochim. Biophys. Acta 1987, 905, 162–172. [Google Scholar] [CrossRef]
- Heberle, F.A.; Wu, J.; Goh, S.L.; Petruzielo, R.S.; Feigenson, G.W. Comparison of three ternary lipid bilayer mixtures: FRET and ESR reveal nanodomains. Biophys J. 2010, 99, 3309–3318. [Google Scholar] [CrossRef] [PubMed]
- Iino, R.; Koyama, I.; Kusumi, A. Single molecule imaging of green fluorescent proteins in living cells: E-cadherin forms oligomers on the free cell surface. Biophys. J. 2001, 80, 2667–2677. [Google Scholar] [CrossRef]
- Daumas, F.; Destainville, N.; Millot, C.; Lopez, A.; Dean, D.; Salome, L. Confined diffusion without fences of a G-protein-coupled receptor as revealed by single particle tracking. Biophys. J. 2003, 84, 356–366. [Google Scholar] [CrossRef]
- Espenel, C.; Margeat, E.; Dosset, P.; Arduise, C.; Le Grimellec, C.; Royer, C.A.; Boucheix, C.; Rubinstein, E.; Milhiet, P.E. Single-molecule analysis of CD9 dynamics and partitioning reveals multiple modes of interaction in the tetraspanin web. J. Cell Biol. 2008, 182, 765–776. [Google Scholar] [CrossRef] [PubMed]
- Feigenson, G.W.; Buboltz, J.T. Ternary phase diagram of dipalmitoyl-PC/dilauroyl-PC/cholesterol: Nanoscopic domain formation driven by cholesterol. Biophys. J. 2001, 80, 2775–2788. [Google Scholar] [CrossRef]
- Garcia-Saez, A.J.; Chiantia, S.; Schwille, P. Effect of line tension on the lateral organization of lipid membranes. J. Biol. Chem. 2007, 282, 33537–33544. [Google Scholar] [CrossRef] [PubMed]
- Grage, S.L.; Keleshian, A.M.; Turdzeladze, T.; Battle, A.R.; Tay, W.C.; May, R.P.; Holt, S.A.; Contera, S.A.; Haertlein, M.; Moulin, M.; et al. Bilayer-mediated clustering and functional interaction of MscL channels. Biophys. J. 2011, 100, 1252–1260. [Google Scholar] [CrossRef] [PubMed]
- Connell, S.D.; Heath, G.; Olmsteda, P.D.; Kisil, A. Critical point fluctuations in supported lipid membranes. Faraday Disc. 2013, 161, 91–111. [Google Scholar] [CrossRef]
- Whited, A.M.; Park, P.S.H. Nanodomain organization of rhodopsin in native human and murine rod outer segment disc membrane. Biochim. Biophys. Acta Biomembr. 2015, 1848, 26–34. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.S.; Khadka, N.K.; Pan, J. Sub-ten-nanometer heterogeneity of solid supported lipid membranes determined by solution atomic force microscopy. Biochim. Biophys. Acta 2016, 1858, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Lang, T.; Rizzoli, S.O. Membrane protein clusters at nanoscale resolution: More than pretty pictures. Physiology 2010, 25, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Heberle, F.A.; Petruzielo, R.S.; Pan, J.; Drazba, P.; Kučerka, N.; Standaert, R.F.; Feigenson, G.W.; Katsaras, J. Bilayer thickness mismatch controls domain size in model membranes. J. Am. Chem. Soc. 2013, 135, 6853–6859. [Google Scholar] [CrossRef] [PubMed]
- Nickels, J.D.; Cheng, X.; Mostofian, B.; Stanley, C.; Lindner, B.; Heberle, F.A.; Perticaroli, S.; Feygenson, M.; Egami, T.; Standaert, R.F.; et al. Mechanical properties of nanoscopic lipid domains. J. Am. Chem. Soc. 2015, 137, 15772–15780. [Google Scholar] [CrossRef] [PubMed]
- Usery, R.D.; Enoki, T.A.; Wickramasinghe, S.P.; Weiner, M.D.; Tsai, W.C.; Kim, M.B.; Wang, S.; Torng, T.L.; Ackerman, D.G.; Heberle, F.A.; et al. Line tension controls liquid-disordered + liquid-ordered domain size transition in lipid bilayers. Biophys. J. 2017, 112, 1431–1443. [Google Scholar] [CrossRef] [PubMed]
- Lingwood, D.; Simons, K. Lipid rafts as a membrane-organizing principle. Science 2010, 327, 46–50. [Google Scholar] [CrossRef] [PubMed]
- Pike, L.J. Rafts defined: A report on the keystone symposium on lipid rafts and cell function. J. Lipid Res. 2006, 47, 1597–1598. [Google Scholar] [CrossRef] [PubMed]
- Heerklotz, H. Triton promotes domain formation in lipid raft mixtures. Biophys. J. 2002, 83, 2693–2701. [Google Scholar] [CrossRef]
- Munro, S. Lipid rafts: Elusive or illusive? Cell 2003, 115, 377–388. [Google Scholar] [CrossRef]
- Harder, T. Formation of functional cell membrane domains: The interplay of lipid- and protein-mediated interactions. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2003, 358, 863–868. [Google Scholar] [CrossRef] [PubMed]
- Hancock, J.F. Lipid rafts: Contentious only from simplistic standpoints. Nat. Rev. Mol. Cell Biol. 2006, 7, 456–462. [Google Scholar] [CrossRef] [PubMed]
- Poveda, J.A.; Fernandez, A.M.; Encinar, J.A.; Gonzalez-Ros, J.M. Protein-promoted membrane domains. Biochim. Biophys. Acta Biomembr. 2008, 1778, 1583–1590. [Google Scholar] [CrossRef] [PubMed]
- Leslie, M. Do Lipid Rafts Exist? Science 2011, 334, 1046–1047. [Google Scholar] [CrossRef] [PubMed]
- Klotzsch, E.; Schuetz, G.J. A critical survey of methods to detect plasma membrane rafts. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20120033. [Google Scholar] [CrossRef] [PubMed]
- Honigmann, A.; Mueller, V.; Ta, H.; Schoenle, A.; Sezgin, E.; Hell, S.W.; Eggeling, C. Scanning STED-FCS reveals spatiotemporal heterogeneity of lipid interaction in the plasma membrane of living cells. Nat. Commun. 2014, 5, 5412. [Google Scholar] [CrossRef] [PubMed]
- Levental, I.; Veatch, S. The continuing mystery of lipid rafts. J. Mol. Biol. 2016, 428, 4749–4764. [Google Scholar] [CrossRef] [PubMed]
- Seul, M.; Andelman, D. Domain shapes and patterns: The phenomenology of modulated phases. Science 1995, 267, 476–483. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, A.; Lebowitz, J.L.; Lieb, E.H. Pattern formation in systems with competing interactions. In Proceedings of the AIP Conference 10th Granada Seminar on Computational Physics, Granada, Spain, 15–19 September 2008. [Google Scholar]
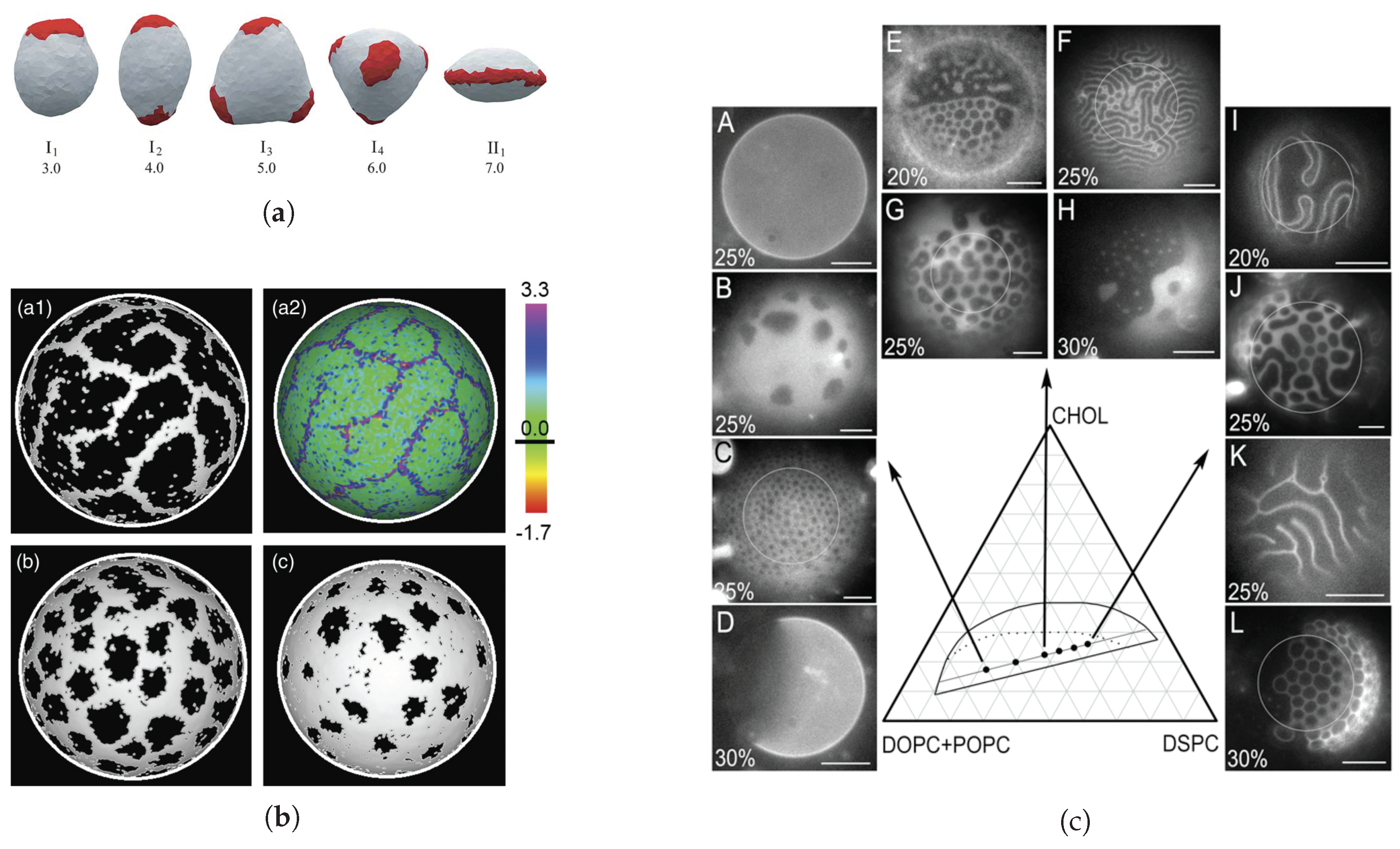
- Lavrentovich, M.O.; Horsley, E.M.; Radja, A.; Sweeney, A.M.; Kamien, R.D. First-order patterning transitions on a sphere as a route to cell morphology. Proc. Natl. Acad. Sci. USA 2016, 113, 5189–5194. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R. Domain-induced budding of fluid membranes. Biophys. J. 1993, 64, 1133–1138. [Google Scholar] [CrossRef]
- Goh, S.L.; Amazon, J.J.; Feigenson, G.W. Toward a better raft model: Modulated phases in the four-component bilayer, DSPC/DOPC/POPC/CHOL. Biophys. J. 2013, 104, 853–862. [Google Scholar] [CrossRef] [PubMed]
- Palmieri, B.; Yamamoto, T.; Brewster, R.C.; Safran, S.A. Line active molecules promote inhomogeneous structures in membranes: Theory, simulations and experiments. Adv. Coll. Interf. Sci. 2014, 208, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Chavent, M.; Duncan, A.L.; Sansom, M.S.P. Molecular dynamics simulations of membrane proteins and their interactions: From nanoscale to mesoscale. Curr. Opin. Struct. Biol. 2016, 40, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Binder, K. (Ed.) Monte Carlo Methods in Statistical Physics; Springer: Berlin, Germany, 1986. [Google Scholar]
- Hu, J.; Weikl, T.; Lipowsky, R. Vesicles with multiple membrane domains. Soft Matter 2011, 7, 6092–6102. [Google Scholar] [CrossRef]
- Barrat, J.-L.; Hansen, J.-P. Basic Concepts for Simple and Complex Liquids; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C Biochem. Biophys. Biol. Virol. 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Foret, L. A simple mechanism of raft formation in two-component fluid membranes. EPL 2005, 71, 508–514. [Google Scholar] [CrossRef]
- Turner, M.S.; Sens, P.; Socci, N.D. Nonequilibrium raftlike membrane domains under continuous recycling. Phys. Rev. Lett. 2005, 95, 168301. [Google Scholar] [CrossRef] [PubMed]
- Leibler, S. Curvature instability in membranes. J. Phys. (Fr.) 1986, 47, 507–516. [Google Scholar] [CrossRef]
- Leibler, S.; Andelman, D. Ordered and curved meso-structures in membranes and amphiphilic films. J. Phys. (Fr.) 1987, 48, 2013–2018. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Dimova, R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 2014, 208, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Baumgart, T.; Hess, S.T.; Webb, W.W.; Jenkins, J.T. Membrane elasticity in giant vesicles with fluid phase coexistence. Biophys. J. 2005, 89, 1067–1080. [Google Scholar] [CrossRef] [PubMed]
- Semrau, S.; Idema, T.; Schmidt, T.; Storm, C. Membrane-mediated interactions measured using membrane domains. Biophys. J. 2009, 96, 4906–4915. [Google Scholar] [CrossRef] [PubMed]
- Gutlederer, E.; Gruhn, T.; Lipowsky, R. Polymorphism of vesicles with multi-domain patterns. Soft Matter 2009, 5, 3303–3311. [Google Scholar] [CrossRef]
- Gueguen, G.; Destainville, N.; Manghi, M. Fluctuation tension and shape transition of vesicles: Renormalisation calculations and Monte Carlo simulations. Soft Matter 2017, 13, 6100–6117. [Google Scholar] [CrossRef] [PubMed]
- Komura, S.; Shimokawa, N.; Andelman, D. Tension-induced morphological transition in mixed lipid bilayers. Langmuir 2006, 22, 6771–6774. [Google Scholar] [CrossRef] [PubMed]
- Stradner, A.; Sedgwick, H.; Cardinaux, F.; Poon, W.C.; Egelhaaf, S.U.; Schurtenberger, P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 2004, 432, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Gotzelmann, B.; Evans, R.; Dietrich, S. Depletion forces in fluids. Phys. Rev. E 1998, 57, 6785–6800. [Google Scholar] [CrossRef]
- Destainville, N. Cluster phases of membrane proteins. Phys. Rev. E 2008, 77, 011905. [Google Scholar] [CrossRef] [PubMed]
- Jarsch, I.K.; Daste, F.; Gallop, J.L. Membrane curvature in cell biology: An integration of molecular mechanisms. J. Cell. Biol. 2016, 214, 375–387. [Google Scholar] [CrossRef] [PubMed]
- Zimmerberg, J.; Kozlov, M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006, 7, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Perlmutter, J.D.; Sachs, J.N. Interleaflet interaction and asymmetry in phase separated lipid bilayers: Molecular dynamics simulations. J. Am. Chem. Soc. 2011, 133, 6563–6577. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R. Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature. Faraday Discuss. 2013, 161, 305–331. [Google Scholar] [CrossRef] [PubMed]
- Milo, R.; Phillips, R. Cell Biology by the Numbers; Garland Science: New York, NY, USA, 2015. [Google Scholar]
- Miao, L.; Seifert, U.; Wortis, M.; Dobereiner, H.G. Budding transitions of fluid-bilayer vesicles: The effect of area-difference elasticity. Phys. Rev. E 1994, 49, 5389–5407. [Google Scholar] [CrossRef]
- Roux, D.; Cates, M.E.; Olsson, U.; Ball, R.C.; Nallet, F.; Bellocq, A.M. Light scattering from a surfactant “sponge” phase: Evidence for a hidden symmetry. Europhys. Lett. 1990, 11, 229–234. [Google Scholar] [CrossRef]
- Gompper, G.; Schick, M. Scattering from internal interfaces in microemulsion and sponge phases. Phys. Rev. E 1994, 49, 1478–1482. [Google Scholar] [CrossRef]
- Schick, M. Membrane heterogeneity: Manifestation of a curvature-induced microemulsion. Phys. Rev. E 2012, 85, 031902. [Google Scholar] [CrossRef] [PubMed]
- Shlomovitz, R.; Schick, M. Model of a raft in both leaves of an asymmetric lipid bilayer. Biophys J. 2013, 105, 1406–1413. [Google Scholar]
- Brazovskii, S.A. Phase transitions of an isotropic system to a non-uniform state. Sov. Phys. JETP 1975, 41, 85–88. [Google Scholar]
- Sunil Kumar, P.B.; Gompper, G.; Lipowsky, R. Modulated phases in multicomponent fluid membranes. Phys. Rev. E 1999, 60, 4610–4618. [Google Scholar] [CrossRef]
- Stevens, M.J. Complementary matching in domain formation within lipid bilayers. J. Am. Chem. Soc. 2005, 127, 15330–15331. [Google Scholar] [CrossRef] [PubMed]
- Shlomovitz, R.; Maibaum, L.; Schick, M. Macroscopic phase separation, modulated phases, and microemulsions: A unified picture of rafts. Biophys. J. 2014, 106, 21–32. [Google Scholar] [CrossRef] [PubMed]
- MacKintosh, F. Mixed fluid bilayers: Effects of confinement. Phys. Rev. E 1994, 50, 2891–2897. [Google Scholar] [CrossRef]
- Gueguen, G.; Destainville, N.; Manghi, M. Mixed lipid bilayers with locally varying spontaneous curvature and bending. Eur. Phys. J. E. 2014, 37, 76. [Google Scholar] [CrossRef] [PubMed]
- Shimobayashi, S.F.; Ichikawa, M.; Taniguchi, T. Direct observations of transition dynamics from macro- to micro-phase separation in asymmetric lipid bilayers induced by externally added glycolipids. EPL 2016, 113, 56005. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; Huang, K.C.; Wingreen, N.S. Lipid localization in bacterial cells through curvature-mediated microphase separation. Biophys. J. 2008, 95, 1034–1049. [Google Scholar] [CrossRef] [PubMed]
- Agudo-Canalejo, J.; Golestanian, R. Pattern formation by curvature-inducing proteins on spherical membranes. New J. Phys. 2017, 19, 125013. [Google Scholar] [CrossRef]
- Williamson, J.J.; Olmsted, P.D. Registered and antiregistered phase separation of mixed amphiphilic bilayers. Biophys. J. 2015, 108, 1963–1976. [Google Scholar] [CrossRef] [PubMed]
- Meinhardt, S.; Vink, R.L.C.; Schmid, F. Monolayer curvature stabilizes nanoscale raft domains in mixed lipid bilayers. Proc. Natl. Acad. Sci. USA 2013, 110, 4476–4481. [Google Scholar] [CrossRef] [PubMed]
- Brodbek, L.; Schmid, F. Interplay of curvature-induced micro- and nanodomain structures in multicomponent lipid bilayers. Int. J. Adv. Eng. Sci. Appl. Math. 2016, 8, 111–120. [Google Scholar] [CrossRef]
- Dan, N.; Pincus, P.; Safran, S.A. Membrane-induced interactions between inclusions. Langmuir 1993, 9, 2768–2771. [Google Scholar] [CrossRef]
- Goulian, M.; Bruinsma, R.; Pincus, P. Long-range forces in heterogeneous fluid membranes. Europhys. Lett. 1993, 22, 145–150. [Google Scholar] [CrossRef]
- Netz, R.R.; Pincus, P. Inhomogeneous fluid membranes: Segregation, ordering, and effective rigidity. Phys. Rev. E 1995, 52, 4114–4128. [Google Scholar] [CrossRef]
- Netz, R.R. Inclusions in fluctuating membranes: Exact results. J. Phys. I (Fr.) 1997, 7, 833–852. [Google Scholar] [CrossRef]
- Dean, D.S.; Manghi, M. Fluctuation-induced interactions between domains in membranes. Phys. Rev. E 2006, 74, 021916. [Google Scholar] [CrossRef] [PubMed]
- Imparato, A.; Shillcock, J.C.; Lipowsky, R. Shape fluctuations and elastic properties of two-component bilayer membranes. Europhys. Lett. 2005, 69, 650–656. [Google Scholar] [CrossRef]
- Brannigan, G.; Brown, F.L.H. Composition dependence of bilayer elasticity. J. Chem. Phys. 2005, 122, 074905. [Google Scholar] [CrossRef] [PubMed]
- Zhong-can, O.-Y.; Helfrich, W. Bending energy of vesicle membranes: General expressions for the first, second, and third variation of the shape energy and applications to spheres and cylinders. Phys. Rev. A 1989, 39, 5280–5288. [Google Scholar] [CrossRef]
- Helfrich, W. Size distributions of vesicles: The role of the effective rigidity of membranes. J. Phys. (Fr.) 1986, 47, 321–329. [Google Scholar] [CrossRef]
- Milner, S.T.; Safran, S.A. Dynamical fluctuations of droplet microemulsions and vesicles. Phys. Rev. A 1987, 36, 4371–4379. [Google Scholar] [CrossRef]
- Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997, 46, 13–137. [Google Scholar] [CrossRef]
- Barbetta, C.; Imparato, A.; Fournier, J.-B. On the surface tension of fluctuating quasi-spherical vesicles. Eur. Phys. J. E 2010, 31, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, T.; Kawasaki, K.; Andelman, D.; Kawakatsu, T. Phase transitions and shapes of two component membranes and vesicles II: Weak segregation limit. J. Phys. II 1994, 4, 1333–1362. [Google Scholar] [CrossRef]
- Baumgart, T.; Hess, S.T.; Webb, W.W. Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature 2003, 425, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Semrau, S.; Idema, T.; Holtzer, L.; Schmidt, T.; Storm, C. Accurate determination of elastic parameters for multicomponent membranes. Phys. Rev. Lett. 2008, 100, 088101. [Google Scholar] [CrossRef] [PubMed]
- Ursell, T.S.; Klug, W.S.; Phillips, R. Morphology and interaction between lipid domains. Proc. Natl. Acad. Sci. USA 2009, 106, 13301–13306. [Google Scholar] [CrossRef] [PubMed]
- Andelman, D.; Kawakatsu, T.; Kawasaki, K. Equilibrium shape of two-component unilamellar membranes and vesicles. Europhys. Lett. 1992, 19, 57–62. [Google Scholar] [CrossRef]
- Kawakatsu, T.; Andelman, D.; Kawasaki, K.; Taniguchi, T. Phase transitions and shapes of two component membranes and vesicles I: Strong segregation limit. J. Phys. II 1993, 3, 971–997. [Google Scholar] [CrossRef]
- Lipowsky, R. Budding of membranes induced by intramembrane domains. J. Phys. II 1992, 2, 1825–1840. [Google Scholar] [CrossRef]
- Julicher, F.; Lipowsky, R. Shape transformations of vesicles with intramembrane domains. Phys. Rev. E 1996, 53, 2670–2683. [Google Scholar] [CrossRef]
- Laradji, M.; Kumar, P.B. Dynamics of domain growth in self-assembled fluid vesicles. Phys. Rev. Lett. 2004, 93, 198105. [Google Scholar] [CrossRef] [PubMed]
- Veatch, S.L.; Keller, S.L. Organization in lipid membranes containing cholesterol. Phys. Rev. Lett. 2002, 89, 268101. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, M.; Imai, M.; Taniguchi, T. Shape deformation of ternary vesicles coupled with phase separation. Phys. Rev. Lett. 2008, 100, 148102. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, M.; Imai, M.; Masui, T.; Komura, S.; Ohta, T. Growth dynamics of domains in ternary fluid vesicles. Biophys. J. 2007, 92, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Bray, A.J. Theory of phase ordering kinetics. Adv. Phys. 1994, 43, 357–459. [Google Scholar] [CrossRef]
- Rozovsky, S.; Kaizuka, Y.; Groves, J.T. Formation and spatio-temporal evolution of periodic structures in lipid bilayers. J. Am. Chem. Soc. 2005, 127, 36–37. [Google Scholar] [CrossRef] [PubMed]
- Saeki, D.; Hamada, T.; Yoshikawa, K. Domain-growth kinetics in a cell-sized liposome. J. Phys. Soc. Jpn. 2006, 75, 013602. [Google Scholar] [CrossRef]
- Stanich, C.A.; Honerkamp-Smith, A.R.; Putzel, G.G.; Warth, C.S.; Lamprecht, A.K.; Mandal, P.; Mann, E.; Hua, T.A.; Keller, S.L. Coarsening dynamics of domains in lipid membranes. Biophys. J. 2013, 105, 444–454. [Google Scholar] [CrossRef] [PubMed]
- Rawicz, W.; Olbrich, K.C.; McIntosh, T.; Needham, D.; Evans, E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000, 79, 328–339. [Google Scholar] [CrossRef]
- Fowler, P.W.; Helie, J.; Duncan, A.; Chavent, M.; Koldso, H.; Sansom, M.S.P. Membrane stiffness is modified by integral membrane proteins. Soft Matter 2016, 12, 7792–7803. [Google Scholar] [CrossRef] [PubMed]
- Usery, R.D.; Enoki, T.A.; Wickramasinghe, S.P.; Nguyen, V.P.; Ackerman, D.G.; Greathouse, D.V.; Koeppe, R.E.; Barrera, F.N.; Feigenson, G.W. Membrane bending moduli of coexisting liquid phases containing transmembrane peptide. Biophys. J. 2018, 114, 2152–2164. [Google Scholar] [CrossRef] [PubMed]
- Amazon, J.J.; Goh, S.L.; Feigenson, G.W. Competition between line tension and curvature stabilizes modulated phase patterns on the surface of giant unilamellar vesicles: A simulation study. Phys. Rev. E 2013, 87, 022708. [Google Scholar] [CrossRef] [PubMed]
- Veatch, S.L.; Keller, S.L. Separation of liquid phases in giant vesicles of ternary mixtures of phospholipids and cholesterol. Biophys J. 2003, 85, 3074–3083. [Google Scholar]
- Gudheti, M.V.; Mlodzianoski, M.; Hess, S.T. Imaging and shape analysis of GUVs as model plasma membranes: Effect of trans DOPC on membrane properties. Biophys. J. 2007, 93, 2011–2023. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, T.; Yanagisawa, M.; Imai, M. Numerical investigations of the dynamics of two-component vesicles. J. Phys. Condens. Matter 2011, 23, 284103. [Google Scholar] [CrossRef] [PubMed]
- Konyakhina, T.M.; Goh, S.L.; Amazon, J.J.; Heberle, F.A.; Wu, J.; Feigenson, G.W. Control of a nanoscopic-to-macroscopic transition: Modulated phases in four-component DSPC/DOPC/POPC/Chol giant unilamellar vesicles. Biophys. J. 2011, 101, L8–L10. [Google Scholar] [CrossRef] [PubMed]
- Amazon, J.J.; Feigenson, G.W. Lattice simulations of phase morphology on lipid bilayers: Renormalization, membrane shape, and electrostatic dipole interactions. Phys. Rev. E 2014, 89, 022702. [Google Scholar] [CrossRef] [PubMed]
- Fournier, J.-B.; Dommersnes, P.G. N-body study of anisotropic membrane inclusions: Membrane mediated interactions and ordered aggregation. Eur. Phys. J. B 1999, 12, 9–12. [Google Scholar]
- Evans, A.R.; Turner, M.S.; Sens, P. Interactions between proteins bound to biomembranes. Phys. Rev. E 2003, 67, 041907. [Google Scholar] [CrossRef] [PubMed]
- Park, J.M.; Lubensky, T.C. Interactions between membrane inclusions on fluctuating membranes. J. Phys. I 1996, 6, 1217–1235. [Google Scholar] [CrossRef]
- Gil, T.; Sabra, M.C.; Ipsen, J.H.; Mouritsen, O.G. Wetting and capillary condensation as means of protein organization in membranes. Biophys. J. 1997, 73, 1728–1741. [Google Scholar] [CrossRef]
- Abney, J.R.; Scalettar, B.A. Molecular crowding and protein organization. In Thermodynamics of Membrane Receptors and Channels; Jackson, M.B., Ed.; CRC Press: Boca Raton, FL, USA, 1993; pp. 183–225. [Google Scholar]
- Liu, J.; Qi, S.; Groves, J.T.; Chakraborty, A.K. Phase segregation on different length scales in a model cell membrane system. J. Phys. Chem. B 2005, 109, 19960–19969. [Google Scholar] [CrossRef] [PubMed]
- Killian, J.A. Hydrophobic mismatch between proteins and lipids in membranes. Biochim. Biophys. Acta 1998, 1376, 401–415. [Google Scholar] [CrossRef]
- Bohinc, K.; Kralj-Iglic, V.; May, S. Interaction between two cylindrical inclusions in a symmetric bilayer. J. Chem. Phys. 2003, 119, 7435–7444. [Google Scholar] [CrossRef]
- Schmidt, U.; Guigas, G.; Weiss, M. Cluster formation of transmembrane proteins due to hydrophobic mismatching. Phys. Rev. Lett. 2008, 101, 128104. [Google Scholar] [CrossRef] [PubMed]
- Yoo, J.; Cui, Q. Membrane-mediated protein-protein interactions and connection to elastic models: A coarse-grained simulation analysis of gramicidin A association. Biophys. J. 2013, 104, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Bories, F.; Constantin, D.; Galatola, P.; Fournier, J.-B. Coupling between inclusions and membranes at the nanoscale. Phys. Rev. Lett. 2018, 120, 128104. [Google Scholar] [CrossRef] [PubMed]
- Brannigan, G.; Brown, F.L.H. Contribution of Gaussian curvature and nonconstant lipid volume to protein deformation of lipid bilayers. Biophys. J. 2007, 92, 864–876. [Google Scholar] [CrossRef] [PubMed]
- Dommersnes, P.G.; Fournier, J.-B. Casimir and mean-field interactions between membrane inclusions subject to external torque. Europhys. Lett. 1999, 46, 256–261. [Google Scholar] [CrossRef]
- Lin, H.K.; Zandi, R.; Mohideen, U.; Pryadko, L.P. Fluctuation-induced forces between inclusions in a fluid membrane under tension. Phys. Rev. Lett. 2011, 107, 228104. [Google Scholar] [CrossRef] [PubMed]
- Weitz, S.; Destainville, N. Attractive asymmetric inclusions in elastic membranes under tension: Cluster phases and membrane invaginations. Soft Matter 2013, 9, 7804–7816. [Google Scholar] [CrossRef]
- Sintes, T.; Baumgartner, A. Protein attraction in membranes induced by lipid fluctuations. Biophys. J. 1997, 73, 2251–2259. [Google Scholar] [CrossRef]
- Borodich, A.; Rojdestvenski, I.; Cottam, M. Lateral heterogeneity of photosystems in thylakoid membranes studied by brownian dynamics simulations. Biophys. J. 2003, 85, 774–789. [Google Scholar] [CrossRef]
- Hinderliter, A.; Biltonen, R.L.; Almeida, P.F.F. Lipid modulation of protein-induced membrane domains as a mechanism for controlling signal transduction. Biochemistry 2004, 43, 7102–7110. [Google Scholar] [CrossRef] [PubMed]
- Reynwar, B.J.; Deserno, M. Membrane composition-mediated protein-protein interactions. Biointerphases 2009, 3, FA117–FA124. [Google Scholar] [CrossRef] [PubMed]
- Van den Bogaart, G.; Meyenberg, K.; Risselada, H.J.; Amin, H.; Willig, K.I.; Hubrich, B.E.; Dier, M.; Hell, S.W.; Grubmüller, H.; Diederichsen, U.; et al. Membrane protein sequestering by ionic protein-lipid interactions. Nature 2011, 479, 552–555. [Google Scholar] [CrossRef] [PubMed]
- Gil, T.; Ipsen, J.H.; Mouritsen, O.G.; Sabra, M.C.; Sperotto, M.M.; Zuckermann, M.J. Theoretical analysis of protein organization in lipid membranes. Biochim. Biophys. Acta Biomembr. 1998, 1376, 245–266. [Google Scholar] [CrossRef]
- Gil, T.; Ipsen, J.H.; Tejero, C.F. Wetting controlled phase transitions in two-dimensional systems of colloids. Phys. Rev. E 1998, 57, 3123–3133. [Google Scholar] [CrossRef]
- Katira, S.; Mandadapu, K.K.; Vaikuntanathan, S.; Smit, B.; Chandler, D. Pre-transition effects mediate forces of assembly between transmembrane proteins. eLife 2016, 5, e13150. [Google Scholar] [CrossRef] [PubMed]
- Machta, B.B.; Veatch, S.L.; Sethna, J.P. Critical Casimir forces in cellular membranes. Phys. Rev. Lett. 2012, 109, 138101. [Google Scholar] [CrossRef] [PubMed]
- De Meyer, F.J.M.; Venturoli, M.; Smit, B. Molecular simulations of lipid mediated protein-protein interactions. Biophys. J. 2008, 95, 1851–1865. [Google Scholar] [CrossRef] [PubMed]
- Periole, X.; Knepp, A.M.; Sakmar, T.P.; Marrink, S.J.; Hubert, T. Structural determinants of the supramolecular organization of G protein-coupled receptors in bilayers. J. Am. Chem. Soc. 2012, 134, 10959–10965. [Google Scholar] [CrossRef] [PubMed]
- Casuso, I.; Sens, P.; Rico, F.; Scheuring, S. Experimental evidence for membrane-mediated protein-protein forces. Biophys. J. 2010, 99, L47–L49. [Google Scholar] [CrossRef] [PubMed]
- Destainville, N.; Foret, L. Thermodynamics of nano-cluster phases: A unifying theory. Phys. Rev. E 2008, 77, 051403. [Google Scholar] [CrossRef] [PubMed]
- Wasnik, V.; Wingreen, N.S.; Mukhopadhyay, R. Modeling curvature-dependent subcellular localization of the small sporulation protein SpoVM in bacillus subtilis. PLoS ONE 2015, 10, e0111971. [Google Scholar] [CrossRef] [PubMed]
- Sieber, J.J.; Willig, K.I.; Kutzner, C.; Gerding-Reimers, C.; Harke, B.; Donnert, G.; Rammner, B.; Eggeling, C.; Hell, S.W.; Grubmüller, H.; et al. Anatomy and dynamics of a supramolecular membrane protein cluster. Science 2007, 317, 1072–1076. [Google Scholar] [CrossRef] [PubMed]
- Gurry, T.; Kahramanogullari, O.; Endres, R.G. Biophysical mechanism for Ras-nanocluster formation and signaling in plasma membrane. PLoS ONE 2009, 4, e6148. [Google Scholar] [CrossRef] [PubMed]
- Gulik-Krzywicki, T.; Seigneuret, M.; Rigaud, J.L. Monomer-oligomer equilibrium of bacteriorhodopsin in reconstituted proteoliposomes. J. Biol. Chem. 1987, 262, 15580–15588. [Google Scholar] [PubMed]
- Homsi, Y.; Schloetel, J.; Scheffer, K.D.; Schmidt, T.H.; Destainville, N.; Florin, N.L.; Lang, T. The extracellular d-domain is essential for the formation of CD81 tetraspanin webs. Biophys. J. 2014, 107, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Merklinger, E.; Schloetel, J.-G.; Weber, P.; Batoulis, H.; Holz, S.; Karnowski, N.; Finke, J.; Lang, T. The packing density of a supramolecular membrane protein cluster is controlled by cytoplasmic interactions. eLife 2017, 6, e20705. [Google Scholar] [CrossRef] [PubMed]
- Rosholm, K.R.; Leijnse, N.; Mantsiou, A.; Tkach, V.; Pedersen, S.L.; Wirth, V.F.; Oddershede, L.B.; Jensen, K.J.; Martinez, K.L.; Hatzakis, N.S.; et al. Membrane curvature regulates ligand-specific membrane sorting of GPCRs in living cells. Nat. Chem. Biol. 2017, 13, 724–729. [Google Scholar] [CrossRef] [PubMed]
- Fournier, J.B.; Dommersnes, P.G. Comment on “Long-range forces in heterogeneous fluid membranes”. Europhys. Lett. 1997, 39, 681–682. [Google Scholar] [CrossRef]
- Weikl, T.R.; Kozlov, M.M.; Helfrich, W. Interaction of conical membrane inclusions: Effect of lateral tension. Phys. Rev. E 1998, 57, 6988–6995. [Google Scholar] [CrossRef]
- Harden, J.L.; MacKintosh, F.C. Shape transformations of domains in mixed-fluid films and bilayer membranes. Europhys. Lett. 1994, 28, 495–500. [Google Scholar] [CrossRef]
- Harden, J.L.; MacKintosh, F.C.; Olmsted, P.D. Budding and domain shape transformations in mixed lipid films and bilayer membranes. Phys. Rev. E 2005, 72, 011903. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, R.; Miettenen, M.S.; Fricke, N.; Lipowsky, R.; Dimova, R. The glycolipid GM1 reshapes asymmetric biomembranes and giant vesicles by curvature generation. Proc. Natl. Acad. Sci. USA 2018, 115, 5756–5761. [Google Scholar] [CrossRef] [PubMed]
- Doyle, D.A.; Morais Cabral, J.; Pfuetzner, R.A.; Kuo, A.; Gulbis, J.M.; Cohen, S.L.; Chait, B.T.; MacKinnon, R. The structure of the potassium channel: Molecular basis of K+ conduction and selectivity. Science 1998, 280, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Bass, R.B.; Strop, P.; Barclay, M.; Rees, D.C. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science 2002, 298, 1582–1587. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Scheerer, P.; Hofmann, K.P.; Choe, H.W.; Ernst, O.P. Crystal structure of the ligand-free G-protein-coupled receptor opsin. Nature 2008, 454, 183–187. [Google Scholar] [CrossRef] [PubMed]
- Manglik, A.; Kruse, A.C.; Kobilka, T.S.; Thian, F.S.; Mathiesen, J.M.; Sunahara, R.K.; Pardo, L.; Weis, W.I.; Kobilka, B.K.; Granier, S. Crystal structure of the μ-opioid receptor bound to a morphinan antagonist. Nature 2012, 485, 321–326. [Google Scholar] [CrossRef] [PubMed]
- Aimon, S.; Callan-Jones, A.; Berthaud, A.; Pinot, M.; Toombes, G.; Bassereau, P. Membrane shape modulates trans-membrane protein distribution. Dev. Cell 2014, 28, 212–218. [Google Scholar] [CrossRef] [PubMed]
- Prevost, C.; Zhao, H.; Manzi, J.; Lemichez, E.; Lappalainen, P.; Callan-Jones, A.; Bassereau, P. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat. Commun. 2015, 6, 8529. [Google Scholar] [CrossRef] [PubMed]
- Blood, P.D.; Voth, G.A. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2006, 103, 15068–15072. [Google Scholar] [CrossRef] [PubMed]
- Pezeshkian, W.; Hansen, A.G.; Johannes, L.; Khandelia, H.; Shillcock, J.C.; Kumar, P.B.S.; Ipsen, J.H. Membrane invagination induced by Shiga toxin B-subunit: From molecular structure to tube formation. Soft Matter 2006, 12, 5164–5171. [Google Scholar] [CrossRef] [PubMed]
- Low, S.H.; Vasanji, A.; Nanduri, J.; He, M.; Sharma, N.; Koo, M.; Drazba, J.; Weimbs, T. Syntaxins 3 and 4 are concentrated in separate clusters on the plasma membrane before the establishment of cell polarity. Mol. Biol. Cell 2006, 17, 977–989. [Google Scholar] [CrossRef] [PubMed]
- Henis, Y.I.; Hancock, J.F.; Prior, I.A. Ras acylation, compartmentalization and signaling nanoclusters (Review). Mol. Membr. Biol. 2009, 26, 80–92. [Google Scholar] [CrossRef] [PubMed]
- Milovanovic, D.; Honigmann, A.; Koike, S.; Gottfert, F.; Pahler, G.; Junius, M.; Müllar, S.; Diederichsen, U.; Janshoff, A.; Grubmüller, H.; et al. Hydrophobic mismatch sorts SNARE proteins into distinct membrane domains. Nat. Commun. 2015, 6, 5984. [Google Scholar] [CrossRef] [PubMed]
- Zuidscherwoude, M.; Gottfert, F.; Dunlock, V.M.E.; Fidgor, C.G.; van den Bogaart, G.; van Spriel, A.B. The tetraspanin web revisited by super-resolution microscopy. Sci. Rep. 2015, 5, 12201. [Google Scholar] [CrossRef] [PubMed]
- Sajman, J.; Trus, M.; Atlas, D.; Sherman, E. The L-type voltage-gated calcium channel co-localizes with syntaxin 1A in nano-clusters at the plasma membrane. Sci. Rep. 2017, 7, 11350. [Google Scholar] [CrossRef] [PubMed]
- Houmadi, R.; Guipouy, D.; Rey-Barroso, J.; Vasconcelos, Z.; Cornet, J.; Manghi, M.; Destainville, N.; Valitutti, S.; Allart, S.; Dupré, L. The Wiskott-Aldrich syndrome protein contributes to the assembly of the LFA-1 nanocluster belt at the lytic synapse. Cell Rep. 2018, 22, 979–991. [Google Scholar] [CrossRef] [PubMed]
- Destainville, N. An alternative scenario for the formation of specialized protein nano-domains (cluster phases) in biomembranes. Europhys. Lett. 2010, 91, 58001. [Google Scholar] [CrossRef]
- Meilhac, N.; Destainville, N. Clusters of proteins in bio-membranes: Insights into the roles of interaction potential shapes and of protein diversity. J. Phys. Chem. B 2011, 115, 7190–7199. [Google Scholar] [CrossRef] [PubMed]
- Plowman, S.J.; Ariotti, N.; Goodall, A.; Parton, R.G.; Hancock, J.F. Electrostatic interactions positively regulate K-Ras nanocluster formation and function. Mol. Cell. Biol. 2008, 28, 4377–4385. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, H.U.; Orłowski, A.; Róg, T.; Nyholm, T.K.; Chai, W.; Feizi, T.; Lingwood, D.; Vattulainen, I.; Simons, K. Lateral sorting in model membranes by cholesterol-mediated hydrophobic matching. Proc. Natl. Acad. Sci. USA 2011, 108, 16628–16633. [Google Scholar] [CrossRef] [PubMed]
- Remorino, A.; De Beco, S.; Cayrac, F.; Di Federico, F.; Cornilleau, G.; Gautreau, A.; Parrini, M.C.; Masson, J.B.; Dahan, M.; Coppey, M. Gradient of Rac1 nanoclusters support spatial patterns of Rac1 signaling. Cell Rep. 2017, 21, 1922–1935. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Kobayashi, T.; Gu, F.; Gruenberg, J. Lipids, lipid domains and lipid-protein interactions in endocytic membrane traffic. Cell Dev. Biol. 1998, 9, 517–526. [Google Scholar] [CrossRef] [PubMed]
- Truong Quang, B.A.; Mani, M.; Markova, O.; Lecuit, T.; Lenne, P.F. Principles of E-cadherin supramolecular organization in vivo. Curr. Biol. 2013, 23, 2197–2207. [Google Scholar] [CrossRef] [PubMed]
- Steinman, R.; Mellman, I.; Muller, W.; Cohn, Z.J. Endocytosis and the recycling of plasma membrane. Cell Biol. 1983, 96, 1–27. [Google Scholar] [CrossRef]
- Hao, M.; Maxfield, F.R. Characterization of rapid membrane internalization and recycling. J. Biol. Chem. 2000, 275, 15279–15286. [Google Scholar] [CrossRef] [PubMed]
- Rosetti, C.M.; Mangiarotti, A.; Wilke, N. Sizes of lipid domains: What do we know from artificial lipid membranes? What are the possible shared features with membrane rafts in cells? Biochim. Biophys. Acta 2017, 1859, 789–802. [Google Scholar] [CrossRef] [PubMed]
- Abney, J.R.; Scalettar, B.A. Fluctuations and membrane heterogeneity. Biophys. Chem. 1995, 57, 27–36. [Google Scholar] [CrossRef]
- Gheber, L.A.; Edidin, M. A model for membrane patchiness: lateral diffusion in the presence of barriers and vesicle traffic. Biophys. J. 1999, 77, 3163–3175. [Google Scholar] [CrossRef]
- Foret, L. Aggregation on a membrane of particles undergoing active exchange with a reservoir. Eur. Phys. J. E 2012, 35, 12. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Sammalkorpi, M.; Haataja, M. Domain formation in the plasma membrane: Roles of nonequilibrium lipid transport and membrane proteins. Phys. Rev. Lett. 2008, 100, 178102. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.; Sagues, F.; Reigada, R. Nonequilibrium patterns in phase-separating ternary membranes. Phys. Rev. E 2009, 80, 011920. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Manghi, M.; Destainville, N. Nanodomains in biomembranes with recycling. J. Phys. Chem. B 2016, 120, 10588–10602. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.; Sagues, F.; Reigada, R. Actively maintained lipid nanodomains in biomembranes. Phys. Rev. E 2008, 77, 021907. [Google Scholar] [CrossRef] [PubMed]
- Vagne, Q.; Turner, M.S.; Sens, P. Sensing Size through Clustering in non-equilibrium membranes and the control of membrane-bound enzymatic reactions. PLoS ONE 2015, 10, e0143470. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Sammalkorpi, M.; Haataja, M. Lipid microdomains: Structural correlations, fluctuations, and formation mechanisms. Phys. Rev. Lett. 2010, 104, 118101. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Sammalkorpi, M.; Haataja, M. Formation and regulation of lipid microdomains in cell membranes: Theory, modeling, and speculation. FEBS Lett. 2010, 584, 1678–1684. [Google Scholar] [CrossRef] [PubMed]
- Prost, J.; Bruinsma, R. Shape fluctuations of active membranes. Europhys. Lett. 1996, 33, 321–326. [Google Scholar] [CrossRef]
- Sabra, M.C.; Mouritsen, O.G. Steady-state compartmentalization of lipid membranes by active proteins. Biophys. J. 1998, 74, 745–752. [Google Scholar] [CrossRef]
- Family, F.; Meakin, P.; Deutch, J.M. Kinetics of coagulation with fragmentation: Scaling behavior and fluctuations. Phys. Rev. Lett. 1986, 57, 727–730. [Google Scholar] [CrossRef] [PubMed]
- Veatch, S.L.; Cicuta, P.; Sengupta, P.; Honerkamp-Smith, A.; Holowka, D.; Baird, B. Critical fluctuations in plasma membrane vesicles. ACS Chem. Biol. 2008, 3, 287–293. [Google Scholar] [CrossRef] [PubMed]
- Brewster, R.; Safran, S.A. Line active hybrid lipids determine domain size in phase separation of saturated and unsaturated lipids. Biophys. J. 2010, 98, L21–L23. [Google Scholar] [CrossRef] [PubMed]
- Cornell, C.E.; Skinkle, A.D.; He, S.; Levental, I.; Levental, K.R.; Keller, S.L. Tuning length scales of small domains in cell-derived membrane and synthetic model membranes. Biophys. J. 2018, 115, 690–701. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp-Smith, A.; Cicuta, P.; Collins, M.D.; Veatch, S.L.; den Nijs, M.; Schick, M.; Keller, S.L. Line tensions, correlation lengths, and critical exponents in lipid membranes near critical points. Biophys. J. 2008, 95, 236–246. [Google Scholar] [CrossRef] [PubMed]
- Baoukina, S.; Rozmanov, D.; Tieleman, D.P. Composition fluctuations in lipid bilayers. Biophys. J. 2017, 113, 2750–2761. [Google Scholar] [CrossRef] [PubMed]
- Guttman, G.; Andelman, D. Electrostatic interactions in two-component membranes. J. Phys. II 1993, 3, 1411–1425. [Google Scholar] [CrossRef]
- Murase, K.; Fujiwara, T.; Umemura, Y.; Suzuki, K.; Iino, R.; Yamashita, H.; Saito, M.; Murakoshi, H.; Ritchie, K.; Kusumi, A. Ultrafine membrane compartments for molecular diffusion as revealed by single molecule techniques. Biophys. J. 2004, 86, 4075–4093. [Google Scholar] [CrossRef] [PubMed]
- Saka, S.K.; Honigmann, A.; Eggeling, C.; Hell, S.W.; Lang, T.; Rizzoli, S.O. Multi-protein assemblies underlie the mesoscale organization of the plasma membrane. Nat. Commun. 2014, 5, 4509. [Google Scholar] [CrossRef] [PubMed]
- Mocsar, G.; Volkó, J.; Rönnlund, D.; Widengren, J.; Nagy, P.; Szöllősi, J.; Tóth, K.; Goldman, C.K.; Damjanovich, S.; Waldmann, T.A.; et al. MHC I expression regulates co-clustering and mobility of interleukin-2 and -15 receptors in T cells. Biophys. J. 2016, 111, 100–112. [Google Scholar] [CrossRef] [PubMed]
- Adkins, M.R.; Zhou, Y.C. Geodesic curvature driven surface microdomain formation. J. Comput. Phys. 2017, 345, 260–274. [Google Scholar] [CrossRef] [PubMed]

| Notation | Name | Section Defined | References |
|---|---|---|---|
| Lo | Liquid-ordered lipid phase | 1 | [7,12,13] |
| Ld | Liquid-disordered lipid phase | 1 | [7,12,13] |
| Membrane surface tension (i.e., energy per unit area) | 2 | [2,11] | |
| Bending elastic modulus or curvature rigidity | 2 | [2,11,15] | |
| Saddle-splay elastic modulus | 2 | [11,15] | |
| Helfrich correlation length: | 2.1.1 | – | |
| Height function (in the Monge representation) | 2 | [11] | |
| Order parameter: local area fraction or phase state (e.g., Lo/Ld) | 2 | [12] | |
| H | Mean curvature ( in the Monge representation) | 2 | [2,11,15] |
| K | Gaussian curvature | 2 | [2,11,15] |
| v | Reduced volume of a vesicle of volume V and area A: | 2.2.1 | [53] |
| Spontaneous or preferred mean curvature | 2 | [11,15] | |
| Domain line tension (i.e., energy per unit length at a 1D phase boundary) | 2 | [18,48] | |
| Invagination length: | 2.2.1 | [48] | |
| or | Coupling coefficient between and H | 2 | [18,45] |
| Critical temperature (at a miscibility critical point) | 2 | [11,12,17,18] | |
| Demixing or phase-separation temperature | 2 | [12,17,18] | |
| Ornstein-Zernike composition correlation length | 2 | [15,54] | |
| Thermal energy J at physiological temperature (37 C) | 1 | [2] | |
| Pressure jump across the membrane (for closed vesicles): | 2.1.3 | [55] | |
| Recycling time (out-of-equilibrium membranes) | 3.1 | [56,57] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Destainville, N.; Manghi, M.; Cornet, J. A Rationale for Mesoscopic Domain Formation in Biomembranes. Biomolecules 2018, 8, 104. https://doi.org/10.3390/biom8040104
Destainville N, Manghi M, Cornet J. A Rationale for Mesoscopic Domain Formation in Biomembranes. Biomolecules. 2018; 8(4):104. https://doi.org/10.3390/biom8040104
Chicago/Turabian StyleDestainville, Nicolas, Manoel Manghi, and Julie Cornet. 2018. "A Rationale for Mesoscopic Domain Formation in Biomembranes" Biomolecules 8, no. 4: 104. https://doi.org/10.3390/biom8040104
APA StyleDestainville, N., Manghi, M., & Cornet, J. (2018). A Rationale for Mesoscopic Domain Formation in Biomembranes. Biomolecules, 8(4), 104. https://doi.org/10.3390/biom8040104





