Detecting Selection on Protein Stability through Statistical Mechanical Models of Folding and Evolution
Abstract
1. Introduction
2. Contact-Based Model of Protein Folding
3. Modeling Selection on Protein Folding Thermodynamics
4. Validations and Limitations of the Model and Assessment of Neutrality
5. Detecting Selection through Null Models Based on Physics and Population Genetics
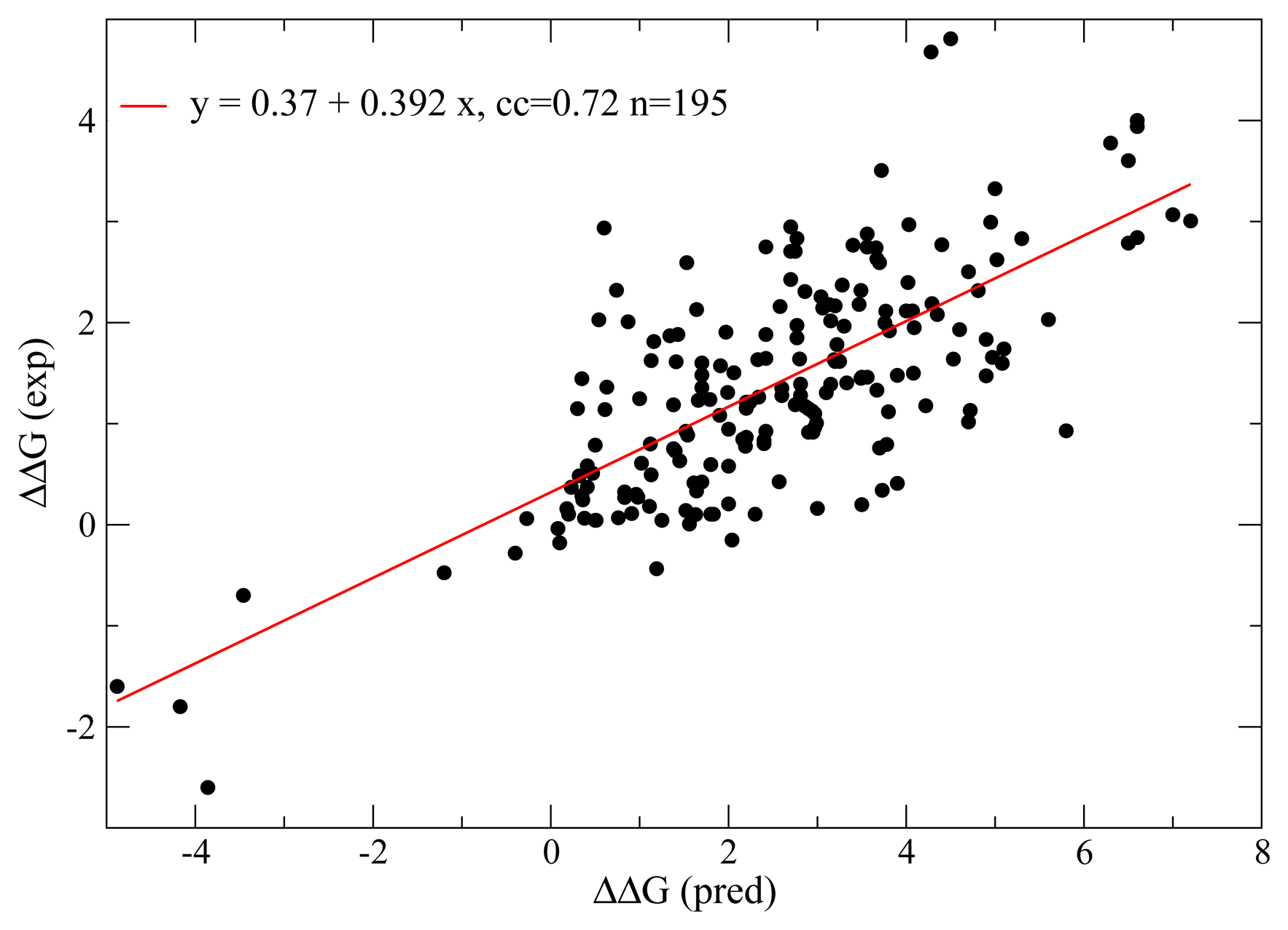
6. Positive Design: Protein Folding Potentials
7. Site-Specific Amino Acid Distributions
7.1. Relationship between Chain Length and Positive Design

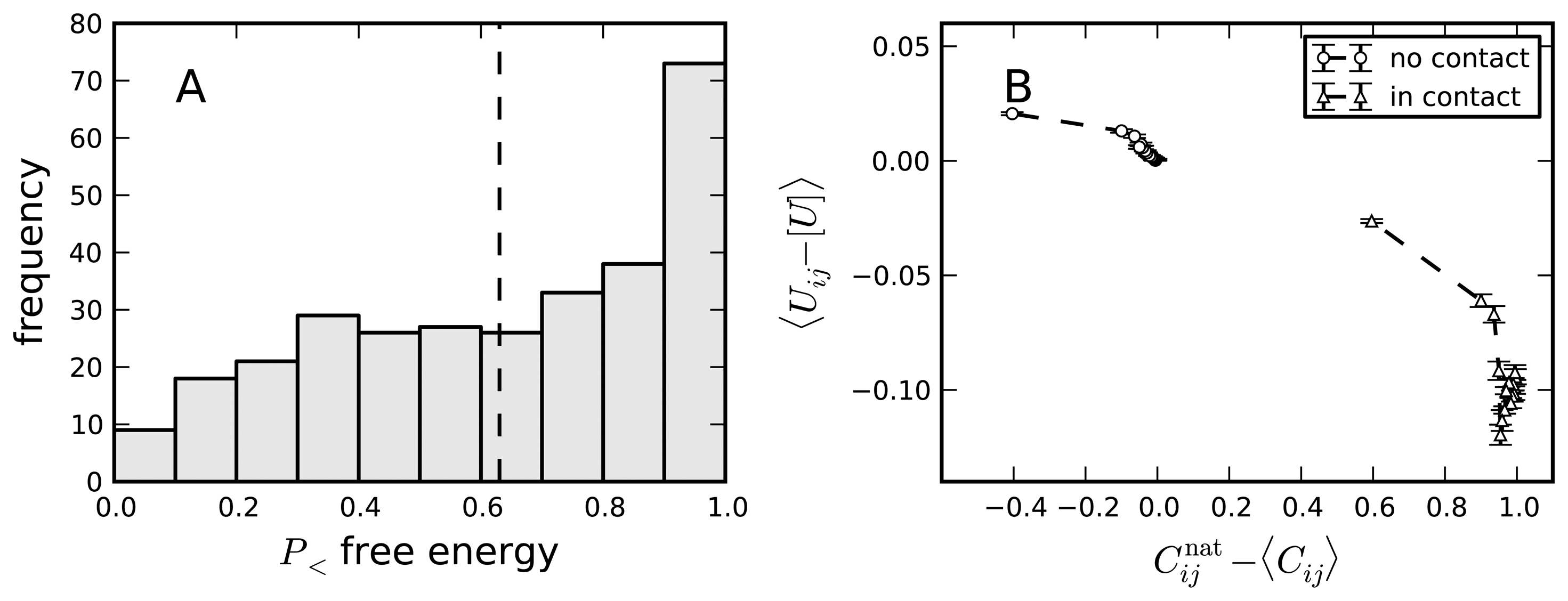
8. Negative Design
9. Selection on Protein Folding Rates
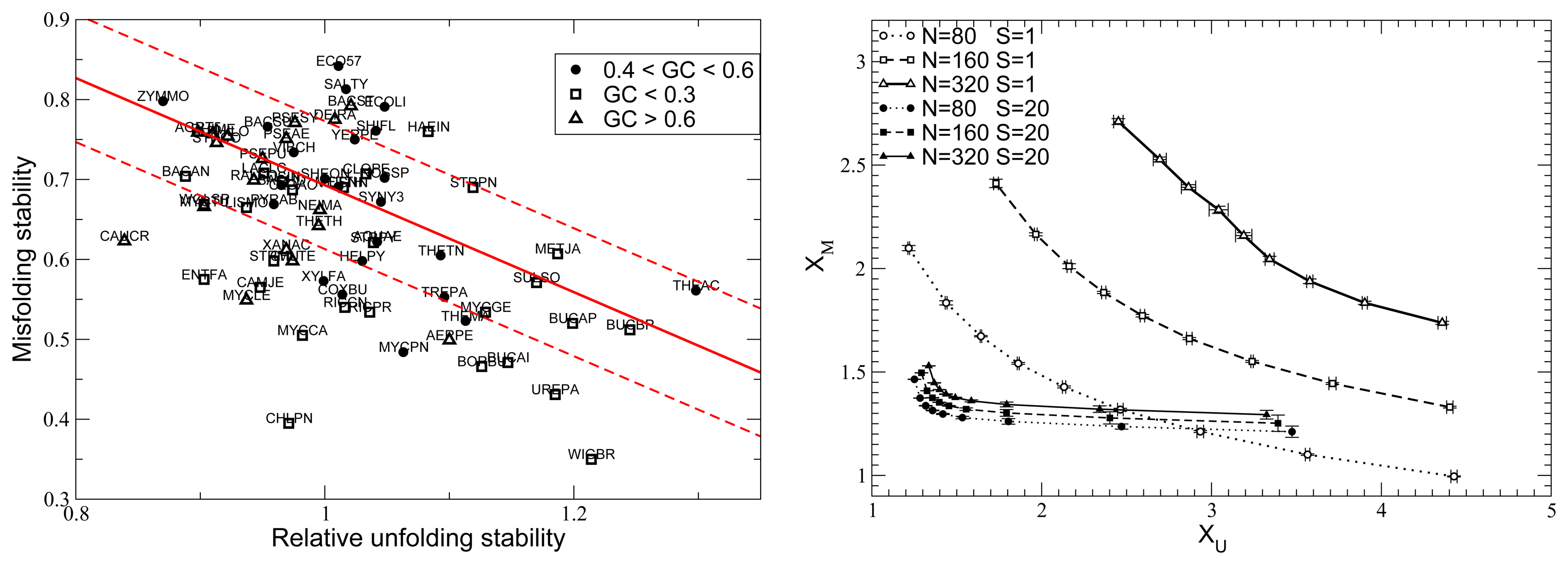
10. Influence of Mutation Bias and Population Size


11. Protein Functional Dynamics with the Elastic Network Model
12. Conclusions
Acknowledgments
Conflicts of Interest
References
- Vendruscolo, M.; Najmanovich, R.; Domany, E. Protein folding in contact map space. Phys. Rev. Lett. 1999, 82, 656–659. [Google Scholar]
- Miyazawa, S.; Jernigan, R. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar]
- Plotkin, S.S.; Onuchic, J.N. Understanding protein folding with energy landscape theory. Part II: Quantitative aspects. Q. Rev. Biophys. 2002, 35, 205–286. [Google Scholar]
- Shakhnovich, E. Protein folding thermodynamics and dynamics: Where physics, chemistry, and biology meet. Chem. Rev. 2006, 106, 1559–1588. [Google Scholar]
- Chan, H.S.; Zhang, Z.; Wallin, S.; Liu, Z. Cooperativity, local-nonlocal coupling, and nonnative interactions: Principles of protein folding from coarse-grained models. Annu. Rev. Phys. Chem. 2011, 62, 301–326. [Google Scholar]
- Karplus, M.; Ichiye, T.; Pettitt, B.M. Configurational entropy of native proteins. Biophys. J. 1987, 52, 1083–1085. [Google Scholar]
- Doig, A.J.; Sternberg, M.J. Side-chain conformational entropy in protein folding. Protein Sci. 1995, 4, 2247–2251. [Google Scholar]
- Galzitskaya, O.V.; Finkelstein, A.V. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. USA 1999, 9, 11299–11304. [Google Scholar]
- Bastolla, U.; Frauenkron, H.; Grassberger, P. Phase diagram of random heteropolymers: Replica approach and application of a new Monte Carlo algorithm. J. Mol. Liq. 2000, 84, 111–129. [Google Scholar]
- Tiana, G.; Sutto, L. Equilibrium properties of realistic random heteropolymers and their relevance for globular and naturally unfolded proteins. Phys. Rev. E 2011, 84, 061910. [Google Scholar]
- Galzitskaya, O.V. Influence of Conformational Entropy on the Protein Folding Rate. Entropy 2010, 12, 961–982. [Google Scholar]
- Uversky, V.N.; Dunker, A.K. Understanding protein non-folding. Biochim. Biophys. Acta 2010, 1804, 1231–1264. [Google Scholar]
- Schuler, B.; Lipman, E.A.; Eaton, W.A. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature 2002, 419, 743–747. [Google Scholar]
- Ohgushi, M.; Wada, A. “Molten-globule state”: A compact form of globular proteins with mobile side-chains. FEBS Lett. 1983, 164, 21–24. [Google Scholar]
- Pande, V.S.; Rokhsar, D.S. Is the molten globule a third phase of proteins? Proc. Natl. Acad. Sci. USA 1998, 95, 1490–1494. [Google Scholar]
- Baldwin, R.L. On-pathway versus off-pathway folding intermediates. Fold Des. 1996, 1, R1–R8. [Google Scholar]
- Fernandez-Recio, J.; Genzor, C.G.; Sancho, J. Apoflavodoxin folding mechanism: An alpha/beta protein with an essentially off-pathway intermediate. Biochemistry 2001, 40, 15234–15245. [Google Scholar]
- Chiti, F.; Dobson, C.M. Protein misfolding, functional amyloid, and human disease. Ann. Rev. Biochem. 2006, 75, 333–366. [Google Scholar]
- Drummond, D.A.; Wilke, C.O. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 2008, 134, 341–352. [Google Scholar]
- Derrida, B. Random Energy Model: An exactly solvable model of disordered systems. Phys. Rev. B 1981, 24, 2613–2626. [Google Scholar]
- Garel, T.; Orland, H. Mean-field model for Protein Folding. Europhys. Lett. 1988, 6, 307–310. [Google Scholar]
- Shakhnovich, E.-I.; Gutin, A.-M. Formation of unique structure in polypeptide chains. Biophys. Chem. 1989, 34, 187–199. [Google Scholar]
- Bryngelson, J.-D.; Onuchic, J.-N.; Socci, N.-D.; Wolynes, P.-G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar]
- Minning, J.; Porto, M.; Bastolla, U. Detecting selection for negative design in proteins through an improved model of the misfolded state. Proteins 2013, 81, 1102–1112. [Google Scholar]
- Bastolla, U.; Vendruscolo, M.; Knapp, E.W. A statistical mechanical method to optimize energy functions for protein folding. Proc. Natl. Acad. Sci. USA 2000, 97, 3977–3981. [Google Scholar]
- Bastolla, U.; Farwer, J.; Knapp, E.-W.; Vendruscolo, M. How to guarantee optimal stability for most representative structures in the protein data bank. Proteins 2001, 44, 79–96. [Google Scholar]
- Godzik, A.; Kolinski, A.; Skolnick, J. Are proteins ideal mixtures of amino acids? Analysis of energy parameter sets. Protein Sci. 1995, 4, 2107–2117. [Google Scholar]
- Bowie, J.U.; LÃijthy, R.; Eisenberg, D. A method to identify protein sequences that fold into a known three-dimensional structure. Science 1991, 253, 164–170. [Google Scholar]
- Jones, D.T.; Taylor, W.R.; Thornton, J.M. A new approach to protein fold recognition. Nature 1992, 358, 86–89. [Google Scholar]
- Gutin, A.M.; Abkevich, V.I.; Shakhnovich, E.I. Evolution-like selection of fast-folding model proteins. Proc. Natl. Acad. Sci. USA 1995, 92, 1282–1286. [Google Scholar]
- Bussemaker, H.J.; Thirumalai, D.; Bhattacharjee, J.K. Thermodynamic stability of folded proteins against mutations. Phys. Rev. Lett. 1997, 79, 3530–3533. [Google Scholar]
- Mirny, L.A.; Abkevich, V.I.; Shakhnovich, E.I. How evolution makes proteins fold quickly. Proc. Natl. Acad. Sci. USA 1998, 95, 4976–4981. [Google Scholar]
- Babajide, A.; Hofacker, I.L.; Sippl, M.J.; Stadler, P.F. Neutral networks in protein space. Fol. Des. 1997, 2, 261–269. [Google Scholar]
- Govindarajan, S.; Goldstein, R.A. Evolution of model proteins on a foldability landscape. Proteins 1997, 29, 461–466. [Google Scholar]
- Tiana, G.; Broglia, R.A.; Roman, H.E.; Vigezzi, E.; Shakhnovich, E.I. Folding and misfolding of designed proteinlike chains with mutations. J. Chem. Phys. 1998, 108, 757–761. [Google Scholar]
- Bastolla, U.; Roman, H.E.; Vendruscolo, M. Neutral evolution of model proteins: Diffusion in sequence space and overdispersion. J. Theor. Biol. 1999, 200, 49–64. [Google Scholar]
- Bornberg-Bauer, E.; Chan, H.S. Modeling evolutionary landscapes: Mutational stability, topology, and superfunnels in sequence space. Proc. Natl. Acad. Sci. USA 1999, 96, 10689–10694. [Google Scholar]
- Dokholyan, N.V.; Shakhnovich, E.I. Understanding hierarchical protein evolution from first principles. J. Mol. Biol. 2001, 312, 289–307. [Google Scholar]
- Taverna, D.M.; Goldstein, R.A. Why are proteins marginally stable? Proteins 2002, 46, 105–109. [Google Scholar]
- Parisi, G.; Echave, J. Structural constraints and emergence of sequence patterns in protein evolution. Mol. Biol. Evol. 2001, 18, 750–756. [Google Scholar]
- Bastolla, U.; Porto, M.; Roman, H.E.; Vendruscolo, M. Statistical properties of neutral evolution. J. Mol. Evol. 2003, 57, S103–S119. [Google Scholar]
- DePristo, M.A.; Weinreich, D.M.; Hartl, D.L. Missense meanderings in sequence space: A biophysical view of protein evolution. Nat. Rev. Genet. 2005, 6, 678–687. [Google Scholar]
- Bloom, J.D.; Silberg, J.J.; Wilke, C.O.; Drummond, D.A.; Adami, C.; Arnold, F.H. Thermodynamic prediction of protein neutrality. Proc. Natl. Acad. Sci. USA 2005, 102, 606–611. [Google Scholar]
- Grahnen, J.A.; Nandakumar, P.; Kubelka, J.; Liberles, D.A. Biophysical and structural considerations for protein sequence evolution. BMC Evol. Biol. 2011, 11, 361. [Google Scholar]
- Wilke, C.O. Bringing molecules back into molecular evolution. PLoS Comput. Biol. 2012, 8, e1002572. [Google Scholar]
- Liberles, D.A.; Teichmann, S.A.; Bahar, I.; Bastolla, U.; Bloom, J.; Bornberg-Bauer, E.; Colwell, L.J.; de Koning, A.P.; Dokholyan, N.V.; Echave, J.; et al. The interface of protein structure, protein biophysics, and molecular evolution. Protein Sci. 2012, 21, 769–785. [Google Scholar]
- Goldstein, R.A. The evolution and evolutionary consequences of marginal thermostability in proteins. Proteins 2011, 79, 1396–1407. [Google Scholar]
- Bahar, I.; Rader, A.J. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 2005, 15, 586–592. [Google Scholar]
- Kimura, M. The neutral theory of molecular evolution; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Durrett, R. Probability models for DNA sequence evolution; Springer-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Sella, G.; Hirsh, A.E. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. USA 2005, 102, 9541–9546. [Google Scholar]
- Bueno, M.; Camacho, C.J.; Sancho, J. SIMPLE estimate of the free energy change due to aliphatic mutations: Superior predictions based on first principles. Proteins 2007, 68, 850–862. [Google Scholar]
- Sali, A.; Shakhnovich, E.; Karplus, M. Kinetics of protein folding. A lattice model study of the requirements for folding to the native state. J. Mol. Biol. 1994, 235, 1614–1636. [Google Scholar]
- Klimov, D.K.; Thirumalai, D. Factors governing the foldability of proteins. Proteins 1996, 26, 411–441. [Google Scholar]
- Goldstein, R.A. Population size dependence of fitness effect distribution and substitution rate probed by biophysical model of protein thermostability. Genome Biol. Evol. 2013, 5, 1584–1593. [Google Scholar]
- Li, W.H.; Wu, C.I.; Luo, C.C. A new method for estimating synonymous and nonsynonymous rates of nucleotide substitution considering the relative likelihood of nucleotide and codon changes. Mol. Biol. Evol. 1985, 2, 150–174. [Google Scholar]
- Ho, S.Y.; Phillips, M.J.; Cooper, A.; Drummond, A.J. Time dependency of molecular rate estimates and systematic overestimation of recent divergence times. Mol. Biol. Evol. 2005, 22, 1561–1568. [Google Scholar]
- Peterson, G.I.; Masel, J. Quantitative prediction of molecular clock and ka/ks at short timescales. Mol. Biol. Evol. 2009, 26, 2595–2603. [Google Scholar]
- McDonald, J.H.; Kreitman, M. Adaptive protein evolution at the Adh locus in Drosophila. Nature 1991, 351, 652–654. [Google Scholar]
- Finkelstein, A.V.; Badretdinov, A.Y.; Gutin, A.M. Why do protein architectures have Boltzmann-like statistics? Proteins 1995, 23, 142–150. [Google Scholar]
- Sippl, M.J. Calculation of conformational ensembles from potentials of mean force. An approach to the knowledge-based prediction of local structures in globular proteins. J. Mol. Biol. 1990, 213, 859–883. [Google Scholar]
- Lui, S.; Tiana, G. The network of stabilizing contacts in proteins studied by coevolutionary data. J. Chem. Phys. 2013. [Google Scholar] [CrossRef]
- Morcos, F.; Pagnani, A.; Lunta, B.; Bertolino, A.; Marks, D.S.; Sander, C.; Zecchina, R.; Onuchic, J.N.; Hwa, T.; Weigt, M. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA 2011, 108, E1293–E1301. [Google Scholar]
- Li, H.; Tang, C.; Wingreen, N.S. Nature of driving force for protein folding: A result from analyzing the statistical potential. Phys. Rev. Lett. 1997, 79, 765–768. [Google Scholar]
- Bastolla, U.; Porto, M.; Roman, H.E.; Vendruscolo, M. Principal eigenvector of contact matrices and hydrophobicity profiles in proteins. Proteins 2005, 58, 22–30. [Google Scholar]
- Bastolla, U.; Ortiz, A.R.; Porto, M.; Teichert, F. Effective connectivity profile: A structural representation that evidences the relationship between protein structures and sequences. Proteins 2008, 73, 872–888. [Google Scholar]
- Bastolla, U.; Porto, M.; Roman, H.E.; Vendruscolo, M. A protein evolution model with independent sites that reproduces site-specific amino acid distributions from the Protein Data Bank. BMC Evol. Biol. 2006, 6, 43. [Google Scholar]
- Bastolla, U.; Demetrius, L. Stability constraints and protein evolution: The role of chain length, composition, and disulphide bonds. Protein Eng. Des. Sel. 2005, 18, 405–415. [Google Scholar]
- Berezovsky, I.N.; Zeldovich, K.B.; Shakhnovich, E.I. Positive and negative design in stability and thermal adaptation of natural proteins. PLoS Comput. Biol. 2007. [Google Scholar] [CrossRef]
- Noivirt-Brik, O.; Unger, R.; Horovitz, A. Analysing the origin of long-range interactions in proteins using lattice models. BMC Struct. Biol. 2009. [Google Scholar] [CrossRef]
- Plotkin, S.S.; Onuchic, J.N. Investigation of routes and funnels in protein folding by free energy functional methods. Proc. Natl. Acad. Sci. USA 2000, 97, 6509–6514. [Google Scholar]
- Oztop, B.; Ejtehadi, M.R.; Plotkin, S.S. Protein folding rates correlate with heterogeneity of folding mechanism. Phys. Rev. Lett. 2004, 93, 208105. [Google Scholar] [CrossRef]
- Clementi, C.; Plotkin, S.S. The effects of nonnative interactions on protein folding rates: Theory and simulation. Protein Sci. 2006, 13, 1750–1766. [Google Scholar]
- Bastolla, U.; Bruscolini, P.; Velasco, J.L. Sequence determinants of protein folding rates: Positive correlation between contact energy and contact range indicates selection for fast folding. Proteins 2012, 80, 2287–2304. [Google Scholar]
- Ivankov, D.N.; Garbuzynskiy, S.O.; Alm, E.; Plaxco, K.W.; Baker, D.; Finkelstein, A.V. Contact order revisited: Influence of protein size on the folding rate. Protein Sci. 2003, 12, 2057–2062. [Google Scholar]
- Bastolla, U.; Moya, A.; Viguera, E.; van Ham, R.C.H.J. Genomic determinants of protein folding thermodynamics. J. Mol. Biol. 2004, 343, 1451–1466. [Google Scholar]
- Fares, M.A.; Moya, A.; Barrio, E. GroEL and the maintenance of bacterial endosymbiosis. Trends Genet. 2004, 20, 413–416. [Google Scholar]
- Fares, M.A.; Ruiz-Gonzalez, M.X.; Moya, A.; Elena, S.F.; Barrio, E. Endosymbiotic bacteria: GroEL buffers against deleterious mutations. Nature 2002. [Google Scholar] [CrossRef]
- Mendez, R.; Fritsche, M.; Porto, M.; Bastolla, U. Mutation bias favors protein folding stability in the evolution of small populations. PLoS Comput. Biol. 2010. [Google Scholar] [CrossRef]
- Rocha, E.P.C.; Feil, E.J. Mutational patterns cannot explain genome composition: Are there any neutral sites in the genomes of bacteria? PLoS Genet. 2010. [Google Scholar] [CrossRef]
- Tirion, M.M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar]
- Taketomi, H.; Ueda, Y.; Go, N. Studies on protein folding, unfolding and fluctuations by computer simulation. 1. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int. J. Pept. Protein Res. 1975, 7, 445–459. [Google Scholar]
- Bryngelson, J.D.; Wolynes, P.G. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 7524–7528. [Google Scholar]
- Tama, F.; Sanejouand, Y.H. Conformational change of proteins arising from normal mode calculations. Protein Eng. 2001, 14, 1–6. [Google Scholar]
- Tobi, D.; Bahar, I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA 2005, 102, 18908–18913. [Google Scholar]
- Mendez, R.; Bastolla, U. Torsional network model: Normal modes in torsion angle space better correlate with conformation changes in proteins. Phys. Rev. Lett. 2010. [Google Scholar] [CrossRef]
- Dos Santos, H.G.; Klett, J.; MÃl'ndez, R.; Bastolla, U. Characterizing conformation changes in proteins through the torsional elastic response. Biochim. Biophys. Acta 2013, 1834, 836–846. [Google Scholar]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bastolla, U. Detecting Selection on Protein Stability through Statistical Mechanical Models of Folding and Evolution. Biomolecules 2014, 4, 291-314. https://doi.org/10.3390/biom4010291
Bastolla U. Detecting Selection on Protein Stability through Statistical Mechanical Models of Folding and Evolution. Biomolecules. 2014; 4(1):291-314. https://doi.org/10.3390/biom4010291
Chicago/Turabian StyleBastolla, Ugo. 2014. "Detecting Selection on Protein Stability through Statistical Mechanical Models of Folding and Evolution" Biomolecules 4, no. 1: 291-314. https://doi.org/10.3390/biom4010291
APA StyleBastolla, U. (2014). Detecting Selection on Protein Stability through Statistical Mechanical Models of Folding and Evolution. Biomolecules, 4(1), 291-314. https://doi.org/10.3390/biom4010291