1. Introduction
Drug–target affinity (DTA) prediction provides a foundation for modern drug discovery, with various benefits that improve efficiency, reduce costs, and increase success rates. Affinity reflects the likelihood of interaction of a drug–target pair, typically measured by
(dissociation constant) or
(inhibition constant). Strong binding is indicated by low
/
(nM to pM), while weak binding corresponds to high
/
(
M to mM). The significance of DTA prediction is well-discussed in the literature, emphasizing its role in accelerating the identification of potential drug candidates and minimizing the risk of failure during clinical trials [
1,
2]. Recent improvements in computational methods [
3,
4,
5,
6] and the availability of relevant data enhance the accuracy and reliability of DTA predictions [
7,
8], aiding in the design of efficient therapeutic strategies and effective treatments for many diseases.
To achieve accurate DTA predictions, the way in which both drugs and targets are represented is a critical determinant of the performance of the models. The proper encoding of these molecular entities is essential for capturing the intricate relationships between their structural and functional properties. Early computational approaches to DTA often relied on simplified representations, such as molecular fingerprints for drugs and amino acid sequences for proteins, to feed machine learning models. Although these methods showed some promise, their inability to fully capture the complexity of molecular interactions limited the predictive power of DTA models [
9,
10,
11]. As the field evolved, researchers began exploring more sophisticated techniques to better model the structural and chemical properties of drugs and targets, leading to the development of advanced representation methods that significantly improved the predictive accuracy and generalizability of DTA models [
12,
13,
14].
Ozturk et al. [
15] proposed DeepDTA, where they utilized 1D convolutional neural networks (CNNs) to extract high-level representations of protein sequences and 1D SMILES representations of the compounds. Before this approach, most computational methods treated drug–target affinity prediction as a binary classification problem. DeepDTA redefined the problem as a continuum of binding strength values, providing a broader view of drug–target interactions.
Nguyen et al. [
16] advanced the field by representing drugs as graphs instead of linear strings and utilized graph neural networks (GNNs) to predict drug–target affinity in their proposed deep learning model called GraphDTA. Building on this trend, Tran et al. [
17] proposed the Deep Neural Computation (DeepNC) model, which consists of multiple graph neural network algorithms.
The rise of natural language-based methods in biomedical research has led to further innovations in DTA modeling [
18,
19,
20,
21]. Qiu et al. [
22] introduced G-K-BertDTA to bridge the gap between the structural and semantic information of molecules. In their approach, drugs were represented as graphs to learn their topological features, and a knowledge-based BERT model was incorporated to obtain the semantic embeddings of the structures, thereby enhancing feature information.
Nevertheless, there are some limitations to the above-mentioned approaches. Firstly, the information on the relative positions of the constituent atoms and bonds is often missing in the drug encoding approaches adopted in these models. In addition, the functional aspects of those drugs, which can provide relevant insights into their interaction with targets, were also not incorporated.
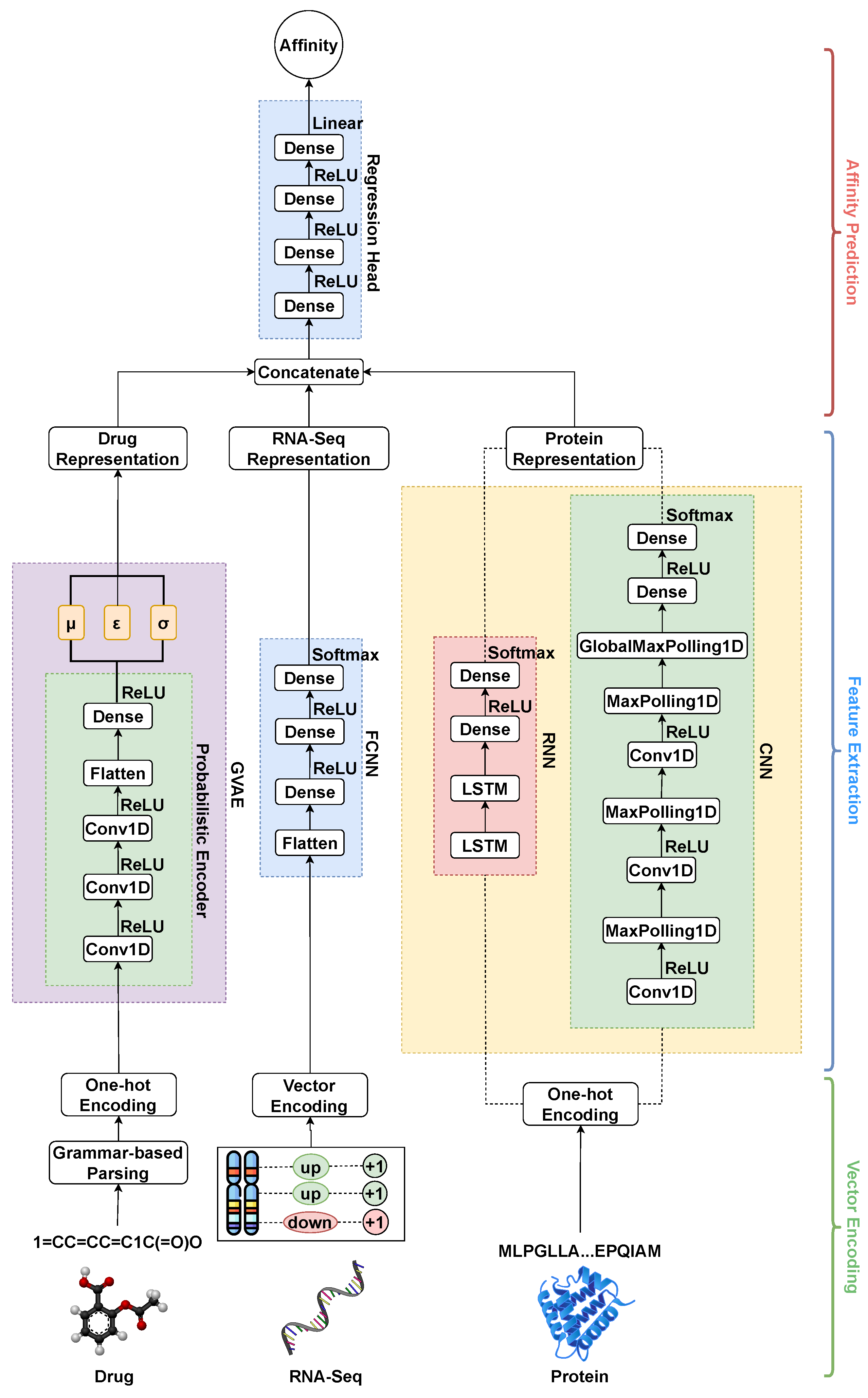
To address these limitations, we utilized the encoding approach for drugs known as the grammar variational autoencoder (GVAE) proposed by Kusner et al. [
23]. The GVAE discusses the parse tree-based encoding of the drug entities, which allows learning from semantic properties and syntactic rules. This approach can learn a more consistent latent space representation in which entities with nearby representations decode to similar outputs. In addition, to incorporate the functional aspect of those drugs, we integrated the chemical perturbation information from the L1000 project [
24]. In the L1000 project, various chemical entities have been used as perturbagens and were tested against multiple human cell lines, primarily linked to several types of cancers, to analyze their gene expression profile. We have utilized these gene expression signatures as the functional feature set for the drugs. Thus, the approach followed in this work utilizes the structural and functional representation of drugs, which enhances the drug–target affinity prediction and outperforms the current state-of-the-art methods.
The paper provides a thorough overview of the background research in
Section 2, along with a detailed explanation of the methodology, dataset preparation, network architecture, and evaluation metrics in
Section 3.
Section 4 presents the results of the proposed method on commonly used benchmark datasets and compares its performance to the current state-of-the-art DTA prediction models. Finally,
Section 5 addresses the limitations of the study and explores opportunities for future research advancements.
5. Conclusions and Future Directions
In this study, we have demonstrated that incorporating chemical perturbation information can enhance drug–target affinity prediction. The core contribution of this research is in its transformation of data from a chemical perturbation assay and utilizing them as an extra modality along with drug and protein structural information. In this work, we transformed the raw chemical perturbation assay data from the L1000 project, a project where a vast array of chemical assays have been performed, and updates to the assays are still ongoing. This research could guide future work on better understanding affinity prediction among biological entities in the absence of the three-dimensional structural information of those entities.
Nevertheless, a fundamental limitation of this research is that information from a chemical perturbation assay may not be available for every drug in the widely used drug–target affinity benchmark datasets. As new drugs are being introduced as potent antidotes for various diseases, corresponding chemical perturbation studies need to be performed on a large scale. In addition, some drugs are also being discarded and prohibited for conventional usage due to the lack of efficacy and severe side effects. Another aspect to consider is the imbalance between active and inactive compounds in a dataset. Chemical perturbation data might help by adding meaningful biological signals, but they could also worsen things if they introduce too much noise. Processed datasets can reduce the imbalance by filtering out redundant inactive data. However, if not handled carefully, they might remove important active compounds or introduce biases that do not reflect real-world data. Future studies should investigate different approaches for transforming chemical perturbation information.
Recent studies have shown that representing drugs as graphs provides a better understanding of the positional aspects of interacting atoms within the compounds, providing deeper insights into the structure–activity relationship (SAR) of the compounds. In addition, the recent availability of predicted 3D structures for the target proteins provides an opportunity to integrate these 3D structural data into the model, therefore enhancing the prediction capabilities of the computational models. This integration can provide deeper insights into the relationship between the structure and function of the proteins, providing a better understanding of structure-based predictive DTA modeling. Moreover, introducing advanced feature extraction methods from biological entities can enhance prediction.
With the continuous developments in natural language-based approaches in deep learning, drug discovery and drug repurposing are fields where the application of such methodologies are becoming popular. As the drugs and proteins are represented as strings, the utilization of natural language-based approaches can enhance the prediction abilities of the computational models. In the future, a conjugation of the existing structure-based approaches and natural language-based approaches can aid in improving the model development for DTA and the related tasks in drug discovery.
In summary, this work underscores the importance of integrating additional data modalities in drug–target affinity prediction.