Abstract
The helical distribution of the electronic density in chiral molecules, such as DNA and bacteriorhodopsin, has been suggested to induce a spin–orbit coupling interaction that may lead to the so-called chirality-induced spin selectivity (CISS) effect. Key ingredients for the theoretical modelling are, in this context, the helically shaped potential of the molecule and, concomitantly, a Rashba-like spin–orbit coupling due to the appearance of a magnetic field in the electron reference frame. Symmetries of these models clearly play a crucial role in explaining the observed effect, but a thorough analysis has been largely ignored in the literature. In this work, we present a study of these symmetries and how they can be exploited to enhance chiral-induced spin selectivity in helical molecular systems.
1. Introduction
The discovery of the spin polarization capability of helical molecules a few years ago [1,2] has demonstrated an intriguing novel physical phenomenon, which has been called chirality-induced spin selectivity (CISS). Although work on spin-dependent effects in chiral systems can be traced back to earlier work by Kessler and others (see Ref. [3]), it was not until 2011 that the previously mentioned two works clearly showed strong spin polarization effects in chiral molecules (DNA in this case) using two different experimental approaches: photoemission experiments [1] and AFM-based electrical transport setups [2]. The CISS effect is very striking since it does not require the presence of any magnetic centers or strong spin–orbit coupling (SOC) effects in the systems where it has been observed [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Its universality in molecular systems displaying a helical shape has put forward the hypothesis that a very close relationship must exist between helical symmetry and spin selectivity. Many theoretical works have been devoted up to now to scrutinize the CISS effect, largely based on spin-dependent transport calculations using scattering matrix or Green’s function techniques [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. In addition, few first-principle calculations have been presented [35,36], further supporting the relation to the helical symmetry. Still, the debate has remained open and there is not a common theoretical framework explaining the CISS effect yet. Most of the previously cited theoretical investigations based on model Hamiltonian approaches assume that the presence of some type of generic SOC in the molecular systems and, based on it, proceed to discuss its consequences for the CISS effect. A major issue has been whether spin polarization can be found in a two-terminal setup without invoking dephasing [26] or non-unitarity effects [29]. Some indications that these factors may not be required were given in Ref. [21] and more recently in Ref. [34], but the discussion remains also open on this point.
In this paper, we consider a very generic model previously used to describe the CISS effect [21,26], which consists of two inter-connected tight-binding chains, mimicking two interacting helices, including spin–orbit interaction and attached to two fermionic reservoirs playing the role of current terminals. We discuss in detail the general symmetries of the model—an issue not addressed previously—and show the parameter ranges where spin polarization can be important. It is interesting to note that our model does not assume any source of dissipation in the molecule. All dissipation takes place deep in the reservoirs, which are assumed to be in local thermodynamic equilibrium with well defined electrochemical potential and temperature. In the next section, we introduce the model and discuss the system energy spectrum by analytically diagonalizing the Hamiltonian. Using non-equilibrium Green’s function techniques, the spin-dependent electrical current is derived from the transmission probability for electrons traversing the two-terminal setup. Thus, we can define an energy-dependent spin polarization function. Special attention is devoted to the general symmetry properties of the spin polarization. Furthermore, we find that spin–flip processes do not contribute to the computed spin polarization, in perfect agreement both with first-principle calculations [35] and with the analysis of photoemission experiments [37].
2. Results
2.1. Tight-Binding Model with Generalized Rashba Interaction
Our system Hamiltonian describes two different helical strands with sites that can be occupied with electrons of spin . Including intrastrand () and interstrand hoppings () as well as a non-zero spin–orbit coupling, we split the system Hamiltonian as , with
where the creation and annihilation electron operators are and , respectively (the superscript ⊺ stands for transpose). The energy of the molecular orbitals in the two strands has been set to zero for simplicity. However, the interstrand coupling needs to be nonzero to achieve non-vanishing spin polarization, as demonstrated in Refs. [21] and [26]. The SOC of the Hamiltonian with strength depends on the spin operator perpendicular to the helical path, which is written in terms of the Pauli matrices as follows:
where is the helix angle, and and are the azymuthal angles in the two helical strands for the B-form of DNA [26].
2.2. Band Structure of a Molecule with Site-Independent SOC
As described in Equation (1), the molecular SOC is site-dependent. However, when one assumes a site-independent SOC ( and ), this model still allows for a finite SOC to exist. Within this approximation, the electron band structure can be easily calculated in the standard way by performing a Fourier transform. The matrix Hamiltonian in momentum space is then
where with and the wavenumber k lies between and for the first Brillouin zone.
In Figure 1, we plot the energy bands calculated from the diagonalization of Equation (3) for three different situations satisfying the requirement ∼ that will be analyzed hereafter. Notice that the condition accounts for a physical scenario where electrons propagating along the two helices, A and B, perform a precession around opposite magnetic fields within the plane. The first case under consideration will be referred to as the symmetric one since and . Furthermore, we will also be dealing with asymmetric cases such as and , x being a scaling factor. The latter has been demonstrated as the most favorable case to obtain an enhanced spin polarization [21,27].
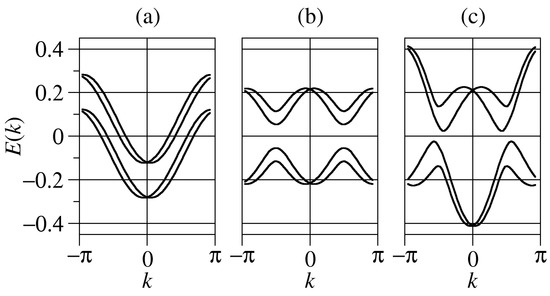
Figure 1.
Energy dispersion relation of the helical system for and in (a) the symmetric configuration with parameters and , (b) the quasi-symmetric configuration with parameters and , and (c) the asymmetric configuration with parameters and .
In the symmetric case [see Figure 1a], the tight-binding bands undergo a horizontal splitting due to the SOC field. This finding is consistent with the shifts observed in Rashba quantum wires with parabolic dispersions [38]. Two separated groups of bands are obtained due to the interstrand hopping term. The asymmetric cases (see Figure 1b,c) are more involved because the nature of the eigenstates (bonding or antibonding) differ in the two strands. Noticeably, a small gap opens for energies around the reference energy. In each case, we recover the spin degeneracy for zero wavenumber. Our results are qualitative since we neglected the site dependence in the SOC potential. However, we do not expect significant departures in the full dependence case.
2.3. Transmission and Spin Polarization
We now discuss charge transport when the molecule is tunnel coupled to two non-magnetic terminals attached at the edges of the helical molecule. We model such connection by adding the following two terms to the system Hamiltonian (1)
where the creation and annihilation electron operators at the leads are and , respectively. Here, the tunneling amplitude is nonzero only when and . Using well-known techniques of non-equilibrium transport calculations [39], after a lengthy but straightforward algebra, we find the electronic transmission probability in terms of advanced and retarded Green’s functions:
Our objective is to calculate the transmission probability per spin and strand, which we define as
where the retarded and advanced Green’s functions are evaluated from the expression . This is exact for independent electrons as the ones considered in this work. are the retarded and advanced electron self-energies due to tunneling. Their matrix elements are the broadening coefficients ’s, which describe the coupling between the molecule and the contacts [40]. When the contacts are metallic, we can take the wide-band limit since their density of states are flat. Thus, the ’s are simply given by a constant, which we take as the energy unit: (, and ). The sum over strands will provide us with the electron transmission per spin
We are now in a position to assess the spin polarization generated in the molecular transport by means of the following energy-dependent quantity:
which will be referred to as spin polarization in what follows.
The transmission completely determines the current for small applied voltages at very low temperature. This description is close to the experiments of Ref. [8] that were performed in the linear response regime with a small applied bias (50 mV). In such a case, a spin polarization of nearly from the linear conductance of the junction was obtained. Thus, we claim that the transmission function, which is proportional to the conductance at very low temperature, may still be a good reference point for the investigation of spin polarization. In different experimental setups, additional non-equilibrium effects play a role, but these are beyond the scope of this work, although they are expected to magnify the CISS effect.
2.4. Analysis of Symmetries
Let us analyze the results derived from Equations (6) and (8) for the three representative cases considered in Section 2.2, namely, symmetric, quasi-symmetric and asymmetric configuration. Since the calculations are fully numerical, we take into account the site dependence of the SOC potential. In Figure 2, Figure 3 and Figure 4, we show all interstrand spin–flip components of the transmission in addition to the spin polarization for each set of parameters. For concreteness, hereafter we will consider a DNA molecule of turns in its B-form, which has bases in a complete turn. Hence, . As a result, our simulations will contain sites. Ab initio calculations calculations suggest values of the intrastrand hopping roughly in the range of 30–80 meV (see, e.g., Ref. [41]) in DNA and we take meV as a typical value. Assuming a lead-molecule coupling of the order of meV yields . As to the SOC, we will take meV, hence .
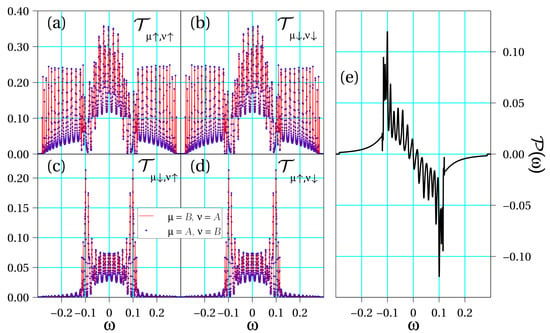
Figure 2.
Transport coefficients obtained for a symmetric molecule: , , , , , , and . Transmission coefficients (a) ; (b) ; (c) ; (d) ; and (e) spin polarization as a function of energy.
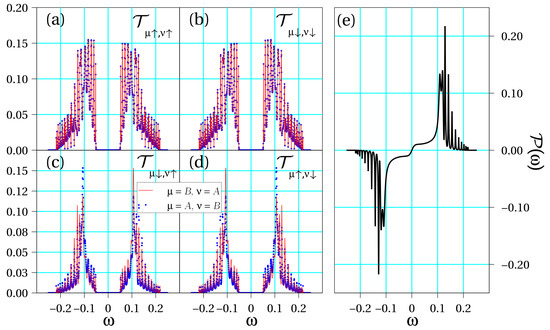
Figure 3.
Transport coefficients obtained for a quasi-symmetric molecules with the same parameters as in Figure 2 but and . Transmission coefficients (a) ; (b) ; (c) ; (d) ; and (e) spin polarization as a function of energy.
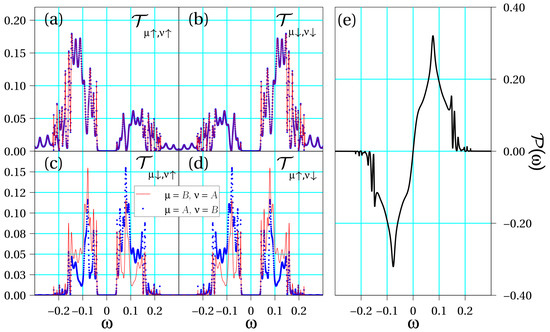
Figure 4.
Transport coefficients obtained for an asymmetric molecule with the same parameters as in Figure 2 but and . Transmission coefficients (a) ; (b) ; (c) ; (d) ; and (e) spin polarization as a function of energy.
Figure 2 shows the curves in different panels for the symmetric situation, namely, when the physical parameters of the two DNA strands are the same. Later, as an intermediate case, Figure 3 shows the same magnitudes when a small asymmetry is introduced in the double-stranded molecular hopping coefficients, (recall that is set as the unit of energy), but the SOC strengths are equal. Finally, Figure 4 summarizes the same physical magnitudes when both DNA strands are clearly asymmetrical with regard to both their different electronic hoppings, , and SOC intensities, .
In all considered cases, we observe that there exist contributions for each set of spins. However, it is most important to mention that the following symmetry condition for spin–flip processes arise from our calculations:
This originates from the fact that the transmission of a Rashba conductor is, quite generally, independent of the magnetization direction, a statement that has been demonstrated for one-dimensional (1D) [42] and quasi-1D systems [43]. Furthermore, for spin-conserving transmission contributions, we observe additional symmetries:
Moreover, the following symmetry conditions for intrastrand contributions also hold (not explicitly shown in the figures for brevity):
The latter conditions lead to the full cancellation of the spin–flip processes such that the components of the transmission which play a role in the spin polarization are and , including the case . Therefore, the resulting spin polarization reads
In fact, the symmetries shown in Equations (10) and (11) imply an energy symmetry in the polarization, which reads
3. Discussion
In this work, we revisit one of the most relevant model Hamiltonians widely used to describe spin-dependent transport in chiral molecular systems [21,26]. In particular, we focus on a description that accounts for a double-stranded helical molecule to mimic DNA molecules in its most common structure, namely, B-form DNA. It is worth noticing that in our study we keep the physical parameters within reasonable values accepted for DNA . We demonstrate that a sizable spin polarization arises in chiral systems with no need of including dephasing effects if the terminal connections are properly simulated [27]. In such a scenario, the asymmetry between the two DNA strands turns out to be a trigger for the spin polarization to arise. Here, we consider three representative cases to analyze this issue. Our reference system is referred to as a symmetrical case, where the two strands are equal. We also consider two other situations where this condition is relaxed. First, in view of some first-principle calculations [44], we introduce a small asymmetry in the two strands by considering their electronic hoppings with opposite signs [45]. Lastly, we obtain spin polarization in a very asymmetrical situation where the two DNA strands are described by different electronic and spin–orbit couplings, the latter being a limiting case for which it was proven that the spin polarization is clearly enhanced [21,27]. In addition, one of the novel interests of the present study is the analysis of the symmetries that arises in the transmission coefficients involved in the spin transport along chiral molecular systems.
Let us now summarize the main conclusions of our work. On the one hand, from Figure 2 and Figure 3, it is clear that even a tiny seed of asymmetry between the two DNA strands lead to a clear enhancement of the spin polarization in the molecule. In particular, just a change of the electronic hopping sign doubles the magnitude of the spin polarization although the energy window within which this enhancement is relevant is still small. However, when the asymmetry between the two strands is further increased as in Figure 4, we obtain an even higher spin polarization and, most importantly, it happens in a clearly wider energy window. From our simulations, not shown here for brevity, it is clear that the opposite signs of the electronic hoppings turns out to be a crucial ingredient to get this effect. This fact is related to the band structures shown in Figure 1, where anti-crossing points arise only if the hoppings parameters have opposite signs. In previous studies [21,32], it was shown that the non-vanishing of spin polarization within a two-strand helical model like the one used in the present study is related to the impossibility of fully removing the SOC from the model via a unitary transformation. In particular, it turns out that asymmetries in the values of the electronic couplings and/or in the strength of the SOC can lead to an increased polarization, a result nicely confirmed in the current investigation. We remark, however, that additionally both strands need to be connected to left and right electrodes in order to get a non-zero polarization.
Regarding the transmission coefficient symmetries, Figure 2, Figure 3 and Figure 4 clearly establish the symmetries summarized in Equations (10) and (11). These symmetries will be valid as long as the energies of the molecular orbitals of the two strands are equal to or symmetric around zero. If this is not the case, then the conditions should be slightly modified. This analysis allows us to demonstrate that the processes responsible for the spin polarization in chiral molecules are those that conserve the spin state. Indeed, it seems plausible that, even in other possible configurations, the spin–flip contributions will be less significant. Our results based on an effective model are in perfect agreement with other recent statements based on ab initio calculations [35] and rate equations for the analysis of photoemission experiments [37].
Author Contributions
Conceptualization, E.D. and F.D.-A.; Methodology, M.A.S., D.S., and R.G.; Software, M.A.S. and E.D.; Formal analysis, F.D.-A. and D.S.; Funding acquisition, F.D.-A., D.S., and G.C.; Investigation, M.A.S., D.S., and E.D.; Writing—original draft, E.D., M.A.S., and R.G.; Writing—review & editing, F.D.-A., D.S., and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science, Innovation and Universities, Grant Nos. MAT2016-75955 and MAT2017-82639. R.G. and G.C. acknowledge financial support from the Volkswagen Stiftung (Grant No. 88366). This work was partly supported by the German Research Foundation (DFG) within the Cluster of Excellence “Center for Advancing Electronics Dresden”. M.S. acknowledges financial support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project-id No. 258499086—SFB1170 “ToCoTronics”, the Free State of Bavaria (Elitenetzwerk Bayern IDK “Topologische Isolatoren”) and the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter—ct.qmat(EXC 2147, Grant No. 39085490).
Acknowledgments
We thank Matthias Geyer and Arezoo Dianat for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyzes, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Göhler, B.; Hamelbeck, V.; Markus, T.Z.; Kettner, M.; Hanne, G.F.; Vager, Z.; Naaman, R.; Zacharias, H. Spin Selectivity in Electron Transmission Through Self-Assembled Monolayers of Double-Stranded DNA. Science 2011, 331, 894. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Markus, T.Z.; Cohen, S.R.; Vager, Z.; Gutierrez, R.; Naaman, R. Spin Specific Electron Conduction Through DNA Oligomers. Nano Lett. 2011, 11, 4652. [Google Scholar] [CrossRef] [PubMed]
- Kessler, J. Polarized Electrons; Springer: Berlin, Germany, 1976. [Google Scholar]
- Kiran, V.; Mathew, S.P.; Cohen, S.R.; Hernández Delgado, I.; Lacour, J.; Naaman, R. Helicenes—A New Class of Organic Spin Filter. Adv. Mat. 2016, 28, 1957. [Google Scholar] [CrossRef] [PubMed]
- Michaeli, K.; Kantor-Uriel, N.; Naaman, R.; Waldeck, D.H. The Electron’s Spin and Molecular Chirality—How are They Related and How do They Affect Life Processes? Chem. Soc. Rev. 2016, 45, 6478. [Google Scholar] [CrossRef] [PubMed]
- Mishra, D.; Markus, T.Z.; Naaman, R.; Kettner, M.; Göhler, B.; Zacharias, H.; Friedman, N.; Sheves, M.; Fontanesi, C. Spin-Dependent Electron Transmission Through Bacteriorhodopsin Embedded in Purple Membrane. Proc. Nat. Acad. Sci. USA 2013, 110, 14872. [Google Scholar] [CrossRef] [PubMed]
- Kiran, V.; Cohen, S.R.; Naaman, R. Structure Dependent Spin Selectivity in Electron Transport Through Oligopeptides. J. Chem. Phys. 2017, 146, 92302. [Google Scholar] [CrossRef]
- Aragonès, A.C.; Medina, E.; Ferrer-Huerta, M.; Gimeno, N.; Teixidó, M.; Palma, J.L.; Tao, N.; Ugalde, J.M.; Giralt, E.; Díez-Pérez, I.; et al. Measuring the Spin-Polarization Power of a Single Chiral Molecule. Small 2017, 13, 1602519. [Google Scholar] [CrossRef]
- Kumar, A.; Capua, E.; Kesharwani, M.K.; Martin, J.M.L.; Sitbon, E.; Waldeck, D.H.; Naaman, R. Chirality-Induced Spin Polarization Places Symmetry Constraints on Biomolecular Interactions. Proc. Natl. Acad. Sci. USA 2017, 114, 2474. [Google Scholar] [CrossRef]
- Mondal, P.C.; Fontanesi, C.; Waldeck, D.H.; Naaman, R. Field and Chirality Effects on Electrochemical Charge Transfer Rates: Spin Dependent Electrochemistry. ACS Nano 2015, 9, 3377. [Google Scholar] [CrossRef]
- Kettner, M.; Göhler, B.; Zacharias, H.; Mishra, D.; Kiran, V.; Naaman, R.; Fontanesi, C.; Waldeck, D.H.; Sȩk, S.; Pawłowski, J.; et al. Spin Filtering in Electron Transport Through Chiral Oligopeptides. J. Phys. Chem. C 2015, 119, 14542. [Google Scholar] [CrossRef]
- Naaman, R.; Waldeck, D.H. Spintronics and Chirality: Spin Selectivity in Electron Transport Through Chiral Molecules. Annu. Rev. Phys. Chem. 2015, 66, 263. [Google Scholar] [CrossRef] [PubMed]
- Zwang, T.J.; Hürlimann, S.; Hill, M.G.; Barton, J.K. Helix-Dependent Spin Filtering Through the DNA Duplex. J. Am. Chem. Soc. 2016, 138, 15551. [Google Scholar] [CrossRef] [PubMed]
- Mtangi, W.; Tassinari, F.; Vankayala, K.; Vargas Jentzsch, A.; Adelizzi, B.; Palmans, A.R.A.; Fontanesi, C.; Meijer, E.W.; Naaman, R. Control of Electrons’ Spin Eliminates Hydrogen Peroxide Formation During Water Splitting. J. Am. Chem. Soc. 2017, 139, 2794. [Google Scholar] [CrossRef] [PubMed]
- Ben Dor, O.; Yochelis, S.; Radko, A.; Vankayala, K.; Capua, E.; Capua, A.; Yang, S.H.; Baczewski, L.T.; Parkin, S.S.P.; Naaman, R.; et al. Magnetization Switching in Ferromagnets by Adsorbed Chiral Molecules Without Current or External Magnetic Field. Nat. Commun. 2017, 8, 14567. [Google Scholar] [CrossRef] [PubMed]
- Kettner, M.; Maslyuk, V.V.; Nürenberg, D.; Seibel, J.; Gutierrez, R.; Cuniberti, G.; Ernst, K.H.; Zacharias, H. Chirality-Dependent Electron Spin Filtering by Molecular Monolayers of Helicenes. J. Phys. Chem. Lett. 2018, 9, 2025. [Google Scholar] [CrossRef] [PubMed]
- Abendroth, J.M.; Cheung, K.M.; Stemer, D.M.; El Hadri, M.S.; Zhao, C.; Fullerton, E.E.; Weiss, P.S. Spin-Dependent Ionization of Chiral Molecular Films. J. Am. Chem. Soc. 2019, 141, 3863. [Google Scholar] [CrossRef] [PubMed]
- Yeganeh, S.; Ratner, M.A.; Medina, E.; Mujica, V. Chiral electron transport: Scattering through helical potentials. J. Chem. Phys. 2009, 131, 014707. [Google Scholar] [CrossRef]
- Medina, E.; López, F.; Ratner, M.A.; Mujica, V. Chiral molecular films as electron polarizers and polarization modulators. Europhys. Lett. 2012, 99, 17006. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Díaz, E.; Naaman, R.; Cuniberti, G. Spin-selective transport through helical molecular systems. Phys. Rev. B 2012, 85, 081404. [Google Scholar] [CrossRef]
- Gutierrez, R.; Díaz, E.; Gaul, C.; Brumme, T.; Domínguez-Adame, F.; Cuniberti, G. Modeling Spin Transport in Helical Fields: Derivation of an Effective Low-Dimensional Hamiltonian. J. Phys. Chem. C 2013, 117, 22276. [Google Scholar] [CrossRef]
- Díaz, E.; Domínguez-Adame, F.; Gutierrez, R.; Cuniberti, G.; Mujica, V. Thermal Decoherence and Disorder Effects on Chiral-Induced Spin Selectivity. J. Phys. Chem. Lett. 2018, 9, 5753. [Google Scholar] [CrossRef] [PubMed]
- Eremko, A.A.; Loktev, V.M. Spin sensitive electron transmission through helical potentials. Phys. Rev. B 2013, 88, 165409. [Google Scholar] [CrossRef]
- Medina, E.; González-Arraga, L.A.; Finkelstein-Shapiro, D.; Berche, B.; Mujica, V. Continuum model for chiral induced spin selectivity in helical molecules. J. Chem. Phys. 2015, 142, 194308. [Google Scholar] [CrossRef] [PubMed]
- Caetano, R.A. Spin–Current and Spin–Splitting in Helicoidal Molecules Due to Spin-Orbit Coupling. Sci. Rep. 2016, 6, 23452. [Google Scholar] [CrossRef] [PubMed]
- Guo, A.M.; Sun, Q.F. Spin-selective transport of electrons in DNA double helix. Phys. Rev. Lett. 2012, 108, 218102. [Google Scholar] [CrossRef]
- Guo, A.M.; Díaz, E.; Gaul, C.; Gutierrez, R.; Domínguez-Adame, F.; Cuniberti, G.; Sun, Q.F. Contact effects in spin transport along double-helical molecules. Phys. Rev. B 2014, 89, 205434. [Google Scholar] [CrossRef]
- Díaz, E.; Albares, P.; Estévez, P.G.; Cerveró, J.M.; Gaul, C.; Diez, E.; Domínguez-Adame, F. Spin Dynamics in Helical Molecules with Nonlinear Interactions. New J. Phys. 2018, 20, 043055. [Google Scholar] [CrossRef]
- Matityahu, S.; Utsumi, Y.; Aharony, A.; Entin-Wohlman, O.; Balseiro, C.A. Spin-dependent transport through a chiral molecule in the presence of spin–orbit interaction and nonunitary effects. Phys. Rev. B 2016, 93, 075407. [Google Scholar] [CrossRef]
- Gersten, J.; Kaasbjerg, K.; Nitzan, A. Induced Spin Filtering in Electron Transmission Through Chiral Molecular Layers Adsorbed on Metals with Strong Spin-Orbit Coupling. J. Chem. Phys. 2013, 139, 114111. [Google Scholar] [CrossRef]
- Hedegard, P.; Dalum, S. Theory of Chiral Induced Spin Selectivity. Nano Lett. 2019, 19, 5253. [Google Scholar]
- Geyer, M.; Gutierrez, R.; Mujica, V.; Cuniberti, G. Chirality-Induced Spin Selectivity in a Coarse-Grained Tight-Binding Model for Helicene. J. Phys. Chem. C 2019, 123, 27230. [Google Scholar] [CrossRef]
- Michaeli, K.; Naaman, R. Origin of Spin-Dependent Tunneling Through Chiral Molecules. J. Phys. Chem. C 2019, 123, 17043. [Google Scholar] [CrossRef]
- Fransson, J. Chirality-Induced Spin Selectivity: The Role of Electron Correlations. J. Phys. Chem. Lett. 2019, 10, 7126. [Google Scholar] [CrossRef] [PubMed]
- Maslyuk, V.V.; Gutierrez, R.; Dianat, A.; Mujica, V.; Cuniberti, G. Enhanced Magnetoresistance in Chiral Molecular Junctions. J. Phys. Chem. Lett. 2018, 9, 5453. [Google Scholar] [CrossRef]
- Zöllner, M.S.; Varela, S.; Medina, E.; Mujica, V.; Herrmann, C. Chiral-Induced Spin Selectivity: A Symmetry Analysis of Electronic Transmission. ChemRxiv 2019. [Google Scholar] [CrossRef]
- Nürenberg, D.; Zacharias, H. Evaluation of spin–flip scattering in chirality-induced spin selectivity using the Riccati equation. Phys. Chem. Chem. Phys. 2019, 21, 3761. [Google Scholar] [CrossRef]
- Moroz, A.V.; Barnes, C.H.W. Effect of the spin–orbit interaction on the band structure and conductance of quasi-one-dimensional systems. Phys. Rev. B 1999, 60, 14272–14285. [Google Scholar] [CrossRef]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors; Springer: Berlin, Germany, 1998. [Google Scholar]
- Ryndyk, D. Theory of Quantum Transport at Nanoscale; Springer: Berlin, Germany, 2016. [Google Scholar]
- Kubar, T.; Woiczikowski, P.B.; Cuniberti, G.; Elstner, M. Efficient Calculation of Charge-Transfer Matrix Elements for Hole Transfer in DNA. J. Phys. Chem. B 2008, 112, 7937. [Google Scholar] [CrossRef]
- Molenkamp, L.W.; Schmidt, G.; Bauer, G.E.W. Rashba Hamiltonian and electron transport. Phys. Rev. B 2001, 64, 121202. [Google Scholar] [CrossRef]
- Sánchez, D.; Serra, L. Fano-Rashba effect in a quantum wire. Phys. Rev. B 2006, 74, 153313. [Google Scholar] [CrossRef]
- Artacho, E.; Machado, M.; Sánchez-Portal, D.; Ordejón, P.; Soler, J.M. Electrons in dry DNA from density functional calculations. Mol. Phys. 2003, 101, 1587. [Google Scholar] [CrossRef][Green Version]
- Díaz, E.; Malyshev, A.V.; Domínguez-Adame, F. Interband optical transitions in DNA-like systems. Phys. Rev. B 2007, 76, 205117. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).