Abstract
Doubly differential cross sections for projectile ionization in fast collisions of few-electron uranium ions with the nitrogen target are calculated within the first order of the relativistic perturbation theory. A comparison with the recent measurements of the energy distribution of forward-emitted electrons is made and good agreement is found.
1. Introduction
For many decades ion-atom collisions serve as a tool for studying basic processes in atomic physics. Nowadays, owing to the usage of storage rings a more efficient and detailed exploration of such processes becomes accessible [1,2]. Storage rings provide a wide range of projectile charge states and velocities, which together with the implementation of various internal targets and detectors leads to unprecedented experimental conditions.
Ionization of highly charged projectile heavy ions can uniquely be studied in storage rings in the inverse kinematics in collisions with gas targets. In this process, called electron loss to the continuum (ELC), the velocity of the ejected “cusp” projectile electrons is close to the projectile velocity [3]. Besides, in such collisions, an electron moving in the beam direction and with can also be originated from ionization of the target, which constitutes the electron capture to the projectile continuum process (ECC). Due to the detection of the projectile charge after the reaction zone, electrons ejected from different centers can be separated in a single experiment [4].
For low-Z projectiles ECC and ELC cross sections were measured from 1970s [4,5,6,7,8]. For highly charged uranium ions a series of measurements was recently performed in the experimental storage ring (ESR) at GSI (Darmstadt, Germany) using a magnetic electron spectrometer [9,10,11,12,13]. Theoretical calculations of ionization probabilities and cross sections based on the first-order perturbation theory were largely discussed in the literature [14,15,16,17,18,19,20,21,22].
In this contribution, we perform computations of the energy distribution of the forward-emitted electrons in the course of ionization of Li- and Be-like uranium ions in near relativistic collisions with the nitrogen target. In the framework of the relativistic first-order perturbation theory, doubly differential cross sections (DDCS) for ionization are obtained in the projectile reference frame. Using the transformation of the cross section to the laboratory reference frame and extraction of the forward part we obtain the desired energy distribution to compare with the recent experimental data [10].
The paper is organized as follows. In Section 2 the basic formalism is outlined, including the formulation of the perturbation theory for the calculation of the doubly differential cross section in the projectile frame in Section 2.1, its transformation to the laboratory frame in Section 2.2, and description of the screening potentials used in Section 2.3. The results for Be- and Li-like ions are presented and discussed in Section 3.1 and Section 3.2, correspondingly. Finally, a summary and outlook are given in Section 4.
Relativistic units are used throughout the paper unless otherwise stated.
2. Basic Formalism
2.1. Doubly Differential Cross Section within the First-Order Perturbation Theory
Let us consider ionization of a projectile ion in the reference frame where it is at rest by a target atom moving along a straight-line trajectory with constant velocity and impact parameter , so that . The projectile ionization may be caused by the target nucleus and target electrons. The total cross section for ionization with good accuracy can be approximated by the incoherent sum of each contribution [23,24]. Moreover, while the nucleus contribution is proportional to , the electron one scales as their number, i.e., target charge for a neutral atom. In what follows, we neglect the ionization by target electrons and consider only the nucleus contribution to the ionization cross section. The transition amplitude from the initial bound projectile state with energy to the final continuum state with energy in the first-order perturbation theory reads as [25]
Here we assume that the z- and x-axes are directed along and , correspondingly, is the Lorentz factor, is the fine-structure constant, is the distance between the projectile electron and the target nucleus, is the Dirac matrix. Moreover, the initial state is characterized by a principal quantum number , angular momentum-parity quantum number , and total angular momentum projection , while the final state is described by an asymptotic momentum and spin projection . Then the DDCS is given by
where the integration over the impact parameter, summation over the final spin projections, and averaging over the initial total angular momentum projections are performed. The integration over the time and impact parameter is convenient to perform introducing the Fourier transform from the space coordinate to the momentum coordinate [15,16]. In this way one obtains
where and
This matrix element is calculated using the plane wave expansion
where are the spherical harmonics and are the spherical Bessel functions [26], together with the expansion of the distorted wave
where is the Clebsch-Gordan coefficient, is the difference between the asymptotic large-distance phase of the Dirac-Coulomb solution and the free Dirac solution [27]. Furthermore, is the Dirac partial wave with a given energy E, angular momentum-parity quantum number , and total angular momentum projection represented by a bispinor
and normalized on the energy scale,
The initial Dirac wave function is also expressed by a bispinor with radial components and normalized to 1. Substituting Equations (5) and (6) into Equation (4), one obtains the following expression for the matrix element in the momentum space:
Then the matrix elements in Equation (9) can be written as [16,22]
where , , the radial integrals are defined by
and angular coefficients read as
In our approach, the integrals (11) are evaluated numerically, while the analytical integration is possible for the case of the wave functions in the pure Coulomb potential [28]. The radial components of the Dirac wave functions and as well as the phase shifts are computed using the RADIAL package [29]. Finally, after substitution of Equation (9) into Equation (3) one arrives at the DDCS for ionization in the form
with
and standing for a Legendre polynomial.
2.2. Lorentz Transformation of the Doubly Differential Cross Section
Up to now, we have derived the formulas for the DDCS for ionization in the projectile reference frame. To make a comparison with experimental data, one should transform it into the laboratory reference frame. The corresponding Lorentz transformation is [25]
where the Lorentz transformation for the energy, momentum, and angle variables reads as
The experimentally obtained energy distribution takes into account only electrons emitted in a cone with an opening angle with respect to the projectile beam direction. This means that the doubly differential cross section in the laboratory reference frame has to be further averaged over the angle interval to give the desired energy spectrum,
It is worth noting that the dependencies of laboratory frame energy and angle on both projectile frame energy and angle, Equation (16), require calculation of the cross section at different energies (angles) in the projectile reference frame, in order to obtain the cross section at a single energy (angle) in the laboratory reference frame. To avoid excessive interpolations, the sufficiently dense uniform two-dimensional grid in the laboratory frame was first transformed to the (nonuniform) projectile-frame grid used for the cross section calculation by Equation (13). Afterwards, the obtained cross section was transformed back to the primary laboratory-frame grid and averaged according to Equations (15)–(17).
2.3. Screening Potential for Electron Wave Functions
The calculation of DDCS for ELC described in Section 2.1 requires initial and final state wave functions, which are the solutions of the one-electron Dirac equation in a central potential. Since the projectiles, we are interested in, are Li- and Be-like ions, the one-particle approximation accompanied by a screening potential should be applied. The simplest choice is the Coulomb potential with some effective charge . The effective charge is smaller than the nuclear charge and accounts for its screening by other electrons. For example, was used in Ref. [10] for the calculation of ionization from the L-shell. Alternatively, more elaborated potentials like the local Dirac-Fock [30], asymptotically corrected [31] exchange Kohn-Sham [32] (without correlations) or Perdew-Zunger [33] can be used. These potentials have correct asymptotic behavior at large r and provide binding energies closer to the experimental values. A generalization of the density functional formalism to the relativistic case can be found in Ref. [34]. We found that the obtained energy distribution of emitted electrons only slightly depends on the type of screening potential. In the results presented in the next section, the Perdew-Zunger (PZ) potential was employed for the wave function calculation.
3. Results and Discussion
The approach outlined above was used for the calculation of the energy distribution of the electrons emitted from the few-electron uranium projectiles in fast collisions with nitrogen molecules. The two corresponding scenarios were recently investigated in the ESR at GSI (Darmstadt, Germany). For the high collision energies considered here, the molecular character of the target can be neglected. The total cross sections for ELC presented below were obtained as a sum of the contributions of each projectile electron (two 1 s and two 2 s electrons for U; two 1 s and one 2 s electron for U) per one nitrogen target atom.
3.1. Be-Like Projectiles
Let us start with presenting the results for the MeV/u U-N collision. Figure 1 shows the DDCS for ELC in the forward direction. The value of the maximal acceptance angle of the spectrometer was adopted in Equation (17). Due to unknown electron detection efficiency, the absolute cross sections were not derived from the data in Ref. [10]. Thus, the shown experimental data of Ref. [10] were renormalized on our results at keV. The obtained results well describe the experimental data, slightly underestimating them at high electron energies, and tend to overestimate at small energies. Also one can see that our results for emitted electron energies larger than 60 keV and smaller than 40 keV agree with the theoretical predictions of Ref. [10] obtained in the framework of the first-order perturbation theory as well. However, in the vicinity of the cusp, which is located at keV, the present results are considerably higher than those of Ref. [10]. The only difference between the two calculations is in screening potentials employed. The binding energies of the initial 2 s states calculated in these potential are very close to each other: keV and keV. Meanwhile, in the additional calculation with the same screening potential as in Ref. [10] we still see the difference in the emitted electron energy distribution in the laboratory frame. Moreover, we also compared the DDCS for ELC in the projectile frame (see Figure 2 of Ref. [10]) and found excellent agreement between the outcomes of two calculations. This could mean that the difference arises at the stage of the Lorentz transformation of the cross section to the laboratory frame and the following averaging over angles. Basically, both calculations describe the experimental data rather well, despite the omission of a possible atomic electron contribution to the electron loss process.
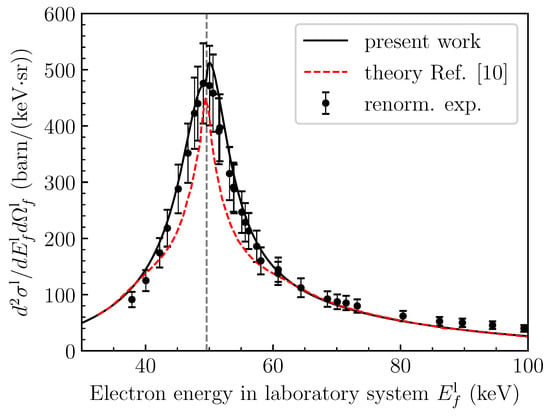
Figure 1.
DDCS for ELC observed at in the MeV/u U-N collision. The theoretical predictions and experimental data of Ref. [10] (renormalized to our results) are also shown. The vertical line at keV corresponds to the cusp.
3.2. Li-Like Projectiles
Let us move to ELC in the MeV/u U-N collision. In the corresponding experiment, only data for the process of radiative electron capture to the continuum have been analyzed up to now [13]. So, we present here our theoretical predictions alone. Figure 2 shows the DDCS for ELC averaged in the angle interval according to Equation (17). Since in operation of the spectrometer there are some effects difficult to estimate, the effective angular acceptance is not known precisely, and the value of can be adopted [13]. The vertical line at keV corresponds to the kinetic energy of the electrons in the electron cooler. This energy defines the ion beam velocity and, hence, it is the energy of the cusp electrons moving with the velocity equal to the projectile velocity. From the figure, one can see that the dependence of DDCS on is mainly located near the cusp, while the wings of the energy distribution are almost independent on the given variation. With decreasing the magnitude of the peak increases. Note that the prefactor in Equation (17) diverges at the limit .
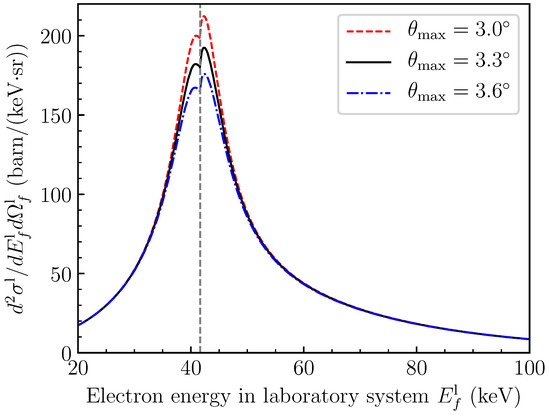
Figure 2.
DDCS for ELC observed at in the MeV/u U-N collision. Presented are the theory for total ELC with different maximum spectrometer acceptance angle . The vertical line at keV corresponds to the cusp.
In Figure 3 the DDCS for ELC is presented for the value of along with the contributions from K- and L-shells.
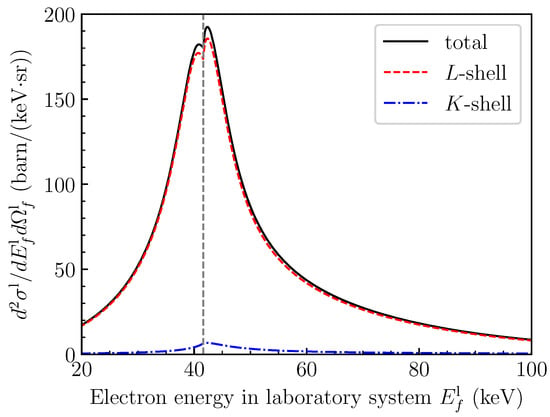
The K-shell ELC is only of the total one, which is caused by the large difference in the ionization potentials for 1 s and 2 s electrons: keV, while keV. However, the additional photon detection made it possible to identify the K-shell contribution in the preceding experiment with Be-like projectiles [10].
4. Summary and Outlook
In this study, the doubly differential cross sections for electron loss to the continuum have been calculated in the framework of the relativistic first-order perturbation theory for few-electron uranium ions colliding with a nitrogen target. The energy distributions of electrons emitted in the projectile beam direction have been presented, and for the MeV/u U-N collision compared with the experimental data of Ref. [10]. For the MeV/u U-N collision we have shown the contributions of the 1 s and 2 s electrons to the total ELC cross section and explore its dependence on the angular acceptance of the spectrometer used in the corresponding experiment (see Ref. [13]).
Besides the considered collisions involving few-electron uranium ions, a number of experiments on various ELC cross sections measurements with 64-electron U projectiles at 30–50 MeV/u energies were performed in Darmstadt [35,36,37]. Their outcome found a strong asymmetry of the cusp shape, which was not predicted by theory [37], so the independent calculation is required. We plan to extend our approach to the description of multielectron projectiles and perform the desired computations.
Author Contributions
A.I.B., Y.S.K., I.I.T., V.M.S. and G.P. contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
Calculations for Li-like projectiles were supported by the Russian Science Foundation (Grant No. 20-62-46006). Calculations for Be-like projectiles were supported by RFBR (Grants No. 18-03-01220, 18-32-00279, 18-32-20063, and 20-02-00199) and the German-Russian Interdisciplinary Science Center (G-RISC) funded by the German Federal Foreign Office via the German Academic Exchange Service (DAAD).
Acknowledgments
We thank P.-M. Hillenbrand for providing us experimental data and K. N. Lyashchenko for valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eichler, J.; Stöhlker, T. Radiative electron capture in relativistic ion–atom collisions and the photoelectric effect in hydrogen-like high-Z systems. Phys. Rep. 2007, 439, 1–99. [Google Scholar] [CrossRef]
- Steck, M.; Litvinov, Y.A. Heavy-ion storage rings and their use in precision experiments with highly charged ions. Prog. Part. Nucl. Phys. 2020, 115, 103811. [Google Scholar]
- Stolterfoht, N.; Schneider, D.; Burch, D.; Wieman, H.; Risley, J.S. Mechanisms for Electron Production in 30-MeV On++O2 Collisions. Phys. Rev. Lett. 1974, 33, 59–62. [Google Scholar] [CrossRef]
- Andersen, L.H.; Frost, M.; Hvelplund, P.; Knudsen, H.; Datz, S. Correlated Two-Electron Effects in Highly Charged Ion-Atom Collisions: Transfer Ionization and Transfer Excitation in 20-MeV Au15++He Collisions. Phys. Rev. Lett. 1984, 52, 518–521. [Google Scholar] [CrossRef]
- Crooks, G.B.; Rudd, M.E. Experimental Evidence for the Mechanism of Charge Transfer into Continuum States. Phys. Rev. Lett. 1970, 25, 1599–1601. [Google Scholar] [CrossRef]
- Dettmann, K.; Harrison, K.G.; Lucas, M.W. Charge exchange to the continuum for light ions in solids. J. Phys. B At. Mol. Phys. 1974, 7, 269–287. [Google Scholar] [CrossRef]
- Vane, C.R.; Sellin, I.A.; Suter, M.; Alton, G.D.; Elston, S.B.; Griffin, P.M.; Thoe, R.S. Z, Velocity, and Charge Dependence of Zero-Degree Electron “Cusps” from Charge Transfer to Continuum States of Bare and Highly Ionized Projectiles. Phys. Rev. Lett. 1978, 40, 1020–1023. [Google Scholar] [CrossRef]
- Breinig, M.; Elston, S.B.; Huldt, S.; Liljeby, L.; Vane, C.R.; Berry, S.D.; Glass, G.A.; Schauer, M.; Sellin, I.A.; Alton, G.D.; et al. Experiments concerning electron capture and loss to the continuum and convoy electron production by highly ionized projectiles in the 0.7–8.5-MeV/u range transversing the rare gases, polycrystalline solids, and axial channels in gold. Phys. Rev. A 1982, 25, 3015–3048. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Atanasov, D.; Banaś, D.; Blumenhagen, K.H.; Brandau, C.; Chen, W.; De Filippo, E.; Gumberidze, A.; Guo, D.L.; et al. Radiative-electron-capture-to-continuum cusp in U88+ + N2 collisions and the high-energy endpoint of electron-nucleus bremsstrahlung. Phys. Rev. A 2014, 90, 022707. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Voitkiv, A.B.; Najjari, B.; Banaś, D.; Blumenhagen, K.H.; Brandau, C.; Chen, W.; De Filippo, E.; Gumberidze, A.; et al. Electron-loss-to-continuum cusp in U88+ + N2 collisions. Phys. Rev. A 2014, 90, 042713. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Jakubassa-Amundsen, D.H.; Monti, J.M.; Banaś, D.; Blumenhagen, K.H.; Brandau, C.; Chen, W.; Fainstein, P.D.; De Filippo, E.; et al. Electron-capture-to-continuum cusp in U88+ + N2 collisions. Phys. Rev. A 2015, 91, 022705. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Litvinov, Y.A.; Stöhlker, T. Forward-angle electron spectroscopy in heavy-ion atom collisions studied at the ESR. J. Phys. Conf. Ser. 2015, 635, 012011. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Groshev, M.E.; Banaś, D.; Benis, E.P.; Brandau, C.; De Filippo, E.; Forstner, O.; Glorius, J.; Grisenti, R.E.; et al. Radiative electron capture to the continuum in U89+ + N2 collisions: Experiment and theory. Phys. Rev. A 2020, 101, 022708. [Google Scholar] [CrossRef]
- Pauli, M.; Rosel, F.; Trautmann, D. Electronic relativistic effects in the semiclassical theory of K-shell ionisation. J. Phys. B At. Mol. Phys. 1978, 11, 2511–2526. [Google Scholar] [CrossRef]
- Amundsen, P.A.; Aashamar, K. Impact parameter dependence of K-shell ionisation by relativistic ions. J. Phys. B At. Mol. Phys. 1981, 14, 4047–4063. [Google Scholar] [CrossRef]
- Valluri, S.R.; Becker, U.; Grün, N.; Scheid, W. K-shell ionisation in relativistic heavy-ion collisions. J. Phys. B At. Mol. Phys. 1984, 17, 4359–4370. [Google Scholar] [CrossRef]
- Becker, U.; Grün, N.; Scheid, W. Cross sections for K-shell ionisation in relativistic heavy-ion collisions. J. Phys. B At. Mol. Phys. 1985, 18, 4589–4595. [Google Scholar] [CrossRef]
- Momberger, K.; Grün, N.; Scheid, W.; Becker, U. Angular distribution of electrons emitted from 1s1/2 and 2s1/2 states in relativistic heavy-ion collisions. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 3269–3273. [Google Scholar] [CrossRef]
- Halabuka, Z.; Perger, W.; Trautmann, D. SCA calculations of the inner shell ionization with Dirac-Fock electronic wave functions. Z. Für Phys. Atoms Mol. Clust. 1994, 29, 151–158. [Google Scholar] [CrossRef]
- Voitkiv, A.; Grün, N.; Scheid, W. Plane-wave Born treatment of projectile-electron excitation and loss in relativistic collisions with atomic targets. Phys. Rev. A 2000, 61, 052704. [Google Scholar] [CrossRef]
- Voitkiv, A.B. Theory of projectile-electron excitation and loss in relativistic collisions with atoms. Phys. Rep. 2004, 392, 191–277. [Google Scholar] [CrossRef]
- Surzhykov, A.; Fritzsche, S. Electron angular and energy distributions following the ionization of highly charged projectile ions. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2711–2721. [Google Scholar] [CrossRef]
- Najjari, B.; Voitkiv, A.B. Excitation of heavy hydrogenlike ions by light atoms in relativistic collisions with large momentum transfers. Phys. Rev. A 2012, 85, 052712. [Google Scholar] [CrossRef]
- Lyashchenko, K.N.; Andreev, O.Y.; Voitkiv, A.B. Electron loss from hydrogen-like highly charged ions in collisions with electrons, protons and light atoms. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 055204. [Google Scholar] [CrossRef]
- Eichler, J.; Meyerhof, W.E. Relativistic Atomic Collisions; Academic Press: San Diego, CA, USA, 1995. [Google Scholar] [CrossRef]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1988. [Google Scholar]
- Rose, M.E. Relativistic Electron Theory; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Jakubassa-Amundsen, D.H.; Amundsen, P.A. Charge transfer in heavy-ion collisions at relativistic velocities. Z. Für Phys. Atoms Nucl. 1980, 298, 13–19. [Google Scholar] [CrossRef][Green Version]
- Salvat, F.; Fernández-Varea, J.; Williamson, W., Jr. Accurate numerical solution of the radial Schrödinger and Dirac wave equations. Comput. Phys. Commun. 1995, 90, 151–168. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Tupitsyn, I.I.; Pachucki, K.; Plunien, G.; Yerokhin, V.A. Radiative and correlation effects on the parity-nonconserving transition amplitude in heavy alkali-metal atoms. Phys. Rev. A 2005, 72, 062105. [Google Scholar] [CrossRef]
- Latter, R. Atomic Energy Levels for the Thomas-Fermi and Thomas-Fermi-Dirac Potential. Phys. Rev. 1955, 99, 510–519. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- MacDonald, A.H.; Vosko, S.H. A relativistic density functional formalism. J. Phys. Solid State Phys. 1979, 12, 2977–2990. [Google Scholar] [CrossRef]
- Weber, G.; Herdrich, M.O.; DuBois, R.D.; Hillenbrand, P.M.; Beyer, H.; Bozyk, L.; Gassner, T.; Grisenti, R.E.; Hagmann, S.; Litvinov, Y.A.; et al. Total projectile electron loss cross sections of U28+ ions in collisions with gaseous targets ranging from hydrogen to krypton. Phys. Rev. ST Accel. Beams 2015, 18, 034403. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Monti, J.M.; Rivarola, R.D.; Blumenhagen, K.H.; Brandau, C.; Chen, W.; DuBois, R.D.; Gumberidze, A.; Guo, D.L.; et al. Electron emission spectra of U28+-ions colliding with gaseous targets. J. Phys. Conf. Ser. 2015, 635, 022049. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Monti, J.M.; Rivarola, R.D.; Blumenhagen, K.H.; Brandau, C.; Chen, W.; DuBois, R.D.; Gumberidze, A.; Guo, D.L.; et al. Strong asymmetry of the electron-loss-to-continuum cusp of multielectron U28+ projectiles in near-relativistic collisions with gaseous targets. Phys. Rev. A 2016, 93, 042709. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).