Positron Scattering from Atoms and Molecules
Abstract
1. Introduction
2. Scattering Parameters: Cross Sections and Spin Polarizations for Atoms
3. and Target Atom Interaction Potential
4. Scattering from Molecules
4.1. Optical Potential Approach
4.2. ab initio R-Matrix Method
5. Results and Discussions
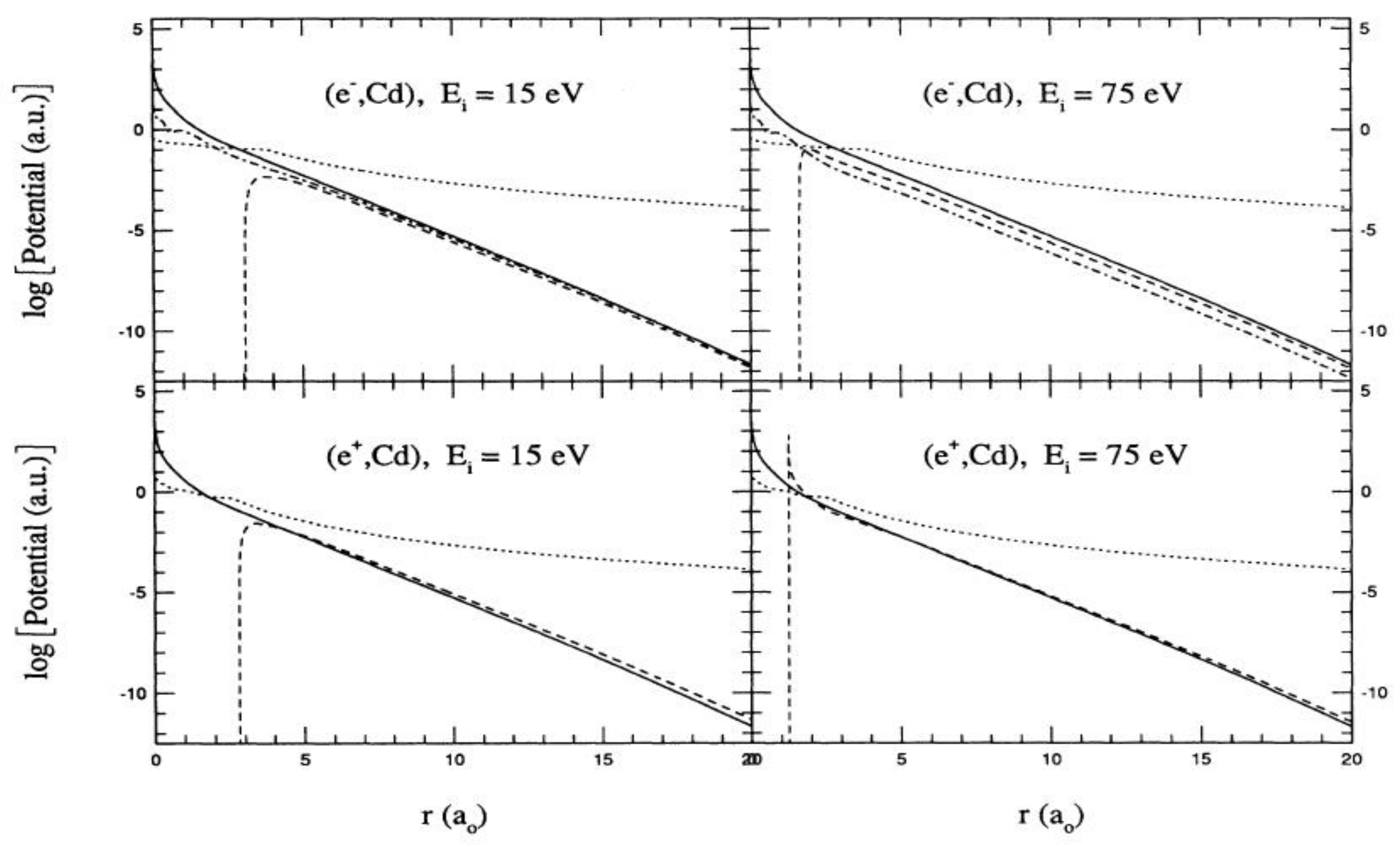
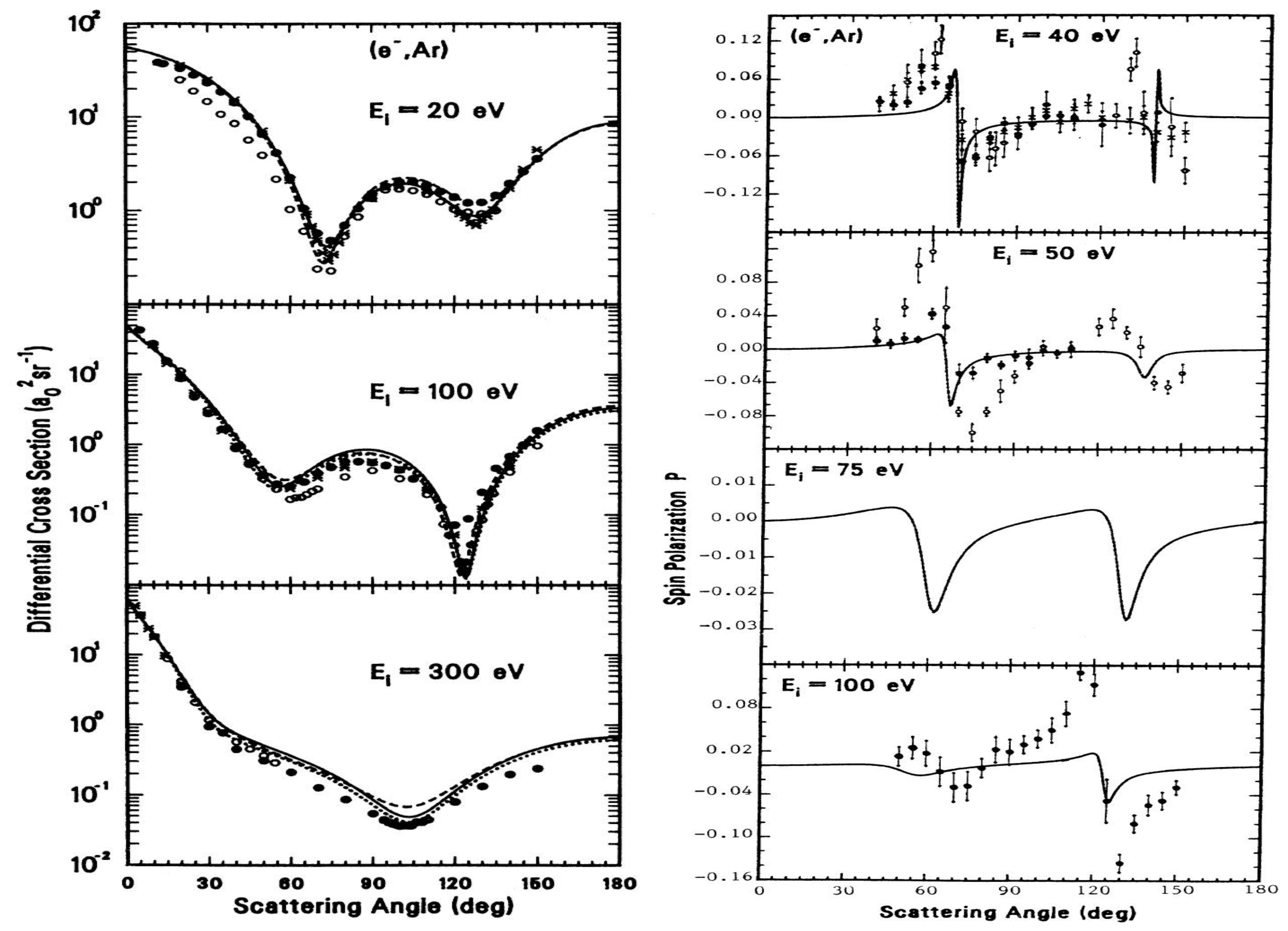
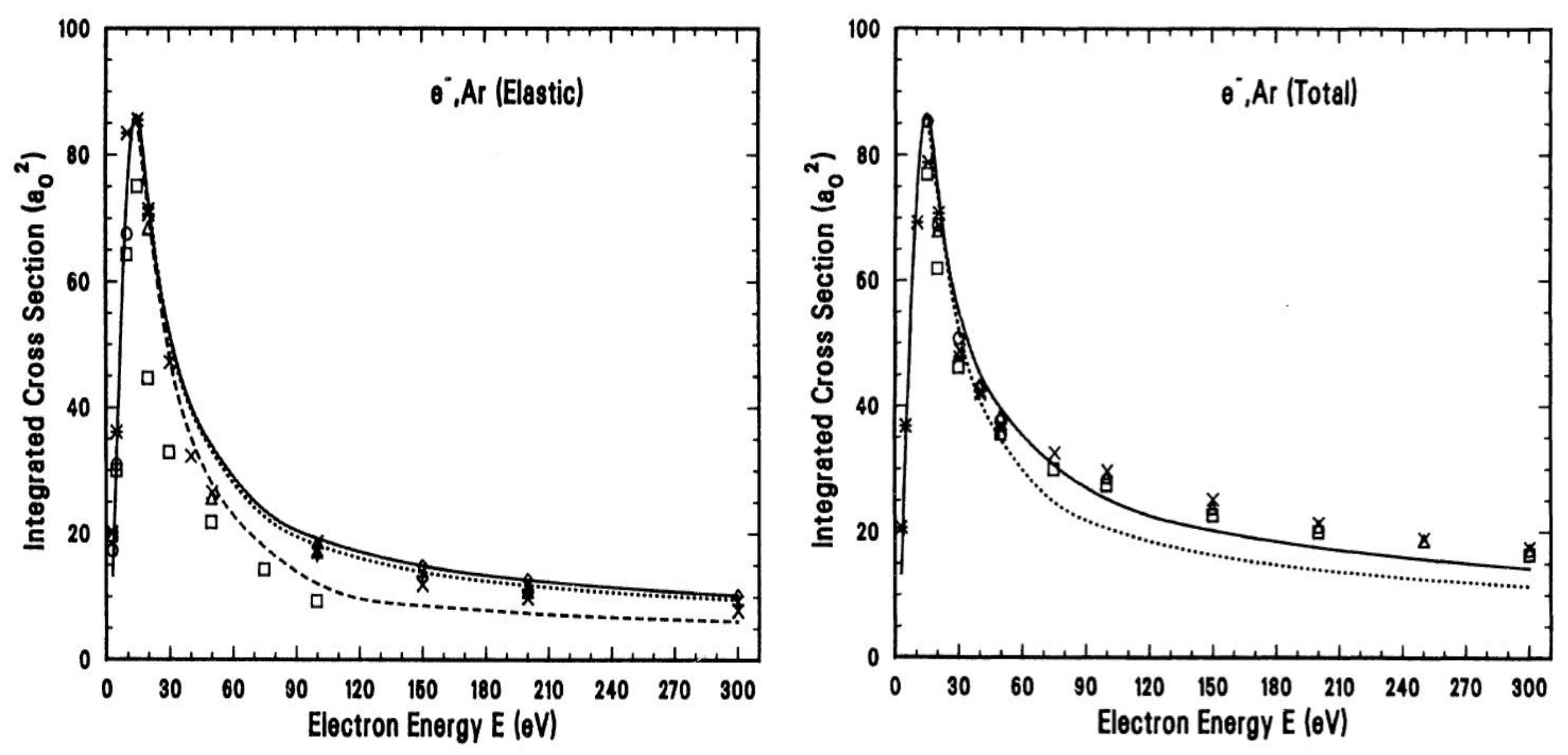
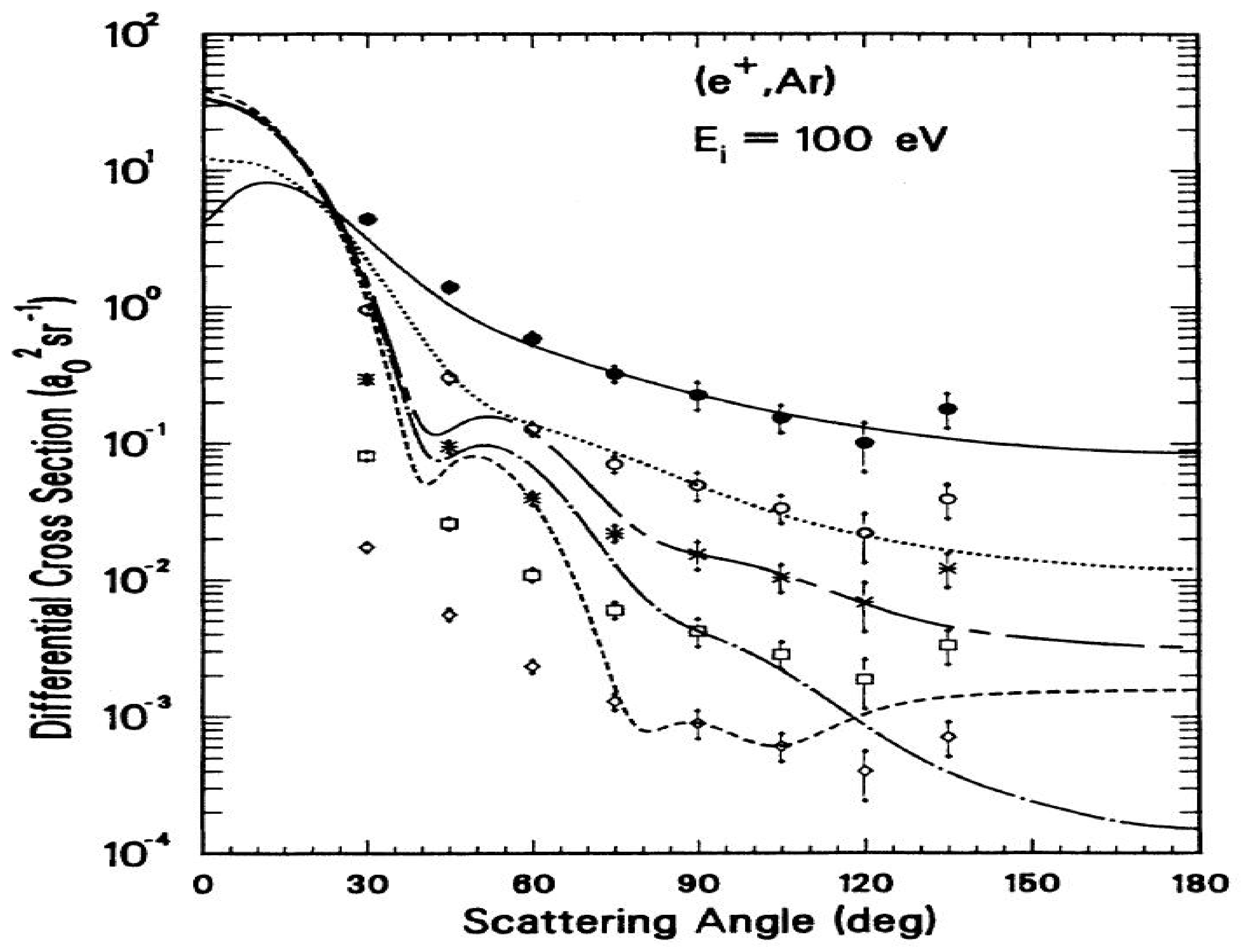
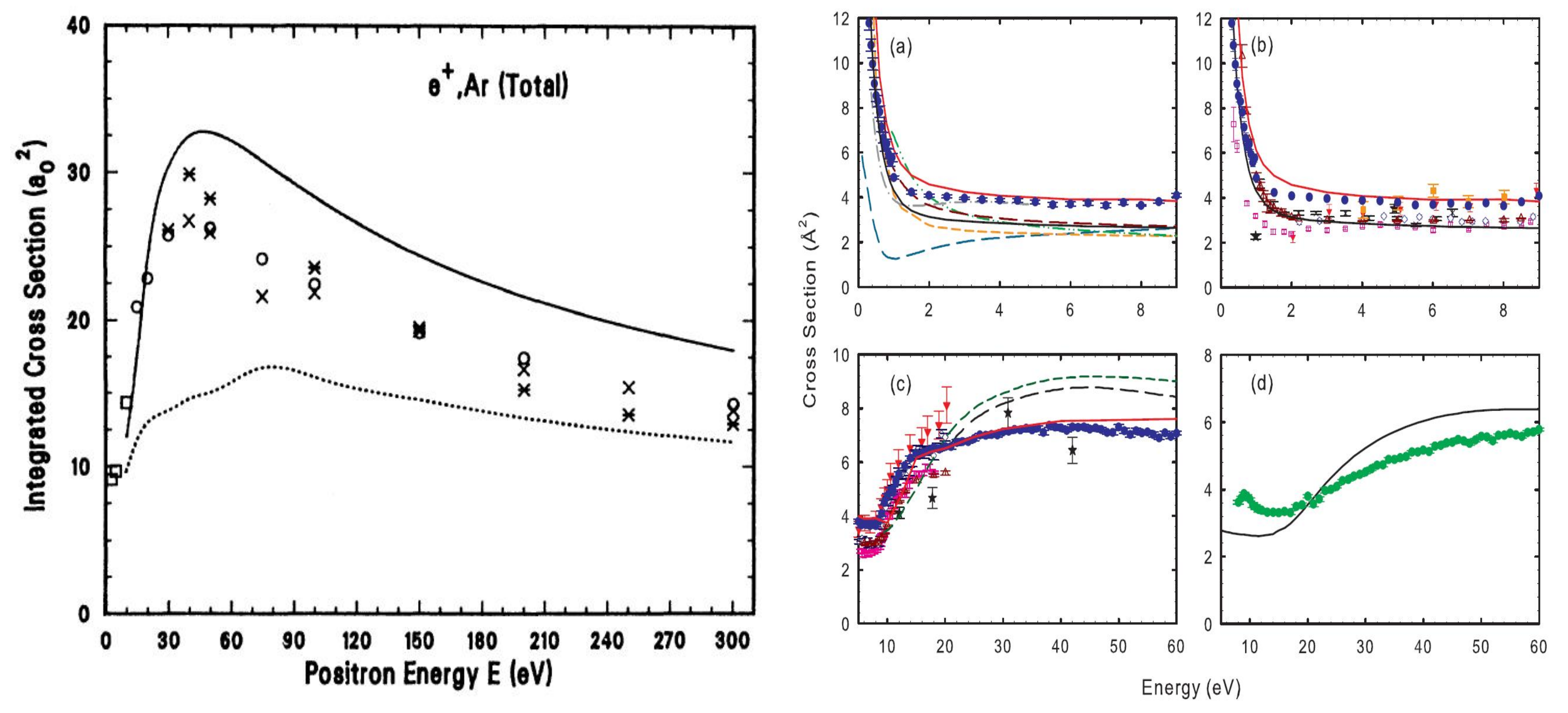
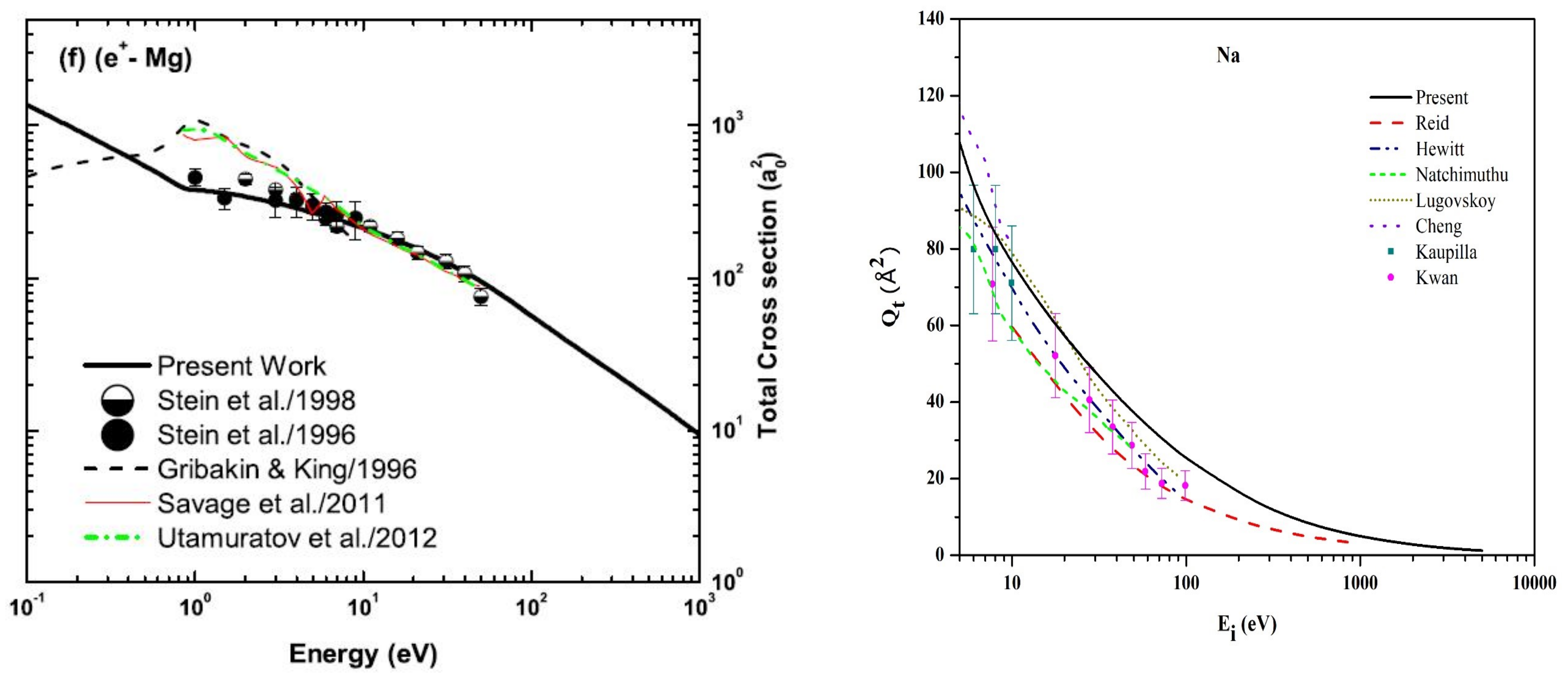
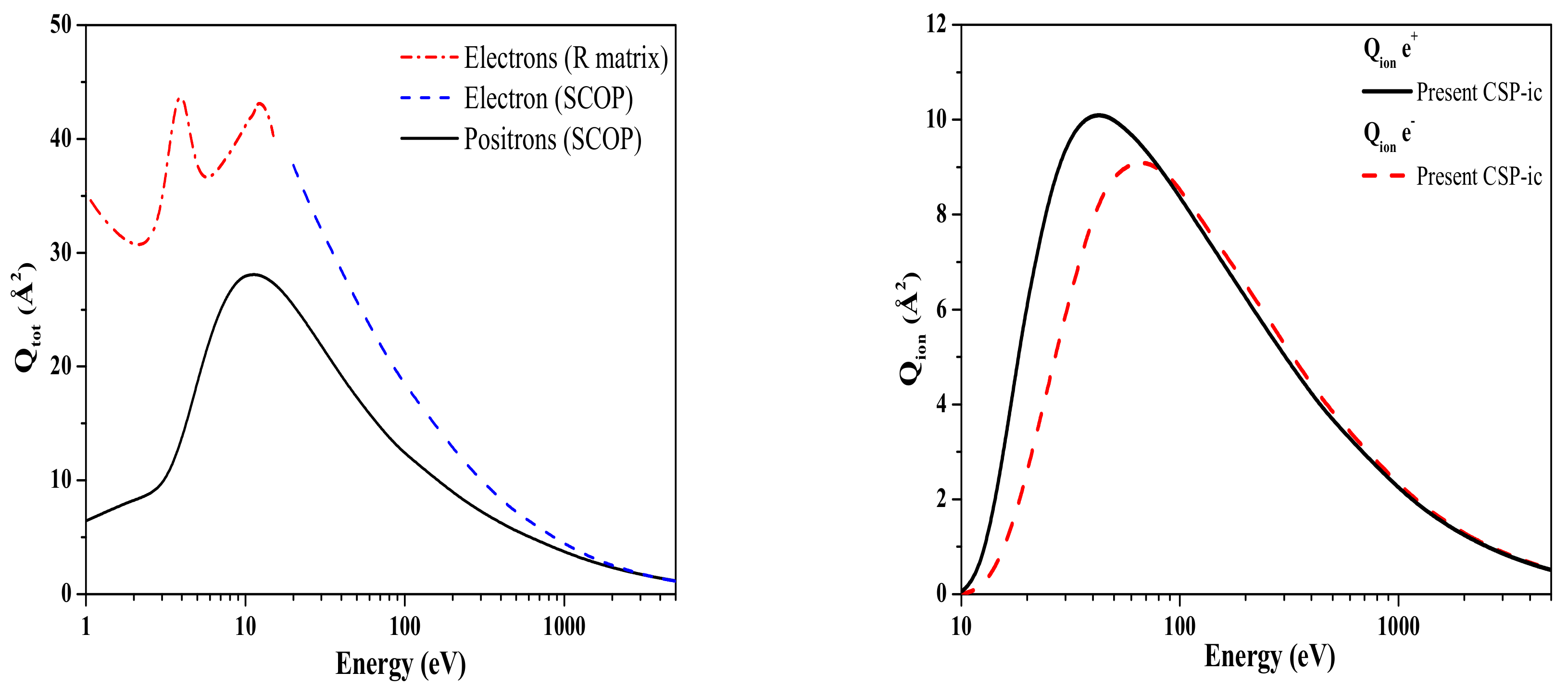
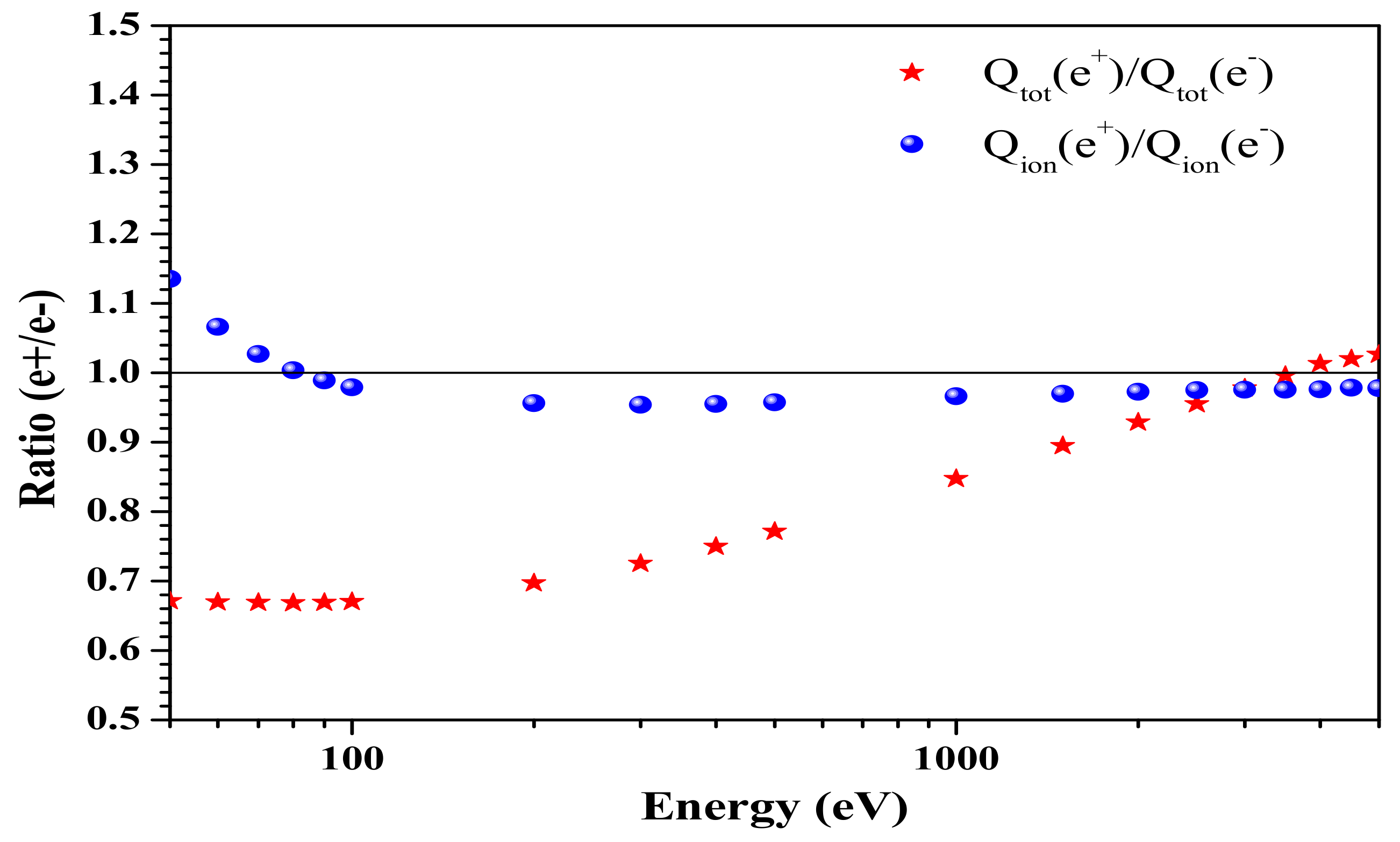
5.1. Cross Sections and Spin Polarization for Scattering from Atoms
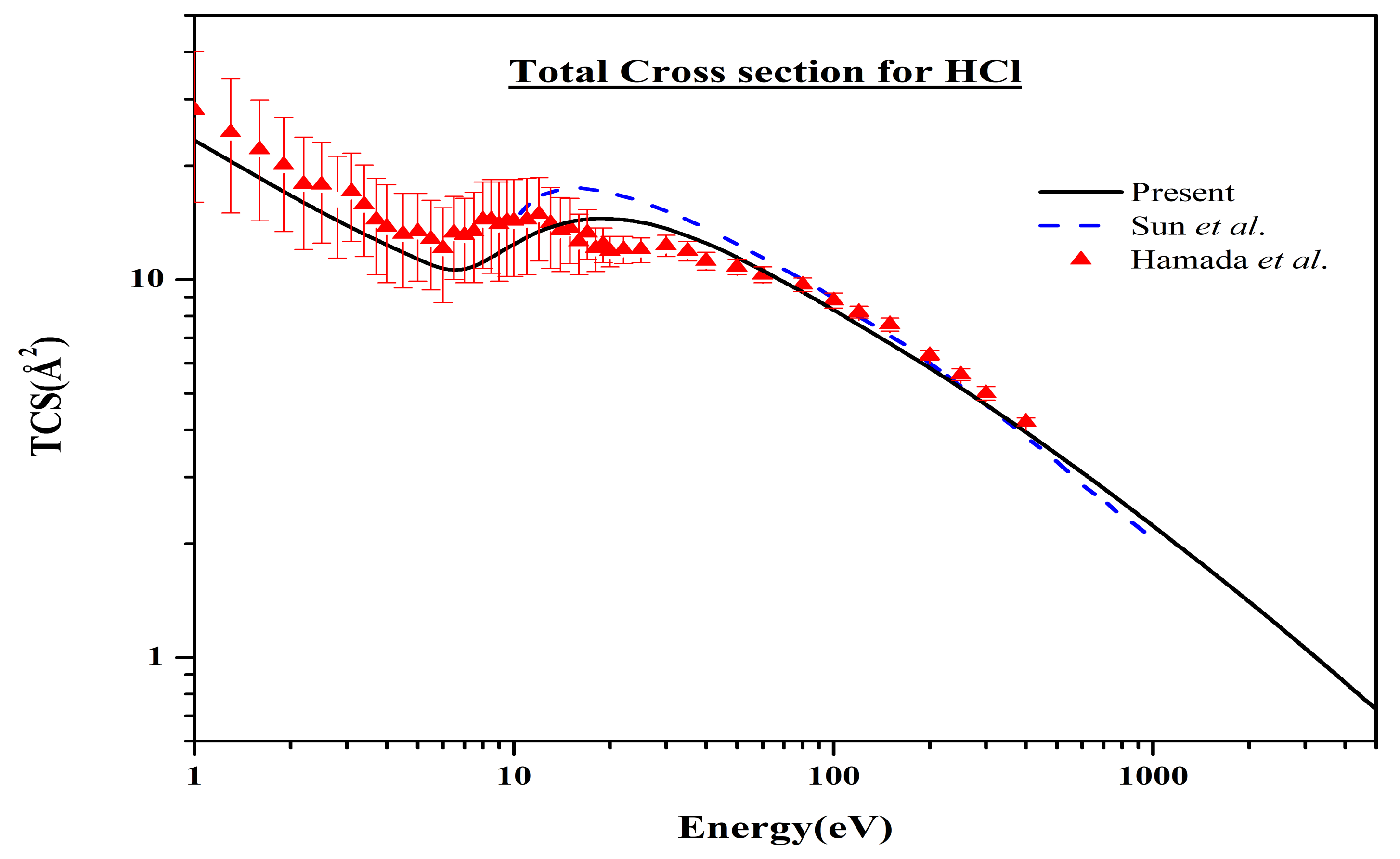
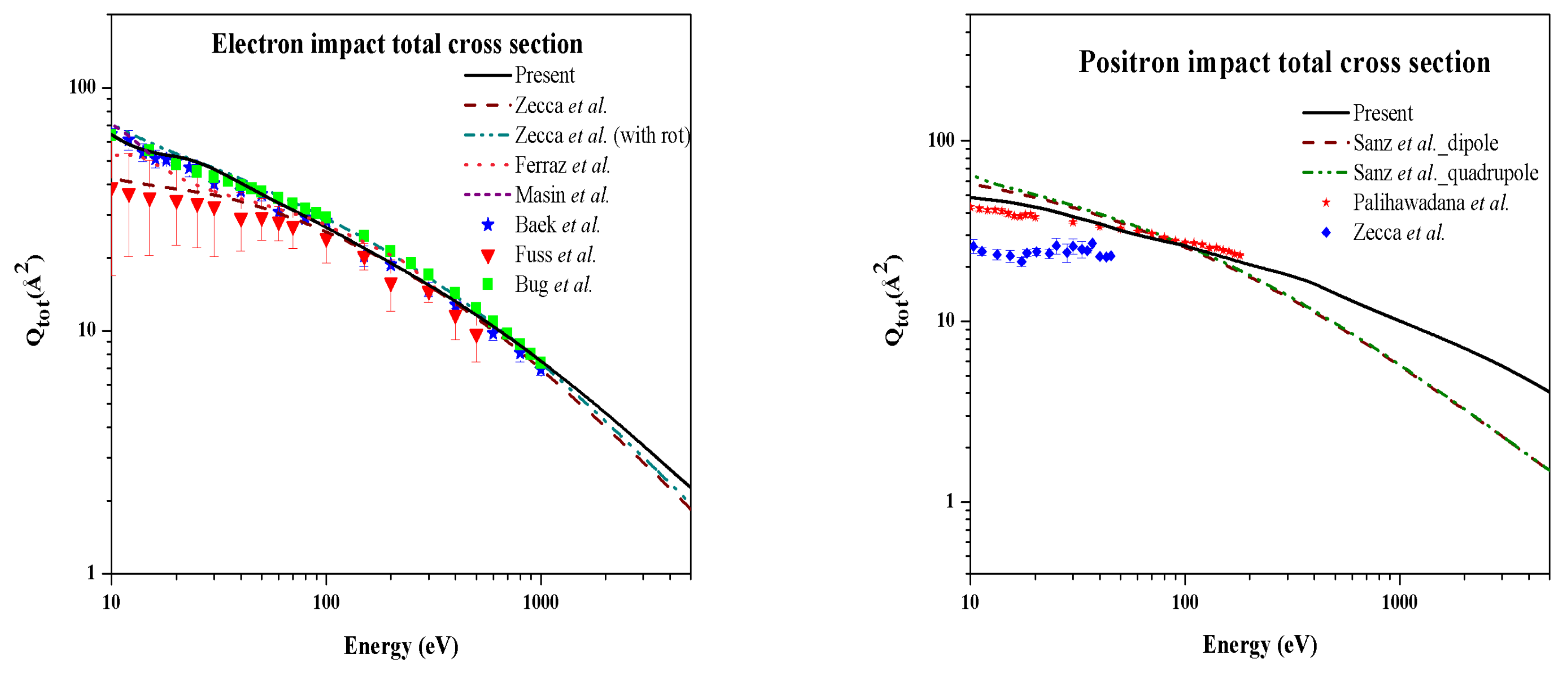
5.2. Scattering from Molecules
6. Conclusions
- Current theoretical methods for electron scattering from inert atoms are well established. However, their predictions for spin polarization may provide a measure of their effective representation.
- Current theoretical method for elastic scattering of positrons from inert gases, single and double electrons systems and molecules have also been developed well, but further studies are needed.
- There is a critical need for improved absorption potential for positron scattering from atoms and molecules.
- Further study is needed to expand the scope for scattering from ions that are abundant in astrophysical plasmas.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nahar, S.N.; Wadehra, J.M. Elastic scattering of positrons and electrons by argon. Phys. Rev. A 1987, 35, 2051–2064. [Google Scholar] [CrossRef]
- Temkin, A. Polarization and Exchange Effects in the Scattering of Electrons from Atoms with Application to Oxygen. Phys. Rev. A 1957, 107, 1004–1012. [Google Scholar] [CrossRef]
- Temkin, A. A Note on the Scattering of Electrons from Atomic Hydrogen. Phys. Rev. A 1959, 116, 358–363. [Google Scholar] [CrossRef]
- McEachran, R.P.; Morgan, D.L.; Ryman, A.G.; Stauffer, A.D. Positron scattering from noble gases. J. Phys. B 1977, 10, 663–677. [Google Scholar] [CrossRef]
- Dasgupta, A.; Bhatia, A.K. Scattering of electrons from argon atoms. Phys. Rev. A 1985, 32, 3335–3343. [Google Scholar] [CrossRef]
- Drachman, R.J. Theory of low energy positrion-helium. Phys. Rev. 1966, 144, 25. [Google Scholar] [CrossRef]
- Campeanu, P.I.; Humberston, J.W. The scattering of p-wave positrons by helium. J. Phys. B 1975, 8, L244. [Google Scholar] [CrossRef]
- Nahar, S.N. Cross sections and spin polarization of e± scattering from cadmium. Phys. Rev. A 1991, 43, 2223–2236. [Google Scholar] [CrossRef]
- Nahar, S.N.; Wadehra, J.M. Relativistic approach for e± scattering from argon. Phys. Rev. A 1991, 53, 1275–1289. [Google Scholar] [CrossRef]
- Hossain, M.I.; Haque, A.K.F.; Patoary, M.A.R.; Uddin, M.A.; Basak, A.K. Elastic scattering of electrons and positrons by atomic magnesium. Eur. Phys. J. D 2016, 70, 41. [Google Scholar] [CrossRef]
- Singh, S.; Naghma, R.; Kaur, J.; Antony, B. Study of elastic and inelastic cross sections by positron impact on inert gases. Eur. Phys. J. D 2018, 72, 69. [Google Scholar] [CrossRef]
- Sinha, N.; Singh, S.; Antony, B. Positron total scattering cross-sections for alkali atoms. J. Phys. B Atomic Mol. Phys. 2018, 51, 015204. [Google Scholar] [CrossRef]
- Reid, D.D.; Wadehra, J.M. Intermediate- to high-energy positrons scattered by alkali-metal atoms. Phys. Rev. A 1998, 57, 4. [Google Scholar] [CrossRef]
- Hewitt, R.N.; Noble, C.J.; Bransden, B.H. Positron collisions with alkali atoms at low and intermediate energies. J. Phys. B Atomic Mol. Opt. Phys. 1993, 26, 3661–3677. [Google Scholar] [CrossRef]
- Lugovskoy, A.V.; Kadyrov, A.S.; Bray, I.; Stelbovics, A.T. Two-center convergent-close-coupling calculations for positron-sodium collisions. Phys. Rev. A 2012, 85, 034701. [Google Scholar] [CrossRef]
- Cheng, Y.-J.; Zhou, Y.-J.; Jiao, L.-G. Total cross sections of positron sodium scattering at low energies. Chin. Phys. B 2012, 21, 013405. [Google Scholar] [CrossRef]
- Canter, K.F.; Coleman, P.G.; Griffith, T.C.; Heyland, G.R. The measurement of total cross sections for positrons of energies 2–400 eV in He, Ne, Ar, and Kr. J. Phys. B Atomic Mol. Phys. 1973, 6, L201–L203. [Google Scholar] [CrossRef]
- Williams, J.F.; Willis, B.A. The scattering of electrons from inert gases. I. Absolute differential elastic cross sections for argon atoms. J. Phys. B. 1975, 8, 1670. [Google Scholar] [CrossRef]
- Bromberg, J.P. Absolute differential cross sections of electrons elastically scattered by the rare gases. I. Small angle scattering between 200 and 700 eV. J. Chem. Phys. 1974, 61, 963. [Google Scholar] [CrossRef]
- Gupta, S.C.; Rees, J.A. Absolute differential cross sections for 100 eV electrons elastically scattered by helium, neon, and argon. J. Phys. B 1975, 8, 1267. [Google Scholar] [CrossRef]
- Kauppila, W.E.; Stein, T.S.; Jesion, G. Direct Observation of a Ramsauer-Townsend Effect in Positron-Argon Collisions. Phys. Rev. Lett. 1976, 36, 580. [Google Scholar] [CrossRef]
- Dubois, R.D.; Rudd, M.E. Differential cross sections for elastic scattering of electrons from argon, neon, nitrogen and carbon monoxide. J. Phys. B 1976, 9, 2657. [Google Scholar] [CrossRef]
- Vuskovic, L.; Kurepa, M.V. Differential cross sections of 60–150 eV electrons elastically scattered in argon. J. Phys. B 1976, 9, 837. [Google Scholar] [CrossRef]
- Jansen, R.H.J.; de Heer, F.J.; Luyken, H.J.; van Wingerden, B.; Blaauw, H.J. Absolute differential cross sections for elastic scattering of electrons by helium, neon, argon and molecular nitrogen. J. Phys. B 1976, 9, 185. [Google Scholar] [CrossRef]
- Kauppila, W.E.; Stein, T.S.; Smart, J.H.; Dababneh, M.S.; Ho, Y.K.; Downing, J.P.; Pol, V. Measurements of total scattering cross sections for intermediate-energy positrons and electrons colliding with helium, neon, and argon. Phys. Rev. A 1981, 24, 725–742. [Google Scholar] [CrossRef]
- Jones, A.C.L.; Makochekanwa, C.; Caradonna, P.; Slaughter, D.S.; Machacek, J.R.; McEachran, R.P.; Sullivan, J.P.; Buckman, S.J.; Stauffer, A.D.; Bray, I.; et al. Positron scattering from neon and argon. Phys. Rev. A 2011, 83, 032701. [Google Scholar] [CrossRef]
- Hyder, G.M.A.; Dababneh, M.S.; Hsieh, Y.-F.; Kauppila, W.E.; Kwan, C.K.; Mahdavi-Hezaveh, M.; Stein, T.S. Positron Differential Elastic-Scattering Cross-Section Measurements for Argon. Phys. Rev. Lett. 1986, 57, 2252. [Google Scholar] [CrossRef]
- Griffith, T.C.; Heyland, G.R. Experimental aspects of the study of the interaction of low-energy positrons with gases. Phys. Rep 1978, 39C, 169–277. [Google Scholar] [CrossRef]
- Tsai, J.-S.; Lebnow, L.; Paul, D.A.L. Measurement of total cross sections (e+, Ne) and (e+, Ar). Can. J. Phys. 1976, 54, 1741. [Google Scholar] [CrossRef]
- Kauppila, W.E.; Kwan, C.K.; Stein, T.S.; Zhou, S. i Evidence for channel-coupling effects in positron scattering by sodium and potassium atoms. J. Phys. B Atomic Mol. Opt. Phys. 1994, 27, L551–L555. [Google Scholar] [CrossRef]
- Kwan, C.K.; Kauppila, W.E.; Lukaszew, R.A.; Parikh, S.P.; Stein, T.S.; Wan, Y.J.; Dababneh, M.S. Total crosssection measurements for positrons and electrons scattered by sodium and potassium atoms. Phys. Rev. 1991, 44, 1620. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.S.; Jiang, J.; Kauppila, W.E.; Kwan, C.K.; Li, H.; Surdutovich, A.; Zhou, S. Measurements of total and (or) positronium-formation cross sections for positrons scattered by alkali, magnesium, and hydrogen atoms. Can. J. Phys. 1996, 74, 313–333. [Google Scholar] [CrossRef]
- Stein, T.; Harte, M.; Jiang, J.; Kauppila, W.; Kwan, C.; Li, H.; Zhou, S. Measurements of positron scattering by hydrogen, alkali metal, and other atoms. Nucl. Instr. Meth. Phys. Res. B 1998, 143, 68–80. [Google Scholar] [CrossRef]
- Ferch, J.; Granitza, B.; Masche, C.; Raith, W. Electron-argon total cross section measurements at low energies by time-of-flight spectroscopy. J. Phys. B 1985, 18, 967. [Google Scholar] [CrossRef]
- Williams, J.F. A phaseshift analysis of experimental angular distributions of electrons elastically scattered from He, Ne and Ar over the range 0.5 to 20 eV. J. Phys. B 1979, 12, 265. [Google Scholar] [CrossRef]
- Charlton, M.; Grifith, T.C.; Heyland, G.R.; Twomey, T.R. Total scattering cross sections for low-energy electrons in helium and argon. J. Phys. B 1980, 13, L239. [Google Scholar] [CrossRef]
- Jost, K.; Bisling, P.G.F.; Eschen, F.; Felsmann, M.; Walther, L. Abstracts of Contributed Papers. In Proceedings of the Thirteenth International Conference on the Physics of Electronic and Atomic Collisions, Berlin, Germany, 27 July–2 August 1983; Eichler, J., Fritsch, W., Hertel, I.V., Stolterfoin, N., Wille, W., Eds.; North-Holland: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Wagenaar, R.W.; de Heer, F.J. Total cross sections for electron scattering from Ar, Kr and Xe. J. Phys. B 1985, 18, 2021. [Google Scholar] [CrossRef]
- Nicket, J.C.; Imre, K.; Register, D.F.; Trajmar, S. Total electron scattering cross sections. I. He, Ne, Ar, Xe. J. Phys. B 1985, 18, 125. [Google Scholar] [CrossRef]
- Mehr, J. Winkelverteilungen elastisch an Edelgas-Atomstrahlen gestreuter Elektronen; Spinpolarisation eines an Argon gestreuten 40 eV-Elektronenstrahls. Z. Phys. 1967, 198, 345. [Google Scholar] [CrossRef]
- Beerlage, M.J.M.; Qing, Z.; Van der Wiel, M.J. The polarisation of electrons elastically scattered from argon and krypton at energies between 10 and 50 eV. J. Phys. B 1981, 14, 4627. [Google Scholar] [CrossRef]
- Schackert, K. Spin polarization of slow electrons elastically scattered by noble gas atomic beams. Z. Phys. 1968, 213, 316. [Google Scholar] [CrossRef]
- Ajmera, M.P.; Chung, K.T. Simplified variational method for P-wave electron-hydrogen scattering. Phys. Rev. A 1974, 10, 1013. [Google Scholar] [CrossRef]
- Drachman, R.J. Positron-Hydrogen Scattering at Low Energies. Phys. Rev. 1965, 138, A1582. [Google Scholar] [CrossRef]
- Bhatia, A.K. Positron Impact Excitation of the 2S State of Atomic Hydrogen. Atoms 2019, 7, 69. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of P-wave electron-Li2+ elastic scattering and photoabsorption in two-electron systems. Phys. Rev. A 1983, 87, 042705. [Google Scholar] [CrossRef]
- Bhatia, A.K. 2006 Electron-wave elastic scattering and photoabsorption in two-electron systems. Phys. Rev. A 2007, 73, 012705. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of electron-hydrogen elastic scattering. Phys. Rev. A 2007, 75, 032713. [Google Scholar] [CrossRef]
- Joshipura, K.N.; Vinodkumar, M.; Limbachiya, C.G.; Antony, B.K. Calculated total cross sections of electron-impact ionization and excitations in tetrahedral (XY4) and SF6 molecules. Phys. Rev. A 2004, 69, 022705. [Google Scholar] [CrossRef]
- Sinha, N.; Patel, D.; Antony, B. Positron Scattering: Total Elastic and Grand Total Cross Sections for Molecules of Astrophysical Importance. ChemistrySelect 2019, 4, 4575–4581. [Google Scholar] [CrossRef]
- Sloan, I.H. The method of polarized orbitals for the elastic scattering of slow electrons by ionized helium and atomic hydrogen. Proc. R. Soc. Lond. 1964, 281, 151–163. [Google Scholar]
- Zhou, Y.; Ratnavelu, K.; McCarthy, I.E. Momentum-space coupled-channel optical method for positron-hydrogen scattering. Phys. Rev. A 2005, 71, 042703. [Google Scholar] [CrossRef]
- Dalgarno, A. Perturbation theory for atomic systems. Proc. R. Soc. A 1959, 251, 282–290. [Google Scholar] [CrossRef]
- Kaneko, S. Electrical Polarizabilities of Rare Gas Atoms by the Hartree-Fock Wave Functions. J. Phys. Soc. Jpn. 1959, 14, 1600–1611. [Google Scholar] [CrossRef]
- McEachran, R.P.; Stauffer, A.D. Positron scattering from helium. J. Phys. B Atomic Mol. Opt. Phys. 2019, 52, 115203. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions. II. Ann. Phys 1962, 19, 287. [Google Scholar] [CrossRef]
- Brown, C.J.; Humberston, J.W. Positronium formation in positron-hydrogen scattering. J. Phys. B Atomic Mol. Opt. Phys. 1985, 18, L401. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Gribakin, G.F.; King, W.A. Many-body calculations of positron scattering and annihilation from noble-gas atoms. J. Phys. B Atomic Mol. Opt. Phys. 1996, 29, 3151. [Google Scholar] [CrossRef][Green Version]
- Green, D.G.; Ludlow, J.A.; Gribakin, G.F. Positron scattering and annihilation on noble-gas atoms. Phys. Rev. A 2014, 90, 032712. [Google Scholar] [CrossRef]
- Germano, J.S.E.; Lima, M.A.P. Schwinger multichannel method for positron-molecule scattering. Phys. Rev. A 1993, 47, 3976. [Google Scholar] [CrossRef]
- Arretche, F.; da Costa, R.F.; Sanchez, S.D.A.; Hisi, A.N.S.; De Oliveira, E.M.; Varella, M.D.N.; Lima, M.A.P. Similarities and differences in e±–molecule scattering: Applications of the Schwinger multichannel method. Nucl. Instrum. Methods Phys. Res. B 2006, 247, 13–19. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Bettega, M.H. Calculated cross sections for elastic scattering of slow positrons by silane. Phys. Rev. A 2017, 96, 042715. [Google Scholar] [CrossRef]
- Higgins, K.; Burke, P.G.; Walters, H.R. Positron scattering by atomic hydrogen at intermediate energies. J. Phys. B Atomic Mol. Opt. Phys. 1990, 23, 1345. [Google Scholar] [CrossRef]
- Scholz, T.; Scott, P.; Burke, P.G. Electron-hydrogen-atom scattering at intermediate energies. J. Phys. B 1988, 21, L139–L145. [Google Scholar] [CrossRef]
- Grant, I.P.; McKenzie, B.J.; Norrington, P.H.; Mayers, D.F.; Pyper, N.C. An atomic multiconfigurational Dirac-Fock package. Comput. Phys. Commun. 1980, 21, 207–231. [Google Scholar] [CrossRef]
- McAlinden, M.T.; Kernoghan, A.A.; Walters, H.R.J. Cross-channel coupling in positron-atom scattering. Hyperfine Interact. 1994, 89, 161–194. [Google Scholar] [CrossRef]
- Mukherjee, T.; Mukherjee, M. Low-energy positron–nitrogen-molecule scattering: A rovibrational close-coupling study. Phys. Rev. A 2015, 91, 062706. [Google Scholar] [CrossRef]
- Jain, A.; Baluja, K.L. Total (elastic plus inelastic) cross sections for electron scattering from diatomic and polyatomic molecules at 10–5000 eV: H2, Li2, HF, CH4, N2, CO, C2H2, HCN, O2, HCl, H2S, PH3, SiH4, and CO2. Phys. Rev. A 1992, 45, 202–218. [Google Scholar] [CrossRef]
- Gao, J.; Peacher, J.L.; Madison, D.H. An elementary method for calculating orientation-averaged fully differential electron-impact ionization cross sections for molecules. J. Chem. Phys. 2005, 123, 204302. [Google Scholar] [CrossRef]
- Madison, D.H.; Al-Hagan, O. The distorted-wave Born approach for calculating electron-impact ionization of molecules. J. Atom. Mol. Opt. Phys. 2010, 2010, 367180. [Google Scholar] [CrossRef]
- Singh, S.; Dutta, S.; Naghma, R.; Antony, B. Theoretical formalism to estimate the positron scattering cross section. J. Phys. Chem. A 2016, 120, 5685–5692. [Google Scholar] [CrossRef]
- Raizada, R.; Baluja, K.L. Total cross sections of positron scattering from various molecules using the rule of additivity. Phys. Rev. A 1997, 55, 1533–1536. [Google Scholar] [CrossRef]
- Morrison, M.A.; Gibson, T.L.; Austin, D. Polarisation potentials for positron-molecule collisions: Positron-H2 scattering. J. Phys. B Atomic Mol. Opt. Phys. 1984, 17, 2725. [Google Scholar] [CrossRef]
- Raj, D. Total cross sections for positron scattering by molecules. Phys. Lett. A 1993, 174, 304–307. [Google Scholar] [CrossRef]
- Khandker, M.H.; Arony, N.T.; Haque, A.K.F.; Maaza, M.; Billah, M.M.; Uddin, M.A. Scattering of e± from N2 in the energy range 1 eV–10 keV. Mol. Phys. 2019, 1–15. [Google Scholar] [CrossRef]
- Horbatsch, M.; Darewych, J.W. Model potential description of low-energy e+-CO2 scattering. J. Phys. B Atomic Mol. Opt. Phys. 1983, 16, 4059. [Google Scholar] [CrossRef]
- Raj, D.; Tomar, S. Scattering of positrons by hydrocarbons at intermediate energies. Indian J. Phys 1996, 70B, 375–383. [Google Scholar]
- Blanco, F.; Ellis-Gibbings, L.; García, G. Screening corrections for the interference contributions to the electron and positron scattering cross sections from polyatomic molecules. Chem. Phys. Lett. 2016, 645, 71–75. [Google Scholar] [CrossRef]
- Srivastava, M.K.; Pathak, A. Total scattering cross sections for intermediate-and high-energy positrons in H2. J. Phys. B Atomic Mol. Opt. Phys. 1981, 14, L579. [Google Scholar] [CrossRef]
- Ellis-Gibbings, L.; Blanco, F.; García, G. Positron interactions with nitrogen and oxygen molecules: Elastic, inelastic and total cross sections. Eur. Phys. J. D 2019, 73, 266. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Girardi, S.; Trainotti, E.; Garcia, G.; Blanco, F.; McEachran, R.P.; Brunger, M.J. Positron scattering from O2. J. Phys. B Atomic Mol. Opt. Phys. 2012, 45, 215206. [Google Scholar] [CrossRef]
- Blanco, F.; Roldán, A.M.; Krupa, K.; McEachran, R.P.; White, R.D.; Marjanović, S.; Petrović, Z.L.; Brunger, M.J.; Machacek, J.R.; Buckman, S.J.; et al. Scattering data for modelling positron tracks in gaseous and liquid water. J. Phys. B Atomic Mol. Opt. Phys. 2016, 49, 145001. [Google Scholar] [CrossRef]
- Tattersall, W.; Chiari, L.; Machacek, J.R.; Erson, E.; White, R.D.; Brunger, M.J.; Buckman, S.J.; Garcia, G.; Blanco, F.; Sullivan, J.P. Positron interactions with water–total elastic, total inelastic, and elastic differential cross section measurements. J. Chem. Phys. 2014, 140, 044320. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Trainotti, E.; Garcia, G.; Blanco, F.; Bettega, M.H.; Sanchez, S.D.A.; Varella, M.T.D.N.; Lima, M.A.; Brunger, M.J. Positron and electron collisions with nitrous oxide: Measured and calculated cross sections. Phys. Rev. A 2013, 88, 022708. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; García, G.; Blanco, F.; Brunger, M.J. Low-energy positron and electron scattering from nitrogen dioxide. J. Phys. B Atomic Mol. Opt. Phys. 2013, 46, 235202. [Google Scholar] [CrossRef]
- Zecca, A.; Trainotti, E.; Chiari, L.; García, G.; Blanco, F.; Bettega, M.H.F.; do N Varella, M.T.; Lima, M.A.P.; Brunger, M.J. An experimental and theoretical investigation into positron and electron scattering from formaldehyde. J. Phys. B Atomic Mol. Opt. Phys. 2011, 44, 195202. [Google Scholar] [CrossRef]
- Chiari, L.; Palihawadana, P.; Machacek, J.R.; Makochekanwa, C.; García, G.; Blanco, F.; McEachran, R.P.; Brunger, M.J.; Buckman, S.J.; Sullivan, J.P. Experimental and theoretical cross sections for positron collisions with 3-hydroxy-tetrahydrofuran. J. Chem. Phys. 2013, 138, 074302. [Google Scholar] [CrossRef] [PubMed]
- Chiari, L.; Zecca, A.; Blanco, F.; García, G.; Brunger, M.J. Cross sections for positron and electron collisions with an analog of the purine nucleobases: Indole. Phys. Rev. A 91, 012711. [CrossRef]
- Anderson, E.K.; Boadle, R.A.; Machacek, J.R.; Chiari, L.; Makochekanwa, C.; Buckman, S.J.; Brunger, M.J.; Garcia, G.; Blanco, F.; Ingolfsson, O.; et al. Low energy positron interactions with uracil—Total scattering, positronium formation, and differential elastic scattering cross sections. J. Chem. Phys. 2014, 141, 034306. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Blanco, F.; García, G.; Brunger, M.J. Experimental and theoretical cross sections for positron scattering from the pentane isomers. J. Chem. Phys. 2016, 144, 084301. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Blanco, F.; García, G.; Perkins, M.V.; Buckman, S.J.; Brunger, M.J. Cross sections for positron impact with 2, 2, 4-trimethylpentane. J. Phys. Chem. A 2014, 118, 6466–6472. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Blanco, F.; García, G.; Brunger, M.J. Positron scattering from vinyl acetate. J. Phys. B Atomic Mol. Opt. Phys. 2014, 47, 175202. [Google Scholar] [CrossRef]
- Sanz, A.G.; Fuss, M.C.; Blanco, F.; Mašín, Z.; Gorfinkiel, J.D.; McEachran, R.P.; Brunger, M.J.; García, G. Cross-section calculations for positron scattering from pyrimidine over an energy range from 0.1 to 10000 eV. Phys. Rev. A 2013, 88, 062704. [Google Scholar] [CrossRef]
- Zecca, A.; Chiari, L.; García, G.; Blanco, F.; Trainotti, E.; Brunger, M.J. Total cross sections for positron and electron scattering from pyrimidine. J. Phys. B Atomic Mol. Opt. Phys. 2010, 43, 215204. [Google Scholar] [CrossRef]
- Stevens, D.; Babij, T.J.; Machacek, J.R.; Buckman, S.J.; Brunger, M.J.; White, R.D.; García, G.; Blanco, F.; Ellis-Gibbings, L.; Sullivan, J.P. Positron scattering from pyridine. J. Chem. Phys. 2018, 148, 144308. [Google Scholar] [CrossRef] [PubMed]
- Zecca, A.; Trainotti, E.; Chiari, L.; Bettega, M.H.F.; Sanchez, S.D.A.; Varella, M.D.N.; Lima, M.A.P.; Brunger, M.J. Positron scattering from the cyclic ethers oxirane, 1, 4-dioxane, and tetrahydropyran. J. Chem. Phys. 2012, 136, 124305. [Google Scholar] [CrossRef] [PubMed]
- Zecca, A.; Chiari, L.; García, G.; Blanco, F.; Trainotti, E.; Brunger, M.J. Total cross-sections for positron and electron scattering from α-tetrahydrofurfuryl alcohol. New J. Phys. 2011, 13, 063019. [Google Scholar] [CrossRef]
- Humberston, J.W.; Van Reeth, P.; Watts, M.S.T.; Meyerhof, W.E. Positron-hydrogen scattering in the vicinity of the positronium formation threshold. J. Phys. B Atomic Mol. Opt. Phys. 1997, 30, 2477. [Google Scholar] [CrossRef]
- Van Reeth, P.; Humberston, J.W. Theoretical studies of threshold features in the cross-sections for low-energy e+–H and e+–He scattering. Nucl. Instrum. Methods Phys. Res. B 2000, 171, 106–112. [Google Scholar] [CrossRef]
- Armour, E.A.G.; Baker, D.J.; Plummer, M. The theoretical treatment of low-energy e+-H2 scattering using the kohn variational method. J. Phys. B Atomic Mol. Opt. Phys. 1990, 23, 3057. [Google Scholar] [CrossRef]
- Weiss, L.I.; Pinho, A.S.; Michelin, S.E.; Fujimoto, M.M. Electronic excitation cross section in positron scattering by H2 molecules using distorted-wave method. Eur. Phys. J. D 2018, 72, 35. [Google Scholar] [CrossRef]
- Basu, M.; Mazumdar, P.S.; Ghosh, A.S. Ionisation cross sections in positron-helium scattering. J. Phys. B Atomic Mol. Opt. Phys. 1985, 18, 369. [Google Scholar] [CrossRef]
- Parcell, L.A.; McEachran, R.P.; Stauffer, A.D. Positron excitation of the 21S state of helium. J. Phys. B Atomic Mol. Opt. Phys. 1983, 16, 4249. [Google Scholar] [CrossRef]
- Khan, P.; Ghosh, A.S. Positronium formation in positron-helium scattering. Phys. Rev. A 1983, 28, 2181–2189. [Google Scholar] [CrossRef]
- Parcell, L.A.; McEachran, R.P.; Stauffer, A.D. Positron scattering from neon. Nucl. Instrum. Methods Phys. Res. B 1998, 143, 37–40. [Google Scholar] [CrossRef]
- Parcell, L.A.; McEachran, R.P.; Stauffer, A.D. Positron scattering from argon and krypton. Nucl. Instrum. Methods Phys. Res. B 2000, 171, 113–118. [Google Scholar] [CrossRef]
- Gribakin, G.F.; Ludlow, J. Many-body theory of positron-atom interactions. Phys. Rev. A 2004, 70, 032720. [Google Scholar] [CrossRef]
- Gribakin, G.F.; King, W.A. Positron scattering from Mg atoms. Can. J. Phys. 1996, 74, 449–459. [Google Scholar] [CrossRef]
- Meyerhof, W.E.; Laricchia, G.; Moxom, J.; Humberston, J.W.; Watts, M.S.T. Positron scattering on atoms and molecules near the positronium threshold. Can. J. Phys. 1996, 74, 427–433. [Google Scholar] [CrossRef]
- Bartschat, K. Direct ionization of heavy noble gases by positron impact. Phys. Rev. A 2005, 71, 032718. [Google Scholar] [CrossRef]
- Moxom, J.; Laricchia, G.; Charlton, M.; Kovar, A.; Meyerhof, W.E. Threshold effects in positron scattering on noble gases. Phys. Rev. A 1994, 50, 3129–3133. [Google Scholar] [CrossRef]
- Danby, G.; Tennyson, J. Positron-HF collisions: Prediction of a weakly bound state. Phys. Rev. Lett. 1988, 61, 2737. [Google Scholar] [CrossRef] [PubMed]
- Tennyson, J. Low-energy, elastic positron-molecule collisions using the R-matrix method: e+-He2 and e+-N2. J. Phys. B Atomic Mol. Opt. Phys. 1986, 19, 4255. [Google Scholar] [CrossRef]
- Danby, G.; Tennyson, J. Differential cross sections for elastic positron-H2 collisions using the R-matrix method. J. Phys. B Atomic Mol. Opt. Phys. 1990, 23, 1005. [Google Scholar] [CrossRef]
- Zhang, R.; Baluja, K.L.; Franz, J.; Tennyson, J. Positron collisions with molecular hydrogen: Cross sections and annihilation parameters calculated using the R-matrix with pseudo-states method. J. Phys. B Atomic Mol. Opt. Phys. 2011, 44, 035203. [Google Scholar] [CrossRef]
- Baluja, K.L.; Zhang, R.; Franz, J.; Tennyson, J. Low-energy positron collisions with water: Elastic and rotationally inelastic scattering. J. Phys. B Atomic Mol. Opt. Phys. 2007, 40, 3515. [Google Scholar] [CrossRef]
- Franz, J.; Baluja, K.L.; Zhang, R.; Tennyson, J. Polarisation effects in low-energy positron–molecule scattering. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 419–424. [Google Scholar] [CrossRef]
- Zhang, R.; Galiatsatos, P.G.; Tennyson, J. Positron collisions with acetylene calculated using the R-matrix with pseudo-states method. J. Phys. B Atomic Mol. Opt. Phys. 2011, 44, 195203. [Google Scholar] [CrossRef]
- Lino, J.L. Improving the wavefunction of the Schwinger multichannel method: Application for positron elastic scattering by He atom. Phys. Scr. 2007, 76, 521. [Google Scholar] [CrossRef]
- Sanchez, S.D.A.; Lima, M.A.P. The influence of f-type function in positron-He/positron-H2 scattering with the Schwinger multichannel method. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 447–451. [Google Scholar] [CrossRef]
- Zanin, G.L.; Tenfen, W.; Arretche, F. Rotational excitation of H 2 by positron impact in adiabatic rotational approximation. Eur. Phys. J. D 2016, 70, 179. [Google Scholar] [CrossRef]
- Varella, M.T.D.N.; Lima, M.A. Near-threshold vibrational excitation of H2 by positron impact: A projection-operator approach. Phys. Rev. A 2007, 76, 052701. [Google Scholar] [CrossRef]
- Lino, J.L. Improving the wavefunction of the Schwinger multichannel method for positron scattering—II: Application for elastic and inelastic e+-H2 scattering. Phys. Scr. 2009, 80, 065303. [Google Scholar] [CrossRef]
- Lino, J.L.; Germano, J.S.E.; Lima, M.A.P. Electronic excitation of H2 by positron impact: An application of the Schwinger multichannel method. J. Phys. B Atomic Mol. Opt. Phys. 1994, 27, 1881. [Google Scholar] [CrossRef][Green Version]
- Lino, J.L.S. Electronic excitation of H2, CO, and N2 by positron impact. Rev. Mex. Fis. 2017, 63, 303–307. [Google Scholar]
- Lino, J.L.; Germano, J.S.; da Silva, E.P.; Lima, M.A. Elastic cross sections and annihilation parameter for e+-H2 scattering using the Schwinger multichannel method. Phys. Rev. A 1998, 58, 3502. [Google Scholar] [CrossRef]
- Seidel, E.P.; Barp, M.V.; Tenfen, W.; Arretche, F. Elastic scattering and rotational excitation of Li2 by positron impact. J. Electron. Spectros. Relat. Phenomena 2018, 227, 9–14. [Google Scholar] [CrossRef]
- de Carvalho, C.R.; do N Varella, M.T.; Lima, M.A.; da Silva, E.P.; Germano, J.S. Progress with the Schwinger multichannel method in positron–molecule scattering. Nucl. Instrum. Methods Phys. Res. B 2000, 171, 33–46. [Google Scholar] [CrossRef]
- Mazon, K.T.; Tenfen, W.; Michelin, S.E.; Arretche, F.; Lee, M.T.; Fujimoto, M.M. Vibrational cross sections for positron scattering by nitrogen molecules. Phys. Rev. A 2010, 82, 032704. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Varella, M.T.D.N.; de Carvalho, C.R.; Lima, M.A. Electronic excitation of N2 by positron impact. Phys. Rev. A 2004, 69, 042703. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Varella, M.T.D.N.; de Carvalho, C.R.; Lima, M.A. Positron impact electronic excitation of N2. Nucl. Instrum. Methods Phys. Res. B 2004, 221, 69–75. [Google Scholar] [CrossRef]
- da Silva, E.P.; Varella, M.T.D.N.; Lima, M.A. Electronic excitation of CO by positron impact. Phys. Rev. A 2005, 72, 062715. [Google Scholar] [CrossRef]
- Sanchez, S.D.A.; Arretche, F.; do N Varella, M.T.; Lima, M.A.P. Low energy positron scattering by SF6 and CO2. Phys. Scr. 2004, T110, 276. [Google Scholar] [CrossRef]
- Sanchez, S.D.A.; Arretche, F.; Lima, M.A.P. Low-energy positron scattering by CO2. Phys. Rev. A 2008, 77, 054703. [Google Scholar] [CrossRef]
- Arretche, F.; Tenfen, W.; Mazon, K.T.; Michelin, S.E.; Lima, M.A.P.; Lee, M.T.; Machado, L.E.; Fujimoto, M.M.; Pessoa, O.A. Low energy scattering of positrons by H2O. Nucl. Instrum. Methods Phys. Res. B 2010, 268, 178–182. [Google Scholar] [CrossRef]
- Arretche, F.; Barp, M.V.; Seidel, E.P.; Tenfen, W. Electronic excitation of H2O by positron impact. Eur. Phys. J. D 2020, 74, 1–7. [Google Scholar] [CrossRef]
- Lino, J.L. Elastic scattering of positrons by H2O at low energies. Rev. Mex. Fis. 2014, 60, 156–160. [Google Scholar]
- Zecca, A.; Chiari, L.; Trainotti, E.; Sarkar, A.; Sanchez, S.D.A.; Bettega, M.H.F.; Varella, M.D.N.; Lima, M.A.P.; Brunger, M.J. Positron scattering from methane. Phys. Rev. A 2012, 85, 012707. [Google Scholar] [CrossRef]
- Zecca, A.; Chiari, L.; Sarkar, A.; Lima, M.A.; Bettega, M.H.; Nixon, K.L.; Brunger, M.J. Positron scattering from formic acid. Phys. Rev. A 2008, 78, 042707. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Blanco, F.; García, G.; Bettega, M.H. Theoretical study on positron scattering by benzene over a broad energy range. Phys. Rev. A 2019, 100, 042705. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Pastega, D.F.; Bettega, M.H. Low-energy positron scattering by pyrimidine. J. Chem. Phys. 2015, 143, 244316. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Sanchez, S.D.A.; Bettega, M.H. Bound state in positron scattering by allene. Phys. Rev. A 2017, 96, 062706. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Bettega, M.H. Elastic collisions of low-energy positrons with tetrahydrofuran. J. Chem. Phys. 2019, 150, 184305. [Google Scholar] [CrossRef] [PubMed]
- Bettega, M.H.; Sanchez, S.D.A.; Varella, M.T.D.N.; Lima, M.A.; Chiari, L.; Zecca, A.; Trainotti, E.; Brunger, M.J. Positron collisions with ethene. Phys. Rev. A 2012, 86, 022709. [Google Scholar] [CrossRef]
- de Carvalho, C.R.; Varella, M.T.D.N.; Lima, M.A.; da Silva, E.P. Elastic positron scattering by C2H2: Differential cross sections and virtual state formation. Phys. Rev. A 2003, 68, 062706. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Trainotti, E.; Bettega, M.H.F.; Sanchez, S.D.A.; Varella, M.D.N.; Lima, M.A.P.; Brunger, M.J. Cross sections for positron scattering from ethane. Phys. Rev. A 2013, 87, 032707. [Google Scholar] [CrossRef]
- Makochekanwa, C.; Kato, H.; Hoshino, M.; Bettega, M.H.F.; Lima, M.A.P.; Sueoka, O.; Tanaka, H. Electron and positron scattering from 1, 1-C2H2F2. J. Chem. Phys. 2007, 126, 164309. [Google Scholar] [CrossRef]
- Moreira, G.M.; Bettega, M.H. Elastic Scattering of Slow Positrons by Pyrazine. J. Phys. Chem. A 2019, 123, 9132–9136. [Google Scholar] [CrossRef]
- Moreira, G.M.; Bettega, M.H. Low-energy positron collisions with CH2O.......H2O complexes. Eur. Phys. J. D 2017, 71, 1–5. [Google Scholar] [CrossRef]
- Nunes, F.B.; Bettega, M.H.; Sanchez, S.D.A. Positron collisions with C3H6 isomers. J. Phys. B Atomic Mol. Opt. Phys. 2015, 48, 165201. [Google Scholar] [CrossRef]
- Nunes, F.B.; Bettega, M.H.; Sanchez, S.D.A. Positron and electron scattering by glycine and alanine: Shape resonances and methylation effect. J. Chem. Phys. 2016, 145, 214313. [Google Scholar] [CrossRef]
- da Silva, E.P.; Germano, J.S.; Lima, M.A. Annihilation Dynamics of Positrons in Molecular Environments: Theoretical Study of Low-Energy Positron-C2H4 Scattering. Phys. Rev. Lett. 1996, 77, 1028. [Google Scholar] [CrossRef]
- Silva, F.M.; Bettega, M.H.; Sanchez, S.D.A. Low-energy positron and electron scattering by methylamine. Eur. Phys. J. D 2014, 68, 12. [Google Scholar] [CrossRef]
- do N Varella, M.T.; Sanchez, S.D.A.; Bettega, M.H.; Lima, M.A.; Chiari, L.; Zecca, A.; Trainotti, E.; Brunger, M.J. Low-energy positron scattering from iodomethane. J. Phys. B Atomic Mol. Opt. Phys. 2013, 46, 175202. [Google Scholar] [CrossRef]
- Ghosh, A.S.; Mukherjee, T.; Biswas, P.K.; Jain, A. Positron-CO collisions using rotational LFCCA. J. Phys. B Atomic Mol. Opt. Phys. 1993, 26, L23. [Google Scholar] [CrossRef]
- Hewitt, R.N.; Noble, C.J.; Bransden, B.H. Positronium formation in positron-hydrogen scattering. J. Phys. B Atomic Mol. Opt. Phys. 1990, 23, 4185. [Google Scholar] [CrossRef]
- Mitroy, J.; Ratnavelu, K. The positron-hydrogen system at low energies. J. Phys. B Atomic Mol. Opt. Phys. 1995, 28, 287. [Google Scholar] [CrossRef]
- Mitroy, J. An calculation of positron-hydrogen scattering at intermediate energies. J. Phys. B Atomic Mol. Opt. Phys. 1996, 29, L263. [Google Scholar] [CrossRef]
- Wakid, S.E.A.; LaBahn, R.W. Positronium formation in positron-hydrogen collisions. Phys. Rev. A 1972, 6, 2039. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, C.D. Hyperspherical close-coupling calculation of positronium formation cross sections in positron-hydrogen scattering at low energies. J. Phys. B Atomic Mol. Opt. Phys. 1994, 27, 5065. [Google Scholar] [CrossRef]
- Kadyrov, A.S.; Bray, I. Two-center convergent close-coupling approach to positron-hydrogen collisions. Phys. Rev. A 2002, 66, 012710. [Google Scholar] [CrossRef]
- Ryzhikh, G.; Mitroy, J. Positron scattering from atomic sodium. J. Phys. B Atomic Mol. Opt. Phys. 1997, 30, 5545. [Google Scholar] [CrossRef]
- Ward, S.J.; Horbatsch, M.; McEachran, R.P.; Stauffer, A.D. Close-coupling approach to positron scattering for lithium, sodium and potassium. J. Phys. B Atomic Mol. Opt. Phys. 1989, 22, 1845. [Google Scholar] [CrossRef]
- Ward, S.J.; Horbatsch, M.; McEachran, R.P.; Stauffer, A.D. Close-coupling approach to positron scattering from potassium. J. Phys. B Atomic Mol. Opt. Phys. 1988, 21, L611. [Google Scholar] [CrossRef]
- Khan, P.; Dutta, S.; Ghosh, A. Positron-lithium scattering using the eigenstate expansion method. J. Phys. B Atomic Mol. Opt. Phys. 1987, 20, 2927. [Google Scholar] [CrossRef]
- Natchimuthu, N.; Ratnavelu, K. Optical potential study of positron scattering by atomic sodium at intermediate energies. Phys. Rev. A 2001, 63, 052707. [Google Scholar] [CrossRef]
- McCarthy, I.E.; Ratnavelu, K.; Zhou, Y. Calculation of total cross sections for electron and positron scattering on sodium and potassium. J. Phys. B Atomic Mol. Opt. Phys. 1993, 26, 2733. [Google Scholar] [CrossRef][Green Version]
- McAlinden, M.T.; Kernoghan, A.A.; Walters, H.R.J. Positron scattering by potassium. J. Phys. B Atomic Mol. Opt. Phys. 1996, 29, 555. [Google Scholar] [CrossRef]
- McAlinden, M.T.; Kernoghan, A.A.; Walters, H.R.J. Positron scattering by lithium. J. Phys. B Atomic Mol. Opt. Phys. 1997, 30, 1543. [Google Scholar] [CrossRef]
- Kernoghan, A.A.; McAlinden, M.T.; Walters, H.R.J. Positron scattering by rubidium and caesium. J. Phys. B Atomic Mol. Opt. Phys. 1996, 29, 3971. [Google Scholar] [CrossRef]
- Mitroy, J.; Ratnavelu, K. Close coupling theory of positron scattering from alkali atoms. Aust. J. Phys. 1994, 47, 721–742. [Google Scholar] [CrossRef]
- Hewitt, R.N.; Joachain, C.J.; Noble, C.J.; Bransden, B.H. Coupled-channel calculations of e+–Mg scattering. Can. J. Phys. 1996, 74, 559–563. [Google Scholar] [CrossRef]
- Utamuratov, R.; Fursa, D.V.; Kadyrov, A.S.; Lugovskoy, A.V.; Savage, J.S.; Bray, I. Two-center convergent-close-coupling calculations of positron scattering on magnesium. Phys. Rev. A 2012, 86, 062702. [Google Scholar] [CrossRef]
- Fursa, D.V.; Bray, I. Convergent close-coupling method for positron scattering from noble gases. New J. Phys. 2012, 14, 035002. [Google Scholar] [CrossRef]
- McEachran, R.P.; Horbatsch, M.; Stauffer, A.D. Positron scattering from rubidium. J. Phys. B Atomic Mol. Opt. Phys. 1991, 24, 1107. [Google Scholar] [CrossRef]
- Utamuratov, R.; Fursa, D.V.; Mori, N.; Kadyrov, A.S.; Bray, I.; Zammit, M.C. Positron-impact electronic excitations and mass stopping power of H2. Phys. Rev. A 2019, 99, 042705. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I.; Chiari, L.; Zecca, A.; Brunger, M.J. Adiabatic-nuclei calculations of positron scattering from molecular hydrogen. Phys. Rev. A 2017, 95, 022707. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Bray, I. Convergent calculations of positron scattering from molecular hydrogen. J. Phys. Conf. Ser. 2015, 635, 012009. [Google Scholar] [CrossRef]
- Utamuratov, R.; Kadyrov, A.S.; Fursa, D.V.; Zammit, M.C.; Bray, I. Two-center close-coupling calculations of positron–molecular-hydrogen scattering. Phys. Rev. A 2015, 92, 032707. [Google Scholar] [CrossRef]
- Weissbluth, M. Atoms and Molecules; Academic Press, Inc.: New York, NY, USA, 1978. [Google Scholar]
- Pradhan, A.K.; Nahar, S.N. Atomic Astrophysics and Spectroscopy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Joachain, C.J. Quantum Collision Theory; North-Holland: Amsterdam, The Netherlands, 1983; Chapter 18. [Google Scholar]
- Clementi, E.; Roetti, C. Roothaan-Hartree-Fock atomic wavefunctions: Basis functions and their coefficients for ground and certain excited states of neutral and ionized atoms, Z ≤ 54. Atomic Data Nucl. Data Tables 1974, 14, 177–478. [Google Scholar] [CrossRef]
- O’Connel, J.K.; Lane, N.F. Non-adjustable exchange-correlation model for electron scattering from closed-shell atoms and molecules. Phys. Rev. A 1983, 27, 1983. [Google Scholar] [CrossRef]
- Jain, A. New parameter-free polarization potentials in low wnergy positron collisions. In Annihilation in Gases and Galaxies; Drachman, R., Ed.; Goddard Space Flight Center: Greenbelt, MD, USA, 1989; p. 71. [Google Scholar]
- Riley, M.E.; Truhlar, D.G. Approximations for the exchange potential in electron scattering. J. Chem. Phys. 1975, 63, 2182. [Google Scholar] [CrossRef]
- Chen, S.; McEachran, R.P.; Stauffer, A.D. Ab initio optical potentials for elastic electron and positron scattering from the heavy noble gases. J. Phys. B 2008, 41, 025201. [Google Scholar] [CrossRef]
- Staszewsa, G.; Schwenke, D.W.; Thurumalai, D.; Truhlar, D.G. Quasifree-scattering model for the imaginary part of the optical potential for electron scattering. Phys. Rev. A 1983, 28, 2740. [Google Scholar] [CrossRef]
- Staszewsa, G.; Schwenke, D.W.; Truhlar, D.G. Investigation of the shape of the imaginary part of the optical-model potential for electron scattering by rare gases. Phys. Rev. A 1984, 29, 3078. [Google Scholar] [CrossRef]
- Fuss, M.C.; Sanz, A.G.; Blanco, F.; Vieira, P.L.; Brunger, M.J.; Garcia, G. Differential and integral electron scattering cross sections from tetrahydrofuran (THF) over a wide energy range: 1–10,000 eV. Eur. Phys. J. D 2014, 68, 161. [Google Scholar] [CrossRef]
- Watson, G.N. Theory of Bessel Functions; Cambridge University Press: London, UK, 1958; p. 368. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Series, Integrals and Products; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Gupta, D.; Antony, B. Electron impact ionization of cycloalkanes, aldehydes, and ketones. J. Chem. Phys. 2014, 141, 054303. [Google Scholar] [CrossRef]
- Singh, S.; Gupta, D.; Antony, B. Plasma relevant electron scattering cross sections of propene. Plasma Sources Sci. Technol. 2018, 27, 105014. [Google Scholar] [CrossRef]
- Singh, S.; Naghma, R.; Kaur, J.; Antony, B. Calculation of total and ionization cross sections for electron scattering by primary benzene compounds. J. Chem. Phys. 2016, 145, 034309. [Google Scholar] [CrossRef]
- Singh, S.; Antony, B. Study of inelastic channels by positron impact on simple molecules. J. Appl. Phys. 2017, 121, 244903. [Google Scholar] [CrossRef]
- Reid, D.D.; Wadehra, J.N. A quasifree model for the absorption effects in positron scattering by atoms. J. Phys. B 1996, 29, L127. [Google Scholar] [CrossRef]
- Singh, S.; Antony, B. Positronium formation and ionization of atoms and diatomic molecules by positron impact. Europhys. Lett. 2017, 119, 50006. [Google Scholar] [CrossRef]
- Wigner, E.P. Resonance Reactions. Phys. Rev. 1946, 70, 606–618. [Google Scholar] [CrossRef]
- Wigner, E.P.; Eisenbud, L. Higher Angular Momenta and Long Range Interaction in Resonance Reactions. Phys. Rev. 1947, 72, 29–40. [Google Scholar] [CrossRef]
- Burke, P.G.; Hibbert, A.; Robb, W.D. Electron scattering by complex atoms. J. Phys. B Atomic Mol. Phys. 1971, 4, 153–161. [Google Scholar] [CrossRef]
- Burke, P.G.; Robb, W.D. The R-Matrix Theory of Atomic Processes. Adv. Atomic Mol. Phys. 1975, 11, 143–214. [Google Scholar]
- Faure, A.; Gorfinkiel, J.D.; Morgan, L.A.; Tennyson, J. GTOBAS: Fitting continuum functions with Gaussian-type orbitals. Comput. Phys. Commun. 2002, 144, 224–241. [Google Scholar] [CrossRef]
- Bloch, C. Une formulation unifiée de la théorie des réactions nucléaires. Nucl. Phys. 1957, 4, 503–528. [Google Scholar] [CrossRef]
- Gailitis, M. New forms of asymptotic expansions for wavefunctions of charged-particle scattering. J. Phys. B Atomic Mol. Phys. 1976, 9, 843–854. [Google Scholar] [CrossRef]
- Morgan, L.A. A generalized R-matrix propagation program for solving coupled second-order differential equations. Comput. Phys. Commun. 1984, 31, 419–422. [Google Scholar] [CrossRef]
- Noble, C.J.; Nesbet, R.K. CFASYM, a program for the calculation of the asymptotic solutions of the coupled equations of electron collision theory. Comput. Phys. Commun. 1984, 33, 399–411. [Google Scholar] [CrossRef]
- Burke, P.G.; Joachain, C.J. Theory of Electron–Atom Collisions; Springer: New York, NY, USA, 1995. [Google Scholar]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comp. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Brunger, M.J.; Buckman, S.J.; Ratnavelu, K. Positron Scattering from Molecules: An Experimental Cross Section Compilation for Positron Transport Studies and Benchmarking Theory. J. Phys. Chem. Ref. Data 2017, 46, 023102. [Google Scholar] [CrossRef]
- Ratnavelu, K.; Brunger, M.J.; Buckman, S.J. Recommended Positron Scattering Cross Sections for Atomic Systems. J. Phys. Chem. Ref. Data 2019, 48, 023102. [Google Scholar] [CrossRef]
- Srivastava, S.K.; Tanaka, H.; Chutjian, A.; Trajmar, S. Elastic scattering of intermediate-energy electrons by Ar and Kr. Phys. Rev. A 1981, 23, 2156. [Google Scholar] [CrossRef]
- Sun, J.; Yu, G.; Jiang, Y.; Zhang, S. Total cross-sections for positron scattering by a series of molecules. Eur. Phys. J. D 1998, 4, 83–88. [Google Scholar] [CrossRef]
- Hamada, A.; Sueoka, O. Total cross section measurements for positrons and electrons colliding with molecules. II. HCl. J. Phys. B Atomic Mol. Opt. Phys. 1994, 27, 5055–5064. [Google Scholar] [CrossRef]
- Masin, Z.; Gorfinkiel, J.D.; Jones, D.B.; Bellm, S.M.; Brunger, M.J. Elastic and inelastic cross sections for low-energy electron collisions with pyrimidine. J. Chem. Phys. 2012, 136, 144310. [Google Scholar] [CrossRef]
- Ferraz, J.; dos Santos, A.; de Souza, G.; Zanelato, A.; Alves, T.; Lee, M.-T.; Brescansin, L.; Lucchese, R.; Machado, L. Cross sections for electron scattering by formaldehyde and pyrimidine in the low-and intermediate energy ranges. Phys. Rev. A 2013, 87, 032717. [Google Scholar] [CrossRef]
- Baek, W.Y.; Arndt, A.; Bug, M.; Rabus, H.; Wang, M. Total electronscattering cross sections of pyrimidine. Phys. Rev. A 2013, 88, 032702. [Google Scholar] [CrossRef]
- Palihawadana, P.; Boadle, R.; Chiari, L.; Erson, E.; Machacek, J.; Brunger, M.J.; Buckman, S.; Sullivan, J. Positron scattering from pyrimidine. Phys. Rev. A 2013, 88, 012717. [Google Scholar] [CrossRef]
- Bug, M.U.; Baek, W.Y.; Rabus, H.; Villagrasa, C.; Meylan, S.; Rosenfeld, A.B. An electron-impact cross section data set (10 eV–1 keV) of DNA constituents based on consistent experimental data: A requisite for Monte Carlo simulations. Radiat. Phys. Chem. 2017, 130, 459–479. [Google Scholar] [CrossRef]
- Fuss, M.C.; Sanz, A.G.; Blanco, F.; Oller, J.C.; Limao-Vieira, P.; Brunger, M.J.; Garcia, G. Total electron-scattering cross sections from pyrimidine as measured using a magnetically confined experimental system. Phys. Rev. A 2013, 88, 042702. [Google Scholar] [CrossRef]
- Sullivan, J.P.; Makochekanwa, C.; Jones, A.; Caradonna, P.; Slaughter, D.S.; Machacek, J.; McEachran, R.P.; Mueller, D.W.; Buckman, S.J. Forward angle scattering effects in the measurement of total cross sections for positron scattering. J. Phys. B Atomic Mol. Opt. Phys. 2011, 44, 035201. [Google Scholar] [CrossRef]
- Sinha, N.; Antony, B. Electron and positron interaction with pyrimidine: A theoretical investigation. J. Appl. Phys. 2018, 123, 124906. [Google Scholar] [CrossRef]
- Singh, S.; Gupta, D.; Antony, B. Electron and positron scattering cross sections for propene. J. Appl. Phys. 2018, 124, 034901. [Google Scholar] [CrossRef]
- Singh, S.; Sen, A.; Antony, B. Positron scattering calculations of elastic, total and momentum transfer cross section for alkaline earth atoms. Int. J. Mass Spectrom. 2018, 428, 22–28. [Google Scholar] [CrossRef]
- Singh, S.; Dutta, S.; Naghma, R.; Antony, B. Positron scattering from simple molecules. J. Phys. B Atomic Mol. Opt. Phys. 2017, 50, 135202. [Google Scholar] [CrossRef]
- Sinha, N.; Singh, S.; Antony, B. Theoretical study of positron scattering by group 14 tetra hydrides: A quantum mechanical approach. Int. J. Quant. Chem. 2018, 118, e25679. [Google Scholar] [CrossRef]
- Sinha, N.; Modak, P.; Singh, S.; Antony, B. Positron scattering from methyl halides. J. Phys. Chem. A 2018, 122, 2513–2522. [Google Scholar] [CrossRef]
- Singh, S.; Antony, B. Positron induced scattering cross sections for hydrocarbons relevant to plasma. Phys. Plasmas 2018, 25, 053503. [Google Scholar] [CrossRef]
- Sinha, N.; Antony, B. Inelastic cross sections for pentane isomers by positron impact. Mol. Phys. 2019, 117, 2527–2534. [Google Scholar] [CrossRef]
- Sinha, N.; Antony, B. Theoretical study of positron scattering from pentane isomers. Chem. Phys. Lett. 2018, 713, 282–288. [Google Scholar] [CrossRef]
| Method | Target(s) | Reference |
|---|---|---|
| IAM | H, NH, CO, CO, O, SF, CF, CCl, CBr, CI, CH, SiH, GeH, PbH | [72] |
| H | [73] | |
| O, CO, CO, SO, CS, OCS, SF | [74] | |
| N | [75] | |
| CO | [76] | |
| Hydrocarbons | [77] | |
| IAM-SCAR(+I) | H, CH | [78,79] |
| N, O | [80] | |
| O | [81] | |
| HO | [82,83] | |
| NO | [84] | |
| NO | [85] | |
| Formaldehyde | [86] | |
| Tetrahydrofuran, 3-hydroxy-tetrahydrofuran | [87] | |
| Indole | [88] | |
| Uracil | [89] | |
| Pentane isomers | [90] | |
| 2,2,4-trimethylpentane | [91] | |
| Vinyl acetate | [92] | |
| Tetrahydrofurfuryl alcohol | ||
| Pyrimidine | [93,94] | |
| Pyridine | [95] | |
| Cyclic ethers (oxirane, 1,4-dioxane, tetrahydropyran) | [96] | |
| Tetrahydrofurfuryl alcohol (THFA) | [97] | |
| KVP | H, He | [57,98,99] |
| H | [100] | |
| DWA | H | |
| H | [101] | |
| Inert gases | [102,103,104,105,106] | |
| MBC | H | [107] |
| Noble gases | [58,59] | |
| Mg | [108] | |
| R-matrix | H | [63,109] |
| Inert gases | [109,110,111] | |
| HF | [112] | |
| He | [113] | |
| H, N | [109,113,114,115] | |
| HO | [116] | |
| CO, Acetylene | [117,118] | |
| SMC | He | [119,120] |
| H | [61,120,121,122,123,124,125,126] | |
| Li | [127] | |
| N | [125,128,129,130,131] | |
| CO | [132] | |
| CO | [120,125,133,134] | |
| HO | [135,136,137] | |
| CH | [138] | |
| Formic acid | [139] | |
| Benzene | [140] | |
| Pyrimidine | [141] | |
| Allene | [142] | |
| Silane | [62] | |
| THF | [143] | |
| Ethene | [144] | |
| Actetylene | [128,145] | |
| Ethane | [146] | |
| 1,1-CHF | [147] | |
| Pyrazine | [148] | |
| Formaldehyde-water complexes | [149] | |
| CH isomers | [150] | |
| Glycine and Alanine | [151] | |
| SF | [133] | |
| CH | [152] | |
| Methylamine | [153] | |
| Iodomethane | [154] | |
| CC | CO | [155] |
| H | [66,156,157,158,159,160,161] | |
| Alkali atoms | [66,162,163,164,165,166,167,168,169,170,171] | |
| Mg | [172,173] | |
| Noble gases | [174,175] | |
| H | [176,177,178,179] | |
| N | [67] |
| Target | Cross Sections | Reference |
|---|---|---|
| Inert gases | , , , | [11] |
| C, N, O | , , , | [71,198] |
| Be, Mg, Ca, Sr, Ba, Ra | , , , , , , | [224] |
| Li, Na, K, Rb, Cs, Fr | [12] | |
| C, N, O | , , , | [71,198] |
| CH, CO, CO, H, N, NO | , , , | [196,225] |
| HO, NH, HCl, OCS, SO | , | [50] |
| SiH, GeH, SnH, PbH | , , | [226] |
| CHF, CHCl, CHBr, CHI | , , , | [227] |
| C, C, CH, CH, CH | , , , , | [228] |
| CH | , | [223] |
| n-pentane, iso-pentane, neo-pentane | , , , | [229,230] |
| CHN | , | [222] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nahar, S.N.; Antony, B. Positron Scattering from Atoms and Molecules. Atoms 2020, 8, 29. https://doi.org/10.3390/atoms8020029
Nahar SN, Antony B. Positron Scattering from Atoms and Molecules. Atoms. 2020; 8(2):29. https://doi.org/10.3390/atoms8020029
Chicago/Turabian StyleNahar, Sultana N., and Bobby Antony. 2020. "Positron Scattering from Atoms and Molecules" Atoms 8, no. 2: 29. https://doi.org/10.3390/atoms8020029
APA StyleNahar, S. N., & Antony, B. (2020). Positron Scattering from Atoms and Molecules. Atoms, 8(2), 29. https://doi.org/10.3390/atoms8020029






