Nature’s Pick-Up Tool, the Stark Effect Induced Gailitis Resonances and Applications

Abstract

A simple universal physical mechanism hidden for more than half a century is unexpectedly discovered from a calculation of low excitation antihydrogen. For ease of reference, this mechanism is named Gailitis resonance. We demonstrate, in great detail, that Gailitis resonances are capable of explaining p+⁷Li low energy nuclear fusion, d-d fusion on a Pd lattice and the initial transient fusion peak in muon catalyzed fusion. Hopefully, these examples will help to identify Gailitis resonances in other systems.

1. Uncovering the Truth from the Nature Takes Time

During the 1960’s, Gailitis and Damburg [1] found weak oscillations in the scattering matrix at energy ε slightly above H(n = 2) energy level in electron-hydrogen scattering calculations. They suggested that the oscillations might have originated from the electric dipole component of the target system.

In an attempt to help the antihydrogen research, a calculation of the total cross section for antihydrogen formation for $\overline{H}$(n ≤ 2) using nine partial waves was carried out [2] for the following reaction, using the modified Faddeev equation,

$$\overline{p}+Ps\left(n=2\right)\to e+\overline{H}\left(n\le 2\right)$$

(1)

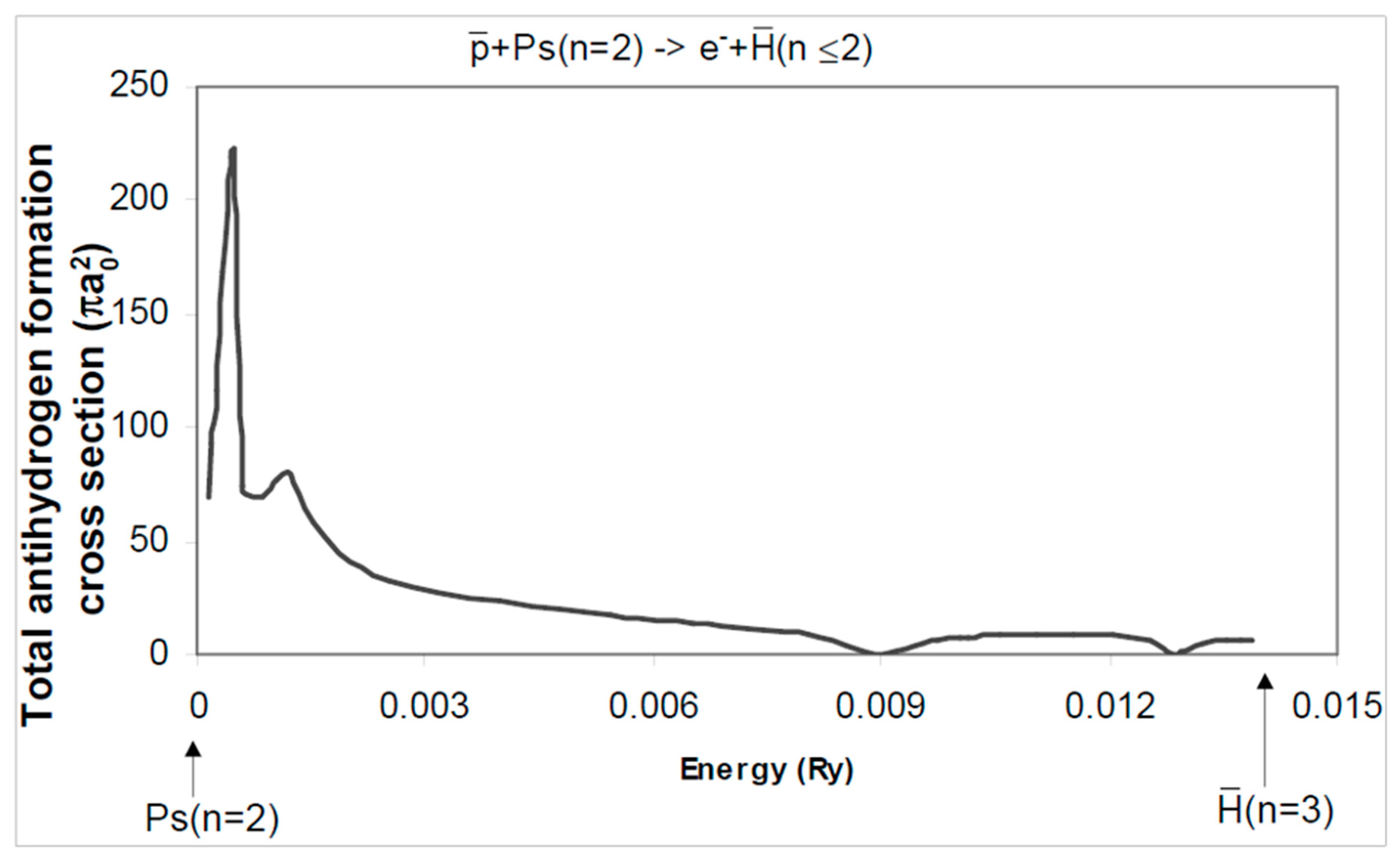
Near the energy region of the Gailitis oscillation, a very large $\overline{H}$(n ≤ 2) formation cross section of 1397πa₀² was found, where a₀ is the Bohr radius. The S-partial wave portion of reaction (1) is plotted in Figure 1 in the energy range between the Ps(n = 2) threshold to the $\overline{H}$(n = 3) threshold.

A couple of resonant-like peaks are clearly visible. However, no previous calculations indicated any resonance in this energy region and subsequent independent calculations also could not reproduce it. Their calculations were carried out with a much shorter cutoff radius than the 450 Bohr radius used in Figure 1.

Ten years later, we decided to investigate the energy region where the questionable cross section peaks were found in Figure 1, using a much larger size job allowed by more powerful computers. The cutoff radius used in [3,4] is 1000 Bohr radius for the following S-state and with six open channel charge conjugation system.

$$\begin{array}{cc}\hfill \mathrm{Channel}\#& \mathrm{Incoming}\mathrm{Channel}\hfill \\ \hfill 1.& e^{+} + H(n=1)\hfill \\ \hfill 2.& e^{+} + H(n=2, l=0)\hfill \\ \hfill 3.& e^{+} + H(n=2, l=1)\hfill \\ \hfill 4.& p + Ps(n=1)\hfill \\ \hfill 5.& p + Ps(n=2, l=0)\hfill \\ \hfill 6.& p + Ps(n=2, l=1)\hfill \end{array}$$

(2)

After numerically solving nearly half a million coupled linear equations, complete sets of beautiful 6 × 6 scattering matrices near each of the three resonances were obtained [3,4].

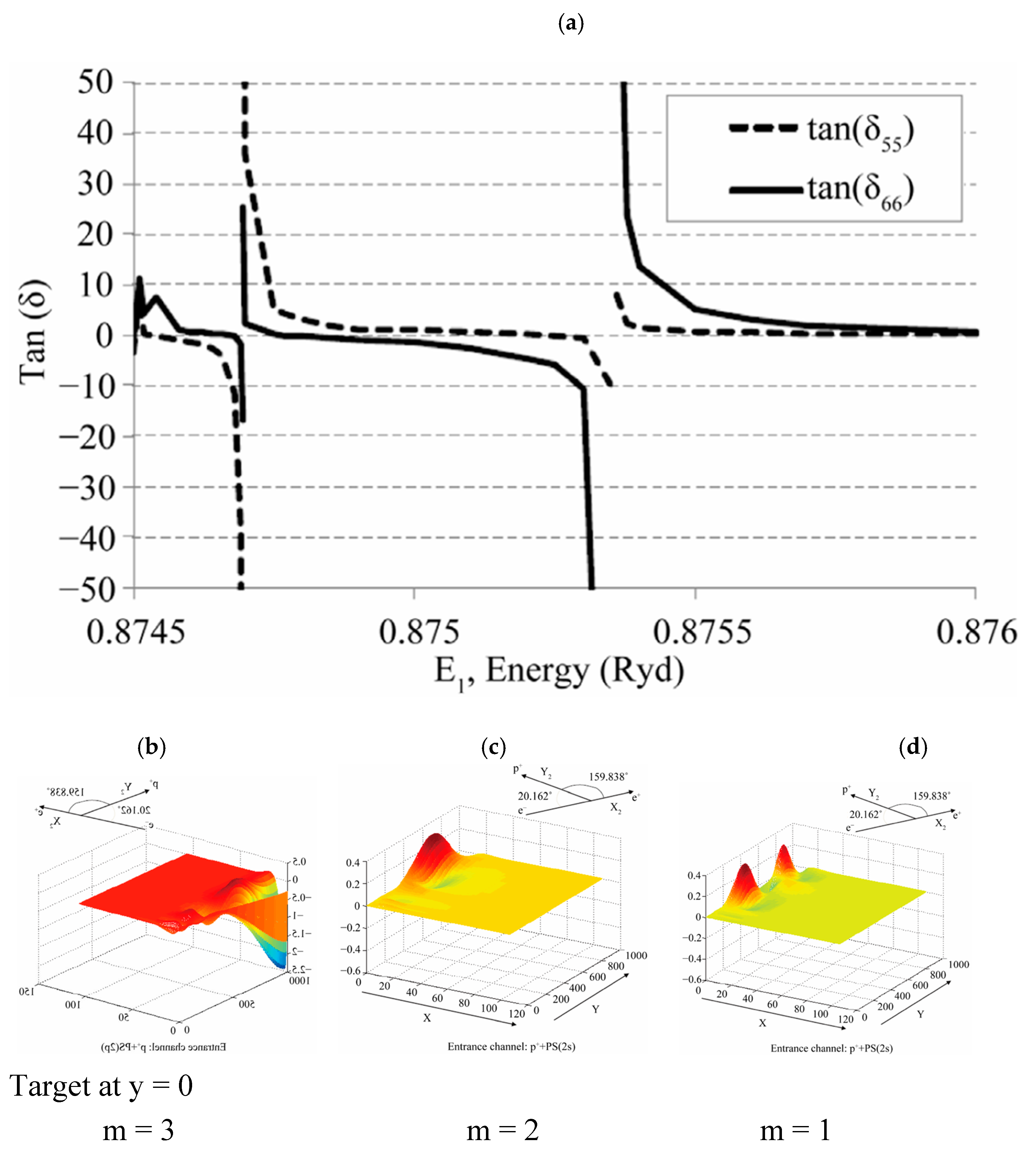
Resonances occur only in channels 5 and 6 of Equation (2), due to their large electric dipole moment. Near resonances, the Faddeev wave amplitudes of channels 5 and 6 and their scattering matrices, tan(δ_ii), i = 5,6, are presented in Figure 2 below.

Apparently, the largest possible run with y_max ≈ 1000a₀ used in our calculations is too short, the third resonance get cut in half. In spite of such defects, these graphs provide enough information to reveal real physics.

Figure 2a is a plot of the K-matrix elements tan(δ_ii), i = 5,6, as a function of the energy E₁, the collision energy with respect to channel 1. Other channel energies are determined in term of E₁. For example the channel energy for channel ε₅ and ε₆ are measured from Ps(n = 2), while E₁ measured from H(n = 1).

Figure 2b is a plot of the Faddeev wave amplitude for channel 6 at energy close to the third resonance.

Figure 2c is a plot of the Faddeev wave amplitude for channel 5 at energy near the second resonance.

Figure 2d is a plot of the Faddeev wave amplitude for channel 5 at energy, not close enough to the first resonance.

All the wave amplitudes of the other Faddeev channels are orders of magnitude smaller.

When the scattering matrix shows singular behavior like Figure 2a, the traditional methods that search for poles in the complex energy plane measure energy and width of the resonances. Here, for the first time, we demonstrate that the Faddeev amplitudes contain all the physics that can be revealed with much less effort.

2. Physics Revealed from Figure 2a

As the proton moves in the attractive electric dipole field from Ps(n = 2) along the y-axis, the phase shift δ suddenly drops from 0⁻ to −π/2. That means that the attractive electric dipole field from Ps(n = 2) suddenly turned strongly repulsive when the energy of the proton matched the electric dipole flipping energies, thus forcing the proton to give up all its energy, and it then turns into an expanding wave packet centered on y_m, where m is a quantum number. From Figure 2b–d, y₁, y₂ can be measured directly, but not y₃. The proton stripped off its energy and turns onto an expanding wave packet. That represents the first of two stages of the lifetime of the Gailitis resonance. The second stage begins when the phase shift suddenly drops from π/2 to 0⁺, indicating a strong attractive force from the target. What will happen during the second stage, which depends only on the host system, is here the Ps. It produces the resonant reaction represented by p + Ps(n = 2) → e⁺ + H(n ≤ 2). Thus, Figure 2a reveals the pick-up action of the Gailitis resonances.

3. Other Common Property of the Gailitis Resonances

It is noticed that the widths of the initial wave packets are equal to their De Broglie wavelengths. In this section, we only use units such that $ħ$ = 1. Thus, the momentum p is related to the De Broglie wavelength p = 1/λ, and ε = p² = (1/λ)². Then, the uncertainty principle is given by Δy Δp = 1. Applied to the Gailitis resonance when Δp→p, we find Δy ≈ 1/p = λ and Δε = (Δp)² = p².

Thus, the Gailitis resonances have another unique property, namely, ε_m/Δε_m = 1 for all m. Due to the incoherent use of units in some of our previous calculations [5], this formula was listed incorrectly as ε_m/Δε_m = 4π².

The lifetime of Gailitis resonances can be calculated using the uncertainty principle in the following form:

ε_m = (1/Δε_m) × 2.42 × 10⁻¹⁷ sec

(3)

where the energy Δε_m is given in Rydberg.

4. Resonant Condition Read from Faddeev Amplitudes

We can relate the known electric dipole moment |μ₁| of the target Ps(n = 2) in the mass normalized Jacobi coordinate system in Figure 2b–d to the resonance energies. The subscript 1 represents the electric dipole moment only, where y²_m = <y²_m> are directly measured at the peaks of the wave packets in Figure 2c,d. However, due to the energy we used to calculate, 2d is too far from the resonant energy. There are two peaks in the wave packet. It is easy to identify which one produced the m = 1 resonance (see [3,4]). Numerically, the resonant equation below comes directly from the wave functions 2c and 2d

ε_m = m|μ₁|/y²_m, where m = 1, 2.

(4)

It is noticed that this is the dipole flipping condition. The value of y₃ cannot be measured from Figure 2b with our limited computer resources. Using a numerical extension of Figure 2b beyond 1000a₀, along with help from Equation (4), y_m, for m = 3 was determined. The properties of the three resonances are listed in

Table 1. ε_m are the resonant energies in units Ryd. ε_m/Δε_m are determined in Section 3. λ_m and y_m are measured directly from Figure 2b–d see Reference. [3] for more detail.

m	εm (Ryd)	εm/Δεm	λm(a0)	ym(a0)
1	5.4436(−4)	1	380.85	296.8
2	0.19436(−3)	1	637.35	702.4
3	0.84344(−4)	1	967.54	1306.0

. All quantities are in mass normalized Jacobi coordinates and |μ₁| = 47.94778.

Please notice, the ε_m resonant energy measured just above the Ps(n = 2) threshold is very small. They are within the range of the fine structure energy width, where the Coulomb degeneracy is removed by the small relativistic perturbation in the pure Coulomb force Hamiltonian that split the Coulomb energy level into a number of independent energy levels depends on the angular momentum quantum number ℓ. The energy width of this fine structure energy levels is very small. All ε_m must lie within this width, thus three-body scattering calculation involves 6-open channels represented in Equation (2).

It is well known in many textbooks that an incoming charge particle p or e⁺ will induce a constant electric dipole moment in the target atom. Consequently, an attractive inverse square force exists that support Gailitis resonance listed in Table 1.

These numbers can also be simply reproduced by the resonant condition Equation (4):

ε_m = m|μ₁|/y²_m,   m = 1, 2, 3.→

(5)

The second column ε_m/Δε_m = 1 indicates that, in the traditional measurements of energy and width of resonances, in the complex energy plane, this ratio must be close to one and all Gailitis resonances lying on this straight line [5]. The present method provides a complete set of properties for all the Gailitis resonances outlined above. These properties are very useful in the search for Gailitis resonances for more complex systems. Such searches have already solved a number of decades old outstanding problems. A few of them are outlined below.

5. Lifetime Rate of Gailitis Resonance in Muon-Catalyzed Fusion

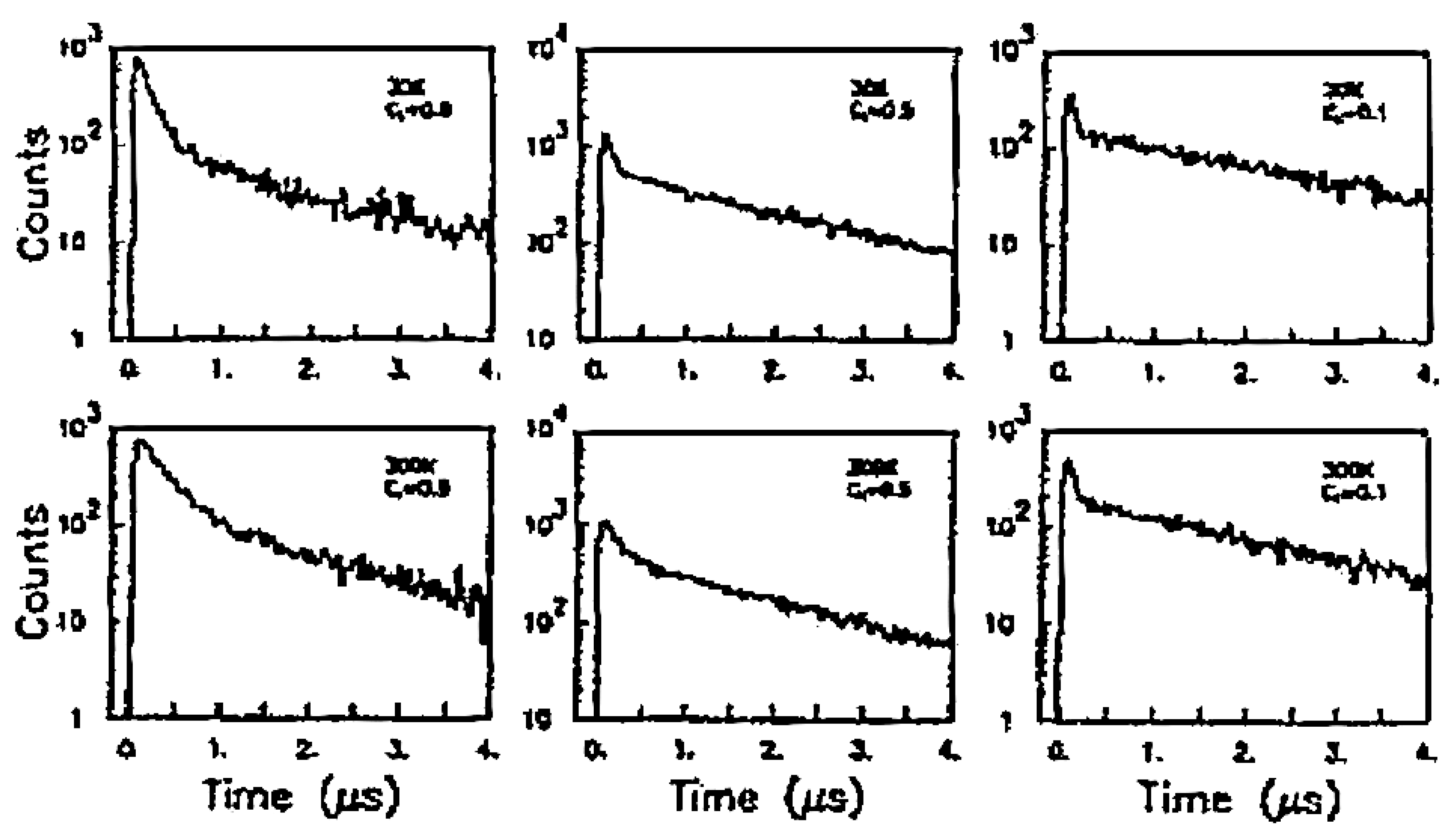
The molecule dtµ is composed of a deuteron and a triton nucleus bound together by a negative muon. The “size” of this molecule is much smaller than a normal molecule bound by an electron. As a result, the probability for the overlap of the two nuclei wave functions is large enough to produce the nuclear reaction:

dtµ → ⁴He + n + μ + 17.6 MeV.

(6)

The number of neutrons, N, counted in the laboratory is given in Figure 3. The mechanism for the formation of large initial peaks was unknown since the publication of the original data [6].

In Reference [7], using the properties of Gailitis resonance and the experimental information that the initial muonic atom tµ was formed at an excited state, n = 14, an estimation found the lifetime of the Gailitis resonance is of the same order of magnitude as the radiative decay lifetime. This is consistent with the data shown in Figure 3. Here at the end of the life of the Gailitis resonance, as Figure 2a shows, it becomes a bound dtµ molecule before the nuclear reaction of Equation (5) takes place.

6. Long-Lived Gailitis Resonance Composed of the Electron-Rydberg Hydrogen Atom

In the Rydberg hydrogen with n~20, the electron was trapped at a very large distance, that is, a very large y_m and λ_m even for the n = 2 system found in Table 1. For Rydberg Gailitis resonances, the lifetime can be expected to exceed its radiation decay lifetime. That seemed to be the case for the earlier stage of research in antihydrogen production when the antihydrogen was created in Rydberg states. The expectation for such states is to radiatively cascade down to low excitation states failed.

7. Nuclear Fusion in (p+⁷Li) -> ⁸Be^* -> 2α

The energy of the Gailitis resonance in p+⁷Li reaction overlaps with that of the compound nuclear energy level centered at 19.9 MeV, with a decay width that extends even below the proton separation energy of ⁸Be (see the arrow in Figure 4).

This compound nuclear energy level has I = 2⁺, the ⁷Li has I₁ = 3/2⁻ and the proton has I₂ = ½, with l = 1⁻ contribution.

One possible vector sum for the resonance is I = 2⁺, that makes a perfect match between the resonance and this compound nuclear energy level Be* (shown by the arrow).

8. S-State Gailitis Resonance (d, Dp)—The “Quasi-Particle”

From the e⁺ + H calculation, it is expected that the activity of the resonance is not strong enough to disturb the lattice. In this section, we assume that the deuteron atom is bound on Pd lattice.

During the first stage of the life of (d, D_p), Figure 5 shows that the wave packet of d is a spherical layer of probability density with maximum located on a spherical surface with resonant radius r₀. A deuterium atom on the lattice is represented by D_p, and it has an electric dipole moment induced by the lattice vibrating phonon, indicating that the electric dipole can be tuned to locate the resonances. Tuning, for example, can be performed using new laser technology to induce a phonon state.

The r₀ remains unchanged during the first stage of the life of the resonance, but the probability density expands both inward and outward from this surface.

During the second stage, starting with a sudden attraction towards D_p, the spherical surface with maximum probability density begins to shrink.

D_p remains on the lattice, unperturbed by the activities of the resonance. As usual, the resonant energies of Gailitis are very small for the long-lived resonances. When the probability cloud begins advancing over the Coulomb barrier, no matter how little, the quasi-particle (d, D_p) is already in a shallow negative attractive tail of the central nuclear potential, far away from the complication of the core nuclear forces.

The role of 4He+ in (d, D_p) fusion.

What does (d, D_p) have in common with ⁴He⁺? They both have one electron and two deuterons d. The ⁴He⁺ is the lowest possible energy system involving these three particles. The most important difference between these two systems concerning this study is the energy difference. Neglecting all small energies involving the lattice and the Gailitis resonance the (d, D_p) is 23.85 MeV above ⁴He⁺. This is the energy needed to separate the two d from the α-particle, the nucleus of ⁴He⁺. Unfortunately, there is no compound nuclear energy level of α to match the nuclear properties of an S-state (d, D_p). Instead of becoming a compound nuclear energy level of α at excitation energy 23.85 MeV (see Figure 6), during the second stage of the life of the (d, D_p), resonant action leads the quasi-particle (d, D_p) into a shallow negative tail of the nuclear potential of D_p, which, in an attempt to expel the intruder, injects it with energy equal to the potential energy drop, as the cloud keeps shrinking.

As soon as the energy accumulation in (d, D_p) reaches the energy of a lattice normal mode phonon, the nuclear energy begins to flow into the lattice, one phonon at a time, until the size of the “quasi-particle” shrinks close to the region where the core nuclear force dominate. Then, the nuclear force takes over the dynamics. The (d, D_p) either reaches the ground state of ⁴He⁺ and still remains on the lattice, or gets kicked out of the lattice as a quasi-particle where background electrons can slow it down, until reducing it to a free ⁴He⁺. This leakage of one phonon at a time is a slow process and the amount leaked each time, one phonon, is negligible for nuclear energy. Namely, only a classical conservation of energy need apply.

9. Discussion

The Gailitis resonances are supported by a very simple physical phenomenon. Why did it take so long to uncover its true nature? The answer is clearly displayed in Figure 2 and Table 1. The most important region is between y = 296.8 a₀ and y = 1306 a₀. Any computer would be hard pressed to accommodate such a large calculation correctly as seen even in some most recent calculations. In other words, the long range Coulomb force is producing unexpectedly long range physics. Present computational methods needs substantial improvements.

This problem is demonstrated clearly with our long struggle for calculating the simplest quantum three-body scattering system in e⁺ + H(n ≤ 2), presented earlier in this report. Table 1 shows that the first Gailitis resonance shows up at y₁ = 296.8a₀. Had we used an effective cut-off, y_max = 300a₀, all the physics of the Gailitis resonances would have remained hidden.

Supercomputers have advanced several generations since our calculations [3,4] and the experimental techniques have also improved, so that we can make measurements in the molecular and atomic level. There is no excuse for us theorists still using the decades old methods that were designed for the needs of decades ago. It is clear that a resonance can represent its own real physical properties, which is more than just a real and imaginary part. We must start with the wave functions for each and every independent open channel.

The quantum 3-body multichannel scattering system presented in our work [3] is only the tip of the iceberg. Ref. [4] is designed to provide interested readers the first step to set up their own code. Critics should help improve it until they can find even better methods that could satisfy the needs of the 21st century.

Scientific processes brought multi-disciplinary physics closer, as shown from the small number of examples presented here; the universal natural mechanism of electric dipole flipping. A lot of other possibilities such as the role of higher order of both the electric and magnetic multipoles will be next. It seems that experimentalists are already moving ahead quickly into these areas.

Clearly, multidisciplinary collaboration can be most fruitful in such an area like the low energy nuclear fusion.