Shannon, Rényi, Tsallis Entropies and Onicescu Information Energy for Low-Lying Singly Excited States of Helium
Abstract
1. Introduction
2. Theoretical Methods
2.1. Determination of Ground and Singly Excited States of Helium via Hylleraas Wave Functions
2.2. Definitions for Electron Density
2.3. Information-Theoretic Quantities in the Position Space
3. Results and Discussion
3.1. Accuracy of Presented Energy and Information-Theoretic Quantities
3.1.1. Energy E
3.1.2. Shannon Entropy S, Rényi Entropy , Tsallis Entropy and Onicescu Information Energy
3.2. Comparison of Shannon Entropy S of the Ground and Four Singly Excited States
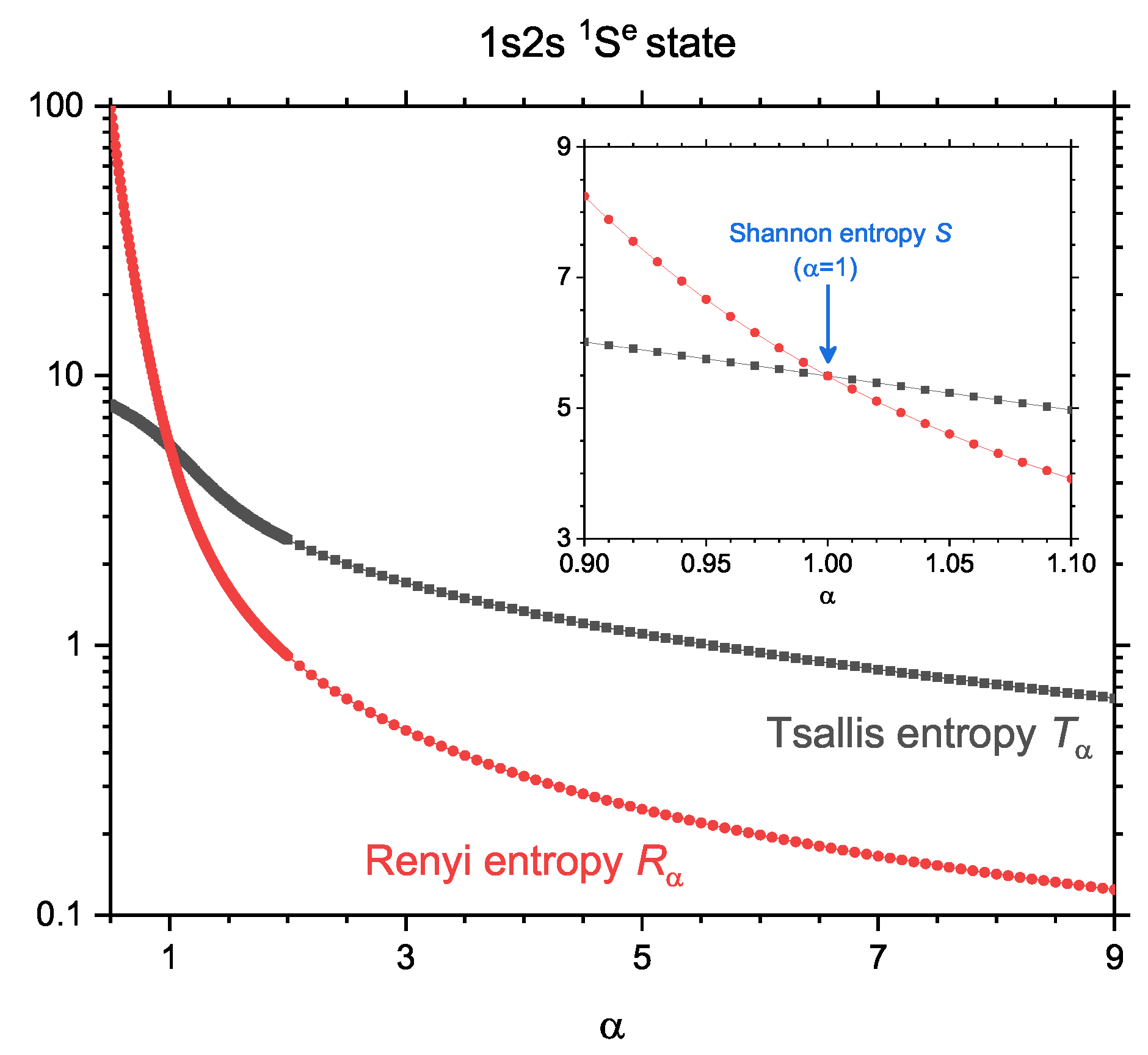
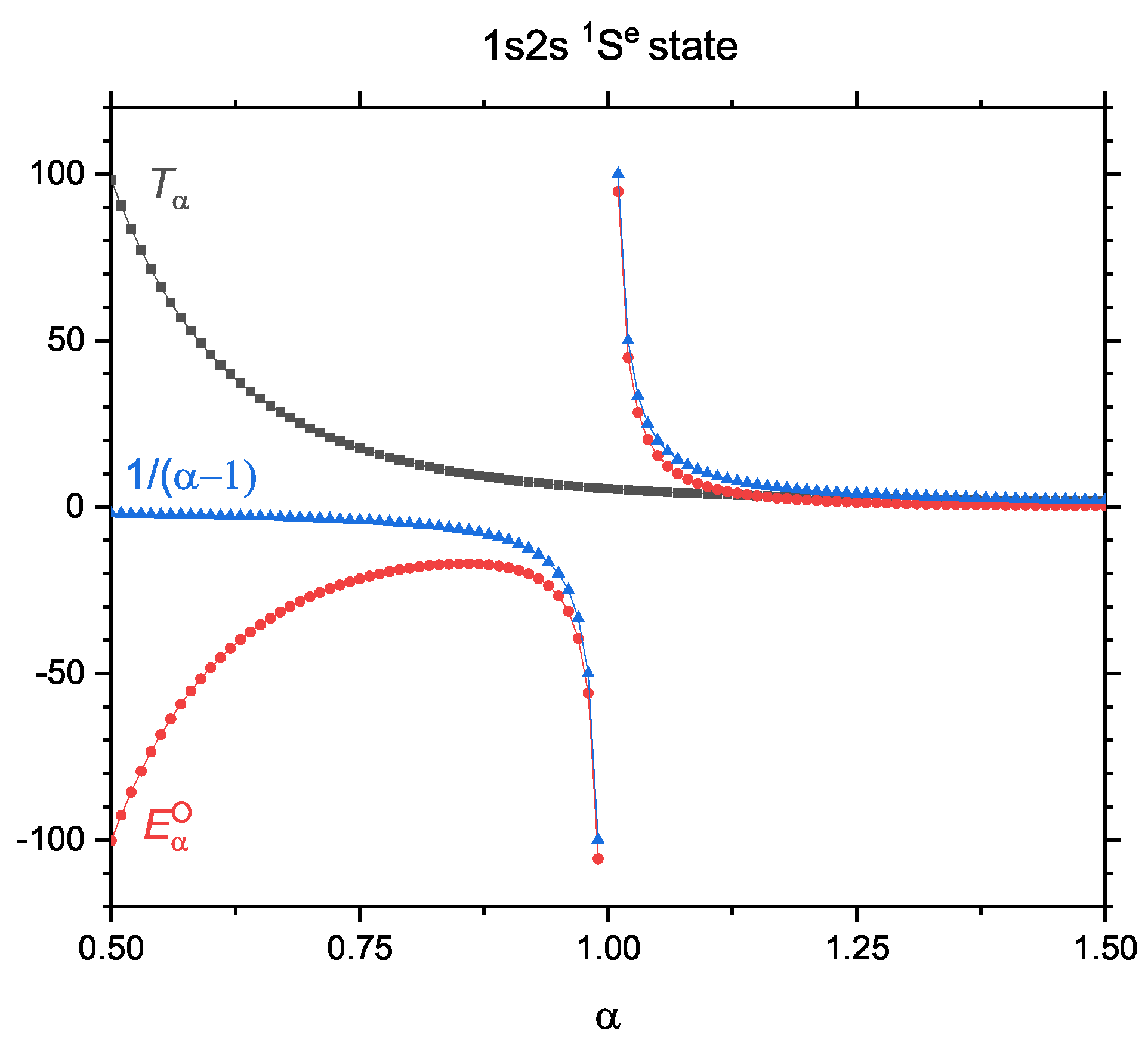
3.3. Comparison of Rényi Entropy , Tsallis Entropy and Onicescu Information Energy of the Ground and Four Singly Excited States
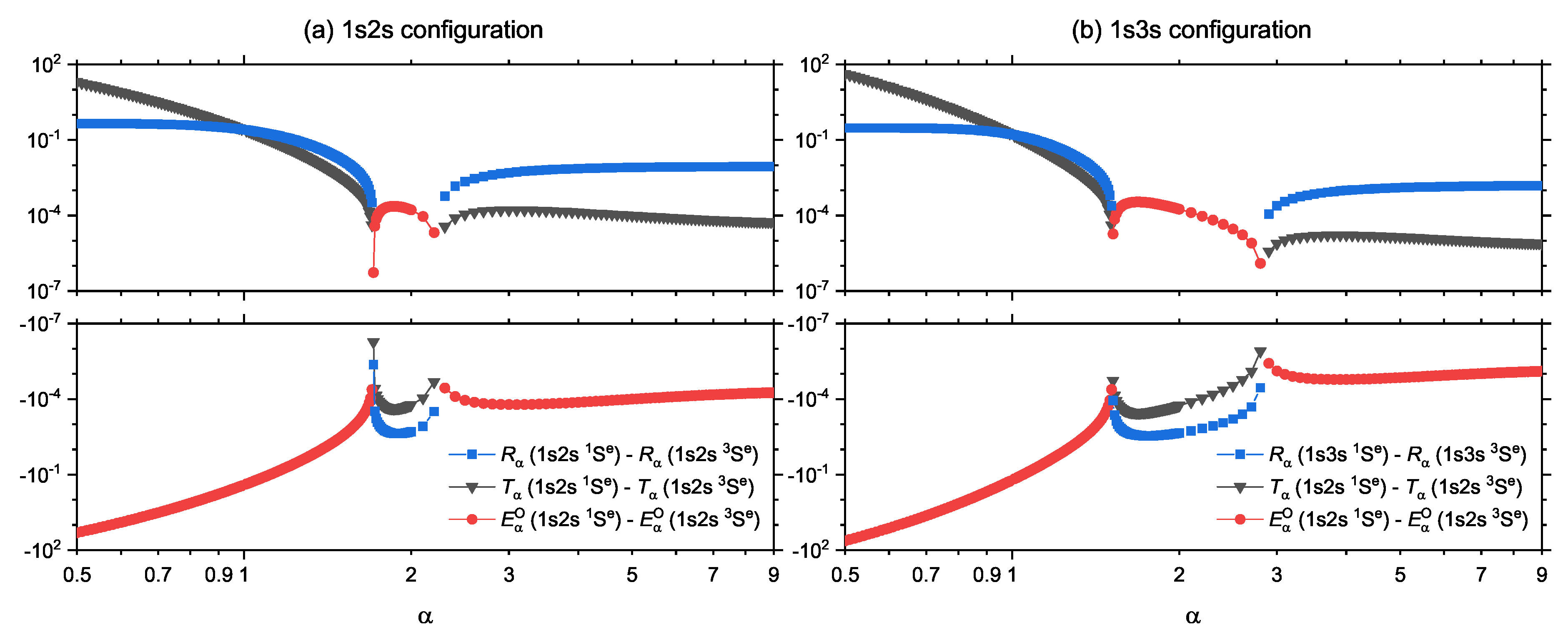
3.4. Singlet–Triplet Reversal of Rényi entropy , Tsallis entropy and Onicescu Information Energy
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chalvet, O.; Daudel, R.; Diner, S.; Malrieu, J.P. (Eds.) Localization and Delocalization in Quantum Chemistry Volume I Atoms and Molecules in the Ground State; Springer: Dordrecht, The Netherlands, 1975; Volume 1. [Google Scholar] [CrossRef]
- Chalvet, O.; Daudel, R.; Diner, S.; Malrieu, J.P. (Eds.) Localization and Delocalization in Quantum Chemistry Volume II Ionized and Excited States; Springer: Dordrecht, The Netherlands, 1976; Volume 2. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Aslangul, C.; Constanciel, R.; Daudel, R.; Kottis, P. Aspects of the Localizability of Electrons in Atoms and Molecules: Loge Theory and Related Methods. Adv. Quantum Chem. 1972, 6, 93–141. [Google Scholar] [CrossRef]
- Sen, K.D. Characteristic features of Shannon information entropy of confined atoms. J. Chem. Phys. 2005, 123, 074110. [Google Scholar] [CrossRef] [PubMed]
- Corzo, H.H.; Laguna, H.G.; Sagar, R.P. Localization-delocalization phenomena in a cyclic box. J. Math. Chem. 2012, 50, 233–248. [Google Scholar] [CrossRef]
- Cedillo, A. Comment on “Localization-delocalization phenomena in a cyclic box” by H. H. Corzo, H. G. Laguna, and R. P. Sagar. J. Math. Chem. 2017, 55, 1889–1892. [Google Scholar] [CrossRef]
- Corzo, H.H.; Castaño, E.; Laguna, H.G.; Sagar, R.P. Measuring localization-delocalization phenomena in a quantum corral. J. Math. Chem. 2013, 51, 179–193. [Google Scholar] [CrossRef]
- Laguna, H.G.; Sagar, R.P. Quantum uncertainties of the confined Harmonic Oscillator in position, momentum and phase-space. Ann. Phys. 2014, 526, 555–566. [Google Scholar] [CrossRef]
- Restrepo Cuartas, J.P.; Sanz-Vicario, J.L. Information and entanglement measures applied to the analysis of complexity in doubly excited states of helium. Phys. Rev. A 2015, 91, 052301. [Google Scholar] [CrossRef]
- Ou, J.H.; Ho, Y.K. Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements. Atoms 2017, 5, 15. [Google Scholar] [CrossRef]
- Ou, J.H.; Ho, Y.K. Shannon information entropy in position space for doubly excited states of helium with finite confinements. Chem. Phys. Lett. 2017, 689, 116–120. [Google Scholar] [CrossRef]
- Rodriguez-Bautista, M.; Vargas, R.; Aquino, N.; Garza, J. Electron-density delocalization in many-electron atoms confined by penetrable walls: A Hartree-Fock study. Int. J. Quantum Chem. 2018, 118, e25571. [Google Scholar] [CrossRef]
- Majumdar, S.; Mukherjee, N.; Roy, A.K. Information entropy and complexity measure in generalized Kratzer potential. Chem. Phys. Lett. 2019, 716, 257–264. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; Neyman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Renyi, A. Probability Theory; North-Holland Publishing Company: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Beadle, E.; Schroeder, J.; Moran, B.; Suvorova, S. An overview of Renyi Entropy and some potential applications. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 1698–1704. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy 2011, 13, 1765–1804. [Google Scholar] [CrossRef]
- Tsallis, C. On the foundations of statistical mechanics. Eur. Phys. J. Spec. Top. 2017, 226, 1433–1443. [Google Scholar] [CrossRef]
- Onicescu, O. Energie Informationnelle. Comptes Rendus Hebd. Seances L’Academie Sci. Ser. A 1966, 263, 841–842. [Google Scholar]
- Iosifescu, M. Octav Onicescu. In Statisticians of the Centuries; Heyde, C.C., Seneta, E., Crépel, P., Fienberg, S.E., Gani, J., Eds.; Springer: New York, NY, USA, 2001; pp. 415–419. [Google Scholar] [CrossRef]
- Angulo, J.C.; Romera, E.; Dehesa, J.S. Inverse atomic densities and inequalities among density functionals. J. Math. Phys. 2000, 41, 7906–7917. [Google Scholar] [CrossRef]
- Romera, E.; Angulo, J.C.; Dehesa, J.S. The Hausdorff entropic moment problem. J. Math. Phys. 2001, 42, 2309. [Google Scholar] [CrossRef]
- Romera, E.; Angulo, J.C.; Dehesa, J.S. Erratum: The Hausdorff entropic moment problem [J. Math. Phys. 42, 2309 (2001)]. J. Math. Phys. 2003, 44, 2354. [Google Scholar] [CrossRef]
- Hô, M.; Sagar, R.P.; Pérez-Jordá, J.M.; Smith, V.H.; Esquivel, R.O. A numerical study of molecular information entropies. Chem. Phys. Lett. 1994, 219, 15–20. [Google Scholar] [CrossRef]
- Hô, M.; Smith, V.H.; Weaver, D.F.; Gatti, C.; Sagar, R.P.; Esquivel, R.O. Molecular similarity based on information entropies and distances. J. Chem. Phys. 1998, 108, 5469–5475. [Google Scholar] [CrossRef]
- Fazal, S.P.; Sen, K.D.; Gutierrez, G.; Fuentealba, P. Shannon entropy of 1-normalized electron density. Indian J. Chem. Sect. A 2000, 39, 48–49. [Google Scholar]
- Massen, S.E. Application of information entropy to nuclei. Phys. Rev. C 2003, 67, 014314. [Google Scholar] [CrossRef]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Shannon-information entropy sum as a correlation measure in atomic systems. Phys. Rev. A 2003, 67, 012507. [Google Scholar] [CrossRef]
- Sen, K.D.; De Proft, F.; Borgoo, A.; Geerlings, P. N-derivative of Shannon entropy of shape function for atoms. Chem. Phys. Lett. 2005, 410, 70–76. [Google Scholar] [CrossRef]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Local correlation measures in atomic systems. J. Chem. Phys. 2005, 122, 084101. [Google Scholar] [CrossRef]
- Moustakidis, C.; Chatzisavvas, K.; Panos, C. Theoretical Quantum-information Properties of Nuclei and Trapped Bose Gases. Int. J. Mod. Phys. E 2005, 14, 1087–1104. [Google Scholar] [CrossRef]
- Chatzisavvas, K.C.; Moustakidis, C.C.; Panos, C.P. Information entropy, information distances, and complexity in atoms. J. Chem. Phys. 2005, 123, 174111. [Google Scholar] [CrossRef]
- Gregori-Puigjané, E.; Mestres, J. SHED: Shannon Entropy Descriptors from Topological Feature Distributions. J. Chem. Inf. Model. 2006, 46, 1615–1622. [Google Scholar] [CrossRef]
- Mohajeri, A.; Dasmeh, P. Evaluating the Nature of Chemical Bonds Based on Probabilistic Models. Int. J. Mod. Phys. C 2007, 18, 1795. [Google Scholar] [CrossRef]
- Romera, E.; Nagy, Á. Rényi information of atoms. Phys. Lett. A 2008, 372, 4918–4922. [Google Scholar] [CrossRef]
- Mohajeri, A.; Alipour, M. Information Energy As an Electron Correlation Measure in Atomic and Molecular Systems. Int. J. Quantum Inf. 2009, 07, 801–809. [Google Scholar] [CrossRef]
- Dehesa, J.S.; López-Rosa, S.; Martínez-Finkelshtein, A.; Yáñez, R.J. Information theory of D-dimensional hydrogenic systems: Application to circular and Rydberg states. Int. J. Quantum Chem. 2009, 110, 1529–1548. [Google Scholar] [CrossRef]
- Nagy, Á.; Romera, E. Relative Rényi entropy for atoms. Int. J. Quantum Chem. 2009, 109, 2490–2494. [Google Scholar] [CrossRef]
- Nagy, Á.; Romera, E. Maximum Rényi entropy principle and the generalized Thomas-Fermi model. Phys. Lett. A 2009, 373, 844–846. [Google Scholar] [CrossRef]
- Antolín, J.; Angulo, J.C. Complexity analysis of ionization processes and isoelectronic series. Int. J. Quantum Chem. 2009, 109, 586–593. [Google Scholar] [CrossRef]
- Antolín, J.; López-Rosa, S.; Angulo, J. Renyi complexities and information planes: Atomic structure in conjugated spaces. Chem. Phys. Lett. 2009, 474, 233–237. [Google Scholar] [CrossRef]
- Delgado-Soler, L.; Toral, R.; Tomás, M.S.; Rubio-Martinez, J. RED: A set of molecular descriptors based on Rényi entropy. J. Chem. Inf. Model. 2009, 49, 2457–2468. [Google Scholar] [CrossRef] [PubMed]
- López-Rosa, S.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa, J.S. Entropy and complexity analysis of hydrogenic Rydberg atoms. J. Math. Phys. 2013, 54, 052109. [Google Scholar] [CrossRef]
- Nagy, Á. Shannon entropy density as a descriptor of Coulomb systems. Chem. Phys. Lett. 2013, 556, 355–358. [Google Scholar] [CrossRef]
- Molina-Espíritu, M.; Esquivel, R.O.; Kohout, M.; Angulo, J.C.; Dobado, J.A.; Dehesa, J.S.; LópezRosa, S.; Soriano-Correa, C. Insight into the informational-structure behavior of the Diels-Alder reaction of cyclopentadiene and maleic anhydride. J. Mol. Model. 2014, 20, 2631. [Google Scholar] [CrossRef] [PubMed]
- Welearegay, M.A.; Balawender, R.; Holas, A. Information and complexity measures in molecular reactivity studies. Phys. Chem. Chem. Phys. 2014, 16, 14928–14946. [Google Scholar] [CrossRef] [PubMed]
- Nagy, Á.; Romera, E. Relative Rényi entropy and fidelity susceptibility. Europhys. Lett. 2015, 109, 60002. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Molina-Espíritu, M.; López-Rosa, S.; Soriano-Correa, C.; Barrientos-Salcedo, C.; Kohout, M.; Dehesa, J.S. Predominant Information Quality Scheme for the Essential Amino Acids: An Information-Theoretical Analysis. ChemPhysChem 2015, 16, 2571–2581. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.H.; Ho, Y.K. Shannon information entropy in position space for two-electron atomic systems. Chem. Phys. Lett. 2015, 633, 261–264. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion. Atoms 2015, 3, 422–432. [Google Scholar] [CrossRef]
- Peng, H.T.; Ho, Y.K. Statistical Correlations of the N-particle Moshinsky Model. Entropy 2015, 17, 1882–1895. [Google Scholar] [CrossRef]
- Rong, C.; Lu, T.; Ayers, P.W.; Chattaraj, P.K.; Liu, S. Scaling properties of information-theoretic quantities in density functional reactivity theory. Phys. Chem. Chem. Phys. 2015, 17, 4977–4988. [Google Scholar] [CrossRef]
- Rong, C.; Lu, T.; Ayers, P.W.; Chattaraj, P.K.; Liu, S. Correction: Scaling properties of information-theoretic quantities in density functional reactivity theory. Phys. Chem. Chem. Phys. 2015, 17, 11110–11111. [Google Scholar] [CrossRef]
- Liu, S.B.; Rong, C.Y.; Wu, Z.M.; Lu, T. Rényi entropy, Tsallis entropy and Onicescu information energy in density functional reactivity theory. Acta Phys.-Chim. Sin. 2015, 31, 2057–2063. [Google Scholar] [CrossRef]
- Esquivel, R.O.; López-Rosa, S.; Molina-Espíritu, M.; Angulo, J.C.; Dehesa, J.S. Information-theoretic space from simple atomic and molecular systems to biological and pharmacological molecules. Theor. Chem. Acc. 2016, 135, 253. [Google Scholar] [CrossRef]
- Liu, S.B. Information-Theoretic Approach in Density Functional Reactivity Theory. Acta Phys.-Chim. Sin. 2016, 32, 98–118. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Rong, C.; Lu, T.; Zhou, P.; Liu, S. Information Functional Theory: Electronic Properties as Functionals of Information for Atoms and Molecules. J. Phys. Chem. A 2016, 120, 3634–3642. [Google Scholar] [CrossRef] [PubMed]
- Alipour, M.; Safari, Z. From information theory to quantitative description of steric effects. Phys. Chem. Chem. Phys. 2016, 18, 17917–17929. [Google Scholar] [CrossRef] [PubMed]
- Toranzo, I.V.; Dehesa, J.S. Rényi, Shannon and Tsallis entropies of Rydberg hydrogenic systems. Europhys. Lett. 2016, 113, 48003. [Google Scholar] [CrossRef]
- Toranzo, I.V.; Puertas-Centeno, D.; Dehesa, J.S. Entropic properties of D-dimensional Rydberg systems. Physica A 2016, 462, 1197–1206. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Toranzo, I.V.; Puertas-Centeno, D. Entropic measures of Rydberg-like harmonic states. Int. J. Quantum Chem. 2017, 117, 48–56. [Google Scholar] [CrossRef]
- Huang, Y.; Rong, C.; Zhang, R.; Liu, S. Evaluating frontier orbital energy and HOMO/LUMO gap with descriptors from density functional reactivity theory. J. Mol. Model. 2017, 23, 3. [Google Scholar] [CrossRef]
- Farid, M.; Abdel-Hady, A.; Nasser, I. Comparative study of the scaling behavior of the Rényi entropy for He-like atoms. J. Phys. Conf. Ser. 2017, 869, 012011. [Google Scholar] [CrossRef]
- Nasser, I.; Zeama, M.; Abdel-Hady, A. The Rényi entropy, a comparative study for He-like atoms using the exponential-cosine screened Coulomb potential. Results Phys. 2017, 7, 3892–3900. [Google Scholar] [CrossRef]
- Zan, L.R.; Jiao, L.G.; Ma, J.; Ho, Y.K. Information-theoretic measures of hydrogen-like ions in weakly coupled Debye plasmas. Phys. Plasmas 2017, 24, 122101. [Google Scholar] [CrossRef]
- Cao, X.; Rong, C.; Zhong, A.; Lu, T.; Liu, S. Molecular acidity: An accurate description with information-theoretic approach in density functional reactivity theory. J. Comput. Chem. 2018, 39, 117–129. [Google Scholar] [CrossRef] [PubMed]
- Jiao, L.G.; Zan, L.R.; Zhang, Y.Z.; Ho, Y.K. Benchmark values of Shannon entropy for spherically confined hydrogen atom. Int. J. Quantum Chem. 2017, 117, e25375. [Google Scholar] [CrossRef]
- Laguna, H.G.; Sagar, R.P. Information theoretical measures from cumulative and survival densities in quantum systems. Int. J. Quantum Chem. 2017, 117, e25387. [Google Scholar] [CrossRef]
- Alipour, M.; Badooei, Z. Toward Electron Correlation and Electronic Properties from the Perspective of Information Functional Theory. J. Phys. Chem. A 2018, 122, 6424–6437. [Google Scholar] [CrossRef]
- Alipour, M. Which information theoretic quantity should we choose for steric analysis of water nanoclusters (H2O)n (n = 6,32,64)? Acta Phys.-Chim. Sin. 2018, 34, 407–413. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures in free and confined hydrogen atom. Int. J. Quantum Chem. 2018, 118, e25596. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures for non-zero l states of confined hydrogen-like ions. Eur. Phys. J. D 2018, 72, 118. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-Entropic Measures in Confined Isotropic Harmonic Oscillator. Adv. Theory Simul. 2018, 1, 1800090. [Google Scholar] [CrossRef]
- Nasser, I.; Zeama, M.; Abdel-Hady, A. The nonadditive entropy for the ground state of helium-like ions using Hellmann potential. Mol. Phys. 2019, 2019, 1612105. [Google Scholar] [CrossRef]
- Zeama, M.; Nasser, I. Tsallis entropy calculation for non-Coulombic helium. Physica A 2019, 528, 121468. [Google Scholar] [CrossRef]
- López-Rosa, S.; Martín, A.L.; Antolín, J.; Angulo, J.C. Electron-pair entropic and complexity measures in atomic systems. Int. J. Quantum Chem. 2019, 119, e25861. [Google Scholar] [CrossRef]
- Ou, J.H.; Ho, Y.K. Benchmark calculations of Rényi, Tsallis entropies, and Onicescu information energy for ground state helium using correlated Hylleraas wave functions. Int. J. Quantum Chem. 2019, 119, e25928. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Omiste, J.J.; Dehesa, J.S. Entropic functionals of Laguerre polynomials and complexity properties of the half-line Coulomb potential. Int. J. Quantum Chem. 2011, 111, 2283–2294. [Google Scholar] [CrossRef]
- Sun, G.H.; Dong, S.H.; Saad, N. Quantum information entropies for an asymmetric trigonometric Rosen-Morse potential. Ann. Phys. 2013, 525, 934–943. [Google Scholar] [CrossRef]
- Dong, S.; Sun, G.H.; Dong, S.H.; Draayer, J. Quantum information entropies for a squared tangent potential well. Phys. Lett. A 2014, 378, 124–130. [Google Scholar] [CrossRef]
- Yahya, W.A.; Oyewumi, K.J.; Sen, K.D. Position and momentum information-theoretic measures of the pseudoharmonic potential. Int. J. Quantum Chem. 2015, 115, 1543–1552. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.; Roy, A.K. Information entropy as a measure of tunneling and quantum confinement in a symmetric double-well potential. Ann. Phys. 2015, 527, 825–845. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Quantum confinement in an asymmetric double-well potential through energy analysis and information entropic measure. Ann. Phys. 2016, 528, 412–433. [Google Scholar] [CrossRef]
- Ghosal, A.; Mukherjee, N.; Roy, A.K. Information entropic measures of a quantum harmonic oscillator in symmetric and asymmetric confinement within an impenetrable box. Ann. Phys. 2016, 528, 796–818. [Google Scholar] [CrossRef]
- Isonguyo, C.N.; Oyewumi, K.J.; Oyun, O.S. Quantum information-theoretic measures for the static screened Coulomb potential. Int. J. Quantum Chem. 2018, 118, e25620. [Google Scholar] [CrossRef]
- Onate, C.A.; Ikot, A.N.; Onyeaju, M.C.; Ebomwonyi, O.; Idiodi, J.O.A. Effect of dissociation energy on Shannon and Rényi entropies. Karbala Int. J. Mod. Sci. 2018, 4, 134–142. [Google Scholar] [CrossRef]
- Olendski, O. Quantum Information Measures of the One-Dimensional Robin Quantum Well. Ann. Phys. 2018, 530, 1700324. [Google Scholar] [CrossRef]
- Olendski, O. Rényi and Tsallis entropies: three analytic examples. Eur. J. Phys. 2019, 40, 025402. [Google Scholar] [CrossRef]
- Ilić, V.M.; Stanković, M.S. A unified characterization of generalized information and certainty measures. Physica A 2014, 415, 229–239. [Google Scholar] [CrossRef]
- Hylleraas, E.A. Über den Grundzustand des Heliumatoms. Z. Phys. 1928, 48, 469–494. [Google Scholar] [CrossRef]
- Hylleraas, E.A. Neue Berechnung der Energie des Heliums im Grundzustande, sowie des tiefsten Terms von Ortho-Helium. Z. Phys. 1929, 54, 347–366. [Google Scholar] [CrossRef]
- Hylleraas, E.A. Über den Grundterm der Zweielektronenprobleme von H−, He, Li+, Be++ usw. Z. Phys. 1930, 65, 209–225. [Google Scholar] [CrossRef]
- Löwdin, P.O. Correlation Problem in Many-Electron Quantum Mechanics I. Review of Different Approaches and Discussion of Some Current Ideas. In Advances in Chemical Physics; Prigogine, I., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1958; Volume 2, Chapter 7; pp. 207–322. [Google Scholar] [CrossRef]
- Yoshizumi, H. Correlation Problem in Many-Electron Quantum Mechanics. II. Bibliographical Survey of the Historical Development with Comments. In Advances in Chemical Physics; Prigogine, I., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1958; Volume 2, Chapter 8; pp. 323–366. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Parr, R.G.; Bartolotti, L.J. Some remarks on the density functional theory of few-electron systems. J. Phys. Chem. 1983, 87, 2810–2815. [Google Scholar] [CrossRef]
- De Proft, F.; Geerlings, P. Contribution of the shape factor σ(r) to atomic and molecular electronegativities. J. Phys. Chem. A 1997, 101, 5344–5346. [Google Scholar] [CrossRef]
- Ayers, P.W.; De Proft, F.; Geerlings, P. Comparison of the utility of the shape function and electron density for predicting periodic properties: Atomic ionization potentials. Phys. Rev. A 2007, 75, 012508. [Google Scholar] [CrossRef]
- Ayers, P.W. Density per particle as a descriptor of Coulombic systems. Proc. Natl. Acad. Sci. USA 2000, 97, 1959–1964. [Google Scholar] [CrossRef] [PubMed]
- De Proft, F.; Ayers, P.W.; Sen, K.D.; Geerlings, P. On the importance of the “density per particle” (shape function) in the density functional theory. J. Chem. Phys. 2004, 120, 9969–9973. [Google Scholar] [CrossRef] [PubMed]
- Calais, J.L.; Löwdin, P.O. A simple method of treating atomic integrals containing functions of r12. J. Mol. Spectrosc. 1962, 8, 203–211. [Google Scholar] [CrossRef]
- Drake, G. High Precision Calculations for Helium. In Springer Handbook of Atomic, Molecular, and Optical Physics; Drake, G., Ed.; Springer: New York, NY, USA, 2006; Chapter 11; pp. 199–219. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantification of Entanglement Entropy in Helium by the Schmidt-Slater Decomposition Method. Few-Body Syst. 2014, 55, 1141–1149. [Google Scholar] [CrossRef]
- Katriel, J.; Montgomery, H.E.; Sen, K.D. Hund’s rule in the (1s2s)1,3S states of the two-electron Debye atom. Phys. Plasmas 2018, 25, 092111. [Google Scholar] [CrossRef]
- Katriel, J.; Montgomery, H.E. Atomic vs. quantum dot open shell spectra. J. Chem. Phys. 2017, 146, 064104. [Google Scholar] [CrossRef]
- Sarsa, A.; Buendía, E.; Gálvez, F.; Katriel, J. Singlet vs. triplet interelectronic repulsion in confined atoms. Chem. Phys. Lett. 2018, 702, 106–110. [Google Scholar] [CrossRef]
- Angulo, J.C.; Dehesa, J.S. Tight rigorous bounds to atomic information entropies. J. Chem. Phys. 1992, 97, 6485–6495. [Google Scholar] [CrossRef]
- Angulo, J.C.; Dehesa, J.S. Erratum: Tight rigorous bounds to atomic information entropies [J. Chem. Phys. 97, 6485 (1992)]. J. Chem. Phys. 1993, 98, 9223. [Google Scholar] [CrossRef]
- Tao, J.; Li, G.; Li, J. Bounds to information entropies for atomic systems. J. Chem. Phys. 1997, 107, 1227–1231. [Google Scholar] [CrossRef]
- Tao, J.; Li, G.; Li, J. Rigorous bounds to information entropies for atomic systems. Phys. Scr. 1997, 56, 284–288. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Zozor, S.; Dehesa, J.S. Upper bounds on Shannon and Rényi entropies for central potentials. J. Math. Phys. 2011, 52, 022105. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Zozor, S.; Dehesa, J.S. Rigorous bounds for Rényi entropies of spherically symmetric potentials. AIP Conf. Proc. 2011, 1305, 192–199. [Google Scholar] [CrossRef]
- Hornyák, I.; Nagy, Á. Inequalities for phase-space Rényi entropies. Int. J. Quantum Chem. 2012, 112, 1285–1290. [Google Scholar] [CrossRef]
- Nahum, A.; Ruhman, J.; Huse, D.A. Dynamics of entanglement and transport in one-dimensional systems with quenched randomness. Phys. Rev. B 2018, 98, 035118. [Google Scholar] [CrossRef]
- Barghathi, H.; Herdman, C.; Maestro, A.D. Rényi Generalization of the Accessible Entanglement Entropy. Phys. Rev. Lett. 2018, 121, 150501. [Google Scholar] [CrossRef]
- Herdman, C.M.; Roy, P.N.; Melko, R.G.; Maestro, A.D. Entanglement area law in superfluid 4He. Nat. Phys. 2017, 13, 556–558. [Google Scholar] [CrossRef]
- Kaufman, A.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Schittko, R.; Preiss, P.M.; Greiner, M. Quantum thermalization through entanglement in an isolated many-body system. Science 2016, 353, 794–800. [Google Scholar] [CrossRef]
- Islam, R.; Ma, R.; Preiss, P.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Greiner, M. Measuring entanglement entropy in a quantum many-body system. Nature 2015, 528, 77–83. [Google Scholar] [CrossRef]
- McMinis, J.; Tubman, N.M. Renyi entropy of the interacting Fermi liquid. Phys. Rev. B 2013, 87, 081108(R). [Google Scholar] [CrossRef]
- Lévay, P.; Nagy, S.; Pipek, J. Elementary formula for entanglement entropies of fermionic systems. Phys. Rev. A 2005, 72, 022302. [Google Scholar] [CrossRef]
- Rouse, I.; Willitsch, S. Superstatistical Energy Distributions of an Ion in an Ultracold Buffer Gas. Phys. Rev. Lett. 2017, 118, 143401. [Google Scholar] [CrossRef] [PubMed]
- Dechant, A.; Kessler, D.A.; Barkai, E. Deviations from Boltzmann-Gibbs Statistics in Confined Optical Lattices. Phys. Rev. Lett. 2015, 115, 173006. [Google Scholar] [CrossRef] [PubMed]
- Douglas, P.; Bergamini, S.; Renzoni, F. Tunable Tsallis Distributions in Dissipative Optical Lattices. Phys. Rev. Lett. 2006, 96, 110601. [Google Scholar] [CrossRef] [PubMed]
- Lutz, E. Anomalous diffusion and Tsallis statistics in an optical lattice. Phys. Rev. A 2003, 67, 051402(R). [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher-Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- Sagar, R.P.; Guevara, N.L. Mutual information and correlation measures in atomic systems. J. Chem. Phys. 2005, 123, 044108. [Google Scholar] [CrossRef] [PubMed]
- Grassi, A. A relationship between atomic correlation energy and Tsallis entropy. Int. J. Quantum Chem. 2008, 108, 774–778. [Google Scholar] [CrossRef]
- Delle Site, L. On the scaling properties of the correlation term of the electron kinetic functional and its relation to the Shannon measure. Europhys. Lett. 2009, 86, 40004. [Google Scholar] [CrossRef]
- Delle Site, L. Erratum: On the scaling properties of the correlation term of the electron kinetic functional and its relation to the Shannon measure. Europhys. Lett. 2009, 88, 19901. [Google Scholar] [CrossRef]
- Grassi, A. A relationship between atomic correlation energy of neutral atoms and generalized entropy. Int. J. Quantum Chem. 2011, 111, 2390–2397. [Google Scholar] [CrossRef]
- Delle Site, L. Shannon entropy and many-electron correlations: Theoretical concepts, numerical results, and Collins conjecture. Int. J. Quantum Chem. 2014, 115, 1396–1404. [Google Scholar] [CrossRef]
- Flores-Gallegos, N. Informational energy as a measure of electron correlation. Chem. Phys. Lett. 2016, 666, 62–67. [Google Scholar] [CrossRef]
- Alipour, M.; Badooei, Z. Information theoretic approach provides a reliable description for kinetic component of correlation energy density functional. Int. J. Quantum Chem. 2018, 118, e25791. [Google Scholar] [CrossRef]
- Collins, D.M. Entropy Maximizations on Electron Density. Z. Naturforsch. A 1993, 48, 68–74. [Google Scholar] [CrossRef]
- López-Rosa, S.; Esquivel, R.O.; Plastino, A.R.; Dehesa, J.S. Quantum entanglement of helium-like systems with varying-Z: compact state-of-the-art CI wave functions. J. Phys. B 2015, 48, 175002. [Google Scholar] [CrossRef]
- Esquivel, R.O.; López-Rosa, S.; Dehesa, J.S. Correlation energy as a measure of non-locality: Quantum entanglement of helium-like systems. Europhys. Lett. 2015, 111, 40009. [Google Scholar] [CrossRef]


| Spin Multiplicity Of The State | Relation between and | Restriction on m and n | Starts from |
|---|---|---|---|
| singlet | |||
| singlet | |||
| triplet | |||
| triplet |
| State | State | ||||
|---|---|---|---|---|---|
| 1s1s | 2.00 | 2.00 | |||
| 1s2s | 1.19 | 2.80 | 1s2s | 2.09 | 0.55 |
| 1s3s | 0.74 | 1.94 | 1s3s | 0.78 | 1.90 |
| State | E | S |
|---|---|---|
| −2.903724371 | 2.70510285 | |
| Drake [105] | −2.9037243770341195 | |
| Lin and Ho [52] | −2.9037243768 | 2.7051028 |
| Ou and Ho [11] | −2.903724371 | 2.70510285 |
| Restrepo Cuartas and Sanz-Vicario [10] | −2.903605 | 2.705 |
| −2.145974042 | 5.49196878 | |
| Drake [105] | −2.145974046054419(6) | |
| Lin and Ho [106] | −2.145974042 | |
| Ou and Ho [11] | −2.145974012 | 5.49196837 |
| Katriel et al. [107] | −2.1459740 | |
| Restrepo Cuartas and Sanz-Vicario [10] | −2.145967 | 5.492 |
| −2.175229377 | 5.23597814 | |
| Drake [105] | −2.17522937823679130 | |
| Lin and Ho [106] | −2.17522937822 | |
| Katriel et al. [107] | −2.1752294 | |
| Restrepo Cuartas and Sanz-Vicario [10] | −2.175229 | 5.236 |
| −2.061271958 | 6.76932178 | |
| Drake [105] | −2.061271989740911(5) | |
| Lin and Ho [106] | −2.06127196 | |
| Restrepo Cuartas and Sanz-Vicario [10] | −2.061270 | 6.769 |
| −2.068 689 066 | 6.605 067 28 | |
| Drake [105] | −2.068 689 067 472 457 19 | |
| Lin and Ho [106] | −2.068 689 06 | |
| Restrepo Cuartas and Sanz-Vicario [10] | −2.068 689 | 6.605 |
| 1s2s | 1s3s | |||
|---|---|---|---|---|
| 0.5 | 7.82736064 | 7.37538422 | 1.00515457 × 101 | 9.75036390 |
| 1 | 5.49196878 | 5.23597814 | 6.76932178 | 6.60506728 |
| 2 | 2.46576126 | 2.46773641 | 2.51349859 | 2.51571175 |
| 3 | 1.70778650 | 1.70278837 | 1.74051392 | 1.74026803 |
| 4 | 1.33674386 | 1.32941893 | 1.36502603 | 1.36403409 |
| 9 | 6.37201665 × 10−1 | 6.28474643 × 10−1 | 6.60262552 × 10−1 | 6.58729039 × 10−1 |
| 1s2s | 1s3s | |||
|---|---|---|---|---|
| 0.5 | 9.81658692 × 101 | 7.79050690 × 101 | 3.02575822 × 102 | 2.59995972 × 102 |
| 1 | 5.49196878 | 5.23597814 | 6.76932178 | 6.60506728 |
| 2 | 9.15055847 × 10−1 | 9.15223459 × 10−1 | 9.19015588 × 10−1 | 9.19194622 × 10−1 |
| 3 | 4.83571213 × 10−1 | 4.83406163 × 10−1 | 4.84612118 × 10−1 | 4.84604549 × 10−1 |
| 4 | 3.27290267 × 10−1 | 3.27156002 × 10−1 | 3.27781851 × 10−1 | 3.27765306 × 10−1 |
| 9 | 1.24236085 × 10−1 | 1.24180846 × 10−1 | 1.24364781 × 10−1 | 1.24356940 × 10−1 |
| 1s2s | 1s3s | |||
|---|---|---|---|---|
| 0.5 | −1.00165869 × 102 | −7.99050690 × 101 | −3.04575822 × 102 | −2.61995972 × 102 |
| 2 | 8.49441529 × 10−2 | 8.47765409 × 10−2 | 8.09844111 × 10−2 | 8.08053779 × 10−2 |
| 3 | 1.64287869 × 10−2 | 1.65938368 × 10−2 | 1.53878810 × 10−2 | 1.53954502 × 10−2 |
| 4 | 6.04306538 × 10−3 | 6.17733033 × 10−3 | 5.55148184 × 10−3 | 5.56802665 × 10−3 |
| 9 | 7.63914364 × 10−4 | 8.19153809 × 10−4 | 6.35218223 × 10−4 | 6.43059145 × 10−4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.-H.; Ho, Y.K. Shannon, Rényi, Tsallis Entropies and Onicescu Information Energy for Low-Lying Singly Excited States of Helium. Atoms 2019, 7, 70. https://doi.org/10.3390/atoms7030070
Ou J-H, Ho YK. Shannon, Rényi, Tsallis Entropies and Onicescu Information Energy for Low-Lying Singly Excited States of Helium. Atoms. 2019; 7(3):70. https://doi.org/10.3390/atoms7030070
Chicago/Turabian StyleOu, Jen-Hao, and Yew Kam Ho. 2019. "Shannon, Rényi, Tsallis Entropies and Onicescu Information Energy for Low-Lying Singly Excited States of Helium" Atoms 7, no. 3: 70. https://doi.org/10.3390/atoms7030070
APA StyleOu, J.-H., & Ho, Y. K. (2019). Shannon, Rényi, Tsallis Entropies and Onicescu Information Energy for Low-Lying Singly Excited States of Helium. Atoms, 7(3), 70. https://doi.org/10.3390/atoms7030070






