Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods
Abstract
1. Introduction
2. Analysis
2.1. Nonlinear Processing of the Zero-Point Field
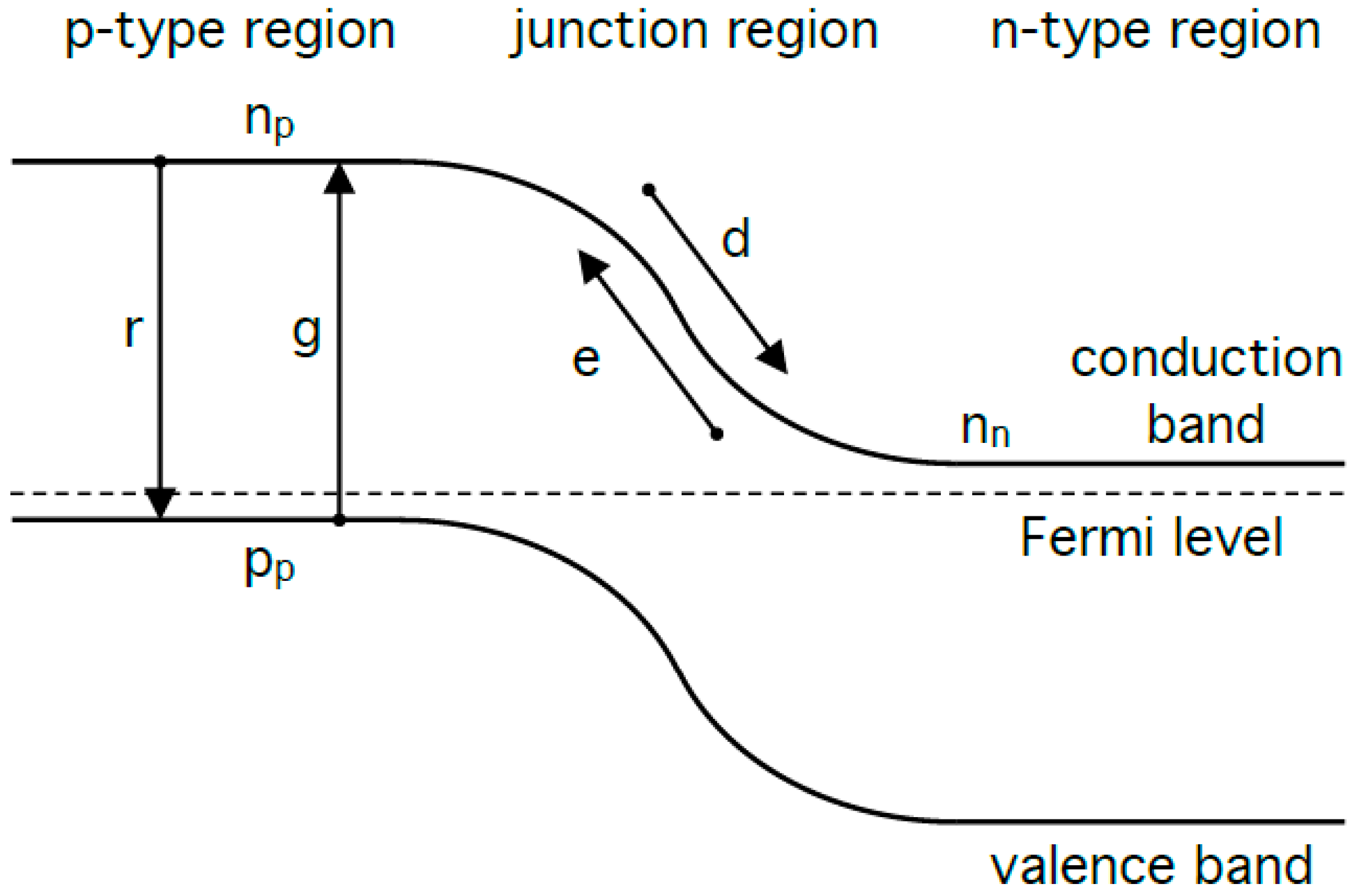
2.1.1. Rectification of Zero-Point Fluctuations in a Diode
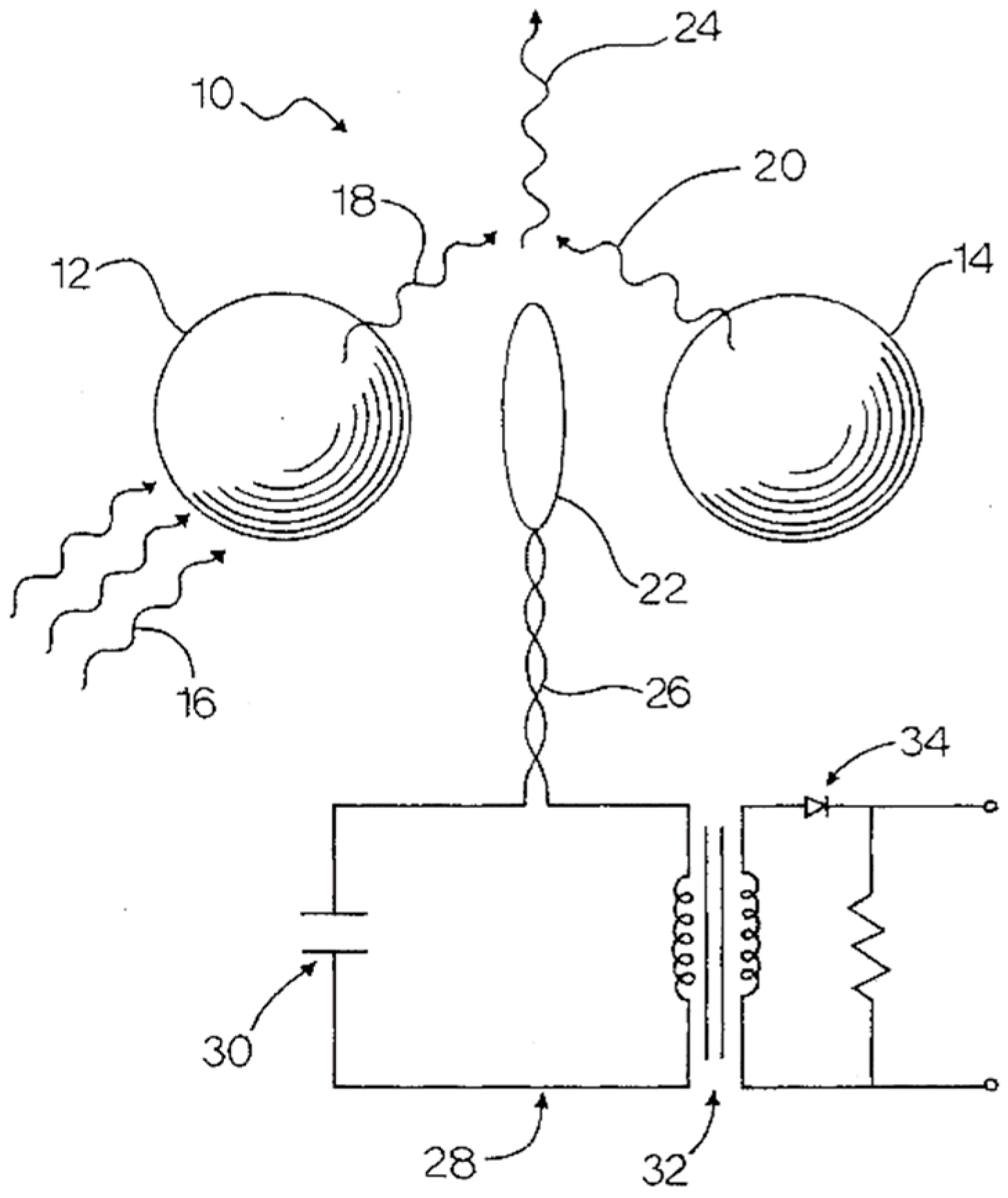
2.1.2. Harvesting of Vacuum Fluctuations Using a Down-Converter and Antenna-Coupled Rectifier
- (a)
- Producing lower beat frequency radiation from the ambient ZPF;
- (b)
- Collecting the beat-frequency radiation at the diode by the antenna;
- (c)
- Rectification of the concentrated radiation by the diode.
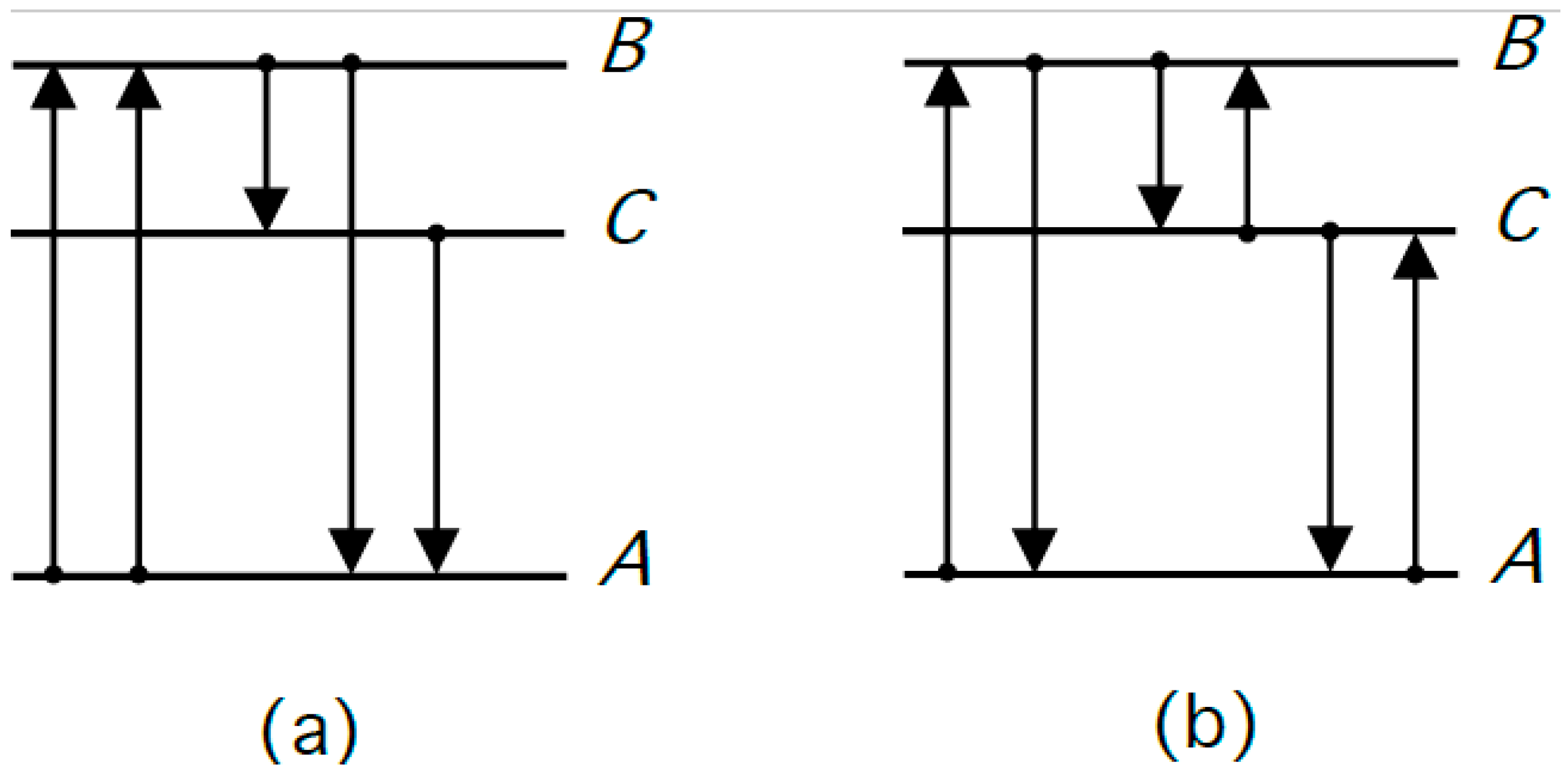
2.1.3. Nonlinear Processing of Background Fields in Nature
2.2. Mechanical Extraction Using Casimir Cavities
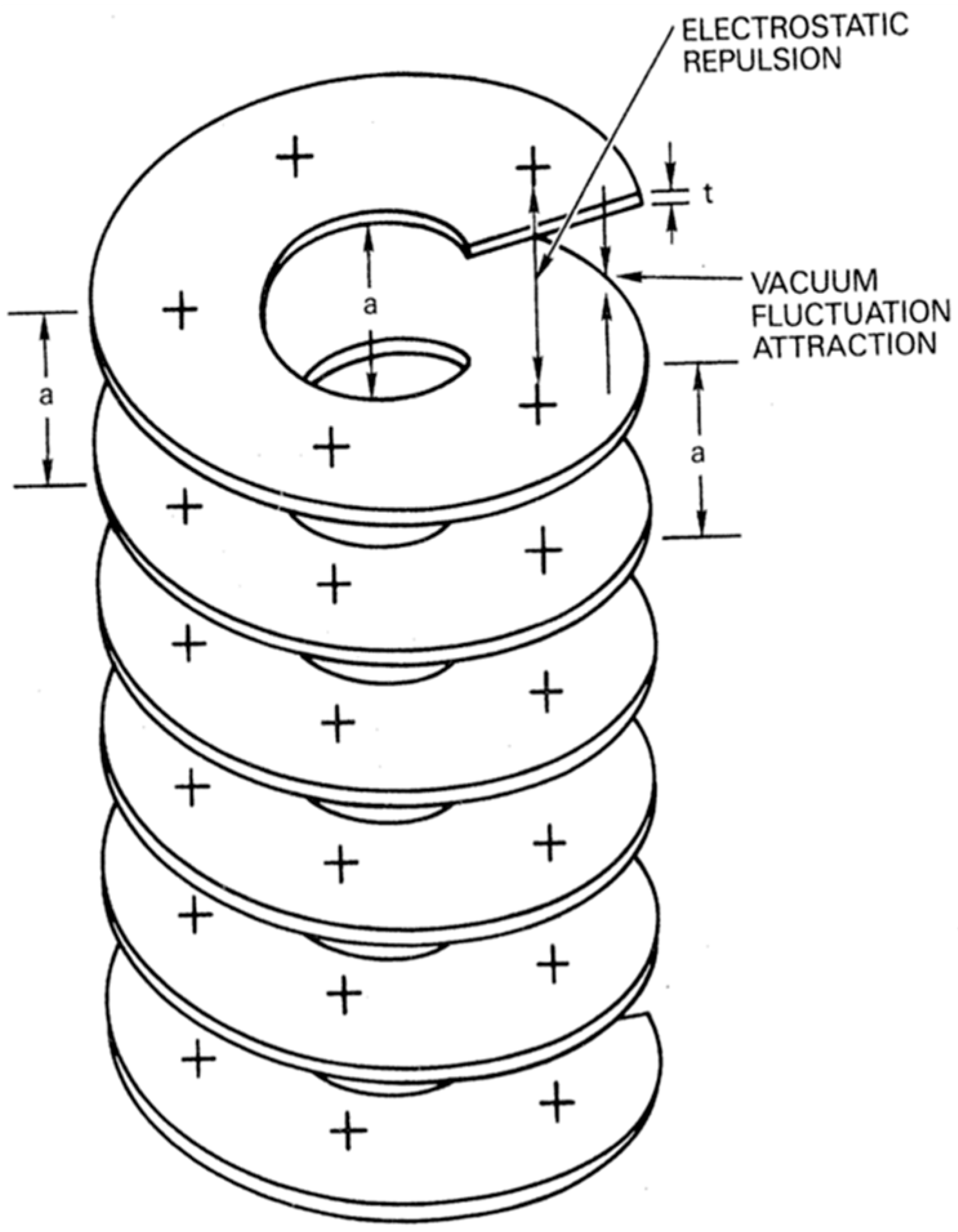
2.2.1. Energy Exchange between Casimir Plates and an Electrical Power Supply
2.2.2. Cyclic Power Extraction from Casimir Cavity Oscillations
2.3. Pumping Atoms through Casimir Cavities
2.3.1. Zero-Point Energy Ground State and Casimir Cavities
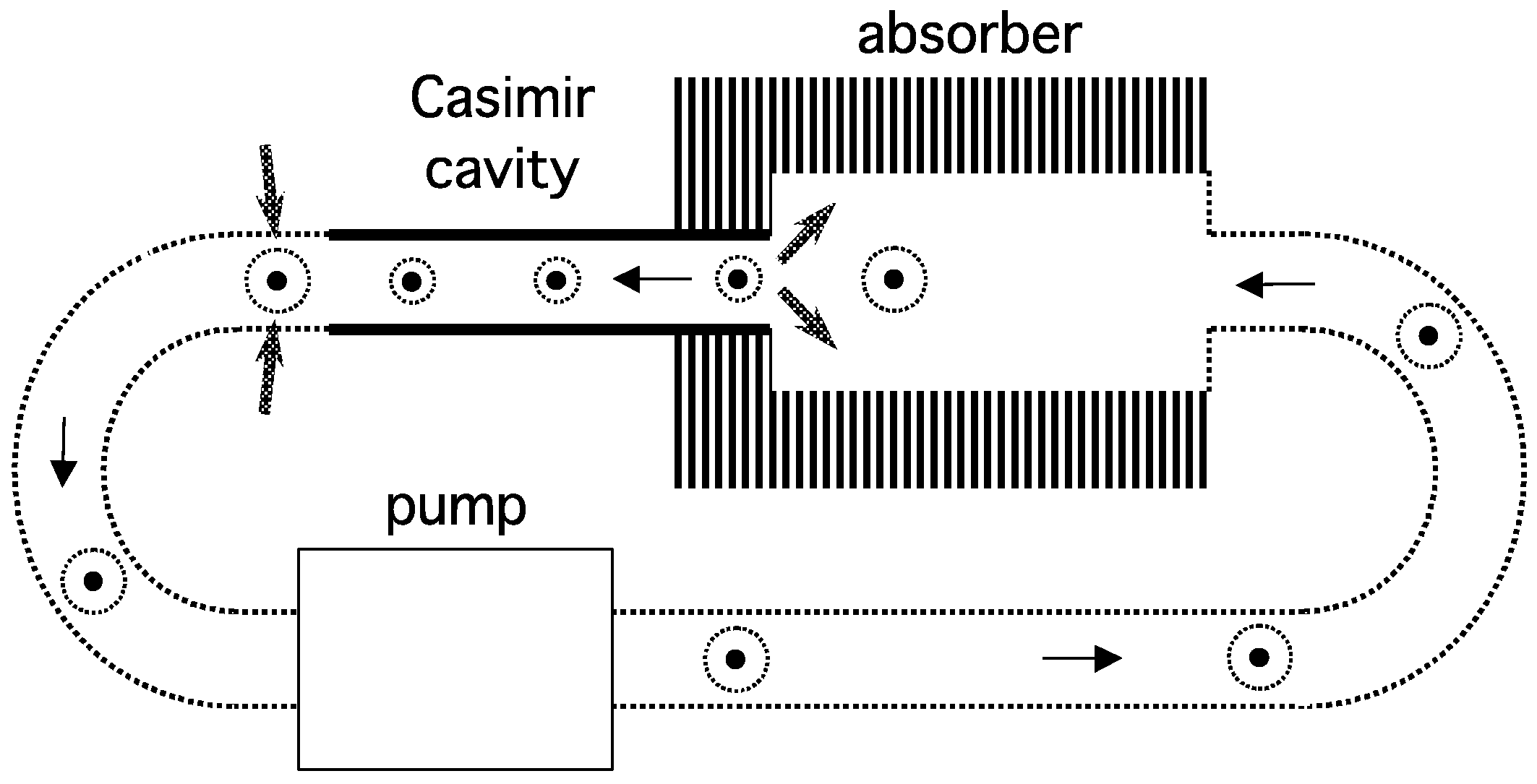
2.3.2. The Extraction Process
2.3.3. Experimental Test of Radiant Emission Due to Gas Flow
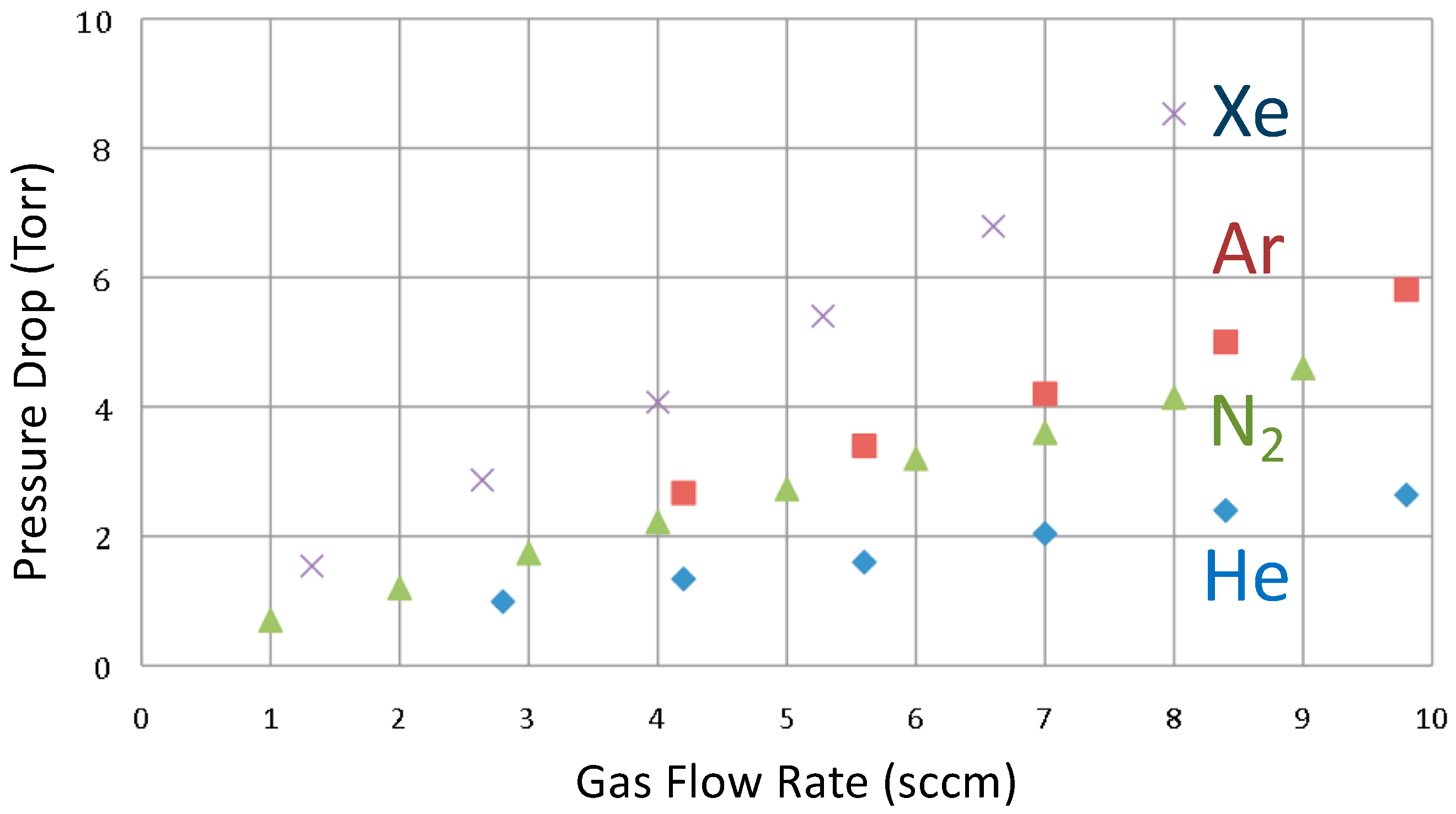
2.3.4. Test of Frictional Heating as a Source for the Observed Radiation
2.3.5. Test of the Joule-Thomson Effect as a Source for the Observed Radiation
2.3.6. Turbulence as a Potential Source for the Observed Radiation
2.3.7. Absorption/Adsorption as a Potential Source for the Observed Radiation
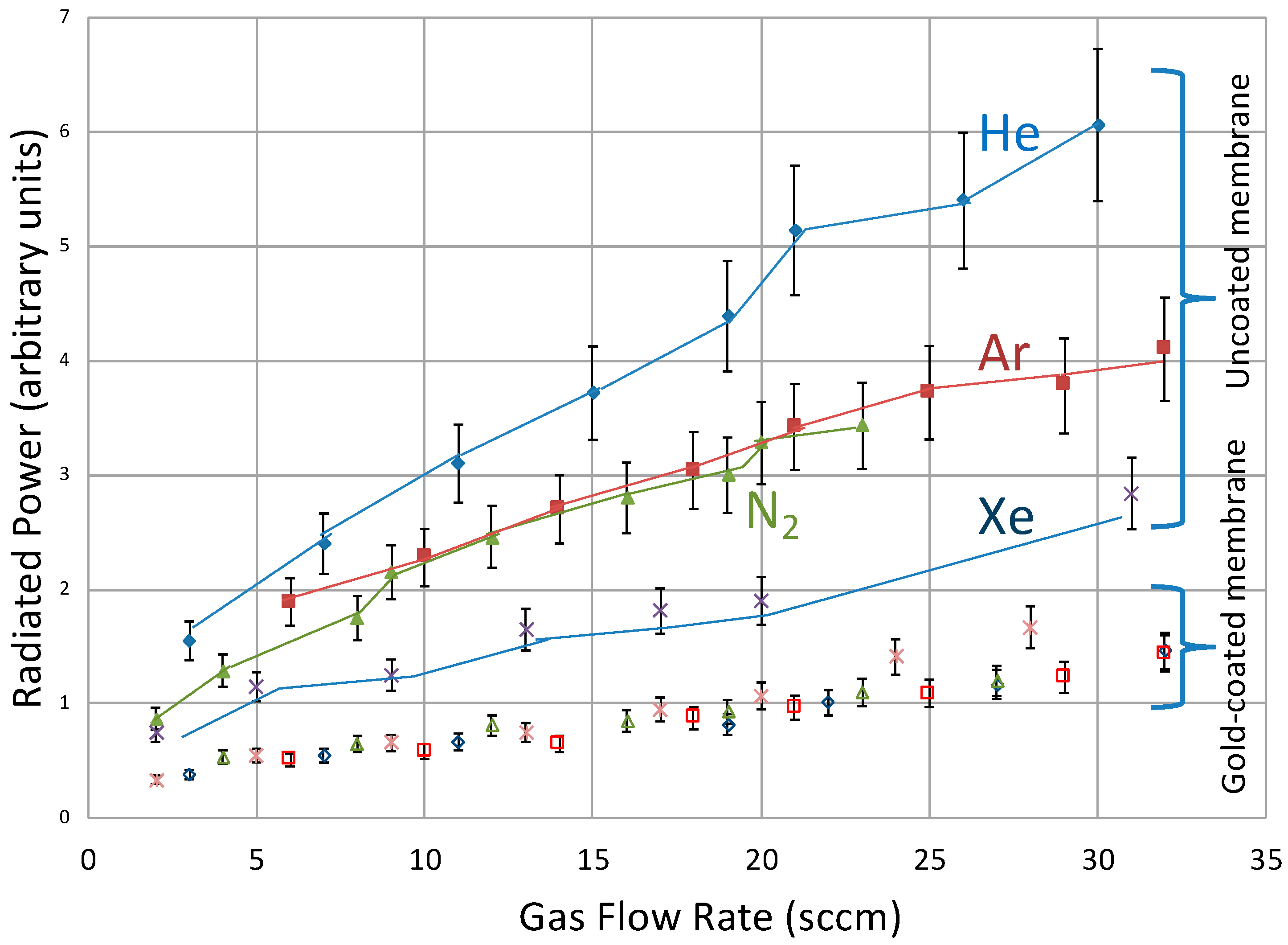
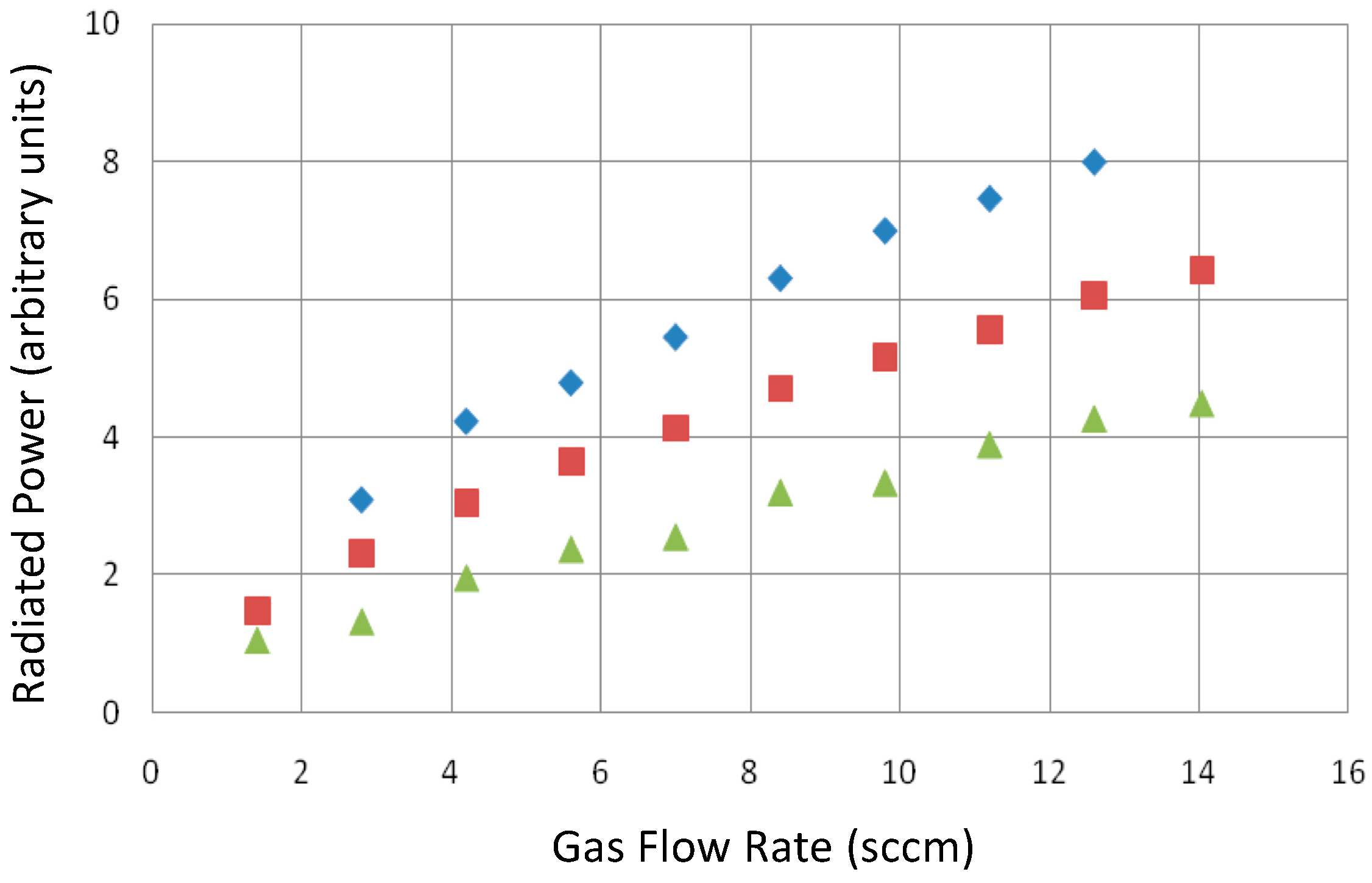
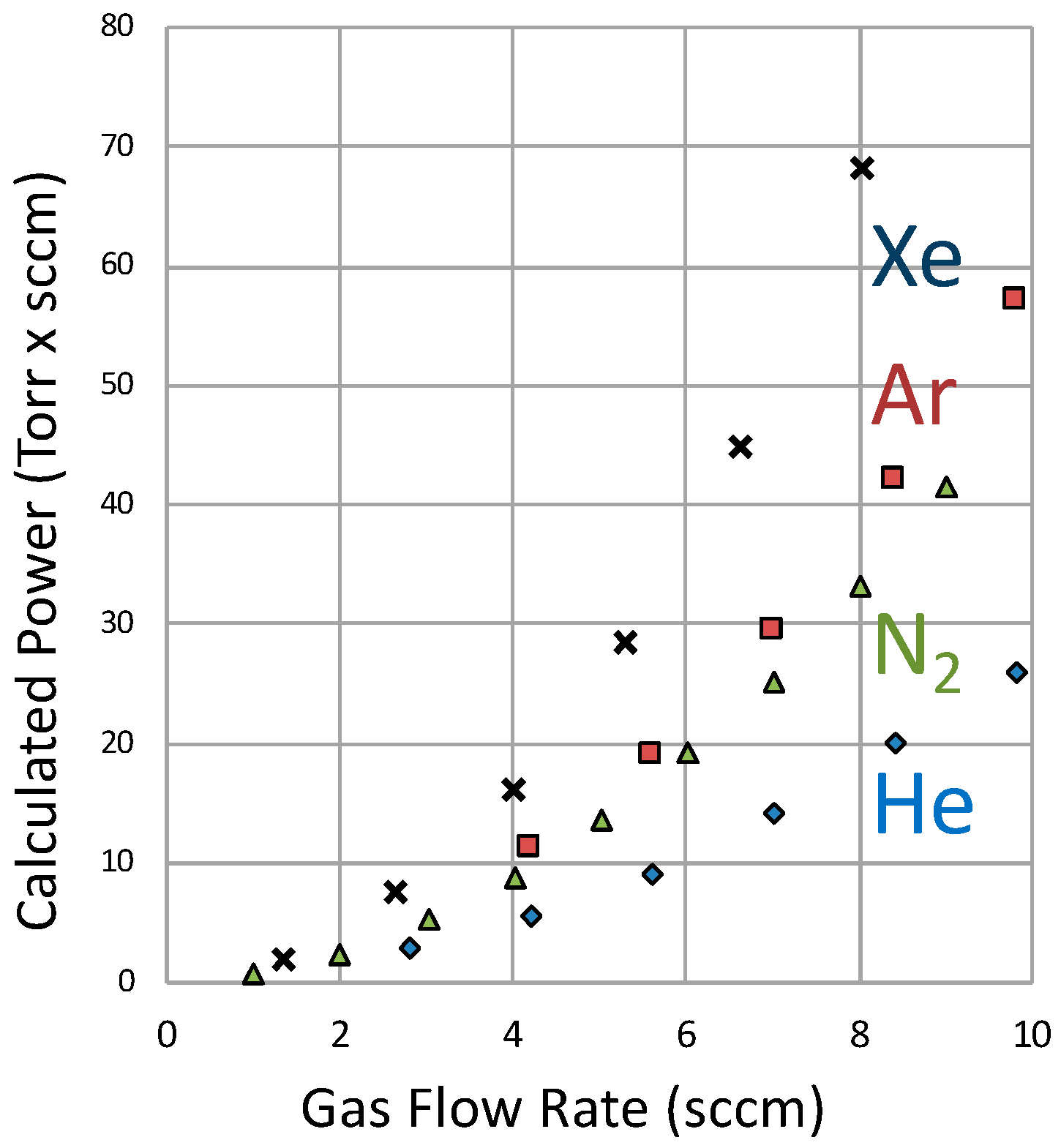
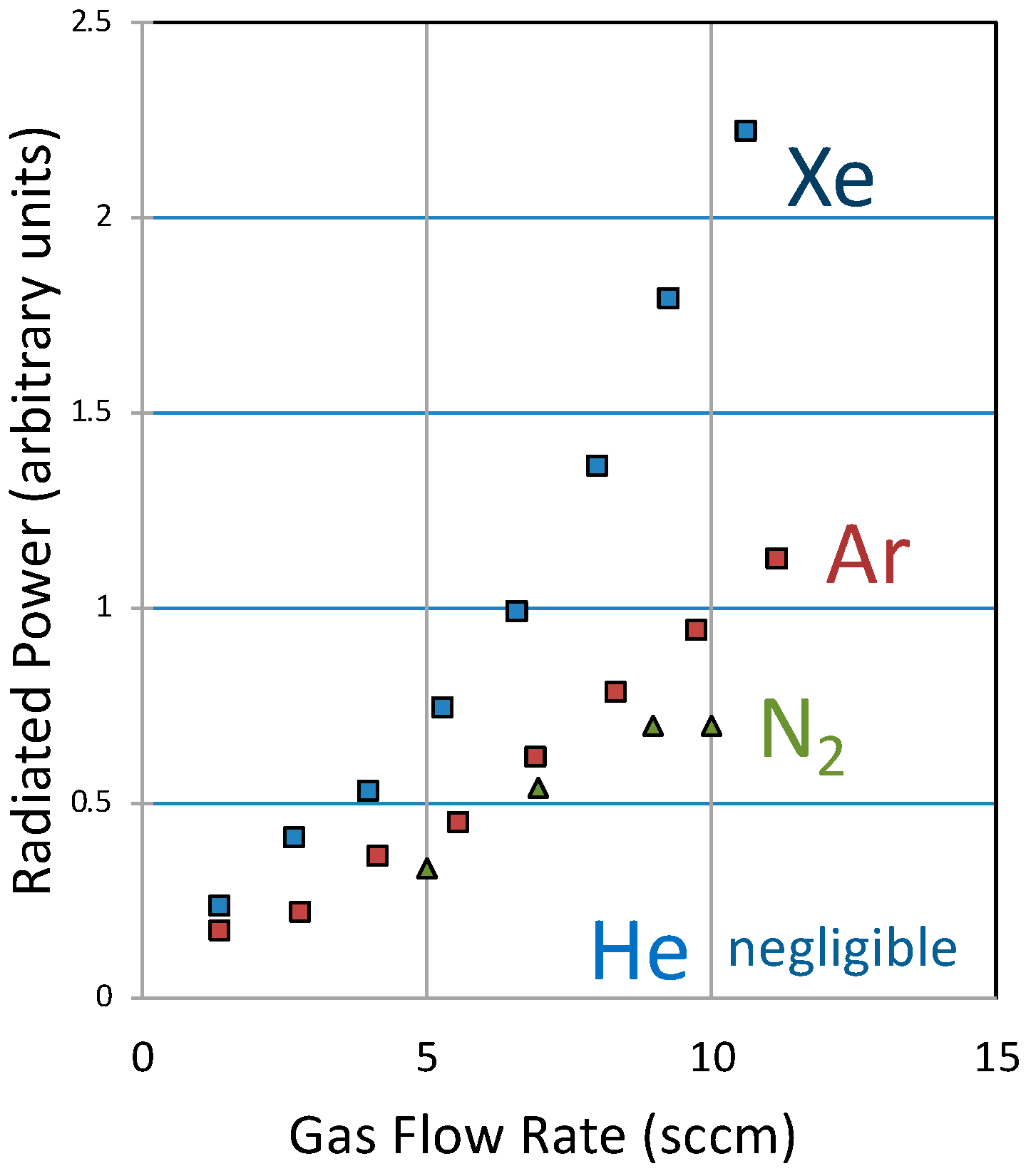
2.3.8. Expected Radiation Power
2.3.9. Deviations from Expected Results
- The measured power is much lower than predicted, as described in the previous section. Some if not all this deviation can be attributed to inconsistent sizes and shapes of the nanopores.
- Another unexpected result is that the uncoated polycarbonate membranes produced much more radiation than the gold-coated devices. It is expected that the metal-walled Casimir cavities are more effective than the dielectric-walled cavities in suppressing interior modes, although the latter does produce the Casimir effect [29] that are only slightly smaller [54]. A likely reason that more radiation was observed from the polycarbonate is that the emitted power heated the cavity walls and the emissivity of the polycarbonate walls and membrane is much greater than that of the gold.
- We expected to see the greatest emission from the xenon atoms. Their outer orbital frequency corresponds to a wavelength (0.1 µm) that is suppressed in the 0.2 µm cavities (suppressed wavelength is ½ the cavity spacing). That suppressed wavelength is farthest from the wavelength corresponding to the helium orbital (0.05 µm). The opposite was observed. We do not know the reason for this, but it may have to do with more total energy being available from the helium atoms.
2.3.10. Violations of the Second Law of Thermodynamics
2.3.11. Future Work to Investigate Gas Flow through Casimir Cavities
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Milonni, P.W. The Quantum Vacuum; Academic Press: Boston, MA, USA, 1994. [Google Scholar]
- Forward, R.L. Extracting electrical energy from the vacuum by cohesion of charged foliated conductors. Phys. Rev. B 1984, 30, 1700–1702. [Google Scholar] [CrossRef]
- Booth, I.J. Energy extraction from the quantum electrodynamic fluctuations of the vacuum state. Specul. Sci. Technol. 1987, 10, 201–204. [Google Scholar]
- Mead, F.B., Jr.; Nachamkin, J. System for Converting Electromagnetic Radiation Energy to Electrical Energy. U.S. Patent No. 5,590,031, 31 December 1996. [Google Scholar]
- Widom, A.; Sassaroli, E.; Srivastava, Y.N.; Swain, J. The Casimir effect and thermodynamic instability. arXiv 1998, arXiv:quant-ph/9803013v1. [Google Scholar]
- Pinto, F. Method for Energy Extraction-II. U.S. Patent No. 6,920,032, 19 July 2005. [Google Scholar]
- Davis, E.; Teofilo, V.L.; Puthoff, H.E.; Nickisch, L.J.; Rueda, A.; Cole, D.C. Review of experimental concepts for studying the quantum vacuum field. Am. Inst. Phys. Conf. Proc. 2006, 813, 1390–1401. [Google Scholar]
- Haisch, B.; Moddel, G. Quantum Vacuum Energy Extraction. U.S. Patent No. 7,379,286, 27 May 2008. [Google Scholar]
- Valone, T.F. Proposed Use of Zero Bias Diode Arrays as Thermal Electric Noise Rectifiers and Non-Thermal Energy Harvesters. Proc Space, Propulsion and Energy Sciences International Forum, Workshop on Future Energy Sources. Am. Inst. Phys. Conf. Proc. 2009, 1103, 501–512. [Google Scholar]
- Bell, D.A. Electrical Noise: Fundamentals and Physical Mechanism; Van Nostrand: London, UK, 1960; p. 60. [Google Scholar]
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad Wet. 1948, 51, 793–795. [Google Scholar]
- Cole, D.C.; Puthoff, H.E. Extracting energy and heat from the vacuum. Phys. Rev. E 1993, 48, 1562–1565. [Google Scholar] [CrossRef]
- Little, S.R. Null Tests of Breakthrough Energy Claims, 42nd AIAA/ASME/SAE/ASEE; Joint Propulsion Conference & Exhibit: Sacramento, CA, USA, 2006; pp. 1–6. [Google Scholar]
- Abbott, D.A.; Davis, B.R.; Phillips, N.J.; Eshraghian, K. Quantum Vacuum Fluctuations, Zero Point Energy and the Question of Observable Noise. Unsolved Problems of Noise in Physics, Biology, Electronic Technology and Information Technology; Doering, C.R., Kiss, L.B., Shlesinger, M.F., Eds.; World Scientific: Singapore, 1997; pp. 131–138. [Google Scholar]
- Sheehan, D.P. Casimir chemistry. J. Chem. Phys. 2009, 131, 104706. [Google Scholar] [CrossRef]
- Joshi, S.; (University of Colorado, Boulder, CO, USA). Internal research, 2016.
- Lef, H.S.; Rex, A.F. Maxwell’s Demon 2: Entropy, Classical and Quantum Information, Computing; IOP: London, UK, 2003. [Google Scholar]
- Capek, V.; Sheehan, D.P. Challenges to the Second Law of Thermodynamics; Springer: Berlin, Germany, 2005. [Google Scholar]
- D’abramo, G. The peculiar status of the second law of thermodynamics and the quest for its violation. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2012, 43, 226–235. [Google Scholar]
- Sheehan, D.P.; Mallin, D.J.; Garamella, J.T.; Sheehan, W.F. This could prove to be a violation of the Second Law: Experimental test of a thermodynamic paradox. Found. Phys. 2014, 44, 235–247. [Google Scholar] [CrossRef]
- McFee, R. Self-rectification in diodes and the second law of thermodynamics. Am. J. Phys. 1971, 39, 814–829. [Google Scholar] [CrossRef]
- Coutre, L.; Zitoun, R. Statistical Thermodynamics and Properties of Matter; Geissler, E., Translator; Overseas Publishers: Amsterdam, The Netherlands, 2000; p. 229. [Google Scholar]
- Bridgman, P.W. Note on the principle of detailed balancing. Phys. Rev. 1928, 31, 101–102. [Google Scholar] [CrossRef]
- Dannon, H.V. Zero-point energy: Thermodynamic equilibrium and Planck radiation law. Gauge Inst. J. 2005, 1, 1–8. [Google Scholar]
- Brown, W.C. Microwave to DC Converter. U.S. Patent No. 3,434,678, 25 March 1969. [Google Scholar]
- Zhu, Z.; Joshi, S.; Grover, S.; Moddel, G. Graphene geometric diodes for terahertz rectennas. J. Phys. D Appl. Phys. 2013, 46, 185101. [Google Scholar] [CrossRef]
- Garret, M.; Grover, S. (Eds.) Rectenna Solar Cells; Springer: New York, NY, USA, 2013. [Google Scholar]
- Burgess, R.E. Noise in receiving aerial systems. Proc. Phys. Soc. 1941, 53, 293–304. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. In Perspectives in Theoretical Physics; Pergamon: Oxford, UK, 1956; Volume 2, pp. 73–83. [Google Scholar]
- Munday, J.N.; Capasso, F.; Parsegian, A. Measured long-range repulsive Casimir–Lifshitz forces. Nature 2009, 457, 170–173. [Google Scholar] [CrossRef]
- Puthoff, H.E. Vacuum Energy Extraction by Conductivity Switching of Casimir Force; Technical Memo Inst. for Advanced Studies: Austin, TX, USA, 1985. [Google Scholar]
- de Man, S.; Iannuzzi, D. On the use of hydrogen switchable mirrors in Casimir force experiments. New J. Phys. 2006, 8, 235–249. [Google Scholar] [CrossRef]
- Scandurra, M. Thermodynamic properties of the quantum vacuum. arXiv 2001, arXiv:Hep-th/0104127v3. [Google Scholar]
- Pinto, F. Engines powered by the forces between atoms. Am. Sci. 2014, 102, 280. [Google Scholar] [CrossRef]
- Sheehan, D.; Nogami, S.H. Hammering with the Quantum Vacuum. Micro Nanosyst. 2011, 3, 348–353. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Phys. Rev. D 2017, 95, 103504. [Google Scholar] [CrossRef]
- Revzen, M.; Opher, R.; Opher, M.; Mann, A. Casimir’s entropy. J. Phys. A Math. Gen. 1997, 30, 7783–7789. [Google Scholar] [CrossRef][Green Version]
- Puthoff, H.E. The energetic vacuum: Implications for energy research. Spect. Sci. Technol. 1990, 13, 47–257. [Google Scholar]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M. Correlation of energy and free energy for the thermal Casimir force between real metals. Phys. Rev. A 2002, 66, 062112. [Google Scholar] [CrossRef]
- Boyer, T.H. Random electrodynamics: The theory of classical electrodynamics with classical electromagnetic zero-point radiation. Phys. Rev. D 1975, 11, 790–808. [Google Scholar] [CrossRef]
- Puthoff, H.E. Quantum ground states as equilibrium particle–vacuum interaction states. Quantum Stud. Math. Found. 2016, 3, 5–10. [Google Scholar] [CrossRef]
- Cole, D.C.; Zou, Y. Quantum mechanical ground state of hydrogen obtained from classical electrodynamics. Phys. Lett. A 2003, 317, 14–20. [Google Scholar] [CrossRef]
- Boyer, T.H. Comments on Cole and Zou’s Calculation of the Hydrogen Ground State in Classical Physics. Found. Phys. Lett. 2003, 16, 613–617. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.M. On the stability of classical orbits of the hydrogen ground state in Stochastic Electrodynamics. Entropy 2016, 18, 135. [Google Scholar] [CrossRef]
- Cetto, A.M.; de la Peña, L. Environmental effects on spontaneous emission and lamb shift, according to stochastic electrodynamics. Phys. Scr. 1988, T21, 27–32. [Google Scholar] [CrossRef]
- Walther, H.; Varcoe, B.T.H.; Englert, B.-G.; Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 2006, 69, 1325–1382. [Google Scholar] [CrossRef]
- Cavalleri, G.; Barbero, F.; Bertazzi, G.; Cesaroni, E.; Tonni, E.; Bosi, L.; Spavieri, G.; Gillies, G.T. A quantitative assessment of stochastic electrodynamics with spin (SEDS): Physical principles and novel applications. Front Phys China 2010, 5, 107–122. [Google Scholar] [CrossRef]
- Puthoff, H.E.; Little, S.R.; Ibison, M. Engineering the zero-point field and polarizable vacuum for interstellar flight. J. Br. Interplanet. Soc. 2002, 55, 137–144. [Google Scholar]
- Dmitriyeva, O.; Moddel, G. Test of zero-point energy emission from gases flowing through Casimir cavities. Phys. Procedia 2012, 38, 8–17. [Google Scholar] [CrossRef][Green Version]
- Roy, S.; Raju, R.; Chuang, H.F.; Cruden, B.A.; Meyyappan, M. Modeling gas flow through microchannels and nanopores. J. Appl. Phys. 2003, 93, 4870–4879. [Google Scholar] [CrossRef]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press: Long Grove, IL, USA, 2009; p. 178. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. Roy. Soc. Lond. Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Iannuzzi, D.; Lisanti, M.; Capasso, F. Effect of hydrogen-switchable mirrors on the Casimir force. Proc. Natl. Acad. Sci. USA 2004, 101, 4019–4023. [Google Scholar] [CrossRef]
- Henriques, C.A.D.O. Study of Atomic Energy Shifts Induced by Casimir Cavities. Master’s Thesis, University of Coimbra, Coimbra, Portugal, 2014. [Google Scholar]
- Koch, R.H.; Van Harlingen, D.J.; Clarke, J. Measurements in quantum noise in resistively shunted Josephson junctions. Phys. Rev. B 1982, 26, 74–87. [Google Scholar] [CrossRef]
- De la Peña, L.; Valdés-Hernández, A.; Cetto, A.M. Statistical consequences of the zero-point energy of the harmonic oscillator. Am. J. Phys. 2008, 76, 947–955. [Google Scholar] [CrossRef]
- Boyer, T.H. Conjectured derivation of the Planck radiation spectrum from Casimir energies. J. Phys. A Math. Gen. 2003, 36, 7425–7440. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moddel, G.; Dmitriyeva, O. Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods. Atoms 2019, 7, 51. https://doi.org/10.3390/atoms7020051
Moddel G, Dmitriyeva O. Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods. Atoms. 2019; 7(2):51. https://doi.org/10.3390/atoms7020051
Chicago/Turabian StyleModdel, Garret, and Olga Dmitriyeva. 2019. "Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods" Atoms 7, no. 2: 51. https://doi.org/10.3390/atoms7020051
APA StyleModdel, G., & Dmitriyeva, O. (2019). Extraction of Zero-Point Energy from the Vacuum: Assessment of Stochastic Electrodynamics-Based Approach as Compared to Other Methods. Atoms, 7(2), 51. https://doi.org/10.3390/atoms7020051




