On the Spatial Uniformity of the Degree of Ionization in a Helium ECR Plasma Produced under a Simple Cusp Field

Abstract

Production of a plasma that has a large degree of ionization (DOI), volume, and spatial and temporal uniformities is a challenge for the improvement of the performance of plasma-based vapor deposition processes. As a potential candidate for the discharge, we investigate plasma parameters arising in helium electron cyclotron resonance (ECR) discharges due to a simple cusp field. Two-dimensional distributions of helium atom emission-line intensities were measured using spectroscopy with multiple viewing chords and then de-convoluted by Abel inversion. The local plasma parameters, including the atomic density, were evaluated using collisional-radiative model analysis. The DOI calculated from the electron and atomic densities reached up to 35% and, in most of the region inside the ECR surface, it was more than 10%.

1. Introduction

A plasma produced using electron cyclotron resonance (ECR) heating under a simple cusp field could have a relatively large degree of ionization (DOI) [1,2]. In a simple cusp field, the field strength increases in the outward direction and the resonance layer forms a closed surface. Electrons escaping from the center of the plasma pass through this surface and their magnetic moments and the magnetic mirror forces are increased by the heating. Electrons are, then, better confined inside the ECR surface, as well as ions, owing to the ambipolar electric field. A relatively large DOI, can thus be obtained with a relatively simple magnetic field configuration.

The DOI is defined as $n_{\mathrm{i}}/(n_{\mathrm{i}}+n_0)$, where $n_{\mathrm{i}}$ and $n_0$ are the total ion and neutral densities, respectively. This expression can be approximated, in the case of low-temperature helium plasmas, as $n_{\mathrm{e}}/(n_{\mathrm{e}}+n_{1^1\mathrm{S}})$, where $n_{\mathrm{e}}$ and $n_{1^1\mathrm{S}}$ are the electron and ground-state helium atom densities, respectively. The number of reports on the DOI attainable by ECR discharges is limited, mainly due to the difficulty in accurately evaluating the spatially-resolved neutral density. In this study, we simultaneously evaluate $n_{\mathrm{e}}$ and $n_{1^1\mathrm{S}}$, using the helium atom (HeI) emission-line intensities and by collisional-radiative (CR) model analysis. This is becoming a standard method, owing to the recent improvements in its measurement accuracy for various types of plasma (see Reference [3] and the references therein). We previously measured a one-dimensional spatial distribution of the DOI [3,4] and found that the DOI increased by up to 30% inside the ECR surface. The purpose of the present study is to extend the measurement to two dimensions in order to confirm the spatial uniformity of the DOI.

2. Method

The excited helium atom densities were evaluated using their emission-line intensities and were then compared with those calculated using a CR model. The adopted model was developed by Goto [5] and Fujimoto [6], and we additionally included the optical escape factor (OEF), which represents the effective reduction of the spontaneous emission coefficient due to radiation trapping [7,8,9]. In our plasma, the density in a state p, which designates a term resolved into the orbital angular momentum (e.g., 2¹P, 2³P, ⋯) is approximately calculated as

$$n_p\simeq r_p^1{n}_{\mathrm{e}}{n}_{1^1\mathrm{S}}+r_p^2{n}_{\mathrm{e}}{n}_{2^1\mathrm{S}}+r_p^3{n}_{\mathrm{e}}{n}_{2^3\mathrm{S}},$$

(1)

where $r_p^1$, $r_p^2$, and $r_p^3$ are coefficients which are functions of $T_{\mathrm{e}}$, $n_{\mathrm{e}}$, and the OEF; and $n_{1^1\mathrm{S}}$, $n_{2^1\mathrm{S}}$, and $n_{2^3\mathrm{S}}$ are the 1¹S (ground) and 2¹S and 2³S (metastable) state densities, respectively. On the right-hand side of Equation (1), the terms, from left to right, represent the production of excited atoms from the ground state atoms, 2¹S metastable atoms and 2³S metastable atoms, respectively. The production of ions through the three-body, radiative and di-electronic recombinations are included in the model but the contributions are negligible in the present plasma because of small electron densities ($n_{\mathrm{e}}$ < 10¹⁸ m⁻³). The small $n_{\mathrm{e}}$ also violates the quasi steady-state approximation [10] for the metastable atoms.

Emission spectra were measured in a wavelength range of 350–750 nm. An example is shown in Figure 1. Eleven emission lines, belonging to n = 2–3 and 2–4 transitions, were used for the analysis; where n is the principal quantum number. As will be described in Section 4, the measured chord-integrated intensities were converted to the radial distributions of the emissivity and the population densities in the n = 3 and 4 states. For the present neutral pressure condition, the effect of the radiation trapping becomes significant for the resonant 1¹S–$n^1$P transitions associated with the ground state. We take into account the OEFs for the 1¹S–3¹P (${\mathsf{\Lambda }}_{3^1\mathrm{P}}$) and 1¹S–4¹P (${\mathsf{\Lambda }}_{4^1\mathrm{P}}$) transitions and determine these factors empirically, assuming that they are independent. The secondary effect—namely, the variation in the densities in the n = 3 and 4 states, as a result of the increase in the $n^1$P state densities (n = 2 and n > 4) due to radiation trapping—was small. Consequently, seven unknown parameters, $T_{\mathrm{e}}$, $n_{\mathrm{e}}$, $n_{1^1\mathrm{S}}$, $n_{2^1\mathrm{S}}$, $n_{2^3\mathrm{S}}$, ${\mathsf{\Lambda }}_{3^1\mathrm{P}}$, and ${\mathsf{\Lambda }}_{4^1\mathrm{P}}$, were determined by fitting the calculated $n_p$ to the measured ones. Although most studies aimed to measure $T_{\mathrm{e}}$ and $n_{\mathrm{e}}$ have used ratios of $n_p$ [5,9,11], we used the absolute values of $n_p$. This enabled us to evaluate $n_{1^1\mathrm{S}}$ at the expense of requiring measurements of absolute emission line intensities.

Figure 1. A spectrum consisting of seven fractional spectra recorded at different wavelengths. They were measured on a viewing chord at a distance of 15 mm from the z-axis and z = 20 mm.

3. Experiments

A pure helium plasma was produced using an ECR discharge device [1,2], as illustrated in Figure 2. At the time of operation, helium gas was fed at a constant flow rate and the pressure at the vacuum chamber was set to 67 mPa. A steady-state plasma was produced for 2.5 s using 2.45 GHz and 0.8 kW microwaves under a simple cusp field. The shape of the ECR surface was a spheroid. A seven-turn internal conductor with a diameter of 12 mm was installed along the axis of the device to produce an additional azimuthal field but was not used for the present study. The surfaces of the internal conductor and the side walls of the vacuum chamber at the axial ends were kept at floating potentials to reduce the loss of plasma.

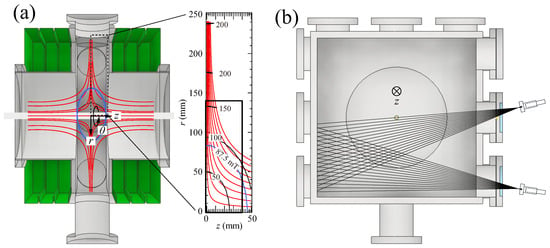
Figure 2. Schematic illustration of the electron cyclotron resonance (ECR) discharge device. (a) Frontal view plane of the device. The red and blue lines represent the magnetic field lines and the ECR surface, respectively. (b) A $r\theta$-plane, where the viewing chords are aligned. The black lines represent the axes of the chords.

Plasma emission was collected using 32 viewing chords, which consisted of two pairs of achromatic lens (Edmund Optics; 12 mm focal length) and 16 bundled optical fibers (Mitsubishi Cable Industries ST230D; 230 and 250 μm core and cladding diameters, 0.2 NA). The chords were aligned on a $r\theta$-plane, as illustrated in Figure 2b and moved to z = 10, 20, and 30 mm, on a shot-by-shot basis. The chords had a diameter of approximately 7 mm around the center of the device. The collected light was transmitted to a spectrometer (Nikon P250; 0.25 m focal length, 600 grooves/mm grating, F/4.5) and 32 spectra were recorded simultaneously using a CMOS detector (Hamamatsu Photonics Orca-Flash 4.0 V2.0; 2048 × 2048 pixels, 6.5 μm pixel size, 16 bit and 100 frames/s). Seven CMOS frames were recorded in a period, where the wavelength-integrated emission intensity was nearly constant and the variation of the spectrum was negligible. Then, the seven spectra were averaged and used for the analysis. The light intensities were absolutely calibrated using a standard tungsten-halogen lamp, taking into account the transmittance of the window. The wavelength resolution, defined as the instrumental width, was approximately 0.6 nm.

4. Results

Figure 1 shows a measured spectrum. It consists of seven fractional spectra measured at different wavelengths. For each of the eleven emission lines indicated in the figure, we applied the following procedures: Firstly, the chord-integrated intensity was evaluated from the area of the line spectrum. The evaluated intensities, with respect to the distances of the chords from the z-axis, were then fitted using a sum of fifteen sigmoid functions. The fitted curve was converted to the radial distribution of the emissivity using Abel inversion. The error bar in the emissivity was evaluated, using a procedure described in Reference [4]. The upper-state density, $n_p\left(r\right)$ and its error were calculated from the emissivity and its uncertainty, using the relation ${ϵ}_{pq}\left(r\right)$ = $(h{\nu }_{pq}/4\pi )n_p\left(r\right)A_{pq}$, where ${ϵ}_{pq}\left(r\right)$ is the emissivity; p and q designate the upper and lower states, respectively; h is Planck’s constant; ${\nu }_{pq}$ is the transition frequency; and $A_{pq}$ is the spontaneous emission coefficient.

We calculated the densities in the n = 3 and 4 states, using the CR model and least-squares fitted them to the measured values, where the input parameters were used as fitting variables and the residues were weighted with the inverse standard deviations of $n_p\left(r\right)$. The $rz$-distributions of the evaluated parameters are shown in Figure 3, where the solid blue line represents the ECR surface and the red dotted lines represent the magnetic field lines. The radial ranges of the plots are limited to where the eleven emission lines were observable, as well as the viewing chords which were not intercepted by the internal conductor. The axial width of the plots corresponds to the 7 mm diameter of the viewing chords. The radial distributions of $T_{\mathrm{e}}$, $n_{\mathrm{e}}$, $n_{1^1\mathrm{S}}$ and the DOI, with their error bars, are shown in Figure 4. The larger errors in the region outside the ECR surface originate from the uncertainty in the CR model fitting, presumably caused by systematic errors in the emissivities.

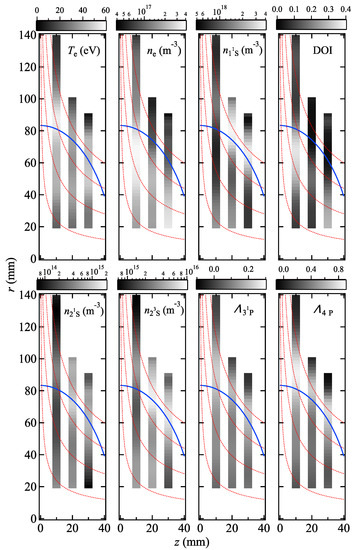
Figure 3. The $rz$-distributions of the plasma parameters, measured in a region designated by the black frame in Figure 2a. The solid blue line represents the ECR surface and the red dotted lines represent the magnetic field lines.

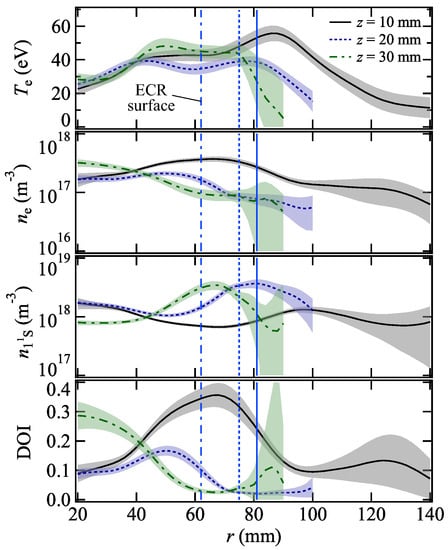
Figure 4. Radial distributions of $T_{\mathrm{e}}$, $n_{\mathrm{e}}$, $n_{1^1\mathrm{S}}$ and the DOI, with error bars.

The evaluated $T_{\mathrm{e}}$ increases, up to 60 eV, near the ECR surface owing to the heating and $n_{\mathrm{e}}$ reaches more than 10¹⁷ m⁻³ inside the ECR surface. Even though the radial distributions of these parameters are independently measured at three different z positions, the two-dimensional $rz$-distributions have close values along the field lines and this tendency is physically consistent with the electron motion along the field lines. Decreased $T_{\mathrm{e}}$ and $n_{\mathrm{e}}$ in a region around z = 10 mm and r = 20 mm are due to perturbation by the internal conductor. A decrease in $n_{\mathrm{e}}$ was also detected by a two-dimensional thermal lithium beam measurement [12]. These reductions could be mitigated by driving a current through the conductor and superposing an azimuthal magnetic field around it [2]. The metastable atom densities reached their maximums near the ECR surface and decreased in the other regions. This can be explained by increased productions as a result of the increased value of $T_{\mathrm{e}}$. The OEFs are peaked slightly outside the ECR surface. In order to confirm their validity, a three-dimensional radiation transport calculation is required; this is a task for future studies. Confirmation of the obtained parameters is not a trivial task and requires elaboration beyond the scope of this study. An advantage of the present method is the empirical determination of these parameters, owing to the reliability of the CR model calculation. The relevance of the parameters, from the viewpoint of the order of magnitude, was discussed in Reference [3,4].

The depletion of $n_{1^1\mathrm{S}}$ inside the ECR surface is attributable to ionization and charge exchange reactions, as well as to an increase in the atomic temperature [13]; $n_{1^1\mathrm{S}}$ at the vacuum chamber wall, evaluated from the pressure at the room temperature, was 1.6 × 10¹⁹ m⁻³ and decreased down to less than 10% inside the ECR surface. The reduction of $n_{1^1\mathrm{S}}$ in the radial edge region was un-physical and contributed to the larger errors. As a result of the increased $n_{\mathrm{e}}$ and decreased $n_{1^1\mathrm{S}}$ inside the ECR surface, the DOI increased up to 35%. Except for the region perturbed by the internal conductor, the DOI was above 10% throughout the interior of the ECR surface.

5. Conclusions

We conducted two-dimensional spectroscopic measurements in a helium ECR plasma produced under a simple cusp field and found that the DOI remained above 10% for the greater portion of the region enclosed by the ECR surface. A decrease in the DOI observed in the central region is attributed to the internal conductor but this could be mitigated by driving a current through the conductor. To confirm the feasibility of application to plasma-based vapor deposition processes, the effects of a floating or biased substrate inserted inside the ECR surface should be investigated in future studies.