Laser-Assisted (e, 2e) Collisions in the Symmetric/Asymmetric Coplanar Geometry
Abstract
1. Introduction
2. Description of (e, 2e) Collision Processes
2.1. Description
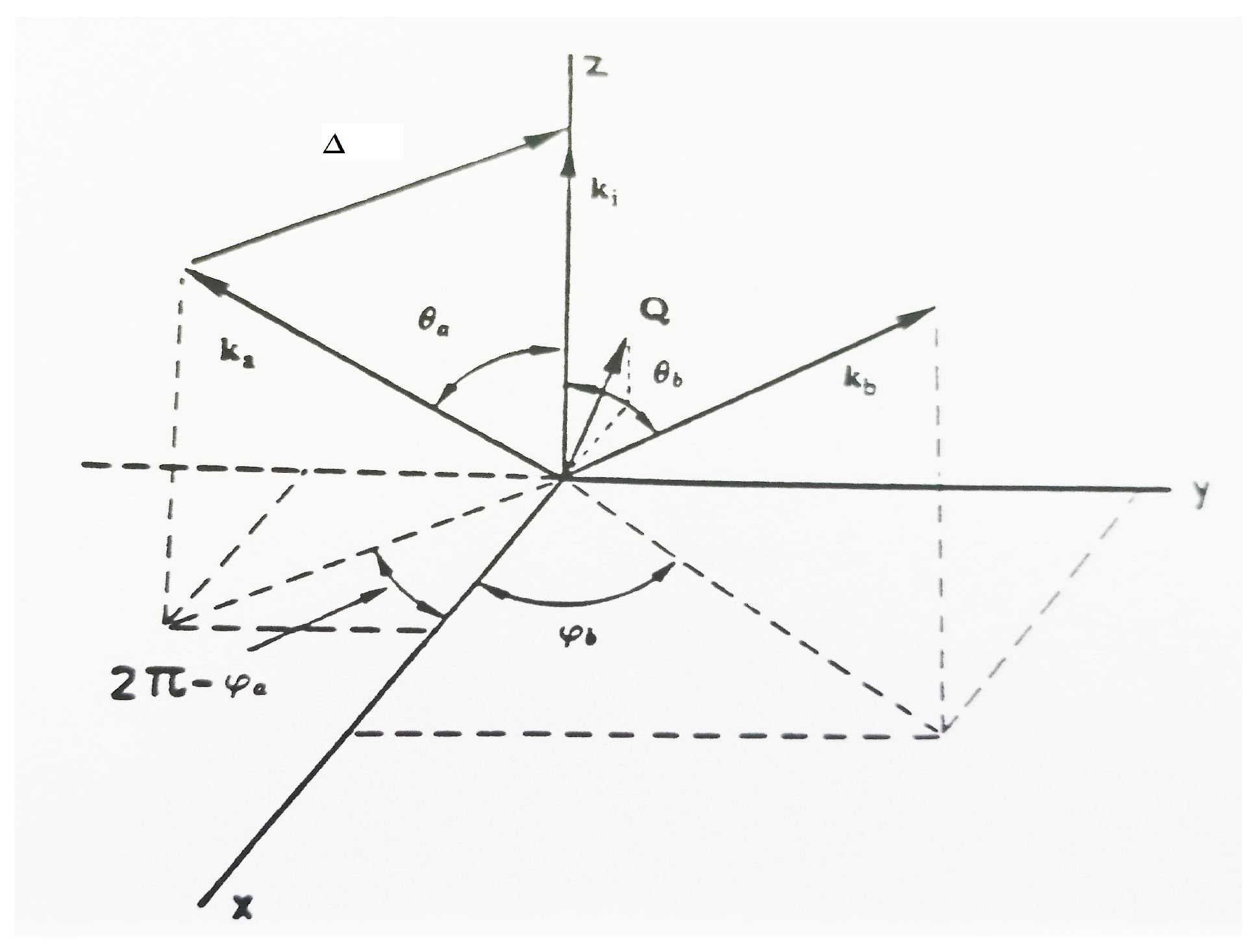
2.2. Kinematics
2.3. Triple Differential Cross Sections
3. Theory of (e, 2e) Collisions in the Presence of a Laser Field
3.1. Description of the Laser Field
3.2. The Wave Function of the Free Electron in the Presence of a Laser Field
3.3. The Dressed Target Wave Function in the Initial State
3.4. The Dressed Target Wave Function in the Final State
- In the case of weak fields, such that . This case has already been discussed above, and we have seen that an appropriate dressed wave function is then given by Equation (14).
- In the limit of low frequencies.
- For sufficiently high electron energies. Indeed, in this case the wave function describing an electron in the field of the residual ion is well approximated by the plane wave , and the operator gives zero when acting on this plane wave.
3.5. The Semi-Perturbative Method
4. Laser-Assisted (e, 2e) Collisions in Atomic Hydrogen in the Coplanar Asymmetric Geometry
4.1. Theory
4.2. Results and Discussion
5. Laser-Assisted (e, 2e) Collisions in Atomic Hydrogen in the Coplanar Symmetric Geometry
5.1. Theory
5.2. Results and Discussion
5.2.1. Triple Differential Cross Sections of Laser-Assisted (e, 2e) Collisions at eV
- (i)
- For laser field strengths lower than V/cm, and for large values of , one can model the (e, 2e) reaction as an electron-electron collision, with () being the momentum of the struck electron before the collision;
- (ii)
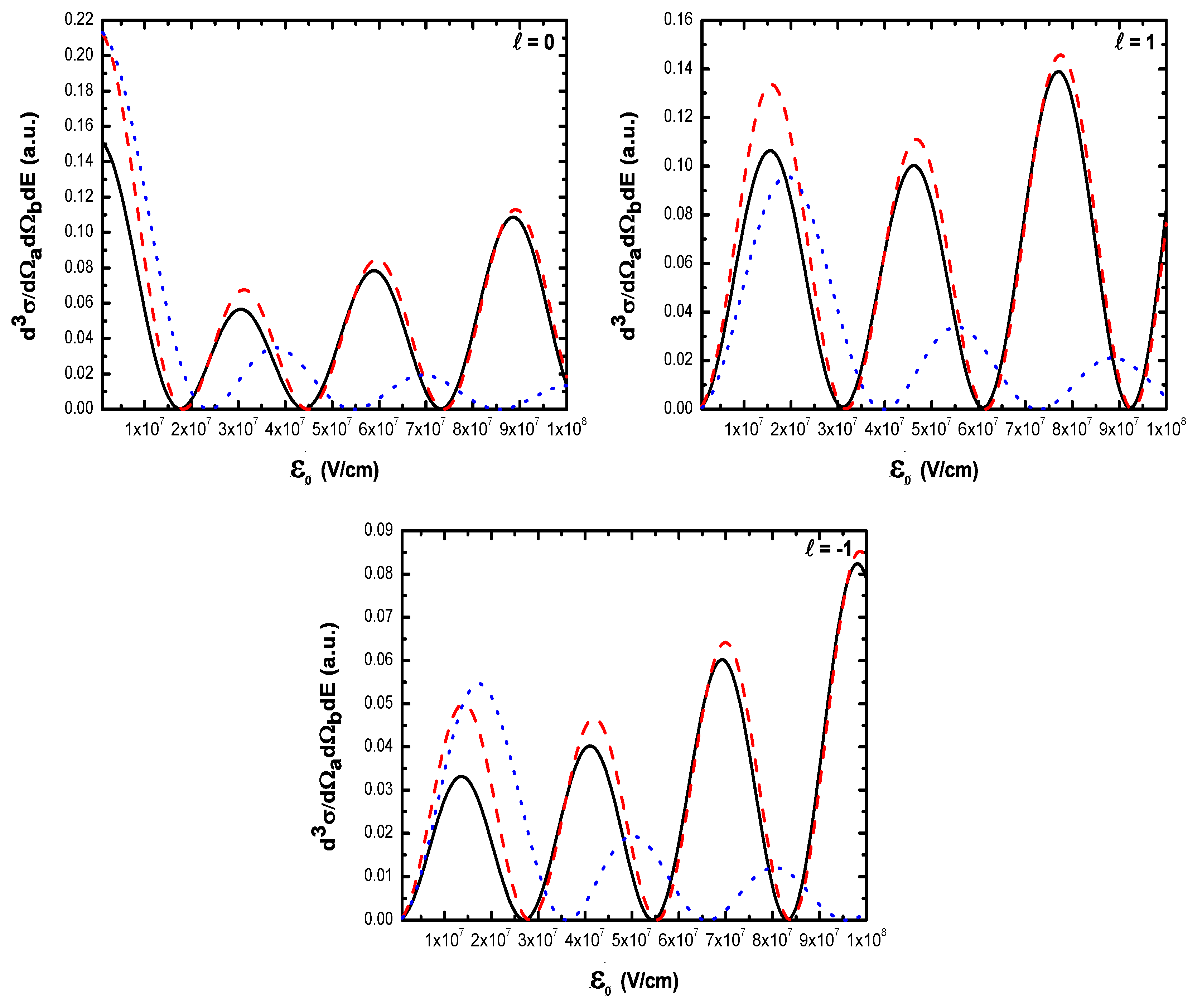
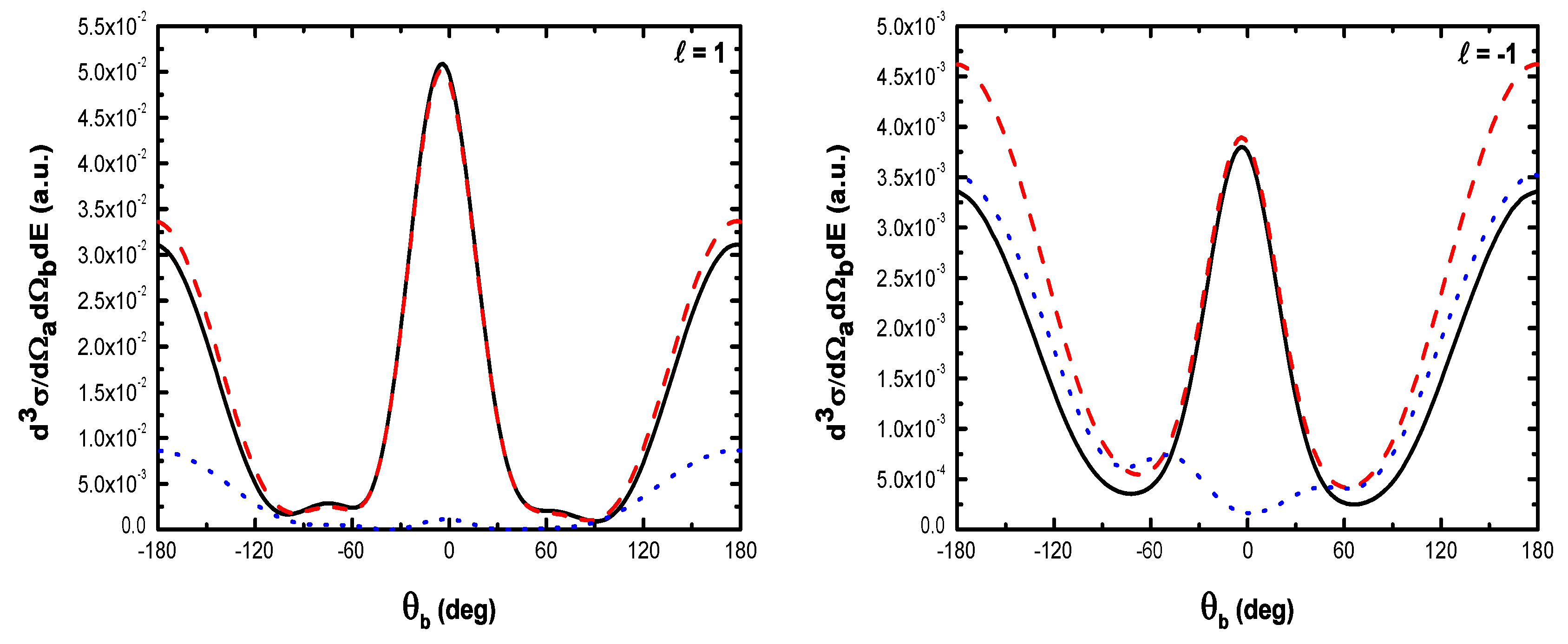
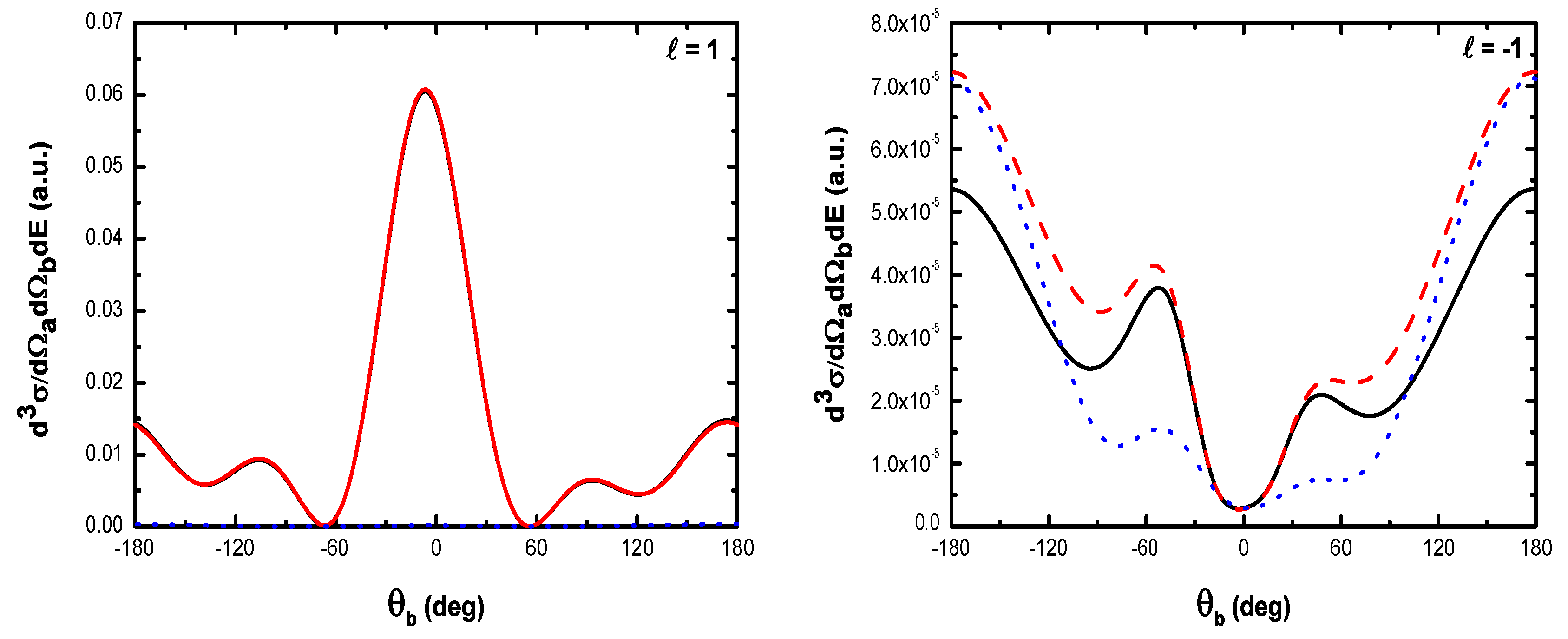
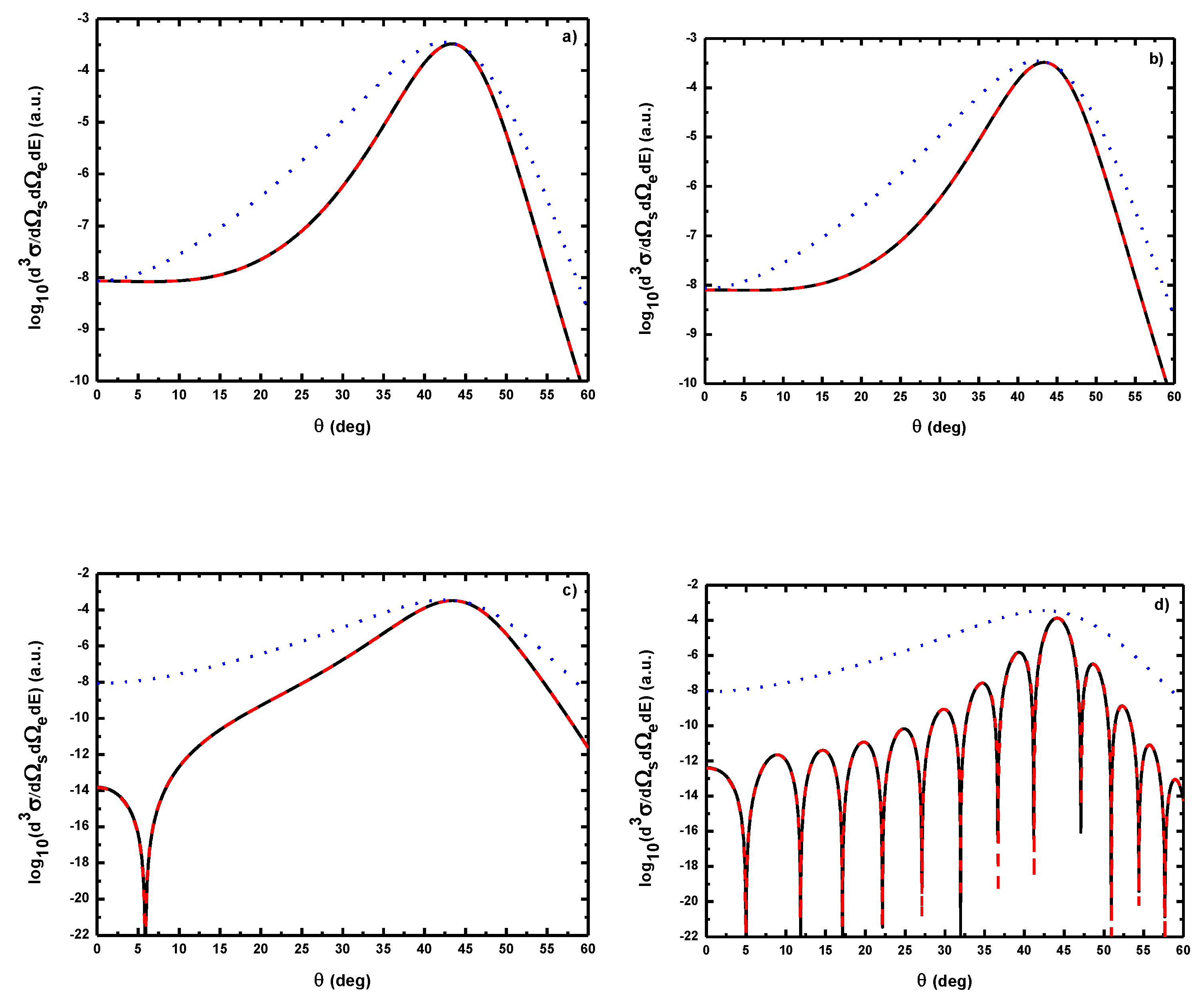
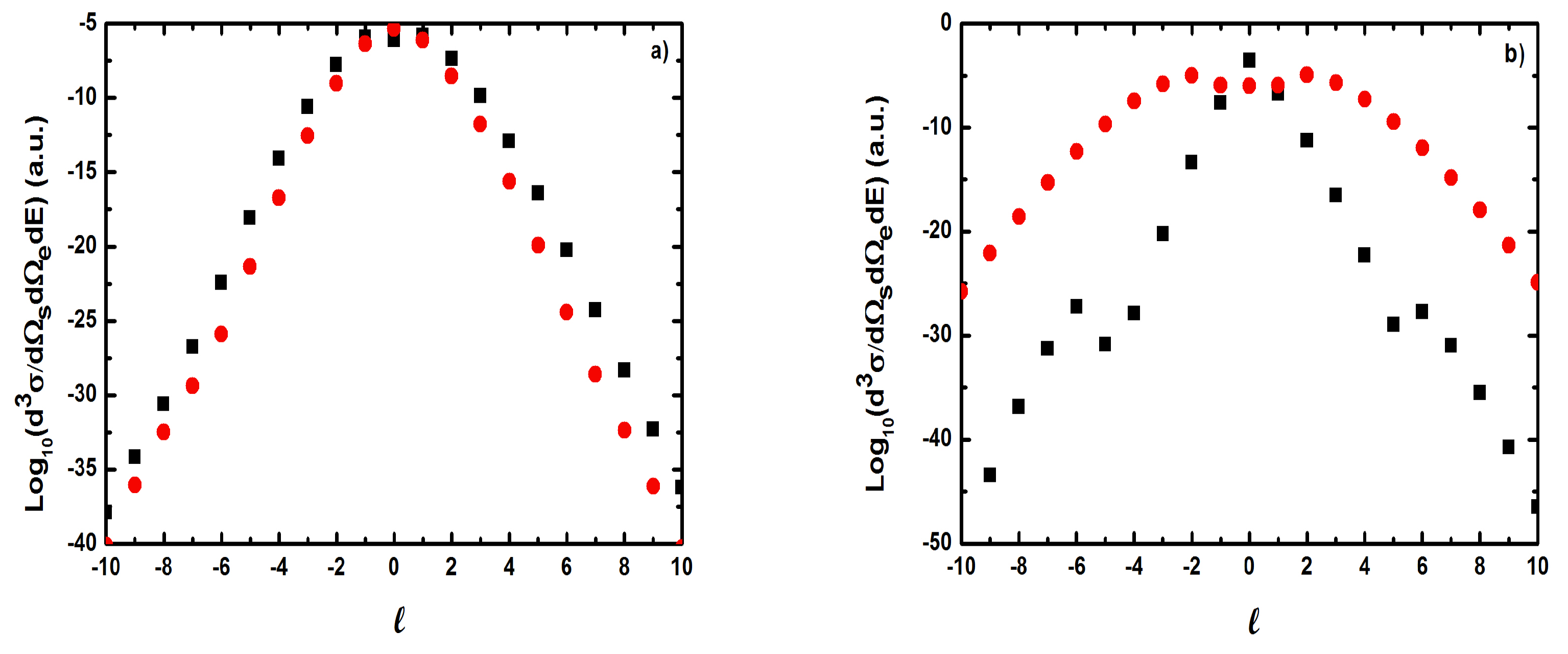
- The magnitude of the cross section for no net exchange of photons is significantly smaller than in the field-free case. This results from the fact that the laser itself does not contribute to the ionization process except for which corresponds to the case where the recoil momentum of the ionized target ( in the present case) is zero, i.e., when the TDCS is maximum. For and the laser field redistributes the ejected electrons in new channels associated to indices in the energy conservation relation [], which are accessible in the ”dressed” continuum of the atomic target. A simplified description of this process is that of two-step processes in the course of which the atomic electron is first brought into the continuum as a result of the collision, and then exchanges photons with the laser field [87]. When the laser intensity increases, an oscillatory phenomenon is observed which is due to the interference between the terms constituting the dominant electronic amplitude given by Equation (61) and the change of sign of the argument of the Bessel function (see below);
- (iii)
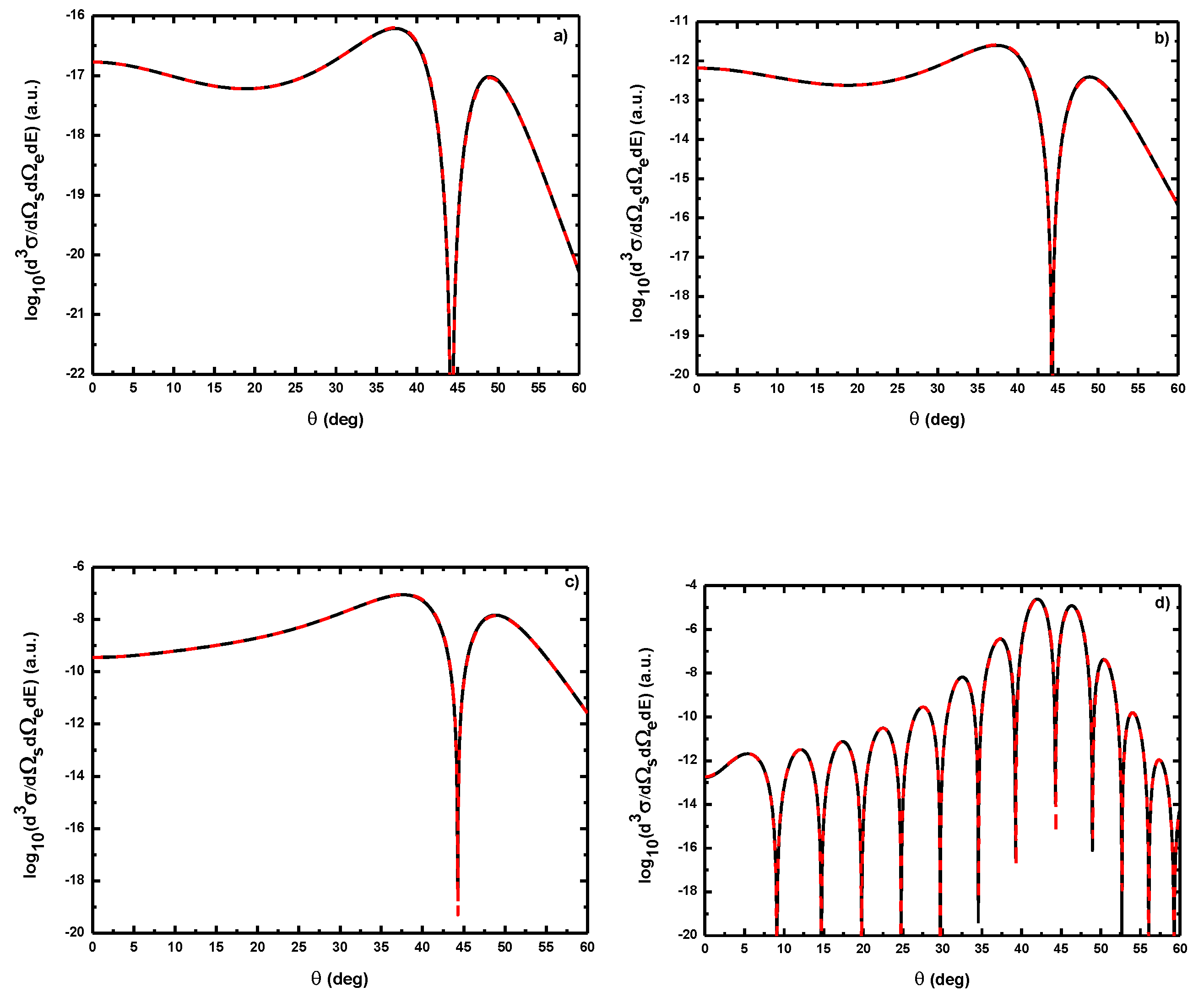
- Figure 19 indicates that, for , the dressing of the target states does not play a dominant role in the physics of the process. In other words, this result shows that the term (Equation (61)) is dominant in the transition amplitude (Equation (60)). This is a signature of coplanar symmetric (e, 2e) collisions in the presence of the laser field in the (e, 2e) spectroscopy region.
- (i)
- , the difference in shape and magnitude between FBA results and those obtained by neglecting the target dressing, at high laser frequencies, is traced to the role played by the explicit introduction of the effects of the atomic target internal structure;
- (ii)
- , the electronic term given by Equation (61) is sufficient in such process so that the atomic target can be described by unperturbed wave function.
5.2.2. Triple Differential Cross Sections of Laser-Assisted (e, 2e) Collisions at eV
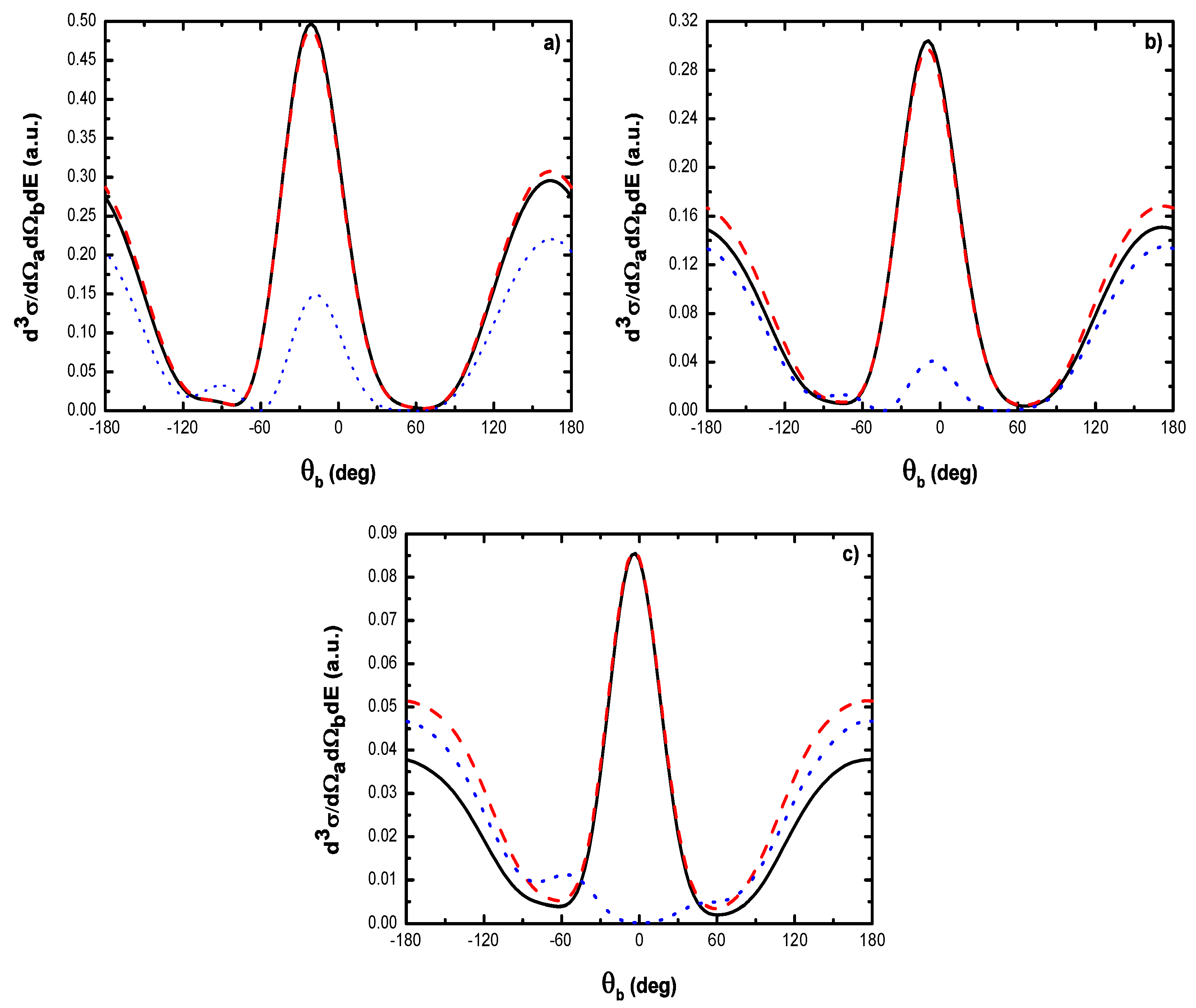
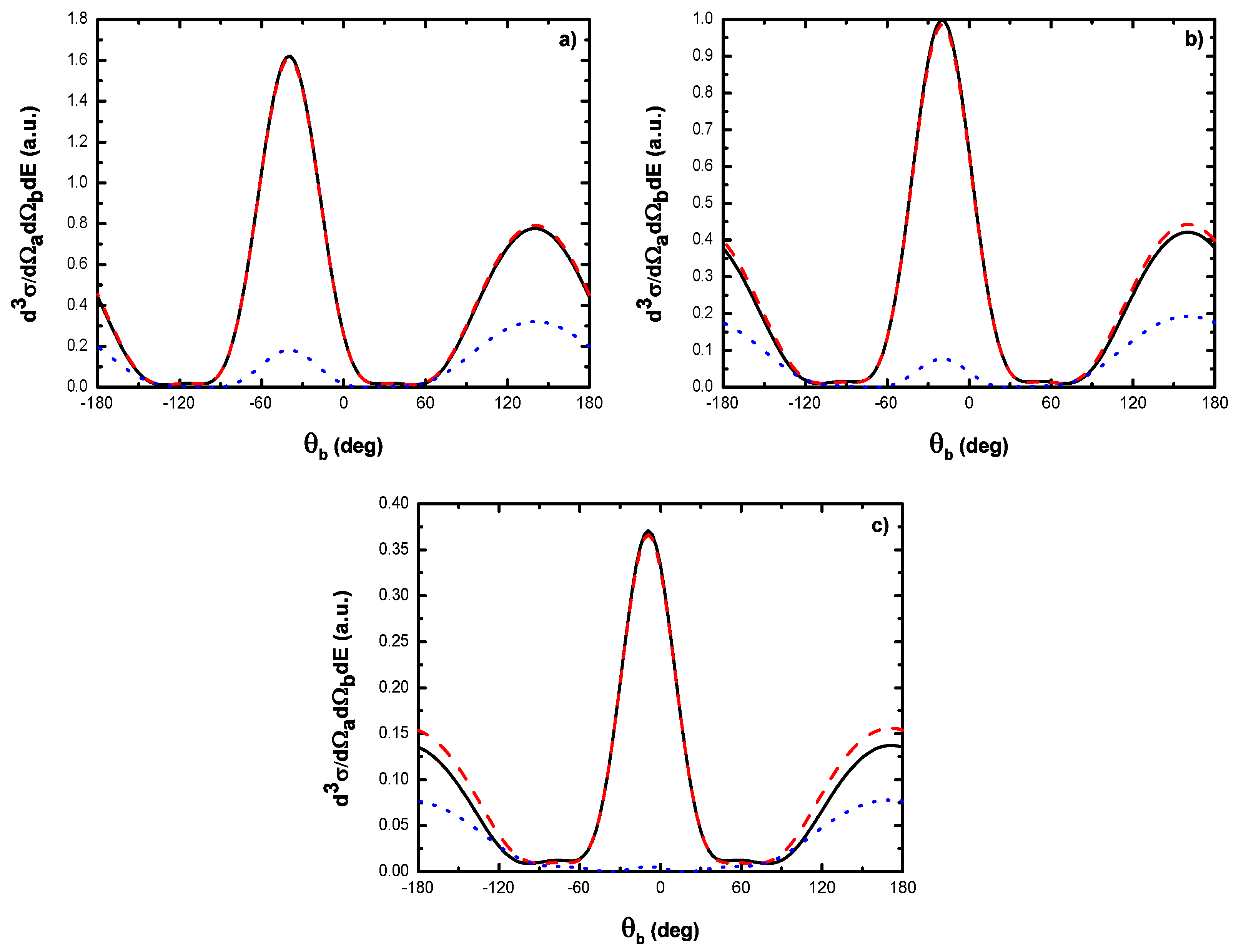
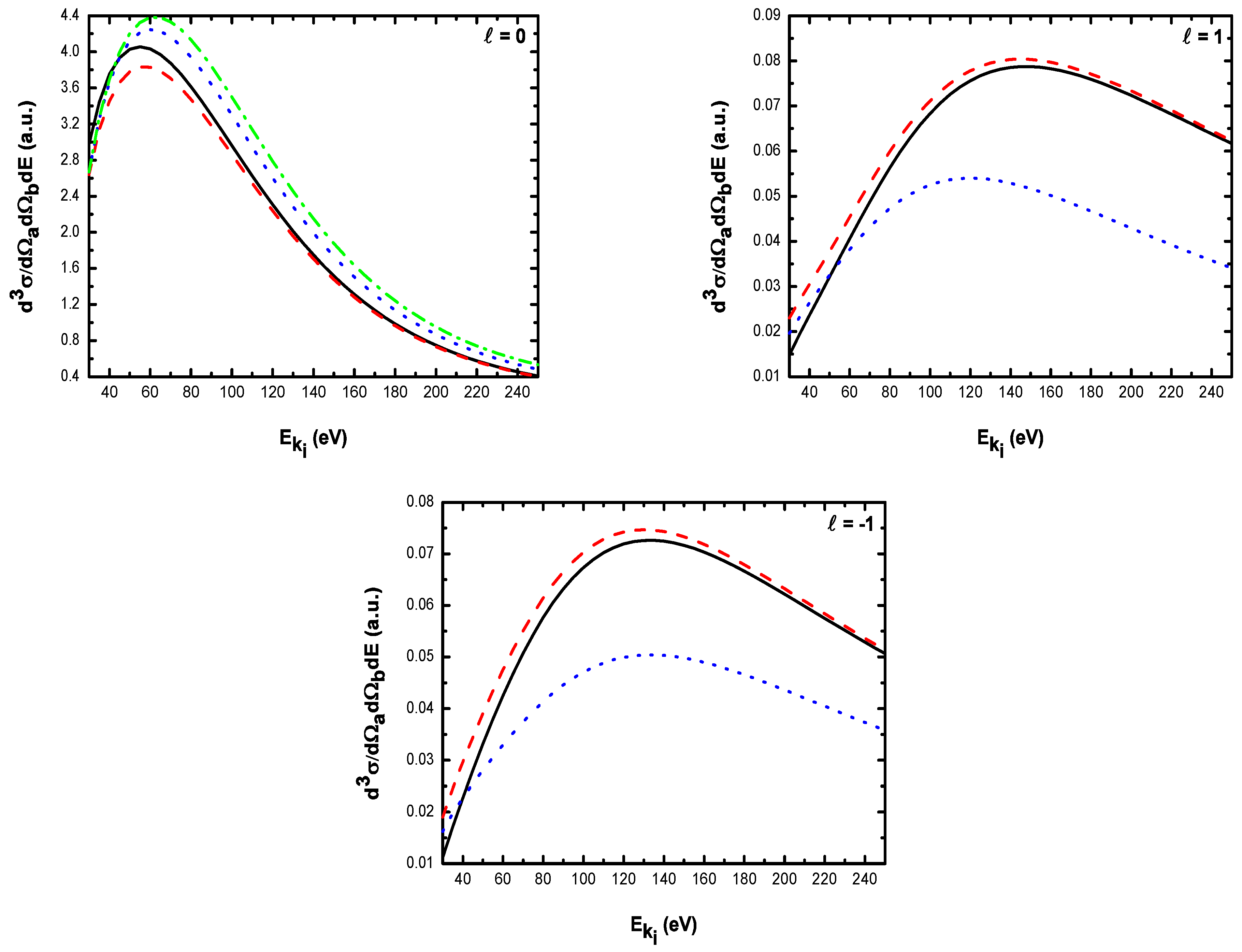
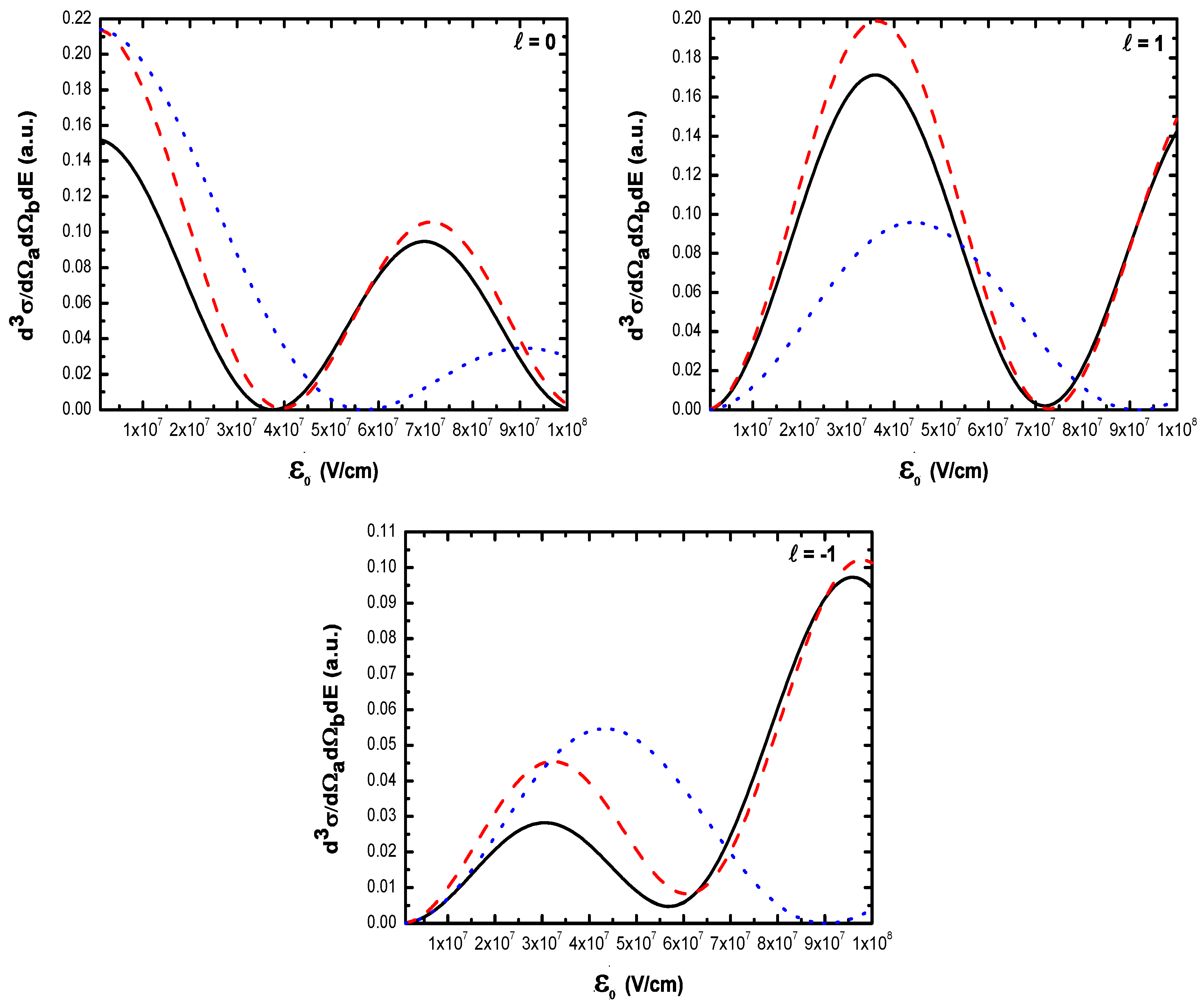
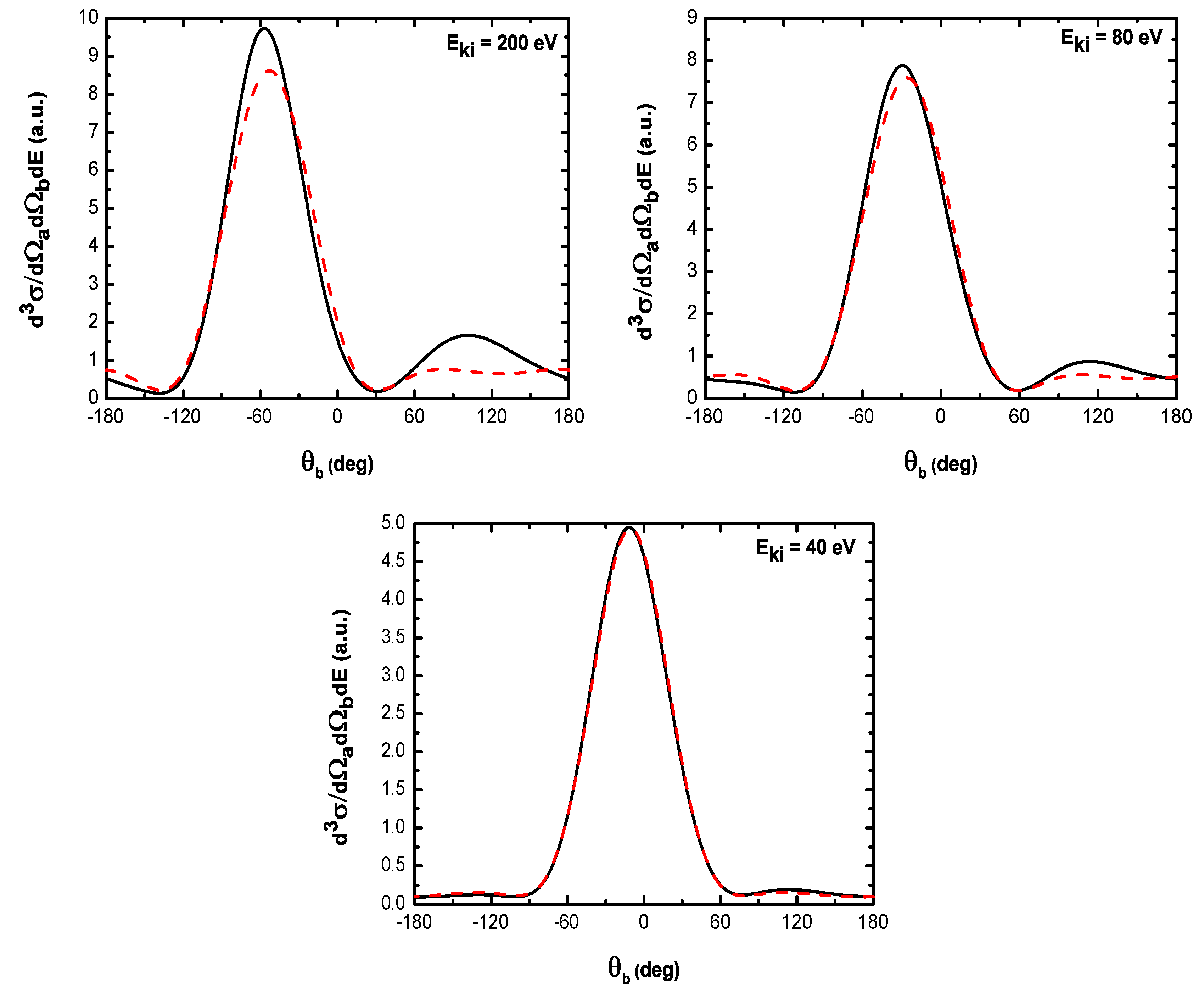
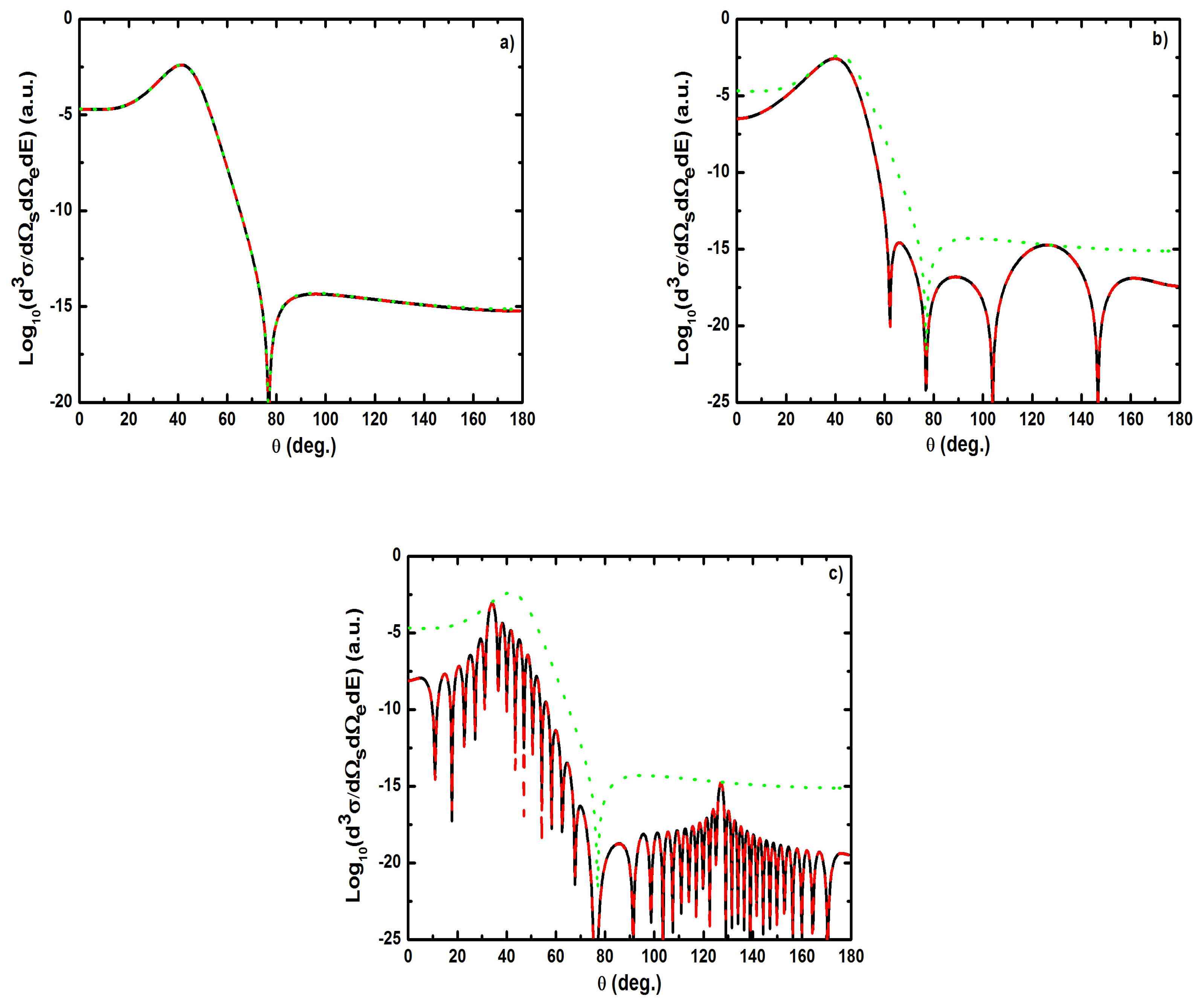
- For electric field strengths that are much smaller than the atomic unit (V/cm) such that perturbation theory is applicable regarding the laser-atom interaction, the attraction between the electron and the nucleus becomes negligible and one can model the (e, 2e) reaction as an electron-electron coupling. In other words, in the (e, 2e) spectroscopy region, the laser-assisted electron-impact ionization of atomic hydrogen in the coplanar symmetric geometry is governed by the electron-electron interaction and one can model the atom by a structureless center of force. Furthermore, for , the dressing of the target states does not play a dominant role in the physics of the process. The first Born approximation to (e, 2e) scattering amplitude with the transfer of ℓ photons Equation (60) can be replaced by the expression (61).
- The magnitude of the cross sections in the presence of the radiation field with no photon exchanged between the projectile-atom system and the laser field is comparable to that in the field-free case. This results from the fact that the laser itself does not contribute to the ionization process [88]. At the (e, 2e) spectroscopy region, the laser field redistributes the ejected electrons in new channels associated with indices in the energy conservation relation, which are accessible in the “dressed” continuum of the atomic target. A simplified description of this process is that of two-step processes in the course of which the atomic electron is first brought into the continuum as a result of the collision, and then exchanges photons with the laser field [88].
- At low laser photon energies and low laser intensities considered here, the dressing of the target states does not play a dominant role in the physics of laser-assisted electron-impact ionization of atomic hydrogen in the coplanar symmetric energy sharing geometry. This result shows, in other words, that under the present conditions the term in Equation (61) is dominant in the (e, 2e) scattering amplitude Equation (60) and one can model the target by a structureless center of force. Note that the atom distortion by the external laser beam will be taken into account at high frequency field (see below). Such a distorted target also acts on the projectile by a long range dipole potential , which requires a nonperturbative treatment of the laser-atom interaction at low incident electron energies.
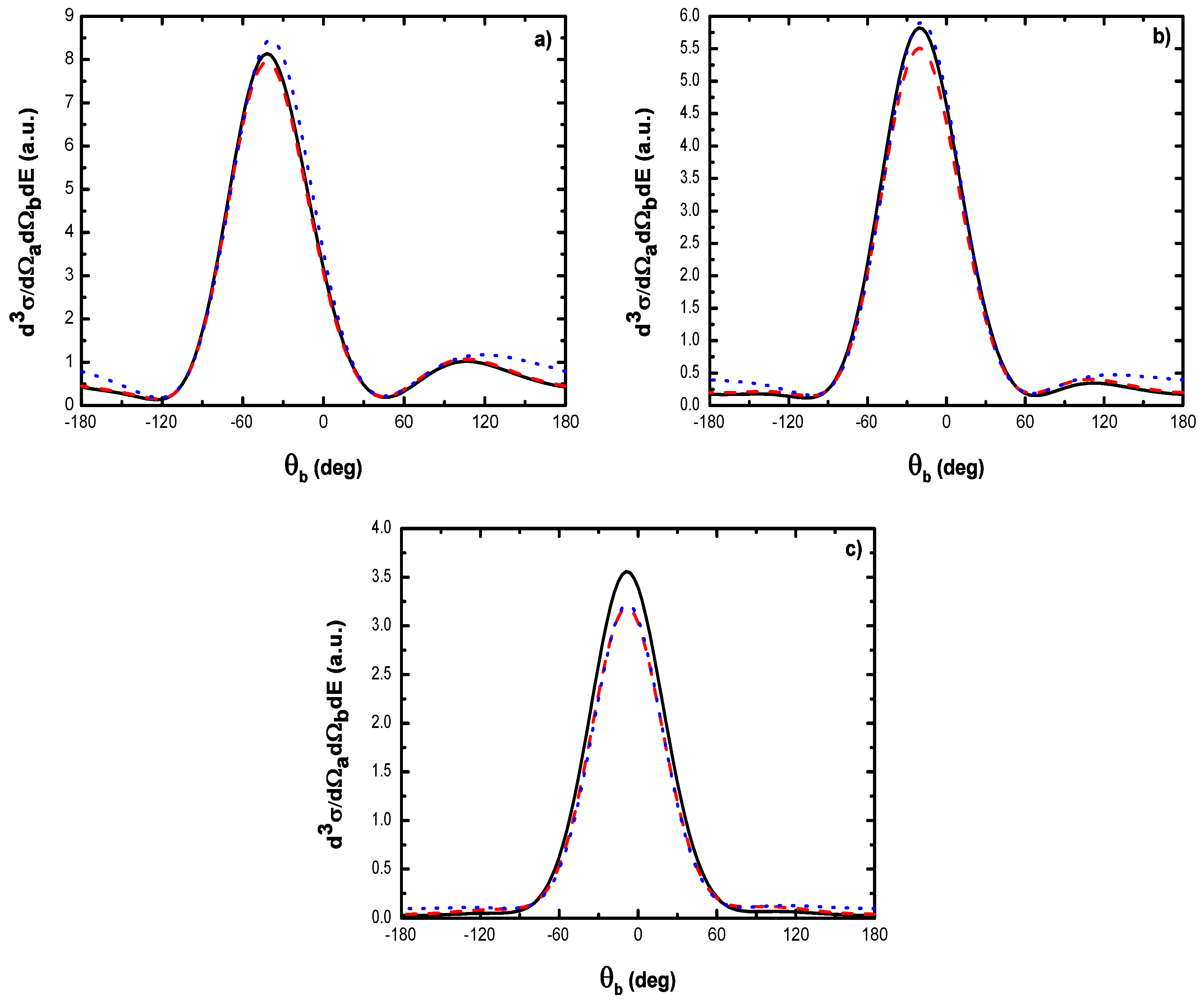
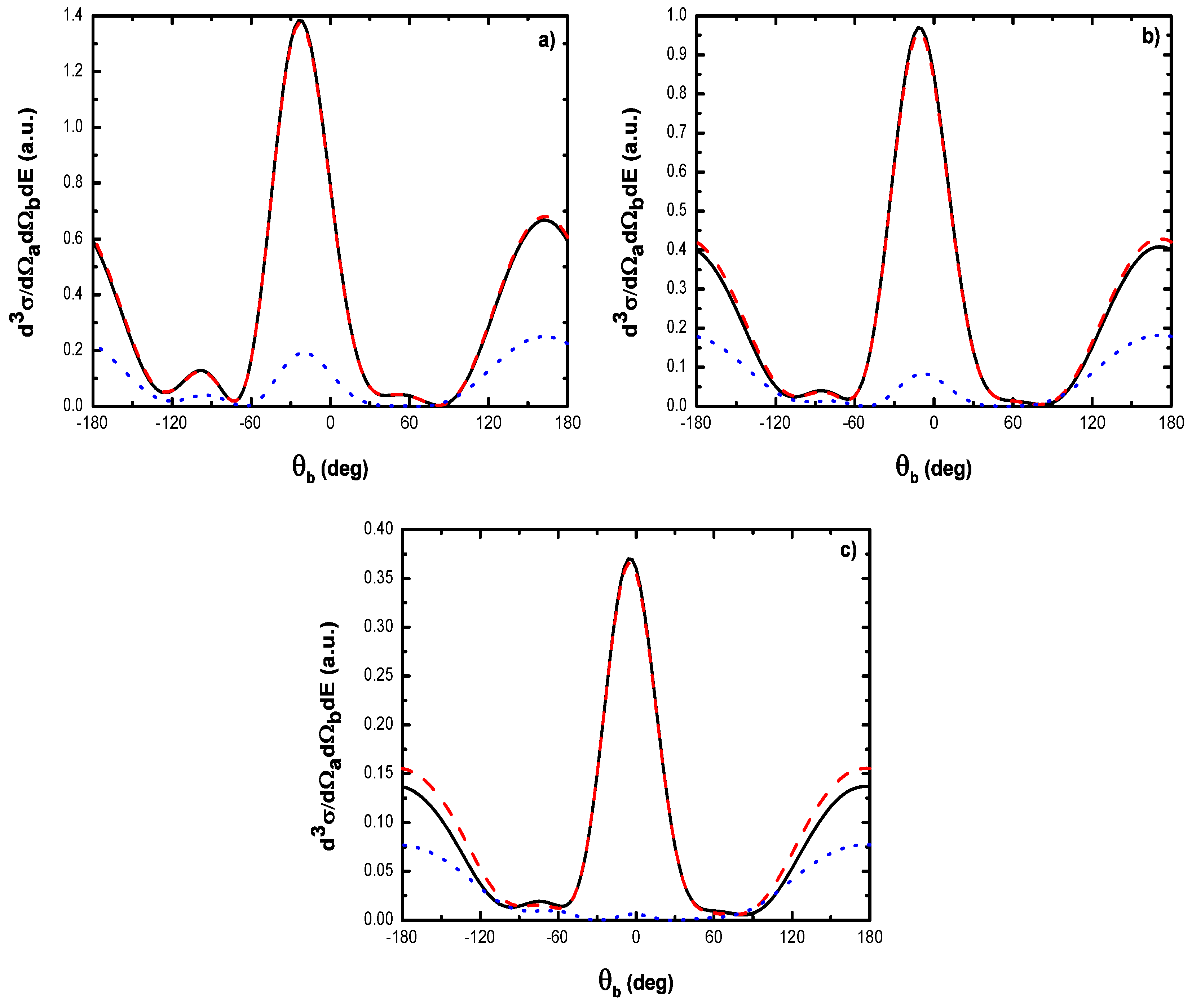
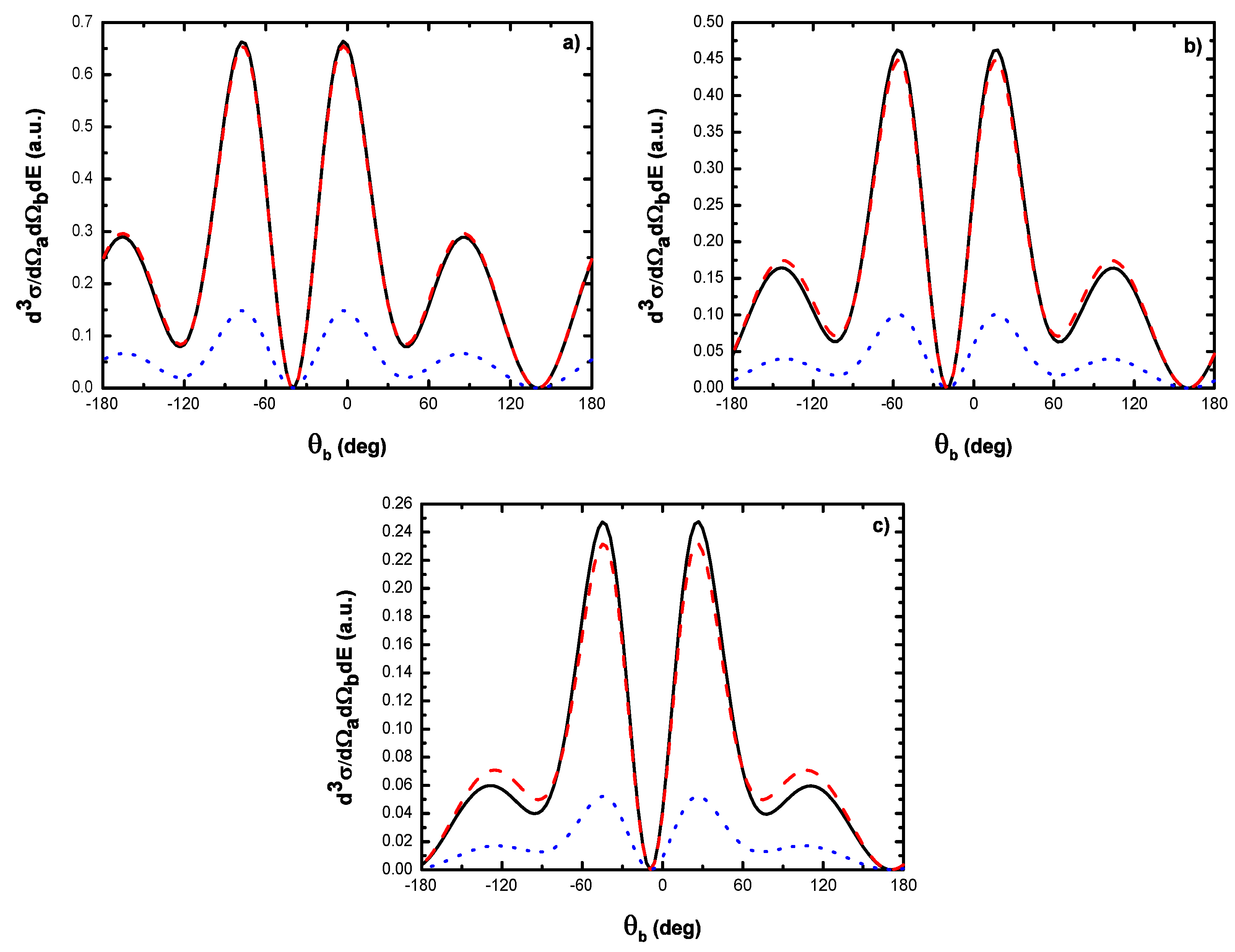
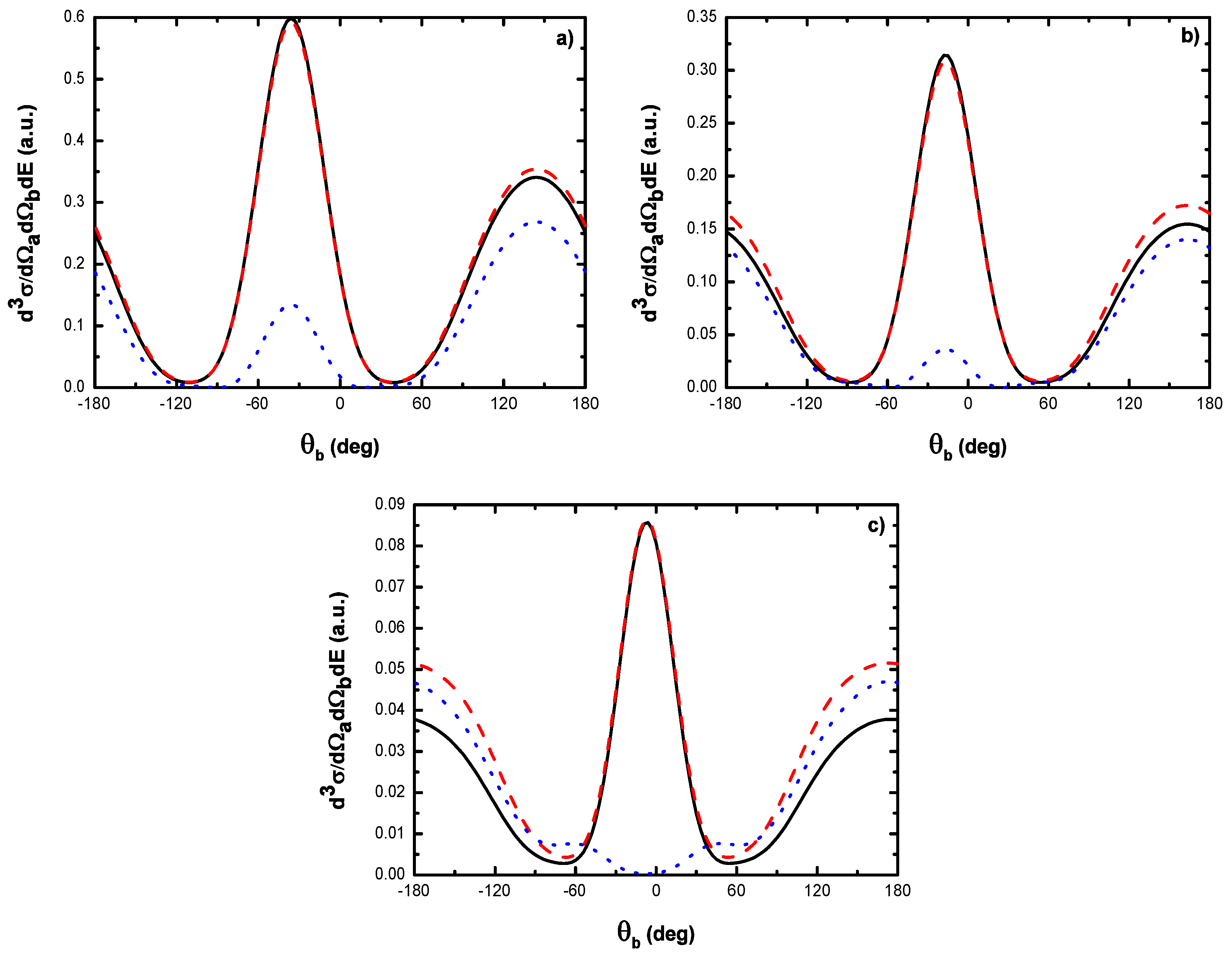
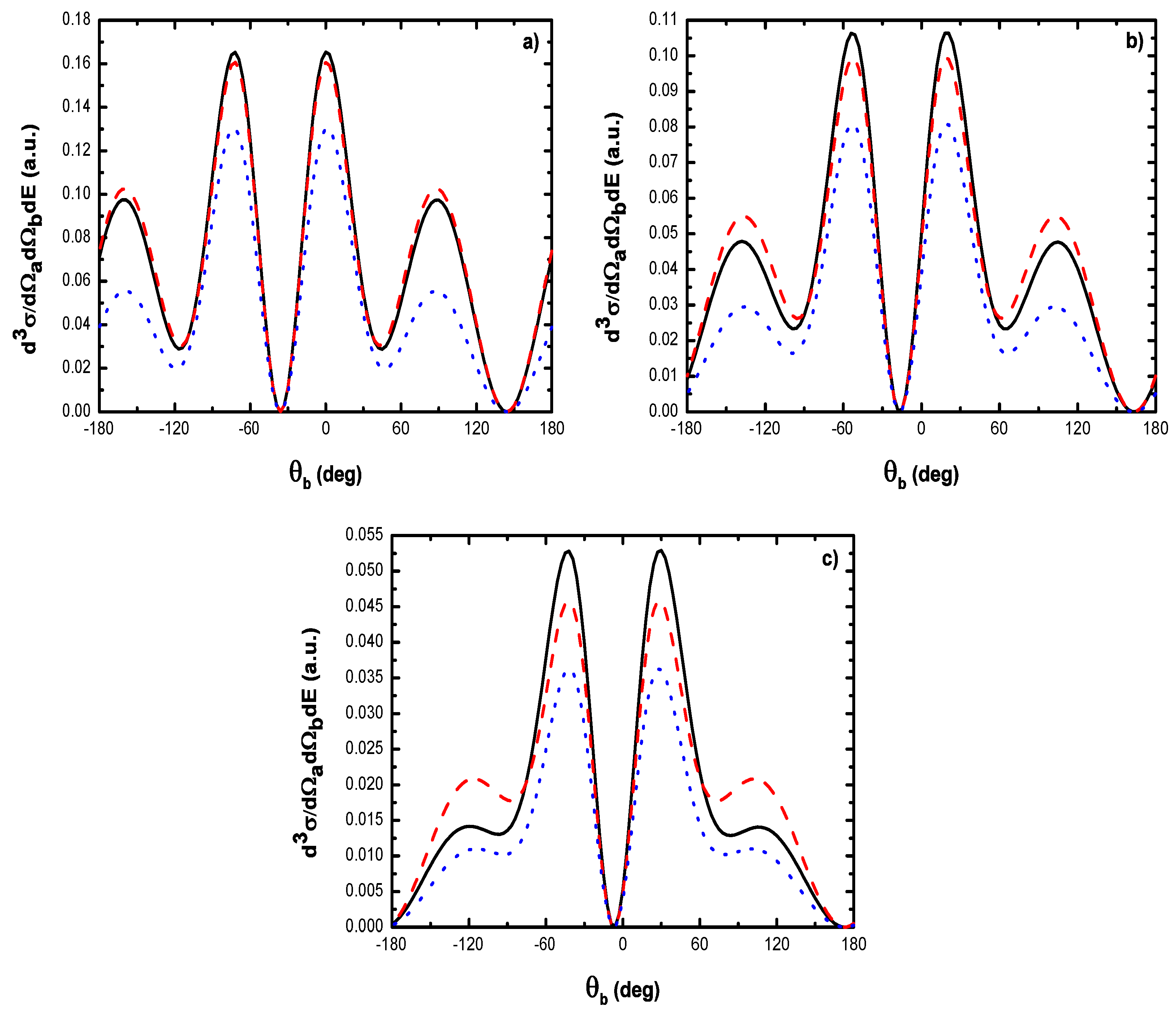
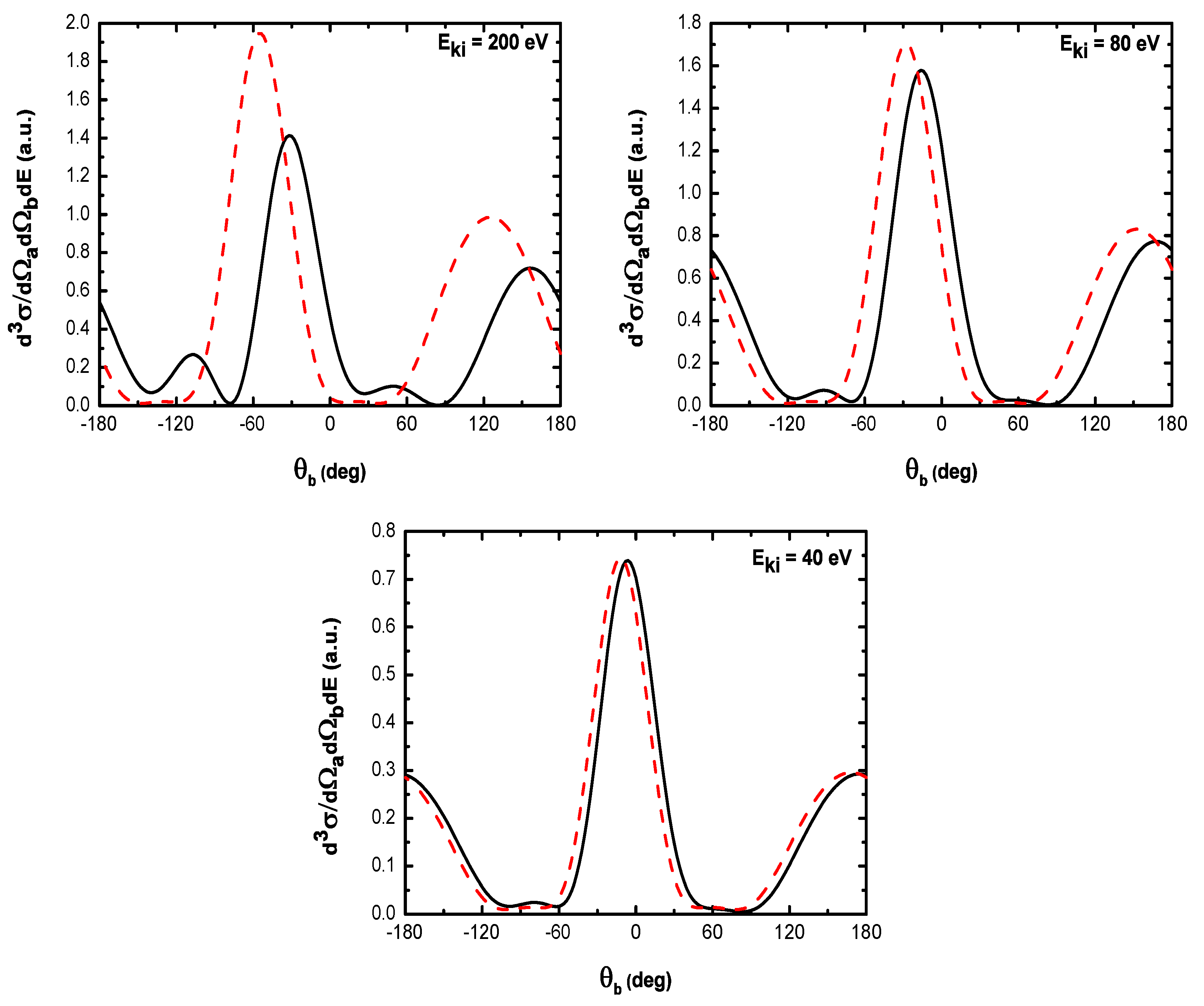
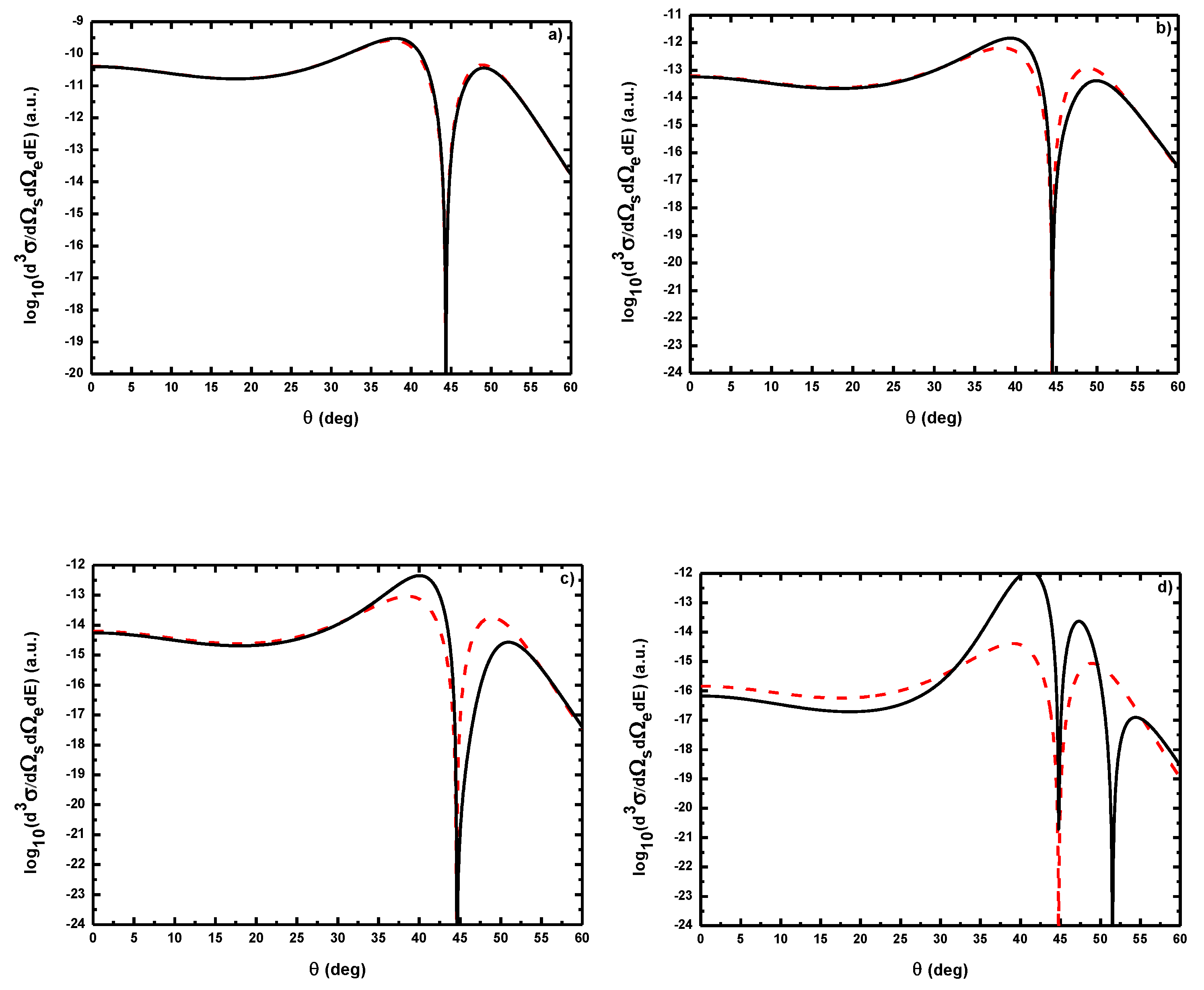
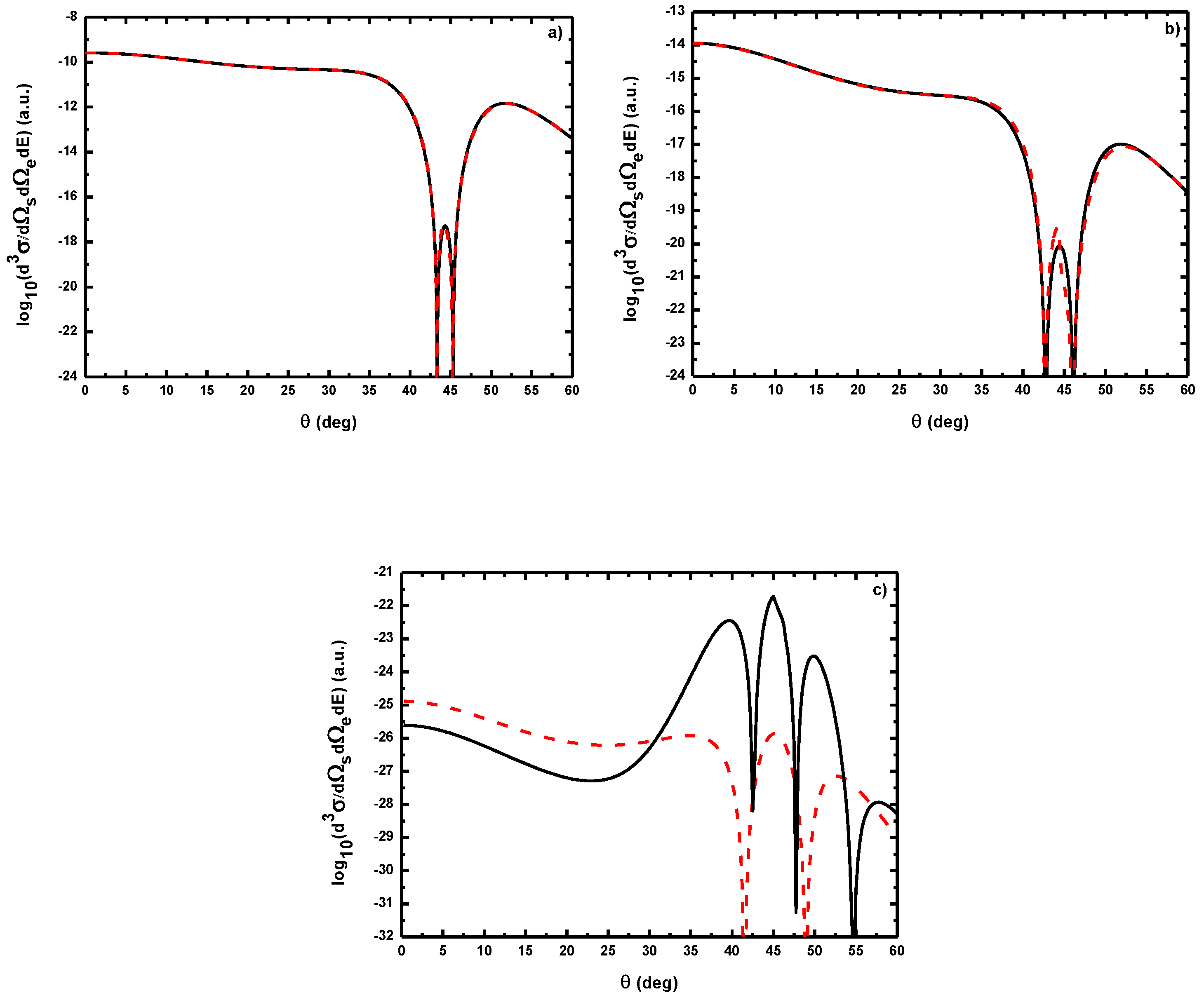
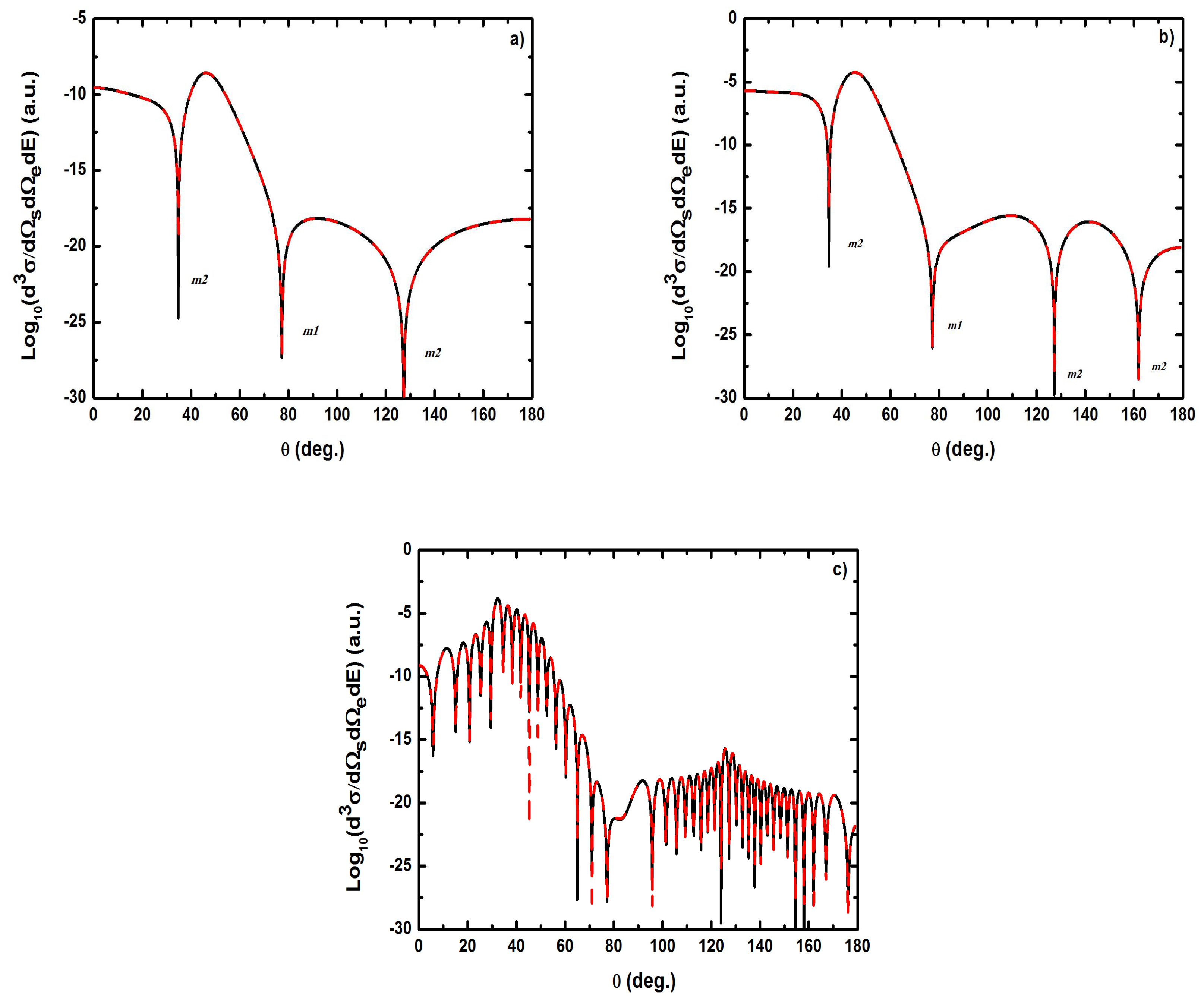
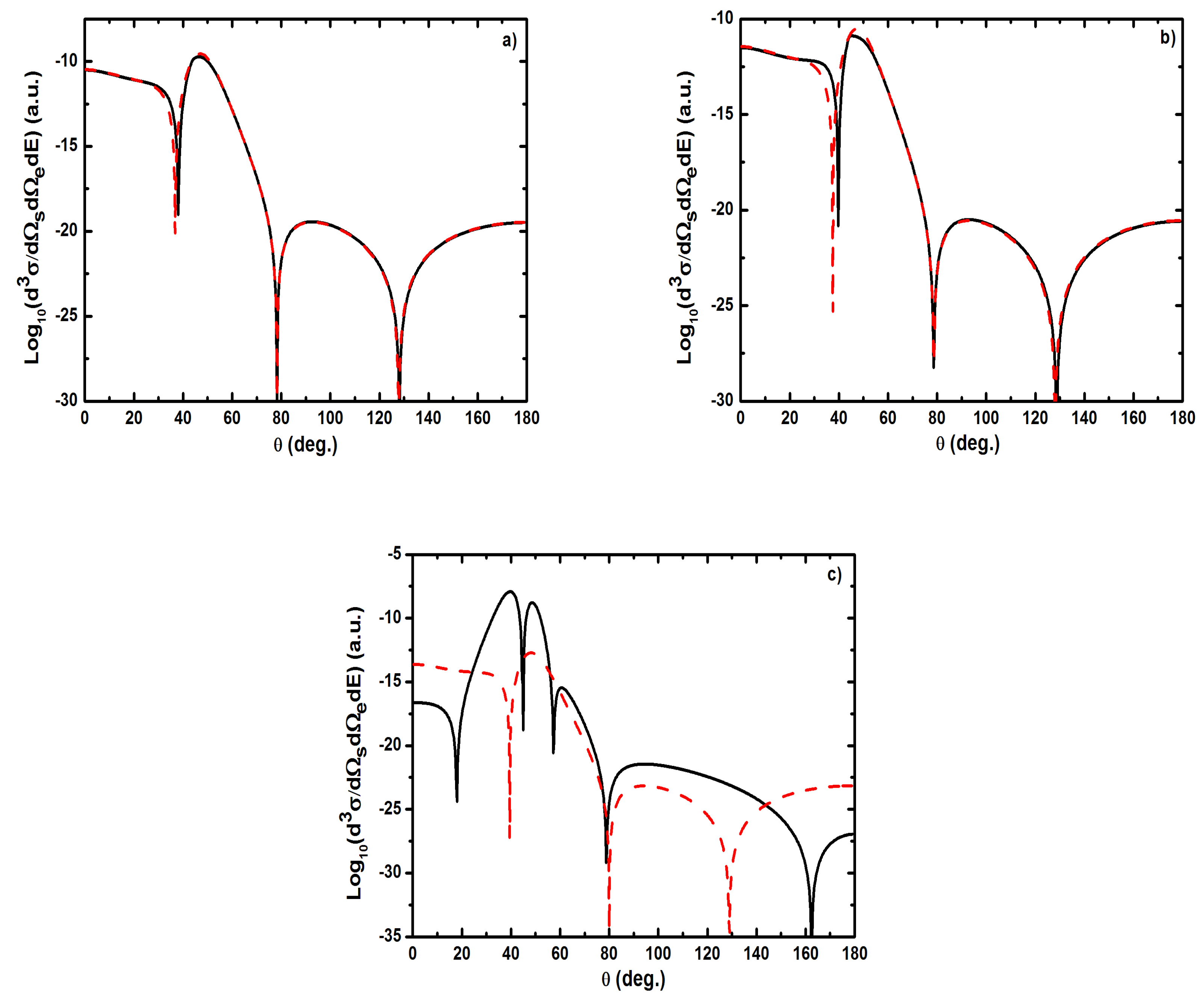
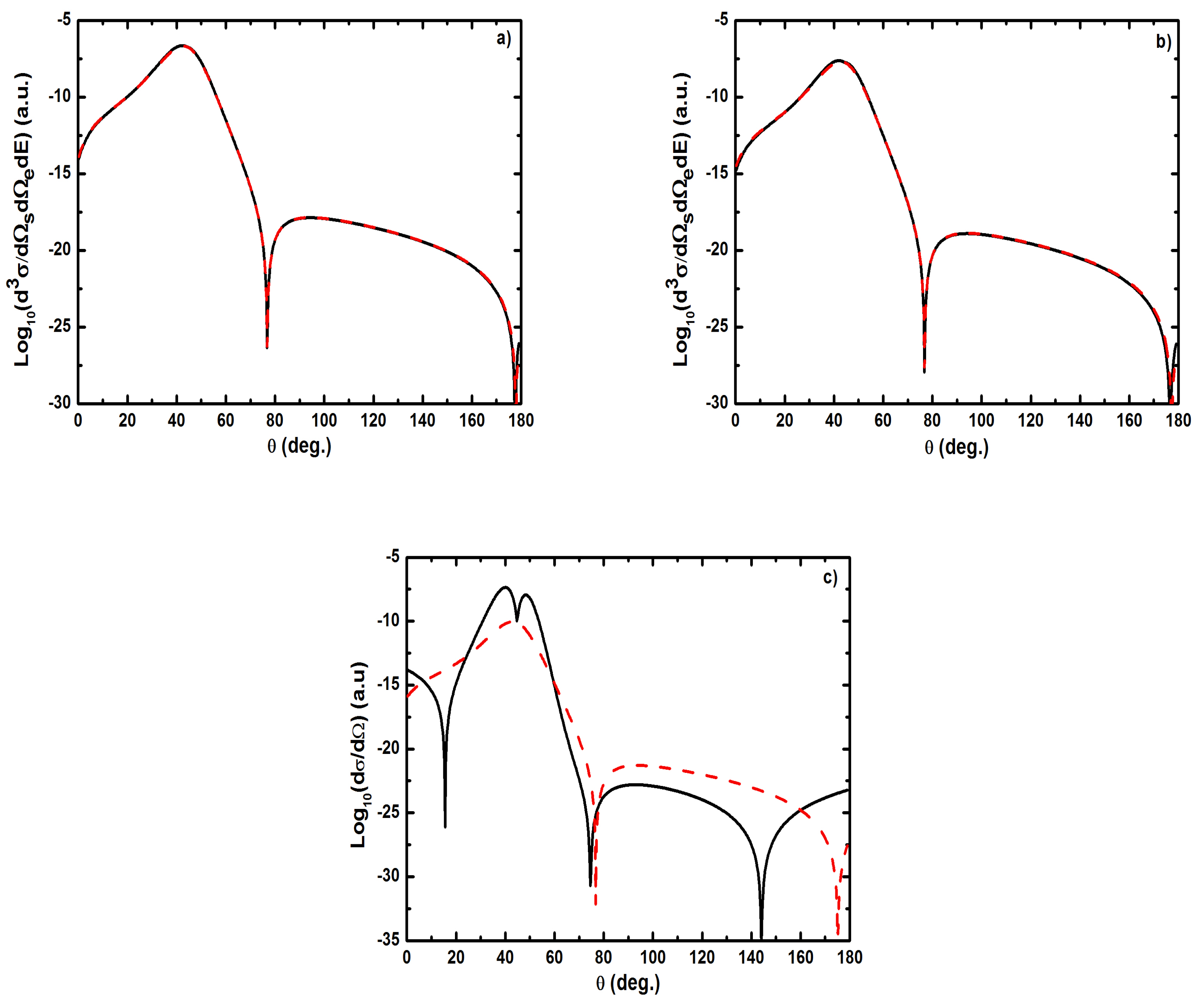
- As shown in Table 1, when the incident electron is fast, the magnitude of the momentum transfer K is never small in a symmetric geometry. On the other hand, the magnitude of the recoil momentum of the residual ion, can be either small, or it can become large. For scattering angles , the values of Q remain small ((e, 2e) spectroscopy region), while Q becomes large for . In the (e, 2e) spectroscopy region, the angular distribution illustrates that the electron-electron interaction which is attributed to the binary peak, is now split into two lobes with different magnitudes, while in large angles symmetric (e, 2e) reactions, the recoil peak (governed by the attraction between the electron and the nucleus) is split into smaller lobes with comparable magnitude. These lobes construct a plateau structures followed by an abrupt cutoff. We clearly observe an oscillatory behavior in the TDCS. This behavior can be traced back to the argument of the Bessel functions entering the expressions of the amplitude Equation (60) (because the dressing effect is less important in this case). For the net absorption of one photon () the results are governed by binary collisions and the recoil collisions are suppressed significantly. We attribute them to the contribution of the intermediate states and the long-range dipole potential affects mainly the distant collisions, which contribute when the energies of the primary electron are weak and the second Born approximation is needed. Outside the (e, 2e) spectroscopy region, Q becomes large and the simple first Born term of Equation (60) is no longer sufficient. Indeed, the second-order contribution of the ground intermediate state is of the same order of magnitude as the first Born term and therefore is essential to a complete description of the ionization amplitude.
- The triply differential cross sections displays two distinct minimums denoted () and (). Both minima correspond to values of the scattering angles for which the cross section is actually zero, nevertheless the origin of these zeros is different for each case. The minimum denoted occurs in fact at angles such that the first Born amplitude for the laser-assisted (e, 2e) process involving the exchange of ℓ photons vanishes. At the relatively low laser intensity considered here, the dressing of the target states does not play a dominant role and under the present conditions the term is dominant and that is zero at scattering angle. In fact, it is the angle that separates the (e, 2e) spectroscopy region (for small scattering angles , the values of Q remain small while in the large angle symmetric (e, 2e) region Q becomes large). On the other hand, the other minimums are due to the argument of the Bessel functions entering the expressions of the amplitudes Equation (60), which grows with and varies with the scattering angle. At higher field strengths, every other laser parameters being fixed, one explores more zeros of the Bessel functions when varying the scattering angle. This clearly gives rise to the observed increase in the number of minima. The same phenomena occurs for the case where the laser polarization vector is perpendicular to the incident momentum (not presented in the present paper).
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Sturmian Expansion of the First-Order Perturbed Wavefunction
Appendix B. Calculation of the Exact Upper Boundary of the Integral Over the Virtual Projectile
References
- Brantov, A.; Rozmus, W.; Sydora, R. Enhanced inverse bremsstrahlung heating rates in a strong laser field. Phys. Plasmas 2003, 10, 3385–3396. [Google Scholar] [CrossRef]
- Wang, F.; Weckert, E.; Ziaja, B. Inverse bremsstrahlung cross section estimated within evolving plasmas using effective ion potentials. J. Plasma Phys. 2009, 75, 289–301. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Differential cross sections for laser-assisted elastic electron scattering from argon. J. Phys. B 1994, 27, 5405. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Low-energy electron-helium scattering in a laser field. J. Phys. B 1996, 29, 5881. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Laser-assisted elastic electron scattering from helium. Can. J. Phys. 2001, 79, 1237–1246. [Google Scholar] [CrossRef]
- Nehari, D.; Holmes, J.; Dunseath, K.M.; Terao-Dunseath, M. Experimental and theoretical study of free-free electron-helium scattering in a CO2 laser field. J. Phys. B 2010, 43, 025203. [Google Scholar] [CrossRef][Green Version]
- DeHarak, B.A.; Ladino, L.; MacAdam, K.B.; Martin, N.L.S. High-energy electron-helium scattering in a Nd: YAG laser field. Phys. Rev. A 2011, 83, 022706. [Google Scholar] [CrossRef]
- Musa, M.O.; MacDonald, A.; Tidswell, L.; Holmes, J.; Wallbank, B. Laser-induced free-free transitions in elastic electron scattering from CO2. J. Phys. B 2010, 43, 175201. [Google Scholar] [CrossRef]
- Mason, N.J.; Newell, W.R. The polarisation dependence of the simultaneous electron-photon excitation cross section of the helium 23S state. J. Phys. B 1990, 23, L179. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Absorption and emission of radiation during electron excitation of the 2 1S and 2 1P states of helium. Phys. Rev. A 1989, 40, 5461. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Simultaneous electron-photon excitation of He 23S: An experimental investigation of the effects of laser intensity and polarisation. J. Phys. B 1990, 23, 2997. [Google Scholar] [CrossRef]
- Luan, S.; Hippler, R.; Lutz, H.O. Simultaneous electron-photon excitation of helium (h(cross) omega = 1.17 eV). J. Phys. B 1991, 24, 3241. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Schulz, M.; Tekaat, T.; Willmann, K. Ionization of helium: Angular correlation of the scattered and ejected electrons. Phys. Rev. Lett. 1969, 22, 89. [Google Scholar] [CrossRef]
- Röder, J.; Ehrhardt, H.; Pan, C.; Starace, A.F.; Bray, I.; Fursa, D.V. Absolute Triply Differential (e, 2e) Cross Section Measurements for H with Comparison to Theory. Phys. Rev. Lett. 1997, 79, 1666. [Google Scholar] [CrossRef]
- Röder, J.; Baertschy, M.; Bray, I. Measurements of the ionization of atomic hydrogen by 17.6-eV electrons. Phys. Rev. A 2003, 67, 010702. [Google Scholar] [CrossRef]
- Childers, J.G.; James, K.E.; Hughes, M.; Bray, I.; Baertschy, M.; Khakoo, M.A. Electron-impact ionization of atomic hydrogen at incident electron energies of 15.6, 17.6, 25, and 40 eV. Phys. Rev. A 2003, 68, 030702. [Google Scholar] [CrossRef]
- Dürr, M.; Dimopoulou, C.; Dorn, A.; Najjari, B.; Bray, I.; Fursa, D.V.; Chen, Z.; Madison, D.H.; Bartschat, K.; Ullrich, J. Single ionization of helium by 102 eV electron impact: three-dimensional images for electron emission. J. Phys. B 2006, 39, 4097. [Google Scholar] [CrossRef]
- Ren, X.; Senftleben, A.; Pflüger, T.; Dorn, A.; Colgan, J.; Pindzola, M.S.; Al-Hagan, O.; Madison, D.H.; Bray, I.; Fursa, D.V.; et al. Tracing multiple scattering patterns in absolute (e, 2e) cross sections for H2 and He over a 4π solid angle. Phys. Rev. A 2010, 82, 032712. [Google Scholar] [CrossRef]
- Ren, X.; Bray, I.; Fursa, D.V.; Colgan, J.; Pindzola, M.S.; Pflüger, T.; Senftleben, A.; Xu, S.; Dorn, A.; Ullrich, J. Electron-impact ionization of helium: A comprehensive experiment benchmarks theory. Phys. Rev. A 2011, 83, 052711. [Google Scholar] [CrossRef]
- Höhr, C.; Dorn, A.; Najjari, B.; Fischer, D.; Schröter, C.D.; Ullrich, J. Electron Impact Ionization in the Presence of a Laser Field: A Kinematically Complete (nγ, 2e) Experiment. Phys. Rev. Lett. 2005, 94, 153201. [Google Scholar]
- Höhr, C.; Dorn, A.; Najjari, B.; Fischer, D.; Schröter, C.D.; Ullrich, J. Laser-assisted electron-impact ionization of atoms. J. Electron Spectrosc. Relat. Phenom. 2007, 161, 172–177. [Google Scholar] [CrossRef]
- Mohan, M.; Chand, P. Electron-impact ionization of the hydrogen atom in the presence of an intense laser beam. Phys. Lett. A 1978, 65, 399–401. [Google Scholar] [CrossRef]
- Cavaliere, P.; Ferrante, G.; Leone, C. Particle-atom ionising collisions in the presence of a laser radiation field. J. Phys. B 1980, 13, 4495. [Google Scholar] [CrossRef]
- Banerji, J.; Mittleman, M.H. Electron-atom ionising collisions in the presence of a low-frequency laser field. J. Phys. B 1981, 14, 3717. [Google Scholar] [CrossRef]
- Cavaliere, P.; Leone, C.; Zangara, R.; Ferrante, G. Effects of a laser field on electron-atom ionizing collisions. Phys. Rev. A 1981, 24, 910. [Google Scholar] [CrossRef]
- Zangara, R.; Cavaliere, P.; Leone, C.; Ferrante, G. Influence of laser properties on particle-atom ionising collisions. J. Phys. B 1982, 15, 3881. [Google Scholar] [CrossRef]
- Zarcone, M.; Moores, D.L.; McDowell, M.R.C. Laser-assisted electron impact ionisation of helium at 256.5 ev. J. Phys. B 1983, 16, L11. [Google Scholar] [CrossRef]
- Mandal, C.K.M.; Ghosh, A.S. Electron-hydrogen ionization in the presence of a laser field. Phys. Rev. A 1984, 30, 2759. [Google Scholar] [CrossRef]
- Joachain, C.J.; Francken, P.; Maquet, A.; Martin, P.; Véniard, V. (e, 2e) Collisions in the Presence of a Laser Field. Phys. Rev. Lett. 1988, 61, 165. [Google Scholar] [CrossRef]
- Martin, P.; Véniard, V.; Maquet, A.; Francken, P.; Joachain, C.J. Electron-impact ionization of atomic hydrogen in the presence of a laser field. Phys. Rev. A 1989, 39, 6178. [Google Scholar] [CrossRef]
- Khalil, D.; Maquet, A.; Taïeb, R.; Joachain, C.J.; Makhoute, A. Laser-assisted collisions in helium. Phys. Rev. A 1997, 56, 4918. [Google Scholar] [CrossRef]
- Makhoute, A.; Khalil, D.; Maquet, A.; Taïeb, R. Light polarization effects in laser-assisted (e, 2e) collisions in helium. J. Phys. B 1999, 32, 3255. [Google Scholar] [CrossRef]
- Jones, S.; Madison, D.H. Slow convergence of the Born approximation for electron-atom ionization. Phys. Rev. A 2002, 66, 062711. [Google Scholar] [CrossRef]
- Li, S.M.; Chenand, J.; Zhou, Z.F. Electron-atomic-hydrogen “elastic” scattering in the presence of a laser field. Eur. Phys. J. D 2002, 19, 157. [Google Scholar] [CrossRef]
- Li, S.M.; Chen, J.; Zhou, Z.F. Ionization of atomic hydrogen by protons in the presence of a laser field. J. Phys. B 2002, 35, 557. [Google Scholar] [CrossRef]
- Duchateau, G.; Cormier, E.; Gayet, R. Coulomb-Volkov approach of ionization by extreme-ultraviolet laser pulses in the subfemtosecond regime. Phys. Rev. A 2002, 66, 023412. [Google Scholar] [CrossRef]
- Colgan, J.; Pindzola, M.S.; Childers, G.; Khakoo, M.A. Low-energy electron-impact single ionization of helium. Phys. Rev. A 2006, 73, 042710. [Google Scholar] [CrossRef]
- Stelbovics, A.T.; Bray, I.; Fursa, D.V.; Bartschat, K. Electron-impact ionization of helium for equal-energy-sharing kinematics. Phys. Rev. A 2005, 71, 052716. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, L.; Zhou, Y. Second-order Born effect in coplanar doubly symmetric (e, 2e) collisions for sodium. Phys. Lett. A 2012, 376, 2122. [Google Scholar] [CrossRef]
- Dal Cappello, C.; Haddadou, A.; Menas, F.; Roy, A.C. The second Born approximation for the single and double ionization of atoms by electrons and positrons. J. Phys. B 2011, 44, 015204. [Google Scholar] [CrossRef]
- Ajana, I.; Makhoute, A.; Khalil, D.; Dubois, A. The second Born approximation in laser-assisted (e, 2e) collisions in hydrogen. J. Phys. B 2014, 47, 175001. [Google Scholar] [CrossRef]
- Makhoute, A.; Ajana, I.; Khalil, D. Low-energy electron-impact laser-assisted ionization of atomic hydrogen. Phys. Rev. A 2014, 90, 053415. [Google Scholar] [CrossRef]
- Ajana, I.; Makhoute, A.; Khalil, D.; Chaddou, S. Exchange effects and second-order Born corrections in laser-assisted collisions with helium atoms. Phys. Rev. A 2015, 91, 043411. [Google Scholar] [CrossRef]
- Makhoute, A.; Ajana, I.; Khalil, D.; Chaddou, S. Second-order Born calculation of laser-assisted single ionization of helium by electrons. Eur. Phys. J. D 2015, 69, 160. [Google Scholar] [CrossRef]
- Ajana, I.; Makhoute, A.; Khalil, D. Laser polarization orientations in (e, 2e) reactions in atoms. Chin. Phys. Lett. 2015, 32, 8083401. [Google Scholar] [CrossRef]
- Makhoute, A.; Ajana, I.; Khalil, D.; Taoutioui, A.; Dubois, A. Signatures of laser photon energy in (e, 2e) reactions in helium. Eur. Phys. J. D 2016, 70, 249. [Google Scholar] [CrossRef]
- Khalil, D.; Tlidi, M.; Makhoute, A.; Ajana, I. Laser-assisted coplanar symmetric (e, 2e) triple differential cross sections. J. Phys. B 2017, 50, 078001. [Google Scholar] [CrossRef]
- Ajana, I.; Agueny, H.; Khalil, D.; Makhoute, A. Laser-assisted (e, 2e) collisions in the coplanar symmetric geometry. J. Phys. B 2018, 51, 225005. [Google Scholar] [CrossRef]
- Li, S.M.; Berakder, J.; Zhang, S.T.; Chen, J. Ionization of one-electron atoms and ions upon charged-particle impact assisted by a laser field. J. Electron. Spectrosc. 2007, 161, 188. [Google Scholar] [CrossRef]
- Ghosh Deb, S.; Roy, S.; Sinha, C. Multiphoton (e, 2e) process of hydrogen atom in strong laser field. Eur. Phys. J. D 2009, 55, 591. [Google Scholar] [CrossRef]
- Kouzakov, K.A.; Yu, V.; Popov, M.; Takahashi, A. Laser-assisted electron momentum spectroscopy. Phys. Rev. A 2010, 82, 023410. [Google Scholar] [CrossRef]
- Bulychev, A.A.; Kouzakov, K.A.; Popov, Y.V. The role of Volkov waves in laser-assisted electron momentum spectroscopy. Phys. Lett. A 2012, 376, 484–487. [Google Scholar] [CrossRef]
- Nixon, K.L.; Murray, A.J. Parametrization of Electron-Impact Ionization Cross Sections from Laser-Excited and Aligned Atoms. Phys. Rev. Lett. 2014, 112, 023202. [Google Scholar] [CrossRef]
- Yamazaki, M.; Oishi, K.; Nakazawa, H.; Zhu, C.; Takahashi, M. Molecular Orbital Imaging of the Acetone S2 Excited State Using Time-Resolved (e, 2e) Electron Momentum Spectroscopy. Phys. Rev. Lett 2015, 114, 103005. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Shan, X.; Liu, Z.; Niu, S.; Wang, E.; Chen, X. Development of an electron momentum spectrometer for time-resolved experiments employing nanosecond pulsed electron beam. Rev. Sci. Instrum. 2018, 89, 033101. [Google Scholar] [CrossRef]
- Zheng, M.Y.; Li, S.M. Laser-assisted ionization of atomic hydrogen by electrons in the second Born approximation. Phys. Rev. A 2010, 82, 023414. [Google Scholar] [CrossRef]
- Volkov, D.M. On a class of solutions of the Dirac equation. Z. Phys. 1935, 94, 250–260. [Google Scholar]
- Ehrhardt, H.; Hesselbacher, K.H.; Jung, K.; Schulz, M.; Willmann, K. Collisional ionization of helium by 250 eV electrons: Experiments with completely determined kinetics. J. Phys. B 1972, 5, 2107. [Google Scholar] [CrossRef]
- Beaty, E.C.; Hesselbacher, K.H.; Hong, S.P.; Moore, I.H. Triple-differential three-dimensional cross sections for low-energy electron impact ionization of helium. J. Phys. B 1977, 10, 611. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Fischer, M.; Jung, K. Triple differential cross section measurements for the electron impact ionization of helium: Comparison with a second Born approximation. Z. Phys. A 1982, 304, 119–124. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Fischer, M.; Jung, K.; Byron, F.W., Jr.; Joachain, C.; Piraux, B. Triply differential cross sections for the ionization of helium by fast electrons. Phys. Rev. Lett. 1982, 48, 1807. [Google Scholar] [CrossRef]
- Lahmam-Bennani, A.; Wellenstein, H.F.; Duguet, A.; Rouault, M. Absolute triple differential cross sections for the 3p ionisation of argon by electron impact. J. Phys. B 1983, 16, 121. [Google Scholar] [CrossRef]
- Lahmam-Bennani, A.; Wellenstein, H.F.; Duguet, A.; Dal Cappello, C. Coincidence electron impact ionisation of helium: Absolute experimental cross sections and comparison with first-order theories. J. Phys. B 1984, 17, 3159. [Google Scholar] [CrossRef]
- Jung, K.; Müller-Fiedler, R.; Schlemmer, P.; Ehrhardt, H.; Kiar, H. Absolute triple differential cross sections of electron impact ionisation of helium at 600 eV collision energy. J. Phys. B 1985, 18, 2955. [Google Scholar] [CrossRef]
- Lahmam-Bennani, A.; Duguet, A.; Dal Cappello, C. High momentum range of electron momentum distributions investigated by means of high energy (e, 2e) collisions. J. Electron Spectrosc. 1986, 40, 141–161. [Google Scholar] [CrossRef]
- Ehrhardt, H.; Jung, K.; Knoth, G.; Schlemmer, P. Differential cross sections of direct single electron impact ionization. Z. Phys. D 1986, 1, 3–32. [Google Scholar] [CrossRef]
- Amaldi, U., Jr.; Egidi, A.; Marconero, R.; Pizzella, G. Use of a two channeltron coincidence in a new line of research in atomic physics. Rev. Sci. Instr. 1969, 40, 1001–1004. [Google Scholar] [CrossRef]
- Weigold, E.; Hood, S.T.; Teubner, P.J.O. Energy and angular correlations of the scattered and ejected electrons in the electron-impact ionization of argon. Phys. Rev. Lett. 1973, 30, 475. [Google Scholar] [CrossRef]
- McCarthy, I.E.; Weigold, E. (e, 2e) spectroscopy. Phys. Rep. 1976, 27, 275. [Google Scholar] [CrossRef]
- Lohmann, B.; Weigold, E. Direct measurement of the electron momentum probability distribution in atomic hydrogen. Phys. Lett. A 1981, 86, 139–141. [Google Scholar] [CrossRef]
- Van Wingerden, B.; Kimman, I.T.; Van Tilburg, V.T.; de Heer, F.J. Triple and double differential cross sections for electron impact ionisation of helium and molecular hydrogen. J. Phys. B 1981, 14, 2475. [Google Scholar] [CrossRef]
- Pochat, A.; Tweed, R.J.; Doritch, M.; Peresse, J. Double and triple differential cross sections for autoionisation of helium by electron impact. J. Phys. B 1982, 15, 2269. [Google Scholar] [CrossRef]
- Pochat, A.; Tweed, R.J.; Peresse, J.; Joachain, C.J.; Piraux, B.; Byron, F.W., Jr. Second-order effects in large-angle coplanar symmetric (e, 2e) processes. J. Phys. B 1983, 16, L775. [Google Scholar] [CrossRef]
- Kimman, J.T.; Pan Guang-Yan, C.; McCurdy, W.; de Heer, F.J. Triple and double differential cross sections for electron impact ionisation of helium for’energy-sharing’kinematics. J. Phys. B 1983, 16, 4203. [Google Scholar] [CrossRef]
- Cook, J.P.D.; McCarthy, I.E.; Stelbovics, A.T.; Weigold, E. Non-coplanar symmetric (e, 2e) momentum profile measurements for helium: an accurate test of helium wavefunctions. J. Phys. B 1984, 17, 2339. [Google Scholar] [CrossRef]
- Byron, F.W., Jr.; Francken, P.; Joachain, C.J. Laser-assisted elastic electron-atom collisions. J. Phys. B 1987, 20, 5487. [Google Scholar] [CrossRef]
- Joachain, C.H. Quantum Collision Theory, 3rd ed.; North-Holland Physics Publishing: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Byron, F.W.; Joachain, C.J. Electron-atom collisions in a strong laser field. J. Phys. B 1984, 17, L295. [Google Scholar] [CrossRef]
- Byron, F.W.; Joachain, C.J. Theory of (e, 2e) Reactions. Phys. Rep. 1989, 179, 211. [Google Scholar] [CrossRef]
- Francken, P.; Attaourti, Y.; Joachain, C.J. Laser-assisted inelastic electron-atom collisions. Phys. Rev. A 1988, 38, 1785. [Google Scholar] [CrossRef]
- Bouzidi, M.; Makhoute, A.; Khalil, D.; Maquet, A.; Joachain, C.J. On the second Born approximation for laser-assisted electron-atom collisions. J. Phys. B 2001, 34, 737. [Google Scholar] [CrossRef]
- Bivona, S.; Burlon, R.; Zangara, R.; Ferrante, G. Electron scattering in strong laser fields. Theoretical models versus recent experiments. J. Phys. B 1985, 18, 3149. [Google Scholar] [CrossRef]
- Francken, P.; Joachain, C.J. Theoretical study of electron-atom collisions in intense laser fields. J. Opt. Soc. Am. B 1990, 7, 554–563. [Google Scholar] [CrossRef]
- Kroll, N.M.; Watson, K.M. Charged-particle scattering in the presence of a strong electromagnetic wave. Phys. Rev. A 1973, 8, 804. [Google Scholar] [CrossRef]
- Ochkur, V.I. The Born-Oppenheimer method in the theory of atomic collisions. Sov. Phys. JETP 1964, 18, 503–508. [Google Scholar]
- Nixon, K.L.; Murray, A.J. (e, 2e) ionization studies of the stable noble gases in a coplanar symmetric geometry. Phys. Rev. A 2013, 87, 022712. [Google Scholar] [CrossRef]
- Mason, N.J. Laser-assisted electron-atom collisions. Rep. Prog. Phys. 1993, 56, 1275. [Google Scholar] [CrossRef]
- Weigold, E.; Noble, C.J.; Hood, S.T.; Fuss, I. Electron impact ionisation of atomic hydrogen: experimental and theoretical (e, 2e) differential cross sections. J. Phys. B 1979, 12, 291. [Google Scholar] [CrossRef]
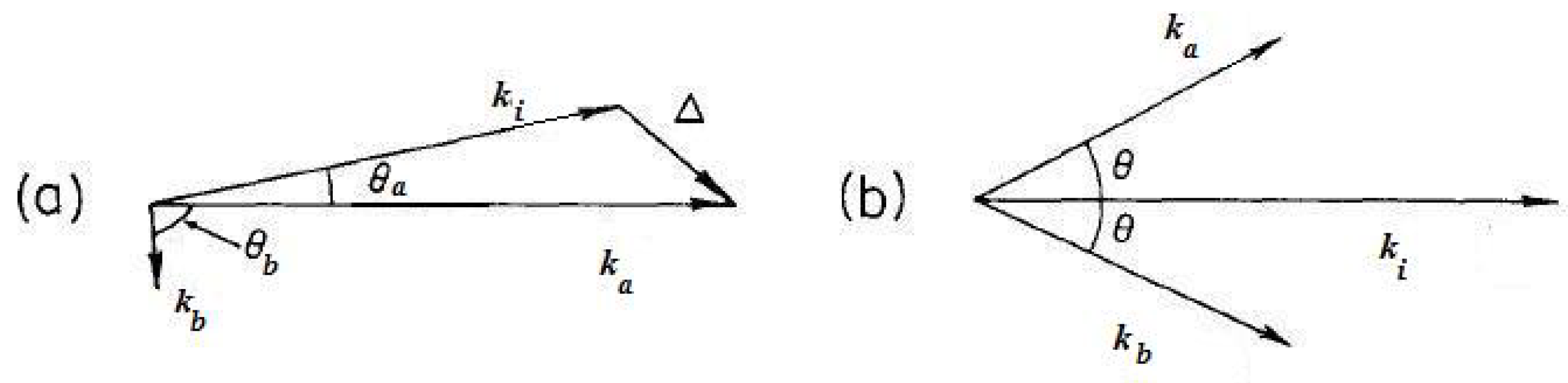


| 0 | 1.83427 | 1.82919 | 1.83936 | 2.39355 | 2.403718 | 2.38338 |
| 10 | 2.03551 | 2.03116 | 2.03986 | 2.26509 | 2.27510 | 2.25507 |
| 20 | 2.54084 | 2.53790 | 2.54378 | 1.88361 | 1.89316 | 1.87405 |
| 30 | 3.19874 | 3.19712 | 3.20073 | 1.26071 | 1.26951 | 1.25189 |
| 40 | 3.91878 | 3.91825 | 3.91933 | 0.41531 | 0.42309 | 0.40751 |
| 50 | 4.65563 | 4.65599 | 4.65527 | 0.62191 | 0.62038 | 0.63345 |
| 60 | 5.38461 | 5.38574 | 5.38348 | 1.83427 | 1.82919 | 1.83936 |
| 70 | 6.09032 | 6.09211 | 6.08852 | 3.17009 | 3.16662 | 3.17357 |
| 80 | 6.76184 | 6.76423 | 6.75946 | 4.59379 | 4.59202 | 4.59556 |
| 90 | 7.39077 | 7.39368 | 7.38786 | 6.06210 | 6.06210 | 6.06210 |
| 100 | 7.79023 | 7.97359 | 7.96686 | 6.53041 | 7.532172 | 7.52864 |
| 130 | 9.35800 | 9.36241 | 9.35358 | 11.49729 | 11.50382 | 11.49075 |
| 150 | 9.95063 | 9.95548 | 9.94579 | 13.38491 | 13.39371 | 13.37609 |
| 180 | 10.28992 | 10.28992 | 10.28483 | 14.51775 | 14.51775 | 14.50750 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makhoute, A.; Khalil, D.; Ajana, I. Laser-Assisted (e, 2e) Collisions in the Symmetric/Asymmetric Coplanar Geometry. Atoms 2019, 7, 40. https://doi.org/10.3390/atoms7020040
Makhoute A, Khalil D, Ajana I. Laser-Assisted (e, 2e) Collisions in the Symmetric/Asymmetric Coplanar Geometry. Atoms. 2019; 7(2):40. https://doi.org/10.3390/atoms7020040
Chicago/Turabian StyleMakhoute, Abdelkader, Driss Khalil, and Imane Ajana. 2019. "Laser-Assisted (e, 2e) Collisions in the Symmetric/Asymmetric Coplanar Geometry" Atoms 7, no. 2: 40. https://doi.org/10.3390/atoms7020040
APA StyleMakhoute, A., Khalil, D., & Ajana, I. (2019). Laser-Assisted (e, 2e) Collisions in the Symmetric/Asymmetric Coplanar Geometry. Atoms, 7(2), 40. https://doi.org/10.3390/atoms7020040





