Distortion of the Ionization Cross Section of He by the Coherence Properties of a C6+ Beam
Abstract
1. Introduction
2. An Incoherent Mixture of Quantum States
2.1. Mathematical Description
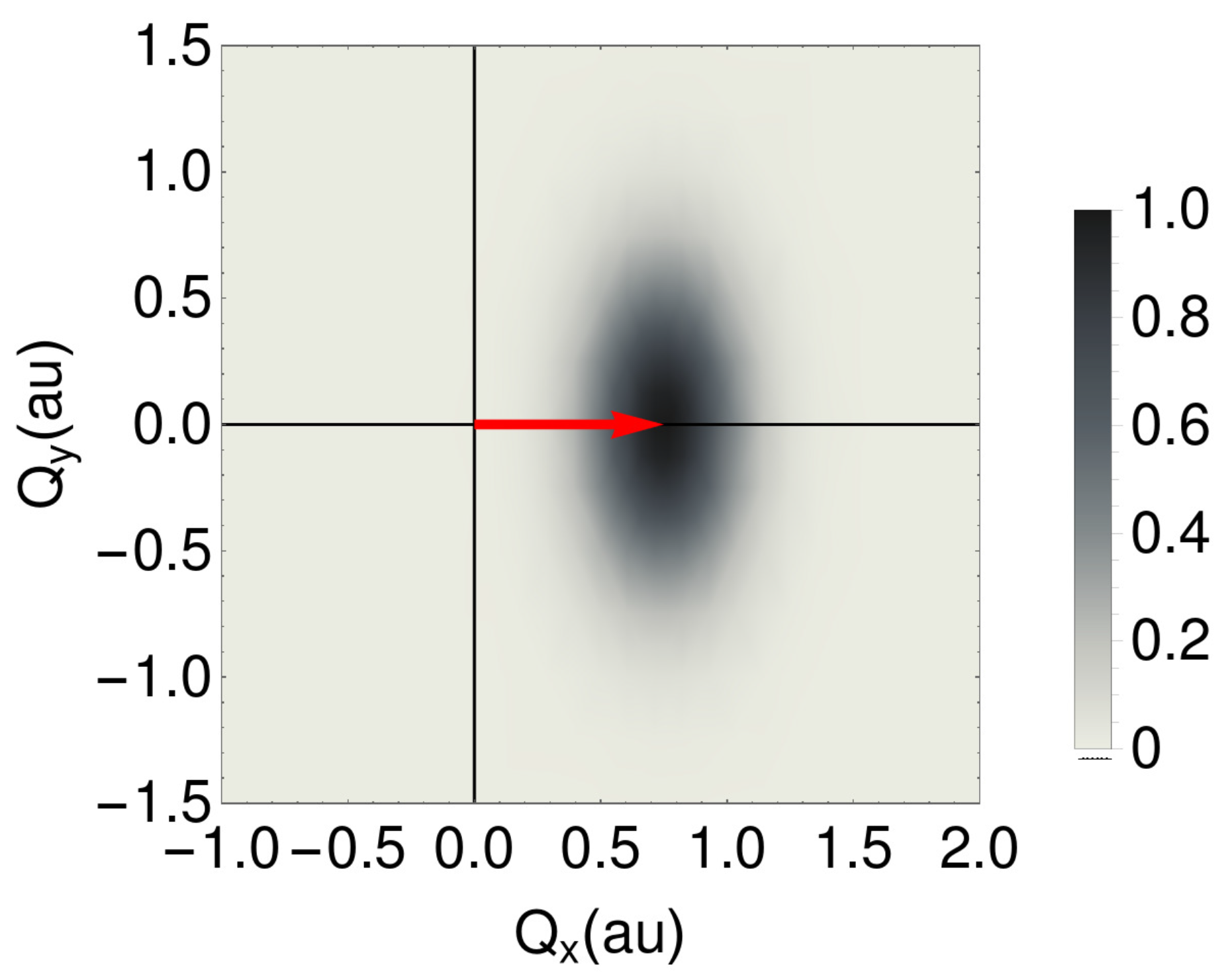
2.2. Calculation of the Incoherent FDCS
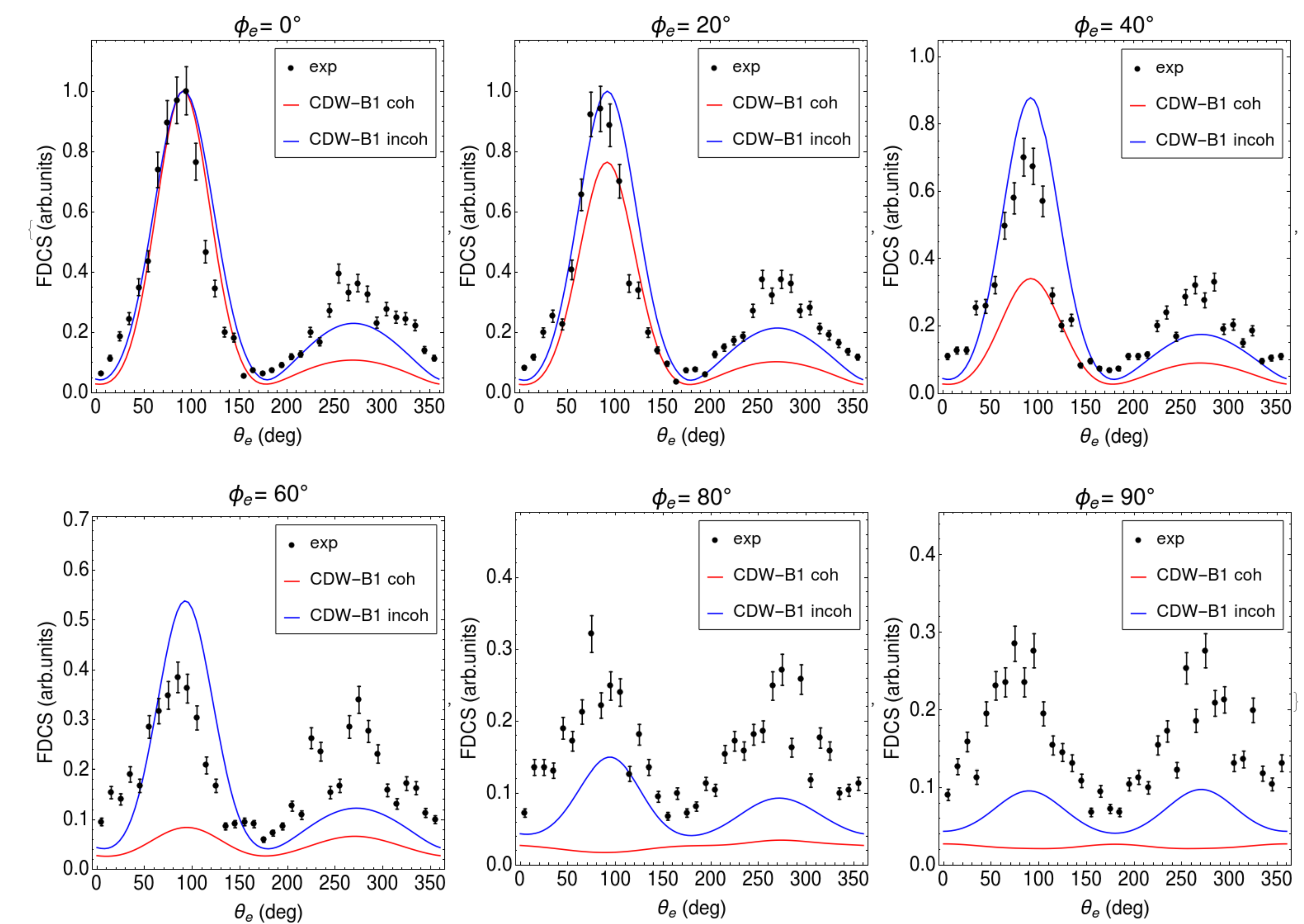
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Egodapitiya, K.N.; Sharma, S.; Hasan, A.; Laforge, A.C.; Madison, D.H.; Moshammer, R.; Schulz, M. Manipulating Atomic Fragmentation Processes by Controlling the Projectile Coherence. Phys. Rev. Lett. 2011, 106, 153202. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Hasan, A.; Egodapitiya, K.N.; Arthanayaka, T.P.; Sakhelashvili, G.; Schulz, M. Projectile coherence effects in electron capture by protons colliding with H2 and He. Phys. Rev. A 2012, 86, 022706. [Google Scholar] [CrossRef]
- Wang, X.; Schneider, K.; LaForge, A.; Kelkar, A.; Grieser, M.; Moshammer, R.; Ullrich, J.; Schulz, M.; Fischer, D. Projectile coherence effects in single ionization of helium. J. Phys. B At. Mol. Phys. 2012, 45, 211001. [Google Scholar] [CrossRef]
- Schneider, K.; Schulz, M.; Wang, X.; Kelkar, A.; Grieser, M.; Krantz, C.; Ullrich, J.; Moshammer, R.; Fischer, D. Role of Projectile Coherence in Close Heavy Ion-Atom Collisions. Phys. Rev. Lett. 2013, 110, 113201. [Google Scholar] [CrossRef] [PubMed]
- Feagin, J.M.; Hargreaves, L. Loss of wave-packet coherence in stationary scattering experiments. Phys. Rev. A 2013, 88, 032705. [Google Scholar] [CrossRef]
- Sharma, S.; Arthanayaka, T.P.; Hasan, A.; Lamichhane, B.R.; Remolina, J.; Smith, A.; Schulz, M. Fully differential study of interference effects in the ionization of H2 by proton impact. Phys. Rev. A 2014, 90, 052710. [Google Scholar] [CrossRef]
- Járai-Szabó, F.; Nagy, L. Theoretical investigations on the projectile coherence effects in fully differential ionization cross sections. Eur. Phys. J. D 2015, 69, 4. [Google Scholar] [CrossRef]
- Arthanayaka, T.P.; Sharma, S.; Lamichhane, B.R.; Hasan, A.; Remolina, J.; Gurung, S.; Sarkadi, L.; Schulz, M. Influence of the post-collision interaction on interference effects in ionization of H2 by proton impact. J. Phys. B At. Mol. Phys. 2015, 48, 175204. [Google Scholar] [CrossRef]
- Arthanayaka, T.; Lamichhane, B.R.; Hasan, A.; Gurung, S.; Remolina, J.; Borbély, S.; Járai-Szabó, F.; Nagy, L.; Schulz, M. Fully differential study of wave packet scattering in ionization of helium by proton impact. J. Phys. B At. Mol. Phys. 2016, 49, 13LT02. [Google Scholar] [CrossRef]
- Sarkadi, L.; Fabre, I.; Navarrete, F.; Barrachina, R.O. Loss of wave-packet coherence in ion-atom collisions. Phys. Rev. A 2016, 93, 032702. [Google Scholar] [CrossRef]
- Fabre, I.; Navarrete, F.; Sarkadi, L.; Barrachina, R.O. Free evolution of an incoherent mixture of states: A quantum mechanical approach to the van Cittert–Zernike theorem. Eur. J. Phys. 2017, 39, 015401. [Google Scholar] [CrossRef]
- Lamichhane, B.R.; Arthanayaka, T.; Remolina, J.; Hasan, A.; Ciappina, M.F.; Navarrete, F.; Barrachina, R.O.; Lomsadze, R.A.; Schulz, M. Fully Differential Study of Capture with Vibrational Dissociation in p+H2 Collisions. Phys. Rev. Lett. 2017, 119, 083402. [Google Scholar] [CrossRef] [PubMed]
- Schulz, M. Chapter Eight—The Role of Projectile Coherence in the Few-Body Dynamics of Simple Atomic Systems. In Advances in Atomic, Molecular, and Optical Physics; Arimondo, E., Lin, C.C., Yelin, S.F., Eds.; Academic Press: New York, NY, USA, 2017; Volume 66, pp. 507–543. [Google Scholar] [CrossRef]
- Gatzke, J.; Navarrete, F.; Ciappina, M.; Gatzke, H.; Chuluunbaatar, O.; Zaytsev, S.A.; Bulychev, A.A.; Kouzakov, K.A.; Galstyan, A.; Waitz, M.; et al. Single ionization of Helium at 0.5–2 MeV proton impact: On the quest for projectile coherence effects. J. Phys. Conf. Ser. 2017, 875, 092006. [Google Scholar] [CrossRef]
- Taylor, J.R. Scattering Theory: The Quantum Theory on Nonrelativistic Collisions; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1972. [Google Scholar]
- Fabre, I.; Navarrete, F.; Sarkadi, L.; Barrachina, R.O. Projectile coherence: The Van Cittert - Zernike theorem revisited. J. Phys. Conf. Ser. 2015, 635, 012001. [Google Scholar] [CrossRef]
- McGovern, M.; Whelan, C.T.; Walters, H.R.J. C6+-impact ionization of helium in the perpendicular plane: Ionization to the ground state, excitation-ionization, and relativistic effects. Phys. Rev. A 2010, 82, 032702. [Google Scholar] [CrossRef]
- Schulz, M.; Moshammer, R.; Fischer, D.; Kollmus, H.; Madison, D.H.; Jones, S.; Ullrich, J. Three-dimensional imaging of atomic four-body processes. Nature 2003, 422, 48. [Google Scholar] [CrossRef] [PubMed]
- Barrachina, R.; Navarrete, F.; Ciappina, M.; Schulz, M. Coherence and contextuality in scattering experiments. In Ion-Atom Collisions: The Few-Body Problem in Dynamic Systems; Schulz, M., Ed.; De Gruyter: Berlin, Germany, in press.
- Navarrete, F.; Ciappina, M.; Sarkadi, L.; Barrachina, R. The role of the wave packet coherence on the ionization cross section of He by p+ and C6+ projectiles. Nucl. Instrum. Methods Phys. Res. B 2017, 408, 165–168. [Google Scholar] [CrossRef]
- Karlovets, D.V.; Kotkin, G.L.; Serbo, V.G. Scattering of wave packets on atoms in the Born approximation. Phys. Rev. A 2015, 92, 052703. [Google Scholar] [CrossRef]
- Fiol, J.; Otranto, S.; Olson, R.E. Fully differential ionization cross sections in fast ion-atom collisions. J. Phys. Conf. Ser. 2007, 88, 012014. [Google Scholar] [CrossRef]
- Fiol, J.; Otranto, S.; Olson, R.E. Momentum-transfer dependence of ionization cross sections for C6++He collisions. J. Phys. Conf. Ser. 2007, 58, 161. [Google Scholar] [CrossRef]
- Fiol, J.; Otranto, S.; Olson, R.E. Critical comparison between theory and experiment for C6++He fully differential ionization cross sections. J. Phys. B At. Mol. Phys. 2006, 39, L285. [Google Scholar] [CrossRef]
- Kouzakov, K.A.; Zaytsev, S.A.; Popov, Y.; Takahashi, M. Singly ionizing 100-MeV/amu C6++He collisions with small momentum transfer. Phys. Rev. A 2012, 86, 032710. [Google Scholar] [CrossRef]
- Colgan, J.; Pindzola, M.S.; Robicheaux, F.; Ciappina, M.F. Fully differential cross sections for the single ionization of He by C6+ ions. J. Phys. B At. Mol. Phys. 2011, 44, 175205. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarrete, F.; Barrachina, R.; Ciappina, M.F. Distortion of the Ionization Cross Section of He by the Coherence Properties of a C6+ Beam. Atoms 2019, 7, 31. https://doi.org/10.3390/atoms7010031
Navarrete F, Barrachina R, Ciappina MF. Distortion of the Ionization Cross Section of He by the Coherence Properties of a C6+ Beam. Atoms. 2019; 7(1):31. https://doi.org/10.3390/atoms7010031
Chicago/Turabian StyleNavarrete, Francisco, Raúl Barrachina, and Marcelo F. Ciappina. 2019. "Distortion of the Ionization Cross Section of He by the Coherence Properties of a C6+ Beam" Atoms 7, no. 1: 31. https://doi.org/10.3390/atoms7010031
APA StyleNavarrete, F., Barrachina, R., & Ciappina, M. F. (2019). Distortion of the Ionization Cross Section of He by the Coherence Properties of a C6+ Beam. Atoms, 7(1), 31. https://doi.org/10.3390/atoms7010031






