Abstract
Differential cross sections (DCS) for single electron capture from helium by heavy ion impact are calculated using a frozen core 3-body model and an active electron 4-body model within the first Born approximation. DCS are presented for H+, He2+, Li3+, and C6+ projectiles with velocities of 1 MeV/amu and 10 MeV/amu. In general, the DCS from the two models are found to differ by about one to two orders of magnitude with the active electron 4-body model showing better agreement with experiment. Comparison of the models reveals two possible sources of the magnitude difference: the inactive electron’s change of state and the projectile–target Coulomb interaction used in the different models. Detailed analysis indicates that the uncaptured electron’s change of state can safely be neglected in the frozen core approximation, but that care must be used in modeling the projectile–target interaction.
1. Introduction
The study of electron capture (or charge transfer) collisions serves researchers in both fundamental and applied fields. On the applied side, electron capture collisions are needed in areas as diverse as plasma physics, astrophysics, and biophysics. Modelers, theorists, and experimentalists in these fields rely on accurate collision cross sections in order to understand phenomena and develop new technologies. Without an accurate knowledge of the most fundamental atomic interactions, more sophisticated systems cannot be adequately understood, and this is where a connection between fundamental and applied physics is needed. From a fundamental standpoint, electron capture collisions can provide valuable information about atomic structure and few-body interactions on the atomic scale. They have been used to study effects such as electron correlation, multi-step processes, and nuclear–nuclear Coulomb effects.
While these collision systems have been studied extensively for the last century, there are still many theoretical, computational, and experimental challenges. In particular, the small projectile scattering angles involved in heavy particle collisions make highly detailed measurements difficult, and only in the last two decades have a significant number of differential cross section measurements become available [1,2,3,4,5,6,7]. The growing body of highly accurate experimental data has spurred the development and application of numerous theoretical models for the study of the electron capture process. While theory’s ability to accurately predict experiments has improved, there are still many remaining challenges. For example, an accurate theoretical treatment of heavy particle continuum wave functions remains quite difficult. Additionally, time-dependent and non-perturbative models often perform better than traditional Born-type models, but they typically rely on classical, semiclassical, or other approximations, and can require significant computational resources [8,9,10,11,12,13].
A frequently used approximation for single electron capture collisions in both perturbative and non-perturbative models is the frozen core approximation in which the uncaptured, inactive electron is assumed to not change state. In the case of a bare particle colliding with a helium atom, the implementation of the frozen core approximation effectively reduces the calculation from a four-body problem to a three-body problem, which greatly improves computational runtimes. The frozen core approximation is also often applied to single ionization and single excitation collisions in which there is an inactive electron that can be modeled as a bystander with only screening effects and no change of state. Naturally, a complete four-body calculation in all of these collision processes represents a more physically accurate description, but the key question is what, if any, limitations exist by using the frozen core approximation.
Theoretical study of the single capture process dates back nearly a century to the first work of Thomas [14] using a classical model and Oppenheimer [15] and Brinkman and Kramers [16] using a quantum mechanical plane wave Born approximation. Since that time, countless additional models have been developed, which are too numerous to list individually. We refer the reader to the review [17] and references cited below for an overview of the history of electron capture studies. However, a brief discussion of a few of the 3-body and 4-body models is relevant to the work here.
Use of the frozen core approximation resulting in a 3-body model has proven effective in many cases. For example, the 3-body continuum distorted wave-eikonal initial state [18], two center basis generator method (TC-BGM) [4], 3-body Coulomb–Born distorted wave formalism [19], and the first order Born approximation with Coulomb boundary conditions [20] have all shown moderate-to-good success in predicting the shape and magnitude of the differential cross section (DCS). While electron correlation cannot be explicitly included in these 3-body models, they all include the Coulomb distortion caused by the residual ion and of nuclear screening. The methods by which these effects are included are what distinguish the models.
Thanks to computational advances, there are also many four-body models in use for the single capture process [2,17,21,22,23,24,25,26,27,28,29,30] with varying degrees of agreement between each other and experiment. These four-body models include the four-body boundary-corrected first Born [31], Coulomb distorted Wave–Born initial state [32], Coulomb distorted wave–four-body [33], four-body boundary-corrected continuum-intermediate-states (BCIS-4B) [31], and Born Distorted Wave–four-body [34] models, among others. The obvious advantage to the four-body models is the inclusion of the initial state electron correlation, although this generally has a minimal effect [8]. The other advantage to four-body models is the ability to include more accurate final state interactions between the outgoing bound state and the residual ion bound state, which is typically the distinguishing feature of the models listed above. With the exception of the TC-BGM model, which is semiclassical, and the BCIS-4B model, which is second order, the models listed above are first order perturbative models. Many of these produce a deep minimum at the so-called dark angle that results from an interference of terms in the perturbation potential. However, inclusion of proper boundary conditions or higher order terms eliminates this feature [8,31]. Despite the plethora of available three-body and four-body models for single electron capture, a focused analysis of the effects of the frozen core approximation in single capture collisions has not been performed. This is the goal of the present investigation.
Previously, we examined the frozen core approximation in electron and heavy ion impact single ionization of helium [35,36], as well as the five-body process of He+ + He electron capture [37]. In our study of single ionization, we found that the initial state projectile–target interaction and the final state ionic potential were most influential on the magnitude and shape of the differential cross sections. The different treatments of these interactions in the three-body and four-body models represent different approximations for screening of the target nucleus and showed clear effects for both electron and heavy ion projectiles.
For the five-body He+ + He single capture collision, our analysis also showed that the model used for screening either the projectile or the target nucleus could significantly affect the shape and magnitude of the DCS. In particular, much like the single ionization case, changes to the initial state projectile–target Coulomb interaction were the primary cause of the differences between the frozen core and active electron DCS. Based on the consistency of these prior studies, we expect the initial state projectile–target interaction to play an important role in the single capture process, as well. In order to focus solely on the effect of the frozen core approximation, we perform calculations with the first Born approximation (FBA), where the effect of the uncaptured electron can be studied in a straightforward manner. Clearly, more sophisticated models are available, but their use introduces additional complexities, making a one-to-one comparison of models more difficult. Our primary aim is to trace any differences in the DCS directly to specific aspects of the theoretical models and approximations. Using two simple models that are identical except for key features is crucial to limiting the possible causes of differences observed in the DCS. Atomic units are used throughout unless otherwise noted.
2. Theory
In both the three-body and four-body models, the DCS are calculated using Jacobi coordinates in the center of mass frame and then converted to the lab frame. The fully differential cross section in the center of mass frame is given by [38]
where is the reduced mass of the scattered projectile and residual ion, is the reduced mass of the initial state projectile and target atom, is the center of mass momentum of the scattered (incident) projectile, and is the transition matrix. The differential cross section in the lab frame is related to that of the center of mass frame by
where δ is the ratio of the speed of the center of mass of the entire collision system in the lab frame V and the speed of the scattered projectile in the center of mass frame , such that . The angle θC is the scattering angle of the projectile in the center of mass frame, which is related to the lab frame scattering angle by
In order to focus on the effects of the frozen core approximation, we use the first Born approximation (FBA) to calculate the transition matrix for single electron capture from a helium target by bare heavy ion impact. We assume the simplest independent electron model for the target atom and use an uncorrelated target helium wave function in the four-body model. It has been shown that for the single capture process, target electron correlation is unimportant and can be neglected [8]. Additionally, electron correlation cannot be explicitly included in a three-body model, and therefore its inclusion in our four-body model would introduce a feature whose effect in comparison to the three-body model could not be directly tested. However, to confirm the assumption that correlation can be neglected, we compare differential cross sections using our uncorrelated four-body model with a similar calculation using a correlated wave function.
In the three-body model, we use a hydrogenic wave function with effective nuclear charge for the target atom. This model minimally accounts for nuclear screening, and most importantly is the same as the independent electron orbitals in the four-body model. The use of a hydrogenic wave function implicitly assumes screening does not play a significant role in the capture process, and to test this assumption, we compare the differential cross sections produced using the three-body model with either the hydrogenic wave function or a 5-Zeta wave function that better models nuclear screening and predicts a more accurate binding energy.
The incident projectile has charge and mass , and we present results here for H+, He2+, Li3+, and C6+ projectiles. In the FBA, the motion of the incident and scattered projectiles is treated as a plane wave in both the initial and final state. The captured electron bound state is given by a hydrogenic wave function that is analytically known.
One advantage of the simplistic FBA used here is that the majority of the calculation can be performed analytically. Additionally, many parts of the three-body and four-body transition matrices are identical, allowing for the most direct comparison of the models. For the analytical calculations, it is useful to keep in mind the hydrogen-like atom momentum space wave function for a nuclear charge Z
For capture to the ground state,
Prior to any analytical calculations, the four-body model requires a 9-dimensional spatial integral and the three-body model requires a 6-dimensional integral. Numerical integration of these integrals is not feasible [27], however use of Equation (4) allows them to be reduced to 3-or 4-dimensional integrals which we perform with standard Gaussian quadrature techniques.
2.1. Active Electron Four-Body Model
In the four-body model, all constituent particles are explicitly included in the calculation with the transition matrix given by
where is the incident (scattered) projectile plane wave with center of mass momentum , is the target helium atom wave function, is the bound electron wave function for the captured electron, and is the bound state of the residual He+ ion. We note that while the target electrons have been labeled here for clarity, their indistinguishability has been properly included by symmetrizing the total final state wave function with respect to the two electrons. The perturbation is given by the Coulomb interaction between the projectile and constituent particles of the helium atom
where are the lab frame position vectors of the projectile and two atomic electrons respectively, and , and are the charges of the projectile, target nucleus, and electron respectively. The Jacobi coordinates are related to the lab frame coordinates by
For the target ground state helium wave function, we use either a one parameter variational wave function that does not include electron correlation given by
or a simple wave function that does include correlation, but still allows for a mostly analytical calculation for capture to the ground state
with , N = 3.182, μ = 0.586, λ = 0.379, and γ = 1.8395. The bound state wave function for the residual He+ ion is simply a 1s hydrogenic wave function for charge given by
2.2. Frozen Core Three-Body Model
In the three-body model, the inactive electron and target nucleus are considered as a single frozen core, with charge . The transition matrix is then given by
where the projectile plane waves are the same as in the four-body model, as is the scattered projectile bound state. The three-body perturbation is
and the target atom wave function is modeled in the simplest case by a single electron bound state given by Equation (13) with to account for screening of the nucleus by the inactive electron. A more sophisticated single electron wave function for the target helium atom is given by a 5-Zeta function
where ai and Zi can be found in [39].
The lab frame coordinates remain the same as in the four-body model, with the exception that the inactive electron is not present and therefore there is no . The Jacobi coordinates for the three-body model can be found by setting = 0 in Equations (7)–(11).
3. Results and Discussion
3.1. Screening and Correlation
We begin by examining the effect of target electron correlation and target nuclear screening in the four-body and three-body models, respectively. In the three-body model, the use of a hydrogenic wave function only minimally includes nuclear screening and does not accurately predict the binding energy, while the 5-Zeta wave function more effectively includes nuclear screening and predicts a more accurate binding energy. Therefore, a comparison of the DCS using the two wave functions will show the effect of target nuclear screening. Figure 1 presents DCS for H+, He2+, Li3+, and C6+ projectiles colliding with helium at velocities of 1 Mev/amu and 10 MeV/amu. The validity of the Born approximation is restricted to energy regimes in which the perturbation parameter is less than unity, and velocities chosen here ensure that this condition is met. A comparison of the three-body models shows that some differences appear, with the 5-Zeta wave function producing DCS that are uniformly about one order of magnitude larger than the hydrogenic wave function. The location of the minimum shifts to larger angles in the model with the 5-Zeta wave function, but generally the shape of the DCS does not change significantly with the choice of the target wave function.
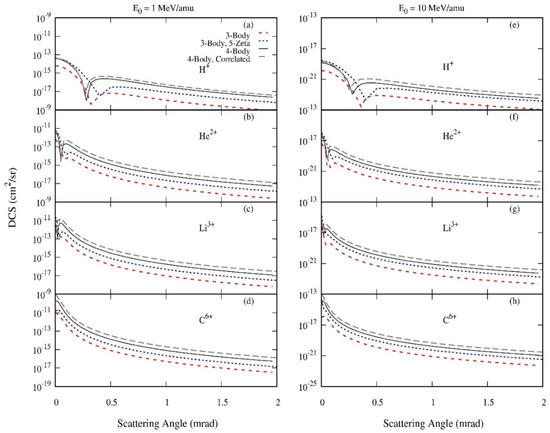
Figure 1.
Differential cross sections for single electron capture to the ground state with the residual He+ ion also in the ground state. The columns contain results for incident projectile velocities of 1 MeV/amu ((a–d)) and 10 MeV/amu ((e–h)). Results are presented for projectiles H+ (a,e), He2+ (b,f), Li3+ (c,g), and C6+ (d,h) the three-body model with either the hydrogenic wave function of Equation (15) or the 5-Zeta wave function of Equation (18) as well as the four-body model with the variational wave function of Equation (13) or the correlated wave function of Equation (14).
In the four-body model, we compare results from either an uncorrelated variational wave function or a correlated target wave function. Again, similar to the three-body model results, a more sophisticated target wave function alters the magnitude of the DCS slightly, but does not affect the shape. The DCS using the correlated wave function is about a factor of two larger at large scattering angles, but nearly identical at small scattering angles. Large angle scattering results from close projectile–nuclear interactions, indicating that electron correlation plays a more important role in close collisions than grazing collisions. In general, the small differences in the DCS between the two target wave functions confirm that electron correlation can safely be neglected in electron capture collisions.
Comparison of the unscreened and uncorrelated three-body and four-body models shows that for all projectiles and velocities, the four-body model is generally one to two orders of magnitude larger than the three-body model, with the DCS most similar at small scattering angles. This is the regime in which nuclear–nuclear interactions are least important. Because the three-body model has a screened nucleus compared to the bare nucleus in the four-body model, one difference between the models is the treatment of target nuclear screening. It is understandable that the models would be most similar at small scattering angles where screening is less important. As scattering angle increases, nuclear–nuclear interactions become more important and the difference in screening treatments between the two models becomes more apparent. Also, as projectile energy increases, the three-body and four-body models become more similar, indicating that projectile screening becomes less important for faster projectiles.
Figure 1 also shows some general trends for both models. As projectile velocity increases, the magnitude of the DCS decreases, as is expected from the total cross sections, which decrease with increasing projectile energy [22]. Also, as projectile charge and mass increase, the DCS increase in magnitude, making capture more likely for heavier and more highly charged ions. The deep minimum in the DCS that is characteristic of FBA models occurs at different scattering angles for the three-body and four-body models. This is expected since the minimum is caused by a cancellation of terms in the perturbation potential, which is different for the two models. The location of the minimum moves to smaller scattering angles as projectile charge and mass increase. However, because projectile charge factors out of the perturbation and results in an overall multiplicative constant, the shift in minimum location as the projectile changes is due to the changing mass of the projectile.
3.2. Frozen Core Effects
Of primary interest here is a direct comparison of the three-body and four-body models in order to study the effects of the frozen core approximation. In this case, we choose the models without correlation or screening. Comparison of the three-body and four-body transition matrices shows two primary differences, both of which originate from the frozen core approximation. First, in the four-body model, the inactive electron in the target atom changes state from the ground state of the He(1s2) atom to the ground state of a hydrogen-like atom with nuclear charge . This electron is completely neglected in the three-body model and is therefore considered not to change state. Second, the perturbation potential is different for the three-body and four-body models. In particular, the four-body perturbation contains a sum of three terms, while the three-body perturbation is only two terms. Past work on the analysis of three-body and four-body models for single ionization has shown that the perturbation potential alters the shape of the fully differential cross sections [35,36]. Additionally, FBA models are known to predict a deep minimum in the electron capture DCS caused by a cancellation of terms in the perturbation [7,40,41,42].
Therefore, we expect that the form of the perturbation will be important in determining the three-body and four-body DCS. To further explore exactly how the inactive electron affects the DCS, we perform a more comprehensive comparison and analysis of the three-body and four-body models. Figure 2 and Figure 3 contain DCS for the same collision systems as Figure 1.
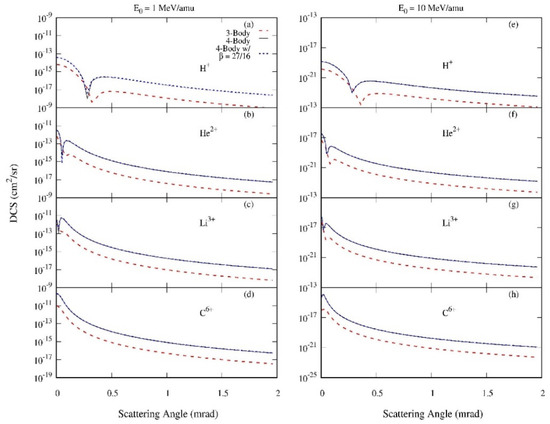
Figure 2.
Same as Figure 1, with DCS calculated using the four-body model with the uncorrelated wave function and the three-body model with the hydrogenic wave function. A calculation using the four-body model (uncorrelated) with is also shown.
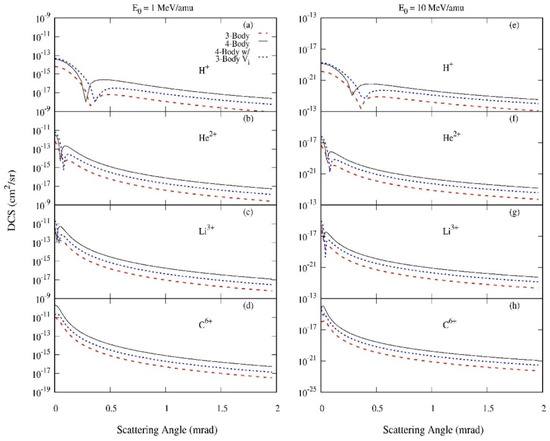
Figure 3.
Same as Figure 3, but results are included for the four-body model using the three-body perturbation of Equation (17), as described in the text.
The treatment of the inactive electron in the four-body model differs in two fundamental ways from that of the three-body model. First, the inactive electron in the four-body model changes state from the ground state of a He(1s2) atom to the ground state of a He+ ion. Second, the Coulomb interaction in the perturbation potential of the four-body model contains three terms, whereas in the three-body model, it only contains two terms. The four-body model perturbation contains the Coulomb interaction of the projectile with each constituent particle of the He+ ion core, but the three-body model perturbation contains only an interaction for the core as a single point particle. Both of these differences between the three-body and four-body models can be individually explored through modifications to the four-body model.
We first examine the effect of the inactive electron changing state from its initial atomic state to its final ionic state in the four-body model. With the one parameter wave function used here for the helium atom, the inactive electron is effectively in a hydrogenic orbital for a nuclear charge of 27/16. After the collision, the electron has transitioned to a hydrogenic orbital for nuclear charge 2. Classically, this corresponds to the electron transitioning to a smaller orbital radius. In the three-body model, the inactive electron is assumed not to change state and therefore it remains in its initial bound state. The inactive electron in the three-body model corresponds to a four-body model in which the final state inactive electron is in the same hydrogenic orbital as it was in the initial state.
To study the effect of the inactive electron’s change of state, we perform a four-body calculation in which the final state He+ ion wave function is hydrogenic with nuclear charge 27/16 (the same as the initial state orbital). All other features of the four-body model are unaltered. Results of the three-body, four-body, and four-body with models are shown in Figure 2. For all projectiles and projectile velocities, the final state He+ ion’s nuclear charge has no discernable effect on the DCS. Closer examination of the two calculations reveals that they differ by at most 10%, with the results for being larger than those for . Thus, we conclude that the change of state of the inactive electron is not the primary cause of the differences between the three-body and four-body DCS. This is consistent with our previous work for the single ionization process, in which the change of state of the inactive electron had a negligible effect on the DCS [35,36].
The other difference between the three-body and four-body models is the perturbation potential used in the calculations. In the three-body model, the frozen core approximation assumes that the Coulomb interaction between the projectile and the He+ core consists of only one term in which the core is fully screened by the inactive electron and therefore modeled as a point particle with charge +1. To test the effect of this approximation, we perform a calculation using the four-body model, but replace the four-body perturbation of Equation (7) with the three-body perturbation of Equation (17). Results are shown in Figure 3, and it is apparent that the choice of perturbation significantly affects the magnitude of the DCS. In particular, the DCS using the four-body model with the three-body perturbation are generally smaller than those of the complete four-body calculation, although not as small as the three-body model. For all projectile energies, the DCS calculated using the four-body model with the three-body perturbation fall between the three-body and four-body models. This indicates that full target nuclear screening in the three-body model results in lower capture cross sections and points to the important role of nuclear–nuclear interactions in the capture process. Clearly the model chosen for the projectile–target interaction significantly alters the DCS much more than the inactive electron changing state. We can then conclude that the concept of the frozen core approximation, in which the inactive electron does not change state, is valid for single electron capture, but that care must be used in modeling the projectile–target interaction. These results are consistent with our past studies of the frozen core approximation and nuclear screening [35,36,37].
3.3. Comparison with Experiment
While the FBA models used here are not expected to perform as well as more sophisticated models, comparison with experiment can provide information regarding the validity of the frozen core approximation. Recent experiments using the COLTRIMS technique have produced a number of highly detailed data sets [1,2,3,4,5,6,7]. Unfortunately, for the single capture process, most experiments were performed with proton projectiles. Only a very limited number of data sets for differential cross sections using other heavy ion projectiles with helium targets are available in the energy regime where the FBA is applicable. Additionally, while the single capture process is well-studied, most available experimental data is for total cross sections, slow projectiles, or hydrogen targets. In Figure 4, Figure 5 and Figure 6, results are shown for the three-body and four-body models using the 5-Zeta and correlated helium wave functions compared with the experiments of [6,7,43].
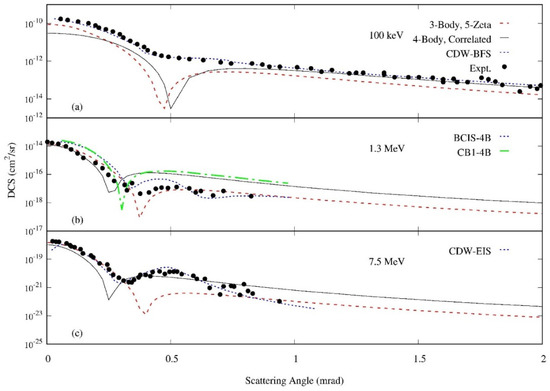
Figure 4.
Differential cross sections for p + He single electron capture to the ground state with the residual He+ ion also in the ground state. Results from the three-body and four-body models are compared to experimental results from (a) [7], (b,c) [6] and the theoretical models from (a) [7], (b) [31], and (c) [47]. For (a), the captured electron is known to be in the ground state in, however for (b,c), the final captured state of the electron is not specified. Incident projectile energies are (a) 100 keV, (b) 1.3 MeV, and (c) 7.5 MeV.
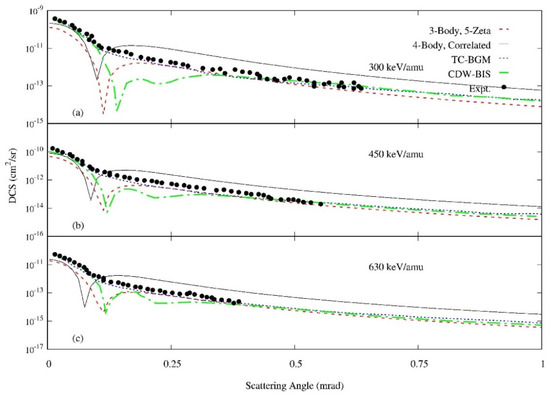
Figure 5.
Differential cross sections for 3He2+ + He single electron capture to the ground state with the residual He+ ion also in the ground state. Results from the three-body and four-body models are compared to experiment [7] and other theoretical models [7,8] Incident projectile energies are (a) 300 keV/amu, (b) 450 keV/amu, and (c) 630 keV/amu. In all cases, the captured electron is known to be in the ground state.
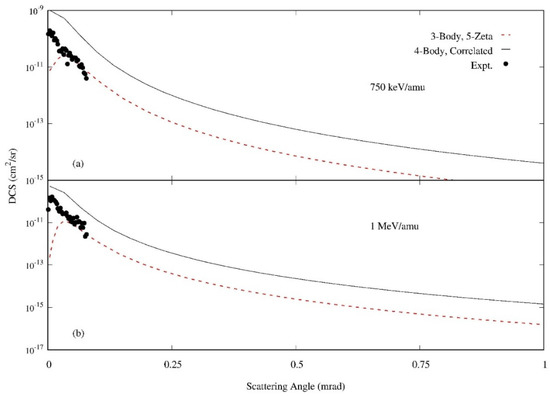
Figure 6.
Differential cross sections for B5+ + He single electron capture to the ground state with the residual He+ ion also in the ground state. Experimental results are from [43]. Incident projectile energies are (a) 750 keV/amu and (b) 1 MeV/amu. In all cases, the captured electron is known to be in the ground state.
There are some important features to note in both the experimental and theoretical DCS results of Figure 4, Figure 5 and Figure 6. First, the experimental DCS exhibit an elbow structure at small scattering angles where the slope of the curve changes. This elbow occurs at the boundary between small and large angle scattering and separates different physical mechanisms. At small angles, projectile–nuclear effects are less important than at large scattering angles. Physically, single capture at small angles is predominantly caused by momentum transfer to the electron, while at large scattering angles, capture occurs through momentum transfer between the nuclei [44,45,46].
The order of magnitude difference at large scattering angles between the three-body and four-body models is evident from Figure 4, Figure 5 and Figure 6, with the four-body model DCS generally larger than the three-body model DCS. This similarity of the models at small scattering angles has also been observed in the He+ + He single capture collision system [37] and can be attributed to nuclear screening being less important in grazing collisions. In general, both models do a surprisingly good job of predicting experiment given their simplicity. However, no clear conclusion can be reached for which model best predicts experiment. In some cases, the four-body model is in better agreement, while in others, three-body model more closely matches the data. For H+ projectiles (Figure 4), both the three-body and four-body models do a reasonable job predicting experiment at small and large scattering angles for the larger projectile velocities. However, both models underestimate the small angle DCS at 100 keV, which may be pushing the limits of the applicability of the FBA model. The deep minimum occurring in the three-body and four-body DCS typically appears near the elbow in the experimental data and causes a clear mismatch between theory and experiment in this region. In Figure 4a, the captured electron is known to be in the ground state, while in Figure 4b,c, the bound state of the captured electron is unknown. From Figure 7 and the Oppenheimer rule, we expect that contributions from excited states will increase the three-body and four-body DCS by about 20%. For each energy, we include predictions of other available theoretical models, which are generally in better agreement with experiment. This is expected since each of the additional models includes better treatments of screening and correlation.
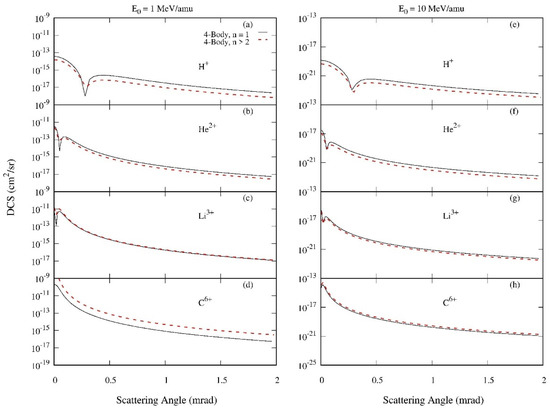
Figure 7.
Differential cross sections using the four-body model (uncorrelated) for capture to the ground state and capture to all excited states up to and including .
In the case of 3He2+ projectiles (Figure 5), similar features are observed. However, in this case the four-body model better predicts experiment at small scattering angle, while at large scattering angles, the three-body model produces better agreement. This indicates that large angle scattering is overestimated by the use of a bare nucleus and that the nuclear–nuclear interaction in the four-body model is too strong. The non-perturbative two center-basis generator method (TC-BGM) model very accurately predicts experiment, while the perturbative Coulomb distorted wave–Born initial state (CDW-BIS) model predicts a similar deep minimum due to interference from the perturbative terms.
In Figure 6, results are shown for the heaviest and most highly charged projectile and agreement between the limited experimental data and the three-body and four-body models is quite poor. This may be due to the relatively large perturbation parameters of (a) and 0.8 (b), making the validity of the FBA questionable for this case. For both velocities, a downturn in the DCS is visible in the three-body model, but is not present for the four-body model. This is likely the presence of the deep minimum appearing at a larger scattering angle in the three-body model than the four-body model.
Lastly, the question of relative importance of capture to the ground state compared to capture to excited states arises. As projectile charge increases, capture into excited states becomes more important. The results presented above assume that the scattered projectile electron is in the ground state and with the exception of Figure 4b,c, this is known for all of the experimental data presented. In Figure 7, we show DCS calculations with the four-body uncorrelated model for capture to the ground state compared to capture to excited states with . In all cases, the inclusion of the DCS had no discernable effect on the sum and therefore inclusion of higher excited states was unnecessary. Figure 7 shows that the likelihood of capture to excited states increases with projectile charge, as expected. With the exception of proton projectiles, capture to excited states is roughly the same order of magnitude as capture to the ground state, and needs to be included if the final bound state is not known.
In summary, we used the first Born approximation in three-body and four-body models of single electron capture to explore the effects of the frozen core approximation. Application of the models to different projectiles and projectile velocities revealed an overall magnitude difference between the models of about one to two orders, with the four-body model predicting larger DCS. The difference in magnitude between the models was traced primarily to the projectile–target Coulomb interaction used in the perturbation. The inactive electron’s change of state from an atomic ground state to an ionic ground state had almost no effect on the DCS. All of these models are consistent with prior studies of the frozen core approximation and point to the need to carefully consider how nuclear screening is included in models. We also confirmed that inclusion of electron correlation in the four-body model had a minimum effect on the DCS. A more sophisticated treatment of target nuclear screening in the three-body model increased the magnitude of the DCS by about one order of magnitude, but did not alter the shape. Both the three-body and four-body models predicted experiments moderately well, with the exception of the B5+ projectiles. While the experimental results that were used here for comparison were able to distinguish capture to the ground state from capture to excited states, this is not always the case. Our calculations showed that capture to excited states is more important for higher charge projectiles, as expected.
Funding
This research was funded by the National Science Foundation, grant numbers PHY-1505217 and PHY-1838550.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ullrich, J.; Moshammer, R.; Dorn, A.; Dörner, R.; Schmidt, L.P.H.; Schmidt-Böcking, H. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 2003, 66, 1463–1545. [Google Scholar] [CrossRef]
- Kim, H.-K.; Schöffler, M.S.; Houamer, S.; Chuluunbaatar, O.; Titze, J.N.; Schmidt, L.P.H.; Jahnke, T.; Schmidt-Böcking, H.; Galstyan, A.; Popov, Y.V.; et al. Electron transfer in fast proton-helium collisions. Phys. Rev. A 2012, 85, 022707. [Google Scholar] [CrossRef]
- Mergel, V.; Dörner, R.; Khayyat, K.; Achler, M.; Weber, T.; Jagutzki, O.; Lüdde, H.J.; Cocke, C.L.; Schmidt-Böcking, H. Strong Correlations in the He Ground State Momentum Wave Function Observed in the Fully Differential Momentum Distributions for the p + He Transfer Ionization Process. Phys. Rev. Lett. 2001, 86, 2257–2260. [Google Scholar] [CrossRef]
- Zapukhlyak, M.; Kirchner, T.; Hasan, A.; Tooke, B.; Schulz, M. Projectile angular-differential cross sections for transfer and transfer excitation in proton collisions with helium. Phys. Rev. A 2008, 77, 012720. [Google Scholar] [CrossRef]
- Fischer, D.; Støchkel, K.; Cederquist, H.; Zettergren, H.; Reinhed, P.; Schuch, R.; Källberg, A.; Simonsson, A.; Schmidt, H.T. Experimental separation of the Thomas charge-transfer process in high-velocity p-He collisions. Phys. Rev. A 2006, 73, 052713. [Google Scholar] [CrossRef]
- Fischer, D.; Gudmundsson, M.; Berényi, Z.; Haag, N.; Johansson, H.A.B.; Misra, D.; Reinhed, P.; Källberg, A.; Simonsson, A.; Støchkel, K.; et al. Importance of Thomas single-electron transfer in fast p-He collisions. Phys. Rev. A 2010, 81, 012714. [Google Scholar] [CrossRef]
- Schöffler, M.S.; Titze, J.; Schmidt, L.P.H.; Jahnke, T.; Neumann, N.; Jagutzki, O.; Schmidt-Böcking, H.; Dörner, R.; Mančev, I. State-selective differential cross sections for single and double electron capture in He+,2+-He and p-He collisions. Phys. Rev. A 2009, 79, 064701. [Google Scholar] [CrossRef]
- Zapukhlyak, M.; Kirchner, T. Projectile angular-differential cross sections for electron transfer processes in ion-helium collisions: Evidence for the applicability of the independent electron model. Phys. Rev. A 2009, 80, 062705. [Google Scholar] [CrossRef]
- Simony, P.R.; McGuire, J.H.; Eichler, J. Exact second Born electron capture for p + He. Phys. Rev. A 1982, 26, 1337–1343. [Google Scholar] [CrossRef]
- Guo, D.L.; Ma, X.; Zhang, R.T.; Zhang, S.F.; Zhu, X.L.; Feng, W.T.; Gao, Y.; Hai, B.; Zhang, M.; Wang, H.B.; et al. State-selective electron capture in 30- and 100-keV He+ + He collisions. Phys. Rev. A 2017, 95, 012707. [Google Scholar] [CrossRef]
- Gao, J.W.; Wu, Y.; Wang, J.G.; Sisourat, N.; Dubois, A. State-selective electron transfer in He+ + He collisions at intermediate energies. Phys. Rev. A 2018, 97, 052709. [Google Scholar] [CrossRef]
- Adivi, E.G.; Bolorizadeh, M.A. Faddeev treatment of single-electron capture by protons in collision with many-electron atoms. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 3321–3338. [Google Scholar] [CrossRef]
- Slim, H.A.; Heck, E.L.; Bransden, B.H.; Flower, D.R. Theoretical differential cross sections for proton-helium scattering at intermediate energies. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2353–2358. [Google Scholar] [CrossRef]
- Leigh, T.H. Fowler Ralph Howard on the capture of electrons by moving electrified particles. Proc. R. Soc. Lond. Ser. A 1927, 114, 561–576. [Google Scholar]
- Oppenheimer, J.R. On the Quantum Theory of the Capture of Electrons. Phys. Rev. 1928, 31, 349–356. [Google Scholar] [CrossRef]
- Brinkman, H.C.; Kramers, H.A. Zur Theorie der Einfangung von Elektronen durch α-Teilchen. Proc. Acad. Sci. Amst. 1930, 33, 973. [Google Scholar]
- Belkić, D.; Mančev, I.; Hanssen, J. Four-body methods for high-energy ion-atom collisions. Rev. Mod. Phys. 2008, 80, 249–314. [Google Scholar] [CrossRef]
- Martínez, A.E.; Deco, G.R.; Rivarola, R.D.; Fainstein, P.D. K-Shell vacancy production in asymmetric collisions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1988, 34, 32–36. [Google Scholar] [CrossRef]
- Ghanbari-Adivi, E. Coulomb–Born distorted wave approximation applied to the proton–helium single-electron capture process. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 165204. [Google Scholar] [CrossRef]
- Dewangan, D.P.; Eichler, J. Electron capture and the long range of the Coulomb interaction. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1987, 23, 160–163. [Google Scholar] [CrossRef]
- Ghanbari-Adivi, E.; Ghavaminia, H. Four-body treatment of the single-electron capture in energetic proton–helium collisions. Phys. Scr. 2014, 89, 105402. [Google Scholar] [CrossRef]
- Halder, S.; Mondal, A.; Samaddar, S.; Mandal, C.R.; Purkait, M. Differential and total cross sections for charge transfer and transfer-excitation in ion-helium collisions. Phys. Rev. A 2017, 96, 032717. [Google Scholar] [CrossRef]
- Belkić, D.; Mančev, I. Formation of H-by double charge exchange in fast proton-helium collisions. Phys. Scr. 1992, 45, 35–42. [Google Scholar] [CrossRef]
- Belkić, D.; Mančev, I. Four-body CDW approximation: dependence of prior and post total cross sections for double charge exchange upon bound-state wave-functions. Phys. Scr. 1993, 47, 18–23. [Google Scholar] [CrossRef]
- Belkić, D. Symmetric double charge exchange in fast collisions of bare nuclei with heliumlike atomic systems. Phys. Rev. A 1993, 47, 189–200. [Google Scholar] [CrossRef]
- Belkic, D. Two-electron capture from helium-like atomic systems by completely stripped projectiles. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 497–508. [Google Scholar] [CrossRef]
- Harris, A.L.; Madison, D.H. Effect of the center-of-mass approximation on the scaling of electron-capture fully differential cross sections. Phys. Rev. A 2014, 90, 022701. [Google Scholar] [CrossRef]
- Mancev, I.; Mergel, V.; Schmidt, L. Electron capture from helium atoms by fast protons. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 2733–2746. [Google Scholar] [CrossRef]
- Samanta, R.; Purkait, M.; Mandal, C.R. Single-electron-capture processes in collisions of He2+, Liq+ (q = 1, 2, 3), C6+, and O8+ ions with helium. Phys. Rev. A 2011, 83, 032706. [Google Scholar] [CrossRef]
- Samaddar, S.; Halder, S.; Mondal, A.; Mandal, C.R.; Purkait, M.; Das, T.K. Single and double electron capture in p-He and α-He collisions. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 065202. [Google Scholar] [CrossRef]
- Mančev, I.; Milojević, N.; Belkić, D. Boundary-corrected four-body continuum-intermediate-state method: Single-electron capture from heliumlike atomic systems by fast nuclei. Phys. Rev. A 2015, 91, 062705. [Google Scholar] [CrossRef]
- Mančev, I. Single-electron capture from helium-like atomic systems by bare projectiles. EPL 2004, 69, 200. [Google Scholar] [CrossRef]
- Mancev, I. Single charge exchange in fast collisions of alpha particles with helium. J. Phys. B At. Mol. Opt. Phys. 2002, 36, 93–104. [Google Scholar] [CrossRef]
- Mančev, I. Electron correlations in single-electron capture from heliumlike atomic systems. Phys. Rev. A 1999, 60, 351–358. [Google Scholar] [CrossRef]
- Harris, A.L.; Morrison, K. Comprehensive study of 3-body and 4-body models of single ionization of helium. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 145202. [Google Scholar] [CrossRef]
- Harris, A.L. Effect of frozen core approximation in heavy-ion impact ionization of helium. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 115203. [Google Scholar] [CrossRef]
- Harris, A.L.; Plumadore, A. Quantum mechanical potentials and inactive electron effects in charge exchange collisions. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 055203. [Google Scholar] [CrossRef]
- McDowell, M.R.C.; Coleman, J.P. Introduction to the Theory of Ion-Atom Collisions; Elsevier Science Publishing Co Inc.: New York, NY, USA, 1970; ISBN 978-0-7204-0166-0. [Google Scholar]
- Clementi, E.; Roetti, C. Roothaan-Hartree-Fock atomic wavefunctions: Basis functions and their coefficients for ground and certain excited states of neutral and ionized atoms, Z ≤ 54. At. Data Nucl. Data Tables 1974, 14, 177–478. [Google Scholar] [CrossRef]
- Ghanbari-Adivi, E.; Ghavaminia, H. Projectile angular-differential cross sections for single electron transfer in fast He+–He collisions. Chin. Phys. B 2015, 24, 033401. [Google Scholar] [CrossRef]
- Belkic, D.; Salin, A. Differential cross sections for charge exchange at high energies. J. Phys. B At. Mol. Phys. 1978, 11, 3905–3911. [Google Scholar] [CrossRef]
- Omidvar, K. Asymptotic form of the charge-exchange cross section in three-body rearrangement collisions. Phys. Rev. A 1975, 12, 911–926. [Google Scholar] [CrossRef]
- Kambara, T.; Igarashi, A.; Watanabe, N.; Nakai, Y.; Kojima, T.M.; Awaya, Y. Recoil-ion momentum distribution of single-electron capture to the ground and excited states in 0.5–He collisions. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 1251–1260. [Google Scholar] [CrossRef]
- Mergel, V.; Dörner, R.; Ullrich, J.; Jagutzki, O.; Lencinas, S.; Nüttgens, S.; Spielberger, L.; Unverzagt, M.; Cocke, C.L.; Olson, R.E.; et al. State Selective Scattering Angle Dependent Capture Cross Sections Measured by Cold Target Recoil Ion Momentum Spectroscopy. Phys. Rev. Lett. 1995, 74, 2200–2203. [Google Scholar] [CrossRef]
- Kamber, E.Y.; Cocke, C.L.; Cheng, S.; Varghese, S.L. Angular Distribution of Fast Protons from Singly and Doubly Ionizing Collisions with He. Phys. Rev. Lett. 1988, 60, 2026–2029. [Google Scholar] [CrossRef]
- Dörner, R.; Ullrich, J.; Schmidt-Böcking, H.; Olson, R.E. Three-body interactions in proton-helium angular scattering. Phys. Rev. Lett. 1989, 63, 147–150. [Google Scholar] [CrossRef]
- Gulyás, L.; Igarashi, A.; Kirchner, T. Projectile scattering in one- and two-electron transitions. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 085205. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).