Simulation of Spectra Code (SOS) for ITER Active Beam Spectroscopy
Abstract
1. Introduction to the SOS Project
2. SOS Physics Background
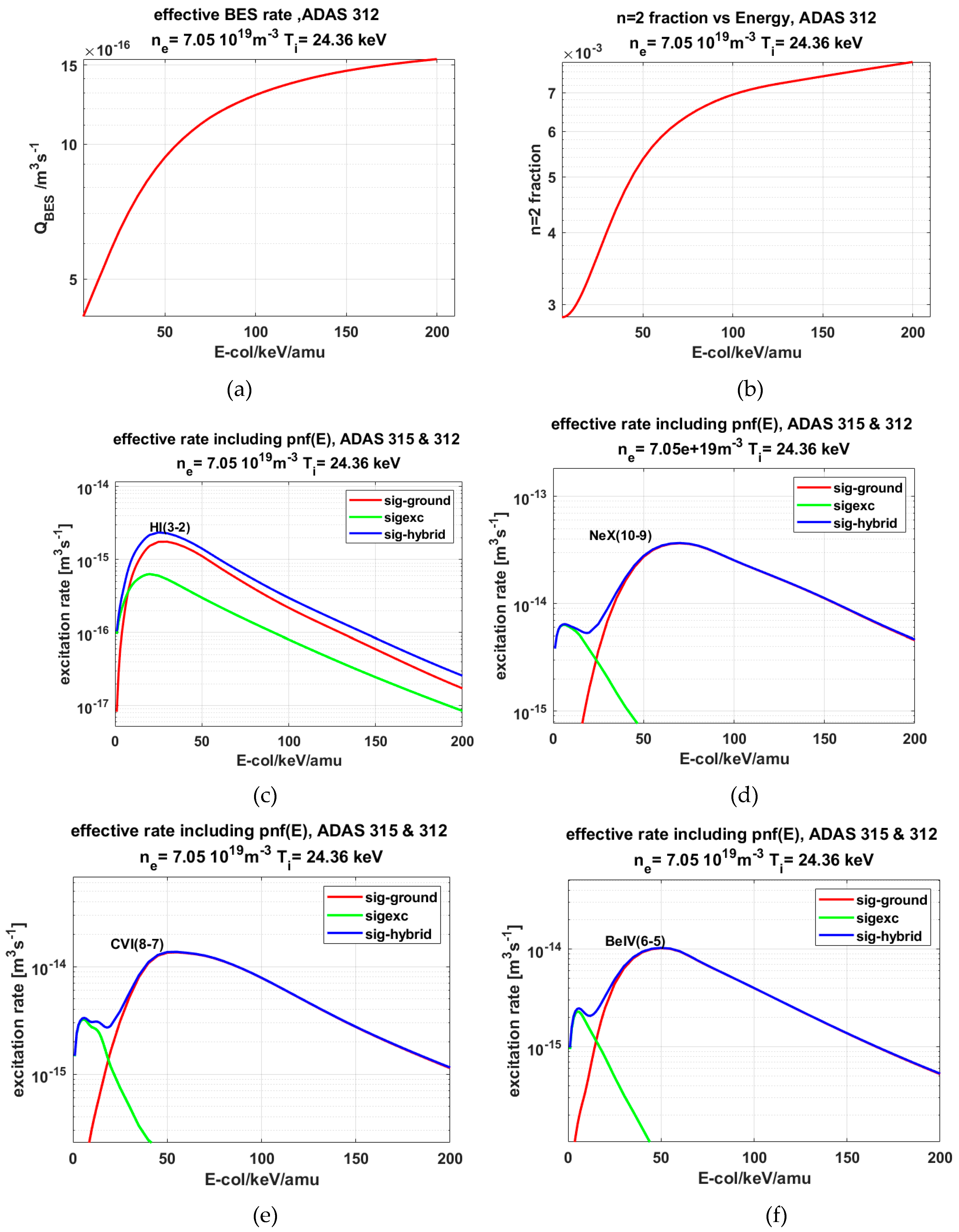
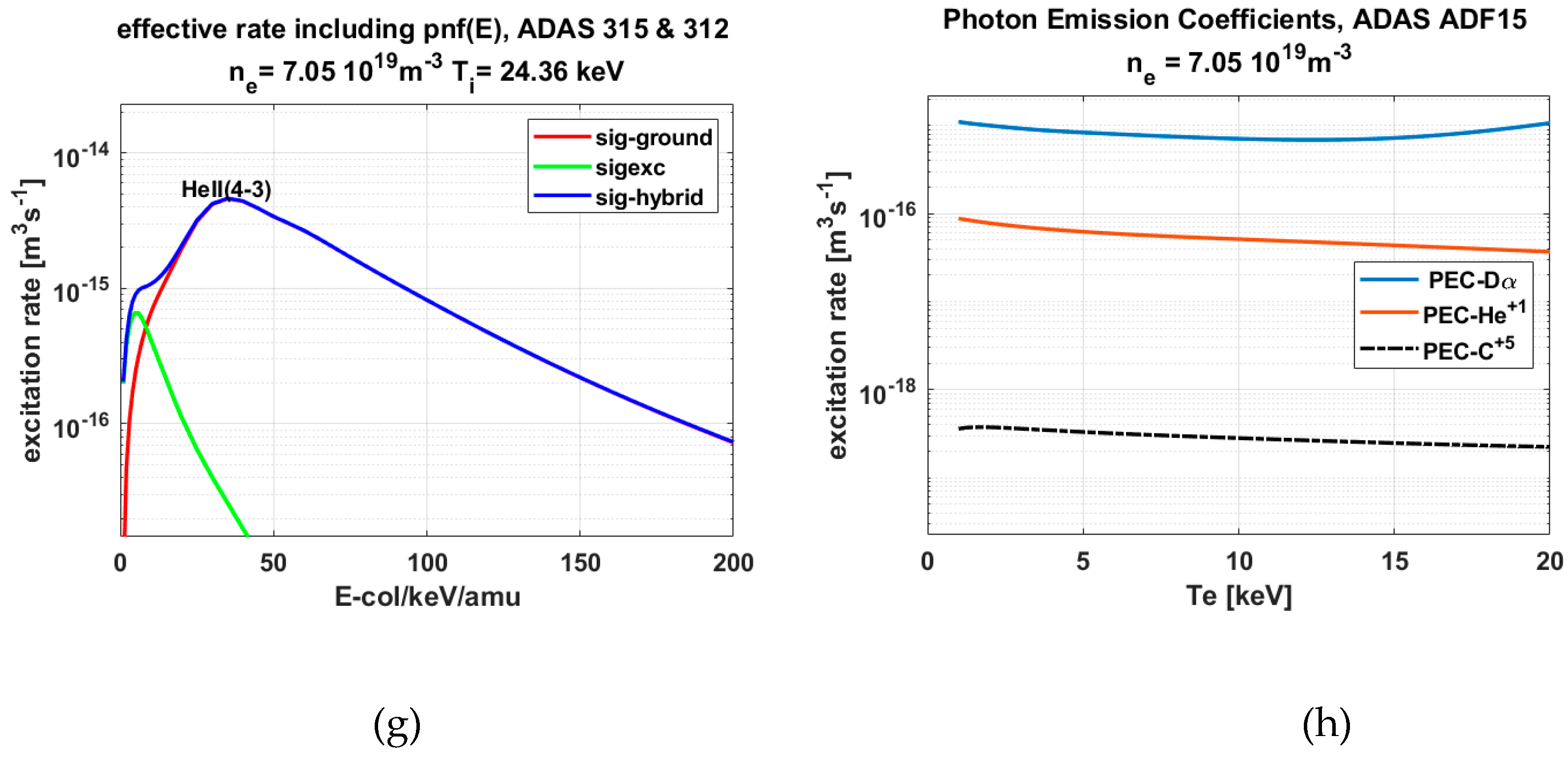
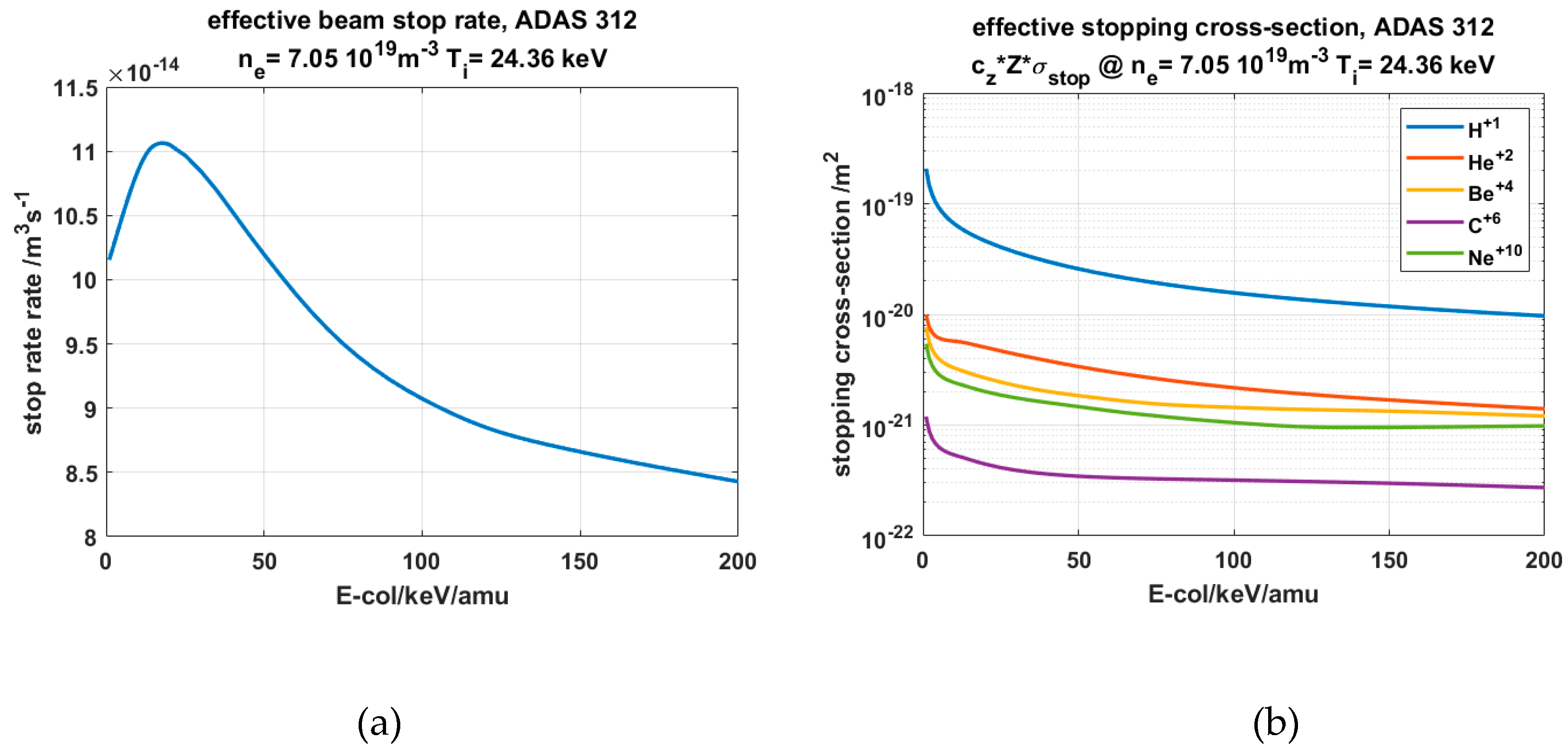
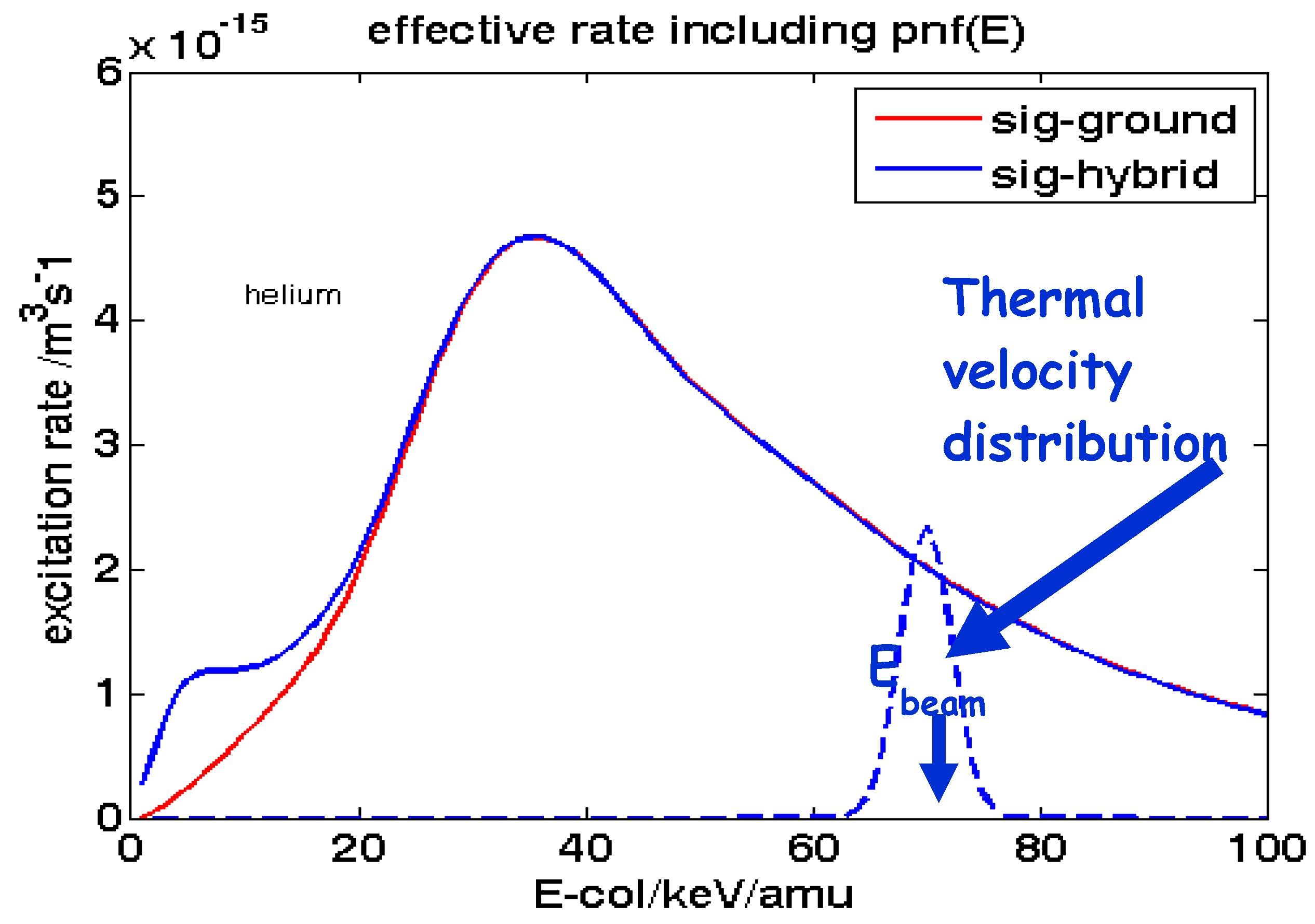
2.1. Atomic Data used in SOS
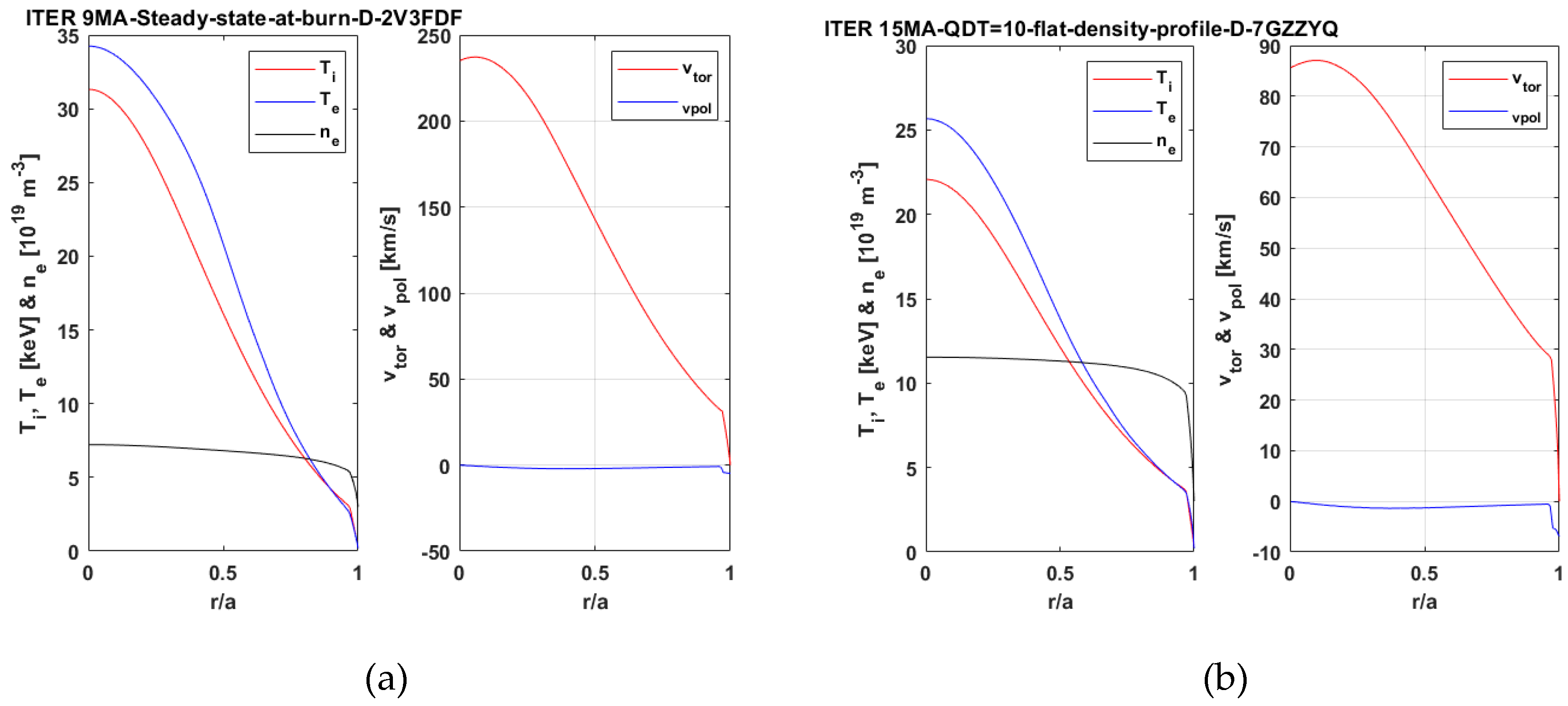
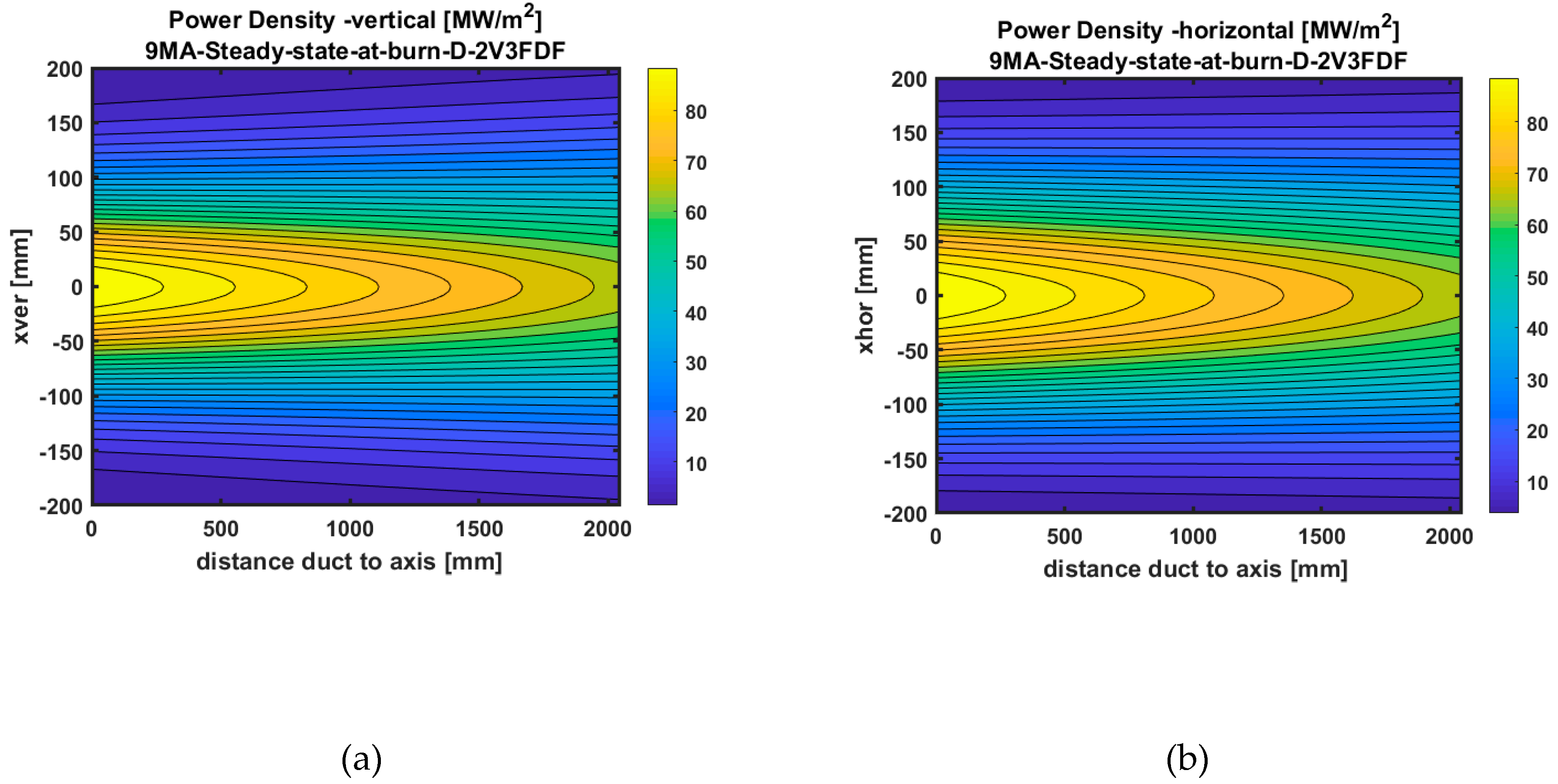
2.2. Neutral Beam Model
2.3. SOS Continuum Radiation Modeling
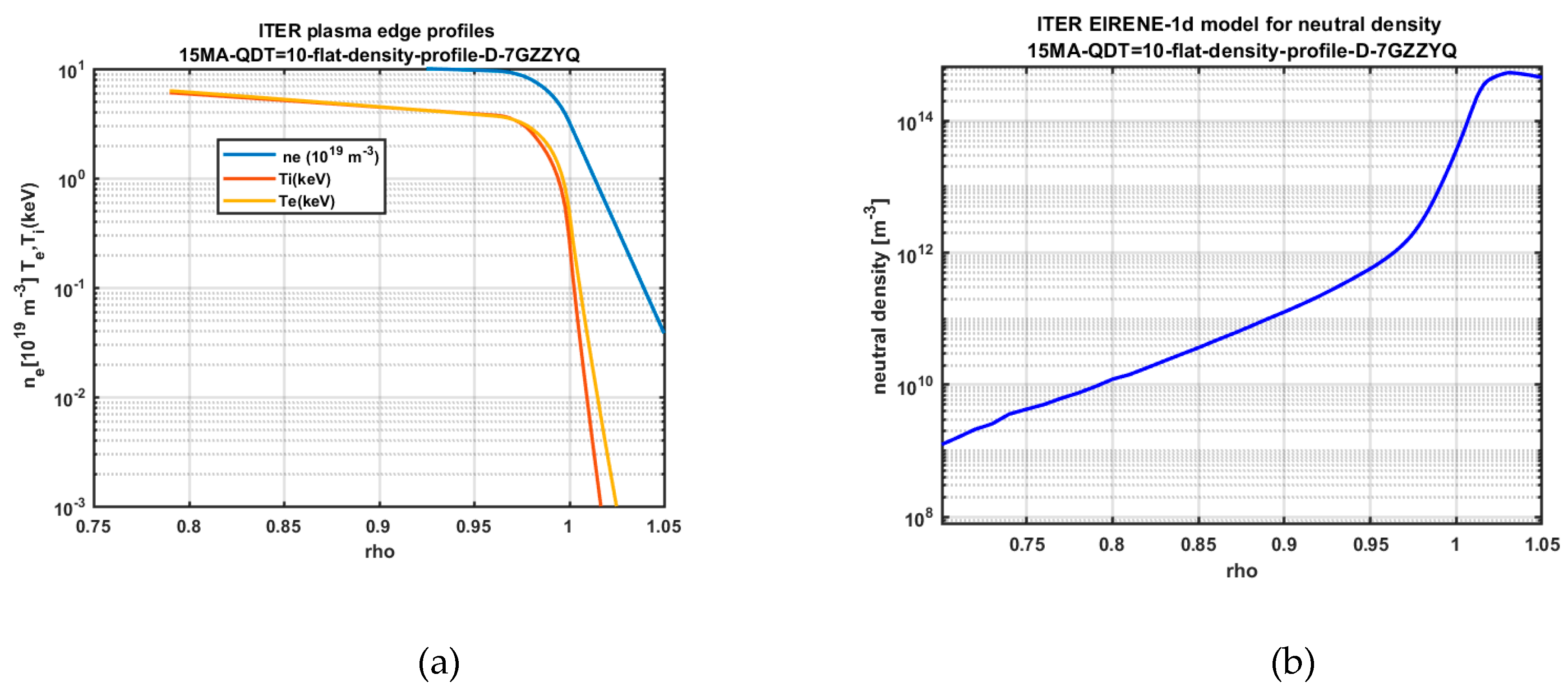
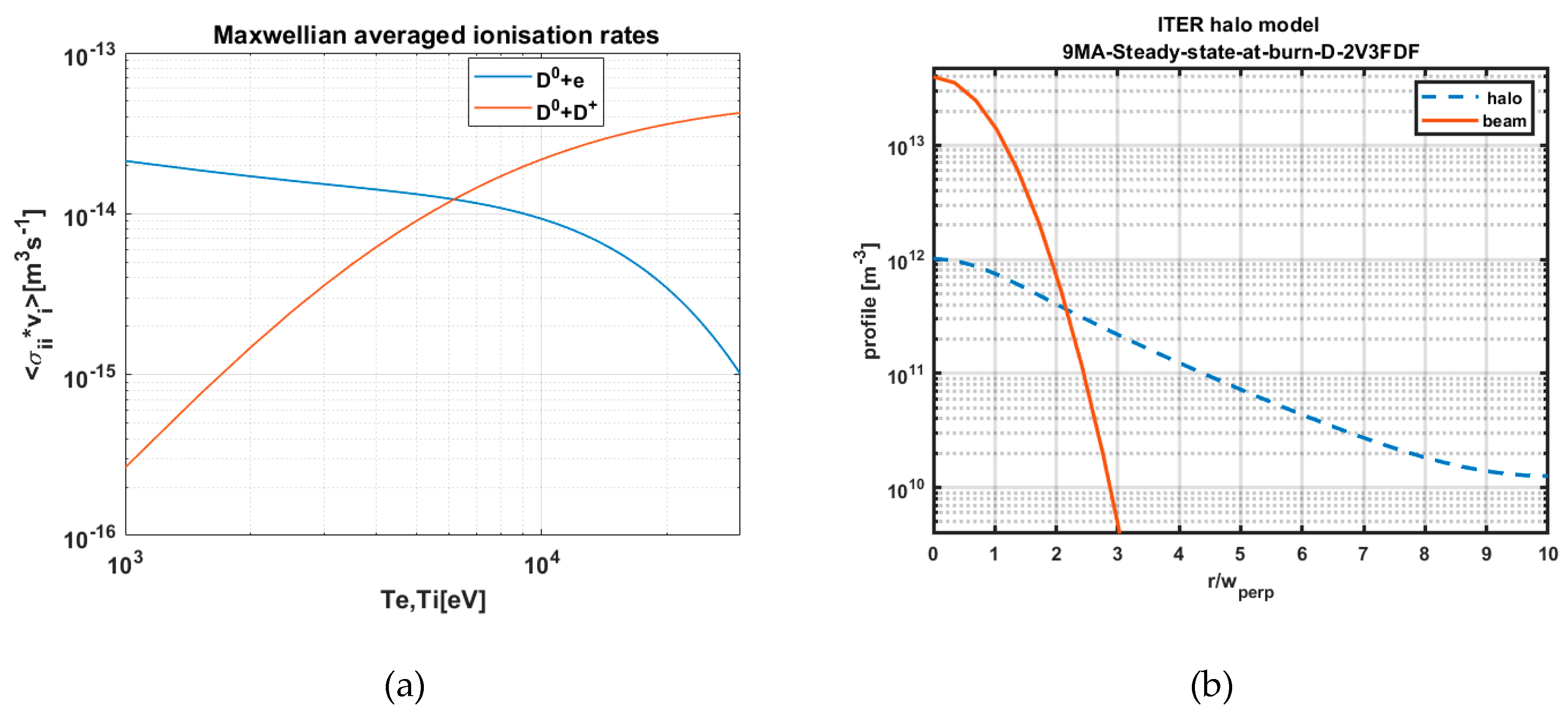
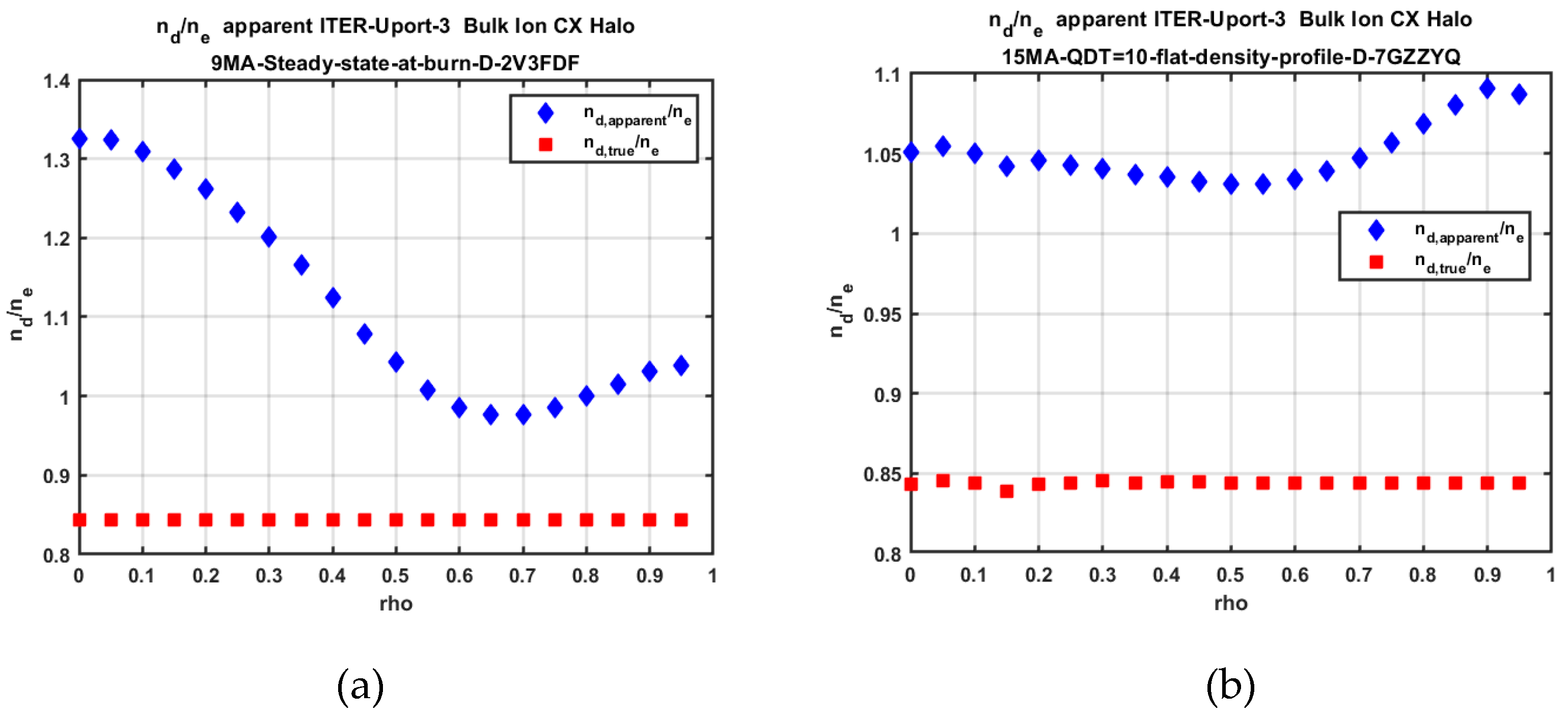
2.4. SOS Modeling of Neutral Density Using EIRENE Code
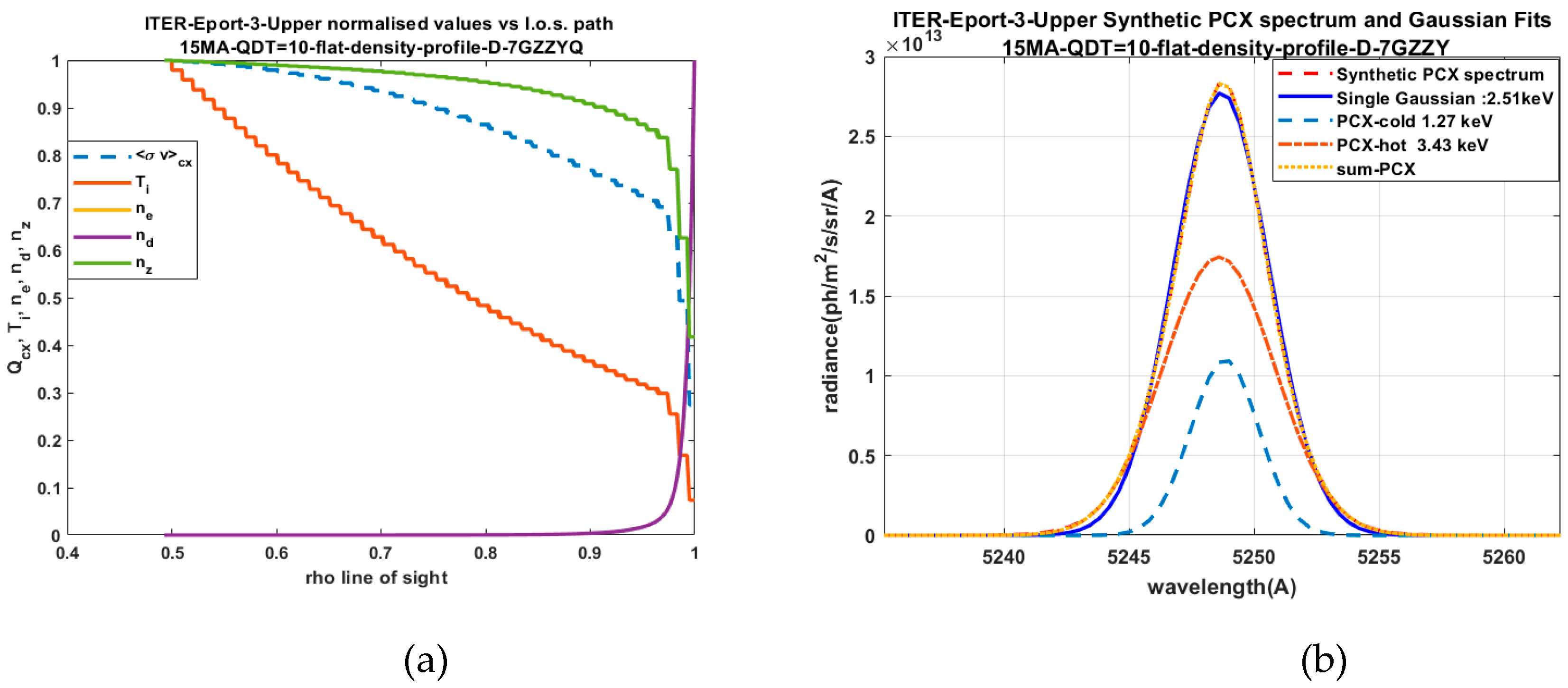
2.5. Passive Charge Exchange Synthetic Line of Sight Integrated Spectra
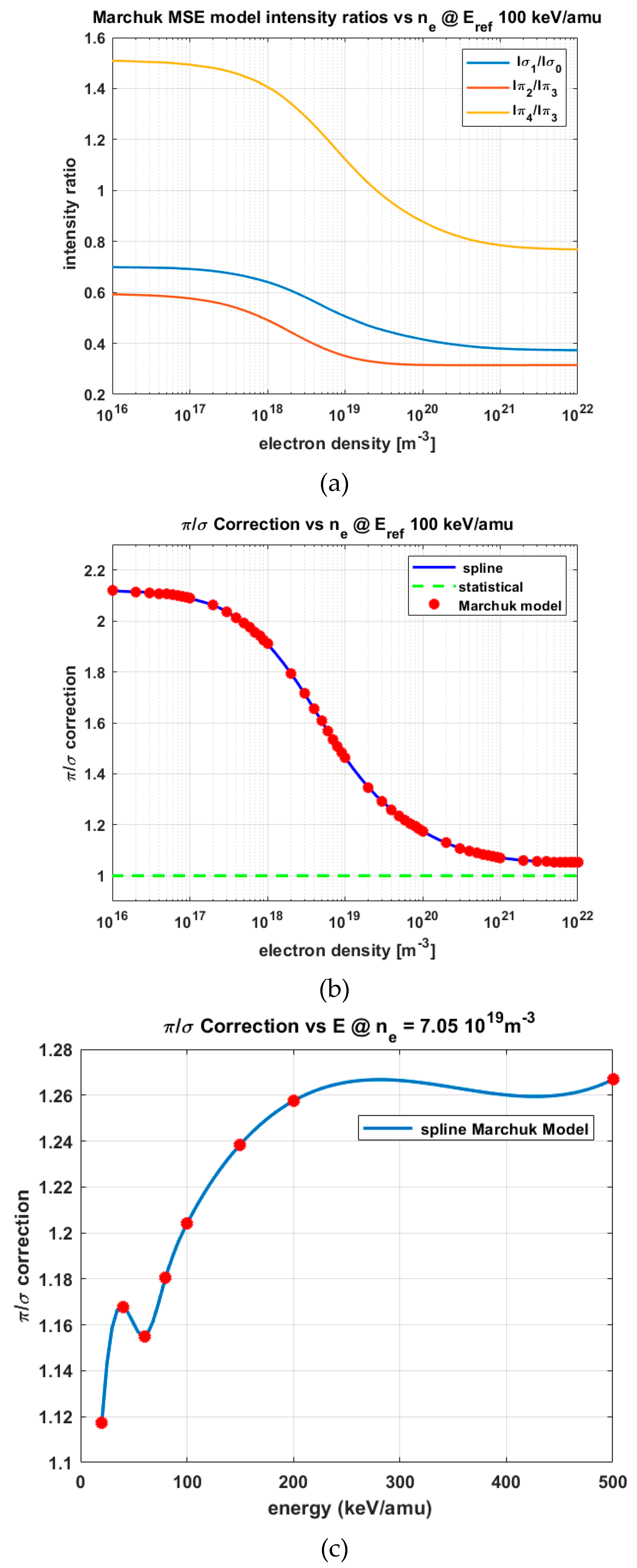
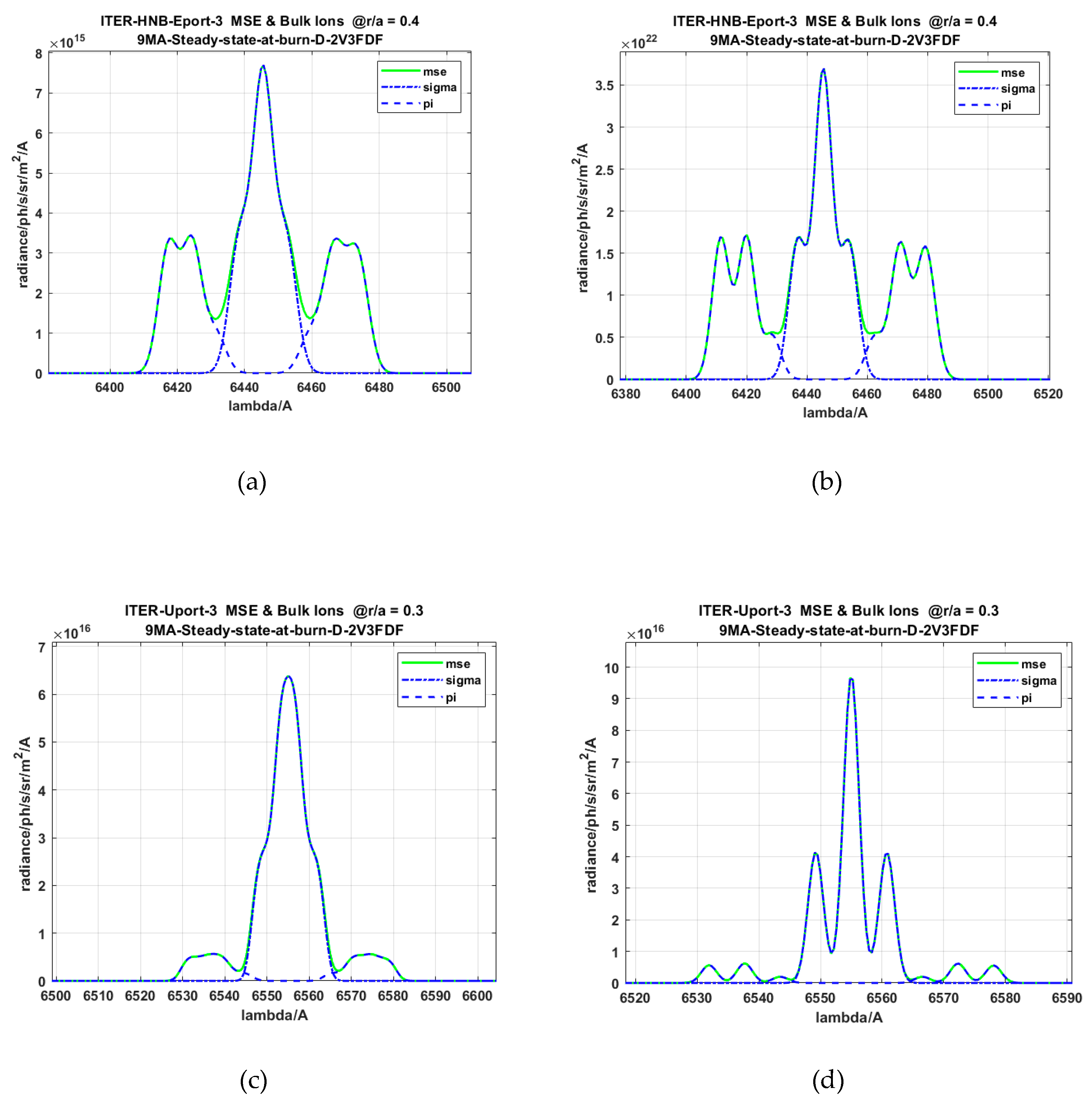
2.6. SOS Modeling of the BES (Motional Stark Effect) Spectrum
Asymmetry of Observed MSE Spectra Caused by Divergence of Neutral Beam Assembly
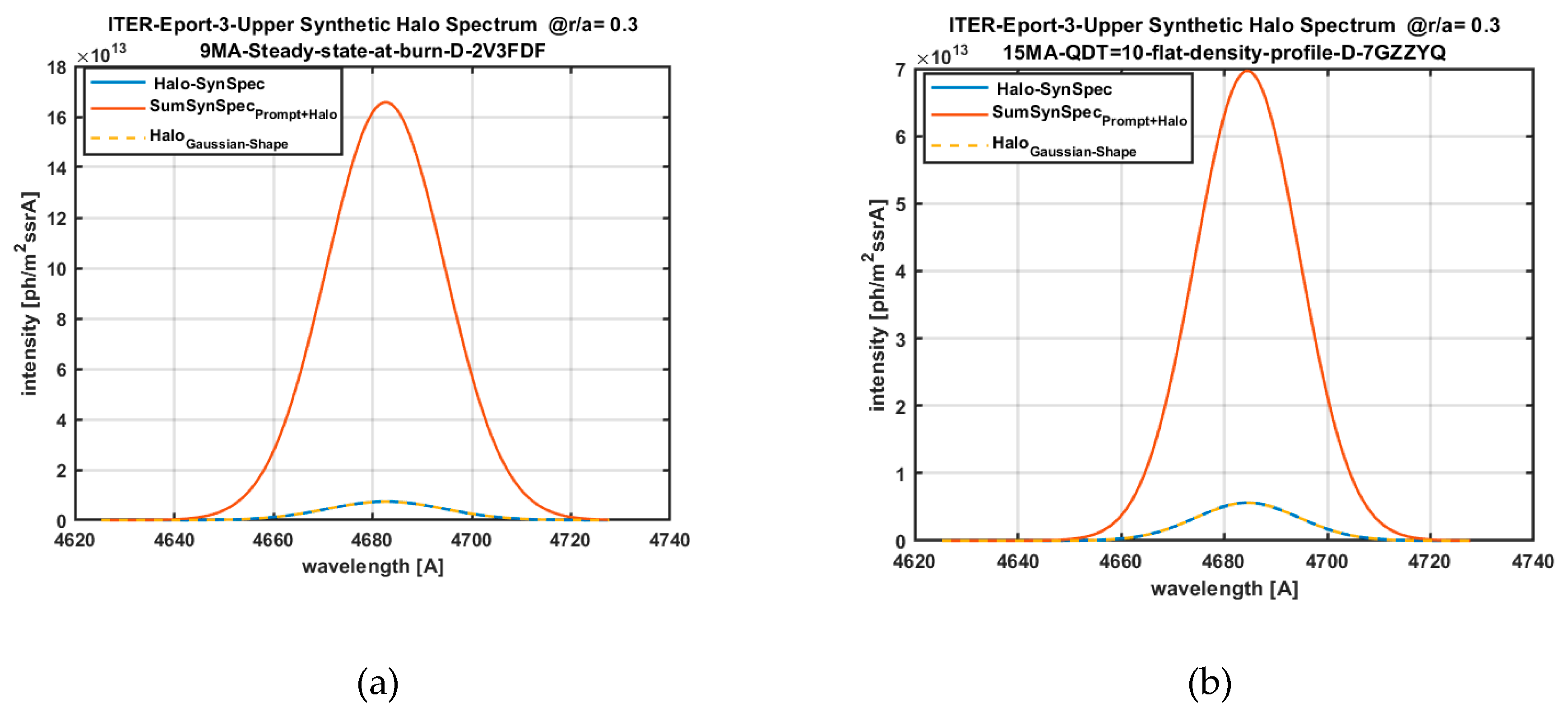
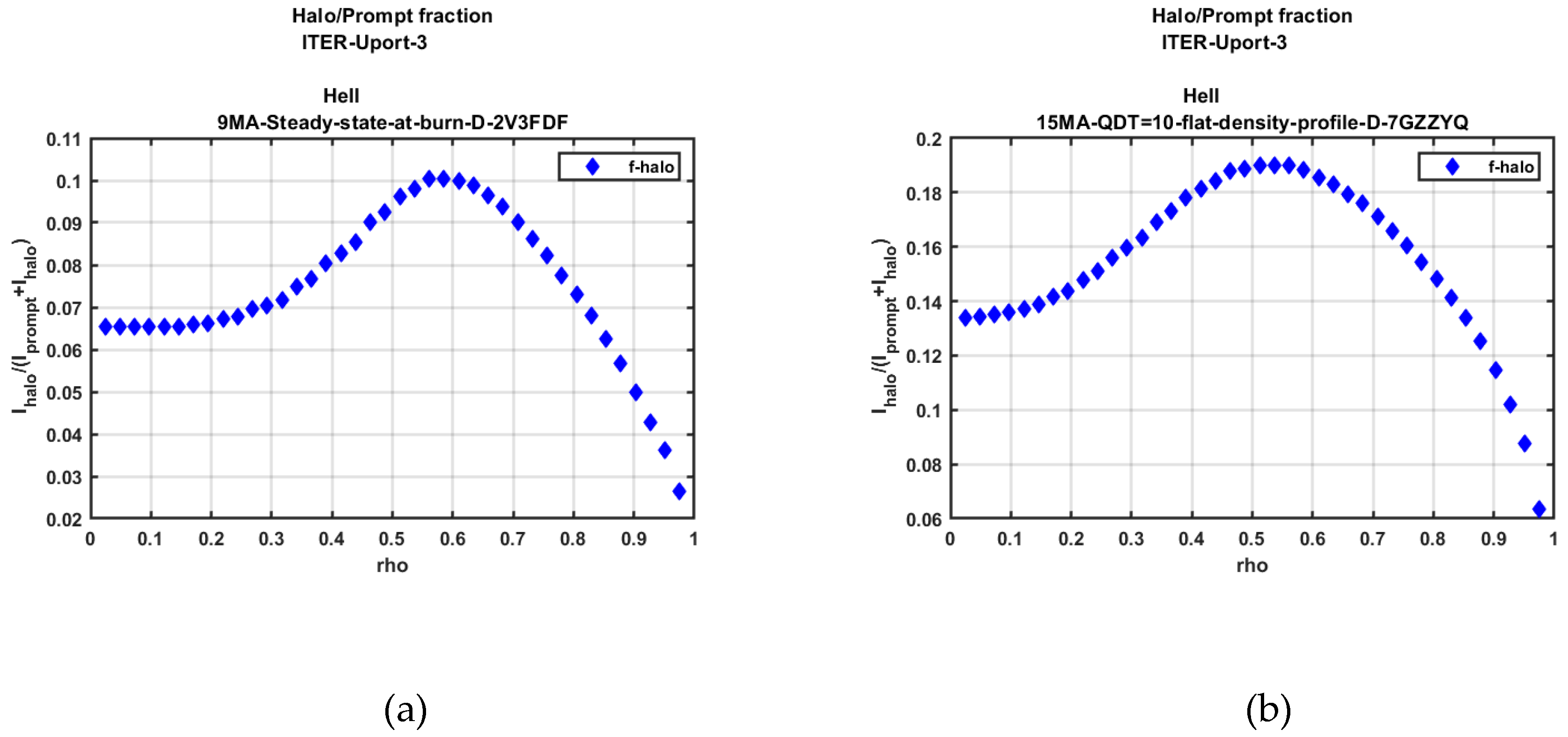
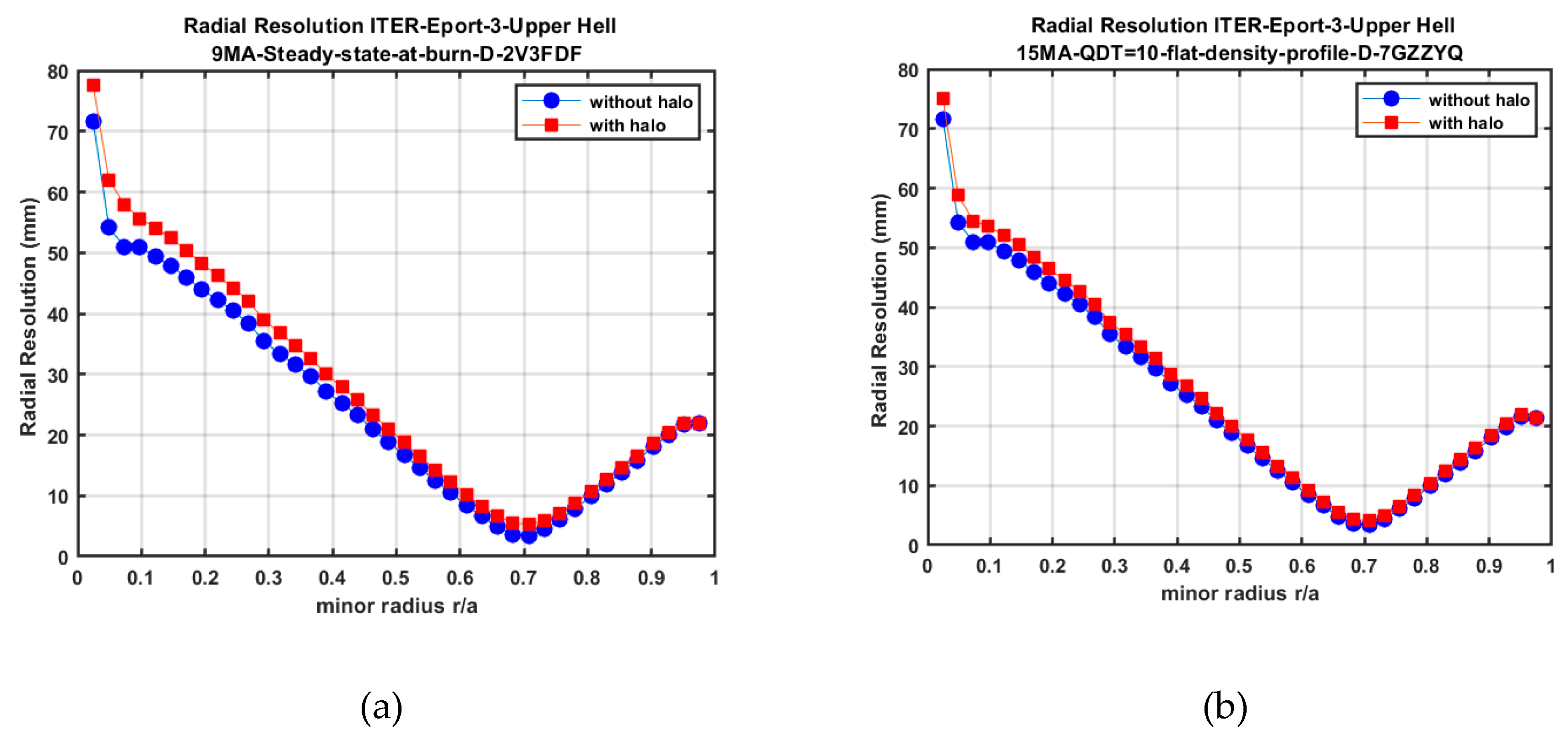
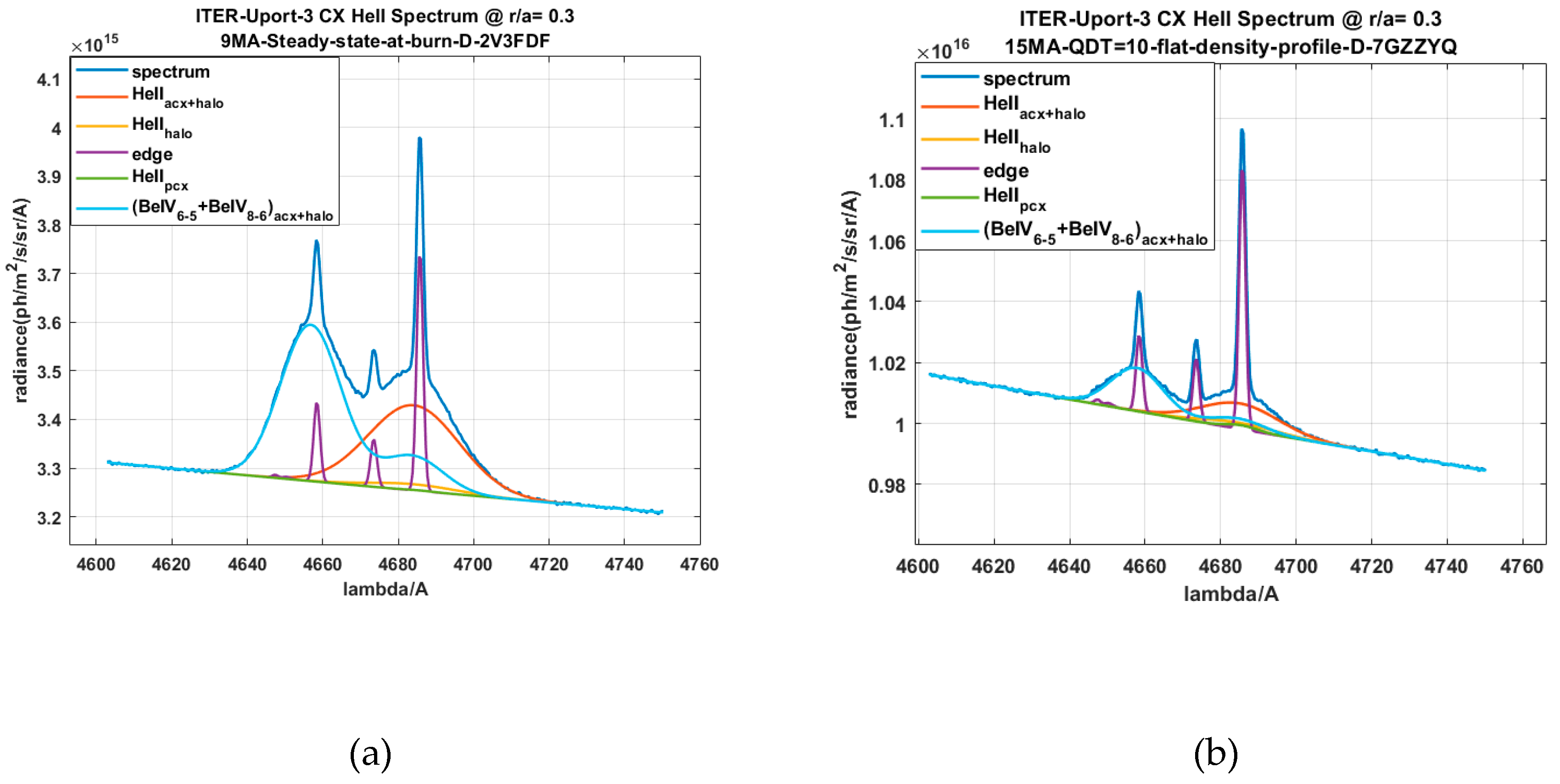
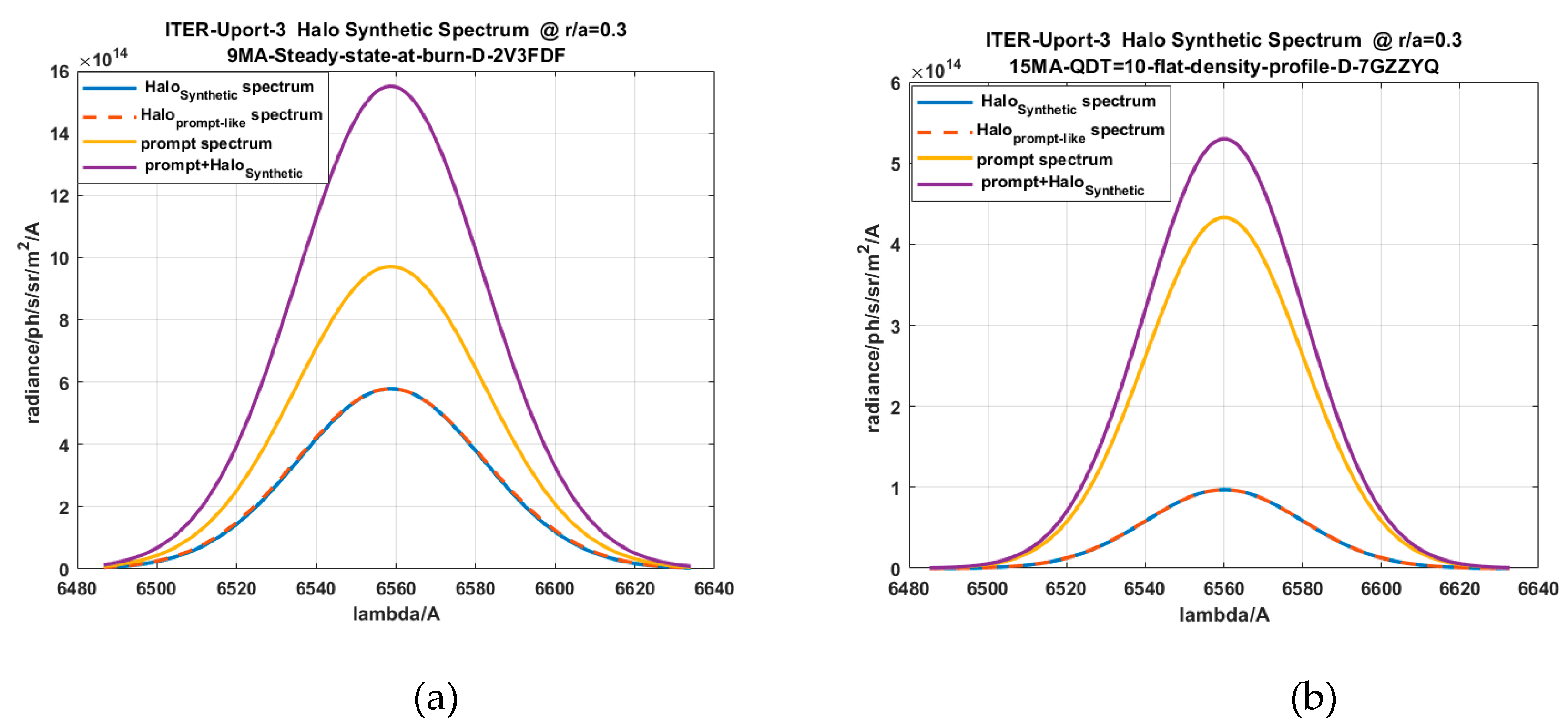
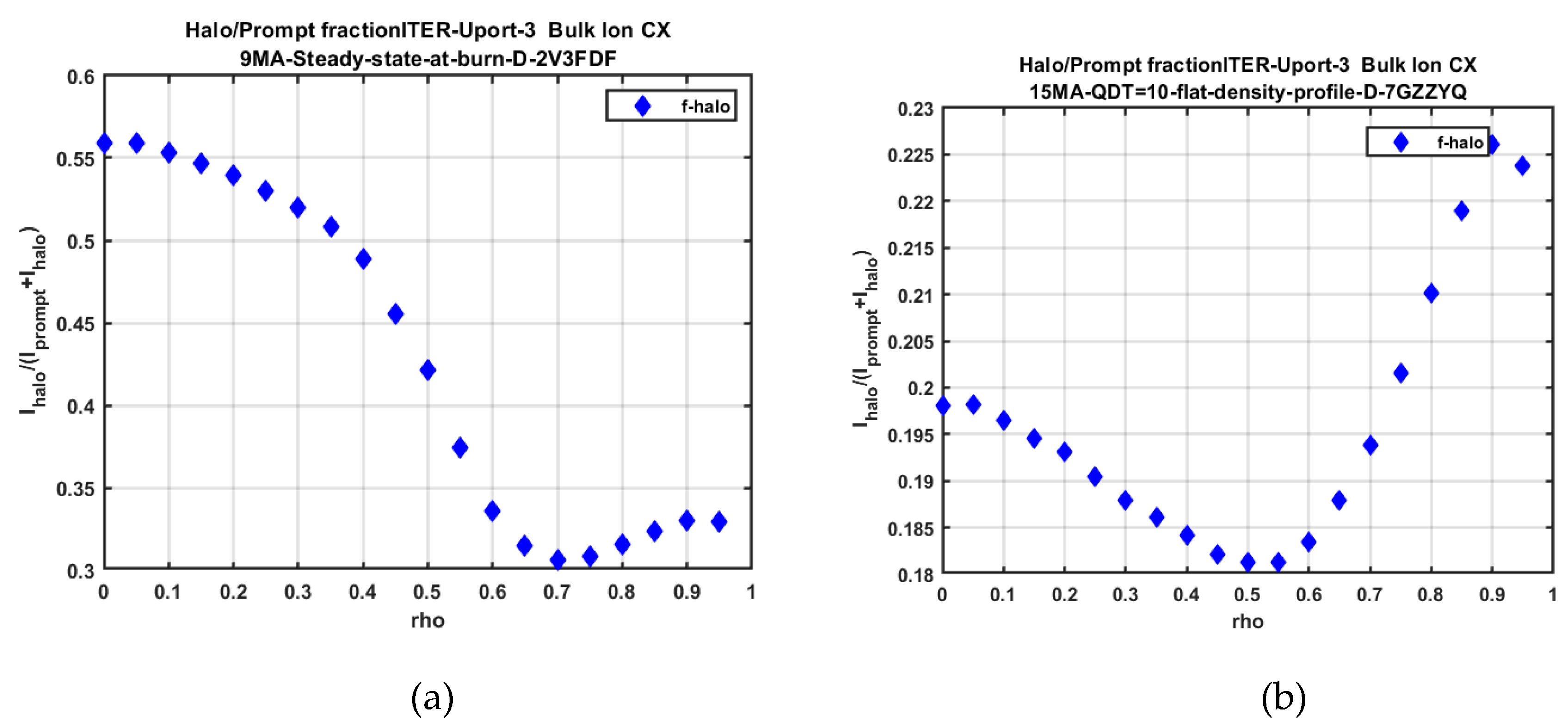
2.7. SOS Halo Model
D-alpha Halo Effect
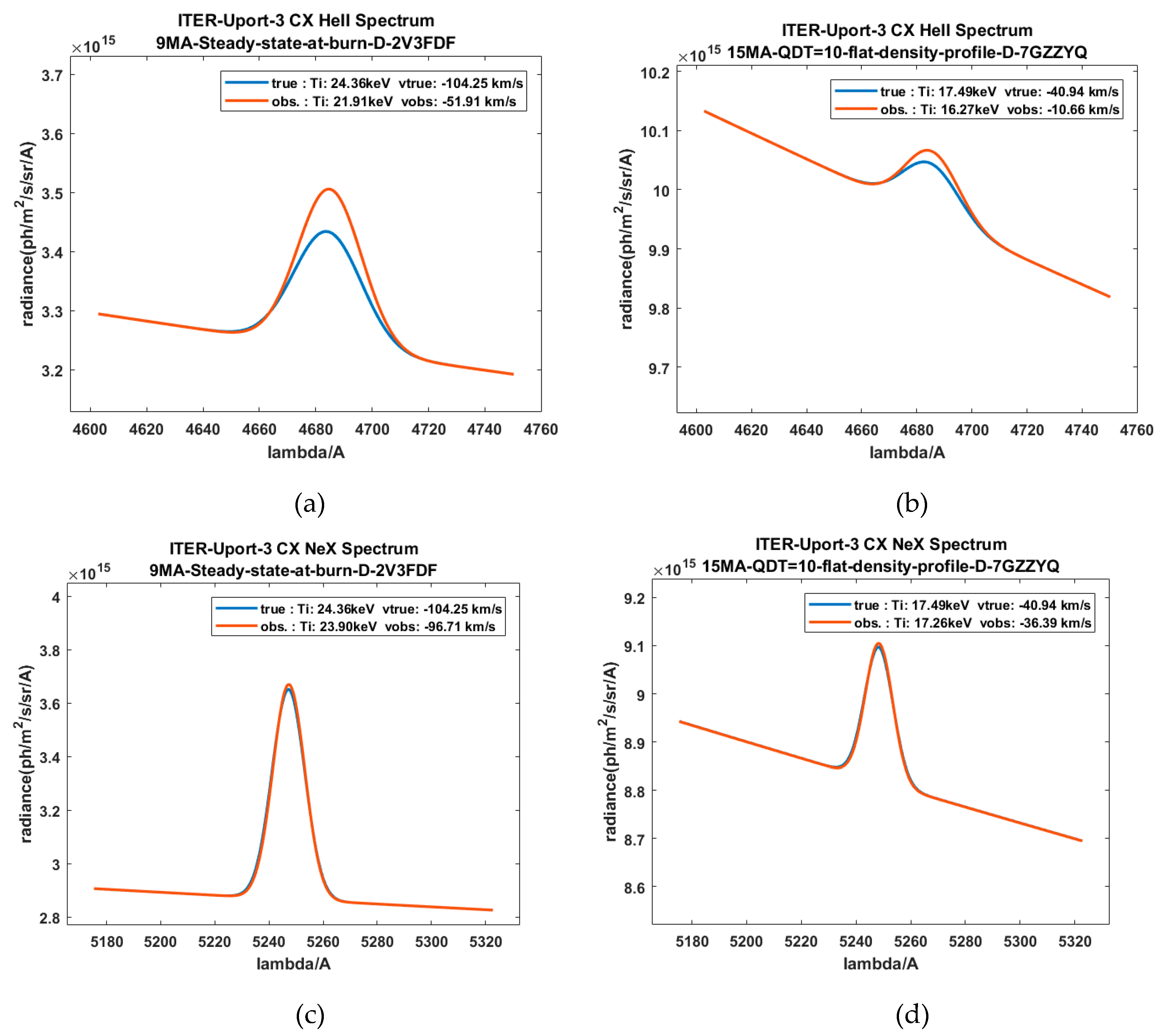
2.8. Impact of Ion Temperature and Plasma Rotation on the Line Shape of CXRS Lines in SOS Model
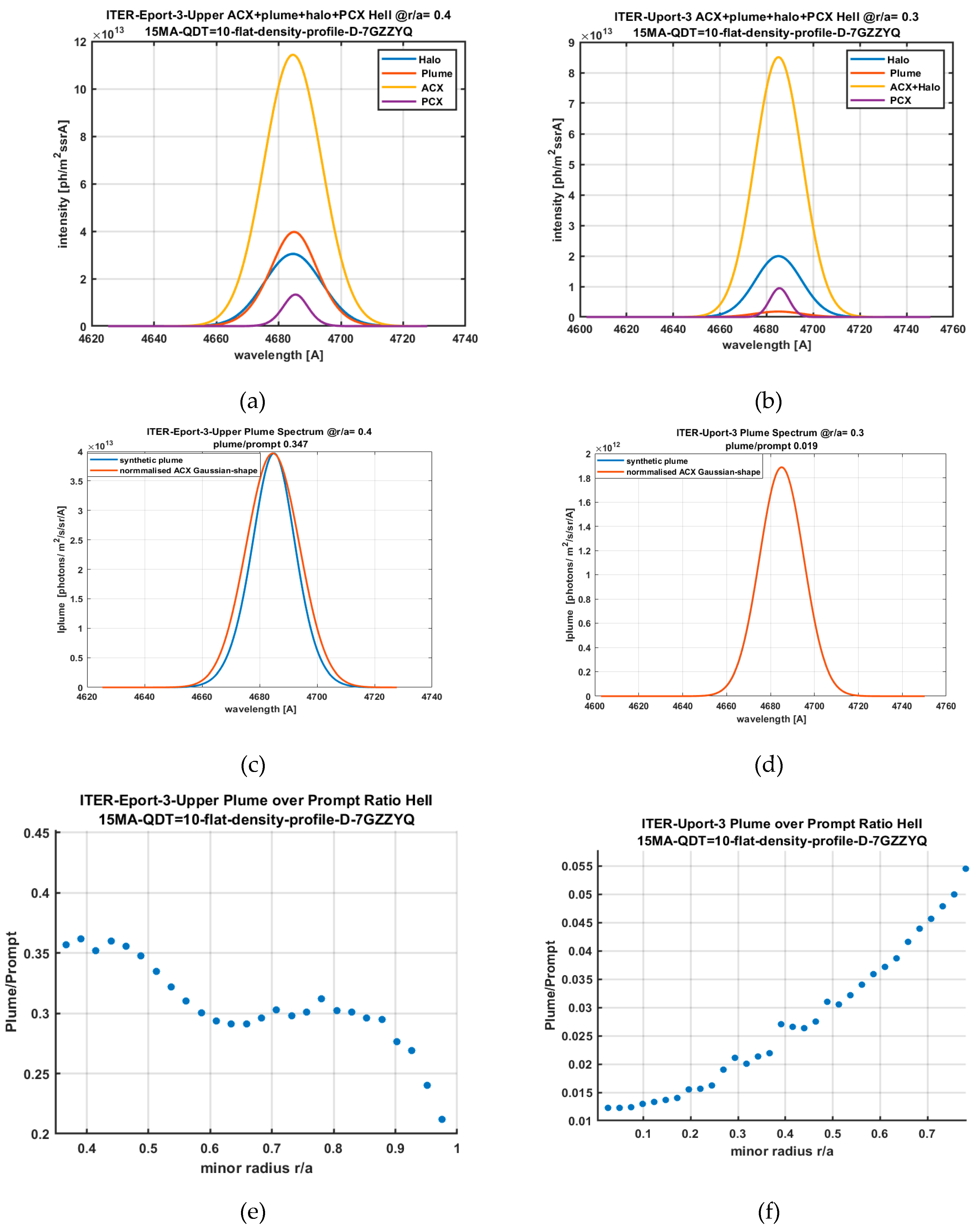
2.9. SOS Modeling of Plume Effect
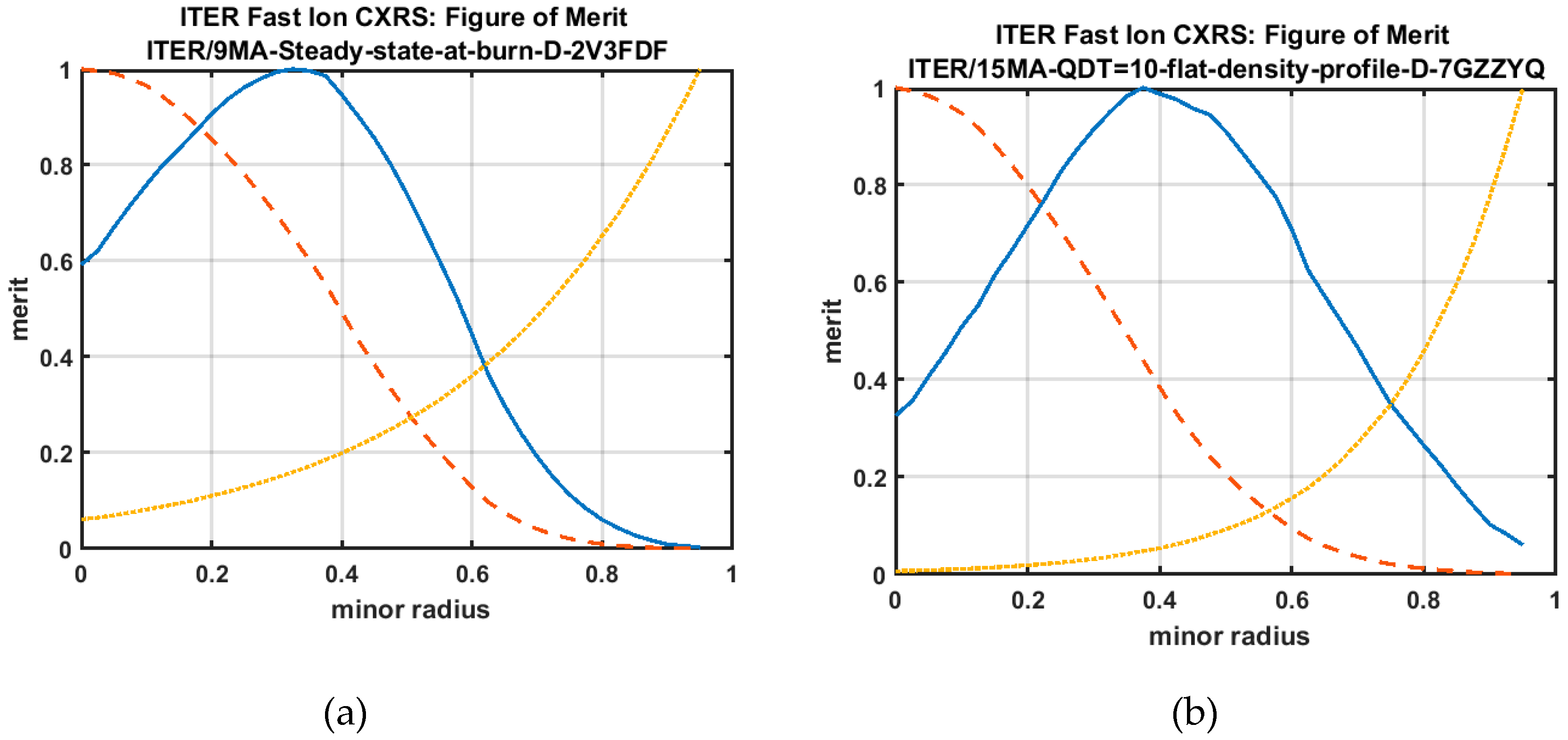
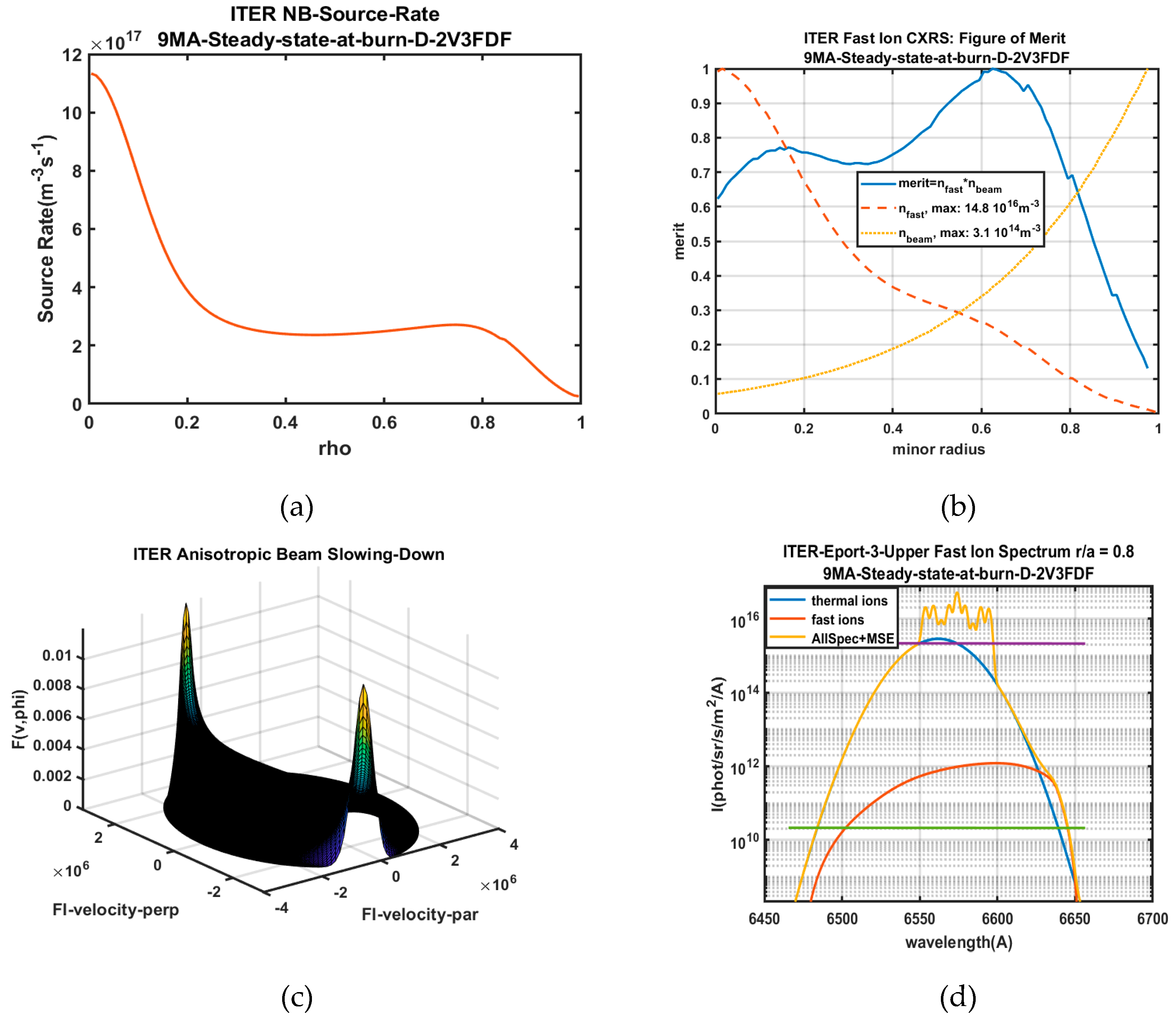
2.10. Fast Ion CXRS
2.10.1. Confined Fusion Alphas
2.10.2. Slowing-Down Beam Ions
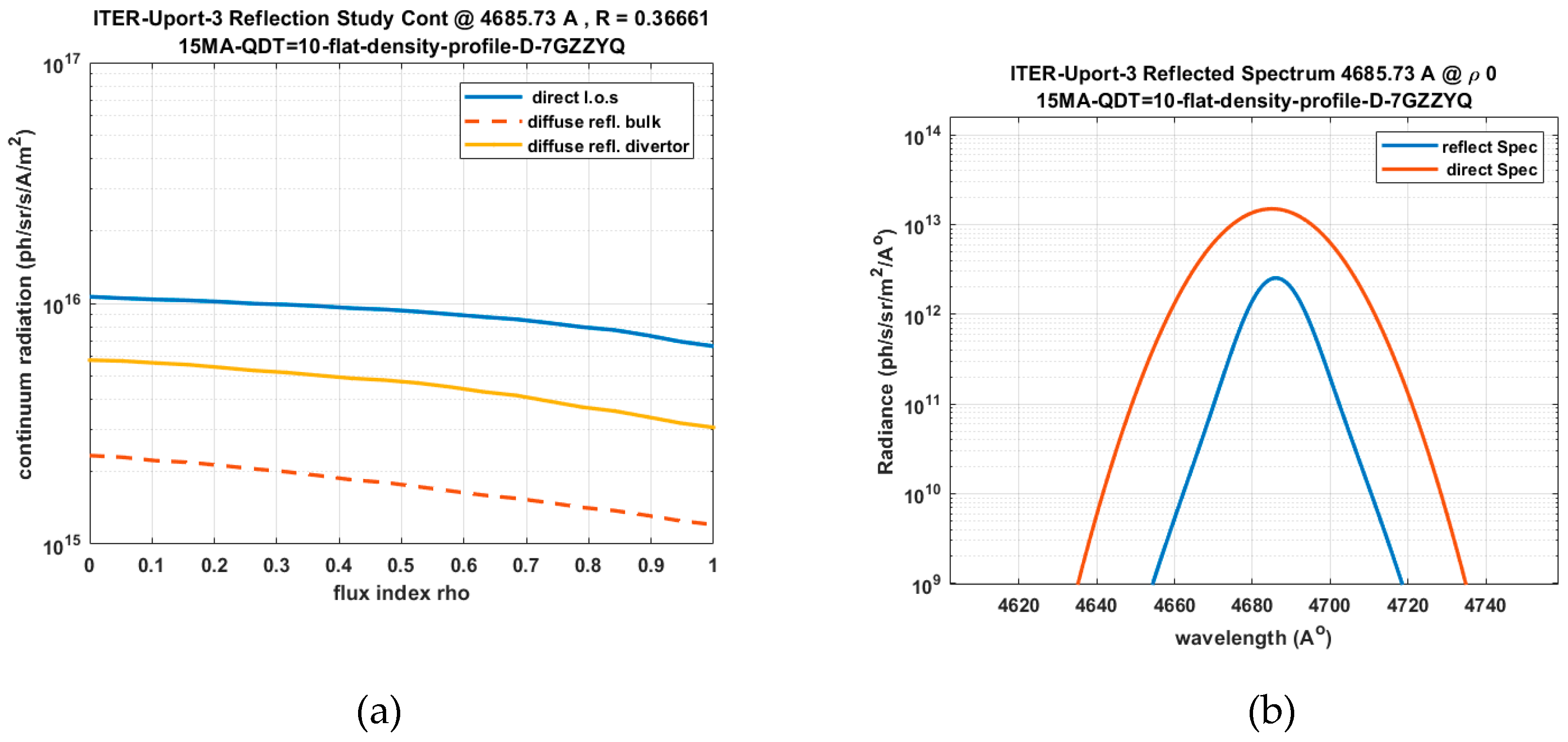
2.11. Wall Reflection Issues
3. Outlook and Future Strategy
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Atomic Data Base ADAS. Available online: http://adas.phys.ac.uk (accessed on 26 February 2019).
- Von Hellermann, M.G.; Biel, W.; Bertschinger, G.; Jupen, C.; O’Mullane, M.; Summers, H.; Whiteford, A. ComplexSpectra in Fusion Plasmas. Phys. Scr. 2005, 120, 19. [Google Scholar] [CrossRef]
- Svensson, J.; Werner, A. Large Scale Bayesian Data Analysis for Nuclear Fusion Experiments. In Proceedings of the 2007 IEEE International Symposium on Intelligent Signal Processing, Xiamen, China, 28 November–1 December 2007. [Google Scholar]
- Arshad, S.A.; Cordey, J.G.; McDonald, D.C.; Farthing, J.; Joffrin, E.; Von Hellermann, M.G.; Roach, C.M.; Svensson, J. Data Validation, Analysis, and Applications for Fusion Plasmas. Fus. Sci. Technol. 2008, 53, 667–669. [Google Scholar] [CrossRef]
- Tugarinov, S.; Krasilnikov, A.; Dokouka, V.; Khayrutdinov, R.; Beigman, I.; Tolstikhina, I.; Vainshtein, L.; Von Hellermann, M.G.; Malaquias, A. Conceptual design of the charge exchange recombination spectroscopy diagnostic for ITER. Rev. Sci. Instr. 2003, 74, 2075–2079. [Google Scholar] [CrossRef]
- Malaquias, A.; Von Hellermann, M.G.; Tugarinov, S.; Lotte, P.; Hawkes, N.; Kuldkepp, M.; Rachlew, E.; Gorshkov, A.; Walker, C.; Costley, A.; et al. Active beam spectroscopy diagnostics for ITER: Present status. Rev. Sci. Instr. 2004, 75, 3393–3398. [Google Scholar] [CrossRef]
- Von Hellermann, M.G.; Jaspers, R.; Biel, W.; Litnovsky, A.; Neubauer, O.; Pap, M.; Hawkes, N.C.; Marren, C.; Walton, B.; Kaschuck, Y.; et al. Status of the DNB based ITER CXRS and BES diagnostic. Rev. Sci. Instr. 2006, 77, 10F516. [Google Scholar] [CrossRef]
- Li, Y.Y.; Fu, J.; Lyu, B.; Du, X.W.; Li, C.Y.; Zhang, Y.; Yin, X.H.; Yu, Y.; Wang, Q.P.; Von Hellermann, M.G.; et al. Development of the charge exchange recombination spectroscopy and the beam emission spectroscopy on the EAST tokamak. Rev. Sci. Instr. 2014, 85, 11E428. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Heidbrink, W.W.; Wan, B.; Von Hellermann, M.G.; Zhu, Y.; Gao, W.; Wu, C.; Li, Y.; Fu, J.; Lyu, B.; et al. Conceptual design of a fast-ion D-alpha diagnostic on experimental advanced superconducting tokamak. Rev. Sci. Instr. 2014, 85, 11E407. [Google Scholar] [CrossRef] [PubMed]
- Von Hellermann, M.G.; Mandl, W.; Summers, H.P.; Weisen, H.; Boileau, A.; Morgan, P.D.; Morsi, H.; Koenig, R.; Stamp, M.F.; Wolf, R. Visible charge exchange spectroscopy at JET. Rev. Sci. Instr. 1990, 61, 3479–3486. [Google Scholar] [CrossRef]
- Whiteford, A.; Von Hellermann, M.G.; Horton, L.D.; Zastrow, K.-D. “CXSFIT—User Manual”, November 2007. Available online: adas.phys.ac.uk/notes/adas_r07-01.pdf (accessed on 26 February 2019).
- Svensson, J.; Von Hellermann, M.G.; König, R. Analysis of Charge Exchange Spectra Using Neural Networks at the JET Tokamak. Plasma Phys. Controll. Fus. 1999, 41, 315. [Google Scholar] [CrossRef]
- Von Hellermann, M.G.; Summers, H.P. Atomic Modelling and Spectroscopic Diagnostics. In Proceedings of the 9th Topical Conference on High Temperature Plasma Diagnostics, Santa Fe, New Mexico, 15–19 March 1992. [Google Scholar]
- Von Hellermann, M.G. Quantitative Spectroscopy for Fusion Plasmas; Akademie Verlag: Berlin, Germany, 1994; pp. 117–130. [Google Scholar]
- Von Hellermann, M.G.; Delabie, E.; Jaspers, R.; Lotte, P.; Summers, H.P. Modelling and Evaluation of Spectra in Beam Aided Spectroscopy. In Proceedings of the 15–19th International Conference on Spectral Line Shapes, Valladolid, Spain, 15–20 June 2008; AIP Conference Proceedings. Volume 1058, pp. 187–194. [Google Scholar]
- Von Hellermann, M.G.; Breger, P.; Frieling, J.G.; König, R.W.T.; Mandl, W.; Maas, A.; Summers, H.P. Analytical Approximation of Cross-Section Effects on Observed CX Spectra in Hot Fusion Plasmas. Plasma Phys. Contr. Fus. 1995, 37, 71. [Google Scholar] [CrossRef]
- Tunklev, M.; Breger, P.; Günther, K.; Von Hellermann, M.G.; König, R.W.T.; O’Mullane, M.; Zastrow, K. Modelling of Passive Charge Exchange Emission and Neutral Background Density Deductions in JET. Plasma Phys. Contr. Fus. 1999, 41, 985–1024. [Google Scholar] [CrossRef]
- Reiter, D.; Baelmans, M.; Börner, P. The EIRENE and B2-EIRENE Codes. Fus. Sci. Technol. 2005, 47, 172–186. [Google Scholar] [CrossRef]
- Stratton, B.; Fonck, R.J.; Ramsay, A.T.; Synakowski, E.J.; Grek, B.; Hill, K.W.; Johnson, D.W.; Mansfield, D.K.; Park, H.; Taylor, G. Charge exchange recombination spectroscopy measurements in the extreme ultraviolet region of central carbon concentrations during high power neutral beam heating in TFTR. Nucl. Fusi. 1990, 30, 675. [Google Scholar] [CrossRef]
- Isler, R. An Overview of CX spectroscopy as plasma diagnostic tool. Plasma Phys. Contr. Fus. 1994, 36, 171. [Google Scholar] [CrossRef]
- Dux, R.; Geiger, B.; McDermott, R.M.; Puetterich, T.; Viezzer, E. Impurity density determination using charge exchange and beam emission spectroscopy. In Proceedings of the 39th EPS Conference on Plasma Physics, Stockholm, Sweden, 2–6 July 2012. [Google Scholar]
- Fonck, R.J.; Darrow, D.S.; Jaehnig, K.P. Determination of Plasma Ion Velocity Distribution via Charge Exchange Recombination Spectroscopy. Phys. Rev. A 1984, 29, 3288. [Google Scholar] [CrossRef]
- Finkenthal, D. The Measurement of Absolute Helium Ion Density Profiles on the DIII-D Tokamak Using Charge Exchange Recombination Spectroscopy. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Stotler, D. Atomic Physics in ITER. In Proceedings of the 5th International Conference on Atomic and Molecular Data and their Applications, Meudon, France, 15–19 October 2006. [Google Scholar]
- Kappatou, A.; McDermott, R.M.; Pütterich, T.; Dux, R.; Geiger, B.; Jaspers, R.J.; Donné, A.J.; Viezzer, E.; Cavedon, M. A forward model of the helium plume effect and the interpretation of helium charge exchange measurement at ASDEX Upgrade. Plasma Phys. Control Fus. 2018, 60, 055006. [Google Scholar] [CrossRef]
- Grisham, L.R.; Post, D.E.; Mikkelsen, D.R. Multi-MeV Li0 Beam as a Diagnostic for Fast Confined Alpha Particles. Nucl. Technol.-Fusion 1983, 3, 121–128. [Google Scholar] [CrossRef]
- Von Hellermann, M.G.; Mandl, W.; Summers, H.P. Investigation of Thermal and Slowing-down Alpha Particles on JET using Charge Exchange Spectroscopy. Plasma Phys. Control Fus. 1991, 33, 1805. [Google Scholar] [CrossRef]
- Von Hellermann, M.G.; Core, W.G.F.; Frieling, J.; Horton, L.D.; Koenig, R.W.T.; Summers, H.P. Observation of Alpha-Particle-Slowing-Down-Spectra in JET He Fuelling Experiments. Plasma Phys. Control Fus. 1993, 35, 799. [Google Scholar] [CrossRef]
- Stratton, B.C.; Fonck, R.J.; McKee, G.R.; Budny, R.V. Observation of sawtooth redistribution of non-thermal confined alpha particles in TFTR DT discharges. Nucl. Fus. 1996, 36, 1586. [Google Scholar] [CrossRef]
- Kappatou, A.; Delabie, E.; Jaspers, R.J.E.; Von Hellermann, M.G. Feasibility of non-thermal helium measurements with charge exchange spectroscopy on ITER. Nucl. Fus. 2012, 52, 043007. [Google Scholar] [CrossRef]
- Lauber, P. Linear Gyrokinetic Description of Fast Particle Effects on the MHD Stabilities in Tokamaks. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2003. [Google Scholar]
- Heidbrink, W.W.; Sadler, G.J. The behaviour of fast ions in tokamak experiments. Nucl. Fus. 1994, 34, 535. [Google Scholar] [CrossRef]
- Heidbrink, W.W.; Burrell, K.H.; Lao, Y.; Pablant, N.A.; Ruskow, E. Hydrogenic fast-ion-diagnostic using Balmer Alpha light. Plasma Phys. Contr. Fus. 2004, 46, 1855. [Google Scholar] [CrossRef]
- Delabie, E.; Jaspers, R.J.E.; Von Hellermann, M.G.; Nielsen, S.K.; Marchuk, O. Charge exchange spectroscopy as a fast ion diagnostic on TEXTOR. Rev. Sci. Instr. 2008, 79, 10E522. [Google Scholar] [CrossRef] [PubMed]
- Geiger, B.; Garcia-Munoz, M.; Hobirk, J.; Tardini, G.; McDermott, R.; Dux, R. Fast-ion D-alpha measurements at ASDEX Upgrade. Plasma Phys. Control. Fus. 2011, 53, 065010. [Google Scholar] [CrossRef]
- Huang, J.; Heidbrink, W.W.; Von Hellermann, M.G.; Stagner, L.; Wu, C.R.; Hou, Y.M.; Chang, J.F.; Ding, S.Y.; Chen, Y.J.; Zhu, Y.B.; et al. Validation of fast-ion-D-alpha spectrum measurements during EAST neutral beam heated plasmas. Rev. Sci. Instr. 2016, 87, 11E542. [Google Scholar] [CrossRef] [PubMed]
- Marchuk, O.; Ralchenko, Y.; Janev, R.K.; Biel, W.; Delabie, E.; Urnov, A.M. Collisional excitation and emission of H- alpha Stark multiplet in fusion plasmas. J. Phys. B 2010, 43, 011002. [Google Scholar] [CrossRef]
- Marchuk, O.; Ralchenko, Y. Populations of Excited Parabolic States of Hydrogen Beam in Fusion Plasmas. In Atomic Processes in Basic and Applied Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Anderson, H.; Von Hellermann, M.G.; Horton, R.H.L.D.; Howman, A.C.; König, R.W.T.; Martin, R.; Olson, R.E.; Summers, H.P. Neutral beam stopping and emission in fusion plasmas I: Deuterium beams. Plasma Phys. Contr. Fus. 2000, 42, 781–806. [Google Scholar] [CrossRef]
- Delabie, E.; Brix, M.; Giroud, C.; Jaspers, R.J.; Marchuk, O.; O’Mullane, M.G.; Ralchenko, Y.; Surrey, E.; Von Hellermann, M.G.; Zastrow, K.D.; et al. Consistency of atomic data for the interpretation of beam emission spectra. Plasma Phys. Control. Fus. 2010, 52, 125008. [Google Scholar] [CrossRef]
- Von Hellermann, M.G.; Jaspers, R.J.E.; Zastrow, H.P. Recent Progress in Beam Emission and CX Spectroscopy. In Advanced Diagnostics for Magnetic and Inertial Fusion; Springer: Boston, MA, USA, 2005. [Google Scholar]
- Hutchinson, I. Principles of Plasma Diagnostics; Cambridge University Press: Cambridge, UK, 1987; p. 170. [Google Scholar]
- Carson, R.T. Coulomb Free-Free Gaunt Factor. Astron. Astrophys. 1988, 189, 319. [Google Scholar]
- Burgess, A.; Summers, H.P. Radiative Gaunt Factors. Mon. Not. R. astr. Soc. 1987, 226, 257–272. [Google Scholar] [CrossRef]
- Levinton, F.M. The multichannel motional stark effect diagnostic on TFTR. Rev. Sci. Instr. 1992, 63, 5157–5160. [Google Scholar] [CrossRef]
- Hawkes, N.C.; Stratton, B.C.; Tala, T.; Challis, C.D.; Conway, G.; DeAngelis, R.; Giroud, C.; Hobirk, J.; Joffrin, E.; Lomas, P.; et al. Observation of Zero Current Density in the Core of JET Discharges with Lower Hybrid Heating and Current Drive. Phys. Rev. Lett. 2001, 87, 115001. [Google Scholar] [CrossRef] [PubMed]
- Boileau, A.; Von Hellermann, M.G.; Mandl, W.; Summers, H.P.; Weisen, H.; Zinoviev, A. Observations of motional Stark features in the Balmer spectrum of deuterium in the JET plasma. J. Phys. B 1989, 22, L145. [Google Scholar] [CrossRef]
- De Bock, M.F.M.; Conway, N.J.; Walsh, M.J.; Carolan, P.G.; Hawkes, N.C. Ab initio modelling of motional Stark effect on MAST. Rev. Sci. Instr. 2008, 79, 10F524. [Google Scholar] [CrossRef] [PubMed]
- Reimer, R.; Marchuk, O.; Geiger, B.; Mc Carthy, P.J.; Dunne, M.; Hobirk, J.; Wolf, R. Influence of non-Local Thermodynamic Equlibrium and Zeeman Effects on magnetic equilibrium reconstruction using spectral Motional Stark Effect Diagnostic. Rev. Sci Inst. 2017, 88, 083509. [Google Scholar] [CrossRef] [PubMed]
- Abdurakhmanov, I.B.; Kadyrov, A.S.; Avazbaez, S.K.; Bray, I. Solution of proton-hydrogen scattering problem using a quantum-mechanical two-center convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 115203. [Google Scholar] [CrossRef]
- Heidbrink, W.W.; liu, D.; Luo, Y.; Ruskov, E.; Geiger, B. A Code that Simulates Fast-Ion Dα and neutral Particle Measurements. Commun. Comput. Phys. 2011, 10, 716. [Google Scholar] [CrossRef]
- Hollmann, E.M.; Pigarov, A.Y.; Denner, R.P. Effects of graphite and molybdenum wall tile reflections on visible light diagnostics in tokamak experiments. Rev. Sci. Instr. 2003, 74, 3984. [Google Scholar] [CrossRef]
- Zastrow, K.D.; Keatings, S.R.; Marot, L.; O’Mullane, M.G.; De Temmerman, G. Modelling the effect of reflection from metallic walls on spectroscopic measurements. Rev. Sci. Instr. 2008, 79, 10F527. [Google Scholar] [CrossRef]
- Banerjee, S.; Vasu, P.; Von Hellermann, M.G.; Jaspers, R.J.E. Wall reflecection modelling for charge exchange recombination spectroscopy (CXRS) measurements on TEXTOR and ITER. Plasma Phys. Contr. Fus. 2010, 52, 125006. [Google Scholar] [CrossRef]
- Lotte, P.; Aumenier, M.H.; Devynk, P.; Fenzi, C.; Martin, V.; Travere, J.M. Wall reflection issues for optical diagnostics in fusion devices. Rev. Sci. Instr. 2010, 81, 10E120. [Google Scholar] [CrossRef] [PubMed]
- Kajita, S.; de Bock, M.; Von Hellermann, M.G.; Kukushkin, A.; Barnsley, R. Ray tracing analysis of stray for charge exchange spectroscopy on ITER. Plasma Phys. Contr. Fus. 2015, 57, 045009. [Google Scholar] [CrossRef]
- Nikolic, D.; Gorczyca, T.W.; Korista, K.T.; Chatzikos, M.; Ferland, G.J.; Guzman, F.; van Hoof, P.A.M.; Williams, R.J.E.; Badnell, N.R. Suppression of Dielectronic Recombination Due to Finite Density Effects. II Analytical Refinement and Application to Density-dependent Ionization Balances and AGN Broad-line Emission. Astrophys. J. Suppl. Ser. 2018, 237, 41. [Google Scholar] [CrossRef]
| 1 | For a detailed description of the SOS modular structure and flow-charts see: https://git.iter.org/projects/DIAG/sos. |

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
von Hellermann, M.; de Bock, M.; Marchuk, O.; Reiter, D.; Serov, S.; Walsh, M. Simulation of Spectra Code (SOS) for ITER Active Beam Spectroscopy. Atoms 2019, 7, 30. https://doi.org/10.3390/atoms7010030
von Hellermann M, de Bock M, Marchuk O, Reiter D, Serov S, Walsh M. Simulation of Spectra Code (SOS) for ITER Active Beam Spectroscopy. Atoms. 2019; 7(1):30. https://doi.org/10.3390/atoms7010030
Chicago/Turabian Stylevon Hellermann, Manfred, Maarten de Bock, Oleksandr Marchuk, Detlev Reiter, Stanislav Serov, and Michael Walsh. 2019. "Simulation of Spectra Code (SOS) for ITER Active Beam Spectroscopy" Atoms 7, no. 1: 30. https://doi.org/10.3390/atoms7010030
APA Stylevon Hellermann, M., de Bock, M., Marchuk, O., Reiter, D., Serov, S., & Walsh, M. (2019). Simulation of Spectra Code (SOS) for ITER Active Beam Spectroscopy. Atoms, 7(1), 30. https://doi.org/10.3390/atoms7010030





