Spectral Modeling of Hydrogen Radiation Emission in Magnetic Fusion Plasmas
Abstract
1. Introduction
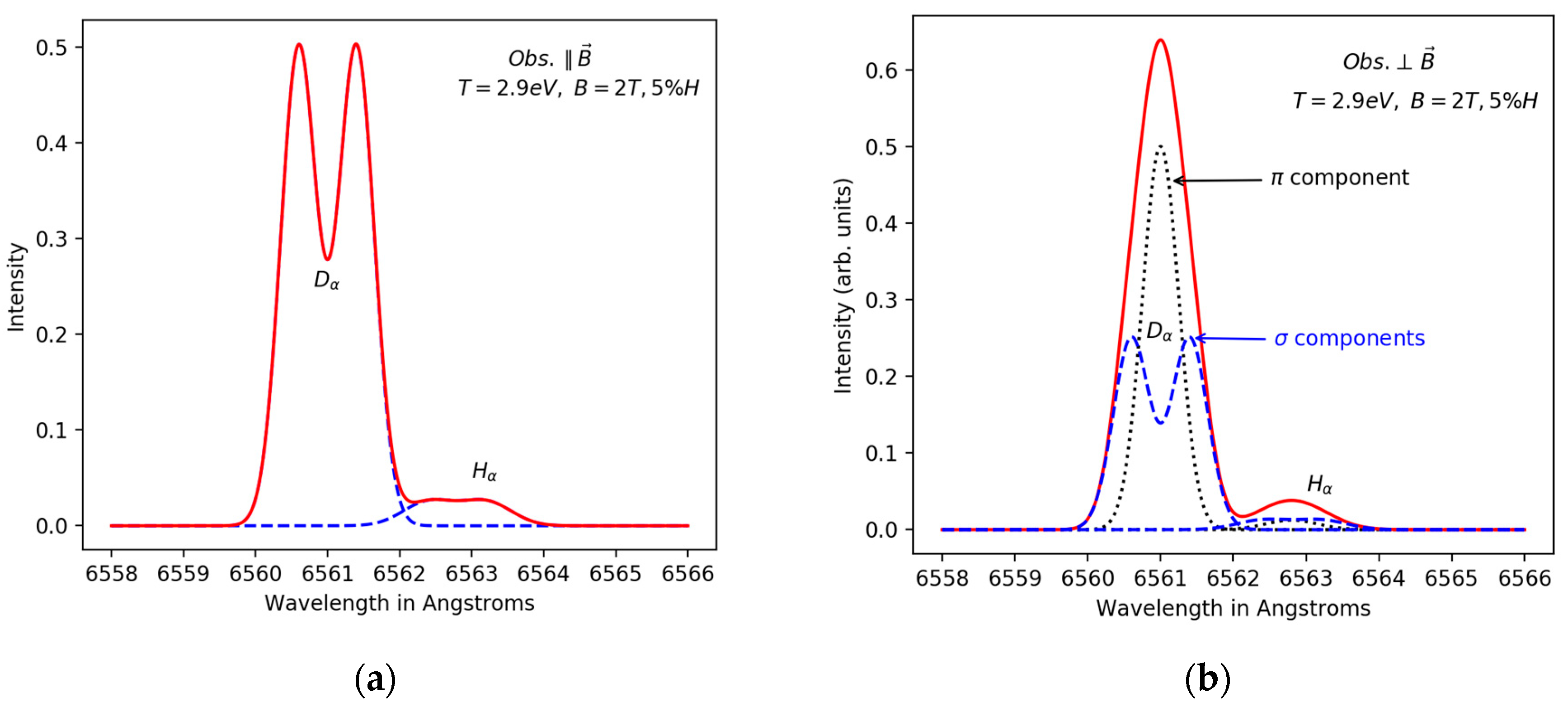
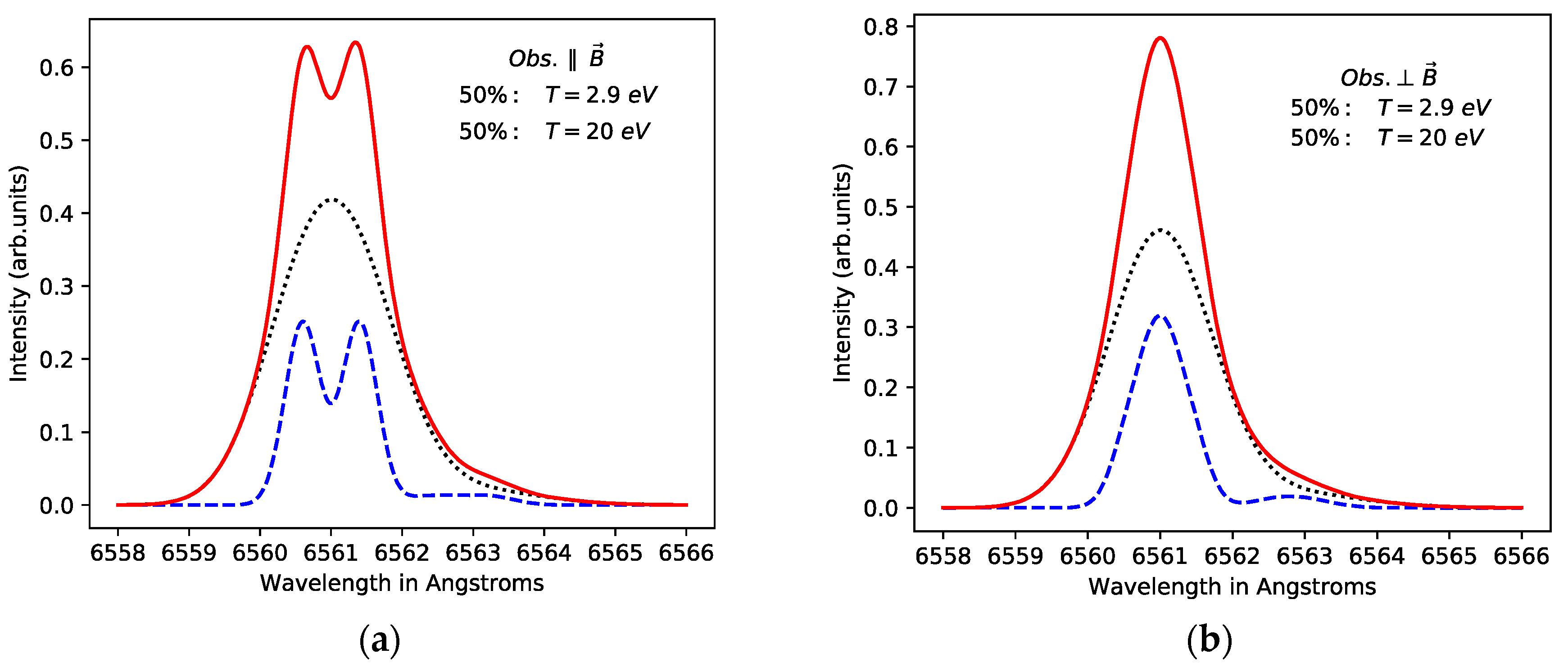
2. The Zeeman–Doppler Hα/Dα Line Profile
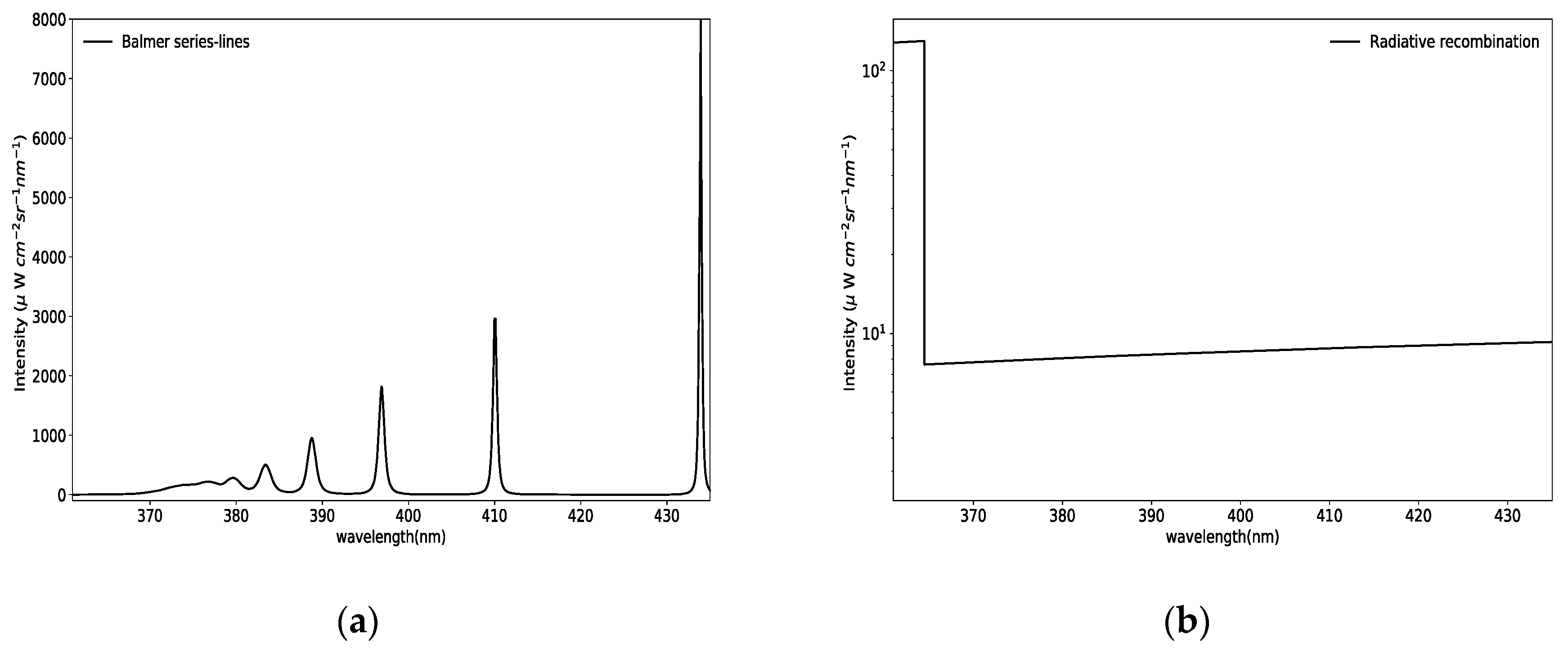
3. The High-n Balmer Lines and Continuum
3.1. Modeling of the Bound–Bound Transitions
3.2. Modeling of the Continuum Radiation
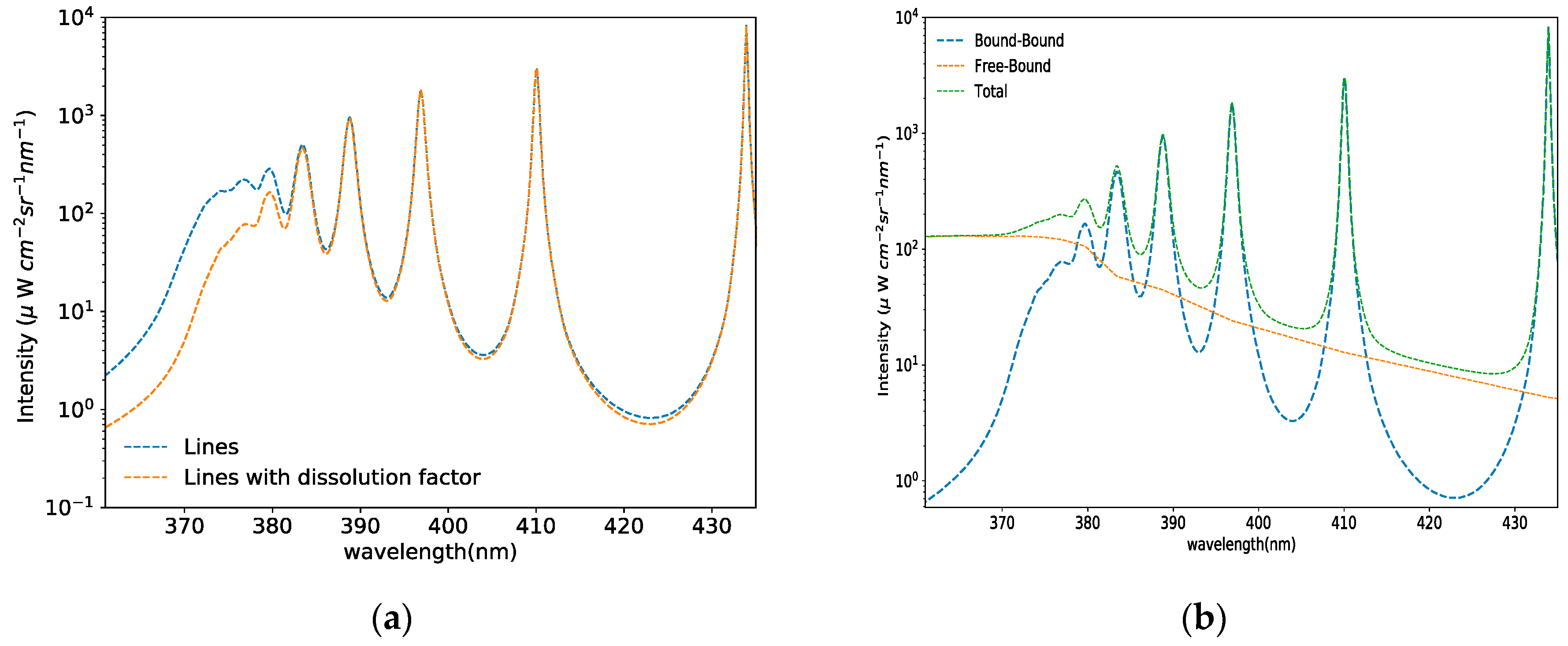
3.3. The Total Spectrum and the Dissolution Approach
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pigarov, A.Y.; Terry, J.L.; Lipschultz, B. Study of the discrete-to-continuum transition in a Balmer spectrum from Alcator C-Mod divertor plasmas. Plasma Phys. Control. Fusion 1998, 40, 2055–2072. [Google Scholar] [CrossRef]
- Krasheninnikov, S.I.; Kukushkin, A.S.; Pshenov, A.A. Divertor plasma detachment. Phys. Plasmas 2016, 23, 055602. [Google Scholar] [CrossRef]
- Loarte, A.; Monk, R.; Martin-Solis, J.; Campbell, D.; Chankin, A.; Clément, S.; Davies, S.; Ehrenberg, J.; Erents, S.; Guo, H.; et al. Plasma detachment in JET Mark I divertor experiments. Nucl. Fusion 1998, 38, 331–371. [Google Scholar] [CrossRef]
- Field, A.R.; Balboa, I.; Drewelow, P.; Flanagan, J.; Guillemaut, C.; Harrison, J.R.; Huber, A.; Huber, V.; Lipschultz, B.; Matthews, G.; et al. Dynamics and stability of divertor detachment in H-mode plasmas on JET. Plasma Phys. Control. Fusion 2017, 59, 095003. [Google Scholar] [CrossRef]
- Potzel, S.; Wischmeier, M.; Bernert, M.; Dux, R.; Müller, H.; Scarabosio, A. A new experimental classification of divertor detachment in ASDEX Upgrade. Nucl. Fusion 2013, 54, 13001. [Google Scholar] [CrossRef]
- Potzel, S.; Dux, R.; Müller, H.W.; Scarabosio, A.; Wischmeier, M. Electron density determination in the divertor volume of ASDEX Upgrade via Stark broadening of the Balmer lines. Plasma Phys. Control. Fusion 2014, 56, 025010. [Google Scholar] [CrossRef]
- Kubo, H.; Takenaga, H.; Sugie, T.; Higashijima, S.; Suzuki, S.; Sakasai, A.; Hosogane, N. The spectral profile of the Ha line emitted from the divertor region of JT-60U. Plasma Phys. Control. Fusion 1998, 40, 1115. [Google Scholar] [CrossRef]
- Koubiti, M.; Marandet, Y.; Escarguel, A.; Capes, H.; Godbert-Mouret, L.; Stamm, R.; De Michelis, C.; Guirlet, R.; Mattioli, M. Analysis of asymmetric Dα spectra emitted in front of a neutralizer plate of the Tore-Supra ergodic divertor. Plasma Phys. Control. Fusion 2002, 44, 261. [Google Scholar] [CrossRef]
- Hey, J.; Chu, C.C.; Mertens, P.H.; Brezinsek, S.; Unternberg, B. Atomic collision processes with ions at the edge of magnetically confined fusion plasmas. J. Phys. B 2004, 37, 2543. [Google Scholar] [CrossRef]
- Neverov, V.S.; Kukushkin, A.B.; Stamp, M.F.; Alkseev, A.G.; Brezinsek, S.; von Hellermann, M.; JET contributors. Determination of divertor stray light in high-resolution main chamber Ha spectroscopy in JET-ILW. Nucl. Fusion 2017, 57, 016031. [Google Scholar] [CrossRef]
- Inglis, D.R.; Teller, E. Ionic depression of series limits in one electron spectra. Astrophys. J. 1939, 90, 439. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef] [PubMed]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.A.; González, M.A.; González-Herrero, D.; Lara, N.; et al. Ion Dynamics Effect on Stark-Broadened Line Shapes: A Cross-Comparison of Various Models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
- Griem, H.; Blaha, M.; Kepple, P. Stark profile clacultaions for Lyman series lines of one electron ions in dense plasmas. Phys. Rev. A 1979, 19, 2421. [Google Scholar] [CrossRef]
- Goto, M.; Sakamoto, R.; Morita, S. Experimental verification of complete LTE plasma formation in hydrogen pellet cloud. PPCF 2007, 49, 1163. [Google Scholar] [CrossRef]
- D’yachkov, L.G. Smooth transition from spectral lines to a continuum in dense hydrogen plasma. High Temp. 2016, 54, 5. [Google Scholar] [CrossRef]
- Stehle, C.; Jacquemot, S. Line shape in hydrogen opacities. Astron. Astrophys 1993, 271, 348. [Google Scholar]
- Iglesias, C.A. Electronic microfield distributions in strongly coupled plasmas. Phys. Rev. A 1983, 28, 1168. [Google Scholar] [CrossRef]
- Sheeba, R.R.; Koubiti, M.; Calisti, A.; Ferri, S.; Marandet, Y.; Rosato, J.; Stamm, R. Synthetic diagnostics based on hydrogen Balmer series in recombining plasmas for WEST tokamak. High Density Energy Phys. 2019. to be submitted to High Energy Density Physics. [Google Scholar]
- Bufferand, H.; Ciraolo, G.; Marandet, Y.; Bucalossi, J.; Ghendrih, P.; Gunn, J.; Mellet, N.; Tamain, P.; Leybros, R.; Fedorczak, N.; et al. Numerical modeling for divertor design of the WEST device with a focus on plasma-wall interactions. Nucl. Fusion 2015, 55, 053025. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koubiti, M.; Sheeba, R.R. Spectral Modeling of Hydrogen Radiation Emission in Magnetic Fusion Plasmas. Atoms 2019, 7, 23. https://doi.org/10.3390/atoms7010023
Koubiti M, Sheeba RR. Spectral Modeling of Hydrogen Radiation Emission in Magnetic Fusion Plasmas. Atoms. 2019; 7(1):23. https://doi.org/10.3390/atoms7010023
Chicago/Turabian StyleKoubiti, Mohammed, and Roshin Raj Sheeba. 2019. "Spectral Modeling of Hydrogen Radiation Emission in Magnetic Fusion Plasmas" Atoms 7, no. 1: 23. https://doi.org/10.3390/atoms7010023
APA StyleKoubiti, M., & Sheeba, R. R. (2019). Spectral Modeling of Hydrogen Radiation Emission in Magnetic Fusion Plasmas. Atoms, 7(1), 23. https://doi.org/10.3390/atoms7010023




