1. Introduction
In the last decade, nuclear fusion started to shift from science to industry, where the tokamak-based ITER is playing the leading role. Runaway electrons (REs) present a potential threat to the safe operation of the future nuclear fusion power plants based on the tokamak principle. Namely, in the latest issue of ITER Physics Basis [
1], REs are considered as the second-highest priority for the ITER disruption mitigation.
COMPASS tokamak [
2] is a suitable and low-risk test bed for studying RE disruption physics and RE model benchmarking. However, one of the common missing RE parameters for comparison of experiment and simulation is RE current or RE density. This article addresses this issue for certain cases.
The basic idea behind the used model was reported on ORMAK tokamak by Fujita [
3]. In contrast to Fujita’s full-theoretical approach, we implemented experimental data from EFIT [
4] and Thomson Scattering [
5] to the calculation. The obtained results are in the acceptable range and their application on density scans and RE localization is presented.
The article starts with a description of an experimental observation of the particular discharge. Theoretical models and detailed description of the settings used in the models for comparison with the experiments are then reported. An estimation of the RE current is the first experimental analysis. Subsequently, the influence of the REs on the current ramp-up phase of the discharge is evaluated. Following that, a principle on how to localize RE beam is done in the next section, using the knowledge of the RE beam current and its maximum energy. Finally, discussions and conclusions are given in the last section with an outlook towards expected future works.
2. Experimental Setup: COMPASS Tokamak
The COMPASS tokamak is a compact experimental fusion facility with a major radius
m and a minor radius
m. The toroidal magnetic field
is in the
–
T range (typically set to
T), coming from 16 toroidal field coils. The plasma current
can reach up to 400 kA using an air-cored transformer. The range for the electron densities is flexible and is typically in the
–
m
domain. Plasma shaping varies from circular and elliptical to single-null D-shaped ITER-like plasmas. When circular, the plasma is limited by a carbon HFS wall. The regular pulse length is
s, although low current circular discharges with RE can last almost 1 s [
6,
7].
The Thomson Scattering diagnostic system in COMPASS uses two Nd:YAG lasers of wavelength 1064 nm with an energy of 1.5 J for each laser. The whole system is oriented vertically and the scattered light is recorded in the radial direction. Each laser has 30 Hz repetition rate, which offers a ms time resolution if the two lasers are operated equidistantly.
The EFIT reconstruction provides relevant quantities on a 2D mesh cross-section of the poloidal plasma plane solving the Grad–Shafranov equation for plasma MHD equilibrium, constrained by the magnetic diagnostics at the COMPASS tokamak (current measured in plasma and field coils, pick-up coils). Additionally, in the analysis addressed here, a toroidal loop voltage in plasma
for computing a maximum RE energy
is calculated using METIS [
8], a Multi-Element Tokamak-oriented Integrated Simulator.
3. Experiment: High RE Current Discharge
The very first magnetic observations of high RE current in the COMPASS tokamak are reported in Ref. [
9] for discharge #7298. The discharge had circular-shaped limited plasma, with toroidal magnetic field
T and plasma current
kA. The plasma density
was lower than
m
in the plasma core as measured by the Thomson Scattering system.
The COMPASS tokamak is well-supplied with the general plasma measurements, which provided us with the following list of observations in the discharge:
Loop voltage measured plasma voltage bellow 1 V, while the typical range is –2 V;
Electron temperature from Thomson Scattering was 1 order of magnitude colder than ordinary tokamak plasma;
Hard X-ray scintillators observed a significant amount of RE losses;
Poloidal internal pick-up coils detected inner structure that is moving outwards;
Vertical field for feedback of horizontal plasma position was increasing during the discharge, even though plasma current was constant;
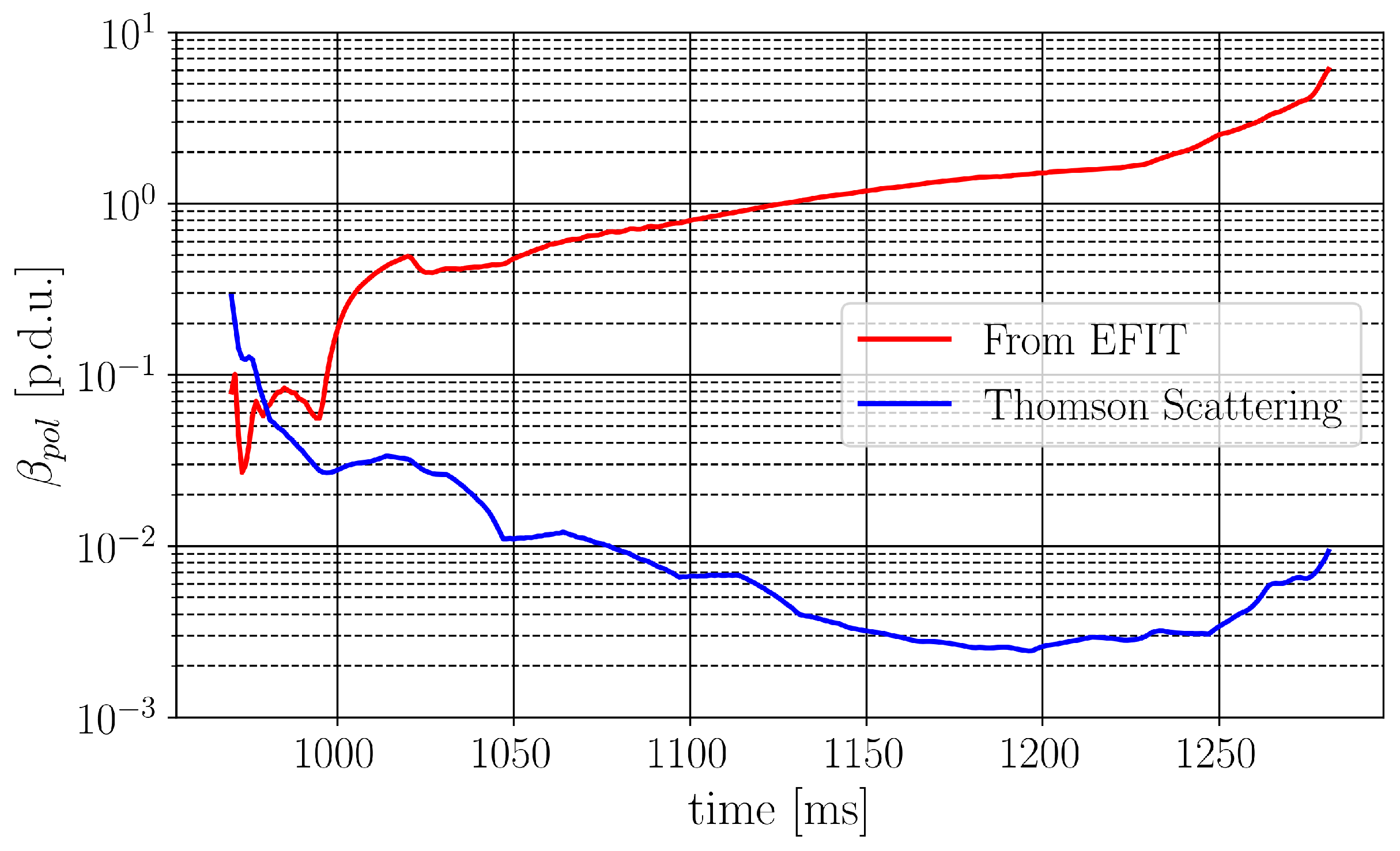
EFIT reconstruction of poloidal cross-section depicted plasma shrinkage towards inner side, due to the increasing magnetic pressure coming from the above-mentioned vertical field;
Plasma pressure in terms of its ratio to the poloidal magnetic field pressure (i.e., poloidal beta ), estimated from EFIT showed unrealistic large values.
All aforementioned information provides us with enough evidence to conclude that RE beam co-existed with the bulk plasma. For more detailed discussion on the measurements, the interested reader is referred to Section 5.1 in Ref. [
10].
4. Method: RE Current Calculation
The overestimate of the
is exploited here for the estimate of the RE current
. The analysis is based on work done by Fujita et al. [
3]. Even though the basic principle used here is the same as Fujita’s, the final approach to the calculation is different. While the original paper estimates all necessary parameters theoretically, we use direct measurements from the Thomson scattering and calculations from EFIT reconstruction. In this section, we only address our changes to the method. The main idea behind the Fujita’s model is an estimate of RE pressure
from the difference between total plasma pressure
(coming from EFIT
)
and pure bulk plasma pressure
(coming from the Thomson Scattering measured radial
profile)
where
r is the radial position along the minor radius
. Examples of
and
are presented in
Figure 1.
The is calculated as an average from obtained values corresponding to results when following conditions and are satisfied simultaneously, to reduce the propagation of error given by this approach. The first condition specifies the accuracy of Thomson Scattering measurements and thereby defines the minimal threshold necessary to distinguish between and and eliminates the error of Thomson Scattering measurements. The second condition is always valid in the case of non-negligible RE pressure and it is artificially taken as a conservative limit.
Furthermore,
is connected to the RE density
where
represents average in both spatial and momentum coordinates,
is relativistic Lorentz factor, and
and
denote the RE velocity in the parallel and perpendicular direction to the magnetic field
, respectively. By estimating the RE energy, one can estimate the RE density
, from which RE current
can be approximately derived using the following expression:
where
is the area of the RE beam cross-section and
is normalized relativistic velocity.
4.1. RE Energy Calculation
The model for maximum obtainable RE energy
is based on Ref. [
11], where radiation losses are subtracted from the acceleration. It is a 0D model, as there is no dimensional dependency, but only time evolution. Particularly, the lost power by synchrotron radiation
and bremsstrahlung radiation
are subtracted from the power gained by the RE thanks to the electric field
to obtain the time dependence of
. The power gain by the toroidal electric field
is simply calculated as
with
standing for the plasma major radius. The synchrotron power loss
where
and
are the classical electron radius and mass, respectively. The curvature radius
is calculated using Equation (9) from Ref. [
12]:
where
at the end of the denominator comes from the average taken over the gyro-motion angle, and where
and
is the drift velocity
with
being the fundamental gyro-frequency. Finally, the angle brackets are making the whole calculation dependent on the RE distribution function (REDF).
4.2. RE Distribution Functions
With mentioning REDF, we need to address its influence on the
calculation. The REDFs used by Fujita et al. and utilized here are monoenergetic
, uniform
, and linear
. The definitions of the first three distributions as functions of RE energy
w are as follows:
with
being the Dirac delta function. The coefficients come from setting the REDF maximum value to 0 at
and then normalizing the REDF to 1.
Furthermore, the exponential REDF
is introduced to present a distribution with a steep decrease that could be important if the avalanche mechanism were to dominate. Additionally, two more REDFs are considered here: skewed Gaussian
[
13]
with
and Maxwell–Jüttner
[
14]
distributions. The (negatively) skewed Gaussian represents a more realistic case of
, as it is not a delta-function. In other words, the negatively skewed Gaussian represents REDF where almost all RE tend towards
but they never reach it. The Maxwell–Jüttner distribution function
is selected as one of the most commonly relativistic distribution functions used in the literature. As all three latter functions have asymptotic behavior towards zero and/or
, normalization has to be different than for the former three. Their parameters are set in such a way that asymptotic edge is smaller than
, while
maximum is located just over
.
4.3. Pitch Angle
Equation (
3) indicates that the pressure separation through the velocities
and
implies knowing the pitch angle
. Fujita et al. omitted the
term and approximated the other one
by
. However, we consider the
influence to be consistent with the estimation of
reported in
Section 4.1, where
plays a role through the parameter
.
Table 1 shows the influence of different REDFs on essential parameters for
calculation. Firstly, it is important to state that averages presented in
Table 1 are done for energy span from 0 to
using the mean of the variable, i.e., neglecting the RE limit at lower energies. The error is negligible due to the high
reached in the COMPASS discharges. The average energy
is calculated for illustration, while
can be seen in Equation (
4).
From Equation (
4), one would expect that the exponential REDF has the smallest
for the same
, as it has the far smallest
. However, due to the term
in Equation (
3) used for the
estimation (by knowing
in Equation (
3)), the result is opposite. Namely, difference in
from
Table 1 of an order of magnitude creates much larger difference in estimated
between REDFs than
does in Equation (
4). Therefore, even though the exponential has by far the smallest
, it has the largest
.
Furthermore, even though two extreme values are taken for
to investigate maximum possible effect from the corresponding variations, the difference due to
is smaller than a few percent for every REDF. Furthermore, the aforementioned
is calculated for
rad, as it is zero at
rad. Here, a significant influence of the pitch angle on the
is observed. Henceforth,
is implemented in
that is relevant for
calculation. Another expected dependence that can be noted from
Table 1 is that the most similar REDF to the monoenergetic one is the skewed Gaussian
REDF, as their parameters are close to each other.
5. Result: COMPASS Discharge 7298
The pitch angle
is taken to be
rad as a mean value found in Ref. [
15]. The RE minor radius
for the RE area
calculation is assumed to be constant and equal to 5 cm. The METIS (with the effective ion charge
) data for the electric field and plasma pressure
from Thomson scattering are interpolated and extrapolated to the EFIT time scale. As EFIT measures before the first and after the last Thomson scattering measurement, the first and the last point of the extrapolated
are approximated to be 95% (arbitrarily taken) of the first and the last Thomson scattering measurement, respectively.
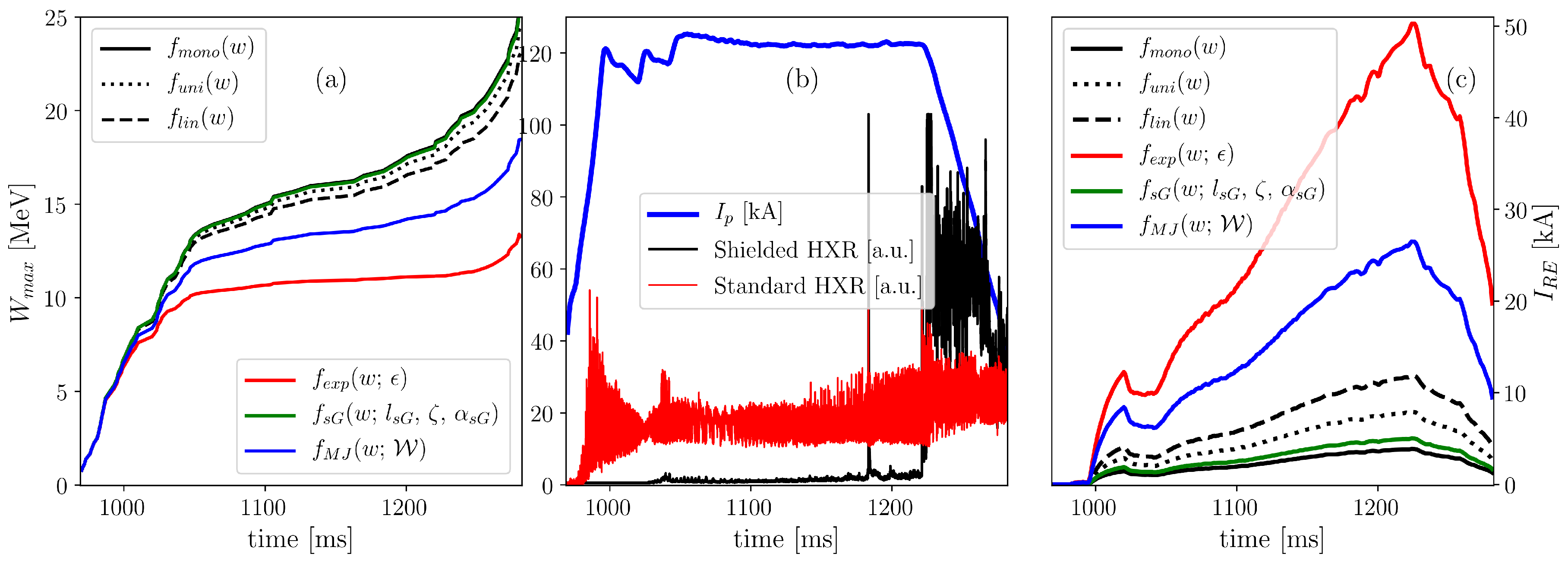
The main result is presented in
Figure 2. The estimate of the RE current
for different RE distribution functions are presented in
Figure 2c and their maximum values are listed in
Table 2. The plasma current
is plotted in
Figure 2b for comparison purposes. In the same figure, Shielded HXR and Standard HXR are also plotted.
The comparison between the
estimate coming from different RE distribution functions described in
Section 4.2 is shown in
Figure 2a and their maximum values are tabulated in
Table 2.
In
Figure 2a, one can see that only
from the exponential
and the Maxwell–Jüttner
distribution function are significantly different, as could be expected from the
values in
Table 1.
Even though
from EFIT increases significantly during the ramp-down phase of the discharge, a relatively strong decrease in RE current
can be seen in
Figure 2c. This is a consequence of the current drop in the total plasma pressure
calculation from EFIT in Equation (
1). It is interesting that the
drop coincides with the RE losses seen from Shielded HXR signal, even though RE losses are not implemented in the calculation. Henceforth, the
decrease can be seen as numerical artifact. However, physical interpretation could be an additional RE energy limit due to the RE beam drift, which is reported in
Section 7. Next, notice that
values span over two orders of magnitude—from a few kA to tens of kA.
Even though
is the most unrealistic of all the used RE distribution functions, it gives minimum
as
,
and
have extreme values. Therefore, we conclude that at least a few kA of current should definitely be driven by the REs in the COMPASS discharge #7298. However, it is not possible to determine which REDF gives the most accurate RE current
estimate from
Figure 2.
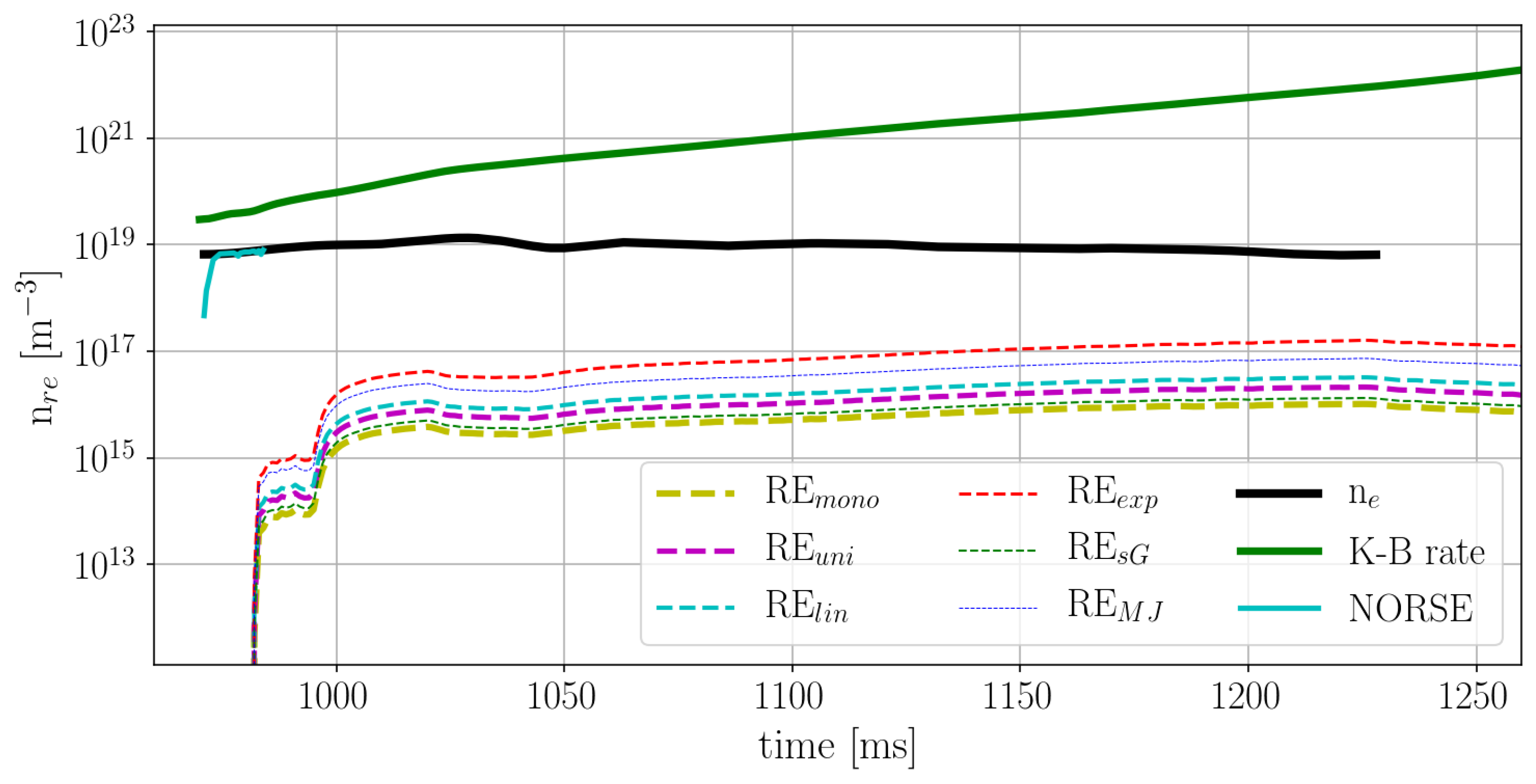
The above experimental results are compared here with the Kruskal–Bernstein theory [
16] and NORSE simulation [
17] in
Figure 3. Kruskal–Bernstein theory is the analytical solution for growth rate of the Dreicer mechanism of RE generation, whose last shape was derived by Connor and Hastie [
16]. The Kruskal–Bernstein equation is a strong function of the
. NORSE calculateS only Dreicer mechanism of RE generation and
,
and
are taken as time-varying parameters, while
and
are constant. Finally, the
is computed by multiplying the total electron density from measurements
with the RE fraction calculated by NORSE.
When applied to the COMPASS discharge #7298, the Kruskal–Bernstein theory predicts RE density larger by 1–3 orders of magnitude than the total . This is a non-physical result of course and we consider this theory not relevant for this particular case. Furthermore, NORSE reaches slide-away regime (i.e., when all electrons runaway) at the very beginning of the discharge. Such early slide-away regime is not supported by the experimental results.
The possible reasons for the overestimating results from Kruskal–Bernstein theory and NORSE simulation could result from overestimating the electric field by METIS or from too high sensitivity of the theories on the parameter. Moreover, RE energy calculation used here is also simplistic and EFIT results could be misleading in the presence of the RE.
6. Application: RE Influence on Ramp-Up
REs are frequently generated during the current ramp-up phase in the COMPASS tokamak. Here, the influence of the RE generation on the plasma current at the end of the ramp-up phase is investigated using the reported model for the RE current .
The density scan in the range 1– m was done during the second RE campaign. The scan consisted of 10 COMPASS discharges from #8552 to #8561. Plasma current was feedback controlled to 130 kA during the flat-top phase and the toroidal magnetic field was T for all discharges.
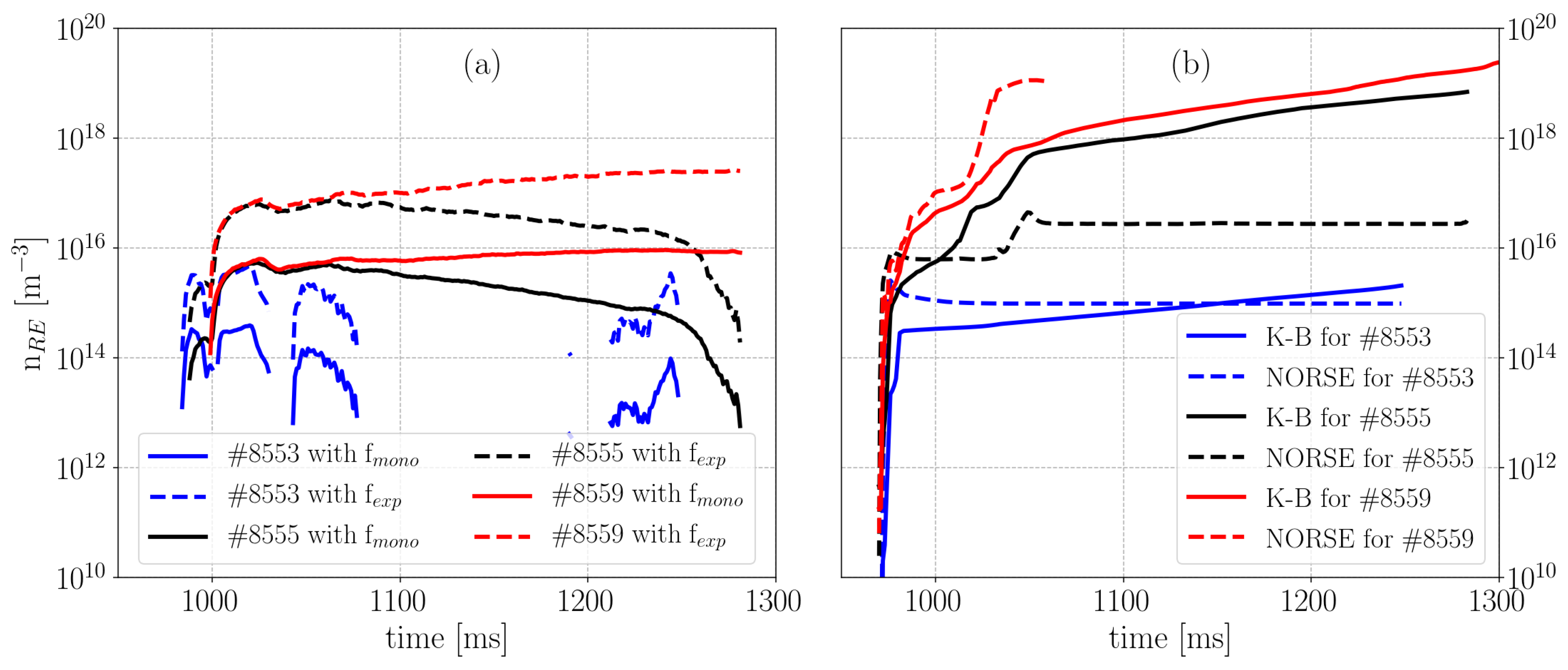
Figure 4a presents an estimate of
, which is more suitable for comparison of the method reported here with Kruskal–Bernstein and NORSE theories. The three discharges were chosen to cover the standard tokamak discharge (#8553), the slide-away regime (#8559) and the transient between the previous two (#8555). To avoid redundant lines,
was calculated only for the two most extreme REDF—the monoenergetic
and the exponential
ones.
The discharge #8553 has
lower by an order of magnitude during the ramp-up phase than the other two discharges (see
Figure 4). Surprisingly, discharges #8555 and #8559 have similar
at the beginning of the discharge. However,
drops for the former discharge as expected from the missing
rise from EFIT and density drop, as observed by the Thomson Scattering system. Finally, the corresponding RE current
at the end of the ramp-up phase for discharges #8553, #8555 and #8559 are
–
kA,
–
kA and
–
kA, respectively. Therefore, the expected trend is observed. Note that the non-continuous line for discharge #8553 comes from the defined thresholds of the method.
To complete the analyses, Kruskal–Bernstein theory and NORSE code were used to theoretically estimate
. The results are presented in
Figure 4b.
First to notice from
Figure 4 is that both theories have the expected trend in density of RE rising from #8553 to #8559. Differently from discharge #7298 in
Figure 3, the Kruskal–Bernstein theory does not give
over
, while
do rise towards
at the end of discharge for #8555 and #8559. For these two discharges, the Kruskal–Bernstein theory does not show a significant difference in
. On the other hand, NORSE estimates that those two discharges are quite different—according to this code #8559 reaches slide-away regime already around 1060 ms, which is probably too early.
Interestingly, in the case of standard discharge #8553, both codes seem to approximately agree in the order of magnitude with the experimental
(between
and
m
). The same is valid when the NORSE simulation is compared with experimental
using
for discharge #8555. However, the NORSE code is not made to predict the drop of
, clearly observed in
Figure 4a and from
from the EFIT reconstruction.
7. Application: RE Localisation
In this section, we investigate the RE energy limit from the RE outward drift through the analytically derived calculation reported by Zehrfeld [
18].
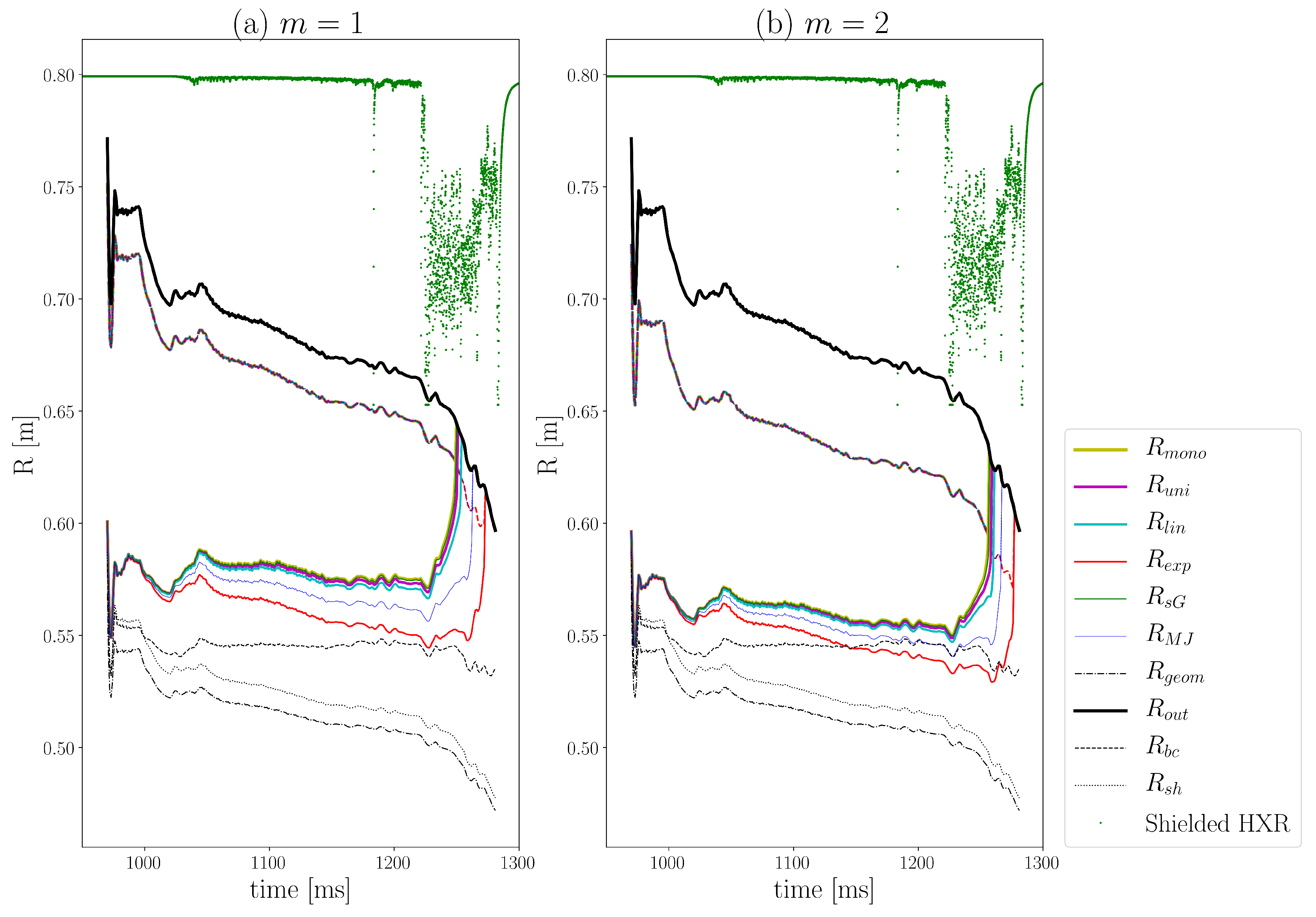
Zehrfeld’s analysis provides the
as a function of the normalized minor radius
. One of the main messages from this analysis is that
profile can have (depending on machine and plasma parameters) maximum value inside plasma (i.e.,
—dashed coinciding colored lines in
Figure 5), which indicates that REs of certain energy can loose confinement before they reach the plasma edge (i.e., the last closed flux surface) that is represented by
in
Figure 5. Namely, peaking parameter of the plasma current profile
m1 proved to be the most significant parameter for RE confinement in respect to the drift. Therefore, knowledge of the
profile can be used for localization of the RE beam. Knowing
at a given time of the discharge, one can find the minimum minor radius
(solid colored lines in
Figure 5) where
, corresponding to the minor radius below which REs with energy
cannot be confined.
Generally, the major radius of plasma geometrical center
and bulk plasma barycenter
do not coincide in the tokamak plasma due to the Shafranov shift [
19]. Additionally, there is RE beam present in the observed discharges shifting the plasma current barycenter
more outwards. All these radii
,
and
are taken from EFIT and shown in
Figure 5 for orientation purposes.
EFIT predicts while Zehrfeld’s method assumes m to be an integer. Accordingly, we used both rounding integers values: and .
One can notice from
Figure 5 that RE orbits are predicted in minor radius of 10–15 cm, which is not very limiting knowing that the COMPASS minor plasma radius is around 20 cm. RE orbits are localized more inside the plasma for higher
m, as could be expected due to the higher peaking of
profile. For the same reason, later significant losses of high energy RE are expected for higher
m, which can be seen by slightly delayed equalization of the RE radius with
(for 5–15 ms) for factor of current profile
than in the
case. However, both timings for significant high energy RE losses are a few tens of milliseconds after the Shielded HXR observes the losses, showing that these losses are probably due to the RE outward drift as
is decreasing and connection of strong Shielded HXR signal and
ramp-down phase is indeed observed in
Figure 2b. On the other hand, this does not explain the interaction on the high-field side seen by the visible cameras.
8. Conclusions
Understanding RE physics gives us better prediction towards understanding RE generation and mitigation in ITER. One basic RE parameter to compare model and experiment is the RE current. Therefore, we have presented here one method for estimating the RE current in the COMPASS tokamak.
The pitch angle showed to be relevant for the RE energy calculation, which plays an internal role in the RE current estimate method. Implementation of the method on the COMPASS discharge #7298 shows that at least a few kA of the total plasma current is driven by the RE. The method is then used for -scan and showed the different amount of RE current present in the plasma at the expected trend. Namely, discharges with lower density have higher RE current. Commonly used Kruskal–Bernstein theory does not appear suitable for high RE current discharges. NORSE, a code built for such discharges, showed to be more sensitive to plasma parameters, but further development is necessary for better prediction of the RE dynamics. Applying the knowledge of RE current to the RE drift energy limit, a crucial role of the limit at the final stage of the COMPASS plasma discharge, is reported.
At the first instance, an implementation of the RE current into the equilibrium simulation is left for future work on the COMPASS tokamak. Furthermore, theories used here are also the most commonly used model basis in the RE research community. However, they obviously overestimate the number of REs. Their further development is far beyond the scope of this article. The results obtained from theories are here to show the issue is oversimplified and demonstrate the need for a better modeling of the RE generation.
Author Contributions
Conceptualization, M.V.; methodology, M.V.; software, M.V., O.F., E.M. and COMPASS IT Team; validation, M.V.; formal analysis, M.V.; investigation, M.V., O.F. and J.M.; resources, J.M.; data curation, M.V. and J.M.; writing—original draft preparation, M.V.; writing—review and editing, M.V., O.F., J.M, and E.M; visualization, M.V. and O.F.; supervision, J.M.; project administration, J.M. and COMPASS department; and funding acquisition, J.M., EUROfusion and COMPASS department.
Funding
This research was funded by Ministry of Education, Youth and Sport of the Czech Republic (MEYS) grant number LM2011021 that supported COMPASS operation and by the Euratom research and training programme 2014-2018 under grant agreement No 633053 with the Co-fund by MEYS project number 8D15001.
Acknowledgments
Erasmum Mundus Joint Doctoral Collage in Fusion Science and Engineering (often abbreviated as “Fusion-DC”) is acknowledged for providing the necessary infrastructure to the first author for his studies. Moreover, we would like to thank to the whole COMPASS team of scientist, engineers and technicians for their fruitful collaboration.
Conflicts of Interest
The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results. In addition, the views and opinions expressed in this work do not necessarily reflect those of the European Commission.
Abbreviations
The following abbreviations are used in this manuscript:
| RE | Runaway Electron |
| REDF | Runaway Electron Distribution Function |
| HXR | Hard X-ray |
References
- Hender, T.; Wesley, J.; Bialek, J.; Bondeson, A.; Boozer, A.; Buttery, R.; Garofalo, A.; Goodman, T.; Granetz, R.; Gribov, Y.; et al. Chapter 3: MHD stability, operational limits and disruptions. Nucl. Fusion 2007, 47, S128. [Google Scholar] [CrossRef]
- Pánek, R.; Adámek, J.; Aftanas, M.; Bílková, P.; Böhm, P.; Cahyna, P.; Cavalier, J.; Dejarnac, R.; Dimitrova, M.; Grover, O.; et al. Status of the COMPASS tokamak and characterization of the first H-mode. Plasma Phys. Control. Fusion 2016, 58, 014015. [Google Scholar] [CrossRef]
- Fujita, T.; Fuke, Y.; Yoshida, Z.; Inoue, N.; Tanihara, T.; Mori, K.; Fukao, M.; Tomita, Y.; Mohri, A. High-Current Runaway Electron Beam in a Tokamak Plasma. J. Phys. Soc. Jpn. 1991, 60, 1237–1246. [Google Scholar] [CrossRef]
- Havlíček, J.; Hronová, O. Magnetic Diagnostics of COMPASS Tokamak. 2010. Available online: http://www.ipp.cas.cz/vedecka_struktura_ufp/tokamak/tokamak_compass/diagnostics/magneticka-diagnostika/index.html (accessed on 16 January 2019).
- Bilkova, P.; Aftanas, M.; Bohm, P.; Weinzettl, V.; Sestak, D.; Melich, R.; Stockel, J.; Scannell, R.; Walsh, M. Design of new Thomson scattering diagnostic system on COMPASS tokamak. Nucl. Instrum. Methods Phys. Res. Sect. A 2010, 623, 656–659. [Google Scholar] [CrossRef]
- Mlynar, J.; Ficker, O.; Vlainic, M.; Weinzettl, V.; Imrisek, M.; Paprok, R.; Rabinski, M.; Jakubowski, M.; the COMPASS Team. Effects of Plasma Control on Runaway Electrons in COMPASS Tokamak. In Proceedings of the 42nd EPS Conference on Plasma Physics, Lisbon, Portugal, 22–26 June 2015; Number P4.102 in ECA. Volume 39E. [Google Scholar]
- Ficker, O.; Mlynar, J.; Vlainic, M.; Macusova, E.; Vondracek, P.; Weinzettl, V.; Urban, J.; Cerovsky, J.; Cavalier, J.; Havlicek, J.; et al. Long slide-away discharges in the COMPASS tokamak. In Proceedings of the 58th Annual Meeting of the APS Division of Plasma Physics, San Jose, CA, USA, 31 October–4 November 2016; Volume 61. [Google Scholar]
- Artaud, J.; Imbeaux, F.; Garcia, J.; Giruzzi, G.; Aniel, T.; Basiuk, V.; BÃcoulet, A.; Bourdelle, C.; Buravand, Y.; Decker, J.; et al. Metis: a fast integrated tokamak modelling tool for scenario design. Nucl. Fusion 2018, 58, 105001. [Google Scholar] [CrossRef]
- Vlainić, M.; Mlynář, J.; Weinzettl, V.; Papřok, R.; Imrísek, M.; Ficker, O.; Vondráček, P.; Havlíček, J. First Dedicated Observations of Runaway Electrons in COMPASS Tokamak. Nukleonika 2015, 60, 249–255. [Google Scholar] [CrossRef][Green Version]
- Vlainic, M. Study of Runaway Electrons at COMPASS Tokamak. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2017. [Google Scholar]
- Yu, J.H.; Hollmann, E.M.; Commaux, N.; Eidietis, N.W.; Humphreys, D.A.; James, A.N.; Jernigan, T.C.; Moyer, R.A. Visible imaging and spectroscopy of disruption runaway electrons in DIII-D. Phys. Plasmas 2013, 20, 042113. [Google Scholar] [CrossRef]
- Pankratov, I.M. Analysis of the synchrotron radiation spectra of runaway electrons. Plasma Phys. Rep. 1999, 25, 145–148. [Google Scholar]
- Azzalini, A. The Skew-Normal and Related Families; Institute of Mathematical Statistics Monographs, Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Jüttner, F. Das Maxwellsche Gesetz der Geschwindigkeitsverteilung in der Relativtheorie. Ann. Phys. 1911, 339, 856–882. [Google Scholar] [CrossRef]
- Vlainic, M.; Vondracek, P.; Mlynar, J.; Weinzettl, V.; Ficker, O.; Varavin, M.; Paprok, R.; Imrisek, M.; Havlicek, J.; Panek, R.; et al. Synchrotron Radiation from Runaway Electrons in COMPASS Tokamak. In Proceedings of the 42nd EPS Conference on Plasma Physics, Lisbon, Portugal, 22–26 June 2015; Number P4.108 in ECA. Volume 39E. [Google Scholar]
- Connor, J.; Hastie, R. Relativistic limitations on runaway electrons. Nucl. Fusion 1975, 15, 415. [Google Scholar] [CrossRef]
- Stahl, A.; Landreman, M.; Embréus, O.; Fülöp, T. NORSE: A solver for the relativistic non-linear Fokker–Planck equation for electrons in a homogeneous plasma. Comput. Phys. Commun. 2017, 212, 269–279. [Google Scholar] [CrossRef]
- Zehrfeld, H.P.; Fussmann, G.; Green, B.J. Electric field effects on relativistic charged particle motion in Tokamaks. Plasma Phys. 1981, 23, 473. [Google Scholar] [CrossRef]
- Shafranov, V.D. Equilibrium of a toroidal pinch in a magnetic field. Soviet Atomic Energy 1962, 13, 1149–1158. [Google Scholar] [CrossRef]
| 1 | m is plasma current profile peaking factor, defined as: . |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).