Coherence-Length Effects in Fast Atom Diffraction at Grazing Incidence
Abstract
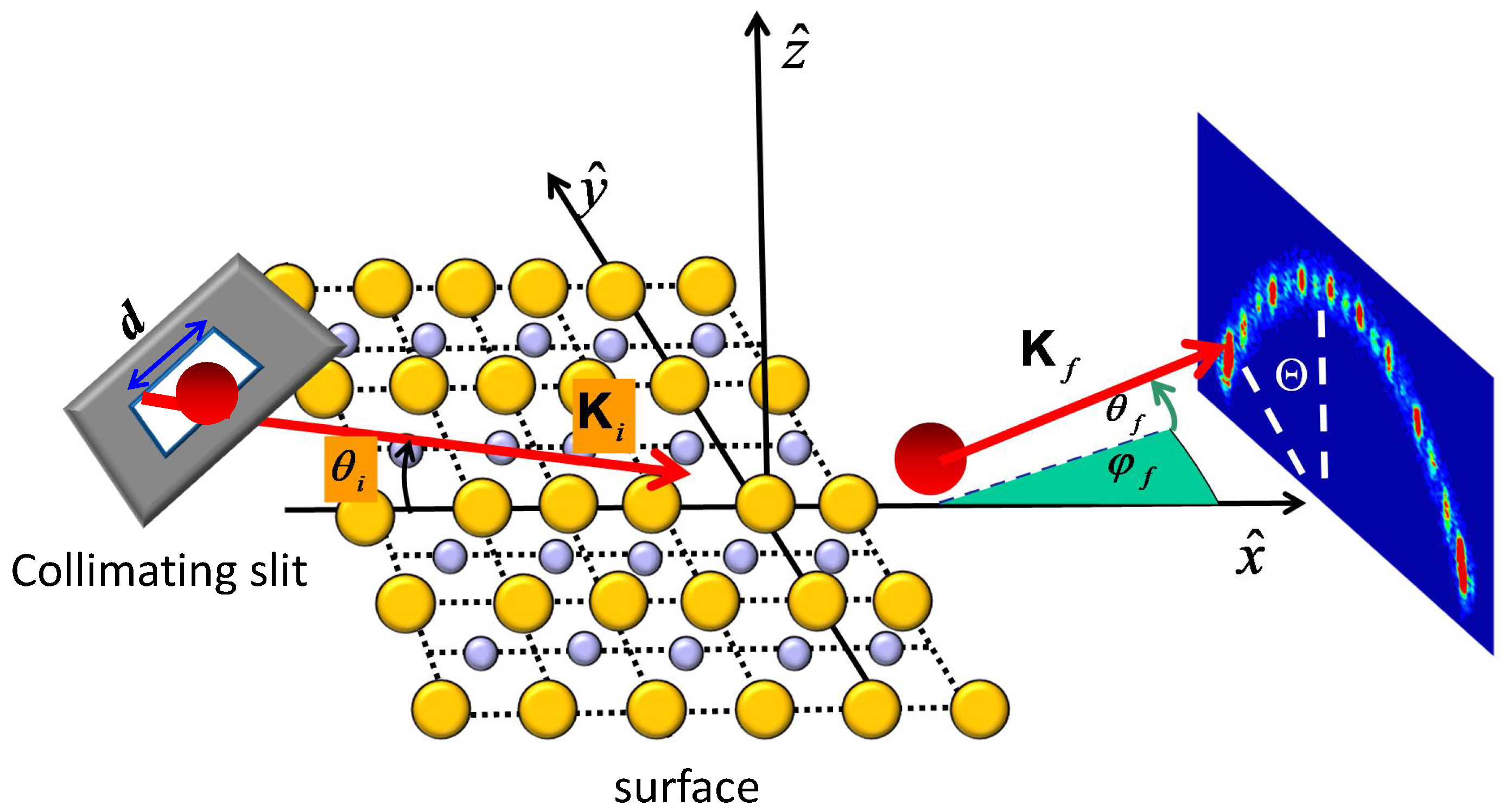
1. Introduction
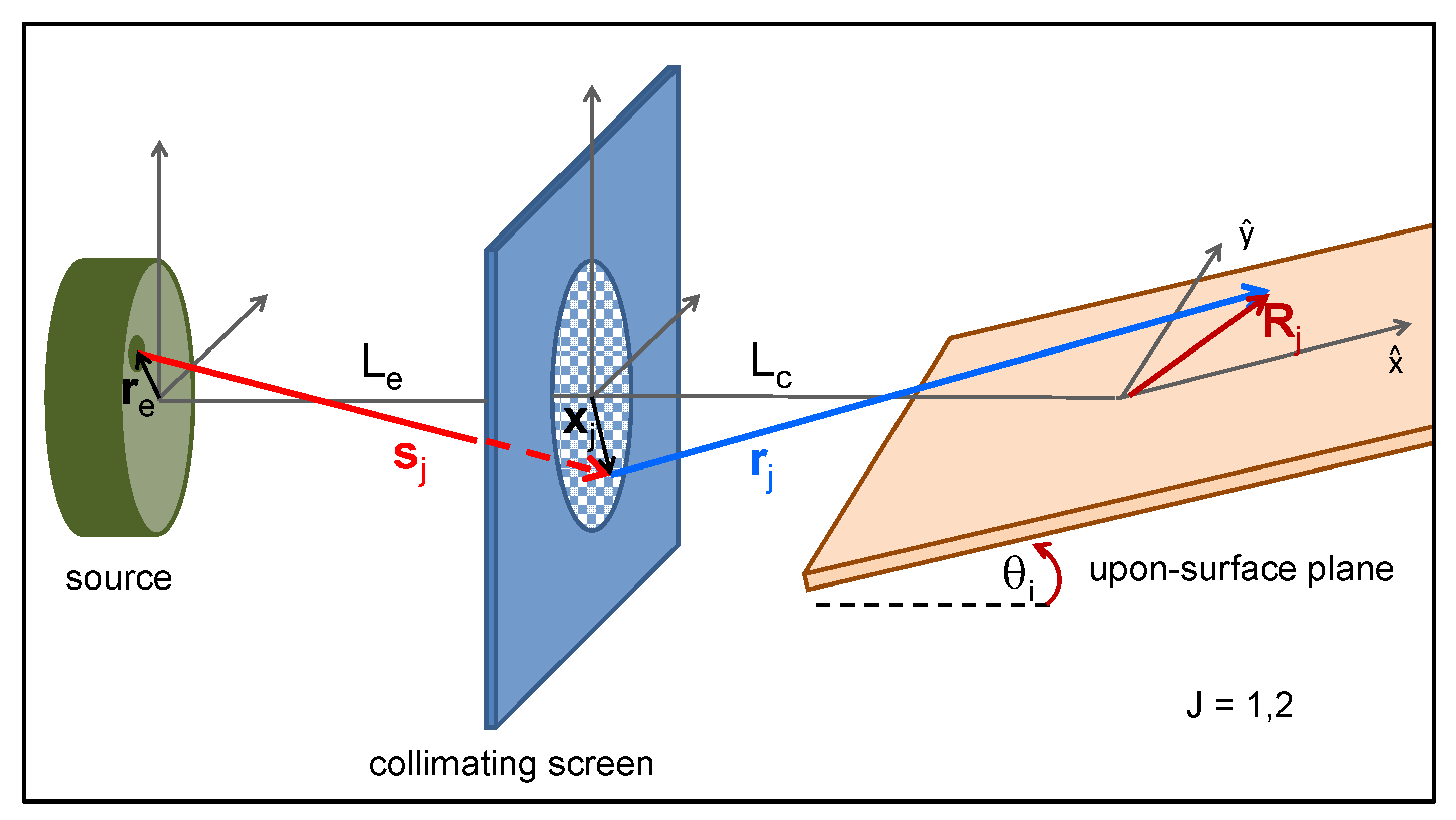
2. Theoretical Model
2.1. Profiles of the Initial Coherent Wave Packet
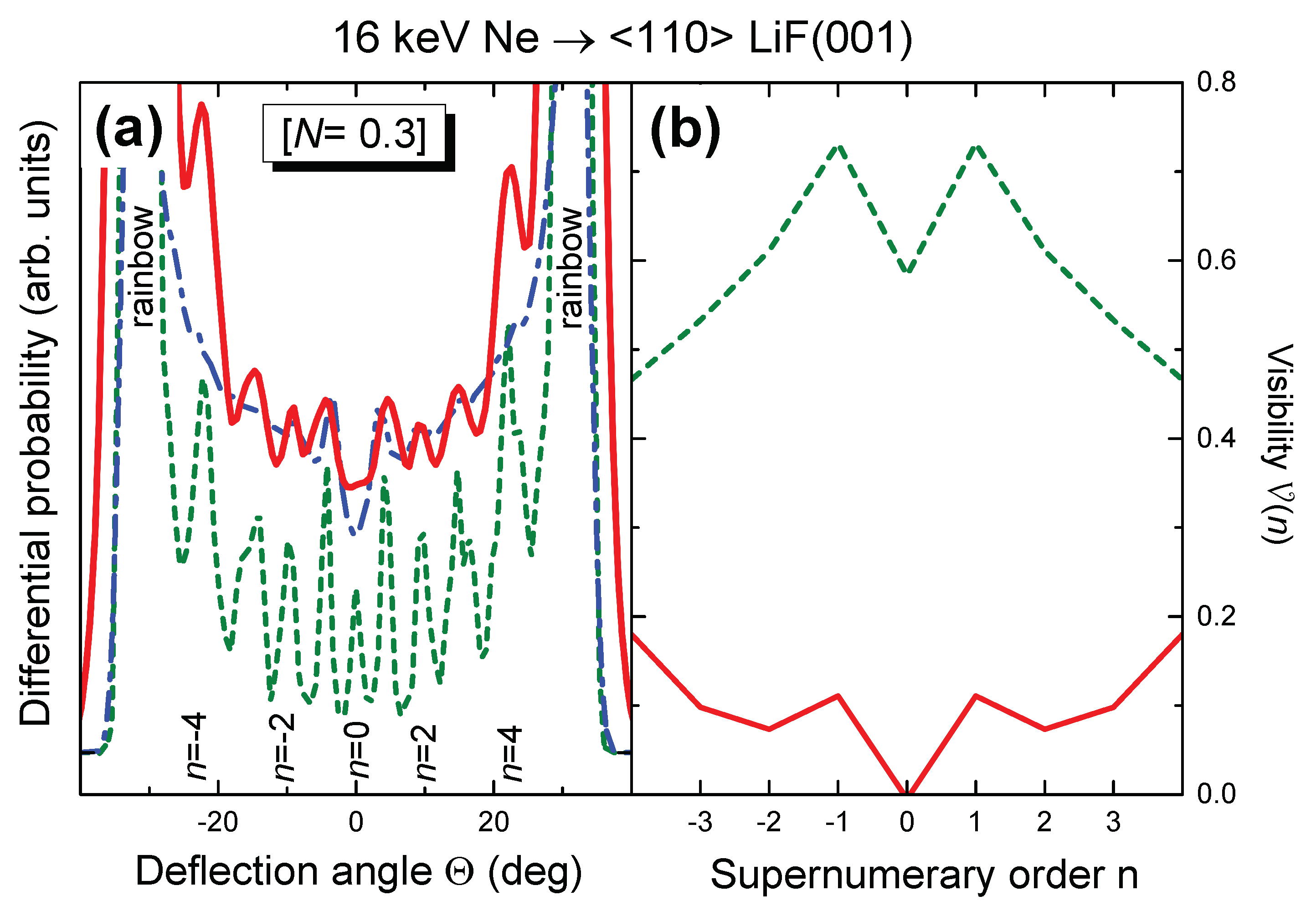
3. Effects due to the Degree of Coherence of the Beam
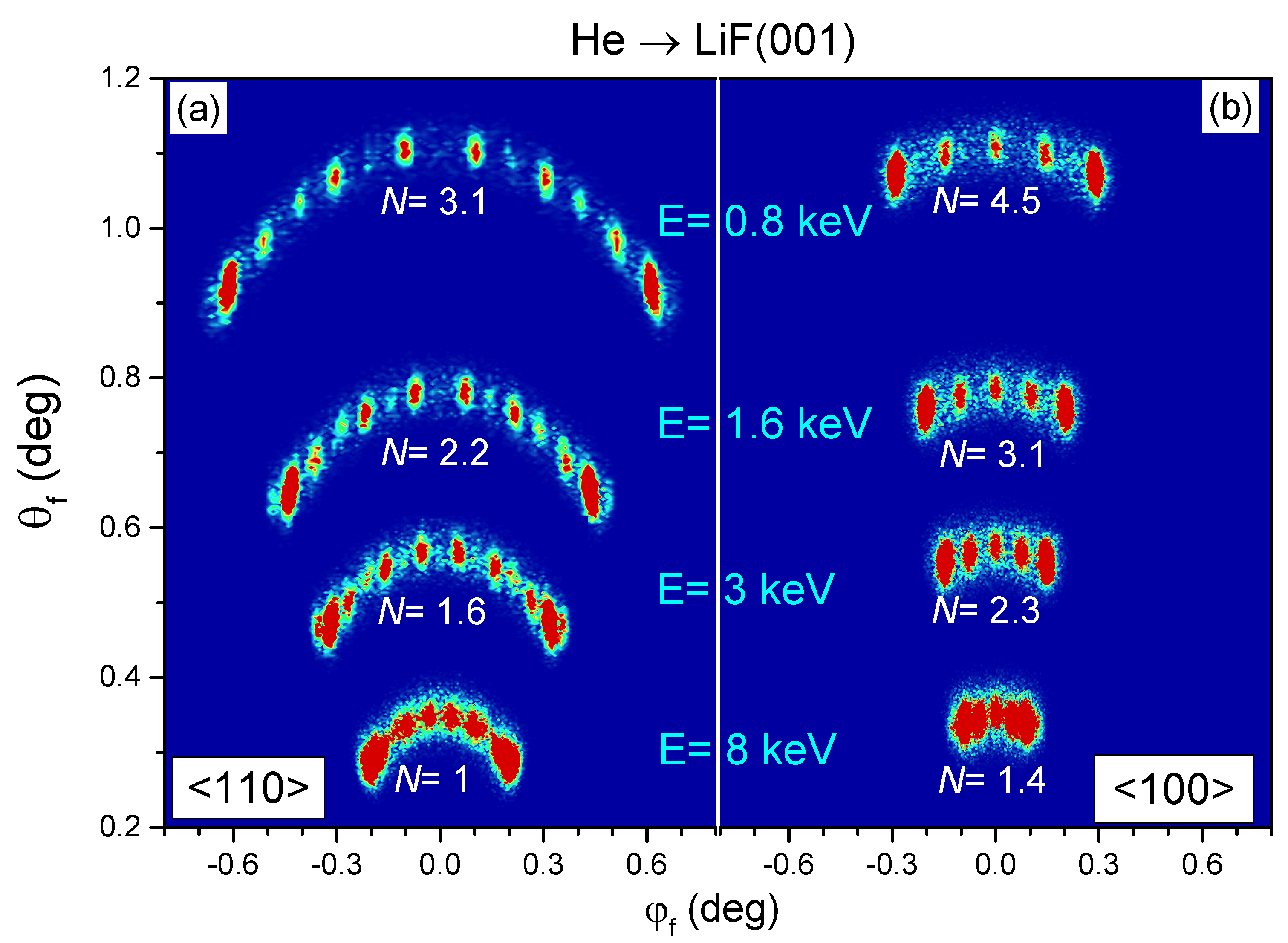
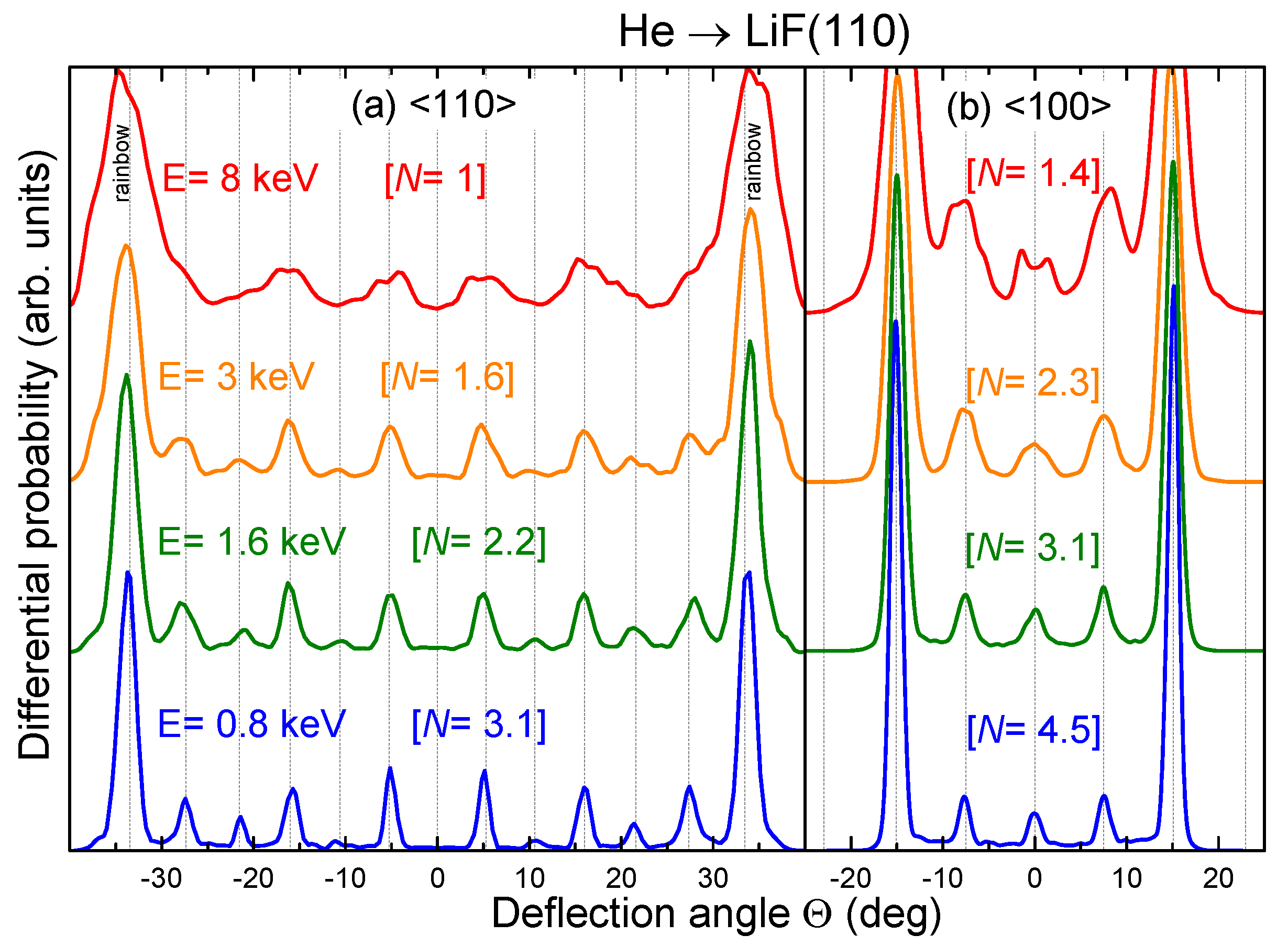
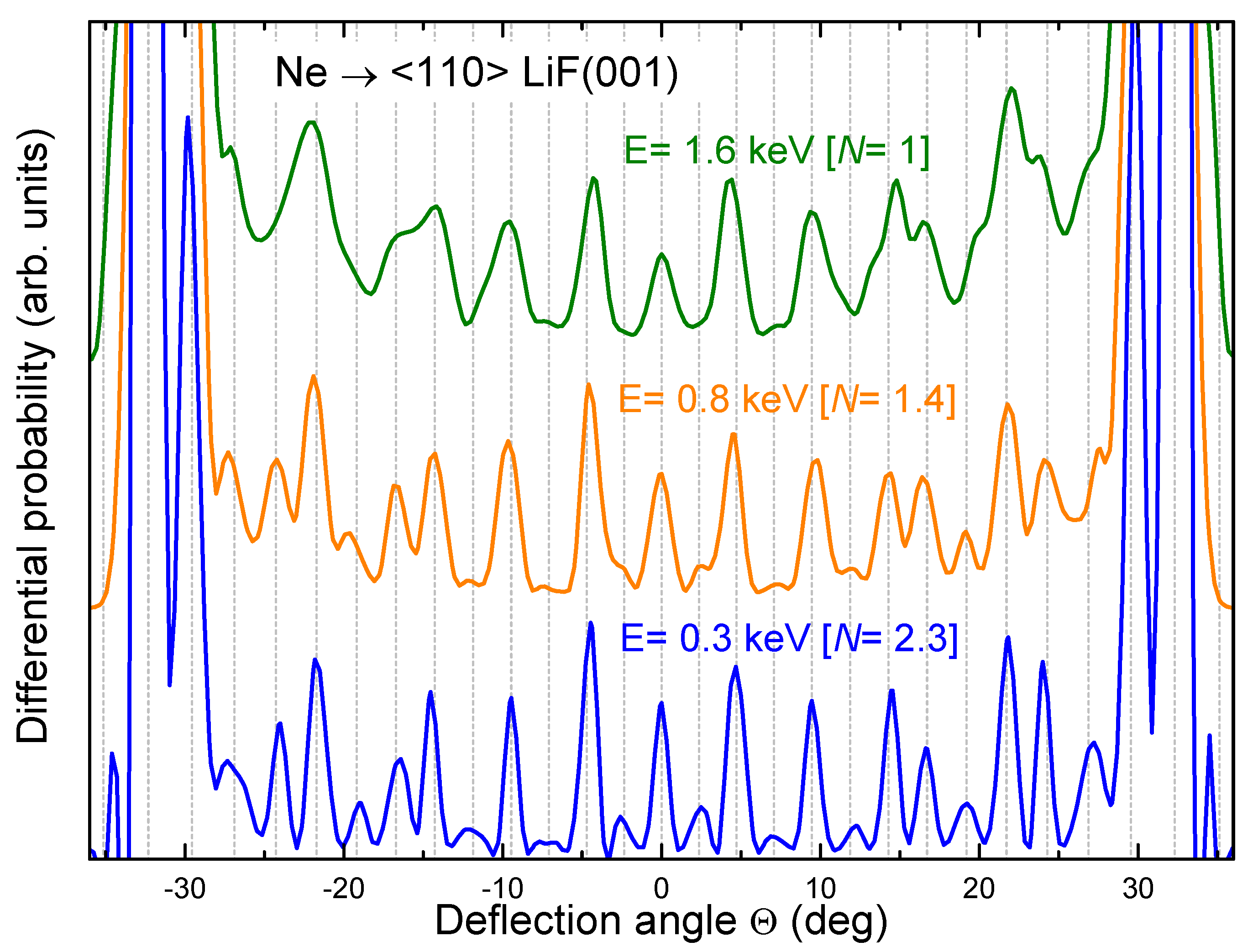
3.1. Influence of the Impact Energy
3.2. Influence of the Incidence Channel
3.3. Influence of the Projectile Mass
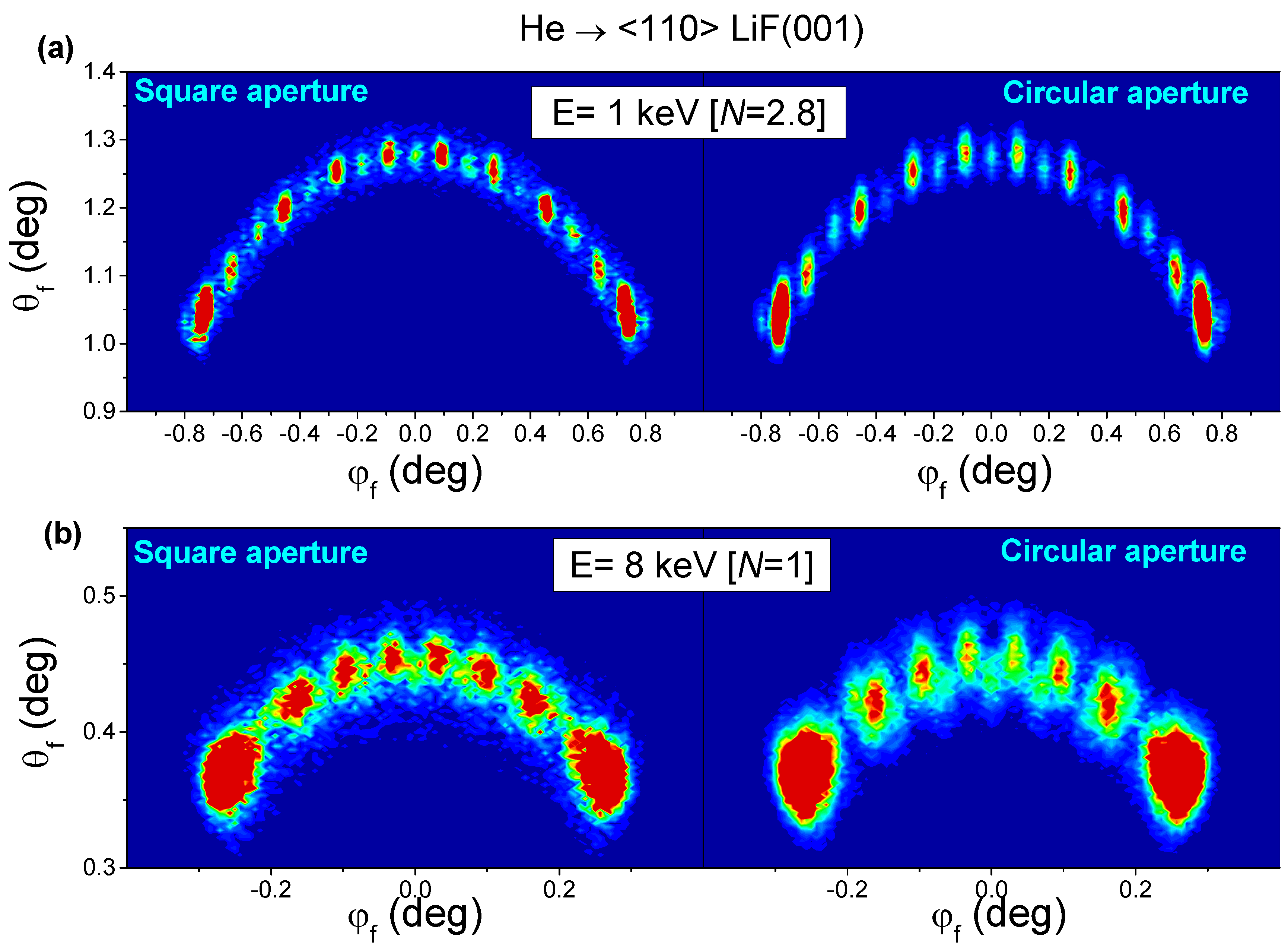
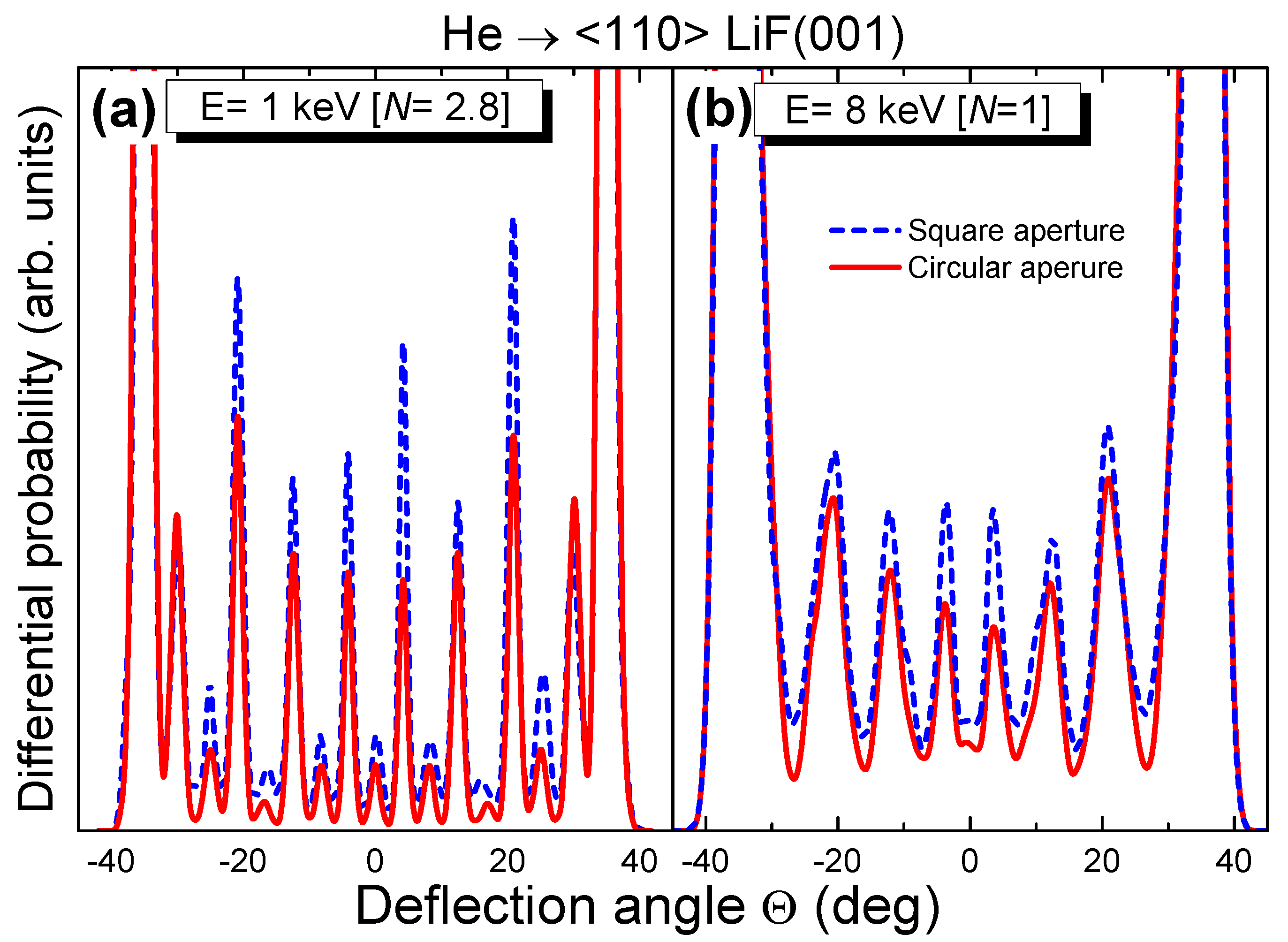
4. Dependence on the Shape of the Collimating Slit: Square versus Circular
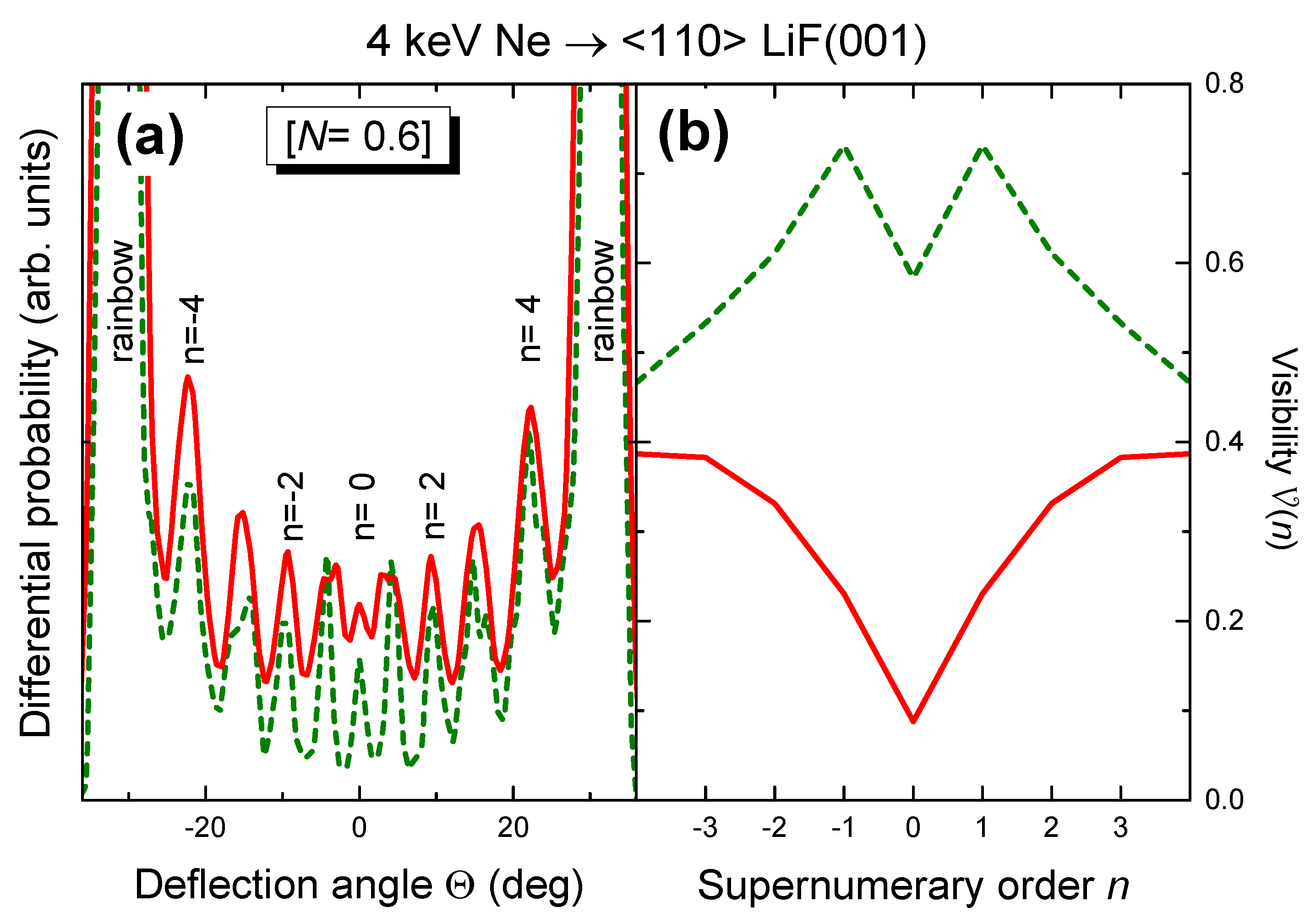
5. Contribution of the Spot-Beam Effect
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Complex Degree of Coherence for an Atomic Beam Passing through a Circular Collimating Aperture
References
- Moix, J.M.; Pollak, E. Heavy atom quantum diffraction by scattering from surfaces. J. Chem. Phys. 2011, 134, 011103. [Google Scholar] [CrossRef] [PubMed]
- Minniti, M.; Díaz, C.; Cuñado, J.L.F.; Politano, A.; Maccariello, D.; Martín, F.; Farías, D.; Miranda, R. Helium, neon and argon diffraction from Ru(0001). J. Phys. Condens. Matter 2012, 24, 354002. [Google Scholar] [CrossRef] [PubMed]
- Seifert, J.; Lienemann, J.; Schüller, A.; Winter, H. Studies on coherence and decoherence in Fast Atom Diffraction. Nucl. Instrum. Methods Phys. Res. B 2015, 350, 99–105. [Google Scholar] [CrossRef]
- Egodapitiya, K.N.; Sharma, S.; Hasan, A.; Laforge, A.C.; Madison, D.H.; Moshammer, R.; Schulz, M. Manipulating Atomic Fragmentation Processes by Controlling the Projectile Coherence. Phys. Rev. Lett. 2011, 106, 153202. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Schneider, K.; LaForge, A.; Kelkar, A.; Grieser, M.; Moshammer, R.; Ullrich, J.; Schulz, M.; Fischer, D. Projectile coherence effects in single ionization of helium. J. Phys. B 2012, 45, 211001. [Google Scholar] [CrossRef]
- Arthanayaka, T.; Lamichhane, B.R.; Hasan, A.; Gurung, S.; Remolina, J.; Borbély, S.; Járai-Szabó, F.; Nagy, L.; Schulz, M. Fully differential study of wave packet scattering in ionization of helium by proton impact. J. Phys. B 2016, 49, 13LT02. [Google Scholar] [CrossRef]
- Karlovets, D.V.; Kotkin, G.L.; Serbo, V.G. Scattering of wave packets on atoms in the Born approximation. Phys. Rev. A 2015, 92, 052703. [Google Scholar] [CrossRef]
- Gassert, H.; Chuluunbaatar, O.; Waitz, M.; Trinter, F.; Kim, H.K.; Bauer, T.; Laucke, A.; Müller, C.; Voigtsberger, J.; Weller, M.; et al. Agreement of Experiment and Theory on the Single Ionization of Helium by Fast Proton Impact. Phys. Rev. Lett. 2016, 116, 073201. [Google Scholar] [CrossRef] [PubMed]
- Sarkadi, L.; Fabre, I.; Navarrete, F.; Barrachina, R.O. Loss of wave-packet coherence in ion-atom collisions. Phys. Rev. A 2016, 93, 032702. [Google Scholar] [CrossRef]
- Navarrete, F.; Ciappina, M.; Sarkadi, L.; Barrachina, R. The role of the wave packet coherence on the ionization cross section of He by p+ and C6+ projectiles. Nucl. Instrum. Methods Phys. Res. B 2017, 408, 165–168. [Google Scholar] [CrossRef]
- Nagy, L.; Járai-Szabó, F.; Borbély, S. The effect of projectile wave packet width on the fully differential ionization cross-sections. J. Phys. B 2018, 51, 144005. [Google Scholar] [CrossRef]
- Schüller, A.; Wethekam, S.; Winter, H. Diffraction of Fast Atomic Projectiles during Grazing Scattering from a LiF(001) Surface. Phys. Rev. Lett. 2007, 98, 016103. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, P.; Khemliche, H.; Borisov, A.G.; Roncin, P. Quantum Scattering of Fast Atoms and Molecules on Surfaces. Phys. Rev. Lett. 2007, 98, 016104. [Google Scholar] [CrossRef] [PubMed]
- Lienemann, J.; Schüller, A.; Blauth, D.; Seifert, J.; Wethekam, S.; Busch, M.; Maass, K.; Winter, H. Coherence during Scattering of Fast H Atoms from a LiF(001) Surface. Phys. Rev. Lett. 2011, 106, 067602. [Google Scholar] [CrossRef] [PubMed]
- Busch, M.; Lienemann, J.; Seifert, J.; Schüller, A.; Winter, H. Decoherence in grazing scattering of fast H and He atoms from a LiF(001) surface. Vacuum 2012, 86, 1618–1623. [Google Scholar] [CrossRef]
- Gravielle, M.S.; Miraglia, J.E. Influence of beam collimation on fast-atom diffraction studied via a semiquantum approach. Phys. Rev. A 2015, 92, 062709. [Google Scholar] [CrossRef]
- Gravielle, M.S.; Miraglia, J.E. Single- and double-slit collimating effects on fast-atom diffraction spectra. Nucl. Instrum. Methods Phys. Res. B 2016, 382, 42–48. [Google Scholar] [CrossRef]
- Gravielle, M.S. Fast interaction of atoms with crystal surfaces: coherent lighting. J. Phys. Conf. Ser. 2017, 875, 012006. [Google Scholar] [CrossRef]
- Frisco, L.; Miraglia, J.E.; Gravielle, M.S. Spot-beam effect in grazing atom-surface collisions: From quantum to classical. J. Phys. Condens. Matter 2018, 30, 405001. [Google Scholar] [CrossRef] [PubMed]
- Schüller, A.; Wethekam, S.; Blauth, D.; Winter, H.; Aigner, F.; Simonović, N.; Solleder, B.; Burgdörfer, J.; Wirtz, L. Rumpling of LiF(001) surface from fast atom diffraction. Phys. Rev. A 2010, 82, 062902. [Google Scholar] [CrossRef]
- Atkinson, P.; Eddrief, M.; Etgens, V.; Khemliche, H.; Debiossac, M.; Momeni, A.; Mulier, M.; Lalmi, B.; Roncin, P. Dynamic grazing incidence fast atom diffraction during molecular beam epitaxial growth of GaAs. Appl. Phys. Lett. 2014, 105, 021602. [Google Scholar] [CrossRef]
- Rubiano, C.A.R.; Bocan, G.A.; Gravielle, M.S.; Bundaleski, N.; Khemliche, H.; Roncin, P. Ab initio potential for the He-Ag(110) interaction investigated using grazing-incidence fast-atom diffraction. Phys. Rev. A 2013, 87, 012903. [Google Scholar] [CrossRef]
- Seifert, J.; Winter, H. Quantitative structure determination using grazing scattering of fast atoms: Oxygen-induced missing-row reconstruction of Mo(112). Phys. Rev. B 2016, 93, 205417. [Google Scholar] [CrossRef]
- Debiossac, M.; Zugarramurdi, A.; Mu, Z.; Lunca-Popa, P.; Mayne, A.J.; Roncin, P. Helium diffraction on SiC grown graphene: Qualitative and quantitative descriptions with the hard-corrugated-wall model. Phys. Rev. B 2016, 94, 205403. [Google Scholar] [CrossRef]
- Seifert, J.; Busch, M.; Meyer, E.; Winter, H. Surface structure of alanine on Cu(110) via grazing scattering of fast atoms and molecules. Phys. Rev. B 2014, 89, 075404. [Google Scholar] [CrossRef]
- Momeni, A.; Casagrande, E.M.S.; Dechaux, A.; Khemliche, H. Ultrafast Crystallization Dynamics at an Organic-Inorganic Interface Revealed in Real Time by Grazing Incidence Fast Atom Diffraction. J. Phys. Chem. Lett. 2018, 9, 908–913. [Google Scholar] [CrossRef] [PubMed]
- Schüller, A.; Blauth, D.; Seifert, J.; Busch, M.; Winter, H.; Gärtner, K.; Włodarczyk, R.; Sauer, J.; Sierka, M. Fast atom diffraction during grazing scattering from a MgO(001) surface. Surf. Sci. 2012, 606, 161–173. [Google Scholar] [CrossRef]
- Schüller, A.; Busch, M.; Seifert, J.; Wethekam, S.; Winter, H.; Gärtner, K. Superstructures of oxygen and sulphur on a Fe(110) surface via fast atom diffraction. Phys. Rev. B 2009, 79, 235425. [Google Scholar] [CrossRef]
- Schüller, A.; Winter, H.; Gravielle, M.S.; Pruneda, J.M.; Miraglia, J.E. He-LiF surface interaction potential from fast atom diffraction. Phys. Rev. A 2009, 80, 062903. [Google Scholar] [CrossRef]
- Zugarramurdi, A.; Debiossac, M.; Lunca-Popa, P.; Mayne, A.J.; Momeni, A.; Borisov, A.G.; Mu, Z.; Roncin, P.; Khemliche, H. Determination of the geometric corrugation of graphene on SiC(0001) by grazing incidence fast atom diffraction. Appl. Phys. Lett. 2015, 106, 101902. [Google Scholar] [CrossRef]
- Debiossac, M.; Roncin, P. Image processing for grazing incidence fast atom diffraction. Nucl. Instrum. Methods Phys. Res. B 2016, 382, 36–41. [Google Scholar] [CrossRef]
- Gravielle, M.S.; Miraglia, J.E. Semiquantum approach for fast atom diffraction: Solving the rainbow divergence. Phys. Rev. A 2014, 90, 052718. [Google Scholar] [CrossRef]
- Winter, H.; Schüller, A. Fast atom diffraction during grazing scattering from surfaces. Prog. Surf. Sci. 2011, 86, 169–221. [Google Scholar] [CrossRef]
- Gravielle, M.S.; Schüller, A.; Winter, H.; Miraglia, J. Fast atom diffraction for grazing scattering of Ne atoms from a LiF(001) surface. Nucl. Instrum. Methods Phys. Res. B 2011, 269, 1208–1211. [Google Scholar] [CrossRef]
- Bocan, G.A.; Fuhr, J.D.; Gravielle, M.S. van der Waals effects on grazing-incidence fast-atom diffraction for H on LiF(001). Phys. Rev. A 2016, 94, 022711. [Google Scholar] [CrossRef]
- Miraglia, J.E.; Gravielle, M.S. Reexamination of the interaction of atoms with a LiF(001) surface. Phys. Rev. A 2017, 95, 022710. [Google Scholar] [CrossRef]
- Bocan, G.A.; Gravielle, M.S. GIFAD for He/KCl(001). Structure in the pattern for 〈110〉 incidence as a measure of the projectile-cation interaction. Nucl. Instrum. Methods Phys. Res. B 2018, 421, 1–6. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Pergamon Press: Oxford, UK, 1986; Chapter 10. [Google Scholar]
- Guantes, R.; Sanz, A.S.; Margalef-Roig, J.; Miret-Artés, S. Atom-surface diffraction: A trajectory description. Surf. Sci. Rep. 2004, 53, 199–330. [Google Scholar] [CrossRef]
- Schaff, J.F.; Langen, T.; Schmiedmayer, J. Interferometry with atoms. Riv. Nuovo Cimento 2014, 7, 509–589. [Google Scholar]
- Tonomura, A. Electron Holography. Prog. Opt. 1986, 23, 183–220. [Google Scholar]
- Cohen-Tannoudji, C.; Diu, B.; Laloë, F. Quantum Mechanics; Willey-VCH: Paris, France, 2011; Chapter I. [Google Scholar]
- Meyer, F.; Folkerts, L.; Schippers, S. Angular and charge state distributions of highly charged ions scattered during low energy surface-channeling interactions with Au(l10). Nucl. Instrum. Methods Phys. Res. B 1995, 100, 366–372. [Google Scholar] [CrossRef]
- Schüller, A.; Winter, H. Supernumerary Rainbows in the Angular Distribution of Scattered Projectiles for Grazing Collisions of Fast Atoms with a LiF(001) Surface. Phys. Rev. Lett. 2008, 100, 097602. [Google Scholar] [CrossRef] [PubMed]
- Farias, D.; Rieder, K.H. Atomic beam diffraction from solid surfaces. Rep. Prog. Phys. 1998, 61, 1575–1664. [Google Scholar] [CrossRef]
- Notice that the parameter n used to label the different supernumerary maxima does not coincide with the supernumerary rainbow order as defined in Ref. [33].
- Roncin, P.; Debiossac, M. Elastic and inelastic diffraction of fast atoms, Debye-Waller factor, and Mössbauer-Lamb-Dicke regime. Phys. Rev. B 2017, 96, 035415. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gravielle, M.S.; Miraglia, J.E.; Frisco, L. Coherence-Length Effects in Fast Atom Diffraction at Grazing Incidence. Atoms 2018, 6, 64. https://doi.org/10.3390/atoms6040064
Gravielle MS, Miraglia JE, Frisco L. Coherence-Length Effects in Fast Atom Diffraction at Grazing Incidence. Atoms. 2018; 6(4):64. https://doi.org/10.3390/atoms6040064
Chicago/Turabian StyleGravielle, María Silvia, Jorge Esteban Miraglia, and Leandro Frisco. 2018. "Coherence-Length Effects in Fast Atom Diffraction at Grazing Incidence" Atoms 6, no. 4: 64. https://doi.org/10.3390/atoms6040064
APA StyleGravielle, M. S., Miraglia, J. E., & Frisco, L. (2018). Coherence-Length Effects in Fast Atom Diffraction at Grazing Incidence. Atoms, 6(4), 64. https://doi.org/10.3390/atoms6040064




