Calculation of Francium Hyperfine Anomaly
Abstract
1. Introduction
2. Theory and Methods
3. Results and Discussion
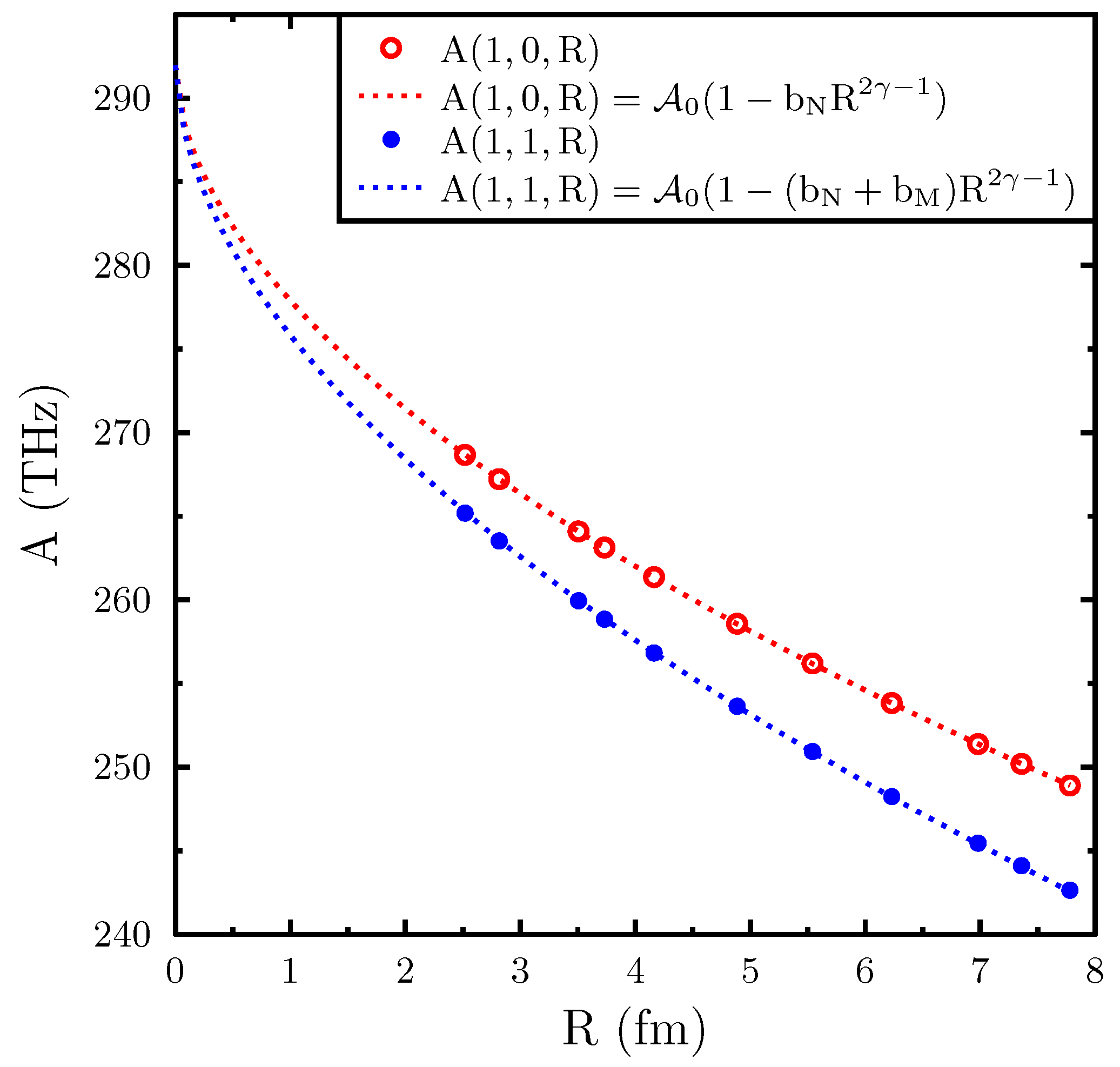
3.1. HFS Anomaly for H-Like Francium Ion
3.2. HFS Anomaly of Neutral Francium Atom
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andreyev, A.; Huyse, M.; Van Duppen, P.; Weissman, L.; Ackermann, D.; Gerl, J.; Hessberger, F.; Hofmann, S.; Kleinböhl, A.; Münzenberg, G.; et al. A triplet of differently shaped spin-zero states in the atomic nucleus 186Pb. Nature 2000, 405, 430–433. [Google Scholar] [CrossRef] [PubMed]
- Bohr, A.; Weisskopf, V.F. The influence of nuclear structure on the hyperfine structure of heavy elements. Phys. Rev. 1950, 77, 94–98. [Google Scholar] [CrossRef]
- Rosenthal, J.E.; Breit, G. The Isotope Shift in Hyperfine Structure. Phys. Rev. 1932, 41, 459–470. [Google Scholar] [CrossRef]
- Crawford, M.; Schawlow, A. Electron-nuclear potential fields from hyperfine structure. Phys. Rev. 1949, 76, 1310. [Google Scholar] [CrossRef]
- Persson, J.R. Table of hyperfine anomaly in atomic systems. At. Data Nucl. Data Tables 2013, 99, 62–68. [Google Scholar] [CrossRef]
- Persson, J.R. Hyperfine structure and hyperfine anomaly in Pb. J. Phys. Commun. 2018, 2, 055028. [Google Scholar] [CrossRef]
- Kozlov, M.; Porsev, S.; Safronova, M.; Tupitsyn, I. CI-MBPT: A package of programs for relativistic atomic calculations based on a method combining configuration interaction and many-body perturbation theory. Comput. Phys. Commun. 2015, 195, 199–213. [Google Scholar] [CrossRef]
- Bratsev, V.F.; Deyneka, G.B.; Tupitsyn, I.I. Application of Hartree-Fock method to calculation of relativistic atomic wave functions. Bull. Acad. Sci. USSR, Phys. Ser. 1977, 41, 173. [Google Scholar]
- Dzuba, V.A.; Flambaum, V.V.; Kozlov, M.G.; Porsev, S.G. Using effective operators in calculating the hyperfine structure of atoms. Sov. Phys. JETP 1998, 87, 885–890. [Google Scholar] [CrossRef]
- Kozlov, M.G.; Porsev, S.G.; Johnson, W.R. Parity non-conservation in Thallium. Phys. Rev. A 2001, 64, 052107. [Google Scholar] [CrossRef]
- Konovalova, E.; Kozlov, M.; Demidov, Y.; Barzakh, A. Calculation of thallium hyperfine anomaly. Rad. Appl. 2017, 2, 181–185. [Google Scholar] [CrossRef]
- Porsev, S.G.; Kozlov, M.G.; Safronova, M.S.; Tupitsyn, I.I. Development of the configuration-interaction + all-order method and application to the parity-nonconserving amplitude and other properties of Pb. Phys. Rev. A 2016, 93, 012501. [Google Scholar] [CrossRef]
- Zhang, J.; Tandecki, M.; Collister, R.; Aubin, S.; Behr, J.; Gomez, E.; Gwinner, G.; Orozco, L.; Pearson, M.; Sprouse, G.; et al. Hyperfine anomalies in Fr: Boundaries of the spherical single particle model. Phys. Rev. Lett. 2015, 115, 042501. [Google Scholar] [CrossRef] [PubMed]
- Grossman, J.; Orozco, L.; Pearson, M.; Simsarian, J.; Sprouse, G.; Zhao, W. Hyperfine anomaly measurements in francium isotopes and the radial distribution of neutrons. Phys. Rev. Lett. 1999, 83, 935. [Google Scholar] [CrossRef]
- Budinčević, I.; Billowes, J.; Bissell, M.; Cocolios, T.E.; De Groote, R.; De Schepper, S.; Fedosseev, V.N.; Flanagan, K.T.; Franchoo, S.; Ruiz, R.G.; et al. Laser spectroscopy of francium isotopes at the borders of the region of reflection asymmetry. Phys. Rev. C 2014, 90, 014317. [Google Scholar] [CrossRef]
- De Groote, R.; Budinčević, I.; Billowes, J.; Bissell, M.; Cocolios, T.E.; Farooq-Smith, G.J.; Fedosseev, V.; Flanagan, K.; Franchoo, S.; Ruiz, R.G.; et al. Use of a continuous wave laser and pockels cell for sensitive high-resolution collinear resonance ionization spectroscopy. Phys. Rev. Lett. 2015, 115, 132501. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, K.; Lynch, K.; Billowes, J.; Bissell, M.; Budinčević, I.; Cocolios, T.E.; De Groote, R.; De Schepper, S.; Fedosseev, V.; Franchoo, S.; et al. Collinear resonance ionization spectroscopy of neutron-deficient francium isotopes. Phys. Rev. Lett. 2013, 111, 212501. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.T.; Corwin, K.; Vogel, K.; Wieman, C.; Dinneen, T.; Maddi, J.; Gould, H. Efficient Collection of 221Fr into a Vapor Cell Magneto-optical Trap. Phys. Rev. Lett. 1997, 79, 994. [Google Scholar] [CrossRef]
- Gomez, E.; Aubin, S.; Orozco, L.; Sprouse, G.; Iskrenova-Tchoukova, E.; Safronova, M. Nuclear Magnetic Moment of 210Fr: A Combined Theoretical and Experimental Approach. Phys. Rev. Lett. 2008, 100, 172502. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, B.; Nandy, D.; Das, B.; Sakemi, Y. Correlation trends in the hyperfine structures of 210,212Fr. Phys. Rev. A 2015, 91, 042507. [Google Scholar] [CrossRef]
- Mårtensson-Pendrill, A.M. Isotopes through the looking glass. Hyperfine Interact. 2000, 127, 41–48. [Google Scholar] [CrossRef]
- Dzuba, V.; Flambaum, V.; Sushkov, O. Relativistic many-body calculations of the hyperfine-structure intervals in caesium and francium atoms. J. Phys. B 1984, 17, 1953. [Google Scholar] [CrossRef]
- Dzuba, V.; Johnson, W.; Safronova, M. Calculation of isotope shifts for cesium and francium. Phys. Rev. A 2005, 72, 022503. [Google Scholar] [CrossRef]
- Kalita, M.; Behr, J.; Gorelov, A.; Pearson, M.; Dehart, A.; Gwinner, G.; Kossin, M.; Aubin, S.; Gomez, E.; Orozco, L.A.; et al. Isotope shifts in the 7S → 8S transition of francium: Measurements and comparison to ab-initio theory. In Proceedings of the APS Division of Atomic, Molecular and Optical Physics Meeting Abstracts, Sacramento, CA, USA, 5–9 June 2017. [Google Scholar]
- Stroke, H.; Blin-Stoyle, R.J.; Jaccarino, V. Configuration mixing and the effects of distributed nuclear magnetization on hyperfine structure in odd-A nuclei. Phys. Rev. 1961, 123, 1326. [Google Scholar] [CrossRef]
- Shabaev, V.M. Hyperfine structure of hydrogen-like ions. J. Phys. B 1994, 27, 5825–5832. [Google Scholar] [CrossRef]
- Andrae, D. Finite nuclear charge density distributions in electronic structure calculations for atoms and molecules. Phys. Rep. 2000, 336, 413–525. [Google Scholar] [CrossRef]
- Büttgenbach, S. Magnetic hyperfine anomalies. Hyperfine Interact. 1984, 20, 1–64. [Google Scholar] [CrossRef]
- Mårtesson-Pendrill, A.M. Magnetic moment distributions in Tl nuclei. Phys. Rev. Lett. 1995, 74, 2184–2187. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Buchinger, F.; Cheal, B.; Crawford, J.; Dilling, J.; Kortelainen, M.; Kwiatkowski, A.; Leary, A.; Levy, C.; Mooshammer, F.; et al. Nuclear moments and charge radii of neutron-deficient francium isotopes and isomers. Phys. Rev. C 2015, 91, 044307. [Google Scholar] [CrossRef]
- Galván, A.P.; Zhao, Y.; Orozco, L.; Gómez, E.; Lange, A.; Baumer, F.; Sprouse, G. Comparison of hyperfine anomalies in the 5S1/2 and 6S1/2 levels of 85Rb and 87Rb. Phys. Lett. B 2007, 655, 114–118. [Google Scholar] [CrossRef]
- Coc, A.; Thibault, C.; Touchard, F.; Duong, H.; Juncar, P.; Liberman, S.; Pinard, J.; Lermé, J.; Vialle, J.; Büttgenbach, S.; et al. Hyperfine structures and isotope shifts of 207–213,220–228Fr; Possible evidence of octupolar deformation. Phys. Lett. B 1985, 163, 66–70. [Google Scholar] [CrossRef]
- Moskowitz, P.; Lombardi, M. Distribution of nuclear magnetization in mercury isotopes. Phys. Lett. B 1973, 46, 334–336. [Google Scholar] [CrossRef]

| (THz) | fit. | 292.0 | 49.5 | 15.2 |
| Reference [26] | 291.5 | 49.5 | 15.1 | |
| fit. | 4.817 | 5.161 | 1.650 | |
| , % | fit. | 14.11 | 15.12 | 4.83 |
| fit. | 0.710 | 0.761 | 0.257 | |
| , % | fit. | 2.08 | 2.23 | 0.75 |
| DHF | 7894.710 | 5.3030 | 0.7646 |
| DHF + Br | 7882.694 | 5.2989 | 0.7642 |
| DHF + MBPT | 10,602.174 | 4.7502 | 0.8584 |
| DHF + MBPT+Br | 10,581.950 | 4.7013 | 0.8506 |
| DHF + RPA | 8684.144 | 5.1092 | 0.8008 |
| DHF + Br + RPA | 8682.028 | 5.1020 | 0.8007 |
| DHF + MBPT + RPA | 11,518.484 | 4.6067 | 0.8844 |
| DHF + MBPT + Br + RPA | 11,507.415 | 4.5516 | 0.8738 |
| DHF | 746.580 | 1.8241 | 0.2842 |
| DHF + Br | 740.251 | 1.8204 | 0.2837 |
| DHF + MBPT | 1130.031 | 1.5661 | 0.3223 |
| DHF + MBPT+Br | 1120.865 | 1.5461 | 0.3160 |
| DHF + RPA | 865.034 | 1.6205 | 0.2606 |
| DHF + Br + RPA | 861.718 | 1.6223 | 0.2627 |
| DHF + MBPT + RPA | 1308.388 | 1.4018 | 0.2929 |
| DHF + MBPT + Br + RPA | 1300.950 | 1.3879 | 0.2891 |
| DHF | 55.524 | 0.0000 | 0.0000 |
| DHF + Br | 55.153 | 0.0000 | 0.0000 |
| DHF + MBPT | 77.870 | 0.0000 | 0.0000 |
| DHF + MBPT + Br | 77.437 | 0.0000 | 0.0000 |
| DHF + RPA | 94.984 | 1.2620 | 0.2769 |
| DHF + Br + RPA | 94.721 | 1.2545 | 0.2742 |
| DHF + MBPT + RPA | 132.482 | 1.2535 | 0.2919 |
| DHF + MBPT + Br + RPA | 131.988 | 1.2382 | 0.2843 |
| Method | (MHz) | (MHz) | (MHz) |
|---|---|---|---|
| DHF | 6668.56 | 706.70 | 55.52 |
| DHF + Br | 6659.37 | 700.78 | 55.15 |
| DHF + MBPT | 9127.20 | 1078.20 | 77.87 |
| DHF + MBPT + Br | 9124.92 | 1070.11 | 77.44 |
| DHF + RPA | 7491.91 | 837.58 | 95.43 |
| DHF + Br + RPA | 7496.66 | 833.22 | 94.73 |
| DHF + MBPT + RPA | 9964.42 | 1254.67 | 127.62 |
| DHF + MBPT + Br + RPA | 9973.44 | 1248.07 | 127.20 |
| FINAL (BR and BW) | 9849.57 | 1242.94 | 126.69 |
| Theory * [19] | 9927 | – | – |
| Theory [20] | 9885.24 | 1279.56 | 104.28 |
| Experiment [14,30,32] | 9856 (113) | 1296 (15) | 106.8 (13) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalova, E.A.; Demidov, Y.A.; Kozlov, M.G.; Barzakh, A.E. Calculation of Francium Hyperfine Anomaly. Atoms 2018, 6, 39. https://doi.org/10.3390/atoms6030039
Konovalova EA, Demidov YA, Kozlov MG, Barzakh AE. Calculation of Francium Hyperfine Anomaly. Atoms. 2018; 6(3):39. https://doi.org/10.3390/atoms6030039
Chicago/Turabian StyleKonovalova, Elena A., Yuriy A. Demidov, Mikhail G. Kozlov, and Anatoly E. Barzakh. 2018. "Calculation of Francium Hyperfine Anomaly" Atoms 6, no. 3: 39. https://doi.org/10.3390/atoms6030039
APA StyleKonovalova, E. A., Demidov, Y. A., Kozlov, M. G., & Barzakh, A. E. (2018). Calculation of Francium Hyperfine Anomaly. Atoms, 6(3), 39. https://doi.org/10.3390/atoms6030039






