Intercombination Transitions in the n = 4 Shell of Zn-, Ga-, and Ge-Like Ions of Elements Kr through Xe
Abstract
1. Introduction
2. Available Data
3. Discussion of Wavelength Data on Cu- through Ge-Like Ions
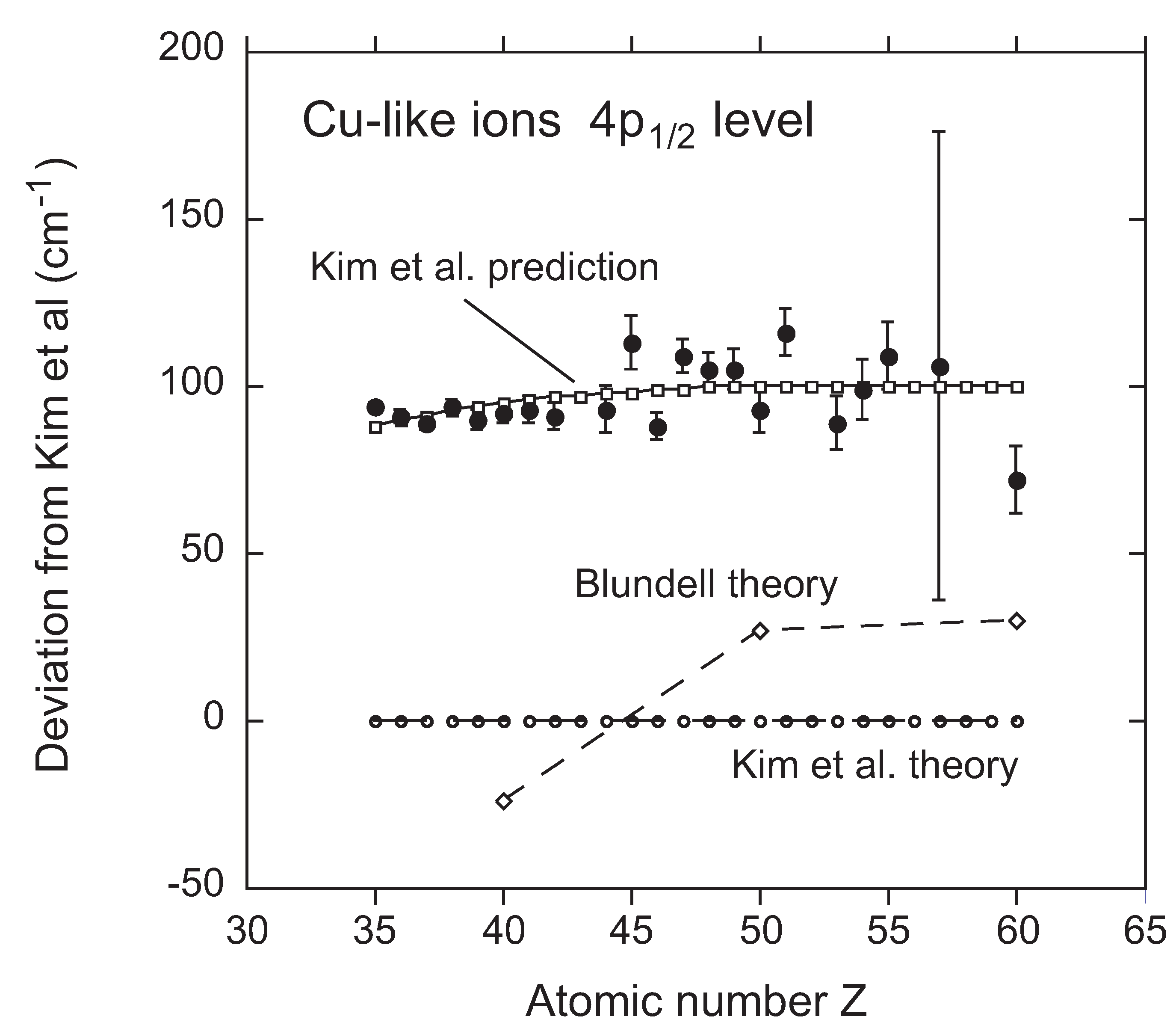
3.1. Cu-Like Ions
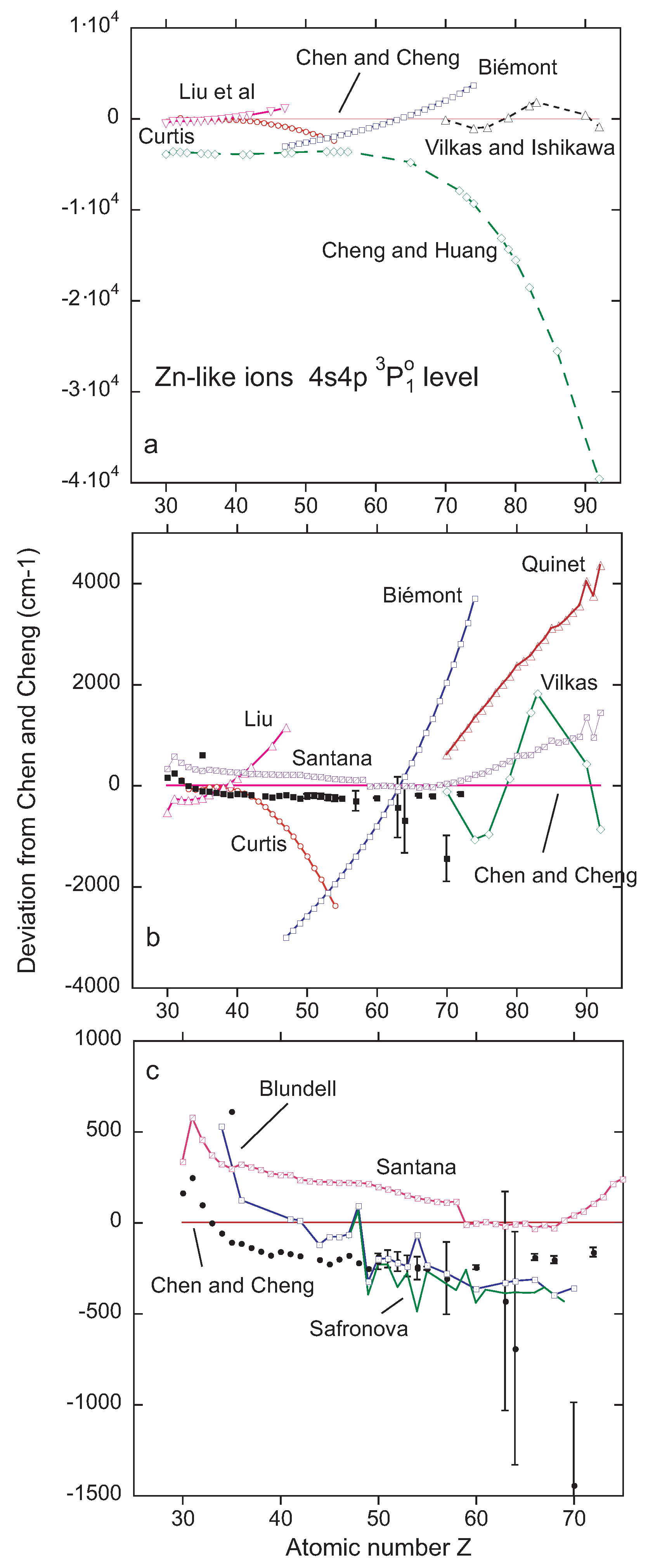
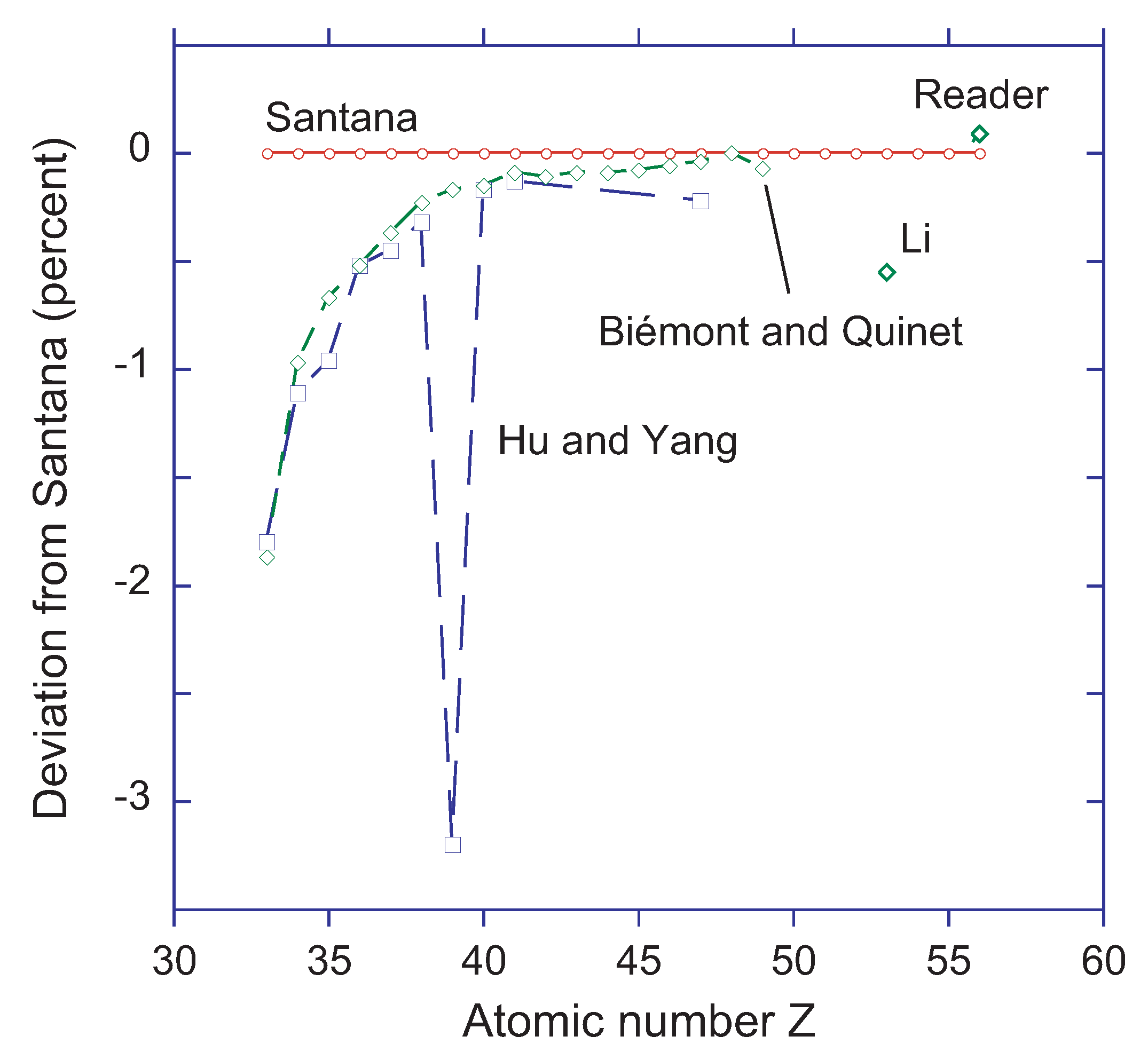
3.2. Zn-Like Ions
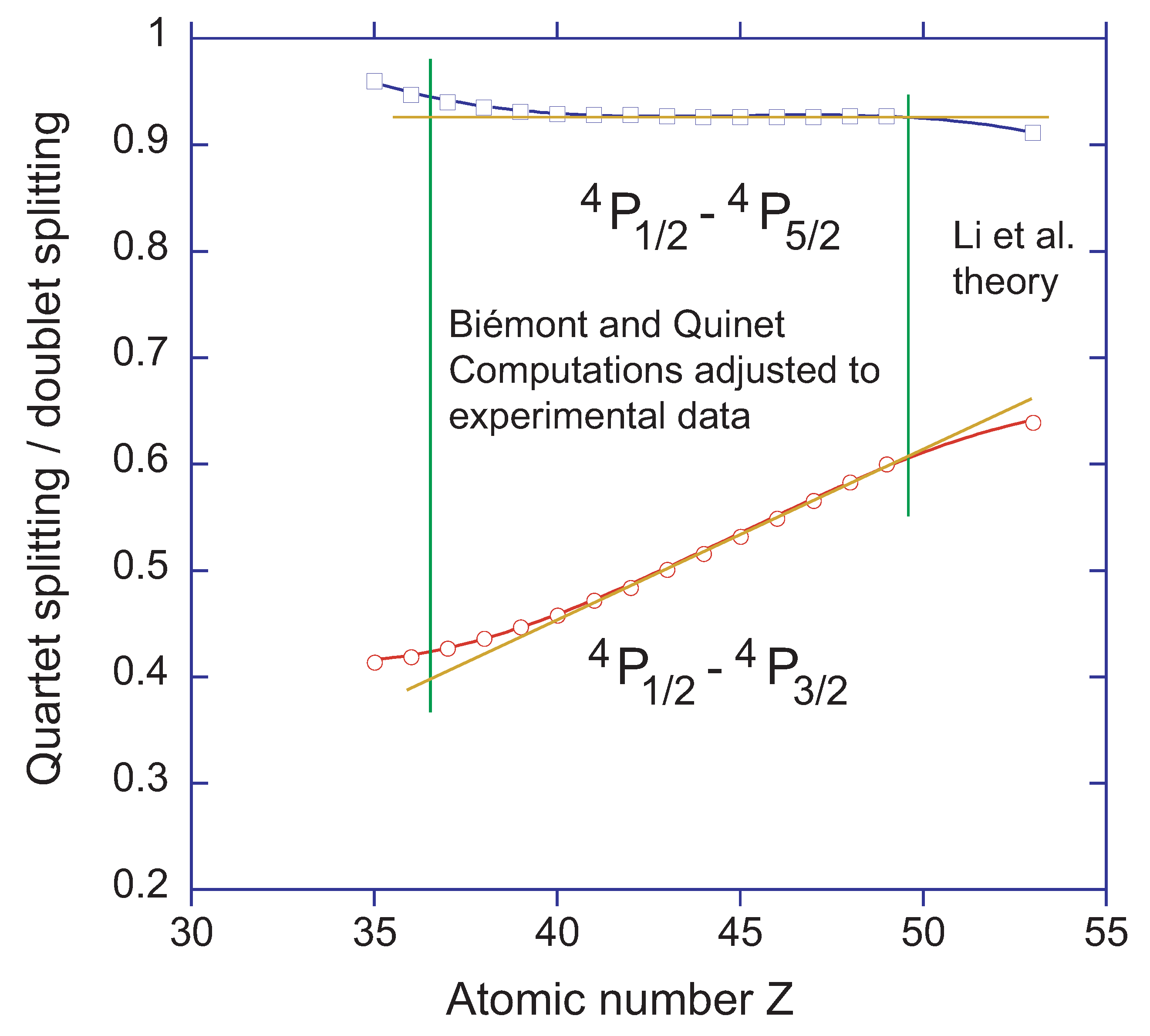
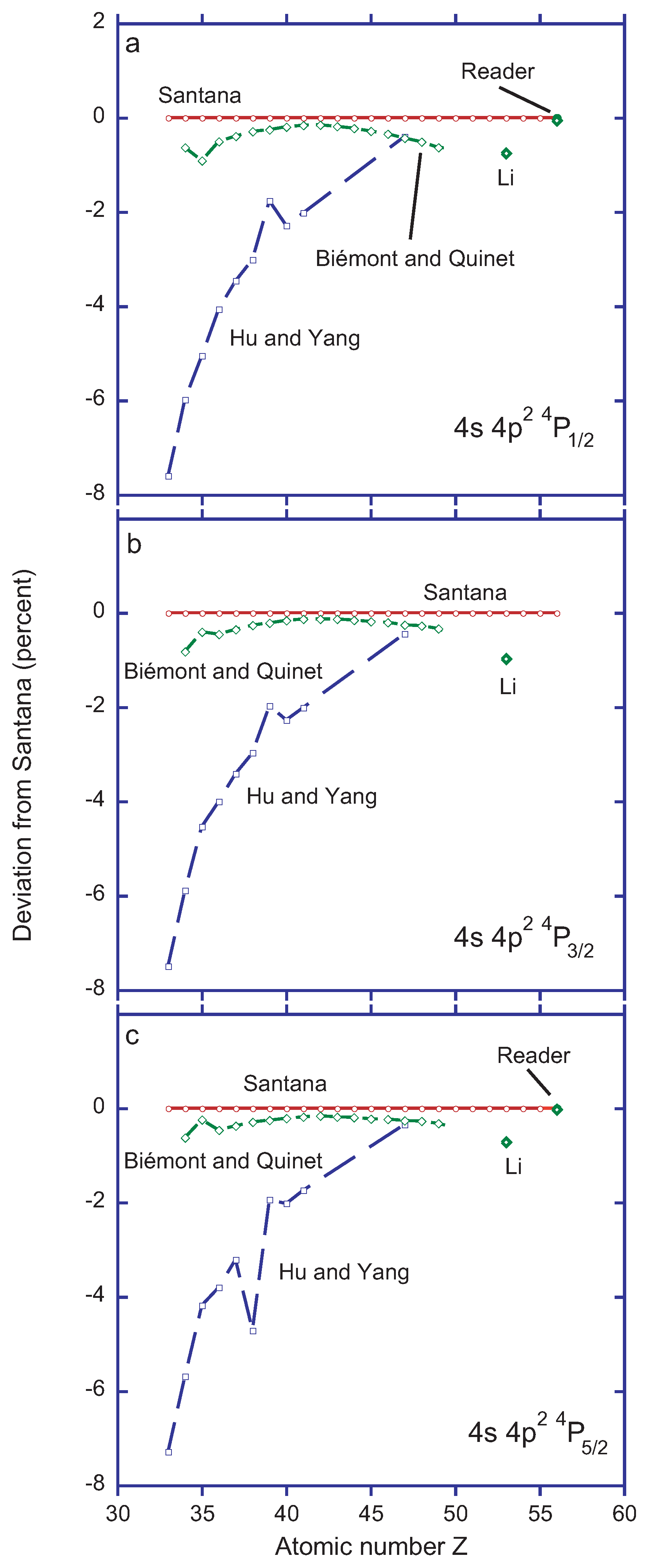
3.3. Ga-Like Ions
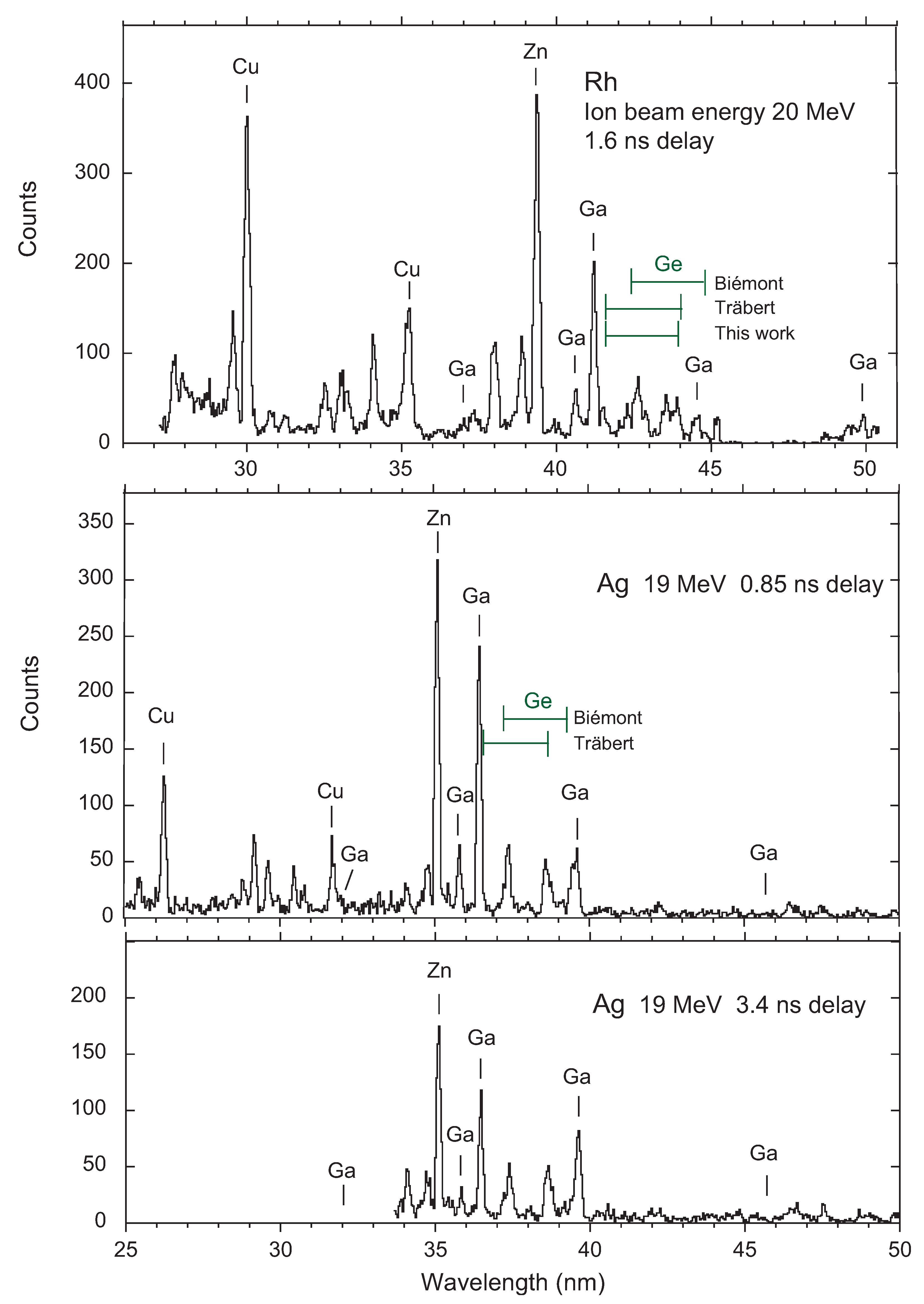
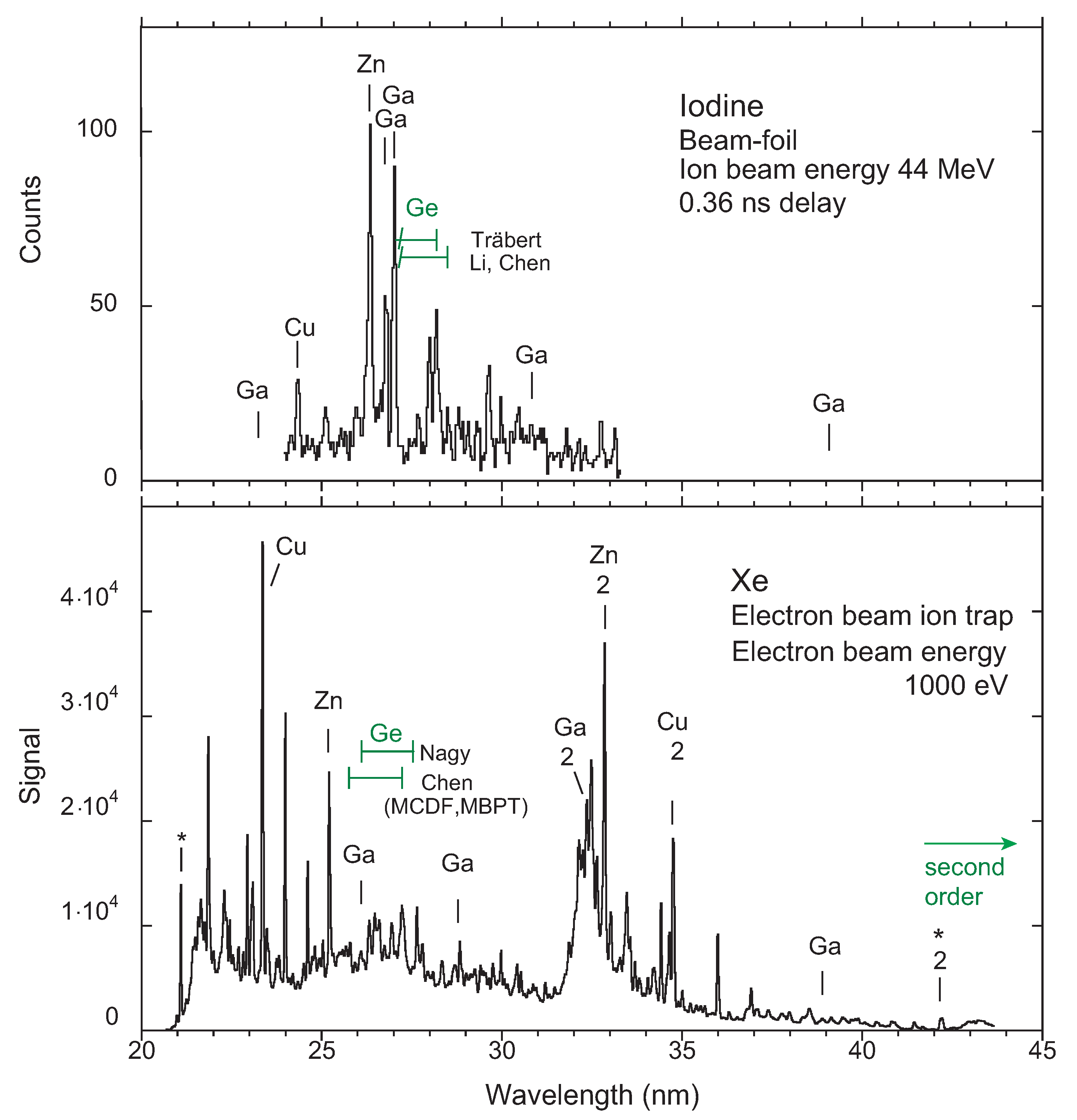
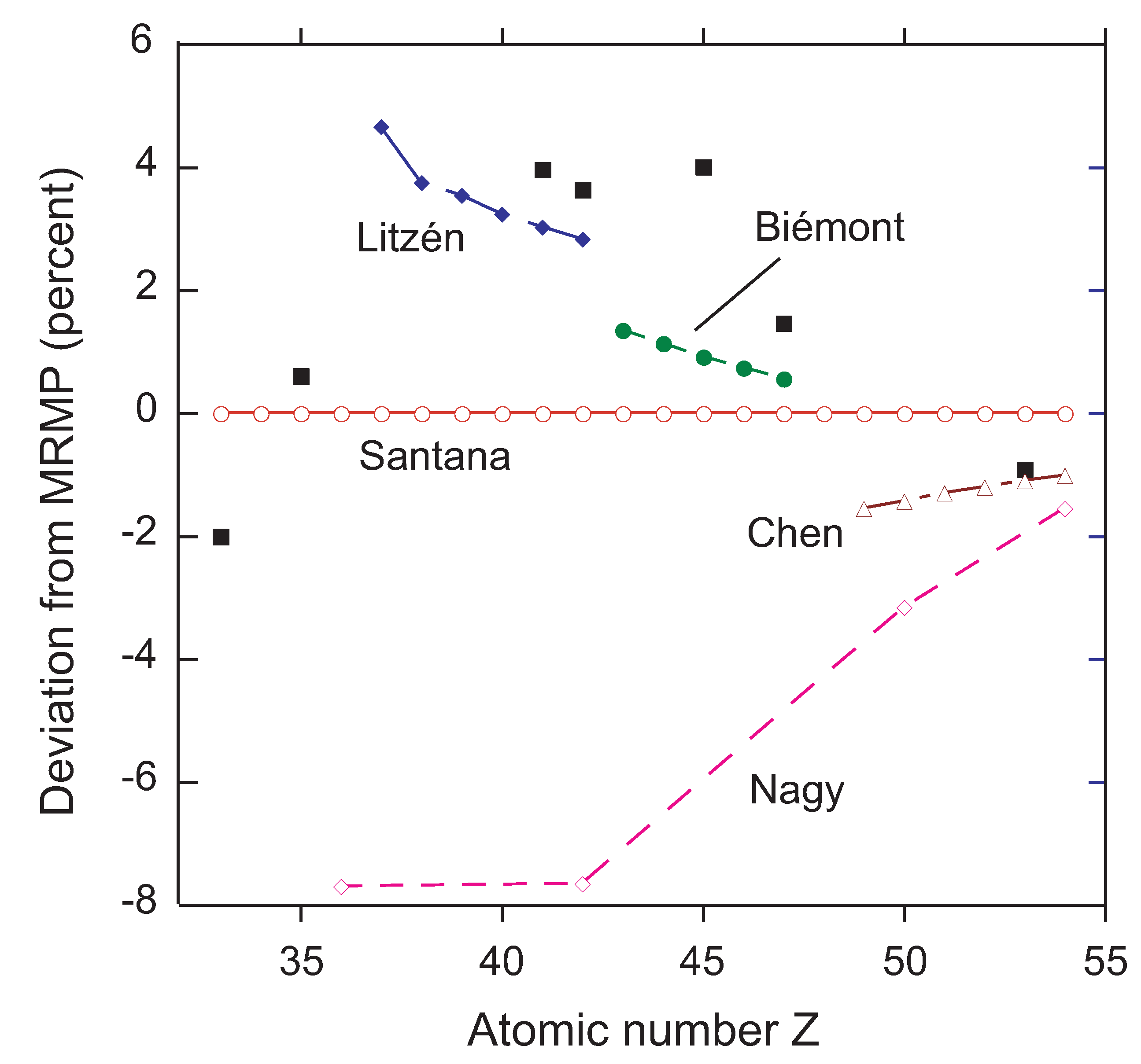
3.4. Ge-Like Ions
4. Discussion and Outlook
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Träbert, E. Beam-foil spectroscopy-quo vadis? Phys. Scr. 2008, 78, 038103. [Google Scholar] [CrossRef]
- Levine, M.A.; Marrs, R.E.; Henderson, J.R.; Knapp, D.A.; Schneider, M.B. The electron beam ion trap: A new instrument for atomic physics measurements. Phys. Scr. 1988, 22, 157–163. [Google Scholar] [CrossRef]
- Levine, M.A.; Marrs, R.E.; Bardsley, J.N.; Beiersdorfer, P.; Bennett, C.L.; Chen, M.H.; Cowan, T.; Dietrich, D.; Henderson, J.R.; Knapp, D.A.; et al. The use of an electron beam ion trap in the study of highly charged ions. Nucl. Instrum. Meth. Phys. Res. 1989, 43, 431–440. [Google Scholar] [CrossRef]
- Beiersdorfer, P. A “brief” history of spectroscopy on EBIT. Can. J. Phys. 2008, 86, 1–10. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Baik, D.H.; Indelicato, P.; Desclaux, J.P. Resonance transition energies of Li-like, Na-like, and Cu-like Ions. Phys. Rev. A 1991, 44, 148–166. [Google Scholar] [CrossRef] [PubMed]
- Blundell, S.A. Calculations of the screened self-energy and vacuum polarization in Li-like, Na-like, and Cu-like ions. Phys. Rev. 1993, 47, 1790–1803. [Google Scholar] [CrossRef]
- Träbert, E. Solar EUV line identifications from beam-foil delayed spectra. Mon. Not. R. Astron. Soc. 1988, 297, 399–404. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H.; Hutton, R.; Martinson, I. Intercombination lines in delayed beam-foil spectra. J. Opt. Soc. Am. B 1988, 5, 2173–2182. [Google Scholar] [CrossRef]
- Utter, S.B.; Beiersdorfer, P.; Träbert, E.; Clothiaux, E.J. Wavelengths of the 4s1/2 4p3/2 resonance lines in Cu-like heavy ions. Phys. Rev. A 2003, 67, 032502. [Google Scholar] [CrossRef]
- Utter, S.B.; Beiersdorfer, P.; Träbert, E. Accurate wavelengths of resonance lines in Zn-like heavy ions. Can. J. Phys. 2003, 81, 911–918. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Chen, H. Wavelengths of the 4s1/2-4p3/2 resonance lines in Cu- and Zn-like heavy ions. Phys. Rev. A 2004, 70, 0325026. [Google Scholar] [CrossRef]
- Chen, M.H.; Cheng, K.-T. A large-scale relativistic configuration-interaction approach: application to the 4s2 4s4p transition energies and E1 rates for Zn-like ions. J. Phys. B Atomic Mol. Phys. 2010, 43, 074019. [Google Scholar] [CrossRef]
- Santana, J.A.; University of Puerto Rico, Cayey, PR, USA. Unpublished work. 2016.
- Edlén, B. Atomic spectra. In Encyclopedia of Physics; Flügge, S., Ed.; Springer: Berlin, Germany, 1964; Volume 27. [Google Scholar]
- Sugar, J.; Musgrove, A. Energy levels of krypton, Kr I through Kr XXXVI. J. Phys. Chem. Ref. Data 1991, 20, 859–916. [Google Scholar] [CrossRef]
- Shirai, T.; Okazaki, K.; Sugar, J. Spectral data for highly ionized krypton, Kr V through Kr XXXVI. J. Phys. Chem. Ref. Data 1995, 24, 1577–1608. [Google Scholar] [CrossRef]
- Saloman, E.B. Energy levels and observed spectral lines of krypton, Kr I through Kr XXXVI. J. Phys. Chem. Ref. Data 2007, 36, 215–386. [Google Scholar] [CrossRef]
- Shirai, T.; Nakai, Y.; Ozawa, K.; Ishii, K.; Sugar, J.; Mori, K. Spectral data for molybdenum ions, Mo VI Mo XLII. J. Phys. Chem. Ref. Data 1987, 16, 327–377. [Google Scholar] [CrossRef]
- Sugar, J.; Musgrove, A. Energy levels of molybdenum, Mo I through Mo XLII. J. Phys. Chem. Ref. Data 1988, 17, 155–239. [Google Scholar] [CrossRef]
- Saloman, E.B. Energy levels and observed spectral lines of xenon, Xe I through Xe LIV. J. Phys. Chem. Ref. Data 2004, 33, 765–921. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.5.2); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018; Available online: https://physics.nist.gov/asd (accessed on 23 Febuary 2018).
- Reader, J.; Acquista, N. Spectrum and energy levels of ten-times ionized yttrium (Y XI). J. Opt. Soc. Am. 1979, 69, 1285–1288. [Google Scholar] [CrossRef]
- Reader, J.; Acquista, N. Spectrum and energy levels of eleven-times ionized zirconium (Zr XII). J. Opt. Soc. Am. 1979, 69, 1659–1662. [Google Scholar] [CrossRef]
- Reader, J.; Acquista, N. Spectrum and energy levels of twelve-times ionized niobium (Nb XIII). J. Opt. Soc. Am. 1980, 70, 317–321. [Google Scholar] [CrossRef]
- Reader, J.; Luther, G.; Acquista, N. Spectrum and energy levels of thirteen-times ionized molybdenum (Mo XIV). J. Opt. Soc. Am. 1979, 69, 144–149. [Google Scholar] [CrossRef]
- Wyart, J.-F.; Reader, J.; Ryabtsev, A. 3d 4p Transitions in the zinclike and copperlike ions Y X; Zr XI, XII; Nb XII, XIII; and Mo XIII, XIV. J. Opt. Soc. Am. 1981, 71, 692–698. [Google Scholar] [CrossRef]
- Reader, J.; Acquista, N.; Cooper, D. Spectra and energy levels of ions in the copper isoelectronic sequence from Ru15+ to Sn21+. J. Opt. Soc. Am. 1983, 73, 1765–1770. [Google Scholar] [CrossRef]
- Seely, J.F.; Brown, C.M.; Behring, W.E. Transitions in Fe-, Co-, Cu-, and Zn-like Ions of W and Re. J. Opt. Soc. Am. B 1989, 6, 3–6. [Google Scholar] [CrossRef]
- Kania, D.R.; MacGowan, B.J.; Keane, C.J.; Brown, C.M.; Ekberg, J.O.; Seely, J.F.; Feldman, U.; Reader, J. Transitions and energy levels for Cu-like Yb41+, Ta44+, and U63+. J. Opt. Soc. Am. B 1990, 7, 1993–1996. [Google Scholar]
- Reader, J.; Acquista, N. 4s-4p resonance transitions in highly charged Cu- and Zn-like ions. Phys. Rev. Lett. 1977, 39, 184–187. [Google Scholar] [CrossRef]
- Reader, J.; Luther, G. Spectra of very highly charged Cu- and Zn-like ions. Phys. Rev. Lett. 1980, 45, 609–613. [Google Scholar] [CrossRef]
- Finkenthal, M.; Bell, R.E.; Moos, H.W.; Bhatia, A.K.; Marmar, E.S.; Terry, J.L.; Rice, J.E. The molybdenum spectrum emitted by a tokamak plasma in the 300–500 range. Phys. Lett. 1981, 82A, 123–126. [Google Scholar] [CrossRef]
- Litzén, U.; Ando, K. 4s-4p transitions including intercombination lines in Zn-like Zr XI, Nb XII, and Mo XIII. Phys. Lett. 1984, 100A, 411–414. [Google Scholar] [CrossRef]
- Acquista, N.; Reader, J. 4s2 1S0 4s4p 1P1 transitions in zinclike ions. J. Opt. Soc. Am. B 1984, 1, 649–651. [Google Scholar] [CrossRef]
- Seely, J.F.; Ekberg, J.O.; Brown, C.M.; Feldman, U.; Behring, W.E.; Reader, J.; Richardson, M.C. Laser produced spectra and QED effects for Fe-, Co-, Cu-, and Zn-like Ions of Au, Pb, Bi, Th, and U. Phys. Rev. Lett. 1986, 57, 2924–2926. [Google Scholar] [CrossRef] [PubMed]
- Finkenthal, M.; Lippmann, A.S.; Huang, L.K.; Yu, T.L.; Stratton, B.C.; Moos, H.W.; Klapisch, M.; Mandelbaum, P.; Bar Shalom, A.; Hodge, W.L.; et al. The spectrum of highly ionized praseodymium and dysprosium from the Texas tokamak. J. Appl. Phys. 1986, 59, 3644–3649. [Google Scholar] [CrossRef]
- Hinnov, E.; Beiersdorfer, P.; Bell, R.; Stevens, J.; Suckewer, S.; von Goeler, S.; Wouters, A.; Dietrich, D.; Gerassimenko, M.; Silver, E. Intercombination lines of the zinc isoelectronic sequence for Z = 50–70. Phys. Rev. A 1987, 35, 4876–4877. [Google Scholar] [CrossRef]
- Cheng, K.T.; Wagner, R.A. Quantum electrodynamics effects in the 4s-4p transitions in Cu-like and Zn-like ions. Phys. Rev. A 1987, 36, 5435–5438. [Google Scholar] [CrossRef]
- Litzén, U.; Reader, J. Spectra and energy levels of ions in the zinc isoelectronic sequence from Rb VIII to Mo XIII. Phys. Rev. A 1987, 36, 5159–5169. [Google Scholar] [CrossRef]
- Kaufman, V.; Sugar, J.; Rowan, W.L. Spectra of copperlike and zinclike xenon: Xe XXV and Xe XXVI. J. Opt. Soc. Am. B 1988, 5, 1273–1274. [Google Scholar] [CrossRef]
- Churilov, S.S.; Ryabtsev, A.N.; Wyart, J.-F. Identification of n = 4, Δn = 0 transitions in the spectra of nickel-like and zinc-like ions through tin. Phys. Scr. 1988, 38, 326–335. [Google Scholar] [CrossRef]
- Litzén, U.; Hansson, A. Additions to the spectra and energy levels of the zinc-like ions Y X-Cd XIX. Phys. Scr. 1989, 40, 468–471. [Google Scholar] [CrossRef]
- Sugar, J.; Kaufman, V.; Baik, D.H.; Kim, Y.-K.; Rowan, W.L. Accurate wavelengths for resonance lines of the Cu and Zn isoelectronic sequences for Pd to Dy. J. Opt. Soc. Am. B 1991, 8, 1795–1798. [Google Scholar] [CrossRef]
- Brown, C.M.; Seely, J.F.; Kania, D.R.; Hammel, B.A.; Back, C.A.; Lee, R.W.; Bar-Shalom, A.; Behring, W.E. Wavelengths and energy levels for the Zn I isoelectronic sequence Sn20+ through U62+. At. Data Nucl. Data Tables 1994, 58, 203–217. [Google Scholar] [CrossRef]
- Träbert, E. Radiative-lifetime measurements on highly-charged ions. In Accelerator-Based Atomic Physics Techniques and Applications; Shafroth, S.M., Austin, J.C., Eds.; American Institute of Physics: Washington, DC, USA, 1997; pp. 567–607. [Google Scholar]
- Träbert, E.; Suleiman, J.; Cheng, S.; Berry, H.G.; Dunford, R.W.; Kanter, E.W.; Kurtz, C.; Livingston, A.E.; Kukla, K.W.; Serpa, F.G.; et al. Experimental transition probabilities of intercombination transitions in Mg-like and Al-like ions of bromine. Phys. Rev. A 1993, 47, 3805–3809. [Google Scholar] [CrossRef] [PubMed]
- Sugar, J.; Träbert, E.; Möller, G.; Heckmann, P.H.; Blanke, J.H.; Martinson, I. Beam-foil study of two-electron transitions in Cu-like ions. Phys. Scr. 1991, 43, 484–489. [Google Scholar] [CrossRef]
- Heckmann, P.H.; Möller, G.; Träbert, E.; Wagner, C.; Martinson, I.; Blanke, J.H.; Sugar, J. Intercombination lines in Zn-like, Ga-like and Ge-like Nb. Phys. Scr. 1991, 44, 151–153. [Google Scholar] [CrossRef]
- Möller, G.; Träbert, E.; Heckmann, P.H.; Sugar, J. 3d9 4s2-3d9 4s4p transitions in Cu I-like Nb XIII. Phys. Scr. 1992, 46, 36–39. [Google Scholar] [CrossRef]
- Träbert, E. Lifetime of the 4s4p P level in foil-excited Zn-like Mo12+ and Ag17+ ions. Phys. Scr. 1989, 39, 592–594. [Google Scholar] [CrossRef]
- Träbert, E.; Pinnington, E.H. Beam-foil lifetimes measured for intercombination transitions in Zn-like and Ga-like ions of Mo. Can. J. Phys. 1993, 71, 128–132. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H.; Doerfert, J.; Granzow, J. Beam-foil lifetimes measured for intercombination transitions in Zn-like ions of Rh and Ag and Ga-like ions of Rh. Phys. Scr. 1993, 47, 780–783. [Google Scholar] [CrossRef]
- Träbert, E.; Heckmann, P.H.; Doerfert, J.; Sugar, J. 3d94s2-3d94s4p transitions from long-lived levels in Cu I-like Rh XVII. Phys. Scr. 1994, 50, 254–257. [Google Scholar] [CrossRef]
- Träbert, E. Identification of intercombination lines in beam-foil spectra of highly ionized Ag. Nucl. Instrum. Meth. Phys. Res. B 1989, 43, 362–365. [Google Scholar] [CrossRef]
- Träbert, E.; Möller, G.; Heckmann, P.H.; Livingston, A.E.; Blanke, J.H. Wavelengths and transition probabilities of intercombination lines in the spectra of Ga- and Ge-like Ag ions. Phys. Scr. 1990, 42, 323–329. [Google Scholar] [CrossRef]
- Träbert, E. EUV beam-foil observations of Cu- through Ge-like ions of iodine. Phys. Scr. T 2011, 144, 014004. [Google Scholar] [CrossRef]
- Li, J.; Träbert, E.; Dong, C.-Z. Energy levels, transition rates and lifetimes for low-lying levels in Cu-, Zn-, Ga- and Ge-like ions of iodine. Phys. Scr. 2011, 83, 015301. [Google Scholar] [CrossRef]
- Johnson, B.M.; Jones, K.W.; Gregory, D.C.; Ekberg, J.O.; Engström, L.; Kruse, T.H.; Cecchi, J.L. Lifetimes and oscillator strengths for the resonance transitions in Cu-like iodine, I XXV. Phys. Scr. 1985, 32, 210–214. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Lepson, J.K.; Chen, H. Extreme ultraviolet spectra of highly charged Xe ions. Phys. Rev. A 2003, 68, 042501. [Google Scholar] [CrossRef]
- Biedermann, C.; Radtke, R.; Fußmann, G.; Schwob, J.-L.; Mandelbaum, P. EUV spectroscopy of highly charged xenon ions. Nucl. Instrum. Meth. Phys. Res. B 2005, 235, 126–130. [Google Scholar] [CrossRef]
- Lepson, J.K.; Beiersdorfer, P.; Brown, G.V.; Kahn, S.M.; Liedahl, D.A.; Mauche, C.W. Utter Cataloguing emission line spectra from Fe VII—Fe XXIV in the extreme ultraviolet. Rev. Mex. Astron. Astrophys. 2000, 9, 137–139. [Google Scholar]
- Lepson, J.K.; Beiersdorfer, P.; Brown, G.V.; Liedahl, D.A.; Utter, S.B.; Brickhouse, N.S.; Dupree, A.K.; Kaastra, J.S.; Mewe, R.; Kahn, S.M. Emission lines of Fe VII-Fe X in the extreme ultraviolet region, 60–140 Å. Astrophys. J. 2002, 578, 648–656. [Google Scholar] [CrossRef]
- Johnson, B.M.; Jones, K.W.; Gregory, D.C.; Kruse, T.H.; Träbert, E. Beam-foil lifetimes of n = 3 levels in Fe XIII to Fe XVI, I. Experiment using position sensitive detection. Phys. Lett. A 1981, 86, 285–288. [Google Scholar] [CrossRef]
- Lepson, J.K.; Beiersdorfer, P.; Clementson, J.; Bitter, M.; Hill, K.W.; Kaita, R.; Skinner, C.H.; Roquemore, A.L.; Zimmer, G. High-resolution time-resolved extreme ultraviolet spectroscopy on NSTX. Rev. Sci. Instrum. 2012, 83, 10D520. [Google Scholar] [CrossRef] [PubMed]
- Weller, M.E.; Beiersdorfer, P.; Soukhanovskii, V.A.; Magee, E.W.; Scotti, F. Three new extreme ultraviolet spectrometers on NSTX-U for impurity monitoring. Rev. Sci. Instrum. 2016, 87, 11E324. [Google Scholar] [CrossRef] [PubMed]
- Biémont, E.; Quinet, P. Oscillator strengths for the gallium-like ions Br V-In XIX. Atomic spectra and oscillator strengths for astrophysics and fusion research. In Proceedings of the 3rd International Collogium of the Royal Netherlands Academy of Arts and Sciences, Amsterdam, The Netherlands, 28–31 August 1989; pp. 138–139. [Google Scholar]
- Litzén, U.; Reader, J. 4s24p2-4s4p3 transition array and energy levels of the germanium-like ions Rb VI-Mo XI. Phys. Scr. S 1989, 39, 468–473. [Google Scholar] [CrossRef]
- Nagy, O.; El Sayed, F. Energies, wavelengths, and transition probabilities for Ge-like Kr, Mo, Sn, and Xe ions. At. Data Nucl. Data Tables 2012, 98, 373–390. [Google Scholar] [CrossRef]
- Biémont, E.; Quinet, P. Energy levels and oscillator strengths for gallium-like ions (Br V–In XIX). J. Quant. Spect. Rad. Transf. 1990, 44, 233–244. [Google Scholar] [CrossRef]
- Biémont, E.; El Himdy, A.; Garnir, H.-P. Oscillator strengths for some n = 4 Δn = 0 transitions of germanium-like ions (Rb VI—Ag XVI). J. Quant. Spect. Rad. Transf. 1990, 43, 437–443. [Google Scholar] [CrossRef]
- Träbert, E.; Magee, E.W.; Beiersdorfer, P.; Lawrence Livermore National Laboratory, Livermore, CA, USA. Unpublished work. 2014.
- Chen, Z.-B.; Wang, K. Energies and transition rates in Ge-like ions between In XVIII and Ce XXVII. At. Data Nucl. Data Tables 2017, 114, 61–261. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Klapisch, M.; Oreg, J. HULLAC, an integrated computer package for atomic processes in plasmas. J. Quant. Spect. Rad. Transf. 2001, 71, 169–188. [Google Scholar] [CrossRef]
- Träbert, E. Extreme ultraviolet spectra of highly charged Fe ions in the laboratory versus the excitation of spectra in astrophysical environments. Can. J. Phys. 2017, 95, 777–782. [Google Scholar] [CrossRef]
- Träbert, E.; Beiersdorfer, P.; Pinnington, E.H.; Utter, S.B.; Vilkas, M.J.; Ishikawa, Y. Experiment and theory in interplay on high-Z few-electron ion spectra from foil-excited ion beams and electron beam ion traps. J. Phys. Conf. Ser. 2007, 58, 93–96. [Google Scholar] [CrossRef]
- Palmeri, P.; Quinet, P.; Biémont, E.; Träbert, E. Wavelengths and transition probabilities for n = 4–n′ = 4 transitions in heavy Cu-like ions (70 ≤ Z ≤ 92). At. Data Nucl. Data Tables 2007, 93, 537–547. [Google Scholar] [CrossRef]
- Curtis, L.J. Isoelectronic studies of the 4s4p 3PJ energy levels in the Zn sequence. J. Opt. Soc. Am. B 1985, 2, 407–410. [Google Scholar] [CrossRef]
- Curtis, L.J. Empirical lifetimes for 4s4p 1,3P1 levels in the zinc isoelectronic sequence. J. Opt. Soc. Am. B 1992, 9, 5–9. [Google Scholar] [CrossRef]
- Huang, K.-N.; Johnson, W.R. Resonance transitions of Mg- and Zn-like ions from multiconfiguration relativistic random-phase approximation. Nucl. Instrum. Meth. B 1985, 9, 502–504. [Google Scholar]
- Biémont, E. Energy levels, wavelengths, transition probabilities, and oscillator strengths for n = 4 − 4 transitions in zinc-like ions. At. Data Nucl. Data Tables 1989, 43, 163–244. [Google Scholar] [CrossRef]
- Biémont, E.; Quinet, P.; Fawcett, B.C. Energy levels and transition probabilities along the Zn isoelectronic sequence. Phys. Scr. 1989, 39, 562–573. [Google Scholar] [CrossRef]
- Quinet, P.; Biémont, E.; Palmeri, P.; Träbert, E. Relativistic atomic data for EUV and X-ray lines in the highly charged Zn-like ions from Yb40+ to U62+. At. Data Nucl. Data Tables 2007, 93, 711–729. [Google Scholar] [CrossRef]
- Liu, Y.; Hutton, R.; Zou, Y.; Andersson, M.; Brage, T. MCDF calculations for the lowest excited states in the Zn-like sequence. J. Phys. B At. Mol. Phys. 2006, 39, 3147–3158. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. Relativistic multireference many-body perturbation calculations on multi-valence-electron systems: Benchmarks on Zn-like ions. Phys. Rev. A 2005, 72, 032512. [Google Scholar] [CrossRef]
- Blundell, S.A.; Johnson, W.R.; Safronova, M.S.; Safronova, U.I. Relativistic many-body calculations of the energies of n = 4 states along the zinc isoelectronic sequence. Phys. Rev. A 2008, 77, 032507. [Google Scholar] [CrossRef]
- Blundell, S.A. Calculation of QED corrections in highly charged Zn-like ions. Can. J. Phys. 2009, 87, 55–65. [Google Scholar] [CrossRef]
- Safronova, U.I.; Safronova, M.S. Relativistic many-body calculations of the oscillator strengths, transition rates and polarizabilities in Zn-like ions. J. Phys. B At. Mol. Phys. 2010, 43, 074025. [Google Scholar] [CrossRef]
- Träbert, E.; Clementson, J.; Beiersdorfer, P.; Santana, J.A.; Ishikawa, Y. Measurements and calculations of Zn-like heavy ions an update. Can. J. Phys. 2011, 89, 1059–1109. [Google Scholar]
- Cheng, T.-C.; Huang, K.-N. Resonance transitions of Zn-like ions from the multiconfiguration relativistic random-phase approximation. Phys. Rev. A 1992, 45, 4367–4373. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Liu, X.; Zhou, C. Energy levels, oscillator strengths, radiative decay rates, and fine-structure collision strengths for the Zn-like ions Nb XII and Mo XIII. At. Data Nucl. Data Tables 2014, 100, 711–729. [Google Scholar] [CrossRef]
- Hu, F.; Mei, M.; Han, C.; Han, B.; Jiang, G.; Yang, J. Correlation effects for nl -n′l′ transitions in nine isoelectronic sequences of silver ions. J. Quant. Spect. Rad. Transf. 2014, 133, 319–328. [Google Scholar] [CrossRef]
- Curtis, L.J.; Reader, J.; Goldsmith, S.; Denne, B.; Hinnov, E. 4s24p 2P intervals in the Ga isoelectronic sequence from Rb6+ to In18+. Phys. Rev. A 1984, 29, 2248–2250. [Google Scholar] [CrossRef]
- Reader, J.; Acquista, N.; Goldsmith, S. 4s24p 4s4p2 and 4s24p 4s25s transitions of galliumlike ions from Rb VII to In XIX. J. Opt. Soc. Am. B 1986, 3, 874–878. [Google Scholar] [CrossRef]
- Litzén, U.; Reader, J. Spectra and energy levels of the galliumlike ions Rb VII-Mo XII. Phys. Scr. 1989, 39, 73–80. [Google Scholar] [CrossRef]
- Litzén, U.; Zeng, X. The 4s24p-4s4p2 transition array and energy levels of the Ga-like ions Ru XIV–In XIX. Phys. Scr. 1991, 43, 262–265. [Google Scholar] [CrossRef]
- Hu, F.; Yang, J.; Wang, C.; Jing, L.; Chen, S.; Jiang, G.; Liu, H.; Hao, L. Multiconfiguration Dirac-Fock calculations on multi-valence-electron systems: Benchmarks on Ga-like ions. Phys. Rev. A 2011, 84, 042506. [Google Scholar] [CrossRef]
- Curtis, L.J. Fine-structure intervals for the lowest P terms in the Cu, Zn, Ga, and Br isoelectronic sequences for Z ≤ 92. Phys. Rev. A 1987, 35, 2089–2094. [Google Scholar] [CrossRef]
- Reader, J.; Gillaspy, J.D.; Osin, D.; Ralchenko, Y. Extreme ultraviolet spectra and analysis of Δn = 0 transitions in highly charged barium. J. Phys. B At. Mol. Phys. 2014, 47, 145003. [Google Scholar] [CrossRef]
- Osin, D.; Reader, J.; Gillaspy, J.D.; Ralchenko, Y. Extreme ultraviolet spectra of highly charged xenon observed with an electron beam ion trap. J. Phys. B At. Mol. Phys. 2012, 45, 245001. [Google Scholar] [CrossRef]
- Singh, A.K.; Goyal, A.; Khatri, I.; Aggarwal, S.; Sharma, R.; Mohan, M. Energy levels, lifetimes and radiative data of Ba XXVI. At. Data Nucl. Data Tab. 2016, 109–110, 339–351. [Google Scholar] [CrossRef]
- Podpaly, Y.A.; Gillaspy, J.D.; Reader, J.; Ralchenko, Y. Measurements and identifications of extreme ultraviolet spectra of highly-charged Sm and Er. J. Phys. B At. Mol. Phys. 2015, 48, 025002. [Google Scholar] [CrossRef]
- Quinet, P.; Biémont, E.; Palmeri, P.; Träbert, E. Multiconfiguration Dirac-Fock wavelengths and transition rates in the X-ray spectra of highly charged Ga-like ions from Yb39+ to U63+. At. Data Nucl. Data Tables 2007, 93, 167–182. [Google Scholar] [CrossRef]
- Ellis, D.G. Problems in the calculation of intercombination line strengths. Phys. Scr. 1989, 40, 12–16. [Google Scholar] [CrossRef]
- Ellis, D.G.; Martinson, I.; Träbert, E. Intercombination transitions in multiply ionized atoms. Comm. At. Mol. Phys. 1989, 22, 241–262. [Google Scholar]
- Träbert, E. Intercombination transitions: Lifetime measurements by beam-foil spectroscopy and other techniques confronted with theoretical trends. Phys. Scr. 1993, 48, 699–713. [Google Scholar] [CrossRef]
- Litzén, U.; Zeng, X. The 4s24p2-4s4p3 transition array and energy levels of the Ge-like ions Ru XIII-Cd XVII. J. Phys. B At. Mol. Phys. 1991, 24, L45–L50. [Google Scholar] [CrossRef]
- Joshi, Y.N.; Budhiraja, C.J. Spectrum of trebly ionized bromine. Can. J. Phys. 1971, 49, 670–677. [Google Scholar] [CrossRef]
- Tauheed, A.; Joshi, Y.N.; Jabeen, S. Revised and extended analysis of trebly ionized bromine: Br IV. Phys. Scr. 2008, 78, 065305. [Google Scholar] [CrossRef]
- Rahimullah, K.; Chaghtai, M.S.Z.; Khatoon, S. 4p-5s Transitions in Y VII, VIII, Zr VIII, IX, Nb lX, X and Mo X, XI. Phys. Scr. 1976, 14, 221–223. [Google Scholar] [CrossRef]
- Breton, C.; DeMichelis, C.; Hecq, W.; Mattioli, M.; Ramette, J.; Saoutic, B.; Bauche, C.-A.; Bauche, J.; Wyart, J.F. Highly ionized xenon spectra (95–260 ) excited in TFR tokamak plasmas. Phys. Scr. 1988, 37, 33. [Google Scholar] [CrossRef]
- O’Sullivan, G.; Costello, J.T.; Kane, M.; Carroll, P.K. 4s24p2-4s24p5s transitions in Ru XIII, Rh XIV and Pd XV. J. Phys. B At. Mol. Phys. 1988, 21, L195–L199. [Google Scholar] [CrossRef]
- Wyart, J.-F.; Artru, M.-C. Addition to the analysis of the Sr VI and Sr VII spectra. Phys. Lett. A 1989, 139, 387–390. [Google Scholar] [CrossRef]
- Dunne, P.; Carroll, P.K.; Corcoran, R.E.; Costello, J.T.; O’Sullivan, G.J. 4s-4p transitions in Ge-like Ru and Rh. J. Phys. B At. Mol. Phys. 1990, 23, L239–L245. [Google Scholar] [CrossRef]
- D’Arcy, R.; Ohashi, H.; Suda, S.; Tanuma, H.; Fujioka, S.; Nishimura, H.; Nishihara, K.; Suzuki, C.; Kato, T.; Koike, F.; et al. Transitions and the effects of configuration interaction in the spectra of Sn XV-Sn XVIII. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 165207. [Google Scholar] [CrossRef]
- Ohashi, H.; Suda, S.; Tanuma, H.; Fujioka, S.; Nishimura, H.; Sasaki, A.; Nishihara, K. EUV emission spectra in collisions of multiply charged Sn ions with He and Xe. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 065204. [Google Scholar] [CrossRef]
- Suzuki, C.; Kato, T.; Sakaue, H.A.; Kato, D.; Sato, K.; Tamura, N.; Sudo, S.; Yamamoto, N.; Tanuma, H.; Ohashi, H.; et al. Analysis of EUV spectra of Sn XIX XXII observed in low-density plasmas in the Large Helical Device. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 074027. [Google Scholar] [CrossRef]
- Palmeri, P.; Quinet, P.; Biémont, E.; Träbert, E. Wavelengths and transition probabilities in heavy Ge-like ions (70 ≤ Z ≤ 92). At. Data Nucl. Data Tables 2007, 93, 355–374. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Träbert, E.; Santana, J.A.; Quinet, P.; Palmeri, P. Intercombination Transitions in the n = 4 Shell of Zn-, Ga-, and Ge-Like Ions of Elements Kr through Xe. Atoms 2018, 6, 40. https://doi.org/10.3390/atoms6030040
Träbert E, Santana JA, Quinet P, Palmeri P. Intercombination Transitions in the n = 4 Shell of Zn-, Ga-, and Ge-Like Ions of Elements Kr through Xe. Atoms. 2018; 6(3):40. https://doi.org/10.3390/atoms6030040
Chicago/Turabian StyleTräbert, Elmar, Juan A. Santana, Pascal Quinet, and Patrick Palmeri. 2018. "Intercombination Transitions in the n = 4 Shell of Zn-, Ga-, and Ge-Like Ions of Elements Kr through Xe" Atoms 6, no. 3: 40. https://doi.org/10.3390/atoms6030040
APA StyleTräbert, E., Santana, J. A., Quinet, P., & Palmeri, P. (2018). Intercombination Transitions in the n = 4 Shell of Zn-, Ga-, and Ge-Like Ions of Elements Kr through Xe. Atoms, 6(3), 40. https://doi.org/10.3390/atoms6030040






