Interaction of Ultrashort Laser Pulses with Atoms in Plasmas

Abstract

The paper is devoted to the investigation of the absorption of ultrashort laser pulses on atoms in plasmas, accounting for the different broadening mechanisms of atomic resonant transitions. The analysis is made in terms of the absorption probability during the entire interaction between the laser pulse and atom. Attention is mainly given to dependence of probability upon the pulse duration and the carrier frequency of the pulse. The results are presented via dimensionless parameters and functions describing the effect of finite pulse duration on atomic spectra for different broadening mechanisms, namely Doppler, Voigt, Holtsmark and their combinations, as well as the Stark line broadening of Rydberg atomic lines.

1. Introduction

The progress in the generation of ultrashort electromagnetic pulses (USPs) [1,2,3] means that it is important to consider their interaction with atomic systems in plasmas. One of the essential advantages of USPs is connected with their short wavelengths, which make it possible for them to excite atomic systems from ground states, in contrast with femtosecond laser pulses in visible spectral ranges.

The interaction of USPs with atomic systems is of great interest for plasma investigations. The long laser pulses in standard diagnostics (fluorescence schemes) usually deal with the excitation of radiative transitions between excited atomic states which belong to the visible spectral range. The contrast of the fluorescence signal in this case is rather small because the populations of excited atomic levels are not very different from one another under standard plasma conditions. At the same time, the carrier frequency of a USP is often in the ultraviolet or even X-ray spectral range, enabling the excitation of atoms and ions in plasmas from their ground states. In this case, the observed fluorescence signal grows by many orders of magnitude due to the large populations of ground states. This opens up new possibilities for plasma diagnostics (see the discussions in [4]).

In this sense, the X-ray radiation of free electron lasers is of special interest, providing possibilities for both highly charged ion excitation from their ground states and for the tuning of laser frequencies [1]. Moreover, the wide frequency spectra of USPs provide the possibility of USP radiation penetrating into optically dense media.

A specific USP results in the appearance of a new parameter in line broadening theory, namely the pulse duration; see also [5,6,7]. This must be considered together with standard line shape parameters such as frequency detuning from atomic transition resonance [8,9]. Thus, one deals with a generalization of the standard broadening theory by introducing new line shapes which depend on both frequency and pulse duration. It is clear that for long pulses, the new line shapes make a smooth transition to the standard one, whereas for short pulses, absorption probabilities as nonlinear functions of pulse duration can be observed.

The USP can be used for plasma investigations both in X-ray and visible spectral ranges. The pulses provided by X-ray free electron lasers (XFEL) are useful for investigations of high temperature, dense plasmas where the radiative transitions in atomic systems such as highly charged ions belong to the X-ray spectral range. At the same time, a USP in the visible spectral range (HHG pulses) can be applied for investigations of low temperature plasmas, where radiative transitions in neutral atoms (for example, alkali atoms, etc.) are only in the visible spectral range. The expressions for radiative transition probabilities in this paper are expressed in terms of universal functions, enabling their application for both of the cases mentioned above. Moreover, such universal representation opens up the possibility of transferring the results of specific investigations to other conditions following the dimensionless parameters of the research.

The present paper is dedicated to the analysis of the absorption of USPs on atoms in plasmas, accounting for different broadening mechanisms, including the Stark broadening of the atomic resonant transition in terms of total absorption probability during the entire pulse action. Specific attention is devoted to the investigations of absorption probability transitions from the nonlinear to the standard linear absorption regime. This research is presented in terms of universal dimensionless parameters, making it possible to estimate the pulse duration effect on the absorption probabilities for different broadening mechanisms related to different plasma conditions.

This research is made within the frame of first-order perturbation theory with respect to pulse amplitude E₀. Thus, the absorption probability is proportional to the squared product of E₀ and pulse duration τ. The probability is therefore quite different for XFEL and HHG pulses. A specific example is considered in [10].

The structure of the paper is as follows: Section 2 contains general formulas for USP absorption line shapes, presented in terms of universal broadening parameters; Section 3 is devoted to the application of general study of the specific broadening mechanisms, namely Doppler, Voigt, Holtsmark and Rydberg spectra; and Section 4 presents the conclusions.

2. General Formulas

The total absorption probability for laser pulses with a Gaussian envelope in dimensionless variables takes the form [7]

$$W\left(\alpha ,\delta \right)=\frac{\pi }{4}\frac{f_0{E}_0^2}{{\omega }_0}\frac{{\alpha }^2}{\mathsf{\Delta }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left\{-{\alpha }^2{\left(\beta -\delta \right)}^2\right\}G\left(\beta \right)d\beta }=\frac{{\pi }^{3/2}}{4}\frac{f_0{E}_0^2}{{\omega }_0}\frac{1}{\mathsf{\Delta }}F\left(\alpha ,\delta \right)$$

(1)

where $G\left({\omega }^{\prime }\right)$ is the spectral line shape of a radiative transition between atomic states. Here, dimensionless variables are introduced:

$$\beta =\frac{{\omega }^{\prime }-{\omega }_0}{\mathsf{\Delta }},\delta =\frac{\omega -{\omega }_0}{\mathsf{\Delta }},\alpha =\mathsf{\Delta }\tau$$

(2)

where ∆ is the spectral width of the line, ${\omega }_0$ and $f_0$ are the frequency and oscillator strength of the electron transition, $E_0$ is the amplitude of electric field strength of the USP, and $\omega$ and $\tau$ are the carrier frequency and pulse duration. The dimensionless absorption probability $F\left(\alpha ,\delta \right)$ is given by the following expression:

$$F\left(\alpha ,\delta \right)=\frac{{\alpha }^2}{\sqrt{\pi }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left\{-{\alpha }^2{\left(\beta -\delta \right)}^2\right\}G\left(\beta \right)d\beta }$$

(3)

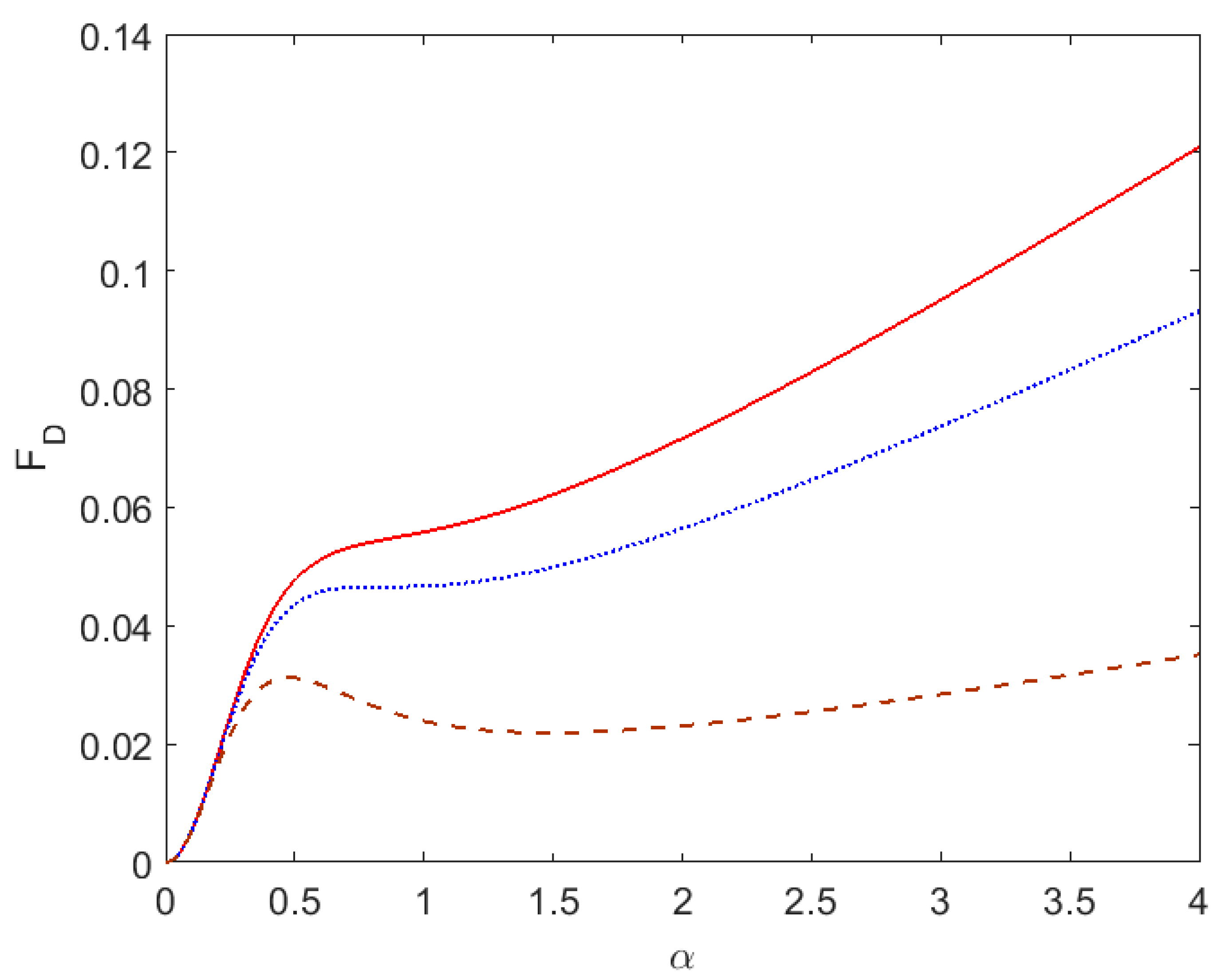
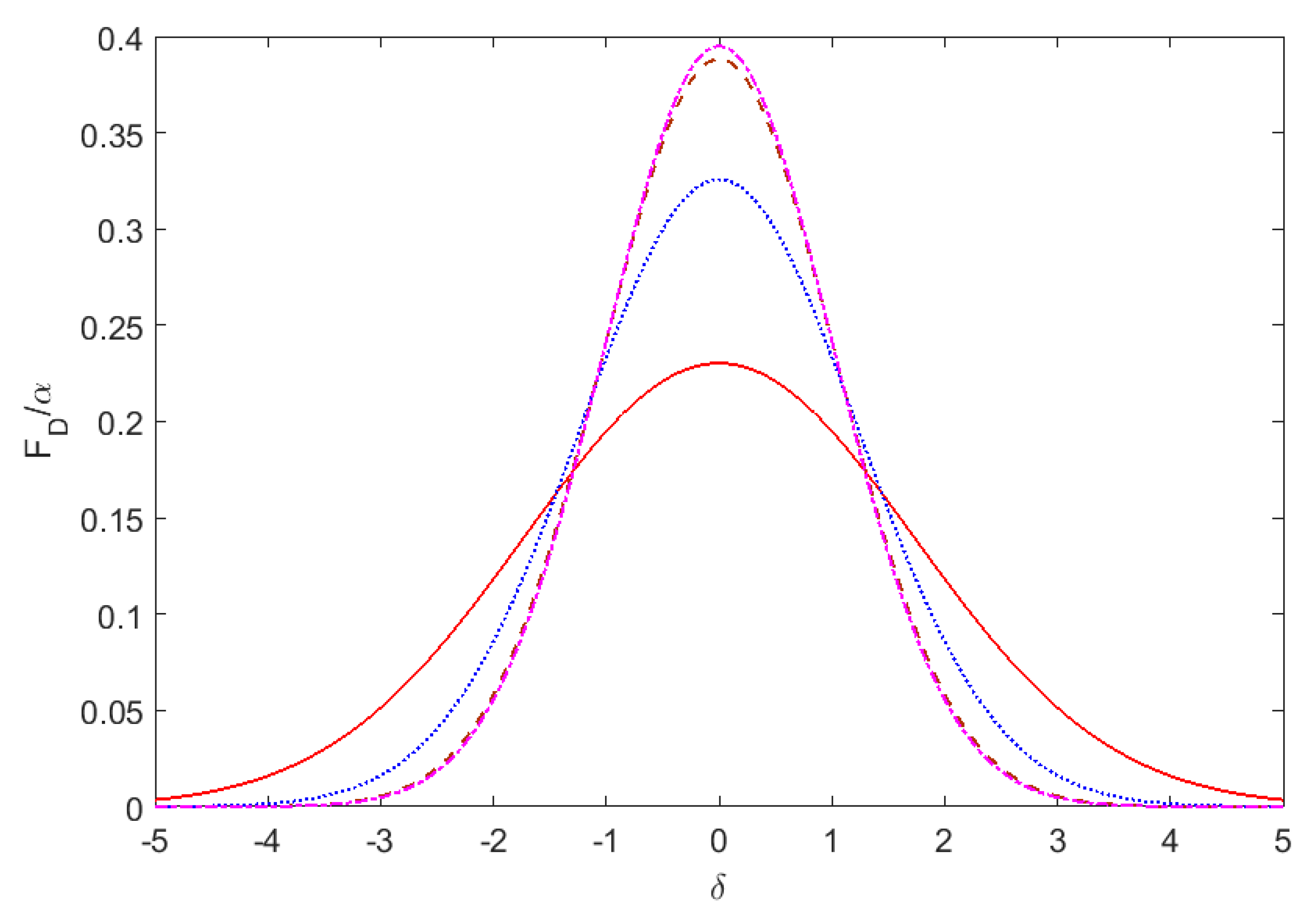
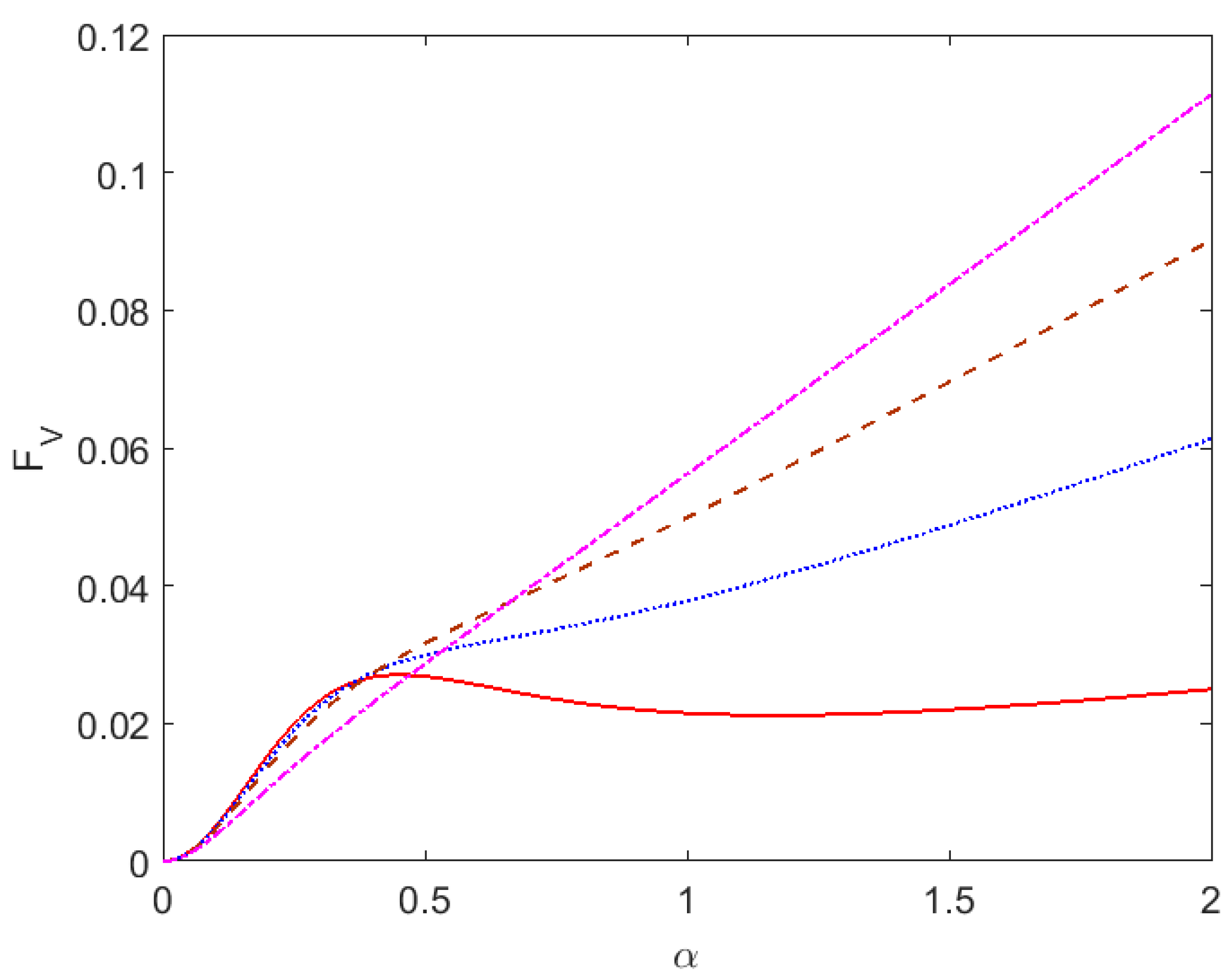
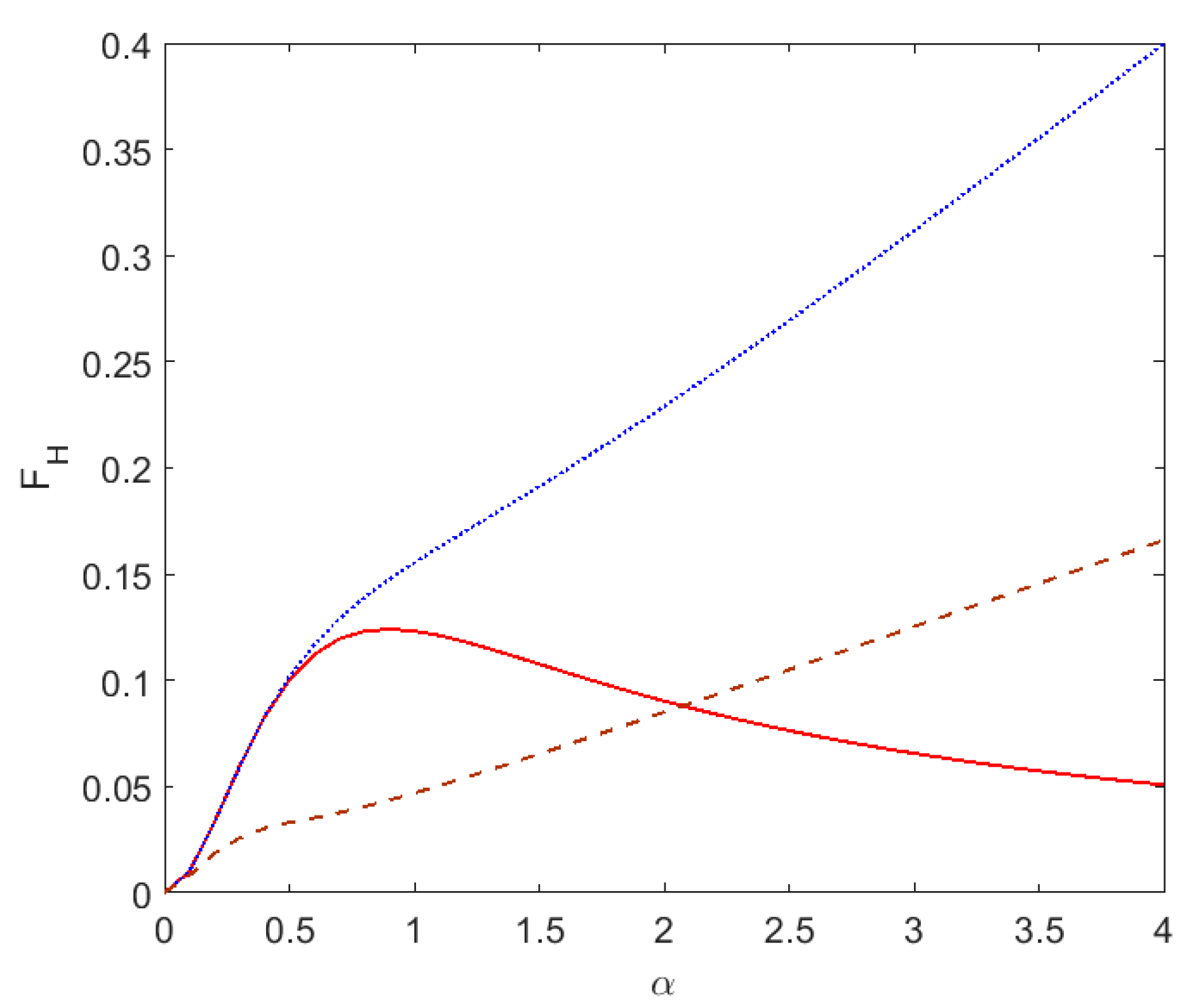
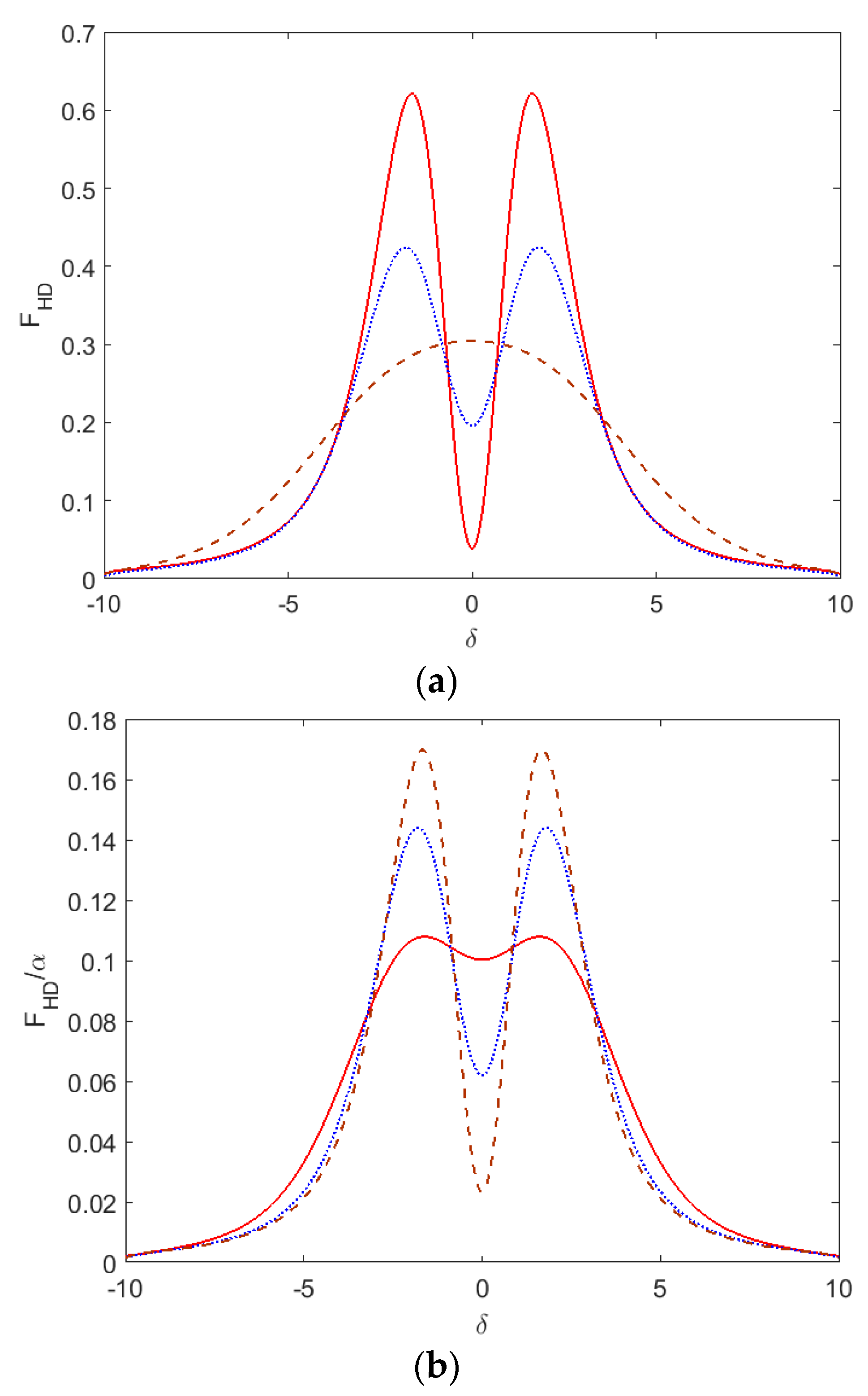
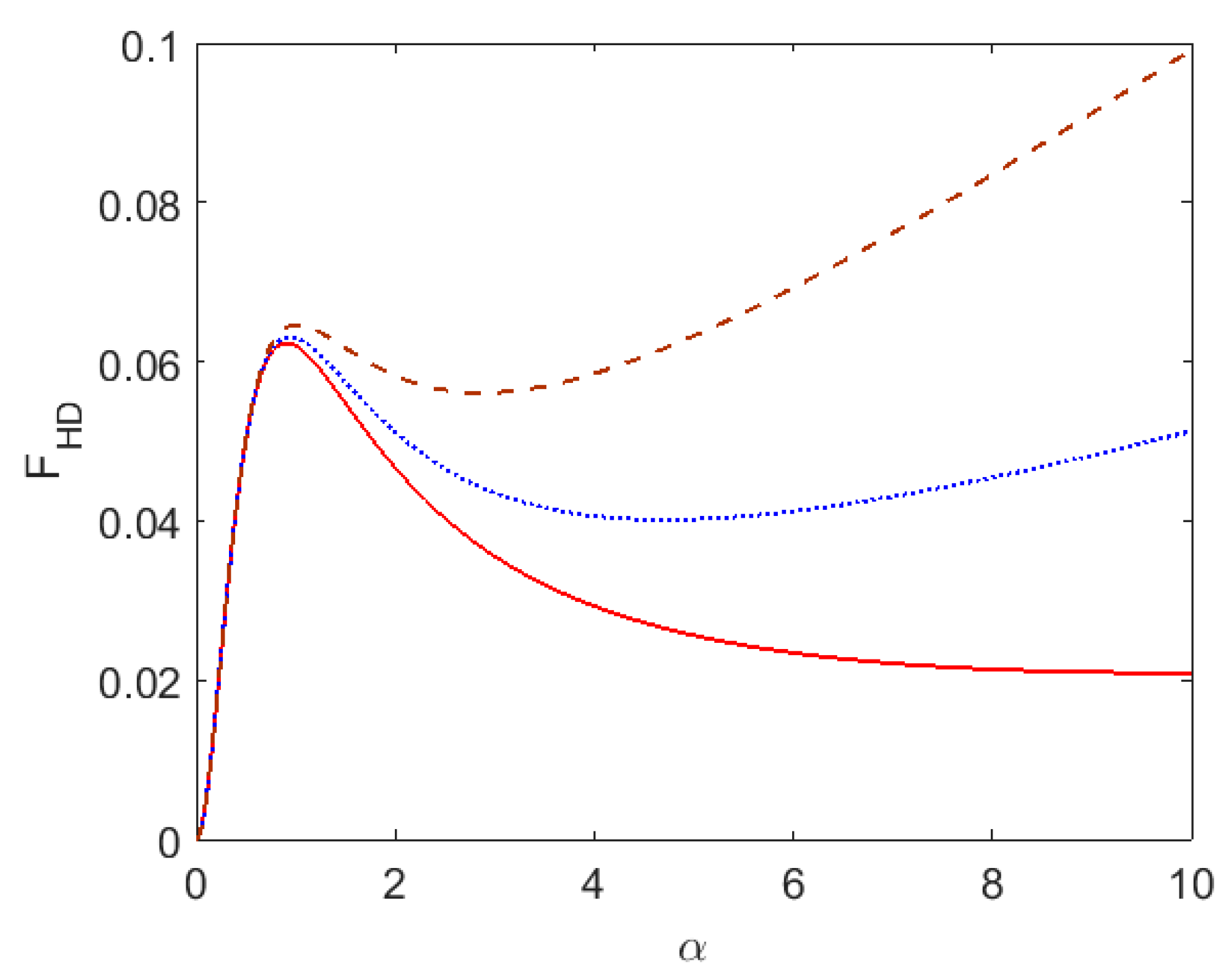
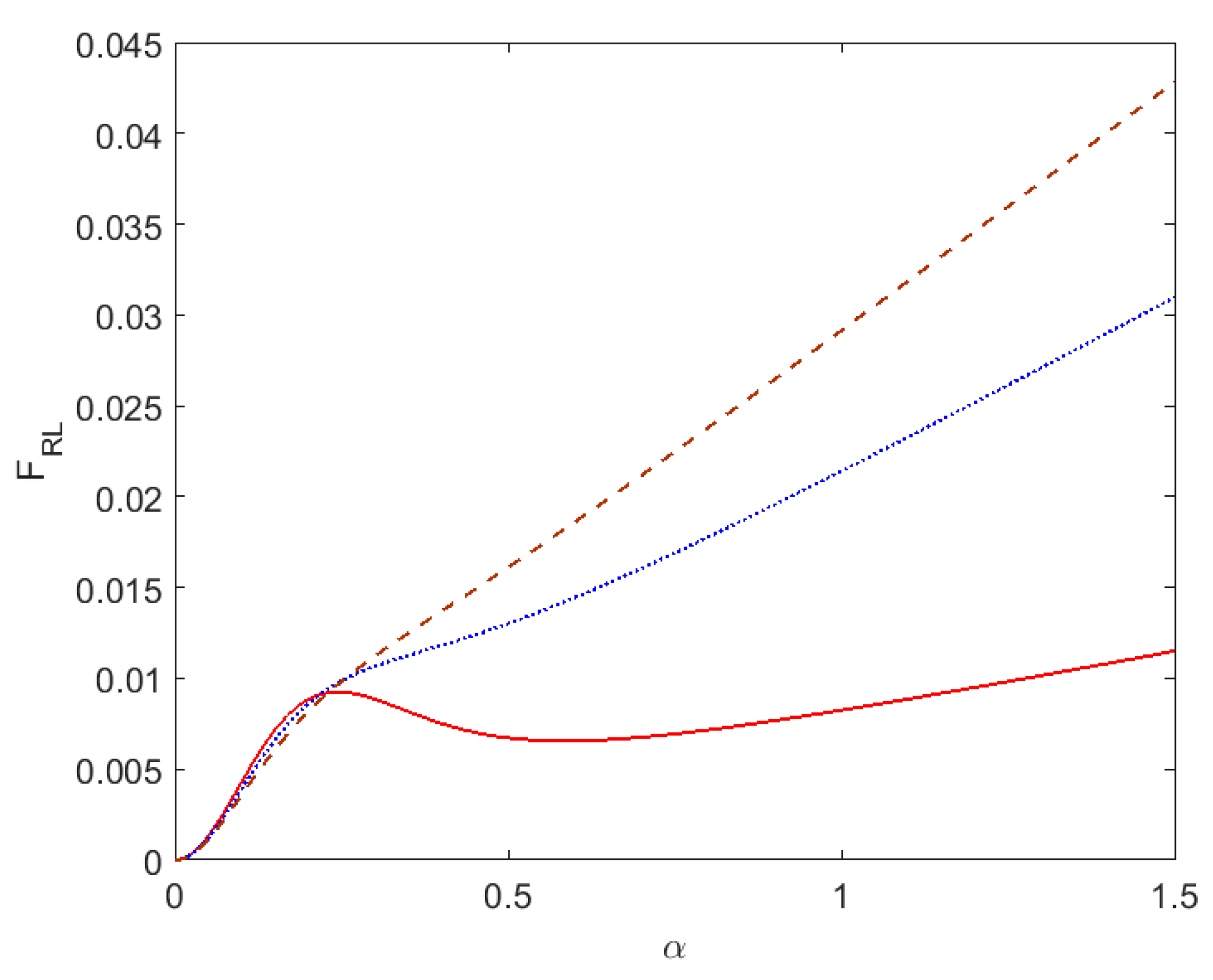
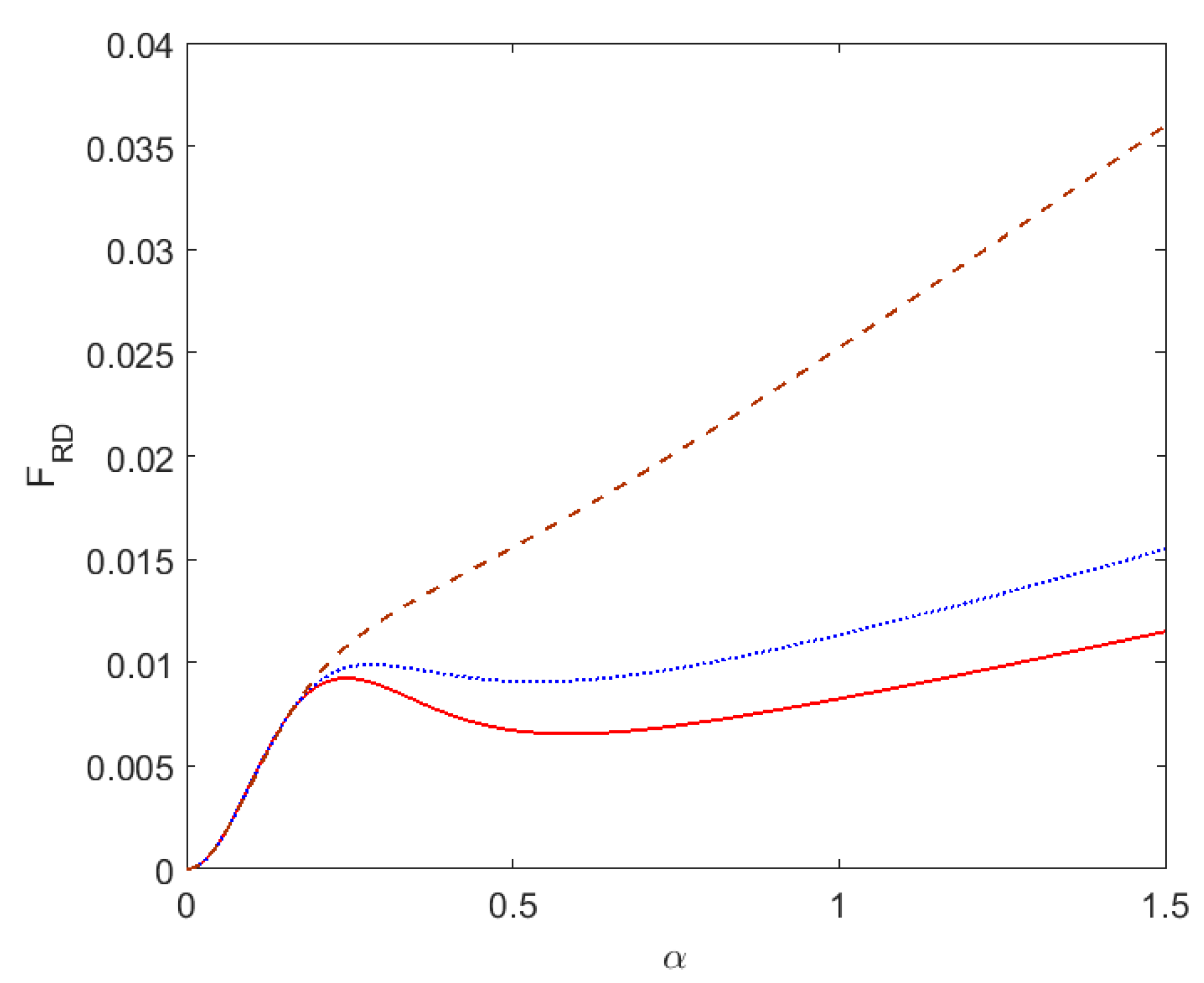
This function describes the dependence of the absorption probability on pulse duration and carrier frequency in terms of dimensionless parameters α and δ. Note that

$$F\left(\alpha ,\delta \right)/\alpha \to G\left(\delta \right)\mathrm{for}\alpha \to \infty$$

(4)

Thus, the function $F\left(\alpha ,\delta \right)$ divided by parameter α presents the line shape of the USP absorption modified by finite pulse duration and becoming the standard one when the value of α goes to infinity.

It should be mentioned that the function $F\left(\alpha ,\delta \right)/\alpha$ integrated over detuning parameter δ is equal to unity.

The influence of pulse duration parameter $\alpha =\mathsf{\Delta }\tau$ on absorption probability for different mechanisms of line broadening in plasmas is considered below.

3. Results and Discussions

3.1. Doppler Broadening

In the case of Doppler broadening, the integral in expression (1) can be calculated analytically, and Formula (1) turns into

$$W_D=\frac{{\pi }^{3/2}}{4}\frac{f_0{E}_0^2}{{\omega }_0}\frac{1}{\mathsf{\Delta }{\omega }_D^2}{F}_D\left(\alpha ,\delta \right)$$

(5)

where

$$F_D\left(\alpha ,\delta \right)=\frac{1}{\sqrt{\pi }}\frac{{\alpha }^2}{\sqrt{2{\alpha }^2+1}}\exp \left\{-\frac{{\alpha }^2{\delta }^2}{2{\alpha }^2+1}\right\}$$

(6)

is the function describing the excitation probability depending on the dimensionless parameters α, and δ. The line shape width ∆ in this case is equal to the standard Doppler line width; see [8]. One can conclude from Equation (6) that

$${\displaystyle \int F_D\left(\alpha ,\delta \right)/\alpha d\delta =1}$$

(7)

for any α. Thus, the normalized line shape has the form

$${\tilde{G}}_D\left(\alpha ,\delta \right)=F_D\left(\alpha ,\delta \right)/\alpha =\frac{1}{\sqrt{\pi }\sigma \left(\alpha \right)}\exp \left(-\frac{{\delta }^2}{2{\sigma }^2\left(\alpha \right)}\right)$$

(8)

where

$$\sigma \left(\alpha \right)=2^{-1/2}\frac{\sqrt{2{\alpha }^2+1}}{\alpha }$$

(9)

is the modified spectral width for Doppler broadening and Gaussian laser pulse. Note that for a large pulse duration, we have $\sigma \left(\alpha >>1\right)\to 1$, which is the standard Doppler line shape.

The Doppler function $F_D\left(\alpha ,\delta \right)$ has extrema which are dependent on the pulse duration parameter $\alpha =\mathsf{\Delta }\tau$ starting from some critical value of the detuning parameter $\delta =\left(\omega -{\omega }_0\right)/\mathsf{\Delta }$. Critical dimensionless detuning, ${\delta }^{\ast }$, is equal to

$${\delta }^{\ast }=\sqrt{3+2\sqrt{2}}\cong 2.414$$

(10)

For $\left|\delta \right|<{\delta }^{\ast }$, extrema in the $F_D\left(\alpha \right)$ function are absent. In the opposite case, the absorption probability dependent on pulse duration has a maximum and minimum, as one can see from Figure 1. For sufficiently long pulses ($\alpha >1$), the dependence of $F_D\left(\alpha \right)$ becomes linear, as is the case in the standard approach for long pulse durations.

Figure 2 presents the distortion of the Doppler line shape by finite duration times of USP. Here, the absorption line shape $F_D\left(\alpha ,\delta \right)/\alpha$ is shown for different values of α. A smooth increase of the Gaussian line shape (8) can be seen in accordance with the decrease of the dispersion factor (9).

3.2. Voigt Line Shape

The Doppler line shape presents the composition of two Gaussian spectral distributions, namely the Doppler line shape and Gaussian shape of USP. Let us consider the important case of the Voigt line shape, which is a composition of two mechanisms of line broadening, namely the Doppler and collisional (impact) mechanisms [8,9]. In this case, we should substitute the Voigt line shape $G_V\left(\beta ,\rho =\gamma /\mathsf{\Delta }\right)$ on the right side of (1) and (3). Therefore, the probability of absorption is a function of three arguments: $F_V\left(\alpha ,\delta ,\rho \right)$ where $\rho =\gamma /\mathsf{\Delta }$ is the ratio between Lorentzian and Gaussian spectral widths, being the standard parameter of Voigt line shapes.

The effect of pulse duration parameter, α, on the transition probability for different ratios, ρ, is presented in Figure 3. It is shown that the transition to the linear dependence takes place for a lower value of the parameter ρ with the increase of the contribution of Lorentzian line wings in the Voigt spectral shape.

3.3. Holtsmark Line Shape

Holtsmark line shapes are the basis for the description of hydrogen spectral line broadening in plasmas [8]. The specifics of such static line shapes are the differences between lines with and without central Stark components, having corresponding peaks and dips in the center of the spectral line. The shape of the unshifted central Stark component is well described by a Voigt line shape with electron impact width. We demonstrate the effect of finite pulse duration on the static line shapes without central components described by Holtsmark distribution.

The Holtsmark distribution has to be substituted into Equations (1) and (3) accounting for a standard static line width ∆ = CF₀, where C is the effective Stark constant for the line under consideration and F₀ (a.u.) = 2.6 N^2/3 (N is ion density) is the standard ion field strength in the Holtsmark distribution. The effect of finite pulse duration α on the Holtsmark static line shape is presented in Figure 4 for different values of detuning δ. This figure shows that, in the case of zero detuning, the line shape determining the absorption probability goes to zero—no absorption in the line center because of the zero in the line shape center. Thus, in the case of nonzero detunings, the absorption probability goes to the standard line dependence on pulse duration for sufficiently long pulses (α > 1).

Figure 5 demonstrates the effect of pulse duration on the Holtsmark–Doppler generalized line shape $F_{HD}\left(\alpha ,\delta ,\xi ={\mathsf{\Delta }}_D/{\mathsf{\Delta }}_H\right)$ for different values of Doppler to Holtsmark line width ratios, ξ, and pulse durations, α. It is seen that the effect of the Doppler broadening produces a decrease of the dip in the center of the static Holtsmark line shape.

It is seen from the comparison of Figure 5a,b that the pulse duration produces approximately the same effect on the static line shapes as Doppler broadening.

The dependences of Holtsmark–Doppler absorption line shapes on the pulse duration parameter, α, for zero detuning and the different ratios of Doppler to Holtsmark widths, ξ, are shown in Figure 6.

A smooth transition of the absorption probability to the linear dependence on pulse duration and a reduction of the absorption probability magnitude at small values of the parameter ξ due to the small value of the Holtsmark line shape in the central part of the spectral line can be observed.

3.4. Line Shapes of Highly Excited Rydberg Atomic States.

Hydrogen line shapes for radiative transitions from highly exited (Rydberg) states to low-excited ones hasvea simplified static line shape, due to the slow variation of the sum of π and σ component intensities for such transitions [11]. This makes it possible to present the corresponding line shapes in a universal manner, taking into account simultaneously both static ion and impact electron contributions as well as Stark–Doppler broadening. We use these results to calculate the USP absorption probability $F_R\left(\alpha ,\delta \right)$ by the substitution of corresponding shapes from [11] into the general Equation (3).

Such a static Stark line shape in this approximation accounting for electron collision broadening γ has the form [11]

$$G_{RL}\left(\beta ,\gamma \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}\cos \left(\beta x\right)\exp \left(-\gamma x-x^{3/2}\right)}$$

(11)

where β is the standard line shape parameter and γ is the ratio of the impact line width to the static width. The effect of pulse duration on absorption probability $F_{RL}\left(\alpha ,\delta ,\gamma \right)$ is shown in Figure 7 for detuning parameter δ = 5 and different relative values of impact to static line widths. It is clear that the transition from static to impact line shape following the increase of the impact width γ facilitates the transition from a linear to nonlinear regime in USP absorption.

The same procedure can be done with account for Stark–Doppler broadening:

$$G_{RD}\left(\beta ,\sigma \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}\cos \left(\beta x\right)\exp \left(-{\sigma }^2{x}^2/2-x^{3/2}\right)}$$

(12)

The effect of pulse duration on the Rydberg Stark–Doppler absorption probability $F_{RD}\left(\alpha ,\delta ,\sigma \right)$ is shown in Figure 8. It is clear that the minimum in such dependence disappears with the increase of Doppler broadening. A comparison of Figure 7 and Figure 8 shows that the Lorentz broadening affects the dependence of the function F(α) more strongly than the Doppler one due to the wider wings in the spectral dependence of the Lorentzian broadening.

From the comparison of Figure 7 and Figure 8 with previous figures describing Doppler, Voigt and Holtsmark line shapes, one can see that, for Rydberg absorption, the function F(α) reaches its maximum at a smaller value of dimensionless pulse duration (α_max ≈ 0.25), while in other cases α_max ≈ 0.5.

The line shapes of radiative transitions are strongly simplified for Rydberg atomic states, making it possible to take into account Stark, collisional and Doppler broadening simultaneously according to equations (11–12). This also simplifies the research of the effect of USPs on atomic transitions for Rydberg lines.

4. Conclusions

The calculations of absorption probabilities in the interaction of USPs with atomic systems in plasmas are made within the frame of perturbation theory regarding the amplitude of laser pulses. The results are expressed in terms of generalized line shapes of the absorption, which contain additional parameters related to pulse duration together with other standard parameters of the broadening theory. Specific broadening mechanisms relative to plasma conditions are considered: Doppler, Voigt, Holtsmark, and their combinations, as well as Stark line broadening of Rydberg atomic lines. The effects of pulse duration on absorption probabilities as well as their spectral dependence are investigated in detail. The specific interest of the research is the transition of the absorption probabilities from nonlinear time dependence at a small pulse duration to linear ones for long pulses depending on carrier frequency detuning from their frequency of transition. The research is presented in universal form, making applications for different atoms and plasma conditions possible.