H-β Line in a Corona Helium Plasma: A Multi-Code Line Shape Comparison
Abstract
:1. Introduction
2. Brief Description of the Codes
3. Code Comparison through Profiles and Line Widths
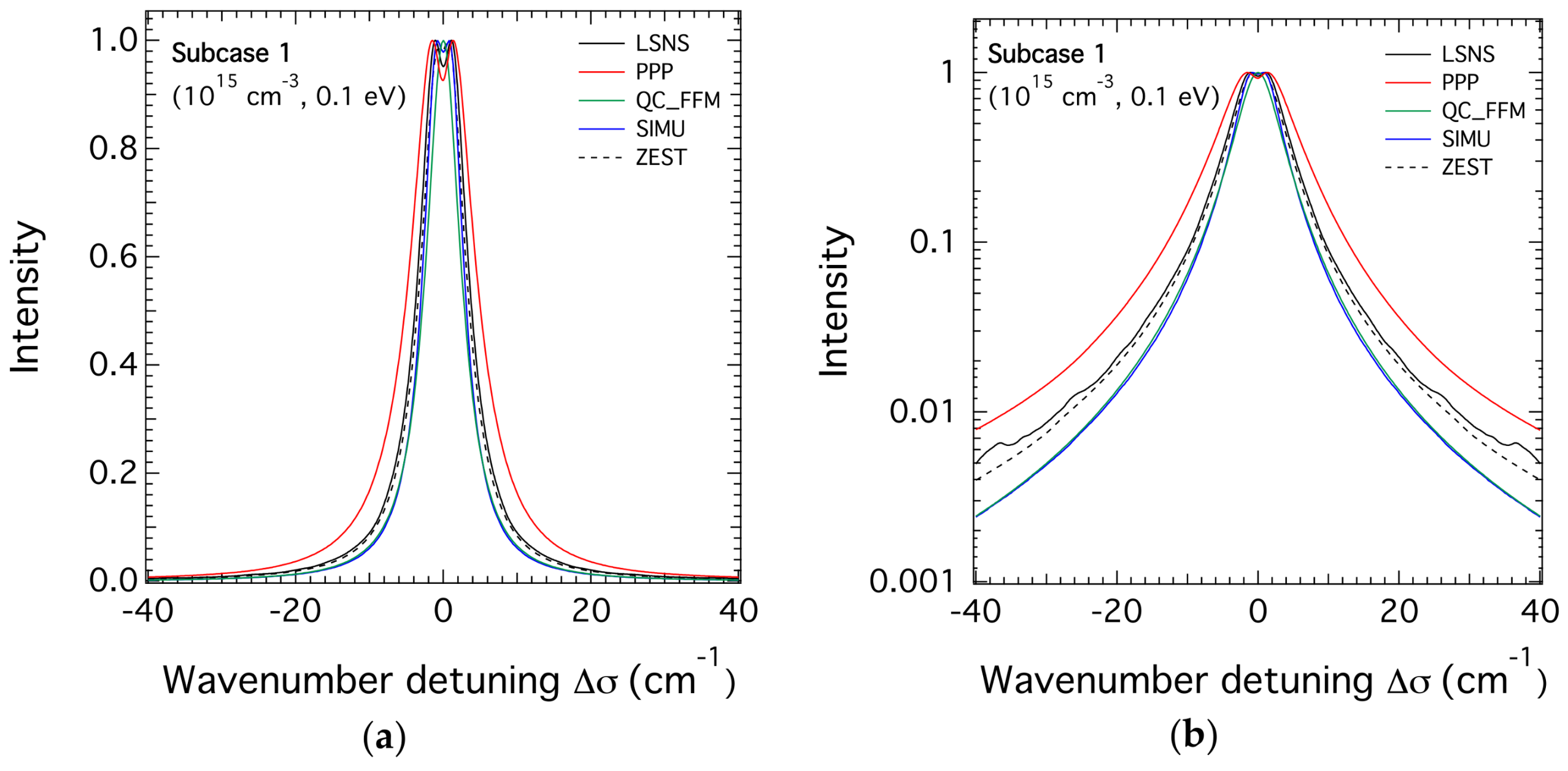
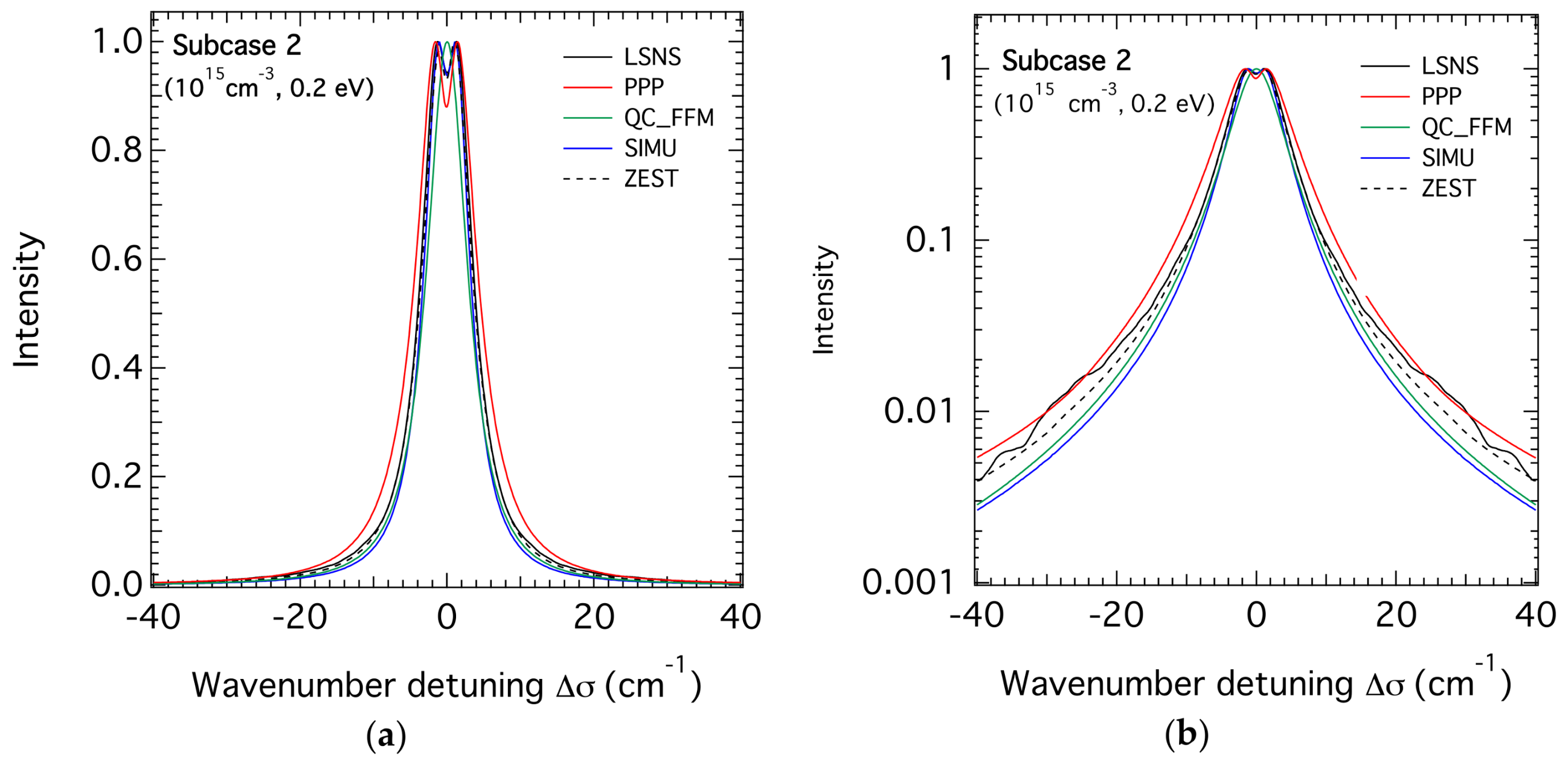
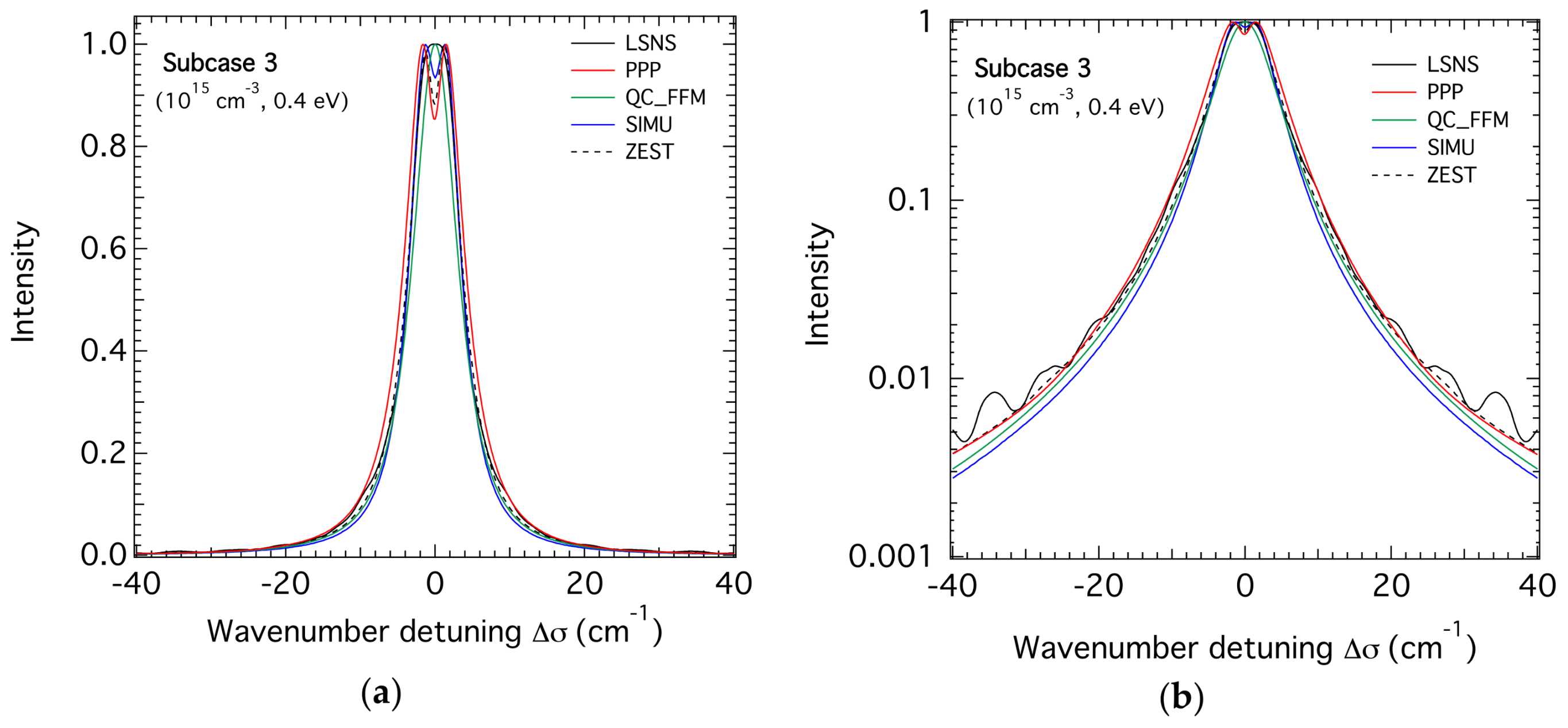
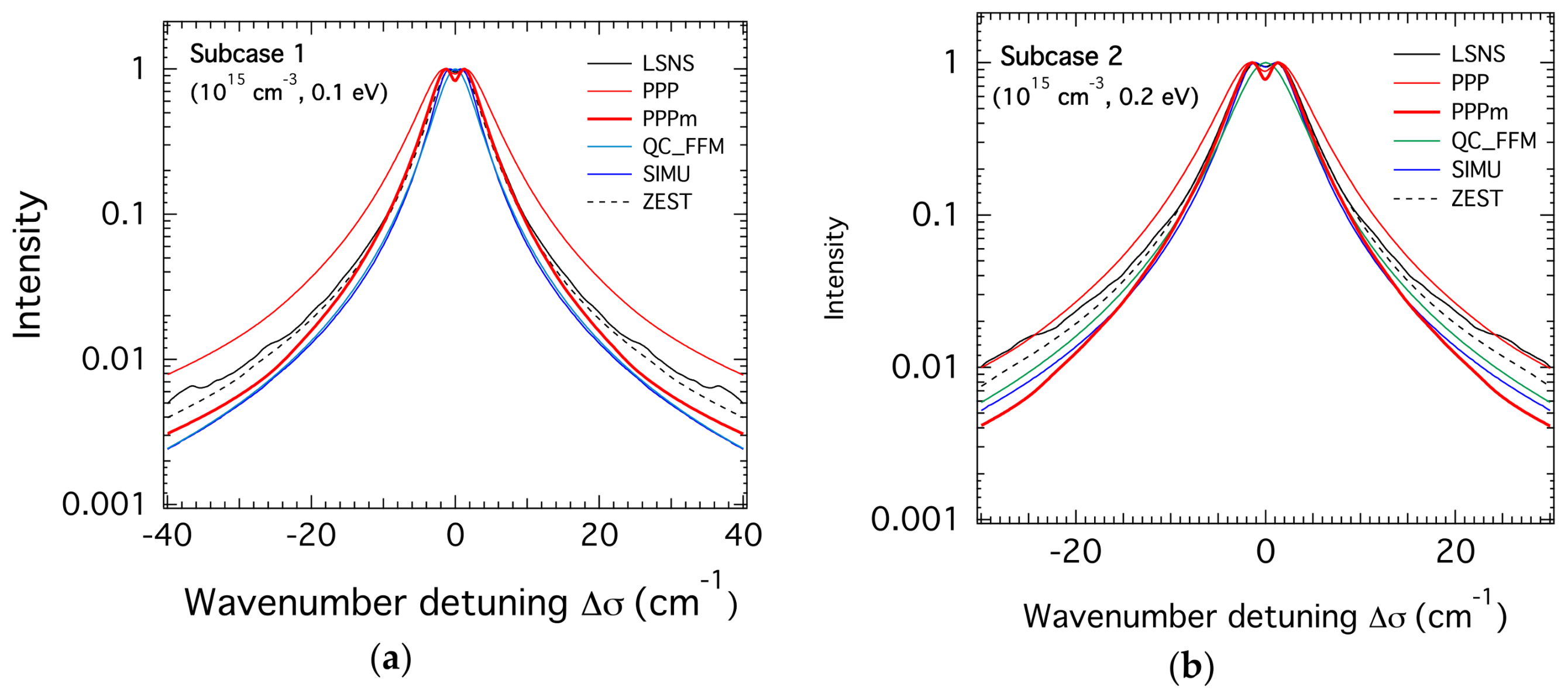
3.1. H-β Line Profiles for the Lower Density
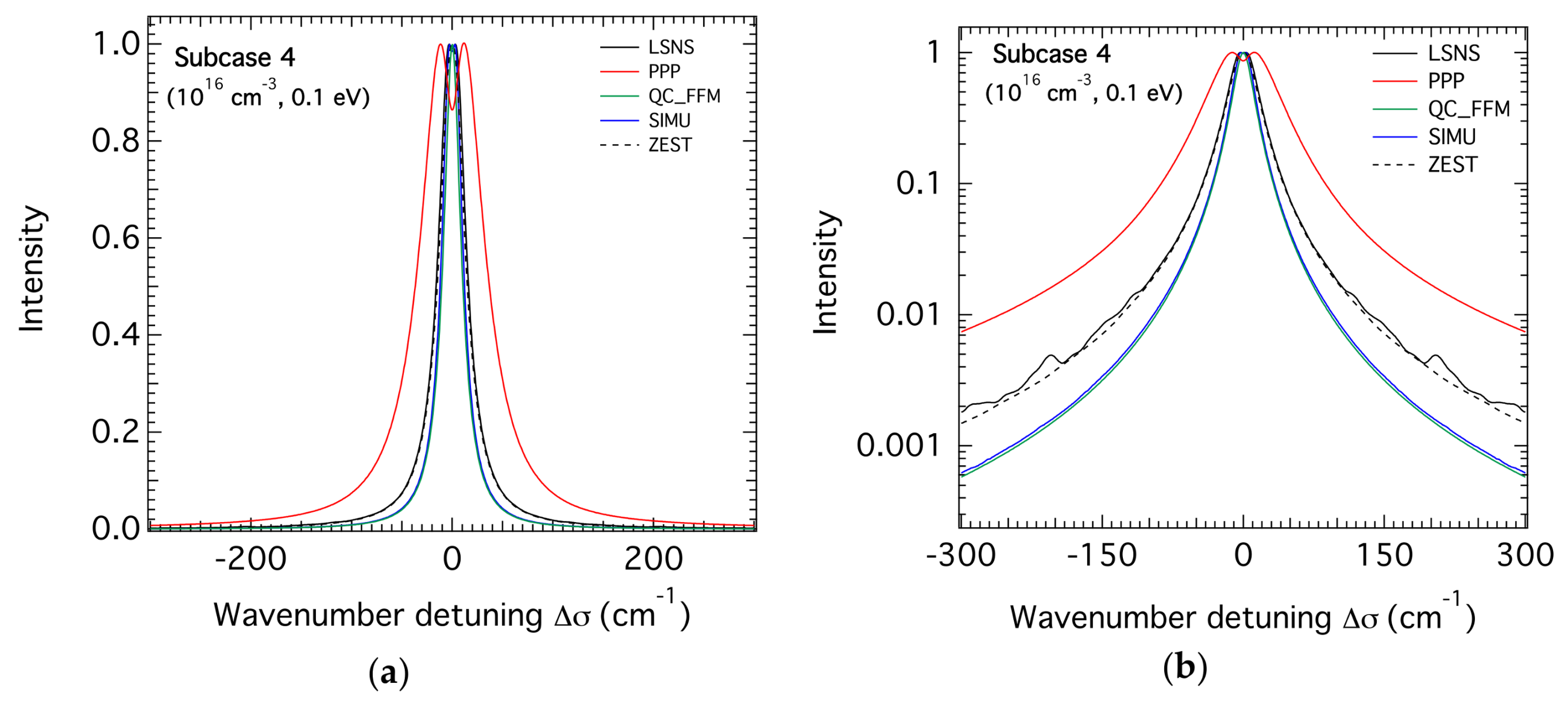
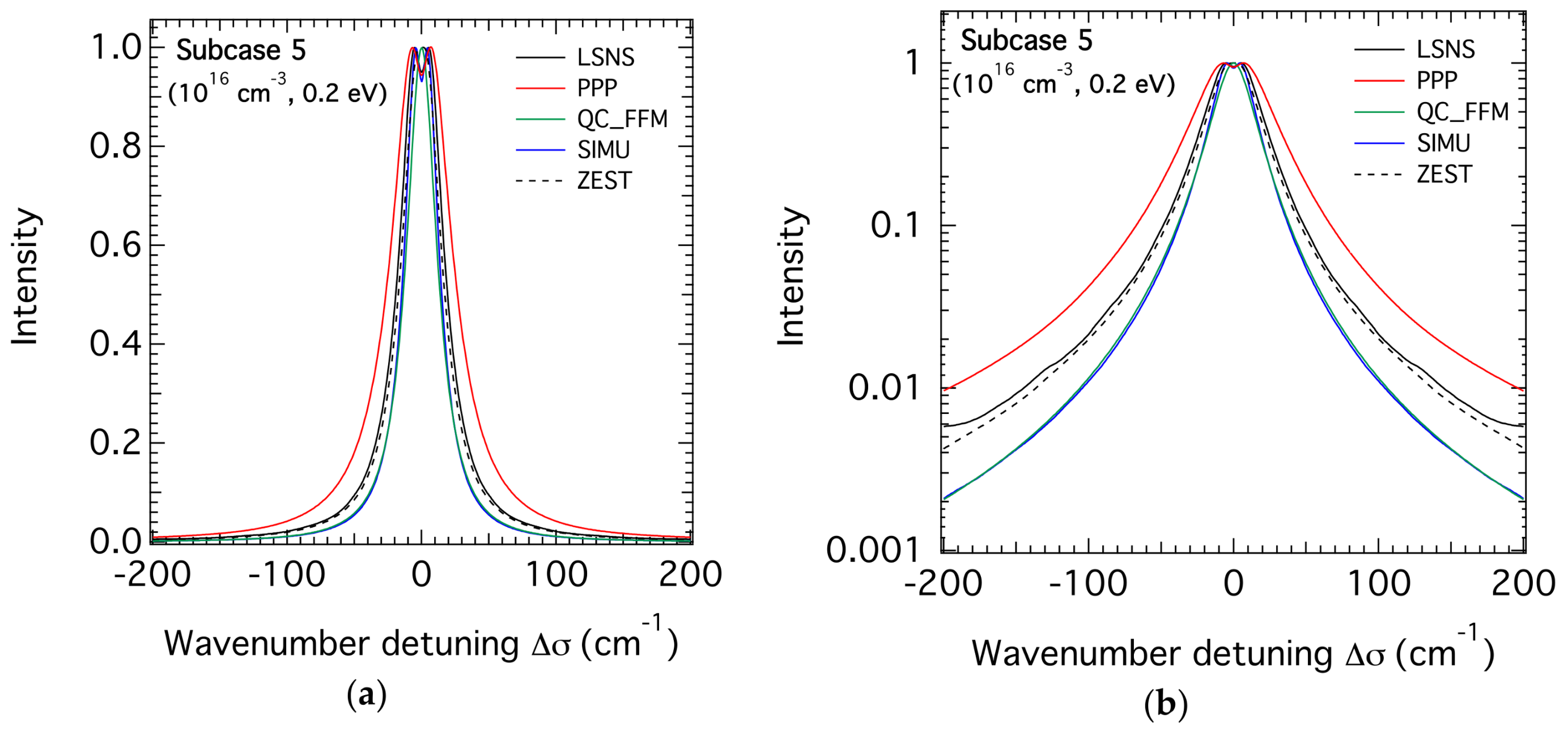
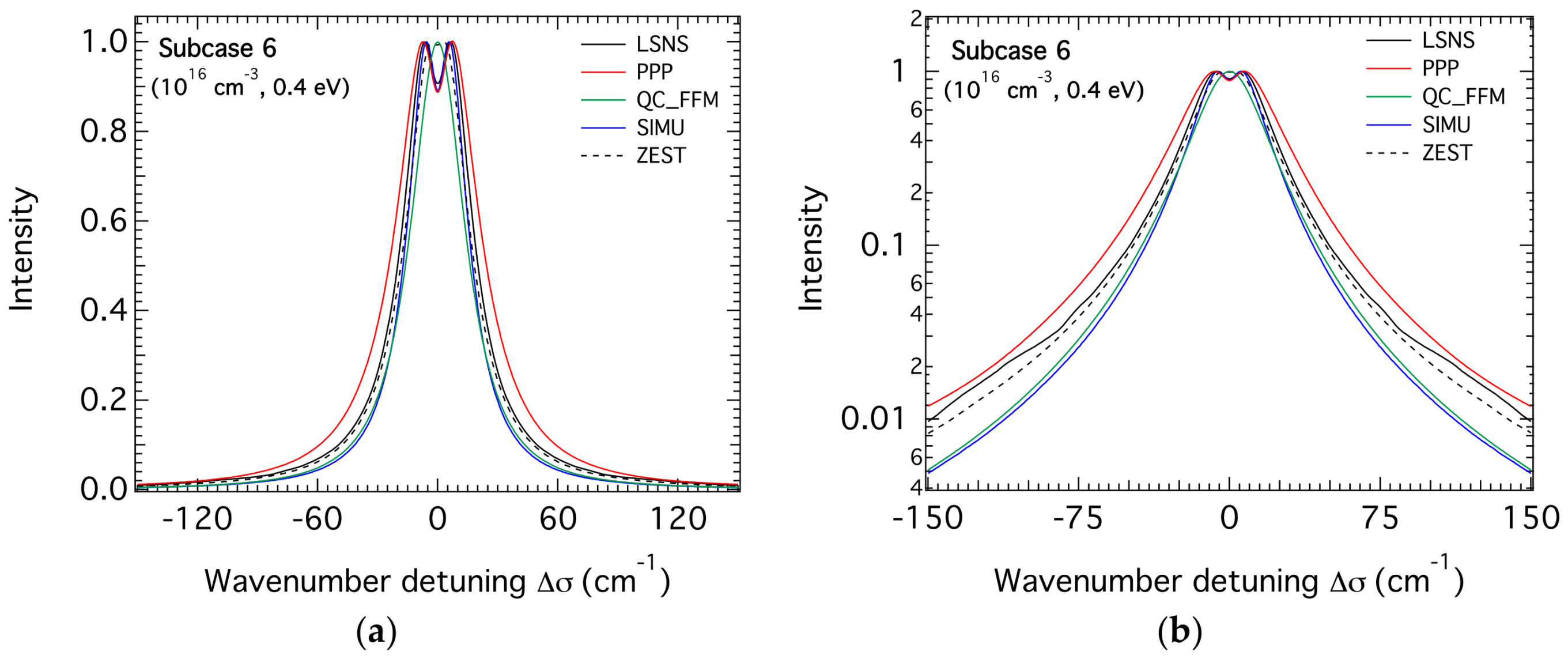
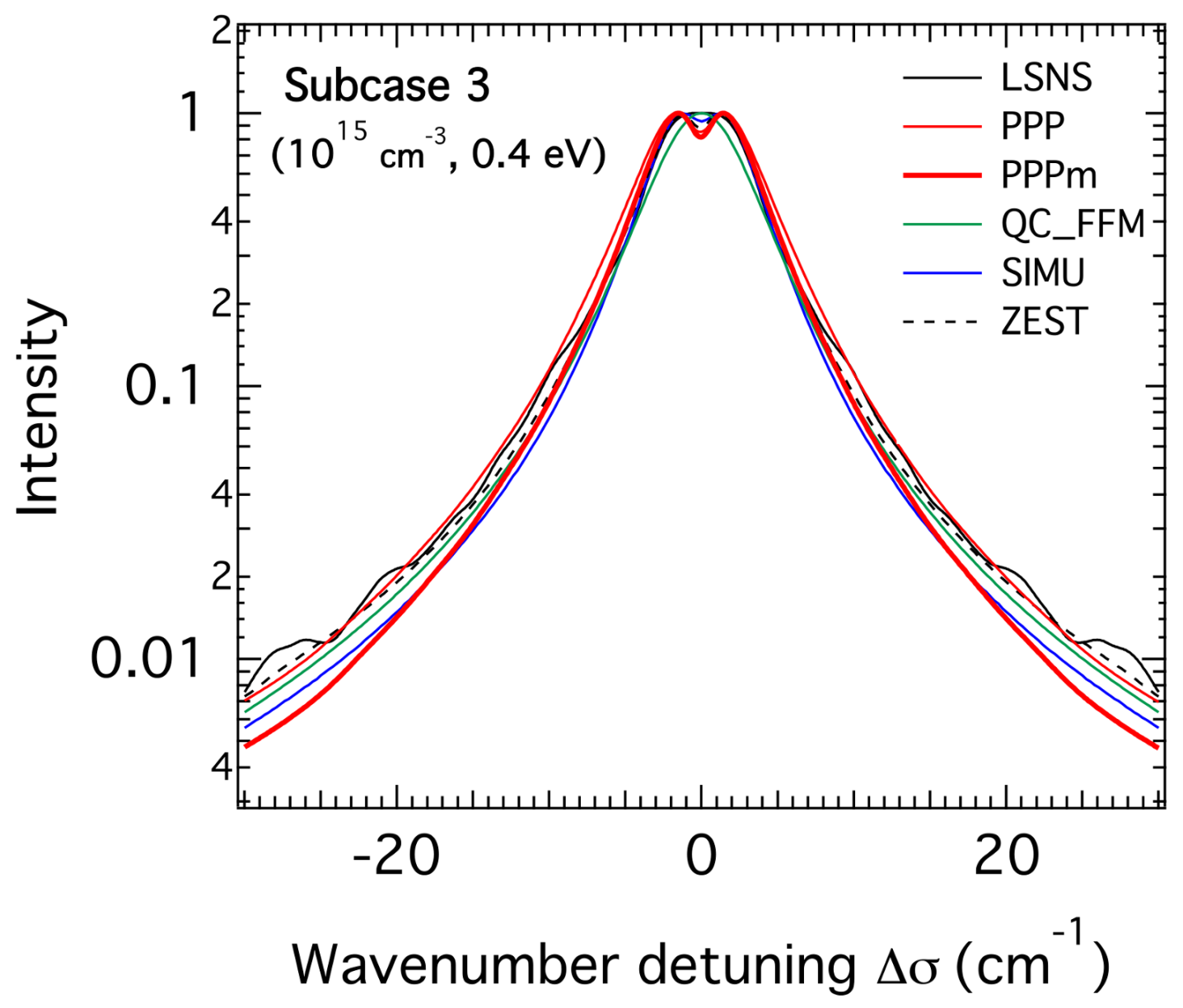
3.2. H-β Line Profiles for the Highest Density
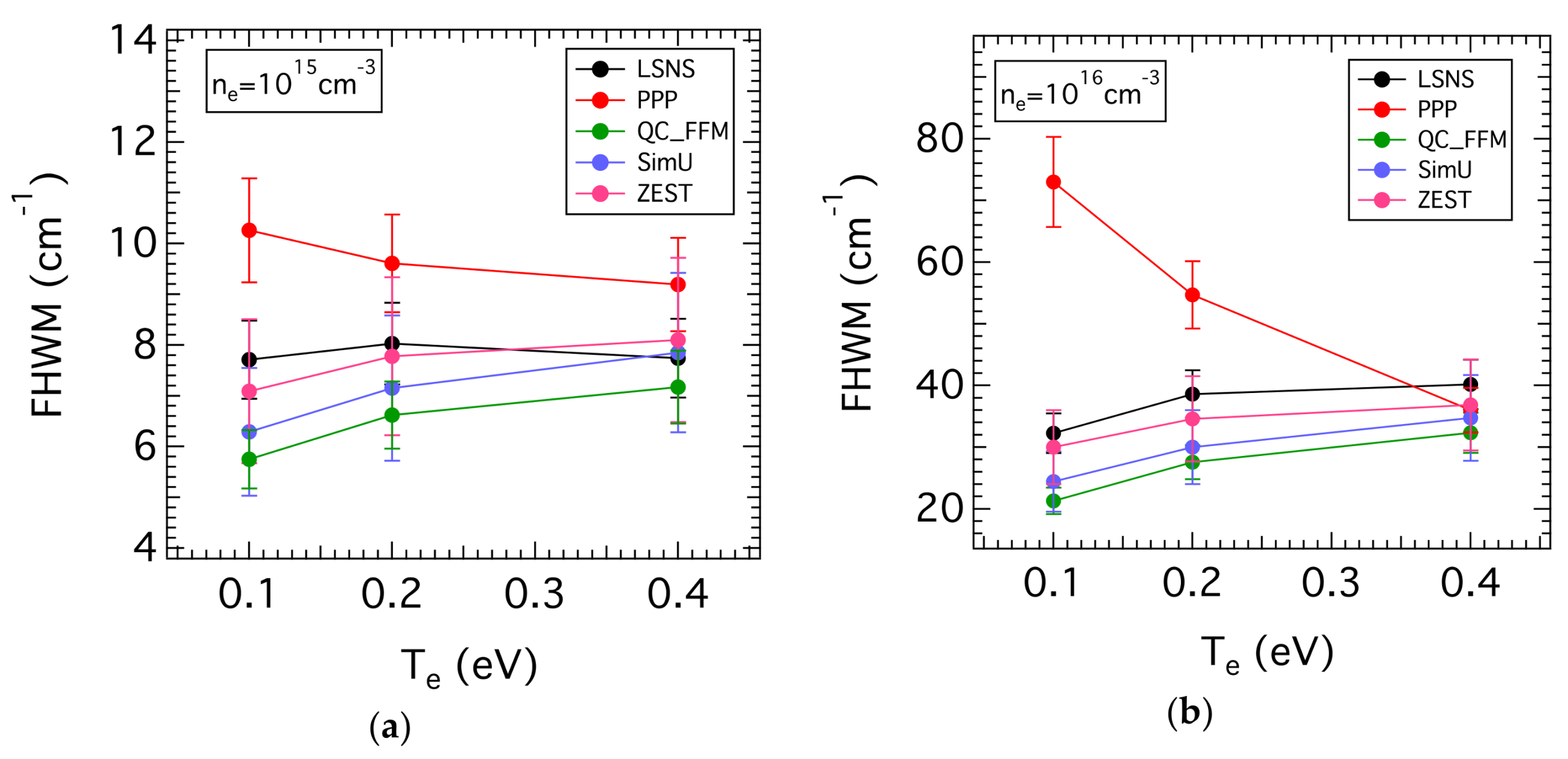
3.3. Comparison of the FWHM of the H-β Line
3.4. Reconsidering the PPP Calculations of the H-β Line
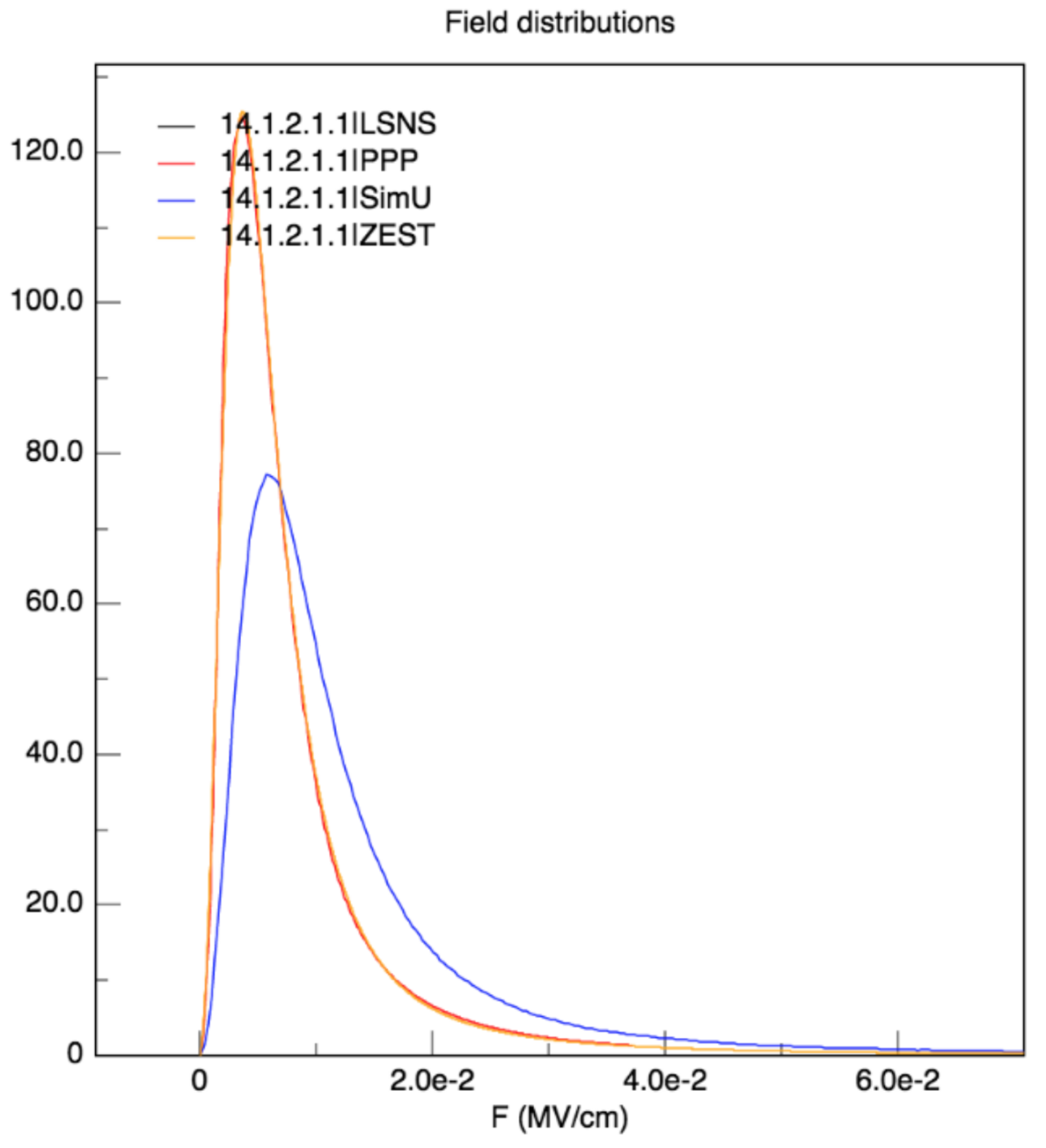
3.5. Electric Microfield Distributions
4. Comparison with Experimental Spectra: Line Shape Fitting
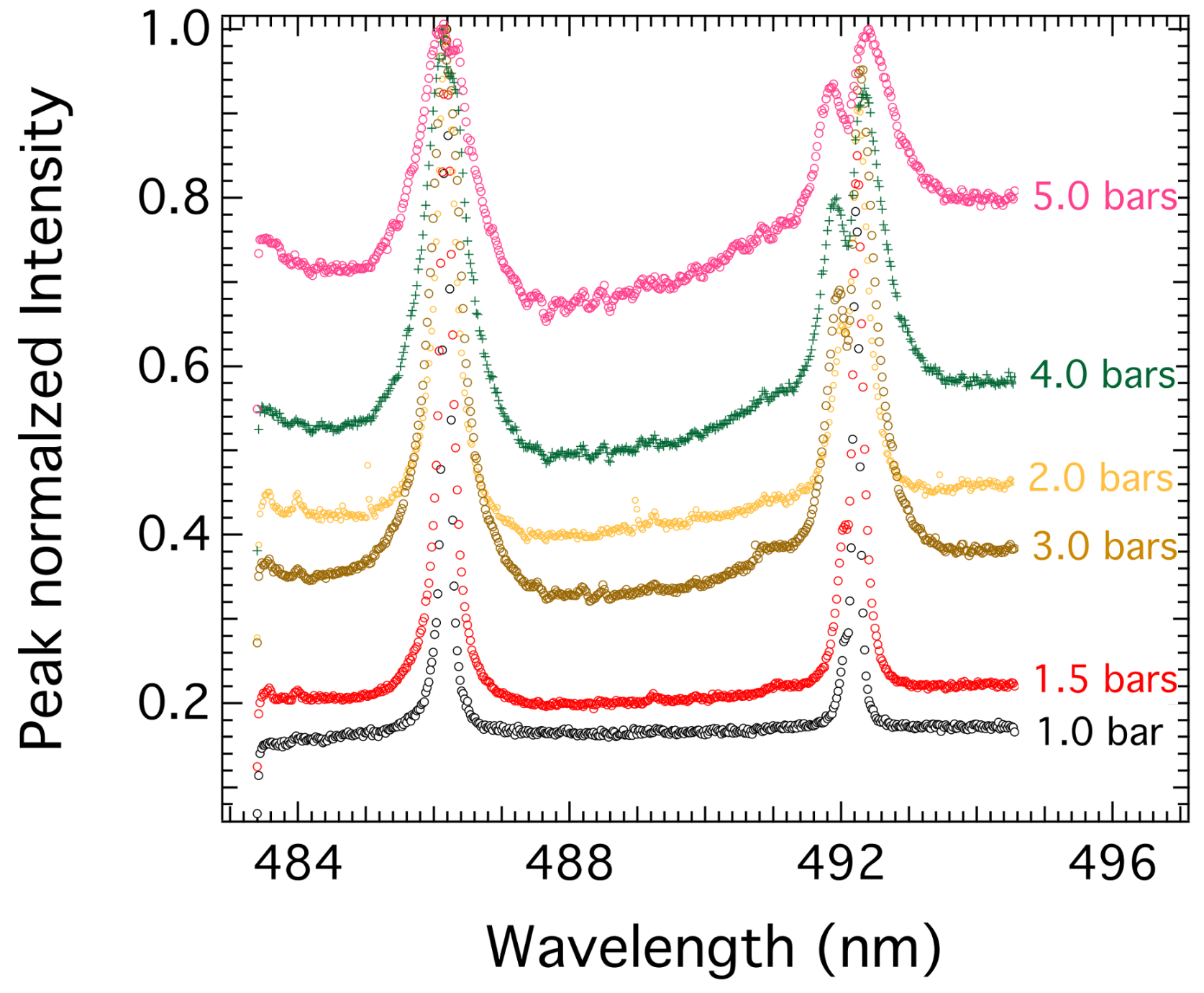
4.1. Introducing the Experimental Spectra
4.2. Broadening Mechanisms of H-β Line in a Helium Plasma
4.3. Comparison with Experimental Data: Spectral Fitting
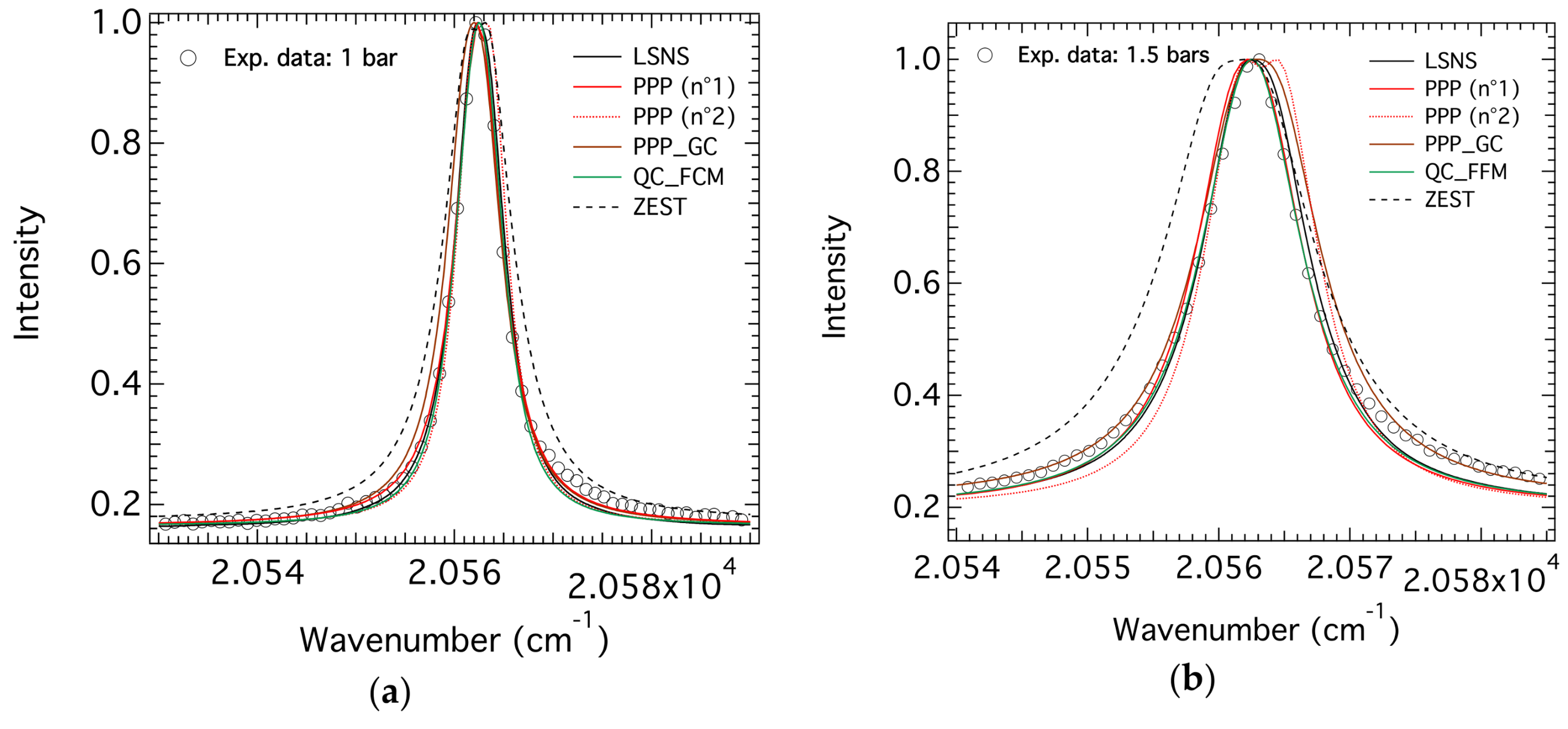
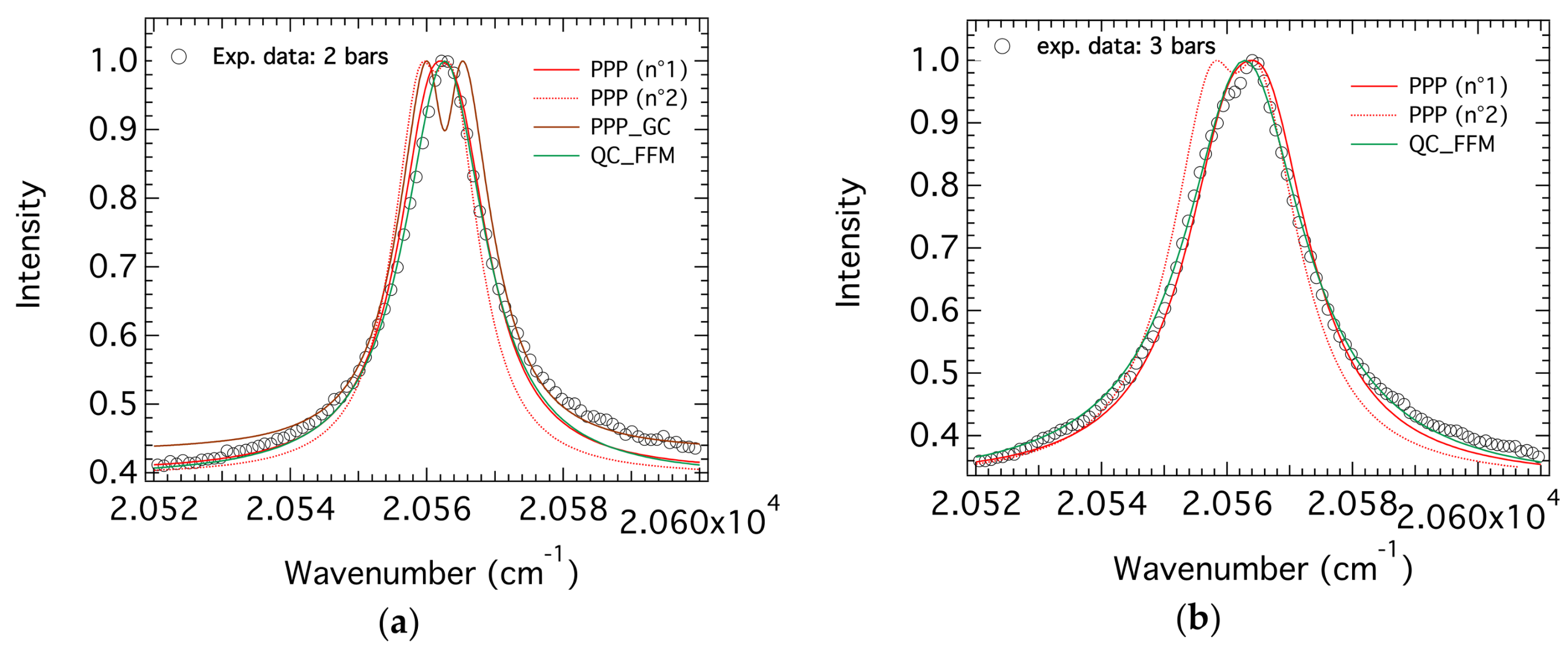
4.3.1. Cases of Low Pressure
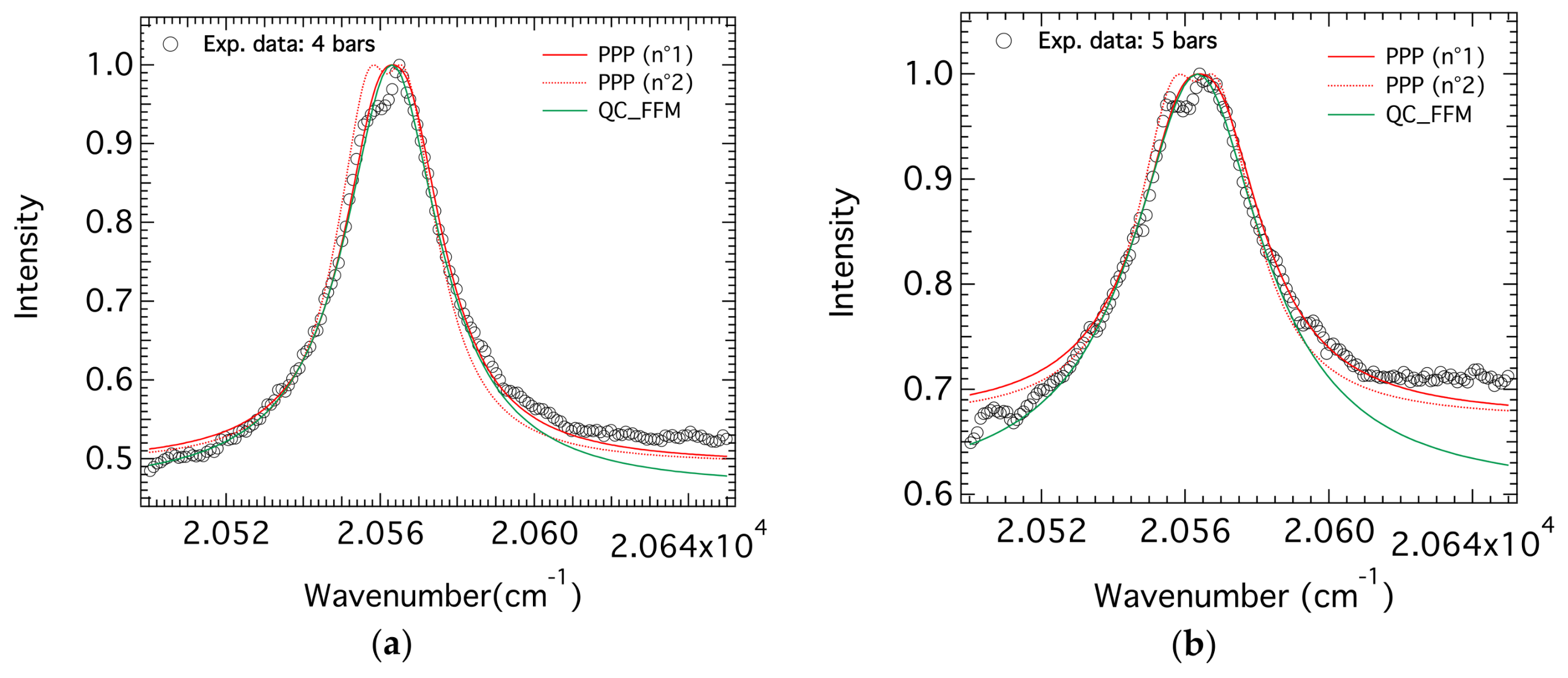
4.3.2. Cases of Intermediate Pressures
4.3.3. Cases of High Pressures
4.4. Interpretation of the Fitting Parameters
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Stambulchik, E. Review of the 1st spectral line shapes in plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528. [Google Scholar] [CrossRef]
- 4th SLSP Workshop. Available online: http://plasma-gate.weizmann.ac.il/projects/slsp/slsp4/ (accessed on 22 February 2018).
- Sheeba, R.R.; Koubiti, M.; Bonifaci, N.; Gilleron, F.; Pain, J.C.; Stambulchik, E. Broadening of the neutral helium 492 nm line in a corona discharge: Code comparison and data fitting. Atoms 2018, 6, 19. [Google Scholar] [CrossRef]
- Rosato, J.; Bufferand, H.; Koubiti, M.; Marandet, Y.; Stamm, R. A table of Balmer γ line shapes for the diagnostic of magnetic fusion plasmas. J. Quant. Spectrosc. Radiat. Transfer 2015, 165, 102–107. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Stambulchik, E.; Alexiou, S.; Griem, H.R.; Kepple, P.C. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. E 2007, 75, 016401. [Google Scholar] [CrossRef] [PubMed]
- Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B.; Lee, R.W. Model for the line shapes of complex ions in hot and dense plasmas. Phys. Rev. A 1990, 42, 5433–5440. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Maron, Y. Quasicontiguous frequency-fluctuation model for calculation of hydrogen and hydrogenlike Stark-broadened line shapes in plasmas. Phys. Rev. E 2013, 87, 053108. [Google Scholar] [CrossRef] [PubMed]
- Gilleron, F.; Pain, J.C. ZEST: A fast code for simulating Zeeman-Stark line-shape functions. Atoms 2018, 6, 11. [Google Scholar] [CrossRef]
- Lee, R.W. Plasma line shapes for selected transitions in Hydrogen-, Helium- and Lithium-like ions. J. Quant. Spectrosc. Radiat. Transf. 1988, 40, 561–568. [Google Scholar] [CrossRef]
- Potekhin, A.; Chabrier, G.; Gilles, D. Electric microfield distributions in electron-ion plasmas. Phys. Rev. E 2002, 65, 036412. [Google Scholar] [CrossRef] [PubMed]
- Gilles, D.; Peyrusse, O. Fast and accurate line shape modeling of the H- and He-like Lyman series for radiative transfer calculations in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1995, 53, 647–661. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef] [PubMed]
- Griem, H.R.; Blaha, M.; Kepple, P.C. Stark-profile calculations for Lyman-series lines of one-electron ions in dense plasmas. Phys. Rev. A 1979, 19, 2421. [Google Scholar] [CrossRef]
- Rosato, J.; Bonifaci, N.; Li, Z.; Stamm, R. A spectroscopic diagnostic of the electron density in a corona discharge. J. Phys. Conf. Ser. 2017, 810, 012057. [Google Scholar] [CrossRef]
- Li, Z.-L.; Bonifaci, N.; Aitken, F.; Denat, A.; von Haeften, K.; Atrazhev, V.M.; Shakhatov, V.A. Spectroscopic investigation of liquid helium excited by a corona discharge: Evidence for bubbles and “red satellites”. Eur. Phys. J. Appl. Phys. 2009, 47, 2821. [Google Scholar] [CrossRef]
- Rosato, J.; Bonifaci, N.; Li, Z.; Stamm, R. Line shape modeling for the diagnostic of the electron density in a corona discharge. Atoms 2017, 5, 35. [Google Scholar] [CrossRef]
- Ali, A.W.; Griem, H.R. Theory of resonance broadening of spectral lines by atom-atom impacts. Phys. Rev. 1965, 4A, A1044. [Google Scholar] [CrossRef]
- Laux, C.O.; Spence, T.G.; Kruger, C.H.; Zare, R.N. Optical diagnostics of atmospheric pressure air plasmas. Plasma Sources Sci. Technol. 2003, 12, 125–138. [Google Scholar] [CrossRef]
- Nikiforov, A.Y.; Leys, C.; Gonzalez, M.A.; Walsh, J.L. Electron density measurement in atmospheric pressure plasma jets: Stark broadening of hydrogenated and non-hydrogenated lines. Plasma Sources Sci. Technol. 2015, 24, 034001. [Google Scholar] [CrossRef]
- Yubero, C.; Dimitrijevic, M.S.; García, M.C.; Calzada, M.D. Using the van der Waals broadening of the spectral atomic lines to measure the gas temperature of an argon microwave plasma at atmospheric pressure. Spectrochim. Acta B 2007, 62, 169–176. [Google Scholar] [CrossRef]
- Allard, N.; Kielkopf, J. The effect of neutral non resonant collisions on atomic spectral lines. Rev. Mod. Phys. 1982, 54, 1103. [Google Scholar] [CrossRef]
- Muñoz, J.; Dimitrijevic, M.S.; Yubero, C.; Calzada, M.D. Using the van der Waals broadening of spectral atomic lines to measure the gas temperature of an argon-helium microwave plasma at atmospheric pressure. Spectrochim. Acta B 2009, 64, 167–172. [Google Scholar] [CrossRef]
- Mossé, C.; Génésio, P.; Bonifaci, N.; Calisti, A. A new procedure to determine the plasma parameters from a genetic algorithm coupled with the spectral line shape PPP. Atoms 2018. submitted. [Google Scholar]
| Plasma Parameters | Codes | ||||||
|---|---|---|---|---|---|---|---|
| (ne, Te = Ti) | LSNS | PPP | QC_FFM | SimU | ZEST | Mean | Factor |
| (1015 cm−3, 0.1 eV) | |||||||
| FWHM (cm−1) | 7.71 | 10.26 | 5.75 | 6.29 | 7.09 | 6.71 | - |
| FWHM ratio | 1.3 | 1.0 | 1.8 | 1.6 | 1.4 | 1.53 | 1.53 |
| (1015 cm−3, 0.2 eV) | |||||||
| FWHM (cm−1) | 8.03 | 9.61 | 6.62 | 7.15 | 7.78 | 7.39 | - |
| FWHM ratio | 1.2 | 1.0 | 1.4 | 1.3 | 1.2 | 1.30 | 1.30 |
| (1015 cm−3, 0.4 eV) | |||||||
| FWHM (cm−1) | 7.74 | 9.19 | 7.17 | 7.85 | 8.10 | 7.71 | - |
| FWHM ratio | 1.2 | 1.0 | 1.3 | 1.2 | 1.1 | 1.19 | 1.19 |
| (1016 cm−3, 0.1 eV) | |||||||
| FWHM (cm−1) | 32.24 | 73.00 | 21.27 | 24.40 | 30.00 | 26.97 | - |
| FWHM ratio | 2.3 | 1.0 | 3.4 | 3.0 | 2.4 | 2.7 | 2.7 |
| (1016 cm−3, 0.2 eV) | |||||||
| FWHM (cm−1) | 38.59 | 54.67 | 27.56 | 29.98 | 34.60 | 32.68 | - |
| FWHM ratio | 1.4 | 1.0 | 2.0 | 1.8 | 1.6 | 1.67 | 1.67 |
| (1016 cm−3, 04 eV) | |||||||
| FWHM (cm−1) | 40.18 | 36.00 | 32.34 | 34.73 | 36.82 | 36.01 | - |
| FWHM ratio | 1.0 | 1.1 | 1.2 | 1.2 | 1.1 | 1.11 | 1.00 |
| Pressure (bars) | (nm) | (nm) | (%) |
|---|---|---|---|
| 1 | 0.051 | 0.143 | 35 |
| 1.5 | 0.076 | 0.206 | 36 |
| 2 | 0.101 | 0.335 | 30 |
| 3 | 0.152 | 0.510 | 30 |
| 4 | 0.202 | 0.604 | 31 |
| 5 | 0.253 | 0.819 | 31 |
| Case n° | P | LSNS | PPP (n°1) | PPP (n°2) | PPP_GC | QC_FFM | ZEST |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.5 | 0.15 | 0.26 | 0.18 | 0.8 | 1.2 |
| 2 | 1.5 | 1.1 | 0.3 | 0.58 | 0.38 | 2.2 | 2.7 |
| 3 | 2 | - | 0.55 | 1.0 | 1.3 | 4.7 | - |
| 4 | 3 | - | 0.9 | 2.0 | - | 10.0 | - |
| 5 | 4 | - | 1.3 | 2.8 | - | 15.0 | - |
| 6 | 5 | - | 1.9 | 3.8 | - | 27.0 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheeba, R.R.; Koubiti, M.; Bonifaci, N.; Gilleron, F.; Mossé, C.; Pain, J.-C.; Rosato, J.; Stambulchik, E. H-β Line in a Corona Helium Plasma: A Multi-Code Line Shape Comparison. Atoms 2018, 6, 29. https://doi.org/10.3390/atoms6020029
Sheeba RR, Koubiti M, Bonifaci N, Gilleron F, Mossé C, Pain J-C, Rosato J, Stambulchik E. H-β Line in a Corona Helium Plasma: A Multi-Code Line Shape Comparison. Atoms. 2018; 6(2):29. https://doi.org/10.3390/atoms6020029
Chicago/Turabian StyleSheeba, Roshin Raj, Mohammed Koubiti, Nelly Bonifaci, Franck Gilleron, Caroline Mossé, Jean-Christophe Pain, Joël Rosato, and Evgeny Stambulchik. 2018. "H-β Line in a Corona Helium Plasma: A Multi-Code Line Shape Comparison" Atoms 6, no. 2: 29. https://doi.org/10.3390/atoms6020029
APA StyleSheeba, R. R., Koubiti, M., Bonifaci, N., Gilleron, F., Mossé, C., Pain, J.-C., Rosato, J., & Stambulchik, E. (2018). H-β Line in a Corona Helium Plasma: A Multi-Code Line Shape Comparison. Atoms, 6(2), 29. https://doi.org/10.3390/atoms6020029







