Revisiting the Stark Width and Shift of He II Pα
Abstract
1. Introduction
2. Experiment
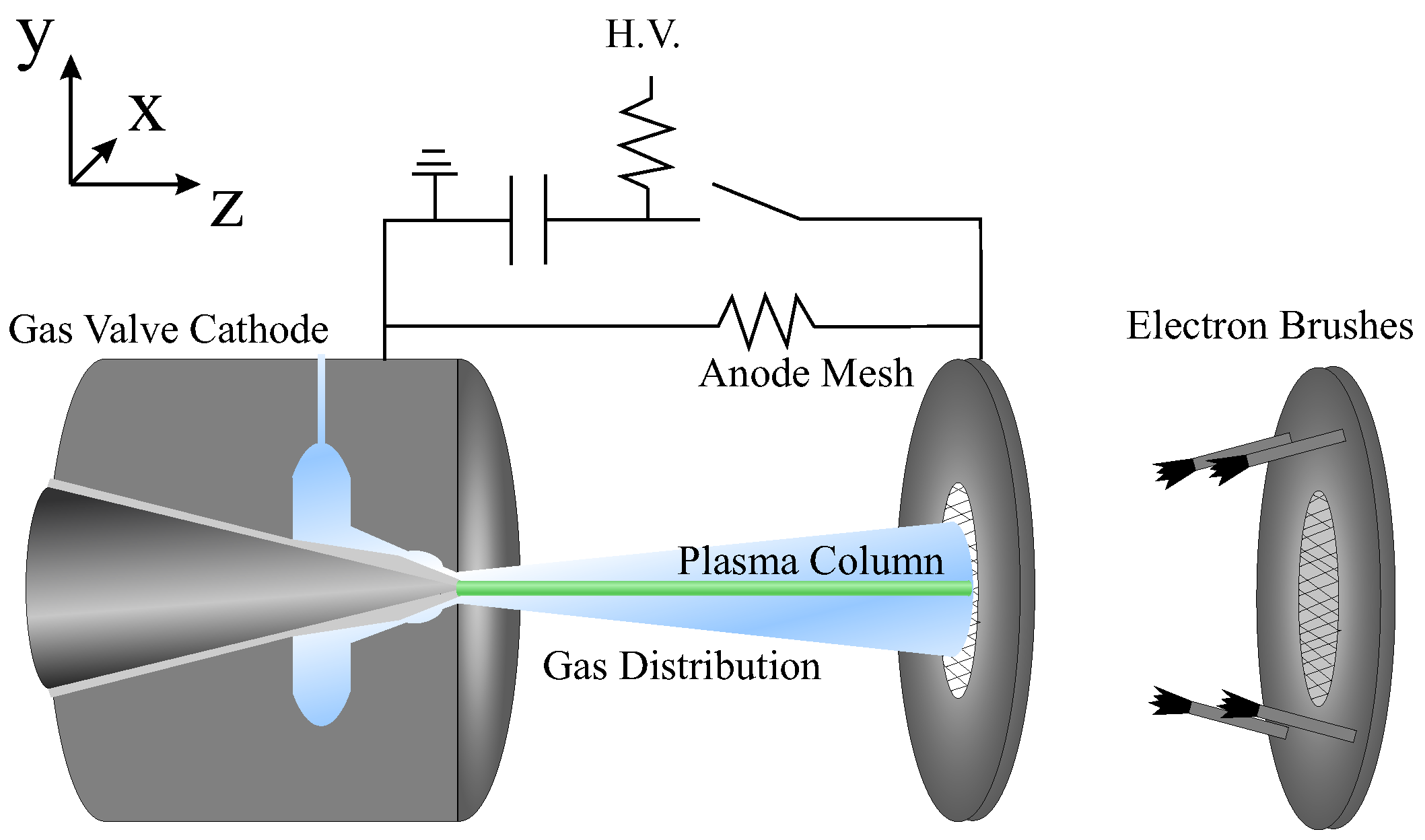
2.1. Experimental Setup
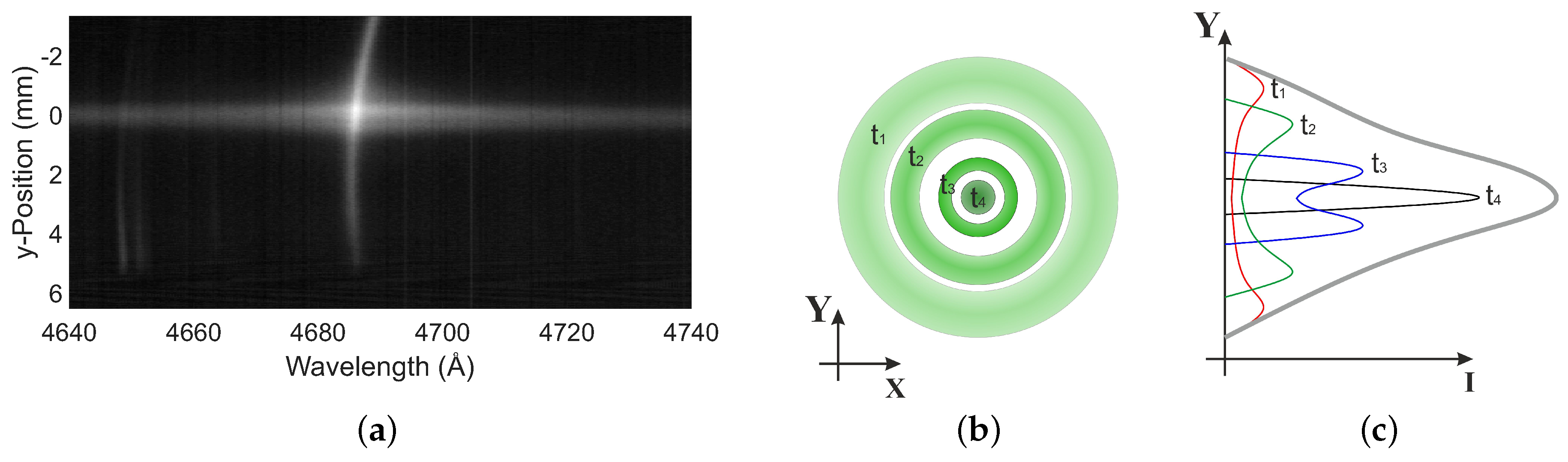
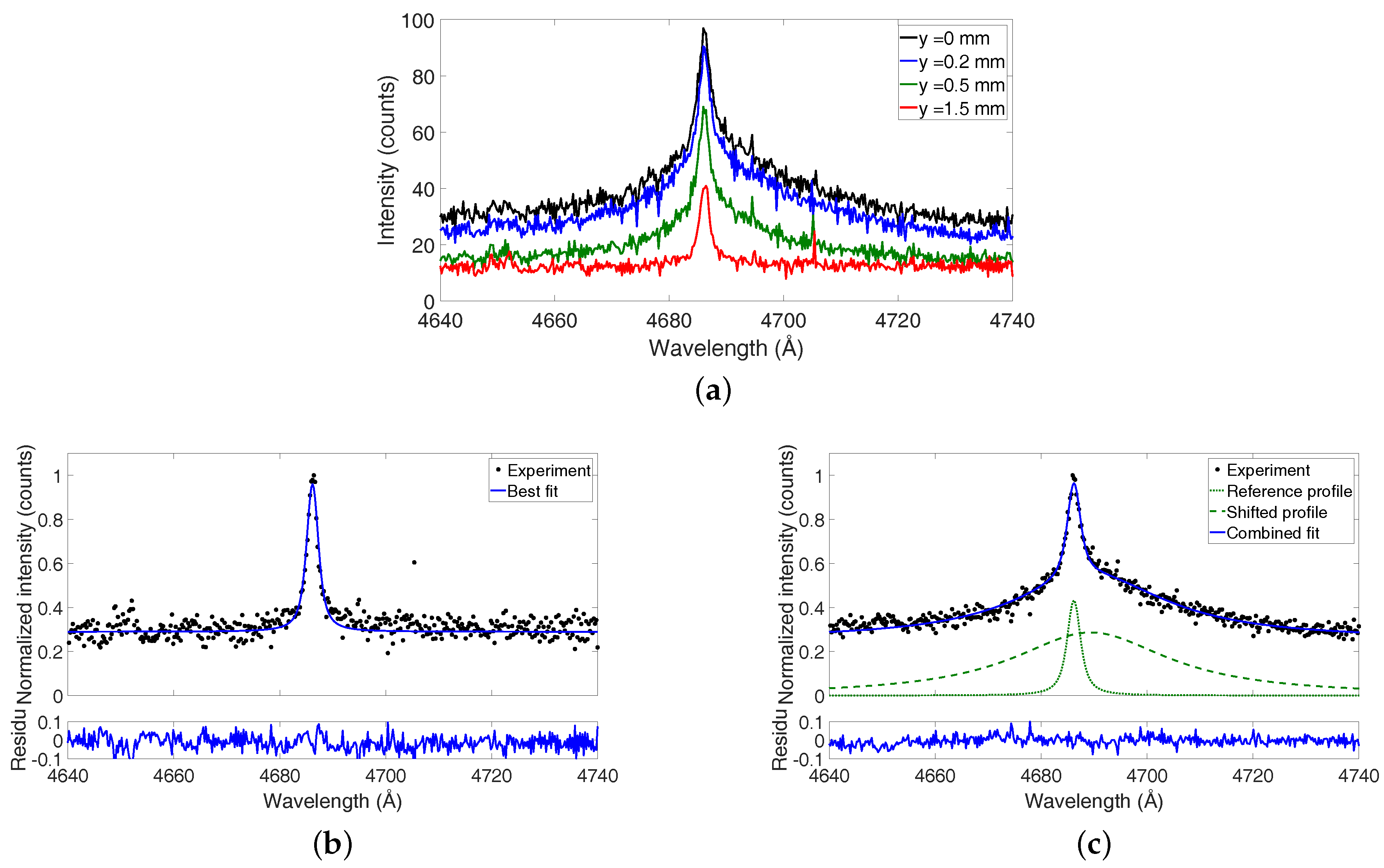
2.2. Experimental Data
3. Code Comparison
3.1. Description of Participating Codes
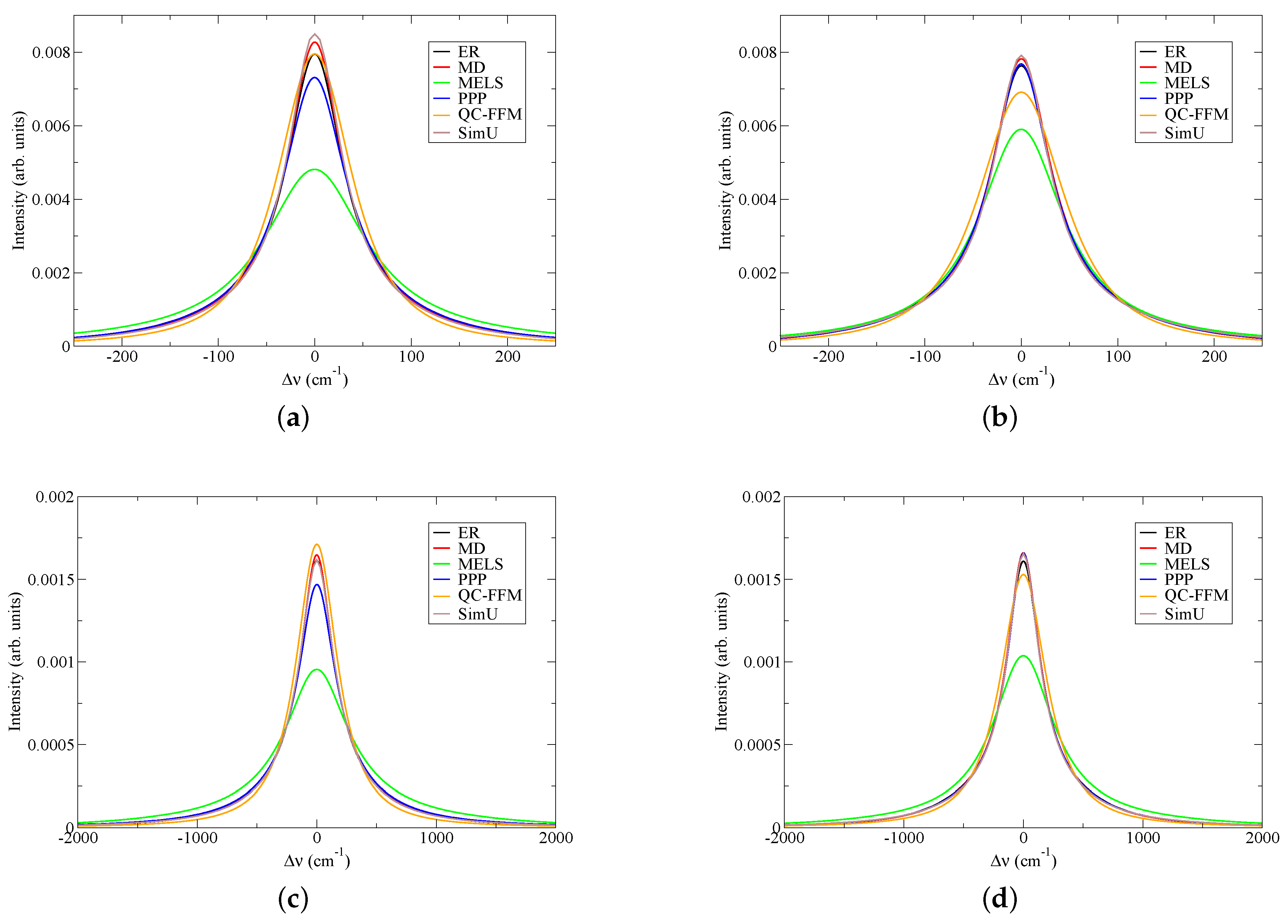
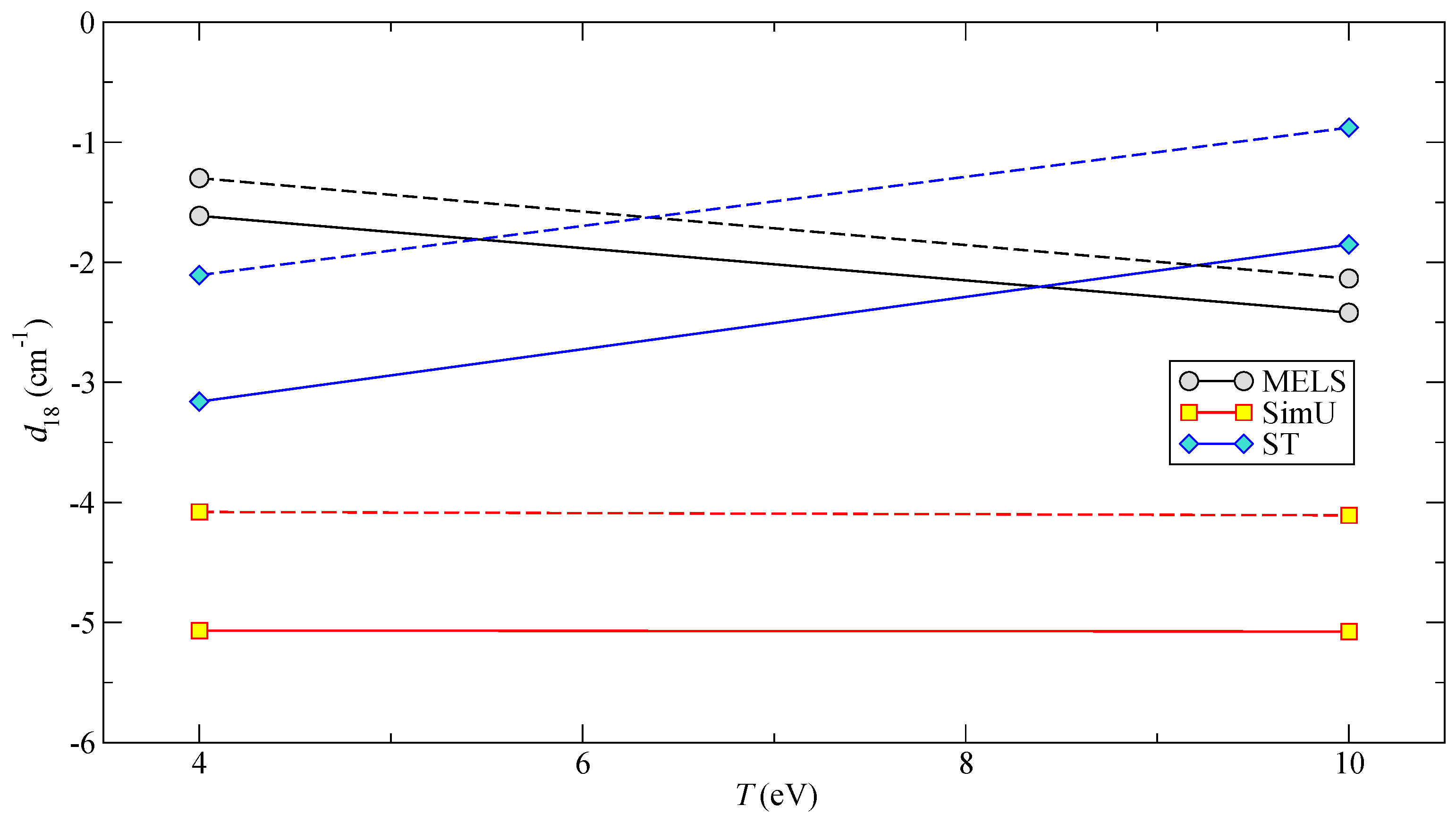
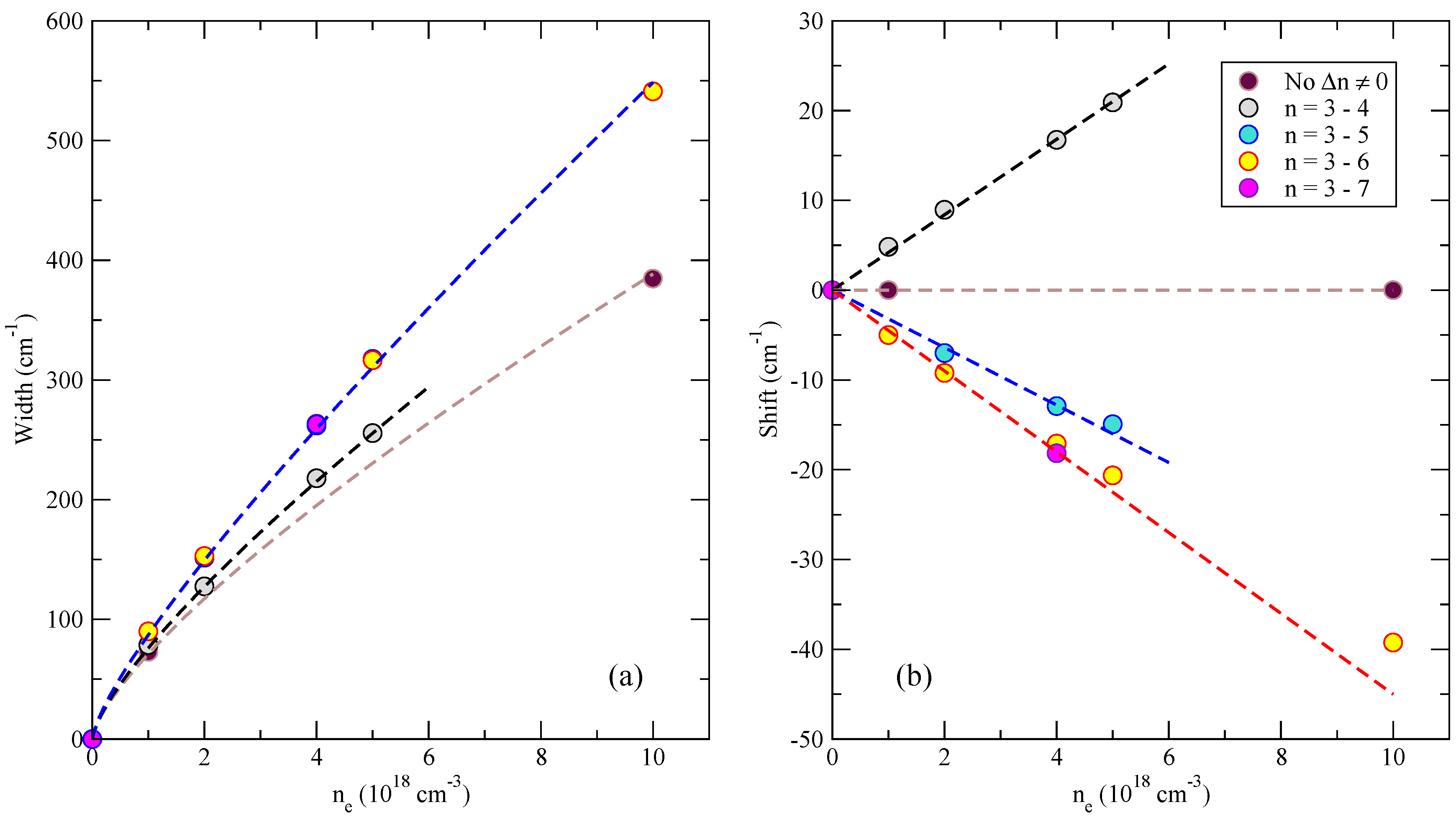
3.2. Code Results in Model Cases
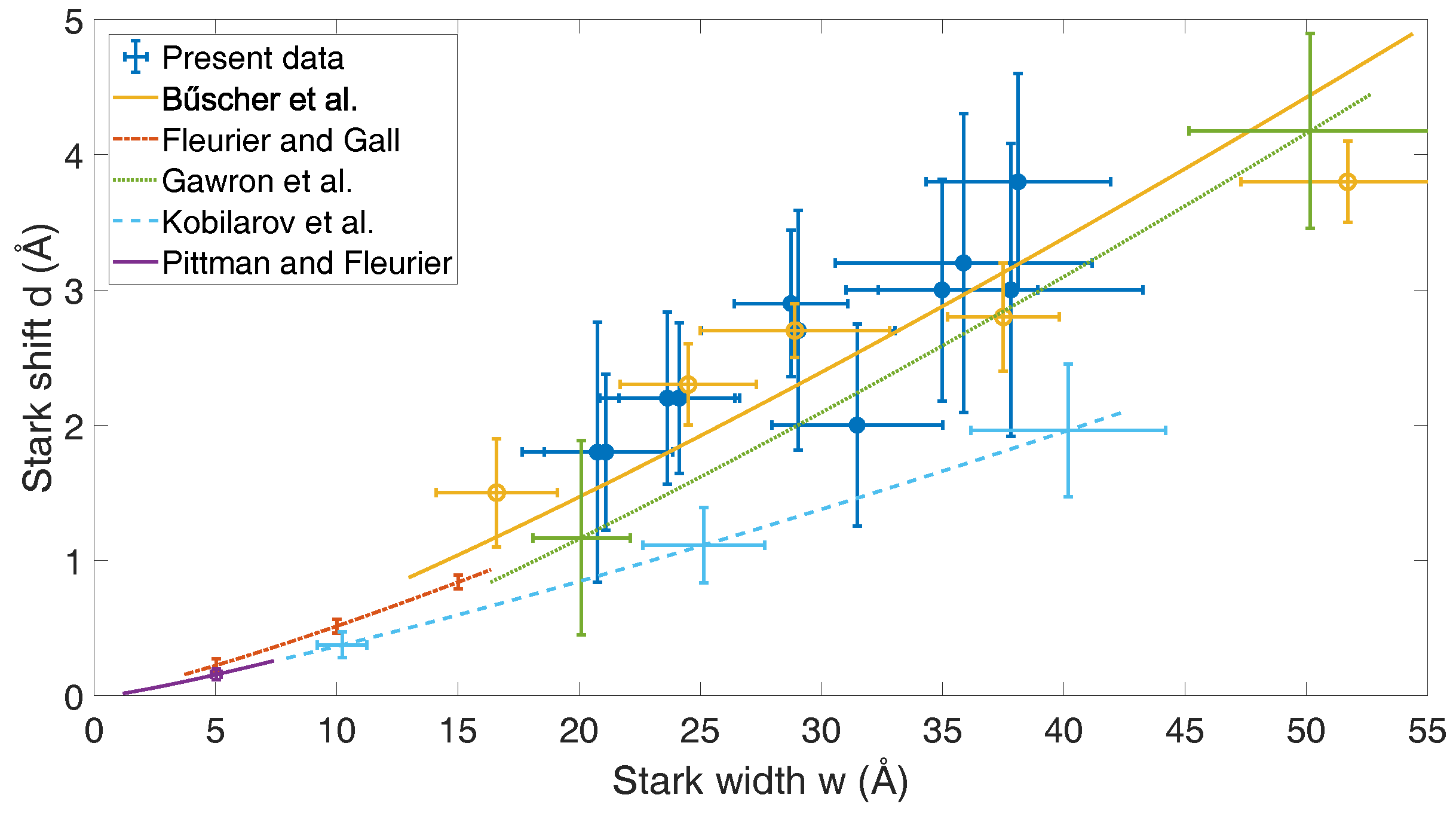
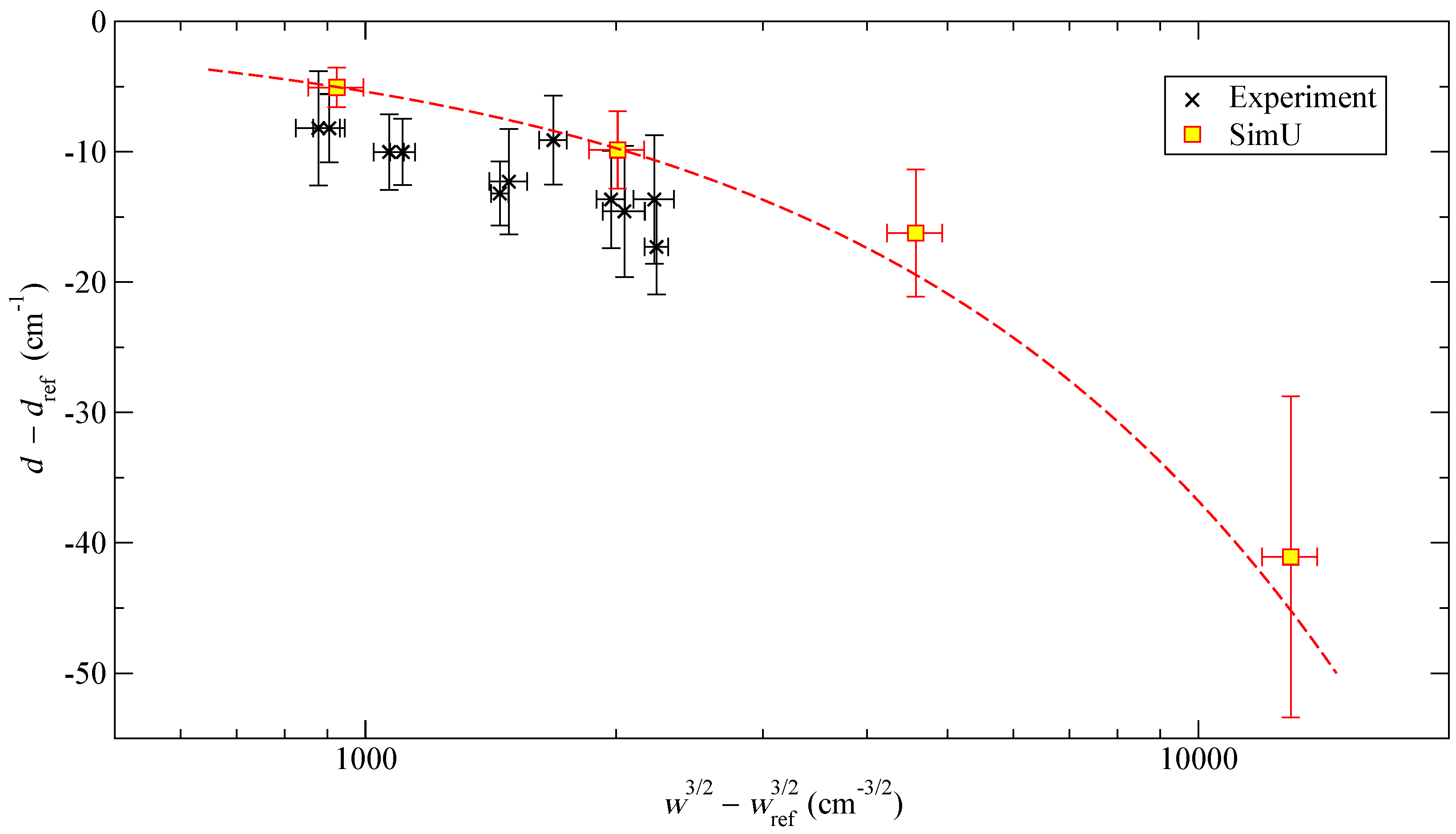
3.3. Experimental Stark Shift and Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Fleurier, C.; Gall, P.L. Shift of the He II Pα line in high density plasmas. J. Phys. B At. Mol. Opt. Phys. 1984, 17, 4311–4322. [Google Scholar] [CrossRef]
- Pittman, T.L.; Fleurier, C. Plasma shifts of the He II Hα and Pα lines. Phys. Rev. A 1986, 33, 1291–1296. [Google Scholar] [CrossRef]
- Kobilarov, R.; Popović, M.V.; Konjević, N. Plasma shift of the He II Pα line. Phys. Rev. A 1988, 37, 1021–1024. [Google Scholar] [CrossRef]
- Gawron, A.; Hey, J.D.; Xu, X.J.; Kunze, H.J. Stark shift of the He II Pα line in a dense plasma. Phys. Rev. A 1989, 40, 7150–7157. [Google Scholar] [CrossRef]
- Büscher, S.; Glenzer, S.; Wrubel, T.; Kunze, H.J. Investigation of the He II Pα and He II Pβ transitions at high densities. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4107–4125. [Google Scholar] [CrossRef]
- Peláez, R.J.; Pérez, C.; González, V.R.; Rodríguez, F.; Aparicio, J.A.; Mar, S. Experimental measurements of shifts and asymmetries of He II Pα and Pβ spectral lines. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2505–2517. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectr. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Rosato, J. Report on the third SLSP code comparison workshop. High Energy Density Phys. 2017, 22, 60–63. [Google Scholar] [CrossRef]
- Gigosos, M.A. Stark broadening models for plasma diagnostics. J. Phys. D Appl. Phys. 2014, 47, 343001. [Google Scholar] [CrossRef]
- Alexiou, S. On the pure dipole shift for hydrogen lines in a plasma. J. Quant. Spectr. Radiat. Transf. 2003, 81, 13–17. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.A.; González, M.Á.; González-Herrero, D.; Lara, N.; et al. Ion dynamics effect on Stark broadened line shapes: A cross comparison of various models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardeñoso, V. New plasma diagnosis tables of hydrogen Stark broadening including ion dynamics. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4795–4838. [Google Scholar] [CrossRef]
- Lara, N. Calculation of Stark Spectra of Strongly Coupled Plasmas Using Molecular Dynamics Simulation. Ph.D. Thesis, Universidad de Valladolid, Valladolid, Spain, 2013. [Google Scholar]
- Iglesias, C.A.; Sonnad, V. Robust algorithm for computing quasi-static Stark broadening of spectral lines. High Energy Density Phys. 2010, 6, 399–405. [Google Scholar] [CrossRef]
- Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B.; Lee, R.W. Model for the line shapes of complex ions in hot and dense plasmas. Phys. Rev. A 1990, 42, 5433–5440. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Maron, Y. Quasicontiguous frequency-fluctuation model for calculation of hydrogen and hydrogenlike Stark-broadened line shapes in plasmas. Phys. Rev. E 2013, 87, 053108. [Google Scholar] [CrossRef] [PubMed]
- Duan, B.; Bari, M.A.; Wu, Z.Q.; Yan, J.; Wang, J.G. Stark-broadened profiles of the Lyman spectral lines in He II ions. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 105701. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Fraile, J.; Torres, F. Hydrogen Stark profiles: A simulation-oriented mathematical simplification. Phys. Rev. A 1985, 31, 3509–3511. [Google Scholar] [CrossRef]
- Tighe, R.J.; Hooper, C.F. Low-frequency electric microfield distributions in a plasma containing multiply-charged ions: Extended calculations. Phys. Rev. A 1977, 15, 1773–1779. [Google Scholar] [CrossRef]
- Dyall, K.G.; Grant, I.P.; Johnson, C.T.; Parpia, F.A.; Plummer, E.P. GRASP: A general-purpose relativistic atomic structure program. Comput. Phys. Commun. 1989, 55, 425–456. [Google Scholar] [CrossRef]
- Iglesias, C.; Rogers, F.; Shepherd, R.; Bar-Shalom, A.; Murillo, M.; Kilcrease, D.; Calisti, A.; Lee, R. Fast electric microfield distribution calculations in extreme matter conditions. J. Quant. Spectr. Radiat. Transf. 2000, 65, 303–315. [Google Scholar] [CrossRef]
- O’Brien, J.T.; Hooper, C.F. A relaxation theory of plasma-broadened He II lines. J. Quant. Spectr. Radiat. Transf. 1974, 14, 479–496. [Google Scholar] [CrossRef]
- Boercker, D.B.; Iglesias, C.A.; Dufty, J.W. Radiative and transport properties of ions in strongly coupled plasmas. Phys. Rev. A 1987, 36, 2254–2264. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Maron, Y. Stark effect of high-n hydrogen-like transitions: Quasi-contiguous approximation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 095703. [Google Scholar] [CrossRef]
- Pfennig, H.; Trefftz, E. Die Druckverbreiterung der diffusen Heliumlinien, Vergleich zwischen Messung und Theorie im quasistatischen Bereich. Z. Naturforsch. A 1966, 21, 697–718. [Google Scholar] [CrossRef]
- Iglesias, C.A. Comparison of electron width models for fast line profile calculations. High Energy Density Phys. 2016, 18, 14–19. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Stamm, R.; Talin, B.; Lee, R.W.; Klein, L. Electronic broadening model for high-n Balmer line profiles. Phys. Rev. E 1998, 58, R6943–R6946. [Google Scholar] [CrossRef]
- Stambulchik, E.; Demura, A.V. Dynamic Stark broadening of Lyman-α. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 035701. [Google Scholar] [CrossRef]
- Demura, A.V. Beyond the linear Stark effect: A retrospective. Atoms 2018. Submitted. [Google Scholar]
- Alexiou, S.; Poquérusse, A. Standard line broadening impact theory for hydrogen including penetrating collisions. Phys. Rev. E 2005, 72, 046404. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Alexiou, S.; Griem, H.R.; Kepple, P.C. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. E 2007, 75, 016401. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Iglesias, C.A. Electron broadening of isolated lines with stationary non-equilibrium level populations. High Energy Density Phys. 2005, 1, 42–51. [Google Scholar] [CrossRef]

| y position (mm) | (Å) | (Å) | (Å) |
|---|---|---|---|
| −1.0 | 2.6 ± 0.1 | 20.8 ± 3.1 | 1.8 ± 1.0 |
| −0.8 | 4.0 ± 0.5 | 23.6 ± 2.8 | 2.2 ± 0.6 |
| −0.5 | 2.9 ± 0.5 | 28.7 ± 2.4 | 2.9 ± 0.5 |
| −0.2 | 3.0 ± 0.7 | 38.1 ± 3.8 | 3.8 ± 0.8 |
| 0.0 | 2.6 ± 0.7 | 35.9 ± 5.3 | 3.2 ± 1.1 |
| 0.1 | 2.4 ± 0.6 | 37.8 ± 5.5 | 3.0 ± 1.1 |
| 0.3 | 2.5 ± 0.5 | 35.0 ± 4.0 | 3.0 ± 0.8 |
| 0.5 | 2.3 ± 0.5 | 29.0 ± 4.0 | 2.7 ± 0.9 |
| Reference | Plasma Source | Working Gas | Observation Direction |
|---|---|---|---|
| Present data | Gas liner z-pinch | He | Radial |
| Büscher et al. [6] | Gas liner z-pinch | H with He doping | Radial |
| Fleurier and Gall [2] | Capillary z-pinch | He | Axial |
| Gawron et al. [5] | Gas liner z-pinch | H with He doping | N/A |
| Kobilarov et al. [4] | Capillary z-pinch | He | Axial |
| Pittman and Fleurier [3] | Capillary z-pinch | He | Axial |
| Code | Type | Quenching | Reference |
|---|---|---|---|
| ER | Simulation | No | [13] |
| MD | Simulation | No | [14] |
| MELS | Model | Yes | [15] |
| PPP | Model | No | [16] |
| QC-FFM | Model | No | [17] |
| SimU | Simulation | Yes | [8] |
| ST | Model | Yes | [18] |
| Code | Levels | Microfields | Electrons | Ion Dynamics |
|---|---|---|---|---|
| MELS | Detailed | APEX [22] | Relaxation impact [23] | BID [24] |
| PPP | Detailed | APEX | Standard theory impact | FFM [25] |
| QC-FFM | QC [26] | Pfennig and Trefftz [27] | FFM w/ impact corr. [17] | FFM w/impact corr. |
| ST | Detailed | Tighe and Hooper [20] | K-matrix impact | – |
| Code | Plasma model | Ion Shielding |
|---|---|---|
| ER | Debye QP’s, straight paths | By electrons only |
| MD | True Coulomb MD | N/A |
| SimU | Debye QP’s with explicit RPI | By electrons and ions |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stollberg, C.; Stambulchik, E.; Duan, B.; Gigosos, M.A.; González Herrero, D.; Iglesias, C.A.; Mossé, C. Revisiting the Stark Width and Shift of He II Pα. Atoms 2018, 6, 23. https://doi.org/10.3390/atoms6020023
Stollberg C, Stambulchik E, Duan B, Gigosos MA, González Herrero D, Iglesias CA, Mossé C. Revisiting the Stark Width and Shift of He II Pα. Atoms. 2018; 6(2):23. https://doi.org/10.3390/atoms6020023
Chicago/Turabian StyleStollberg, Christine, Evgeny Stambulchik, Bin Duan, Marco A. Gigosos, Diego González Herrero, Carlos A. Iglesias, and Caroline Mossé. 2018. "Revisiting the Stark Width and Shift of He II Pα" Atoms 6, no. 2: 23. https://doi.org/10.3390/atoms6020023
APA StyleStollberg, C., Stambulchik, E., Duan, B., Gigosos, M. A., González Herrero, D., Iglesias, C. A., & Mossé, C. (2018). Revisiting the Stark Width and Shift of He II Pα. Atoms, 6(2), 23. https://doi.org/10.3390/atoms6020023






