Numerical Methods for the Time-Dependent Schrödinger Equation: Beyond Short-Time Propagators

Abstract

This article reviews several numerical methods for the time-dependent Schrödinger Equation (TDSE). We consider both the most commonly used approach—short-time propagation, which solves the TDSE by assuming that the Hamiltonian is time-independent over sufficiently small (time) intervals—as well as a number of higher-order alternatives. Our goal is to dispel the notion that the latter are too computationally demanding for practical use. To that end, we cover methods whose numerical building blocks are shared by short-time propagators or can be handled by standard libraries. Moreover, we make the case that these methods are best positioned to take advantage of parallel computing environments. One of the alternatives considered is a “double DVR” solver, which applies an expansion in a product basis of functions in space and time to obtain a solution (over all space and at multiple time points simultaneously) with a single linear system solve. To our knowledge, and despite its simplicity, this approach has not previously been applied to the TDSE.

1. Introduction

Suppose that $\psi (r,t)$ is the wave function of a quantum system, dependent on both time t and a radial spatial variable r. The evolution of $\psi$ is governed by the famous time-dependent Schrödinger Equation (TDSE), which—in atomic units—takes the form

$$i{\displaystyle \frac{\partial }{\partial t}}\psi (r,t)=H(r,t)\psi (r,t)$$

(1)

for $H(r,t)$ a corresponding Hamiltonian operator. We can decompose H as $H(r,t)=H_0\left(r\right)+W(r,t)$ for a time-independent operator $H_0\left(r\right)$ and a time-dependent operator $W(r,t)$. The former corresponds to the kinetic energy of the system while the latter collects time-dependent potential terms. Solutions to the TDSE are central to understanding and modeling a variety of phenomena in quantum mechanics. Examples include photoionization [1,2], molecular dynamics [3], and the behavior of Bose–Einstein condensates [4], among many others.

Despite its continued importance, numerical tools for the TDSE have been somewhat slow to evolve. The most commonly used approach is what we call short-time propagation, wherein the TDSE is converted to a set of coupled differential equations in time of the form

$$i{\displaystyle \frac{\partial }{\partial t}}\mathit{\psi }\left(t\right)=\mathbf{H}\left(t\right)\mathit{\psi }\left(t\right),$$

(2)

obtained by representing $\psi (r,t)$ and $H(r,t)$ in a certain spatial basis, and $\mathit{\psi }\left(t\right)$ is computed from a known value $\mathit{\psi }\left(t_0\right)$ as

$$\mathit{\psi }\left(t\right)\approx e^{-i(t-t_0)\widehat{\mathbf{H}}}\mathit{\psi }\left(t_0\right)$$

(3)

with $\widehat{\mathbf{H}}=\mathbf{H}\left({\displaystyle \frac{t-t_0}{2}}\right).$ Equivalently, a solution at time $t_0$ is propagated to a solution at time t by assuming that the Hamiltonian $H(r,t)$ is time-independent over the interval $[t_0,t]$ and can be represented (in an appropriate spatial basis) by $\widehat{\mathbf{H}}$, in which case (3) is exact. While there are many ways to execute this procedure (see [5] and Section 2) all of them are limited by the central assumption that $H(r,t)$ can be well-approximated by a time-independent operator over $[t_0,t]$. As a result, short-time propagators are typically accurate only when $[t_0,t]$ is small, and therefore computing $\psi (r,t)$ via short-time propagation, at even modest times, requires repeated, serial application of (3).

While short-time propagators date back to at least the late 40’s [6,7,8,9], they have remained popular both in the literature and among practitioners. When nine research groups were tasked with solving the same TDSE in a recent 2018 collaboration [10], for example, twelve of the combined fourteen methods used were some variant of short-time propagator (with the remaining two leveraging general solvers like Runge–Kutta [11]). This is in spite of a growing collection of methods [12,13,14,15] designed specifically to avoid the primary drawback of short-time propagation—i.e., its relegation to small time steps. The question therefore remains: can these newer methods provide realistic gains for researchers and, if so, why have they failed to gain wider traction?

In this article, we explore this question by revisiting both short-time propagators and their alternatives. Our goal is to make a case for the latter, specifically for use in high-performance computing environments, where problems are large and parallelization can be fully exploited. In doing so, we add a “double DVR” approach to the family of short-time alternatives, which—to our knowledge—has not been previously applied to the TDSE.

The remainder of the article is organized as follows. Section 2 covers short-time propagators in further detail. We then explore alternatives in Section 3, focusing in particular on the Magnus expansion [16], the aforementioned double DVR, and the Iterative Volterra Propagator (ITVOLT) developed in [15]. We then close the article with a handful of comments on software for the TDSE, noting that perhaps the most important advantage of short-time propagators to this point has been their ease of implementation.

Scope and Terminology

Before moving on, we pause to clarify the scope of this survey and the terminology used throughout. First, we note that the restriction to a radial wave function is made primarily to simplify the discussion; all of the methods considered can be posed in an arbitrary number of spatial dimensions, although working out the numerical details for the newer methods (ITVOLT and the double DVR) is still an open problem, as is a robust comparison with the popular solvers for that setting [17,18,19,20].

In a similar vein, we do not consider boundary conditions. The choice of a boundary—e.g., bound state vs. ionization vs. periodic boundaries, as dictated by the problem—primarily affects the setup of the TDSE. In the case of open systems such as ionization problems, spurious reflections are typically handled by modifying the Hamiltonian in (2), for example by adding a complex absorber [21]. Alternatively, an exterior complex scaling (ECS) [22] or R-matrix [23] setup can be employed. Importantly, the solvers we present are more or less unaffected by these choices, except for adjustments necessary to work with complex Hamiltonians, which in particular necessitate different methods for handling (matrix) exponentiation. The major change if ECS or absorbers are used is that these exponentials may no longer be unitary. The R-matrix approach can mitigate this problem.

Above, we drew a distinction between “short-time propagators” and other, higher-order solvers. To avoid confusion, we emphasize that all of the methods considered here propagate a solution to the TDSE over successive time intervals, whose size $\Delta t$ is up to the user and may be “small” or “large.” The aforementioned short-time propagators are labeled as such since they can only possibly be accurate for smaller time steps. Equivalently, they are low-order accurate in $\Delta t$. In contrast, the methods considered in Section 3 offer numerical levers (i.e., quadrature points, basis functions, etc.) that can be adjusted to achieve higher accuracy regardless of $\Delta t$.

Finally, we emphasize that the TDSE is heavily problem-dependent, meaning the optimal numerical method for use in one setting may not be the best choice in another. Single-particle scattering [24], for example, is handled differently than either multi-electron atomics in strong laser fields [25] or molecular photochemistry [26]. Here, we focus on single or fewer than three particle descriptions that can be applied to problems of scattering, single or double ionization in strong laser fields, or bound state treatments. With this in mind, we note that static grids/time-independent spatial basis functions (used to obtain (3)) are not always suitable.

2. Short-Time Propagators: Pros and Cons

To solve (1) via short-time propagation, we first need to convert the TDSE into (3)—i.e., by representing $\psi (r,t)$ and $H(r,t)$ in space as $\mathit{\psi }\left(t\right)$ and $\mathbf{H}\left(t\right)$, respectively. To avoid confusion, we will always use bold notation to represent these quantities. Additionally, we assume that $\psi (r,t)$ and $H(r,t)$ are represented over all space for the length of the propagation; in practice, adaptive representations (e.g., as in [27]) can be used to improve efficiency.

Typically, $\mathit{\psi }\left(t\right)$ and $\mathbf{H}\left(t\right)$ are derived by either (1) discretizing the TDSE over a spatial grid or (2) expanding $\psi (r,t)$ in a spatial function basis. In case (1), $\mathit{\psi }\left(t\right)$ is a time-dependent vector whose entries record the values of the wave function at the grid points. The corresponding $\mathbf{H}\left(t\right)$ is then a time-dependent matrix, obtained by approximating the spatial derivative (i.e., from the kinetic energy term of $H(r,t)$) with a finite-difference formula on the grid [28]. The use of a finite-difference approximation here lends structure to $\mathbf{H}\left(t\right)$, which is usually not only banded but also symmetric (provided the grid points are equally spaced).

Alternatively, $\mathit{\psi }\left(t\right)$ and $\mathbf{H}\left(t\right)$ can be obtained by replacing the wave function with a time-dependent expansion

$$\psi (r,t)=\sum _j{c}_j\left(t\right){\varphi }_j\left(r\right)$$

(4)

for a corresponding spatial function basis $\left\{{\varphi }_j\left(r\right)\right\}$. If this basis is orthonormal with respect to an inner product $\langle ·|·\rangle$, (3) can be derived by inserting (4) into the TDSE and computing the inner product of each side with the basis functions. In this case, $\mathit{\psi }\left(t\right)$ records the coefficients $c_j\left(t\right)$, while the entries of $\mathbf{H}\left(t\right)$ are given by

$$\langle {\varphi }_j\left(r\right)\left|H(r,t)\right|{\varphi }_k\left(r\right)\rangle ={\int }_{-\infty }^{\infty }{\varphi }_j{\left(r\right)}^{\ast }H(r,t){\varphi }_k\left(r\right)w\left(r\right)dr$$

(5)

for an appropriate weight function $w\left(r\right)$. In practice, evaluating these “matrix elements” reduces to applying a suitable quadrature. If the ${\varphi }_j$’s are polynomials, as is typical, we can leverage the well-known connection between orthogonal polynomials and quadrature rules (see, e.g., [29]) to obtain one that integrates products of the basis functions exactly. This describes the well-known Discrete Variable Representation (DVR) approach [30,31,32], “discrete” here referring to the fact that the basis functions are, in some sense, localized around the corresponding quadrature points. Once again, a clever choice of basis can ensure that $\mathbf{H}\left(t\right)$ has favorable structure (e.g., is also banded and symmetric).

Suppose now that $\mathit{\psi }\left(t_0\right)$ is known at some initial time $t_0$. Modulo error introduced by the chosen spatial representation, the value of the wave function at any subsequent time can be computed as $\mathit{\psi }\left(t\right)=\mathbf{U}(t,t_0)\mathit{\psi }\left(t_0\right)$ for time-evolution operator

$$\mathbf{U}(t,t_0)=1+\sum _{n=1}^{\infty }{(-i)}^n{\int }_{t_0}^{t}d{t}_1^{\prime }{\int }_{t_0}^{t_1^{\prime }}d{t}_2^{\prime }\dots {\int }_{t_0}^{t_{n-1}^{\prime }}d{t}_n^{\prime }\mathbf{H}\left(t_1^{\prime }\right)\mathbf{H}\left(t_2^{\prime }\right)\cdots \mathbf{H}\left(t_n^{\prime }\right).$$

(6)

This sum is known as a Dyson series, and its fields $\mathbf{H}\left(t^{\prime }\right)$ are time ordered—i.e., $t_1^{\prime }>t_2^{\prime }>\cdots >t_n^{\prime }$. As a general approach to the TDSE, short-time propagation is based around the following observation: when $\mathbf{H}$ is time-independent, (6) reduces to a simple exponential $\mathbf{U}(t,t_0)=e^{-i(t-t_0)\mathbf{H}}$. Hence, assuming that $\mathbf{H}\left(t\right)$ is constant over $[t_0,t]$ and perhaps equal to $\widehat{\mathbf{H}}\left({\displaystyle \frac{t-t_0}{2}}\right)$, the next value of the wave function can be obtained (approximately) as $e^{-i(t-t_0)\widehat{\mathbf{H}}}\mathit{\psi }\left(t_0\right)$. Note that while taking $\widehat{\mathbf{H}}$ to be the midpoint value of the Hamiltonian here is perhaps the most common choice, it is by no means required.

From here, we just need to decide how to evaluate the exponential. There is no shortage of options [33], though our preference is for methods that can efficiently apply an exponential to a single vector. In the physics literature, the most popular choices are Crank-Nicolson [7], higher-order Padé approximations [34], Krylov-subspace methods (i.e., Lanczos) [35], Chebyshev expansion [36], and various split-operator techniques [24,37,38]. See [5] for a survey comparing these methods in depth on the same TDSE.

Regardless of the specific method used, short-time propagators are unitary, a simple consequence of the fact that the exponential $e^{i\mathbf{A}}$ is unitary if $\mathbf{A}$ is Hermitian. This is an important upshot of the approach, as the true time-evolution operator $\mathbf{U}$ is also unitary. Of course, a unitary propagator is not necessarily an accurate one, though they are less likely to suffer numerical instability.

The majority of research on short-time propagators has focused on deriving and testing various combinations of its two key ingredients: (1) the spatial representation that yields $\mathit{\psi }\left(t\right)$ and $\mathbf{H}\left(t\right)$ and (2) the method for handling the subsequent exponential (see again [5,10]). In all cases, exploiting available structure is the key to efficiency, recalling that ingredient (1) may be chosen to ensure that $\widehat{\mathbf{H}}$ is sparse or banded. As we might expect, the most popular approaches for handling the exponential are well-suited to leverage this structure. Take Crank-Nicolson as an example, which replaces $e^{-i(t-t_0)\widehat{\mathbf{H}}}$ with the (1,1) Padé approximant

$$e^{-i(t-t_0)\widehat{\mathbf{H}}}\approx {\displaystyle \frac{\mathbf{I}-i\left(\frac{t-t_0}{2}\right)\widehat{\mathbf{H}}}{\mathbf{I}+i\left(\frac{t-t_0}{2}\right)\widehat{\mathbf{H}}}}.$$

(7)

When $\widehat{\mathbf{H}}$ is banded, computing $\mathit{\psi }\left(t\right)$ via (7) requires solving a simple banded linear system, whose coefficient matrix is $\mathbf{I}+i\left({\displaystyle \frac{t-t_0}{2}}\right)\widehat{\mathbf{H}}$. The other methods are similar, reliant only on basic numerical linear algebra routines that can be outsourced to publicly available and robustly tested libraries (e.g., LAPACK).

This combination of simplicity and flexibility is the primary reason for the popularity of short-time propagation. Indeed, short-time propagators are so straightforward to implement that the aforementioned survey [5] suggested them as a useful introduction to computational methods for undergraduate physics students. Of course, their drawbacks are also clear. When $\mathbf{H}\left(t\right)$ varies significantly over short time intervals, the fundamental assumption of the approach, that $\mathbf{U}(t,t_0)$ can be well-approximated by the exponential $e^{-i(t-t_0)\widehat{\mathbf{H}}}$, deteriorates, unless the step size becomes (potentially prohibitively) small.

A somewhat less-discussed limitation is their resistance to parallelization. At its core, the short-time propagation approach is inherently serial, as the value of $\mathit{\psi }\left(t_0\right)$ is required to obtain the next value $\mathit{\psi }\left(t\right)$. Accordingly, short-time propagators can exploit data parallelism only; that is, they can spread $\mathit{\psi }\left(t\right)$ over multiple processors and potentially break each exponential into pieces that can be done in parallel, but they cannot go any further (e.g., to compute the wavefunction at multiple time points simultaneously), while parallelization of this kind has been considered in the literature (see for example [39]) it may not be enough to make full use of computing resources.

3. Taking Larger Time Steps

We turn now to a survey of short-time propagation alternatives, focusing on three in particular: (1) the Magnus expansion [16], (2) ITVOLT [15], and (3) a double DVR approach. Our goal is to highlight methods that can solve the TDSE over larger time intervals without requiring much additional work—e.g., by reusing kernels from the short-time approach (for example, methods for handling matrix exponentials). A common thread is the use of Lagrange polynomials/quadratures, which are convenient to work with and stable if implemented properly [40]. While we focus our presentation on the TDSE, it should be noted that all of the methods considered in this section extend to arbitrary PDE’s. ITVOLT, for example, can be interpreted as a specialization of more general exponential integrators [41].

3.1. Magnus Expansion

We start with the Magnus expansion—a fairly straightforward generalization of the short-time approach. The idea here is to use an alternative approximation to the Dyson series (6), in this case setting $\mathbf{U}(t,t_0)=e^{-i\mathbf{\Omega }(t,t_0)}$ for

$$\mathbf{\Omega }(t,t_0)=\sum _{k=1}^{\infty }{\mathbf{\Omega }}_k(t,t_0),$$

(8)

where each term ${\mathbf{\Omega }}_k(t,t_0)$ is a nested integral of commutators involving $\mathbf{H}\left(t\right)$. The first few take the form

$$\begin{array}{l}{\mathbf{\Omega }}_1(t,t_0)={\int }_{t_0}^t\mathbf{H}\left(t_1\right)d{t}_1\\ {\mathbf{\Omega }}_2(t,t_0)={\int }_{t_0}^{t}d{t}_1{\int }_{t_0}^{t_1}[\mathbf{H}\left(t_1\right),\mathbf{H}\left(t_2\right)]d{t}_2\\ {\mathbf{\Omega }}_3(t,t_0)={\int }_{t_0}^{t}d{t}_1{\int }_{t_0}^{t_1}d{t}_2{\int }_{t_0}^{t_2}\left([\mathbf{H}\left(t_1\right),[\mathbf{H}\left(t_2\right),\mathbf{H}\left(t_3\right)]]+[\mathbf{H}\left(t_3\right),[\mathbf{H}\left(t_2\right),\mathbf{H}\left(t_1\right)]]\right)d{t}_3\end{array}$$

(9)

for $[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A}$ the standard commutator. As suggested by its name, this expansion was first derived by Magnus [16].

The Magnus expansion implies a simple propagator for the TDSE: set $\mathit{\psi }\left(t\right)=e^{-i\widehat{\mathbf{\Omega }}(t,t_0)}$ for $\widehat{\mathbf{\Omega }}(t,t_0)$ an approximation of $\mathbf{\Omega }(t,t_0)$. Obtaining this approximation requires the following:

• Truncating the expansion (in most settings, taking only the first handful of terms will be practical).
• Computing the surviving ${\mathbf{\Omega }}_k(t,t_0)$—i.e., approximating their nested integrals by quadrature.
• Evaluating the resulting exponential, with the aforementioned split-operator techniques being the natural choice.

As with short-time propagation, this high-level strategy yields a family of solvers—e.g., [42,43,44]—each of which applies a different procedure for handling the individual steps. In general, keeping k terms in the expansion yields a method that is order $2k$ in the time step $\Delta t=t-t_0$, assuming these terms are approximated sufficiently accurately and modulo constants that depend on $\mathbf{H}$ [45]. For additional details on the convergence of (8), see [46].

If we assume that $\mathbf{H}$ is time-independent over $[t_0,t]$, the approach outlined above reduces to short-time propagation (since any term in (8) involving commutators will vanish, and ${\mathbf{\Omega }}_1(t,t_0)$ can be evaluated exactly). Accordingly, the aforementioned convergence results imply that short-time propagation is, at best, a second order method in $\Delta t$; Magnus, meanwhile, can reach much higher accuracy even if only a few terms in the series are kept. Moreover, it retains one of the primary benefits of short-time propagation: regardless of where we truncate/how we approximate the expansion, the resulting propagator is unitary.

3.2. ITVOLT

Our next alternative ITVOLT [15], short for Iterative Volterra Propagator, approaches the TDSE by way of an equivalent Volterra integral equation. Once again, the starting point here is the coupled system (3). If we write $\mathbf{H}\left(t\right)$ as the sum of a time-independent operator ${\mathbf{H}}_0$ and a time-dependent operator $\mathbf{W}\left(t\right)$, sticking with the same spatial representation as before, we can rewrite this expression as

$$i{\displaystyle \frac{\partial }{\partial t}}\mathit{\psi }\left(t\right)=\left[{\mathbf{H}}_0+\mathbf{W}\left({\displaystyle \frac{t_i+t_f}{2}}\right)\right]\mathit{\psi }\left(t\right)+\left[\mathbf{W}\left(t\right)-\mathbf{W}\left({\displaystyle \frac{t_i+t_f}{2}}\right)\right]\mathit{\psi }\left(t\right)$$

(10)

for $t_i\le t\le t_f$. Setting $\widehat{\mathbf{H}}={\mathbf{H}}_0+\mathbf{W}\left({\displaystyle \frac{t_i+t_f}{2}}\right)$ and $\mathbf{V}\left(t\right)=\mathbf{W}\left(t\right)-\mathbf{W}\left({\displaystyle \frac{t_i+t_f}{2}}\right)$ and integrating, we obtain

$$\mathit{\psi }\left(t\right)=e^{-i(t-t_i)\widehat{\mathbf{H}}}\mathit{\psi }\left(t_i\right)-i{\int }_{t_i}^t{e}^{-i(t-s)\widehat{\mathbf{H}}}\mathbf{V}\left(s\right)\mathit{\psi }\left(s\right)ds.$$

(11)

For $t_i\le t\le t_f$, this Volterra equation is an exact solution to the TDSE (again, modulo error attributable to the spatial representation).

ITVOLT computes this solution over successive time steps $[{\tau }_j,{\tau }_{j+1}]$ by applying a Gauss–Lobatto quadrature to the integral (equivalently, by expanding the integrand in Lagrange polynomials). This results in a system of equations at the quadrature points of the form

$$\mathit{\psi }\left(t_p\right)=e^{-i(t_p-{\tau }_j){\widehat{\mathbf{H}}}_j}\mathit{\psi }\left({\tau }_j\right)-i\sum _{l=1}^n{w}_{p,l}{e}^{-i(t_p-t_l){\widehat{\mathbf{H}}}_j}{\mathbf{V}}_j\left(t_l\right)\mathit{\psi }\left(t_l\right),$$

(12)

which can be solved directly or iteratively. Here, ${\tau }_j=t_1<t_2<\cdots <t_n={\tau }_{j+1}$ and ${\left\{w_{p,l}\right\}}_{p,l=1}^n$ are the quadrature points and weights, respectively. The latter carries two indices as (1) a unique set of weights is needed for each upper bound on the integral in (11) and (2) the quadrature is global in the sense that all n points are used to evaluate the Volterra equation at any $t_p$. We also index ${\widehat{\mathbf{H}}}_j$ and ${\mathbf{V}}_j\left(t\right)$ by j to emphasize their dependence on (the midpoint of) the current time interval. We note that adding and subtracting the midpoint value of $\mathbf{W}\left(t\right)$ in (10) contributes to numerical efficiency by limiting the time-dependence of $\mathbf{V}\left(t\right)$, which dictates the number of quadrature points necessary to approximate the integral accurately. As a result, the inhomogeneous term of the Volterra equation is exactly the short-time approximation from the previous section, though $t_p-{\tau }_j$ may not be small.

Several versions of ITVOLT were put forward in [15], each of which solves (12) in a different way. In the simplest case, ITVOLT runs a basic Jacobi-like iteration, repeatedly evaluating (12) beginning with the (short-time) inhomogeneous term. More advanced options leverage standard solvers like the Krylov-subspace-based GMRES [47], which, unlike the Jacobi iteration, is guaranteed to converge. Of course, constructing and solving (12) also requires handling matrix exponentials, with the discussion from Section 2 carried over.1 However (12) is handled, ITVOLT is not a unitary solver for the TDSE—i.e., it does not necessarily preserve the norm of $\mathit{\psi }\left(t\right)$, while this can pose numerical problems, it comes with a silver lining: ${\left|\right|\mathit{\psi }\left(t\right)\left|\right|}_2$ can now be used as a conduit for accuracy, which is particularly useful when the TDSE of interest has no known analytic solution.

In comparison to short-time propagators, whose fundamental source of numerical error is the approximation $\mathbf{H}\left(t\right)\approx \widehat{\mathbf{H}}$, ITVOLT is primarily limited by the accuracy of the quadrature used. If we take n points on the interval $[{\tau }_j,{\tau }_{j+1}]$ of size $\Delta \tau ={\tau }_{j+1}-{\tau }_j$, for example, standard results for Lagrange interpolation (see, e.g., [48] (Chapter 6)) imply that the error incurred by moving from the exact Volterra equation to the approximate system—that is, the spectral norm difference between the true solution and the solution to (12)—can be bounded by $C{\displaystyle \frac{\Delta {\tau }^{n+1}}{n!}}$ for C a constant that depends on the maximum value of the n-th derivative of the integrand of (11). This is the power of the Volterra equation approach: the experiments presented in [15] demonstrate that, even for large values of $\Delta \tau$, adding one or two additional quadrature points can dramatically improve accuracy. Again, we note here the importance of controlling the time-dependence of $\mathbf{V}\left(t\right)$—e.g., to ensure that the constant C is manageable.

ITVOLT was not the first Volterra-based method proposed for the TDSE. Earlier work by Ndong et al. [13] and Schaefer et al. [14] presented a similar, though somewhat more involved, approach. The benefit of ITVOLT specifically is its simplicity and flexibility. That is, practitioners are free to (1) use any method for handling the necessary exponentials and (2) choose any iterative/direct method for solving the resulting system of equations (with the cheap Jacobi iteration available for large problems done with limited computational resources). All the while, the only additional building blocks needed are standard routines for computing Gauss–Lobatto quadrature points/weights. In this way, ITVOLT is fairly straightforward to implement, and in particular can be easily built on top of existing software for short-time propagators.

The payoff for this modest overhead is the ability to take much larger step sizes $[{\tau }_j,{\tau }_{j+1}]$ and in effect to solve for the wave function at multiple times (i.e., the quadrature points) simultaneously. In this way, ITVOLT is capable of moving beyond the data parallelism of short-time propagation.

3.3. Double DVR

Our final alternative to short-time propagation is a method that is, in some sense, dual to ITVOLT. The idea here is to again derive a large system of equations that defines the wave function $\psi (r,t)$ over all space and at multiple time points simultaneously. In this case, however, such a system is obtained via what we call a double DVR. As above, DVR is short for Discrete Variable Representation, while “double” refers to the fact that a DVR-like expansion is applied in both space and time.

To this point, we have discussed DVR’s as something to use in tandem with other methods—e.g., to represent the TDSE in space before applying another solver, including short-time propagators and ITVOLT. The key insight of the double DVR approach is that this second step can be avoided, meaning we can use a DVR expansion to solve the TDSE directly, provided the function basis is time-dependent. Like ITVOLT, this is not strictly new; expansions in time-dependent function bases have been explored before, for example in the multi-configuration time-dependent Hartree (MCTDH) method [17]. Our contribution is to demonstrate that this high-level approach can be implemented both with less complicated machinery and in a way that is applicable to any TDSE. In particular, the method we propose is simpler than that of [17] in two key ways: (1) the coefficients in the expansion are time-independent and (2) the function basis is a straightforward product of functions in time and space. For the latter, we take a cue from the standard DVR approach, while in this article we focus on the simple case where the wave function depends only on a radial spatial variable, when working in multiple spatial dimension, the typical choice for a DVR is an analogous product basis of single variable functions (see for example [39]).

The double DVR method solves the TDSE on successive time intervals $[{\tau }_j,{\tau }_{j+1}]$ by expanding the wave function as

$$\psi (r,t)=\sum _{j,p}{c}_{j,p}{\varphi }_j\left(r\right)l_p\left(t\right)$$

(13)

for $\left\{{\varphi }_j\left(r\right)\right\}$, again, a spatial function basis and $\left\{l_p\left(t\right)\right\}$ a set of (scaled) Lagrange polynomials with roots at a set of Gauss–Lobatto quadrature points ${\tau }_j=t_1<t_2<\cdots <t_n={\tau }_{j+1}$ in $[{\tau }_j,{\tau }_{j+1}]$. Note that these are the same time points used by ITVOLT. Moreover, the Lagrange polynomials are indexed so that $l_p\left(t_q\right)=0$ if $p\ne q$ and scaled by the square roots of the corresponding Gauss–Lobatto quadrature weights so that they have unit norm (with respect to the standard inner product on continuous functions).

Since the coefficients $c_{j,p}$ are time-independent on $[{\tau }_j,{\tau }_{j+1}]$, they can be obtained as the solution to a (large) system of equations, which can be generated as follows. First, we insert (13) into the TDSE to obtain

$$i\sum _{j,p}{c}_{j,p}{\varphi }_j\left(r\right)l_p^{\prime }\left(t\right)=\sum _{j,p}{c}_{j,p}H(r,t){\varphi }_j\left(r\right)l_p\left(t\right).$$

(14)

Integrating both sides of (14) against $l_q\left(t\right)$ yields

$$i\sum _j\left(\sum _p{c}_{j,p}{l}_p^{\prime }\left(t_q\right)\right){\varphi }_j\left(r\right)=\sum _j{c}_{j,q}H(r,t_q){\varphi }_j\left(r\right).$$

(15)

The simplification here follows from the fact that the time dependence of $H(r,t)$ comes from the potential term $W(r,t)$, which is a scalar function of space and time. Taking next the inner product with ${\varphi }_k\left(r\right)$ gives

$$i\sum _p{c}_{k,p}{l}_p^{\prime }\left(t_q\right)=\sum _j{c}_{j,q}\langle {\varphi }_k\left(r\right)|H(r,t_q)|{\varphi }_j\left(r\right)\rangle .$$

(16)

This defines a system of equations in the coefficients $c_{j,p}$, with one equation derived from each pair of basis functions $l_q\left(t\right)$ and ${\varphi }_k\left(r\right)$. The right-hand side of this system corresponds to terms involving the coefficients $c_{j,1}$, which are assumed to be known.

Many of the numerical details from ITVOLT similarly apply to the double DVR:

• The method is flexible, in that the system (16) can be solved in a variety of ways, both direct and iterative.
• It is not explicitly unitary and therefore will not (in general) preserve the norm of the wave function.
• Accuracy is limited by the number of basis functions $l_p\left(t\right)$ and ${\varphi }_j\left(r\right)$ used, with the former linked to the number of Gauss–Lobatto points selected in $[{\tau }_j,{\tau }_{j+1}]$.

Note that the double DVR approach, unlike the other methods considered in this article, does not require evaluating matrix exponentials. Nevertheless, it can still be computationally demanding. To promote efficiency, the spatial basis functions $\left\{{\varphi }_j\left(r\right)\right\}$ should be chosen to limit the number of terms on the right hand side of (16)—e.g., so that the full system can be arranged in a (block) banded fashion.

Again, we emphasize that—by solving for the wave function at multiple time points simultaneously—the double DVR is inherently parallel in a way that standard short-time propagators are not. Like ITVOLT, it is therefore poised to take advantage of additional computational resources, if available.

Example 1.

Consider the driven harmonic oscillator [49], whose Hamiltonian is

$$H(r,t)=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^2}{\partial r^2}}+{\displaystyle \frac{1}{2}}{r}^2+rE\left(t\right)$$

(17)

for an electric field $E\left(t\right)=E_0{sin}^2(\pi t/T)cos\left(t\right)$ with amplitude $E_0$ and final propagation time T. If we choose the eigenfunctions of the unforced oscillator as spatial basis functions—i.e., in atomic units,

$${\varphi }_j\left(r\right)={\displaystyle \frac{1}{{\pi }^{1/4}\sqrt{2^{j}j!}}}{e}^{-{\displaystyle \frac{r^2}{2}}}{H}_j\left(r\right)$$

(18)

for $H_j\left(r\right)$ the j-th Hermite polynomial, then (16) reduces to

$$i\sum _p{c}_{k,p}·l_p^{\prime }\left(t_q\right)=c_{k-1,q}\left(E\left(t_q\right)\sqrt{{\displaystyle \frac{k}{2}}}\right)+c_{k,q}·{\mathcal{E}}_k+c_{k+1,q}\left(E\left(t_q\right)\sqrt{{\displaystyle \frac{k+1}{2}}}\right),$$

(19)

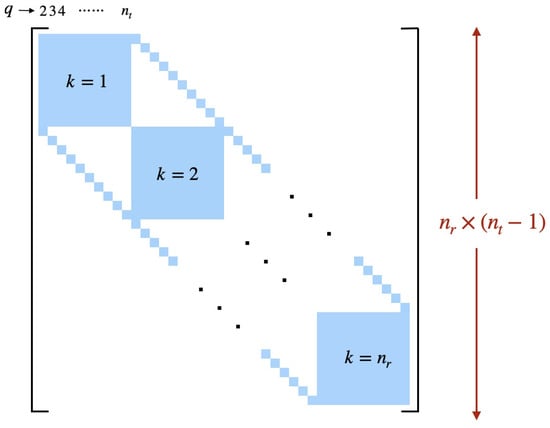
where ${\mathcal{E}}_k=k+{\displaystyle \frac{1}{2}}$ is the energy corresponding to ${\varphi }_k\left(r\right)$. By grouping coefficients by their spatial index, this system is block tridiagonal (see Figure 1).

3.4. Comparison

To close this section, we summarize in

Table 1. Numerical details for the TDSE solvers considered in this paper. Asymptotic accuracies in terms of $\Delta t$ are modulo error due to the spatial representation, which is incurred equally by all methods. Obtaining a similar result for the double DVR is an open problem.

	Method
	Short-Time Prop	Magnus	ITVOLT	Double DVR
Main source of error	Approximation $\mathbf{H}\left(t\right)\approx \widehat{\mathbf{H}}$	Truncation order (k)	Number of quad. points ($n_t$)	Number of basis functions
Unitary?	Yes	Yes	No	No
Parallelism	Space	Space	Time and space	Time and space
Accuracy on $\Delta t$	$O(\Delta t^2)$	$O(\Delta t^{2k})$	$O(\Delta t^{n_t+1})$	Open
Computational Bottleneck	Exponential of $-i\Delta t\widehat{\mathbf{H}}$	Evaluating ${\mathbf{\Omega }}_1,\dots ,{\mathbf{\Omega }}_k$	Iterating/solving (12)	Solving (16)

the numerical properties of the methods considered above. This data should be weighed against the computational complexity of each solver, which we briefly describe here.

For each time step of size $\Delta t$, short-time propagation is clearly the cheapest method, requiring only the application of a single exponential on a vector. If $\mathbf{H}\left(t\right)$ is $n_r\times n_r$, this can be done in $O\left(k{n}_r^2\right)$ operations for modest k (e.g., the number of steps in a Krylov method) and possibly $O\left(k{n}_{r}b\right)$ if $\mathbf{H}\left(t\right)$ is banded with total bandwidth b. By comparison, each iteration used to solve (12) in ITVOLT requires evaluating $O\left(n_t^2\right)$ exponential-vector products for $n_t$ the number of quadrature points used, which results in a per-step cost of $O\left(m·n_t^2·k{n}_r^2\right)$ or $O\left(m·n_t^2·k{n}_{r}b\right)$, assuming m iterations are needed to reach suitable accuracy and again depending on the sparsity of $\mathbf{H}\left(t\right)$. Of course, this applies only to the cheapest, Jacobi-like version of ITVOLT; if (12) is instead solved directly, the cost may balloon to as much as $O\left(n_t^3{n}_r^3\right)$. This is similarly the worst-cast cost of the double DVR approach, assuming no exploitable structure is available and a direct method is used to solve (16), where $n_r$ and $n_t$ are now the number of spatial/time basis functions used in each step. The Magnus expansion sits somewhere in the middle: the dominant cost there is the evaluation of the ${\mathbf{\Omega }}_{\mathit{k}}$, each of which requires $O\left(n_t^k{n}_r^3\right)$ operations if an $n_t$-point quadrature rule is used to evaluate the integrals of (9) over $[t_0,t_0+\Delta t]$. Again, this reduces some if $\mathbf{H}\left(t\right)$ is banded.

4. Conclusions

This paper reviewed a collection of solvers for the TDSE, including commonly used short-time propagators and alternative methods that can take larger time steps. We hope that the details presented here demystify the latter and encourage practitioners to adopt them, particularly for use on large problems where computing resources that can fully exploit additional parallelization are available.

In the introduction, we noted that one of the reasons for the enduring popularity of short-time propagators is their ease of implementation and, accordingly, the breadth of software available for them (see for example [50] and the software accompanying [5]). As a result, we use this article to make a call for open-source implementations of other methods, including—but not limited to—those considered in Section 3. With this in mind, we note that a Fortran implementation of ITVOLT is publicly available,2 though it remains to be parallelized.