Theoretical Calculation of Ground and Electronically Excited States of MgRb+ and SrRb+ Molecular Ions: Electronic Structure and Prospects of Photo-Association
Abstract
1. Introduction
2. Methods of Calculation
3. Results and Discussion
3.1. Adiabatic Potential Energy Curves (PECs) and Spectroscopic Constants
3.2. Permanent and Transition Dipole Moments (PDMs and TDMs)
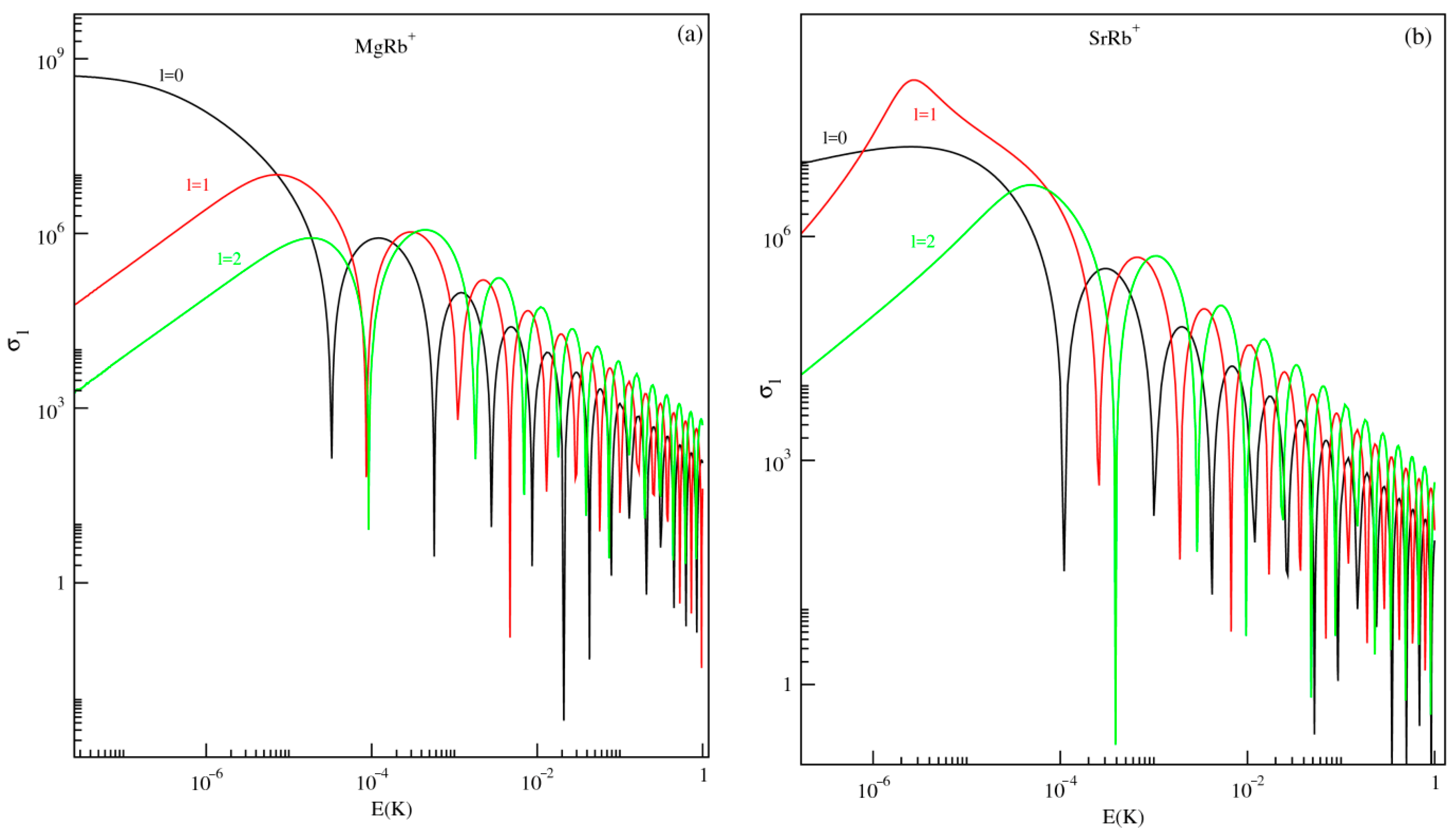
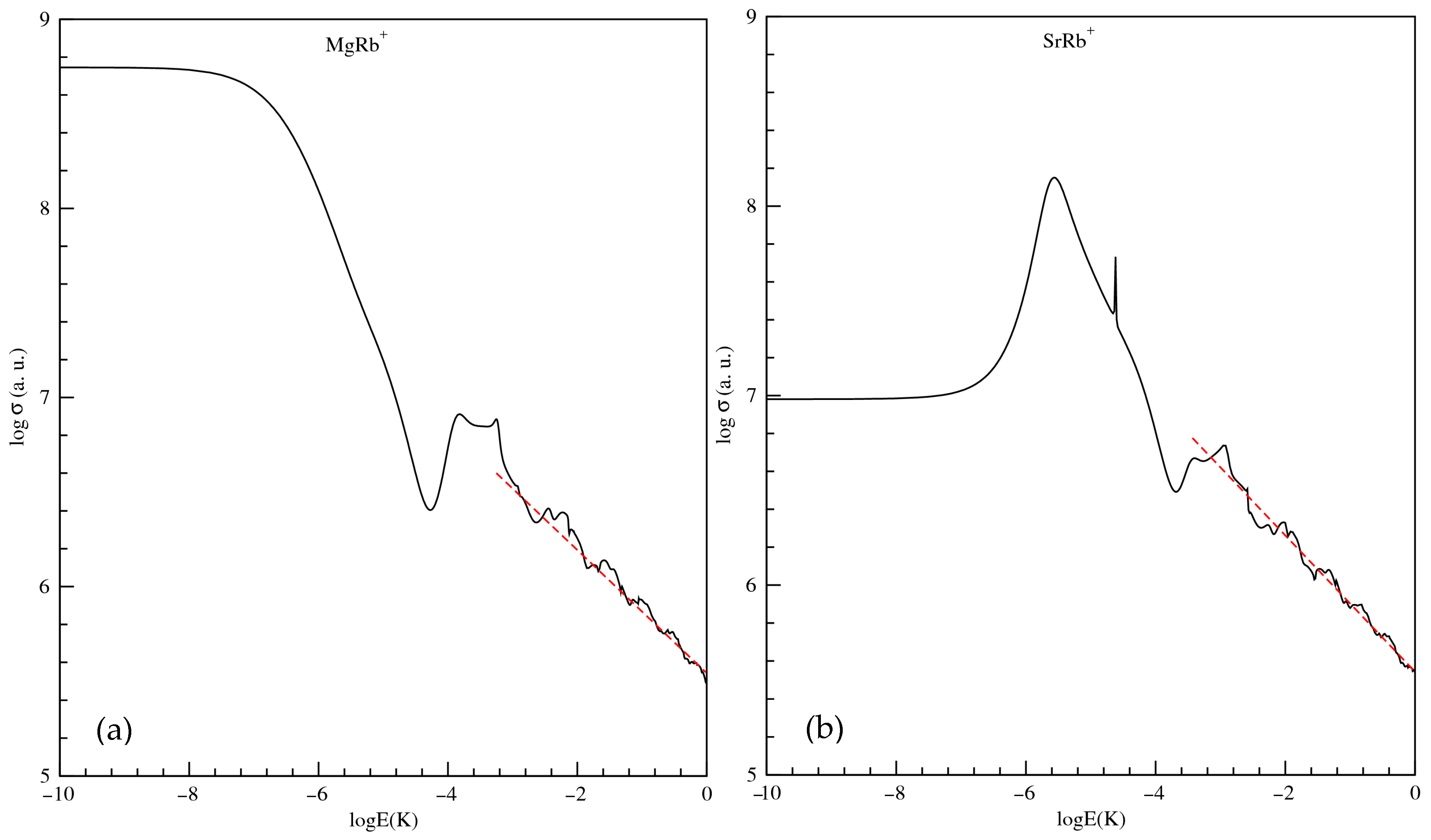
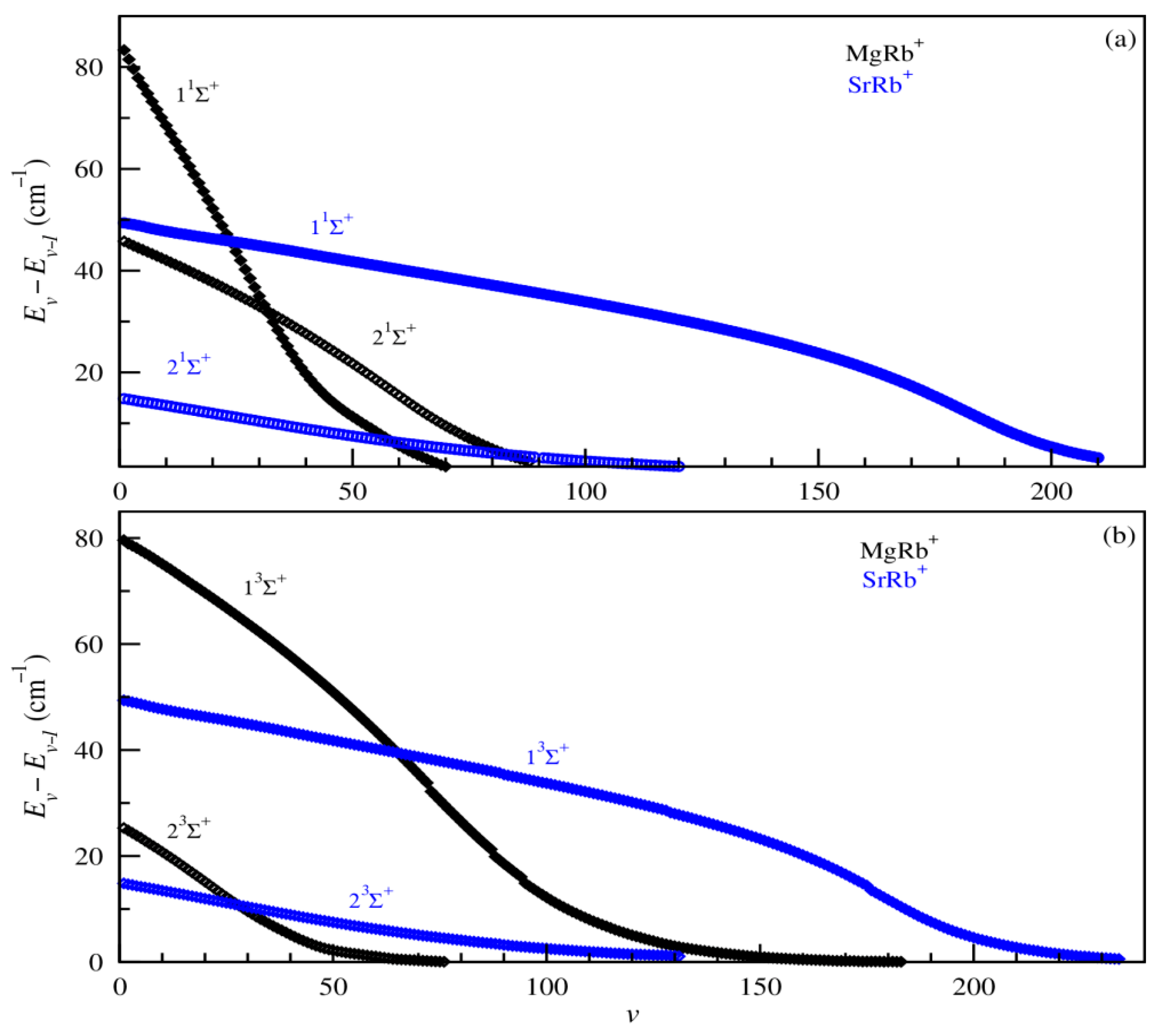
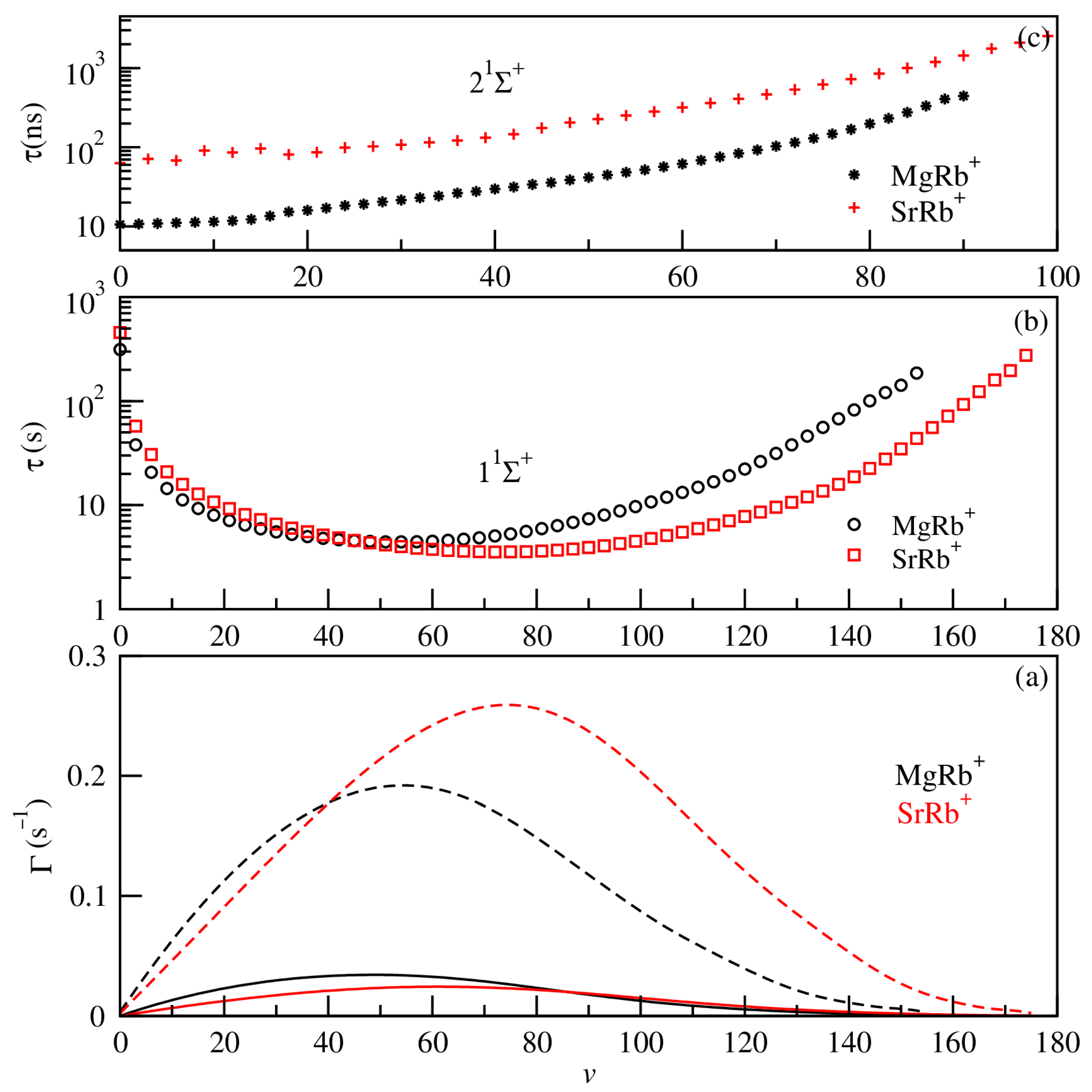
3.3. Exploitation of Results: Atom–Ion Elastic Scattering Proprieties, Vibrational Levels, Radiative Lifetimes, and the Possibility of Formation via Photoassociation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tomza, M.; Jachymski, K.; Gerritsma, R.; Negretti, A.; Calarco, T.; Idziaszek, Z.; Julienne, P.S. Cold hybrid ion-atom systems. Rev. Mod. Phys. 2019, 91, 035001. [Google Scholar] [CrossRef]
- Tscherbul, T.V.; Brumer, P.; Buchachenko, A.A. Spin-orbit interactions and quantum spin dynamics in cold ion-atom collisions. Phys. Rev. Lett. 2016, 117, 143201. [Google Scholar] [PubMed]
- Willitsch, S. Ion-atom hybrid systems. In Ion Traps for Tomorrow’s Applications; IOS Press: Amsterdam, The Netherlands, 2015; pp. 255–268. [Google Scholar]
- Eberle, P.; Dörfler, A.D.; von Planta, C.; Ravi, K.; Haas, D.; Zhang, D.; van de Meerakker, S.Y.T.; Willitsch, S. Ion-atom and ion-molecule hybrid systems: Ion-neutral chemistry at ultralow energies. J. Phys. Conf. Ser. 2015, 635, 012012. [Google Scholar]
- Eberle, P.; Dörfler, A.D.; von Planta, C.; Ravi, K.; Willitsch, S. A Dynamic Ion–Atom Hybrid Trap for High-Resolution Cold-Collision Studies. ChemPhysChem 2016, 17, 3769–3775. [Google Scholar] [CrossRef]
- Pérez Ríos, J. Cold chemical reactions between molecular ions and neutral atoms. In An Introduction to Cold and Ultracold Chemistry: Atoms Molecules Ions and Rydbergs; Springer: Berlin/Heidelberg, Germany, 2020; pp. 215–233. [Google Scholar]
- Côté, R.; Dalgarno, A. Ultracold atom-ion collisions. Phys. Rev. A 2000, 62, 012709. [Google Scholar] [CrossRef]
- Zipkes, C.; Palzer, S.; Ratschbacher, L.; Sias, C.; Köhl, M. Cold heteronuclear atom-ion collisions. Phys. Rev. Lett. 2010, 105, 133201. [Google Scholar] [CrossRef]
- Ravi, K.; Lee, S.; Sharma, A.; Werth, G.; Rangwala, S.A. Cooling and stabilization by collisions in a mixed ion–atom system. Nat. Commun. 2012, 3, 1–7. [Google Scholar] [CrossRef]
- Png, W.H.; Hsu, T.; Liu, T.W.; Lin, G.D.; Chang, M.S. Quantum computing with trapped ions: An overview. IEEE Nanotechnol. Mag. 2022, 16, 30–36. [Google Scholar] [CrossRef]
- Doerk, H.; Idziaszek, Z.; Calarco, T. Atom-ion quantum gate. Phys. Rev. A—At. Mol. Opt. Phys. 2010, 81, 012708. [Google Scholar]
- Perego, E.; Duca, L.; Sias, C. Electro-optical ion trap for experiments with atom-ion quantum hybrid systems. Appl. Sci. 2020, 10, 2222. [Google Scholar] [CrossRef]
- Thielemann, F.; Siemund, J.; von Schoenfeld, D.; Wu, W.; Weckesser, P.; Jachymski, K.; Walker, T.; Schaetz, T. Exploring atom-ion Feshbach resonances below the s-wave limit. Phys. Rev. X 2025, 15, 011051. [Google Scholar]
- Weckesser, P.; Thielemann, F.; Wiater, D.; Wojciechowska, A.; Karpa, L.; Jachymski, K.; Tomza, M.; Walker, T.; Schaetz, T. Observation of Feshbach resonances between a single ion and ultracold atoms. Nature 2021, 600, 429–433. [Google Scholar] [CrossRef]
- Xing, X.; Weckesser, P.; Thielemann, F.; Jónás, T.; Vexiau, R.; Bouloufa-Maafa, N.; Luc-Koenig, E.; Madison, K.W.; Orbán, A.; Xie, T.; et al. Competing excitation quenching and charge exchange in ultracold Li-Ba+ collisions. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 245201. [Google Scholar]
- Takahashi, Y. Quantum simulation of quantum many-body systems with ultracold two-electron atoms in an optical lattice. Proc. Jpn. Acad. Ser. B 2022, 98, 141–160. [Google Scholar]
- Côté, R. Ultracold hybrid atom–ion systems. In Advances in Atomic, Molecular, and Optical Physics; Academic Press: Cambridge, MA, USA, 2016; Volume 65, pp. 67–126. [Google Scholar]
- Ladjimi, H.; Zrafi, W.; Farjallah, M.; Bejaoui, M.; Berriche, H. Electronic structure, cold ion–atom elastic collision properties and possibility of laser cooling of BeCs+ molecular ion. Phys. Chem. Chem. Phys. 2022, 24, 18511–18522. [Google Scholar] [PubMed]
- Mahdian, A. Elastic and Inelastic Collisions in an Atom-Ion Experiment. Ph.D. Thesis, Universität Ulm, Ulm, Germany, 2023. [Google Scholar]
- Gacesa, M.; Montgomery, J.A., Jr.; Michels, H.H.; Côté, R. Production of NaCa+ molecular ions in the ground state from cold atom-ion mixtures by photoassociation via an intermediate state. Phys. Rev. A 2016, 94, 013407. [Google Scholar]
- da Silva, H., Jr.; Raoult, M.; Aymar, M.; Dulieu, O. Formation of molecular ions by radiative association of cold trapped atoms and ions. New J. Phys. 2015, 17, 045015. [Google Scholar] [CrossRef]
- Ladjimi, H.; Sardar, D.; Farjallah, M.; Alharzali, N.; Naskar, S.; Mlika, R.; Berriche, H.; Deb, B. Spectroscopic properties of the molecular ions BeX+ (X = Na, K, Rb): Forming cold molecular ions from an ion–atom mixture by stimulated Raman adiabatic process. Mol. Phys. 2018, 116, 1812–1826. [Google Scholar] [CrossRef]
- Sardar, D.; Naskar, S.; Pal, A.; Berriche, H.; Deb, B. Formation of a molecular ion by photoassociative Raman processes. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 245202. [Google Scholar] [CrossRef]
- Mølhave, K.; Drewsen, M. Formation of translationally cold MgH+ and MgD+ molecules in an ion trap. Phys. Rev. A 2000, 62, 011401. [Google Scholar] [CrossRef]
- Staanum, P.F.; Højbjerre, K.; Wester, R.; Drewsen, M. Probing isotope effects in chemical reactions using single ions. Phys. Rev. Lett. 2008, 100, 243003. [Google Scholar] [CrossRef]
- Bertelsen, A.; Vogelius, I.S.; Jørgensen, S.; Kosloff, R.; Drewsen, M. Photo-dissociation of Cold MgH ions: Towards rotational temperature measurements and controlled dissociation. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2004, 31, 403–408. [Google Scholar]
- Jørgensen, S.; Drewsen, M.; Kosloff, R. Intensity and wavelength control of a single molecule reaction: Simulation of photodissociation of cold-trapped MgH+. J. Chem. Phys. 2005, 123, 94302. [Google Scholar] [CrossRef] [PubMed]
- Aymar, M.; Dulieu, O. The electronic structure of the alkaline-earth-atom (Ca, Sr, Ba) hydride molecular ions. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215103. [Google Scholar] [CrossRef]
- Belayouni, S.; Ghanmi, C.; Berriche, H. Adiabatic and quasi-diabatic investigation of the strontium hydride cation SrH+: Structure, spectroscopy, and dipole moments. Can. J. Phys. 2016, 94, 791–802. [Google Scholar] [CrossRef]
- Shi, D.; Liu, X.; Shan, S.; Xu, H.; Yan, B. Configuration interaction study on the low-lying electronic states of strontium hydride cation including spin-orbit coupling. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2017, 180, 29–36. [Google Scholar] [CrossRef]
- Allouche, A.R.; Spiegelmann, F.; Aubert-Frécon, M. Theoretical study of the low-lying electronic states of the BaH+ molecular ion. Chem. Phys. Lett. 1993, 204, 343–349. [Google Scholar]
- Śmiałkowski, M.; Tomza, M. Interactions and chemical reactions in ionic alkali-metal and alkaline-earth-metal diatomic AB+ and triatomic A 2 B+ systems. Phys. Rev. A 2020, 101, 012501. [Google Scholar]
- Hall, F.H.; Eberle, P.; Hegi, G.; Raoult, M.; Aymar, M.; Dulieu, O.; Willitsch, S. Ion-neutral chemistry at ultralow energies: Dynamics of reactive collisions between laser-cooled Ca+ ions and Rb atoms in an ion-atom hybrid trap. Mol. Phys. 2013, 111, 2020–2032. [Google Scholar] [CrossRef]
- Ben-shlomi, R.; Pinkas, M.; Meir, Z.; Sikorsky, T.; Katz, O.; Akerman, N.; Ozeri, R. High-energy-resolution measurements of an ultracold-atom–ion collisional cross section. Phys. Rev. A 2021, 103, 032805. [Google Scholar]
- Smith, W.W.; Goodman, D.S.; Sivarajah, I.; Wells, J.E.; Banerjee, S.; Côté, R.; Michels, H.H.; Mongtomery, J.A.; Narducci, F.A. Experiments with an ion-neutral hybrid trap: Cold charge-exchange collisions. Appl. Phys. B 2014, 114, 75–80. [Google Scholar]
- Meir, Z.; Sikorsky, T.; Ben-Shlomi, R.; Akerman, N.; Dallal, Y.; Ozeri, R. Dynamics of a ground-state cooled ion colliding with ultracold atoms. Phys. Rev. Lett. 2016, 117, 243401. [Google Scholar] [CrossRef]
- Zipkes, C.; Palzer, S.; Sias, C.; Köhl, M. A trapped single ion inside a Bose–Einstein condensate. Nature 2010, 464, 388–391. [Google Scholar] [CrossRef]
- Hall, F.H.; Aymar, M.; Raoult, M.; Dulieu, O.; Willitsch, S. Light-assisted cold chemical reactions of barium ions with rubidium atoms. Mol. Phys. 2013, 111, 1683–1690. [Google Scholar] [CrossRef]
- ElOualhazi, R.; Berriche, H. Electronic structure and spectra of the MgLi+ ionic molecule. J. Phys. Chem. A 2016, 120, 452–465. [Google Scholar] [CrossRef] [PubMed]
- Akkari, S.; Zrafi, W.; Ladjimi, H.; Bejaoui, M.; Dhiflaoui, J.; Berriche, H. Electronic structure of ground and low-lying excited states of BaLi+ molecular ion: Spin-orbit effect, radiative lifetimes and Franck-Condon factor. Phys. Scr. 2024, 99, 035403. [Google Scholar] [CrossRef]
- Zrafi, W.; Ladjimi, H.; Said, H.; Berriche, H.; Tomza, M. Ab initio electronic structure and prospects for the formation of ultracold calcium–alkali-metal-atom molecular ions. New J. Phys. 2020, 22, 073015. [Google Scholar]
- Aymar, M.; Guérout, R.; Dulieu, O. Structure of the alkali-metal-atom+ strontium molecular ions: Towards photoassociation and formation of cold molecular ions. J. Chem. Phys. 2011, 135, 6. [Google Scholar] [CrossRef]
- Fuentealba, P.; Reyes, O. Pseudopotential calculations on the ground state of the alkaline-earth monohydride ions. Mol. Phys. 1987, 62, 1291–1296. [Google Scholar] [CrossRef]
- Foucrault, M.; Millié, P.; Daudey, J.P. Nonperturbative method for core–valence correlation in pseudopotential calculations: Application to the Rb2 and Cs2 molecules. J. Chem. Phys. 1992, 96, 1257–1264. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Jou, F.C.; Kelleher, D.E.; Kramida, A.E.; Musgrove, A.; Reader, J.; Olsen, K. NIST Atomic Spectra Database (Version 3.0.1); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2006. Available online: https://webbook.nist.gov/chemistry/ (accessed on 3 May 2025).
- Aymar, M.; Guérout, R.; Sahlaoui, M.; Dulieu, O. Electronic structure of the magnesium hydride molecular ion. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 154025. [Google Scholar] [CrossRef]
- Kaupp, M.; Schleyer, P.V.R.; Stoll, H.; Preuss, H. Pseudopotential approaches to Ca, Sr, and Ba hydrides. Why are some alkaline earth MX2 compounds bent? J. Chem. Phys. 1991, 94, 1360–1366. [Google Scholar] [CrossRef]
- Zrafi, W.; Hela, L.; Berriche, H. Accurate ab initio calculations of adiabatic energy and dipole moment: Prospects for the formation of cold Alkaline-Earth-Francium molecular ions ALKE-Fr+ (ALKE = Be, Mg, Ca, and Sr). Phys. Scr. 2023, 98, 125403. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Nagle, J.K. 2018 Table of static dipole polarizabilities of the neutral elements in the periodic table. Mol. Phys. 2019, 117, 1200–1225. [Google Scholar]
- Cooley, J.W. An improved eigenvalue corrector formula for solving the Schrödinger equation for central fields. Math. Comput. 1961, 15, 363–374. [Google Scholar]
- Schweizer, W. Discrete Variable Method. In Numerical Quantum Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 155–207. [Google Scholar] [CrossRef]
- Zemke, W.T.; Crooks, J.B.; Stwalley, W.C. Radiative and nonradiative lifetimes for vibrational levels of the A 1Σ+ state of 7LiH. J. Chem. Phys. 1978, 68, 4628–4630. [Google Scholar] [CrossRef]
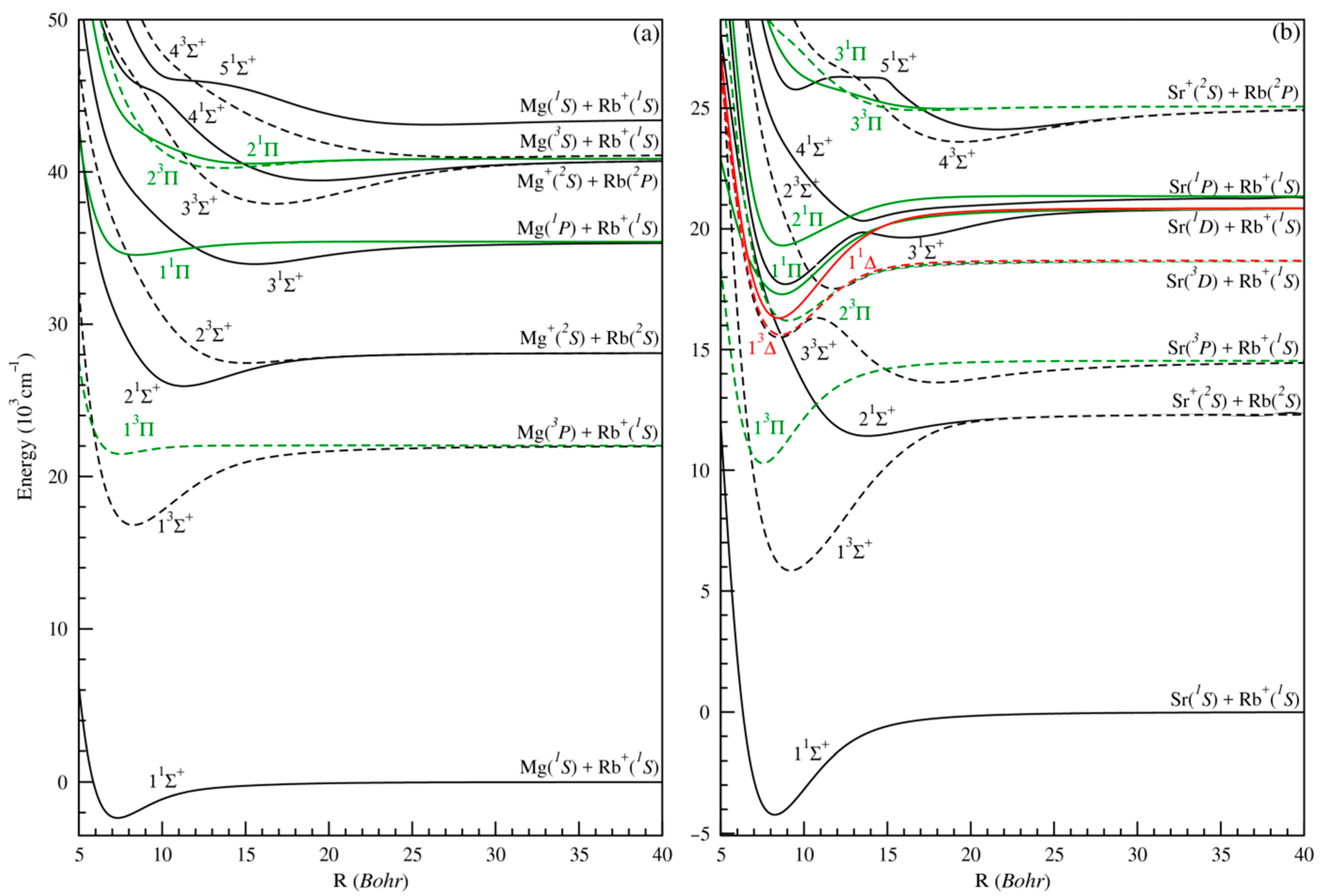
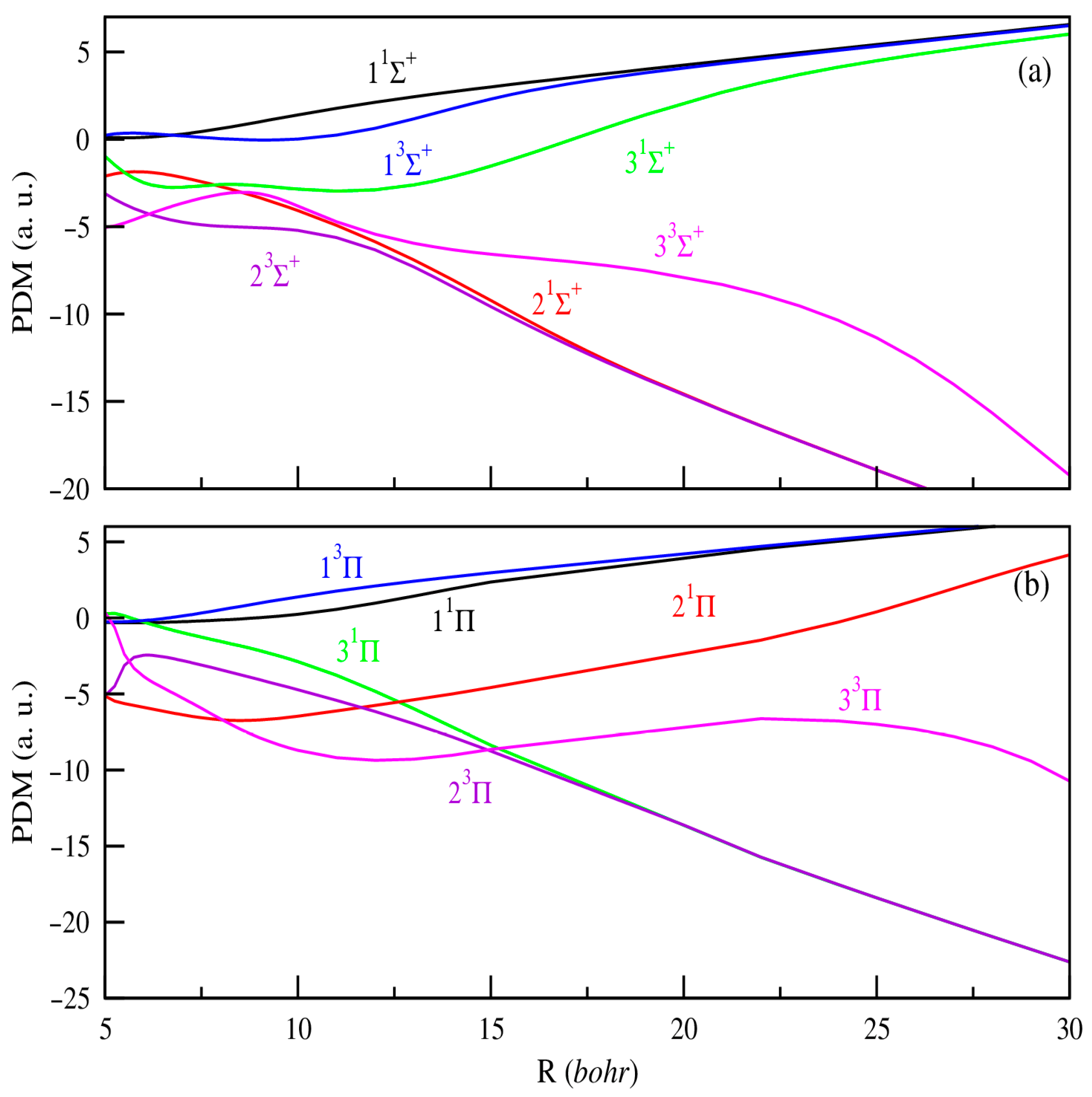
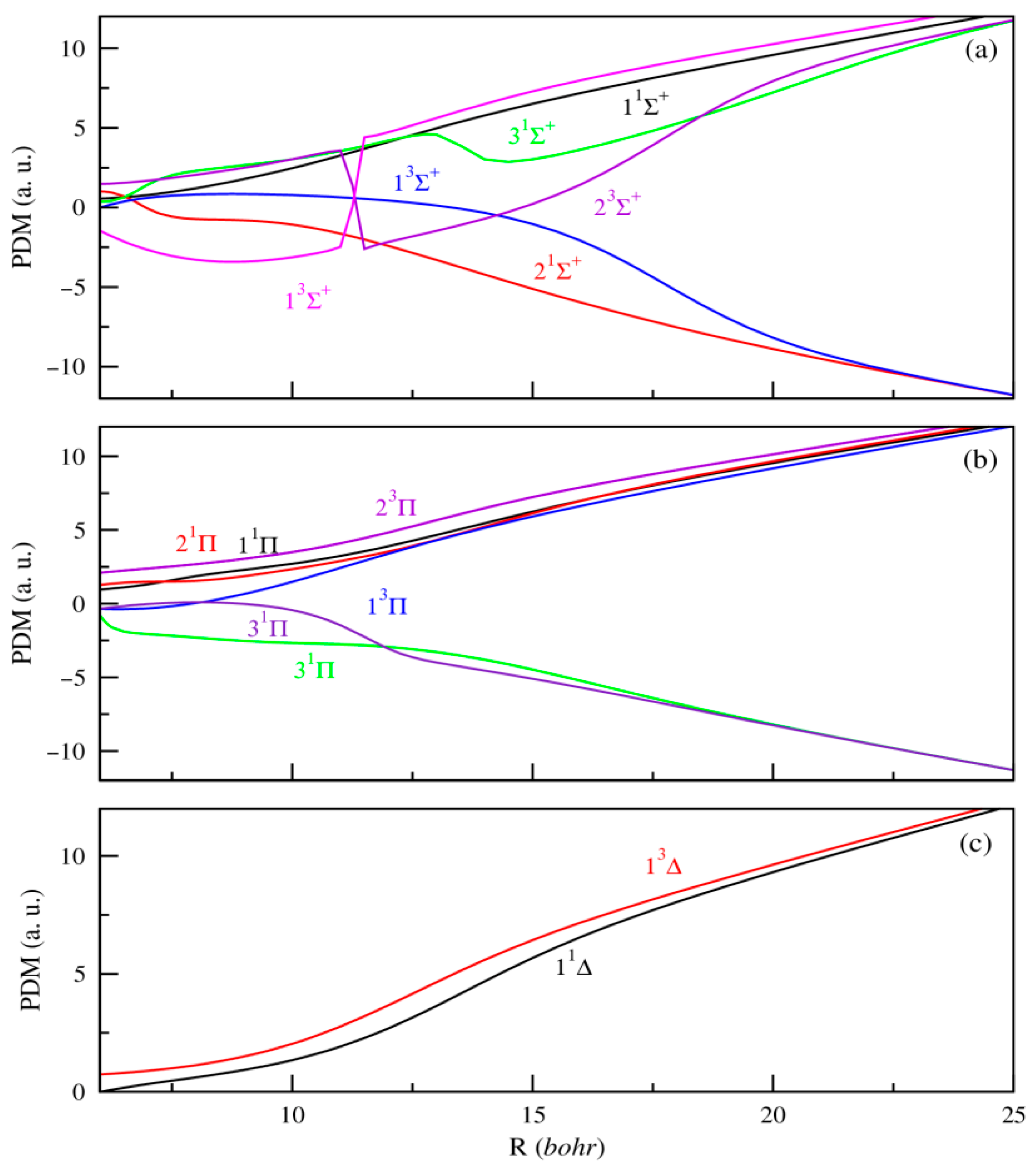
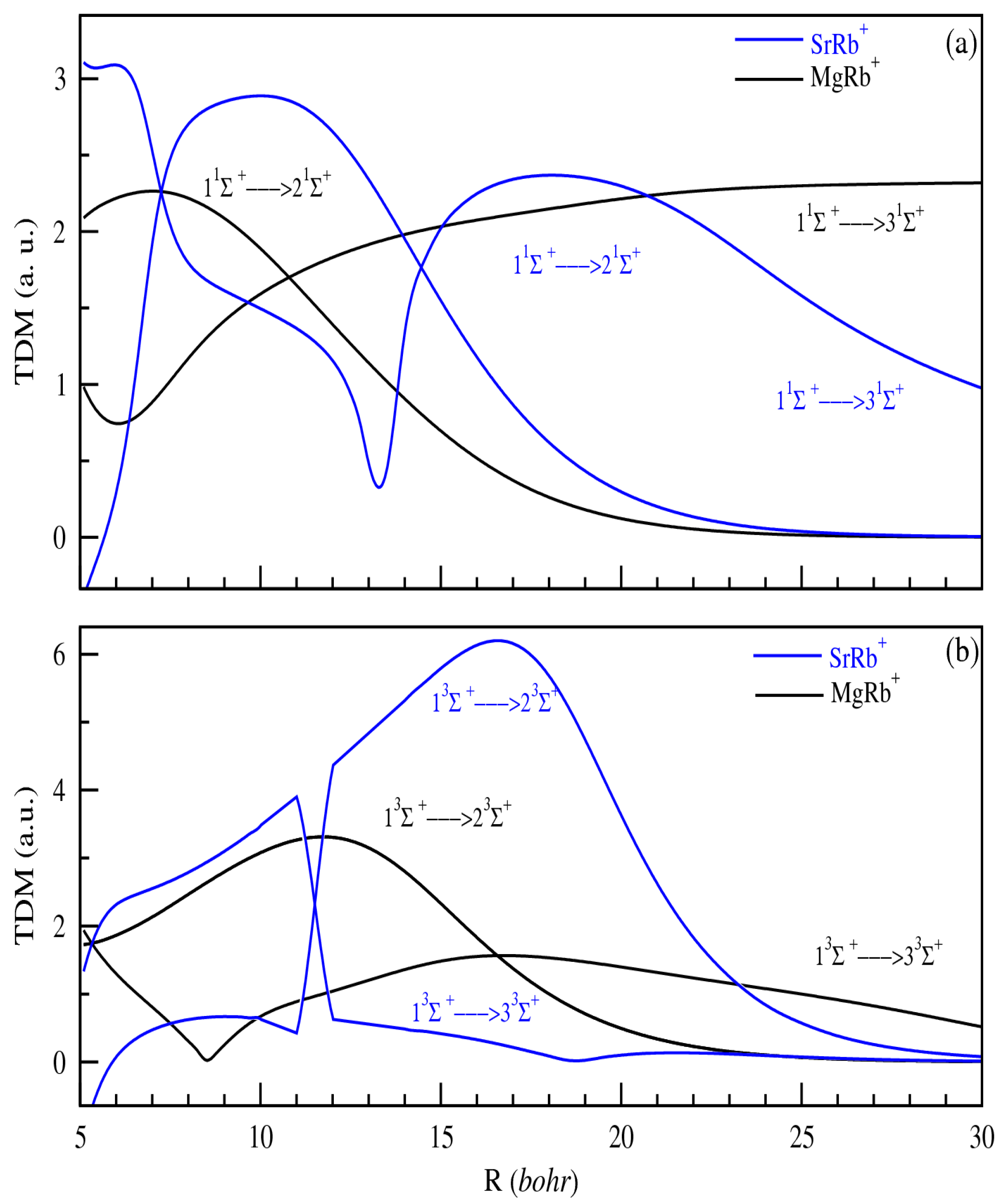
| Rb | Mg | Sr | |
|---|---|---|---|
| α | 9.245 | 0.46904 | 5.51 |
| 2.5213 | 0.900 | 2.0893 | |
| 2.279 | 1.25499 | 2.1170 | |
| 2.511 | 1.500 | 1.64471 | |
| 2.511 | 1.500 | 1.64471 |
| Ion | State | Asymptotic Limit | This Work | Exp [45] | Theo [42] | Theo [39] |
|---|---|---|---|---|---|---|
| MgRb+ | ||||||
| X1Σ+ | Mg(1S(3s2)) + Rb+ | 0 | 0 | |||
| 13Σ+, 13Π | Mg(3P(3s3p)) + Rb+ | 21,875 | 21,994 | |||
| 21 Σ+, 23Σ+ | Mg+(2S(3s)) + Rb(2S(5s)) | 27,978 | 28,116 | |||
| 31Σ+, 11Π | Mg(1P(3s3p)) + Rb+ | 35,049 | 35,181 | |||
| 41Σ+, 21Π, 33Σ+, 23Π | Mg+(2S(3s)) + Rb(2P(5p)) | 40,715 | 40,853 | |||
| 43Σ+ | Mg(3S(3s4s)) + Rb+ | 41,195 | 41,154 | |||
| 51Σ+ | Mg(1S(3s4s)) + Rb+ | 43,501 | 43,472 | |||
| SrRb+ | ||||||
| X1Σ+ | Sr(1S(5s2)) + Rb+ | 0 | 0 | 0 | 0 | |
| 21Σ+, 13Σ+ | Sr+(2S(5s)) + Rb(2S(5s)) | 12,402 | 12,147 | 12,441 | - | |
| 23Σ+, 13Π | Sr(3P(5s5p)) + Rb+ | 14,965 | 14,710 | 14,627 | 14,548 | |
| 33Σ+, 23Π, 13∆ | Sr(3D(5s4d)) + Rb+ | 18,722 | 18,258 | 18,795 | 18,242 | |
| 31Σ+, 11Π, 11∆ | Sr(1D(5s4d)) + Rb+ | 20,893 | 20,150 | 20,810 | 20,209 | |
| 41Σ+, 21Π | Sr(1P(5s5p)) + Rb+ | 21,480 | 21,699 | 21,455 | 21,459 | |
| 51Σ+, 31Π, 43Σ+, 33Π | Sr+(2S(5s)) + Rb(2P(5p)) | 25,139 | 24,884 | - | - |
| State | Re (Bohr) | De (cm−1) | Te (cm−1) | ωe (cm−1) | ωexe (cm−1) | Be (cm−1) | Reference |
|---|---|---|---|---|---|---|---|
| X1Σ | 7.33 | 2352 | 0 | 84.19 | 0.83 | 0.059151 | This work |
| 7.41 | 2237 | 0 | 84.1 | 0.058600 | [32] | ||
| 21Σ+ | 11.29 | 2182 | 28,285 | 45.96 | 0.18 | 0.024964 | This work |
| 31Σ+ | 15.57 | 1454 | 36,296 | 28.22 | 0.08 | 0.013123 | This work |
| 41Σ+ | 19.42 | 1416 | 41,787 | 21.82 | 0.06 | 0.008437 | This work |
| 51Σ+ | 26.14 | 375 | 45,450 | 11.65 | 0.07 | 0.004656 | This work |
| 11Π | 8.44 | 852 | 36,899 | 40.03 | 0.55 | 0.044675 | This work |
| 21Π | 15.34 | 304 | 42,901 | 17.52 | 0.18 | 0.013519 | This work |
| 31Π | 18.34 | 896 | 48,425 | 16.43 | 0.06 | 0.009462 | This work |
| 11∆ * | Repulsive | This work | |||||
| 13Σ+ | 8.27 | 5198 | 19,166 | 80.35 | 0.30 | 0.046547 | This work |
| 23Σ+ | 15.04 | 668 | 29,799 | 25.75 | 0.23 | 0.014060 | This work |
| 33Σ+ | 16.68 | 2947 | 40,256 | 29.84 | 0.05 | 0.011440 | This work |
| 43Σ+ | 29.05 | 192 | 43,313 | 7.74 | 0.08 | 0.003770 | This work |
| 13Π | 7.51 | 535 | 23,830 | 55.84 | 1.32 | 0.056425 | This work |
| 23Π | 13.62 | 599 | 42,606 | 23.53 | 0.16 | 0.017156 | This work |
| 33Π | 18.78 | 1128 | 48,693 | 17.70 | 0.05 | 0.009024 | This work |
| 13∆ * | Repulsive | This work |
| State | Re (Bohr) | ∆Rₑ (%) | De (cm−1) | ∆Dₑ (%) | Te (cm−1) | ωe (cm−1) | ∆ωₑ (%) | ωexe (cm−1) | Be (cm−1) | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| X1Σ+ | 8.24 | 4225 | 58.09 | 0.18 | 0.020494 | This work | ||||
| 8.34 | 1.2 | 4247 | 59.00 | 1.6 | 0.020100 | [32] | ||||
| 8.23 | 0.1 | 4266 | 1.0 | 59.41 | 2.3 | 0.0205 | [21] | |||
| 8.2 | 0.5 | 4285 | 1.4 | 58.00 | 0.2 | [42] | ||||
| 21Σ+ | 13.81 | 895 | 15,645 | 20.68 | 0.11 | 0.007297 | This work | |||
| 13.79 | 0.1 | 933 | 4.2 | 15,752.3 | 20.94 | 1.3 | 0.0073 | [21] | ||
| 13.8 | 0.1 | 960 | 7.3 | 21.00 | 1.5 | [42] | ||||
| 31Σ+ | 8.88 | 3143 | 21,933 | 46.60 | 0.12 | 0.017632 | This work | |||
| 8.09 | 8.9 | 3122 | 0.7 | 47.00 | 0.9 | [42] | ||||
| 2nd well | 16.02 | 1216 | 23,861 | 16.47 | 0.055 | 0.001518 | This work | |||
| 15.8 | 1.4 | 1132 | 6.9 | 16.00 | 2.9 | [42] | ||||
| 41Σ+ | 13.52 | 1000 | 24,557 | 37.19 | 0.49 | 0.007611 | This work | |||
| 13.6 | 0.6 | 1012 | 1.2 | 31.00 | 16.6 | [42] | ||||
| 51Σ+ | 9.50 | 723 * | This work | |||||||
| 14.39 | 1231 * | This work | ||||||||
| 21.64 | 933 | 28,342 | 12.18 | 0.45 | 0.015415 | This work | ||||
| 13Σ+ | 9.20 | 6474 | 10,068 | 49.57 | 0.09 | 0.016450 | This work | |||
| 9.20 | 6544 | 1.1 | 49.00 | 1.2 | [42] | |||||
| 23Σ+ | 8.52 | 976 * | This work | |||||||
| 8.5 | 0.2 | 954 | 2.3 | 49.00 | [42] | |||||
| 2nd well | 17.98 | 881 | 17,863 | 14.99 | 0.16 | 0.019179 | This work | |||
| 18.00 | 0.1 | 893 | 1.4 | 15.00 | 0.1 | [42] | ||||
| 33Σ+ | 11.26 | 1694 | 21,207 | 123.97 | 6.46 | 0.010977 | This work | |||
| 11.00 | 2.3 | 1923 | 13.5 | [42] | ||||||
| 43Σ+ | 19.39 | 1445 | 27,830 | 15.48 | 0.03 | 0.003701 | This work | |||
| 11Π | 8.67 | 3563 | 21,515 | 43.66 | 0.08 | 0.018522 | This work | |||
| 8.7 | 0.3 | 3561 | 0.1 | 44.00 | 0.8 | [42] | ||||
| 21Π | 8.71 | 2024 | 23,535 | 39.82 | 0.31 | 0.018340 | This work | |||
| 8.7 | 0.1 | 2049 | 1.2 | 40.00 | 0.5 | [42] | ||||
| 31Π | 18.65 | 76 | 29,204 | 6.48 | 0.14 | 0.003999 | This work | |||
| 13Π | 7.54 | 4229 | 14,518 | 63.72 | 0.20 | 0.024448 | This work | |||
| 7.6 | 0.8 | 4240 | 0.3 | 64.00 | 0.4 | [42] | ||||
| 23Π | 9.04 | 2479 | 20,423 | 43.57 | 0.13 | 0.017045 | This work | |||
| 9.0 | 0.4 | 2551 | 2.9 | 44.00 | 0.1 | [42] | ||||
| 33Π | 17.07 | 139 | 29,141 | 8.38 | 0.11 | 0.004775 | This work | |||
| 11∆ | 8.49 | 4551 | 20,527 | 51.11 | 0.11 | 0.019320 | This work | |||
| 8.5 | 0.1 | 4533 | 0.4 | 52.00 | 1.6 | [42] | ||||
| 13∆ | 8.6 | 3068 | 19,834 | 48.09 | 0.12 | 0.018818 | This work | |||
| 8.6 | 3150 | 2.7 | 49.00 | 1.7 | [42] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farjallah, M.; Ladjimi, H.; Zrafi, W.; Berriche, H. Theoretical Calculation of Ground and Electronically Excited States of MgRb+ and SrRb+ Molecular Ions: Electronic Structure and Prospects of Photo-Association. Atoms 2025, 13, 69. https://doi.org/10.3390/atoms13080069
Farjallah M, Ladjimi H, Zrafi W, Berriche H. Theoretical Calculation of Ground and Electronically Excited States of MgRb+ and SrRb+ Molecular Ions: Electronic Structure and Prospects of Photo-Association. Atoms. 2025; 13(8):69. https://doi.org/10.3390/atoms13080069
Chicago/Turabian StyleFarjallah, Mohamed, Hela Ladjimi, Wissem Zrafi, and Hamid Berriche. 2025. "Theoretical Calculation of Ground and Electronically Excited States of MgRb+ and SrRb+ Molecular Ions: Electronic Structure and Prospects of Photo-Association" Atoms 13, no. 8: 69. https://doi.org/10.3390/atoms13080069
APA StyleFarjallah, M., Ladjimi, H., Zrafi, W., & Berriche, H. (2025). Theoretical Calculation of Ground and Electronically Excited States of MgRb+ and SrRb+ Molecular Ions: Electronic Structure and Prospects of Photo-Association. Atoms, 13(8), 69. https://doi.org/10.3390/atoms13080069






