1. Introduction
The Earth’s atmospheric radiation environment is highly variable and includes multiple sources of ionizing radiation. The primary source of thermal energy for the Earth is solar radiation. This energy is transmitted through radiation and converted into heat when it reaches the Earth’s surface. Among the various forms of solar radiation, extreme ultraviolet (EUV) light is a significant contributor to the energy input into Earth’s and other planetary atmospheres. To maintain energy balance, Earth also radiates energy back into space. However, some of this outgoing radiation is trapped by greenhouse gases and re-emitted toward the surface, resulting in planetary warming—an effect widely known as the greenhouse effect.
Streams of charged particles from the Sun, particularly during intense space weather events, can significantly influence Earth’s climate and atmospheric conditions (see [
1,
2,
3] and references therein). Among the most impactful contributors to space radiation are solar energetic particles, which are high-energy particles (ranging from keV to GeV) composed mainly of protons, electrons, and heavy ions with a high atomic number, as well as high-energy components of galactic cosmic rays.
The ozone layer—a vital shield located in the upper atmosphere—absorbs between 93% and 99% of the sun’s ultraviolet (UV) radiation, thereby protecting life on Earth. In addition to CFCs, solar energetic particles have also been shown to contribute to ozone reduction, particularly during solar storms (see [
1,
2,
3] and references therein). During these storms, elevated levels of solar protons in the upper atmosphere can break apart molecules, creating reactive compounds that deplete the ozone.
Currently, there is considerable concern that human-induced increases in greenhouse gases could cause substantial global warming. Over the past century, the levels of these naturally occurring gases have surged due to human activities. Additionally, industrially manufactured compounds such as CF3CH2F (HFC-134a, also known as R134a) have also seen rising concentrations in the atmosphere in recent decades.
Due to its chemical and physical characteristics, CF
3CH
2F has been identified as the most effective replacement for CFC-12 in refrigeration and air conditioning systems [
1,
2,
3]. The environmental impact of a substance is commonly assessed based on its potential to deplete the ozone layer and enhance the greenhouse effect. The latter is quantified using the Global Warming Potential (GWP), which compares the energy absorbed by the emissions of 1 ton of a substance over a specified period—typically 100 years—to that absorbed by 1 ton of CO
2, which has a GWP of 1. The Ozone Depletion Potential (ODP), in contrast, is measured relative to the reference compound CCl
3F.
CF
3CH
2F is currently the most abundant hydrofluorocarbon in the atmosphere, with concentrations about five times higher than those of other HFCs [
1]. Before the 1990s, the production of CF
3CH
2F was minimal, but it has grown considerably since then. However, emissions are not directly tied to production levels; rather, they occur during use and after disposal.
CF
3CH
2F, like many hydrofluorocarbons, contains a CF
3 group. Studies [
1,
2,
3] indicate that CF
3 groups do not significantly contribute to ozone depletion. Although CF
3CH
2F has a negligible ODP, its atmospheric breakdown can release fluorine atoms. In the upper atmosphere, protons and photons in the extreme ultraviolet and x-ray ranges provide critical energy that can ionize, excite, and dissociate neutral gas molecules.
Thus, refrigerant gases currently in use, such as the CF
3CH
2F, pose significant environmental threats due to their strong contributions to the greenhouse effect and/or their destructive impact on the ozone layer. To mitigate these effects, regulations have been introduced to restrict the production and use of certain gases [
2]. The greenhouse effect is measured in terms of GWP, while the effect on the ozone layer is measured using ODP. The CF
3CH
2F molecule has a GWP of 1430, an ODP of 0, and a lifetime of 14 years. It has been the subject of several studies [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11].
Gas detectors are widely employed in nuclear and high-energy physics applications for detecting, tracking, and triggering charged particles, such as muons. These detectors are valued for their simplicity and reliability; however, careful consideration must be given to factors such as gas–material interactions, gas purification processes, and the presence of contaminants in gas mixtures [
11].
The energy loss of charged particles as they pass through matter is a topic of considerable importance in both atomic and nuclear physics. In nuclear experiments, accurately determining the reaction energy often requires precise knowledge of the stopping cross-sections of the target materials. This is especially critical for proton energies below 1 MeV, where the stopping cross-sections rise sharply with decreasing energy and reach a peak near 100 keV.
Since oscillator strengths are essential for determining the stopping powers of bound electrons, it is important to calculate them accurately for molecules. The electronic stopping power of high-velocity ions, represented by |−dE/dx|, can be derived from the photon absorption cross-section of the target material. This is because the electromagnetic field of a fast-moving ion can be approximated as a flux of virtual photons accompanying the ion. As the ion travels through the medium, some of these virtual photons are absorbed by the target’s electrons. The ion then regenerates the virtual photons through its electric current; however, this regeneration draws energy from the ion’s center-of-mass motion. Consequently, the absorption of virtual photons corresponds to an energy loss by the ion’s electrons. In this context, |−dE/dx| can be interpreted as the average opacity for virtual photon absorption.
The aim of this paper is to discuss some of the important properties of the interaction between photons, protons, and the CF3CH2F molecule, an eco-friendly refrigerant used in particle gas detectors.
2. Results
Understanding how atoms and molecules are ionized by both charged particles and photons is crucial for a comprehensive grasp of how matter responds to electromagnetic fields. When assuming collision speeds that are fast but still within the non-relativistic regime, this connection has been widely explored in atomic physics [
12,
13,
14]. In the framework of non-relativistic Bethe–Born (NBB) dipole approximation, the ionization of atoms by projectiles during collisions involving small momentum transfer is often analyzed by highlighting its resemblance to ionization through photon absorption (i.e., the photoelectric effect).The Weizsäcker–Williams (WW) approach, also known as the equivalent photon method, is a commonly used technique in atomic and molecular physics for estimating electron ejection resulting from collisions between atoms and molecules and high-speed charged projectiles. The frequency spectrum of virtual photons is as follows [
14]:
where
q is the projectile charge;
v is its speed;
c is the speed of light;
α =
e2/
ħc is the fine structure constant; and
a ≅ 1 is a dimensionless number.
This method is applicable because, for collisions with sufficiently large impact parameters, the electromagnetic field of the incoming projectile can closely resemble that of a pulse of radiation. Consequently, ionization cross-sections resulting from interactions with charged particles can be directly compared to those resulting from photoabsorption. The WW method is even sometimes applied to non-relativistic fast collisions involving light targets [
12], where it continues to provide reasonably accurate predictions for ionization cross-sections.
As a charged particle or photon travels through a material, it inevitably interacts with the medium, transferring part of its energy and leading to ionization. This interaction results in the creation of an ion–electron pair, consisting of an ionized atom and a liberated electron. For charged particles, the energy loss during this process is commonly described by the stopping power, denoted as |−dE/dx|, where E represents the particle’s energy and x is the distance traversed within the medium.
Since the energy transfer in typical stopping experiments occurs from the projectile’s kinetic energy to the target material through electronic excitations, it is reasonable to expect that the transition strength—quantified by the oscillator strength—plays a significant role in the process.
2.1. Photoabsorption
In the regime of high-energy collisions, the first Born approximation is expected to be valid. So, the results for the ionization cross-section induced by proton collision should be comparable to that of photoionization. Accordingly, we calculated the photoionization cross-sections to compare them with those obtained for proton impact in the high-energy limit. The photoionization cross-section is related to the optical oscillator strength (OOS) according to the following:
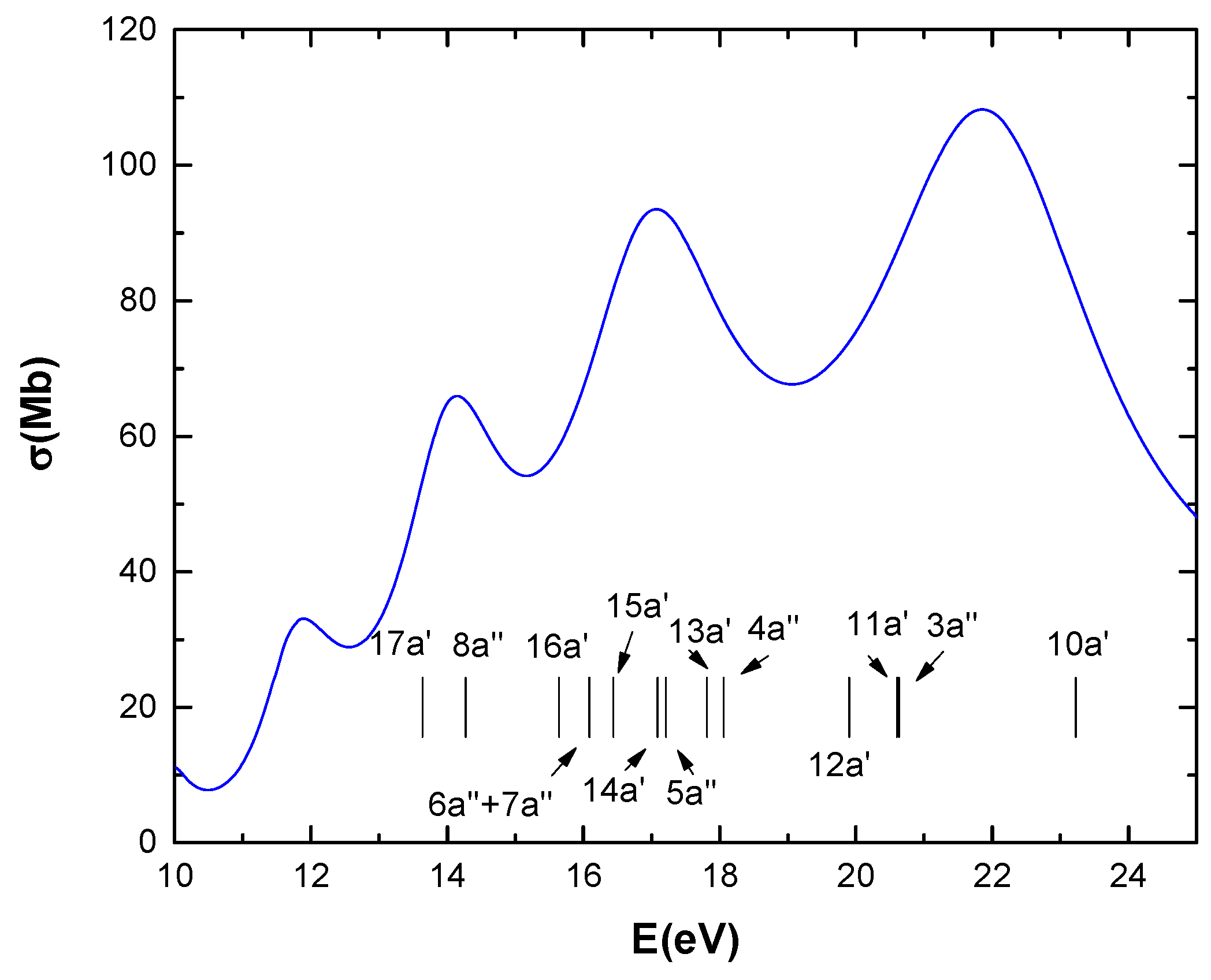
Figure 1 presents the time-dependent density-functional theory (TDDFT) calculations for the photoabsorption cross-sections of CF
3CH
2F as a function of photon energy.
In
Figure 1, the calculated total photoabsorption cross-section is shown in the 10–25 eV range. Above the ionization energy (13.64 eV), this essentially represents the photoionization cross-section. The distinct peaks suggest the possibility of discrete resonances within the continuum. Above the ionization potential, for instance in the 15–25 eV range, the total cross-section ranges from 54 to 110 Mb.
2.2. Proton Impact Ionization
Figure 2 shows the calculated ionization cross-sections of the CF
3CH
2F molecule due to proton impact as a function of projectile energy. These are compared to the electron impact ionization cross-section from the binary-encounter-Bethe (BEB) model [
9], as well as to the classical ionization cross-section [
13].
According to theoretical models based on first-order Born approximations, the cross-section for ionization processes (σ
+) is directly proportional to the natural logarithm of the velocity and the square of the electric charge divided by the velocity, as shown in the following equation:
. In this context, since electrons and protons have charges of the same magnitude (although with opposite signs), it is expected that both will have similar cross-sections in high-energy regimes when they have the same velocities. This equivalence is justified by the dominance of the Coulomb interaction and the validity of the Born approximation in this energy range. Thus, the BEB calculations for electron impact [
9] were used to normalize Rudd’s model [
12] at high projectile energy.
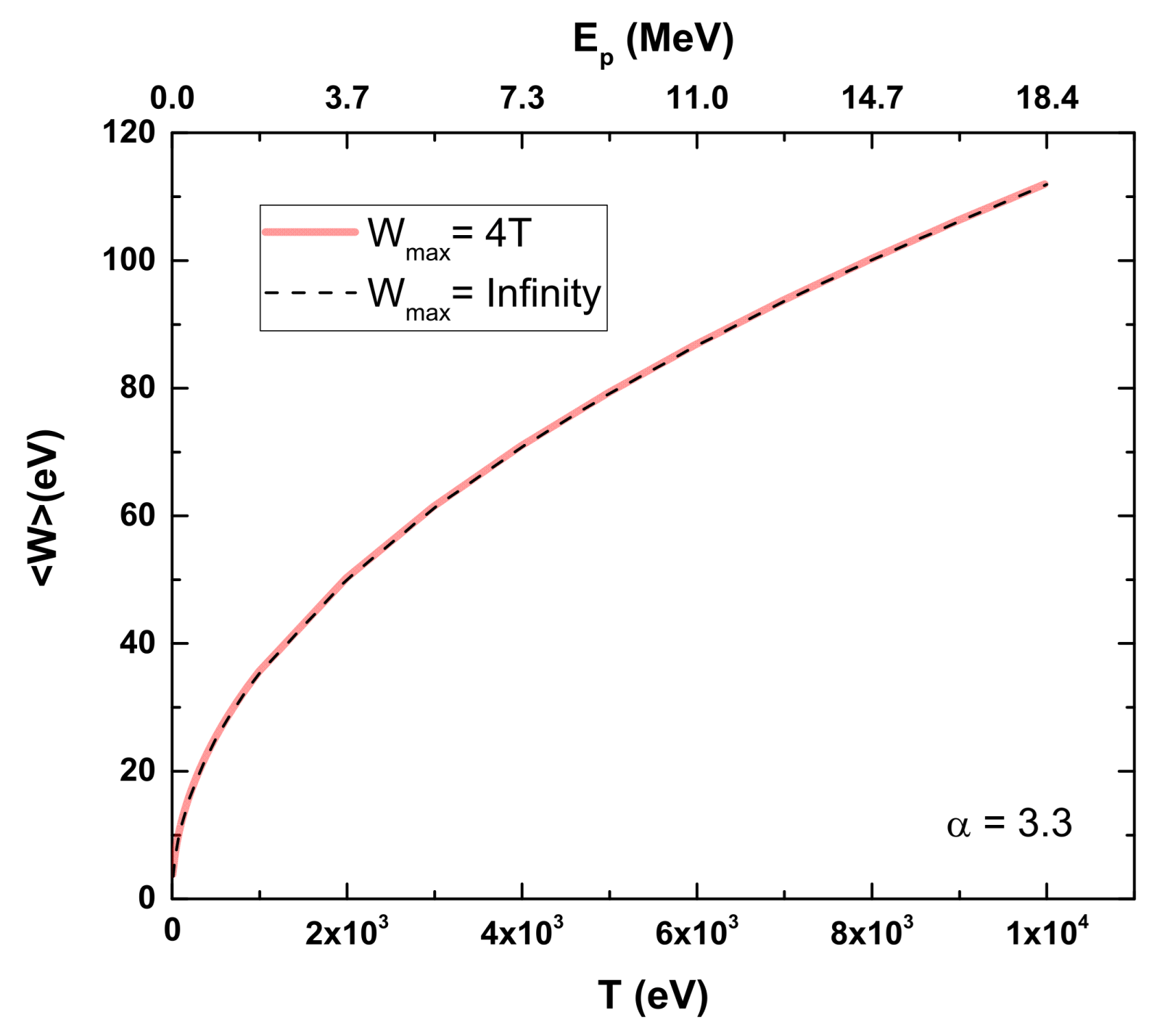
Another notable quantity that can be determined is the mean energy 〈
W〉 of the secondary electrons, expressed as follows:
According to Rudd’s model, low-energy transfers will be more relevant in these calculations, making the ionization of the valence shell a noticeable factor.
Figure 3 shows our results for CF
3CH
2F, illustrating Equation (3) with
Wmax = ∞ and comparing it to the more realistic limit of
Wmax = 4T. No significant differences are observed between the two curves as a function of the proton energy.
The penetration of charged particles through matter has been extensively investigated through both theoretical analyses and experimental studies for over a hundred years. Despite these efforts, the inherently many-body nature of atomic and molecular systems presents significant challenges in achieving a comprehensive understanding of the mechanisms involved in the deceleration of projectiles. The electronic stopping cross-section reflects the response of a material’s electrons to the energy deposited by an incoming projectile, often resulting in electronic excitations.
The electronic stopping power curve is typically divided into three distinct regimes, each corresponding to different dominant energy loss processes based on their likelihood of occurrence. At high projectile velocities, energy dissipation is primarily due to the ionization of individual atoms. As the projectile’s speed decreases, processes such as electron capture, electron loss, and electronic excitations begin to play a more prominent role [
15,
16].
An analytical approximation for projectiles in the moderately relativistic regime (0.1 < (βγ =
p/Mc) < 1000) can be found by using the Bethe–Bloch equation [
8,
9,
10], as follows:
where
is the mean energy loss per length;
ρ is the density of the medium;
I = 95.0294 eV is the mean excitation energy; and
δ(
βγ) is the density effect correction function to the energy loss.
K is a constant given by
K = 4
πNA(
re2mec2r2) and
, where
M is the mass of the incoming particle [
11].
In each inelastic collision, a specific amount of energy Δ
E is transferred from the incoming particle to the medium. The stopping cross-section associated with ionization is expressed in the following equation [
17,
18,
19,
20]:
The stopping power
S is defined as the average energy loss per unit path length of the projectile. It can be evaluated as the ratio of the average energy loss in a collision, as follows [
15,
16,
17,
18]:
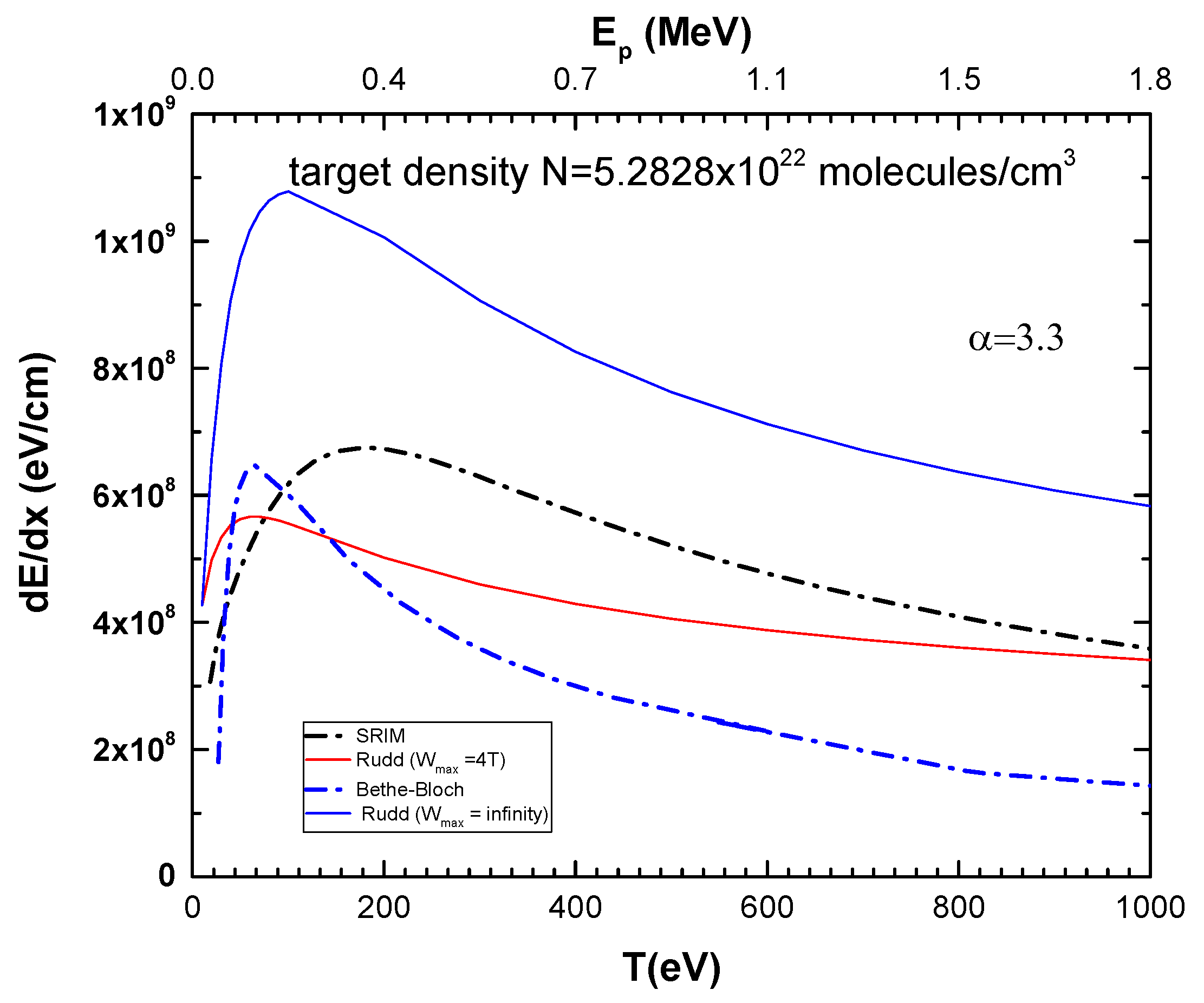
In
Figure 4, we show the results for the electronic stopping cross-section across the low to high collision range, obtained using Rudd’s model [
10], with
Wmax = ∞ and
Wmax = 4T. These are compared with the Bethe–Bloch expression, Equation (1), the classical model [
13], and the results from the Stopping and Range of Ions in Matter (SRIM) program [
17,
18], for the CF
3CH
2F molecule. The target density was taken as
N = 5.28 × 10
22 molecules/cm
3. From
Figure 4, it can be observed that Rudd’s model with
Wmax = ∞ overestimates the stopping power by a factor of two in comparison to the other models. This is because it overestimates the contribution of the SDCS, where the kinetic energy of the ejected electrons does not obey the momentum and energy conservation laws. On the other hand, Rudd’s model with
Wmax = 4T, SRIM, and Bethe–Bloch stopping powers present different proton energy dependencies, although they generally agree within 25% to a factor of two, depending on the energy range.
3. Discussion
As seen in the previous section, Rudd’s model, SRIM, and Bethe–Bloch stopping powers present different proton energy dependencies, although there is generally a relative agreement.
The SRIM program [
15] is widely recognized as a reliable tool for simulating ion–solid interactions, particularly for light ions, where it demonstrates high accuracy. Simulations involving light ions—such as hydrogen and helium—typically show strong agreement with experimental data, with errors generally below 5%. However, for heavy ions—especially in the low-energy regime—SRIM predictions often diverge from experimental observations. These discrepancies are largely attributed to limitations in the modeling of nuclear and electronic stopping powers. The accuracy of SRIM calculations becomes especially sensitive to energies below 20keV, where nuclear stopping dominates. Furthermore, some studies suggest that SRIM may overestimate the electronic stopping power of slow heavy ions in light-element targets.
A significant factor contributing to these discrepancies is the limited availability of experimental data for heavy ion stopping power, which hampers the validation and refinement of the underlying models. Precise determination of the nuclear stopping power at low energy remains a critical challenge, as it directly affects range and energy deposition predictions. In some cases, SRIM has been found to underestimate the ion range compared to experimental measurements. Nevertheless, the SRIM software continues to evolve through regular updates informed by experimental results and theoretical developments. The core of the SRIM package is the Transport of Ions in Matter (TRIM) program, which performs detailed Monte Carlo simulations of ion trajectories through matter.
Complementary to SRIM, the Bethe–Bloch formula, Equation (3), provides a theoretical framework for calculating the stopping power of charged particles as they pass through matter. It is especially effective at high energy and is widely applied in both particle and materials physics. However, the uncorrected Bethe equation loses accuracy at low energies—typically below 1–10 keV, depending on the atomic number of the target—where additional corrections are required. This further highlights the challenges in modeling ion–solid interactions across a broad energy range and the importance of integrating both empirical data and theoretical refinements into simulation tools.
Solar proton eruptions, which occur more often during periods of solar maximum, are capable of inducing ionization, molecular breakup (dissociation), dissociative ionization, and electronic excitation processes in the middle layers of the atmosphere. Consequently, intense solar proton events can significantly modify the chemical composition of the polar middle atmosphere.
When these energetic protons enter the atmosphere, they—and the secondary electrons they generate—can interact with molecules such as CF
3CFH
2 (R-134a). These interactions may lead to the formation of neutral and charged molecular fragments, such as CF
3+, CH
2F
+, etc. [
9], through dissociation or dissociative ionization processes during collisions.
As for the comparison between photoionization and ionization by protons, above the ionization potential, for instance in the 15–25 eV range, the total cross-section ranges from 54 to 110 Mb, which is the same order of magnitude found in
Figure 2 for high proton energies (10
3 eV < T < 10
4 eV). While this is not surprising, it serves as an indirect form of internal validation for the calculations.
5. Conclusions
In this work, Rudd’s semiempirical model was applied to evaluate proton impact ionization cross-sections in the CF3CH2F molecule using a parameterized approach. The calculations accounted for contributions from both the outer and inner electron shells to accurately estimate the average energy of secondary electrons, as well as the single and total differential cross-sections. In addition, photoionization cross-sections were computed to validate the proton-induced ionization results at high energies. In addition, we calculated the photoionization cross-section to compare it with the one obtained for proton impact in the high-energy limit.
The Rudd model offers a key advantage in its compatibility with numerical tools, making it suitable for computational applications. Its versatility also allows for adaptation to a wide range of molecular targets by adjusting molecular parameters such as the number of electron shells and binding energies. However, a significant challenge remains in the validation of the model’s predictions, primarily due to the limited availability of experimental data suitable for benchmarking.
A comparison between the Rudd and BEB models reveals strong agreement in the analyzed energy range (100–200 keV). This consistency stems from both models accounting for the molecular structure of the target and from the fact that protons and electrons possess charges of the same magnitude, supporting a coherent description of ionization processes at these energies. In contrast, the SRIM and Bethe models exhibit notable discrepancies relative to the obtained data. These models are generally more applicable to lower energy regimes and do not explicitly include molecular structural effects, which reduces their predictive reliability for complex molecules like CF3CH2F in the high-energy range considered here.
It is important to note that this study focused exclusively on the ionization process. As a result, the findings should not be generalized to other interaction mechanisms. A more comprehensive investigation would require the inclusion of additional processes such as charge transfer, electronic excitation, and elastic scattering. However, the experimental data necessary for validating these processes remain incomplete at present.