Energy Levels, Lifetimes, and Transition Properties for N iii – v

Abstract

We present excitation energies, transition wavelengths, electric dipole (E1) transition rates, oscillator strengths, line strengths, and lifetimes for the 86 lowest states up to and including $1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7\mathrm{f}$ in N iii, the 125 lowest states up to and including $1{\mathrm{s}}^{2}2\mathrm{s}7\mathrm{f}$ in N iv, and the 53 lowest states up to $1{\mathrm{s}}^{2}8\mathrm{g}$ in N v using the multiconfiguration Dirac–Hartree–Fock (MCDHF) and relativistic configuration interaction (RCI) methods. The computed results are then compared with data from the Atomic Spectra Database of the National Institute of Standards and Technology (NIST-ASD), experimental results, and other theoretical studies. For all levels in N iii – v, the root mean square energy differences from the NIST values are 130, 103, and 6 cm⁻¹, respectively. Compared to previous multiconfiguration Hartree–Fock and the Breit–Pauli (MCHF-BP) calculations, 89.3%, 98.5%, and 100% of the $log\left(gf\right)$ values for N iii – v agree within 5%, respectively.

1. Introduction

Emission lines from multiply ionized nitrogen N iii – v are commonly observed in the spectra of various astrophysical objects. Analyzing these spectral lines provides valuable insights into the chemical abundance and physical characteristics of such objects [1,2,3,4,5]. For example, Cameron et al. [4] observed the brightness of N iii $\lambda$ 1750 and N iv $\lambda$ 1486 lines, proposing their use in analyzing the N/O abundance ratio by comparing them with faint O iii lines. Rivero González et al. [2,3] used N iii and N iv emission lines for the abundance analysis of O-type stars. Chayer et al. [1] pointed out that N v $\lambda$ 1240 doublet lines can be used in the determination of element abundances. In this context, accurate atomic data such as energy levels and oscillator strengths are crucial for analyzing chemical abundances and reliably interpreting observed spectra.

Given the astrophysical importance of these ions, numerous studies have been conducted in the past. The full lists of published papers can be accessed from the NIST Atomic Transition Probability Bibliographic database [6]. The majority of transition probabilities related to multiply ionized nitrogen N iii – v originate from theoretical calculations. The current sets of calculated electric dipole transition probabilities (A) in the Atomic Spectra Database of the National Institute of Standards and Technology (NIST-ASD; see Kramida et al. [7]) are primarily based on Opacity Project calculations: Fernley et al. [8] for N iii, Tully et al. [9] for N iv, and Peach et al. [10] for N iv. Additionally, the A values from Bell et al. [11] for N iii, Hibbert [12] for N iv, and Bièmont [13], Lindgård and Nielsen [14] for N v, along with experimental values from Fang et al. [15] and compilation data from Allard et al. [16], have also been included in the NIST-ASD. Bell et al. [11] calculated the A values for the transitions among the 20 lowest-lying fine structure levels of the $1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p},1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2,1{\mathrm{s}}^{2}2{\mathrm{p}}^3,1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}3l(l\le 2)$ states in N iii, employing CIV3 code. Similarly, Hibbert [12] utilized the same code to compute the oscillator strengths of transitions involving $1{\mathrm{s}}^{2}2\mathrm{s}3l{}^3\mathrm{L}(l\le 2)$ terms in N iv. Fang et al. [15] used a cylindrical radio frequency ion trap to measure the A values belonging to the $1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^4\mathrm{P}-1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}^{\mathrm{o}}$ transitions. The other existing experimental transition probabilities were obtained from lifetime measurements [17,18,19,20,21], beam-foil experiments [22,23,24,25], and the analysis of the relative intensities of the spectral lines emitted by these ions [26,27].

Froese Fischer and co-workers have conducted detailed investigations of N iii [28,29], N iv [28,30], and N v [31,32], focusing on the low-lying levels. They employed multiconfiguration Hartree–Fock and the Breit–Pauli (MCHF-BP) approximation to compute the energy levels and various transition properties, including transition probabilities, oscillator strengths, and lifetimes. Using CIV3 code, Hibbert et al. also performed calculations on the energy levels and A values for the transitions among the levels of low-lying configurations in N iii [11,33,34], and N iv [12,35].

Calculations involving additional energy levels, such as those for $n>3$, and their corresponding transitions are also available. For example, Fernández-Menchero et al. [36] adopted AUTOSTRUCTURE code, Aggarwal et al. [37] used the General-purpose Relativistic Atomic Structure Package (GRASP), and Fernández-Menchero et al. [38] utilized the B-spline box-based close-coupling method to calculate the atomic data in N iv. However, these calculations included only limited electron correlation effects, which affected their accuracy. In addition, Wang et al. [39] carried out calculations of energies and transition parameters in N iv using the multiconfiguration Dirac–Hartree–Fock (MCDHF) and relativistic configuration interaction (RCI) method.

As part of our series of work on obtaining accurate atomic data of astrophysically important CNO elements [40,41,42], new calculations were performed for the lowest 86, 125, and 53 states in N iii – v, respectively, using the fully relativistic MCDHF and RCI method. The electric dipole (E1) transition data among these levels, including wavelengths, transition rates, line strengths, and oscillator strengths, along with the corresponding lifetimes, are provided.

2. Calculations

The fully relativistic MCDHF method [43], implemented through Grasp2018 [44,45], was adopted in the present work. In this method, an atomic state function (ASF) $\Psi \left(\gamma JP\right)$, is expanded over configuration state functions (CSFs);

$$\Psi \left(\gamma JP\right)=\sum _i{c}_i\Phi \left({\gamma }_{i}JP\right)$$

(1)

Here, J and P represent the total angular momentum and parity of the system, respectively; ${\gamma }_i$ is a set of quantum numbers used to specify a CSF in addition to JP; and $c_i$ is the mixing coefficient.

The CSFs are $jj$-coupled many-electron functions, which are constructed from the products of one-electron Dirac orbitals [46]. Using the extended optimal level (EOL) scheme [47], the radial components of the Dirac orbitals and the expansion coefficients of the targeted states are optimized in a relativistic self-consistent field procedure. This optimization is achieved by solving the MCDHF equations, which are derived through the variational approach. The primary quantum electrodynamic (QED) effects, namely, vacuum polarization and self-energy, along with the Breit interaction, are included in the following RCI calculation, using the radial functions obtained from the MCDHF optimization.

We started the calculations with a Dirac–Hartree–Fock (DHF) calculation based on a set of multireference (MR) configurations. The configurations included in the MR set for each ion are listed in the first column in

Table 1. Summary of the computational schemes for N iii – v. MR refers to the multireference sets, while AS denotes the active sets of orbitals used in the calculations.

MR in MCDHF	MR in RCI	AS
	N iii, ${\mathrm{N}}_{\mathrm{levels}}=86$
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}nl$($n\le 6,l\le 4$)	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2$, $1{\mathrm{s}}^{2}2{\mathrm{s}}^2\{n_1(\mathrm{s},\mathrm{p},\mathrm{d}),n_2\mathrm{f},n_3\mathrm{g}\}$	{$12\mathrm{s},12\mathrm{p},12\mathrm{d},12\mathrm{f},$
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7l$($l\le 3$)	$(3\le n_1\le 7$, $4\le n_2\le 7,5\le n_3\le 6)$	$10\mathrm{g},8\mathrm{h}$}
$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2$, $1{\mathrm{s}}^{2}2{\mathrm{p}}^3$,	$1{\mathrm{s}}^{2}2{\mathrm{p}}^3$, $1{\mathrm{s}}^{2}2{\mathrm{p}}^2\{n_1(\mathrm{s},\mathrm{p},\mathrm{d}),n_2\mathrm{f},n_3\mathrm{g}\}$
$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}3l$($l\le 2$)	$(3\le n_1\le 7,4\le n_2\le 7,5\le n_3\le 6)$
	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}3l$($l\le 2$)
	N iv, ${\mathrm{N}}_{\mathrm{levels}}=125$
$1{\mathrm{s}}^{2}2\mathrm{s}nl$($n\le 7,l\le 4$), $2\mathrm{s}6\mathrm{h}$, $1{\mathrm{s}}^{2}2\mathrm{p}3\mathrm{d}$,	$1{\mathrm{s}}^{2}2\mathrm{s}nl$ ($n\le 7,l\le 4$),$1{\mathrm{s}}^{2}2\mathrm{s}6\mathrm{h}$	{$12\mathrm{s},12\mathrm{p},12\mathrm{d},12\mathrm{f},$
$1{\mathrm{s}}^{2}2{\mathrm{p}}^2$, $2\mathrm{p}{n}_1$$\{\mathrm{s},\mathrm{p}$}$(3\le n_1\le 4)$	$1{\mathrm{s}}^{2}2{\mathrm{p}}^2$, $1{\mathrm{s}}^{2}2\mathrm{p}{n}_1${$\mathrm{s},\mathrm{p},\mathrm{d}$}$(3\le n_1\le 4)$	$11\mathrm{g},8\mathrm{h},7\mathrm{i}$}
	N v, ${\mathrm{N}}_{\mathrm{levels}}=53$
$1{\mathrm{s}}^{2}nl$ ($n\le 8,l\le 4$)	$1{\mathrm{s}}^{2}nl$ ($n\le 8,l\le 4$)	{$14\mathrm{s},14\mathrm{p},14\mathrm{d},$
$1{\mathrm{s}}^{2}6\mathrm{h}$	$1{\mathrm{s}}^{2}6\mathrm{h}$	$12\mathrm{f},12\mathrm{g},8\mathrm{h},7\mathrm{i}$}

. The CSFs were then produced and progressively expanded using the multireference singles and doubles (MR-SD) method, allowing single and double excitations from the electrons of the MR sets to the orbitals in the active set (AS) [43,48,49]. During this stage, different computational strategies were employed to compute the atomic properties for distinct ions. The CSFs were produced by allowing SD substitution from the $n=2$ shells for N iii – v, with the restriction that at most one substitution was allowed for N iii. The $1{\mathrm{s}}^2$ core shell was kept frozen for N iii and N iv, while a maximum of one substitution from this core was permitted for N v.

In the subsequent RCI calculations, the MR sets for N iii and N iv were expanded to include configurations with considerable contributions to the total wave functions. Higher-order configuration interaction effects were accounted for by permitting SD excitations from this extended MR set, as depicted in the second column in Table 1. For N iii, the CSF expansions in the final RCI calculation were generated by allowing SD substitutions from all subshells of the extended MR configurations, with the restriction that only one substitution could occur from the $1{\mathrm{s}}^2$ core. In the case of N iv, the CSFs were formed by allowing single, double, and triple (SDT) substitutions from all orbitals of the extended MR configurations, with the restriction of a maximum of one excitation from the $1{\mathrm{s}}^2$ atomic core. As for N v, the CSF expansions were enlarged by enabling all SDT substitutions from the extended MR orbitals to the largest AS of the orbitals. The maximum AS for N iii – v are presented in the last column in Table 1.

3. Results and Discussion

3.1. Energies

The computed excitation energies for the lowest 86, 125, and 53 levels of the corresponding targeted configurations in N iii, N iv, and N v, respectively, from the present MCDHF and RCI calculations are shown in

Table A1. Energies in cm⁻¹ and lifetimes (in s) in both the Babushkin (${\tau }_B$) and Coulomb (${\tau }_C$) gauges for N iii.

No.	State	LS Composition	ERCI	ENIST	ΔE	τB	τC
1	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	94% + 4% $1{\mathrm{s}}^{2}2{\mathrm{p}}^3{}^2\mathrm{P}^{\mathrm{o}}$	0.00	0.0	0
2	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	94% + 4% $1{\mathrm{s}}^{2}2{\mathrm{p}}^3{}^2\mathrm{P}^{\mathrm{o}}$	173.78	174.4	−0.62
3	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^4\mathrm{P}_{1/2}$	98%	57,104.87	57,187.1	−82.23	1.4484E-03	8.3602E-04
4	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^4\mathrm{P}_{3/2}$	98%	57,164.21	57,246.8	−82.59	1.4611E-02	6.0757E-03
5	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^4\mathrm{P}_{5/2}$	98%	57,244.73	57,327.9	−83.17	3.6222E-03	2.1712E-03
6	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^2\mathrm{D}_{5/2}$	95%	101,135.78	101,023.9	111.88	2.0026E-09	2.0036E-09
7	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^2\mathrm{D}_{3/2}$	95%	101,142.65	101,030.6	112.05	1.9911E-09	1.9943E-09
8	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^2\mathrm{S}_{1/2}$	94%	131,247.74	131,004.3	243.44	3.5818E-10	3.5948E-10
9	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^2\mathrm{P}_{1/2}$	95%	146,073.61	145,875.7	197.91	1.7616E-10	1.7656E-10
10	$1{\mathrm{s}}^{2}2\mathrm{s}2{\mathrm{p}}^2{}^2\mathrm{P}_{2/3}$	95%	146,183.65	145,985.8	197.85	1.7606E-10	1.7649E-10

Note: Only the first 10 rows are shown here. The labels in the second column are assigned based on the components with the highest expansion coefficients given in the third column. These components are detailed in the third column, listing up to three LS components (expressed in LS coupling notation) that each contribute more than 2% to the total wave function. ΔE signifies the deviation (E_RCI − E_NIST) etween the MCDHF/RCI-calculated values and the compiled values from the NIST-ASD [7]. The complete dataset is provided in Supplementary Materials, Table S1.

,

Table A2. Energies in cm⁻¹ and lifetimes (in s) in both the Babushkin (${\tau }_B$) and Coulomb (${\tau }_C$) gauges for N iv.

No.	State	LS Composition	ERCI	ENIST	ΔE	τB	τC
1	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	93% + 7% $1{\mathrm{s}}^{2}2{\mathrm{p}}^2\left({}^1\mathrm{S}\right){}^1\mathrm{S}$	0.00	0.0
2	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{}^3\mathrm{P}_0^{\mathrm{o}}$	99%	67,218.09	67,209.2	8.89
3	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{}^3\mathrm{P}_1^{\mathrm{o}}$	99%	67,280.48	67,272.3	8.18	1.7650E-03	1.0861E-03
4	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{}^3\mathrm{P}_2^{\mathrm{o}}$	99%	67,423.74	67,416.3	7.44
5	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{}^1\mathrm{P}_1^{\mathrm{o}}$	97%	130,884.90	130,693.9	191.00	4.2939E-10	4.2901E-10
6	$1{\mathrm{s}}^{2}2{\mathrm{p}}^2{}^3\mathrm{P}_0$	99%	175,629.30	175,535.4	93.90	5.6849E-10	5.6776E-10
7	$1{\mathrm{s}}^{2}2{\mathrm{p}}^2{}^3\mathrm{P}_1$	99%	175,702.22	175,608.1	94.12	5.6791E-10	5.6724E-10
8	$1{\mathrm{s}}^{2}2{\mathrm{p}}^2{}^3\mathrm{P}_2$	99%	175,825.93	175,732.9	93.03	5.6699E-10	5.6644E-10
9	$1{\mathrm{s}}^{2}2{\mathrm{p}}^2{}^1\mathrm{D}_2$	97%	189,096.28	188,882.5	213.78	4.3058E-09	4.3106E-09
10	$1{\mathrm{s}}^{2}2{\mathrm{p}}^2{}^1\mathrm{S}_0$	90% + 6% $1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}$	235,850.37	235,369.3	481.07	3.3962E-10	3.3914E-10

Note: Only the first 10 rows are shown here. The labels in the second column are assigned based on the components with the highest expansion coefficients given in the third column. These components are detailed in the third column, listing up to three LS components (expressed in LS coupling notation) that each contribute more than 2% to the total wave function. ΔE signifies the deviation (E_RCI − E_NIST) between the MCDHF/RCI-calculated values and the compiled values from the NIST-ASD [7]. The complete dataset is provided in Supplementary Materials, Table S2.

and

Table A3. Energies in cm⁻¹ and lifetimes (in s) in both the Babushkin (${\tau }_B$) and Coulomb (${\tau }_C$) gauges for N v.

No.	State	LS Composition	ERCI	ENIST	ΔE	τB	τC
1	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	100%	0.00	0.0	0.00
2	$1{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	100%	80,483.16	80,463.2	19.96	2.9768E-09	2.9749E-09
3	$1{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	100%	80,742.57	80,721.9	20.67	2.9464E-09	2.9465E-09
4	$1{\mathrm{s}}^{2}3\mathrm{s}{}^2\mathrm{S}_{1/2}$	100%	456,125.29	456,126.6	−1.31	1.0988E-10	1.0989E-10
5	$1{\mathrm{s}}^{2}3\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	100%	477,769.77	477,765.7	4.07	8.2299E-11	8.2267E-11
6	$1{\mathrm{s}}^{2}3\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	100%	477,846.18	477,842.0	4.18	8.2476E-11	8.2444E-11
7	$1{\mathrm{s}}^{2}3\mathrm{d}{}^2\mathrm{D}_{3/2}$	100%	484,400.96	484,404.3	−3.34	2.3552E-11	2.3548E-11
8	$1{\mathrm{s}}^{2}3\mathrm{d}{}^2\mathrm{D}_{5/2}$	100%	484,423.58	484,426.3	−2.72	2.3564E-11	2.3562E-11
9	$1{\mathrm{s}}^{2}4\mathrm{s}{}^2\mathrm{S}_{1/2}$	100%	606,349.72	606,348.8	0.92	1.7275E-10	1.7273E-10
10	$1{\mathrm{s}}^{2}4\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	100%	615,144.99	615,141.0	3.99	1.3371E-10	1.3366E-10

Note: Only the first 10 rows are shown here. The labels in the second column are assigned based on the components with the highest expansion coefficients given in the third column. These components are detailed in the third column, listing up to three LS components (expressed in LS coupling notation) that each contribute more than 2% to the total wave function. ΔE signifies the deviation (E_RCI − E_NIST) between the MCDHF/RCI-calculated values and the compiled values from the NIST-ASD [7]. The complete dataset is provided in Supplementary Materials, Table S3.

. The lifetimes in both the Babushkin and Coulomb gauges, along with the experimental excitation energies compiled in the NIST-ASD, are also displayed. In the relativistic calculations, the wave functions for the states are represented as expansions over $jj$-coupled CSFs. To compare these with the compiled values in the NIST-ASD, a transformation method from $jj$-coupled CSFs to $LSJ$-coupled CSFs [50] was employed, providing the atomic state functions in the $LSJ$ labeling system.

We noticed that the labeling order of levels #29 $1{\mathrm{s}}^{2}2\mathrm{p}3\mathrm{p}{}^3\mathrm{S}_1$ and #37 $1{\mathrm{s}}^{2}2\mathrm{s}4\mathrm{s}{}^3\mathrm{S}_1$ for N iv is inverted compared to the order used by the NIST-ASD. Upon careful examination, we found that the weights for the first two eigenvector components of level #29 are 69% ($1{\mathrm{s}}^{2}2\mathrm{p}3\mathrm{p}{}^3\mathrm{S}_1$) and 27% ($1{\mathrm{s}}^{2}2\mathrm{s}4\mathrm{s}{}^3\mathrm{S}_1$), while those of level #37 are 71% ($1{\mathrm{s}}^{2}2\mathrm{s}4\mathrm{s}{}^3\mathrm{S}_1$) and 28% ($1{\mathrm{s}}^{2}2\mathrm{p}3\mathrm{p}{}^3\mathrm{S}_1$). The two levels, characterized by relatively pure LS coupling, exhibit some degree of mixing; however, this mixing is not significant. This suggests that the assignments for the two levels in the NIST-ASD should be interchanged: specifically, the 487,607.4 ${\mathrm{cm}}^{-1}$ should be assigned to the $1{\mathrm{s}}^{2}2\mathrm{p}3\mathrm{p}{}^3\mathrm{S}_1$ level and 498,045.50 ${\mathrm{cm}}^{-1}$ designated as the $1{\mathrm{s}}^{2}2\mathrm{p}4\mathrm{s}{}^3\mathrm{S}_1$ level. This finding is consistent with the results reported by Wang et al. [39]. Ultimately, our comparisons of these two levels are based on their energy ordering rather than their original assignments.

From Table A1, Table A2 and Table A3, it is clear that the computed energies agree quite well with the NIST-ASD values, with differences ($\Delta E$ = $E_{RCI}-E_{\mathrm{NIST}}$) smaller than 150 ${\mathrm{cm}}^{-1}$ for the majority of states. The most notable deviation is observed in the level $1{\mathrm{s}}^{2}2\mathrm{s}7\mathrm{s}{}^1\mathrm{S}_0$ of N iv, with a difference of 596 ${\mathrm{cm}}^{-1}$. For all levels in N iii – v, the root-mean-square differences from the NIST values are 130, 103, and 6 ${\mathrm{cm}}^{-1}$, respectively.

3.2. Transition Properties

The computed wavelengths ($\lambda$) and transition properties, including transition rate (A), oscillator strength ($gf$), and line strength (S) for the E1 transitions, are provided in

Table A4. Electric dipole transition data for N iii from the present calculations.

Upper	Lower	λ (Å)		S (a.u. of ${\mathit{a}}_0^2{\mathit{e}}^2$)		gf		A (s−1)		dT
		RCI	NIST	B	C	B	C	B	C
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7\mathrm{d}{}^2\mathrm{D}_{3/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	276.286	276.193	2.832E-02	2.833E-02	3.115E-02	3.116E-02	6.808E+08	6.812E+08	0.001
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7\mathrm{d}{}^2\mathrm{D}_{5/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	276.419	276.326	5.096E-02	5.097E-02	5.602E-02	5.603E-02	8.156E+08	8.158E+08	0.000
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7\mathrm{d}{}^2\mathrm{D}_{3/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	276.419	276.326	5.670E-03	5.672E-03	6.233E-03	6.235E-03	1.361E+08	1.362E+08	0.000
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7\mathrm{s}{}^2\mathrm{S}_{1/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	278.527	278.437	2.080E-03	2.066E-03	2.270E-03	2.254E-03	9.764E+07	9.695E+07	0.007
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}7\mathrm{s}{}^2\mathrm{S}_{1/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	278.662	278.572	4.181E-03	4.150E-03	4.559E-03	4.526E-03	1.959E+08	1.945E+08	0.007
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}6\mathrm{d}{}^2\mathrm{D}_{3/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	282.171	282.063	4.874E-02	4.865E-02	5.249E-02	5.239E-02	1.100E+09	1.098E+09	0.002
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}6\mathrm{d}{}^2\mathrm{D}_{5/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	282.308	282.202	8.773E-02	8.756E-02	9.443E-02	9.424E-02	1.318E+09	1.316E+09	0.002
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}6\mathrm{d}{}^2\mathrm{D}_{3/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	282.309	282.202	9.759E-03	9.741E-03	1.050E-02	1.048E-02	2.199E+08	2.195E+08	0.002
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}6\mathrm{s}{}^2\mathrm{S}_{1/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}^{\mathrm{o}}$	285.959	285.857	3.600E-03	3.577E-03	3.825E-03	3.801E-03	1.561E+08	1.551E+08	0.006
$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}6\mathrm{s}{}^2\mathrm{S}_{1/2}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}^{\mathrm{o}}$	286.101	286.000	7.233E-03	7.186E-03	7.682E-03	7.632E-03	3.132E+08	3.112E+08	0.007

Note: Only the first 10 rows are shown here. Upper and lower states, wavelength in vacuum, λ, line strength, S, in Babushkin (B) and Coulomb (B) gauges, weighted oscillator strength, gf, in B and C gauges, transition probability, A, in B and C gauges, and the relative difference between two gauges of A values, dT. Note that the third column presents λ from our current MCDHF and RCI calculations, whereas the fourth column lists the NIST-ASD Ritz wavelength values. For the wavelengths marked with an asterisk (*), at least one of the energy levels involved in the transition was not available in from the NIST-ASD [7]. The complete dataset is provided in Supplementary Materials, Table S4.

,

Table A5. Electric dipole transition data for N iv from the present calculations.

Upper	Lower	λ (Å)		S (a.u. of ${\mathit{a}}_0^2{\mathit{e}}^2$)		gf		A (s−1)		dT
		RCI	NIST	B	C	B	C	B	C
$1{\mathrm{s}}^{2}2\mathrm{s}7\mathrm{p}{}^1\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	170.093	170.074	7.745E-03	7.827E-03	1.383E-02	1.398E-02	1.063E+09	1.075E+09	0.011
$1{\mathrm{s}}^{2}2\mathrm{s}7\mathrm{p}{}^3\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	170.293	170.293 *	1.433E-07	1.433E-07	2.556E-07	2.556E-07	1.960E+04	1.960E+04	0.000
$1{\mathrm{s}}^{2}2\mathrm{p}4\mathrm{s}{}^1\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	172.168	172.171	2.034E-06	2.137E-06	3.588E-06	3.770E-06	2.691E+05	2.828E+05	0.048
$1{\mathrm{s}}^{2}2\mathrm{p}4\mathrm{s}{}^3\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	172.992	172.997	1.607E-06	1.597E-06	2.822E-06	2.804E-06	2.097E+05	2.083E+05	0.007
$1{\mathrm{s}}^{2}2\mathrm{s}6\mathrm{p}{}^3\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	174.414	174.414 *	3.515E-08	3.426E-08	6.122E-08	5.967E-08	4.475E+03	4.362E+03	0.025
$1{\mathrm{s}}^{2}2\mathrm{s}6\mathrm{p}{}^1\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	174.622	174.602	1.353E-02	1.354E-02	2.354E-02	2.355E-02	1.717E+09	1.718E+09	0.000
$1{\mathrm{s}}^{2}2\mathrm{s}5\mathrm{p}{}^1\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	181.766	181.741	2.544E-02	2.543E-02	4.252E-02	4.250E-02	2.862E+09	2.861E+09	0.000
$1{\mathrm{s}}^{2}2\mathrm{s}5\mathrm{p}{}^3\mathrm{P}_1^{\mathrm{o}}$	$1{\mathrm{s}}^{2}2{\mathrm{s}}^2{}^1\mathrm{S}_0$	181.802	181.802 *	5.623E-05	5.616E-05	9.395E-05	9.383E-05	6.320E+06	6.312E+06	0.001
$1{\mathrm{s}}^{2}2\mathrm{s}7\mathrm{g}{}^3\mathrm{G}_3$	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{}^3\mathrm{P}_2^{\mathrm{o}}$	191.892	191.889 *	3.151E-13	4.365E-13	4.989E-13	6.910E-13	1.291E-02	1.788E-02	0.278
$1{\mathrm{s}}^{2}2\mathrm{s}7\mathrm{d}{}^3\mathrm{D}_1$	$1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{}^3\mathrm{P}_0^{\mathrm{o}}$	191.905	191.875	7.761E-03	7.763E-03	1.229E-02	1.229E-02	7.420E+08	7.422E+08	0.000

Note: Only the first 10 rows are shown here. Upper and lower states, wavelength in vacuum, λ, line strength, S, in Babushkin (B) and Coulomb (B) gauges, weighted oscillator strength, gf, in B and C gauges, transition probability, A, in B and C gauges, and the relative difference between two gauges of A values, dT. Note that the third column presents λ from our current MCDHF and RCI calculations, whereas the fourth column lists the NIST-ASD Ritz wavelength values. For the wavelengths marked with an asterisk (*), at least one of the energy levels involved in the transition was not available in the NIST-ASD [7]. The complete dataset is provided in Supplementary Materials, Table S5.

and

Table A6. Electric dipole transition data for N v from the present calculations.

Upper	Lower	λ (Å)		S (a.u. of ${\mathit{a}}_0^2{\mathit{e}}^2$)		gf		A (s−1)		dT
		RCI	NIST	B	C	B	C	B	C
$1{\mathrm{s}}^{2}8\mathrm{p}{}^2\mathrm{P}_{3/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	133.992	133.993	3.604E-03	3.604E-03	8.170E-03	8.171E-03	7.588E+08	7.589E+08	0.000
$1{\mathrm{s}}^{2}8\mathrm{p}{}^2\mathrm{P}_{1/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	133.992	133.993	1.807E-03	1.807E-03	4.096E-03	4.097E-03	7.608E+08	7.610E+08	0.000
$1{\mathrm{s}}^{2}7\mathrm{p}{}^2\mathrm{P}_{3/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	136.423	136.424	5.679E-03	5.681E-03	1.264E-02	1.265E-02	1.133E+09	1.133E+09	0.000
$1{\mathrm{s}}^{2}7\mathrm{p}{}^2\mathrm{P}_{1/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	136.424	136.425	2.846E-03	2.847E-03	6.337E-03	6.340E-03	1.136E+09	1.136E+09	0.000
$1{\mathrm{s}}^{2}6\mathrm{p}{}^2\mathrm{P}_{3/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	140.355	140.356	9.774E-03	9.777E-03	2.115E-02	2.116E-02	1.790E+09	1.791E+09	0.000
$1{\mathrm{s}}^{2}6\mathrm{p}{}^2\mathrm{P}_{1/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	140.357	140.358	4.897E-03	4.900E-03	1.060E-02	1.060E-02	1.794E+09	1.795E+09	0.000
$1{\mathrm{s}}^{2}5\mathrm{p}{}^2\mathrm{P}_{3/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	147.423	147.424	1.933E-02	1.933E-02	3.982E-02	3.984E-02	3.055E+09	3.057E+09	0.000
$1{\mathrm{s}}^{2}5\mathrm{p}{}^2\mathrm{P}_{1/2}$	$1{\mathrm{s}}^{2}2\mathrm{s}{}^2\mathrm{S}_{1/2}$	147.426	147.427	9.683E-03	9.687E-03	1.995E-02	1.996E-02	3.061E+09	3.063E+09	0.000
$1{\mathrm{s}}^{2}8\mathrm{d}{}^2\mathrm{D}_{3/2}$	$1{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{1/2}$	150.112	150.108	8.068E-03	8.060E-03	1.633E-02	1.631E-02	1.208E+09	1.207E+09	0.001
$1{\mathrm{s}}^{2}8\mathrm{d}{}^2\mathrm{D}_{5/2}$	$1{\mathrm{s}}^{2}2\mathrm{p}{}^2\mathrm{P}_{3/2}$	150.170	150.166	1.449E-02	1.451E-02	2.931E-02	2.935E-02	1.445E+09	1.447E+09	0.001

Note: Only the first 10 rows are shown here. Upper and lower states, wavelength in vacuum, λ, line strength, S, in Babushkin (B) and Coulomb (B) gauges, weighted oscillator strength, gf, in B and C gauges, transition probability, A, in B and C gauges, and the relative difference between two gauges of A values, dT. Note that the third column presents λ from our current MCDHF and RCI calculations, whereas the fourth column lists the NIST-ASD Ritz wavelength values. The complete dataset is provided in Supplementary Materials, Table S6.

for N iii to N v, respectively. All transition parameters are presented in both the Babushkin and Coulomb gauges. Note that the wavelengths derived from the experimental energy levels compiled in the NIST-ASD are also listed, and the transition parameters A and $gf$ were adjusted to match the NIST-ASD wavelength values.In addition, Table A4, Table A5 and Table A6 also include the relative differences in the transition rates between the Babushkin and Coulomb gauges, denoted as $\mathrm{d}\mathrm{T} = |{\mathrm{A}}_{\mathrm{B}}-{\mathrm{A}}_{\mathrm{C}}|/\max ({\mathrm{A}}_{\mathrm{B}},{\mathrm{A}}_{\mathrm{C}})$. We can see that the agreement of the Babushkin and Coulomb gauges is within 10% for most of the transitions. The average values of $\mathrm{d}\mathrm{T}$ for all the E1 transitions presented are 6.50%, 1.86%, and 0.87%, corresponding to the transitions of N iii through N v, respectively.

A comparison of the present computed transition data with other theoretical and experimental results allows an overall assessment of their accuracy. Note that the comparisons with other results described in the following sections are all based on the experimental-wavelength-adjusted values. In Figure 1, the present computed $log\left(gf\right)$ values, in the Babushkin gauge, are compared with selected values from the NIST-ASD, which have an estimated accuracy of better than 25%. It can be seen from the figure that our computations are in good agreement with the NIST values for the majority of transitions. However, the agreements are worse for transitions involving levels that interact strongly with other states in N iii and N iv. Most of these transitions originate from the Opacity Project calculations, which employed a non-relativistic approach and relied on the $LS$-coupling scheme. Nonetheless, these non-relativistic calculations and the associated $LS$-coupling scheme are inappropriate for cases with strong relativistic configuration interaction effects.

The $log\left(gf\right)$ values obtained in the present work were also compared with the results from MCHF-BP [28,31] and configuration interaction (CI) calculations [34], as shown in Figure 2. The analysis reveals a strong agreement between the $log\left(gf\right)$ values computed in this work and those from other sources, particularly for transitions with $log\left(gf\right)$ values exceeding −4. Specifically, when comparing the present results with the CI calculations by Correge and Hibbert [34] for N iii, all available transitions agree within 16%, with 47 out of 51 common transitions demonstrating relative differences of less than 5%. Additionally, when the present MCDHF/RCI results are compared with the MCHF-BP calculations [28,31], the proportions of transitions with relative differences below 5% are 89.3%, 98.5%, and 100% for N iii – v, respectively.

In Figure 3, we compare our computed A values (wavelength-adjusted) in the Babushkin gauge with the experimental values measured by Djeniže et al. [27]. The experimental A values were obtained by using values compiled in the NIST-ASD as a reference. It is observed that the computed A values agree with the experimental values within the experimental uncertainties, except for the $1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{(}^3\mathrm{P})3\mathrm{d}{}^4\mathrm{P}_{5/2}-1{\mathrm{s}}^{2}2\mathrm{s}2\mathrm{p}{(}^3\mathrm{P})3\mathrm{p}{}^4\mathrm{S}_{3/2}$ and $1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}5\mathrm{f}{}^2\mathrm{F}_{7/2}-1{\mathrm{s}}^{2}2{\mathrm{s}}^{2}4\mathrm{d}{}^2\mathrm{D}_{5/2}$ transitions. The computed transition A values are $5.369\times {10}^7{\mathrm{s}}^{-1}$ and $1.707\times {10}^8{\mathrm{s}}^{-1}$, while the measured values are $8.10\times {10}^7{\mathrm{s}}^{-1}$ and $1.30\times {10}^8{\mathrm{s}}^{-1}$, resulting in differences of 34% and 31%. The A values from the NIST Atomic Spectra Database (NIST-ASD) for these transitions are $5.42\times {10}^7{\mathrm{s}}^{-1}$ and $1.88\times {10}^8{\mathrm{s}}^{-1}$, with which our computed values show excellent agreement.

4. Conclusions

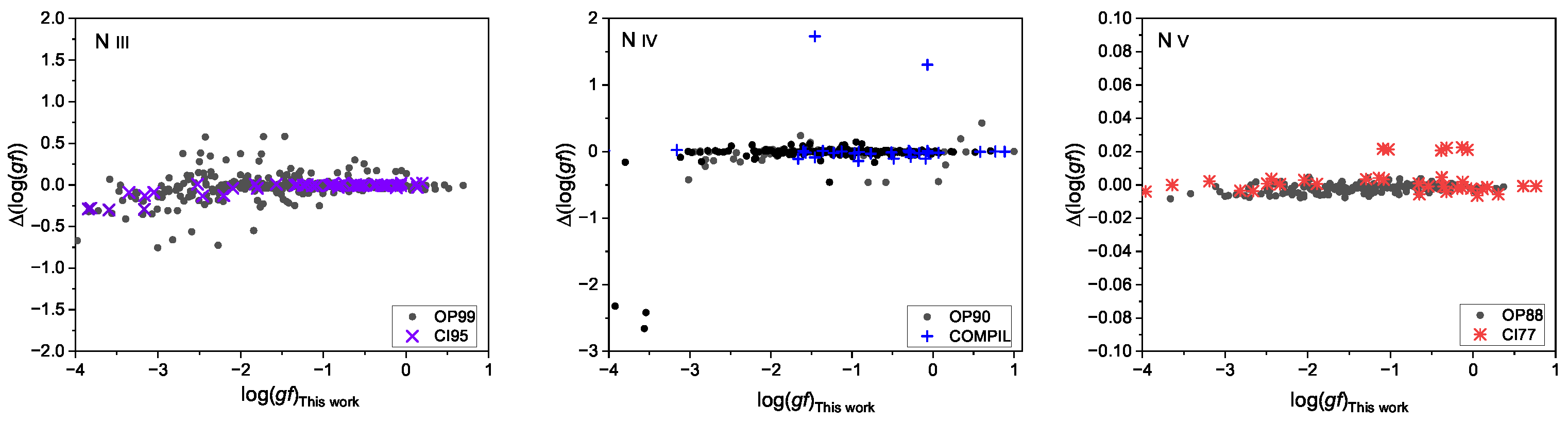
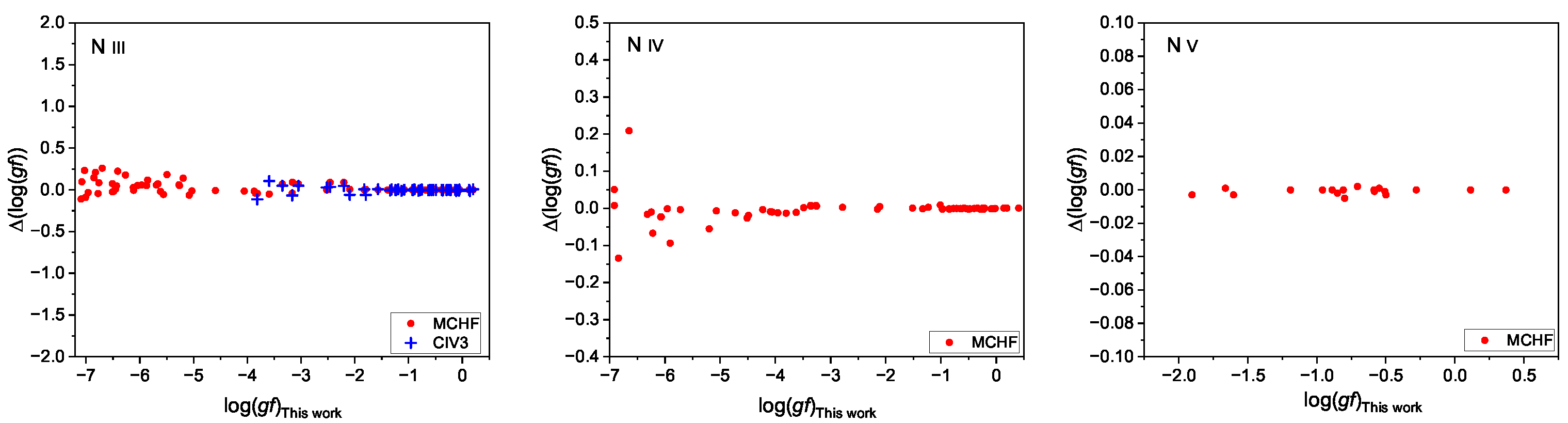
Using the MCDHF and RCI method, we present an extensive and accurate dataset of excitation energies, lifetimes, wavelengths, E1 line strengths, transition rates, and oscillator strengths for N iii – v. Our calculated level energies show excellent agreement with the observed values. The root mean square differences from the NIST values are 130, 103, and 6 ${\mathrm{cm}}^{-1}$, respectively.The accuracy of the transition data was validated through extensive comparisons with the NIST-ASD as well as previous theoretical and experimental results, and the overall agreement was good. However, for some transitions where levels deviate significantly from pure $LS$ coupling, i.e., with strong relativistic configuration interaction effects and relativistic QED effects, the agreement between our computed $log\left(gf\right)$ values and the NIST-compiled values is poorer. We suggest that the current results be used as a reference for N iii – v for various astrophysical applications.