Challenges in Atomic Spectroscopy of Low-Ionisation-Stage Heavy Elements for Astrophysics
Abstract
1. Introduction
2. Measuring Fine Structure Transitions of Heavy Elements
3. Producing Low-Ionisation-Stage Heavy Element Atomic Spectra
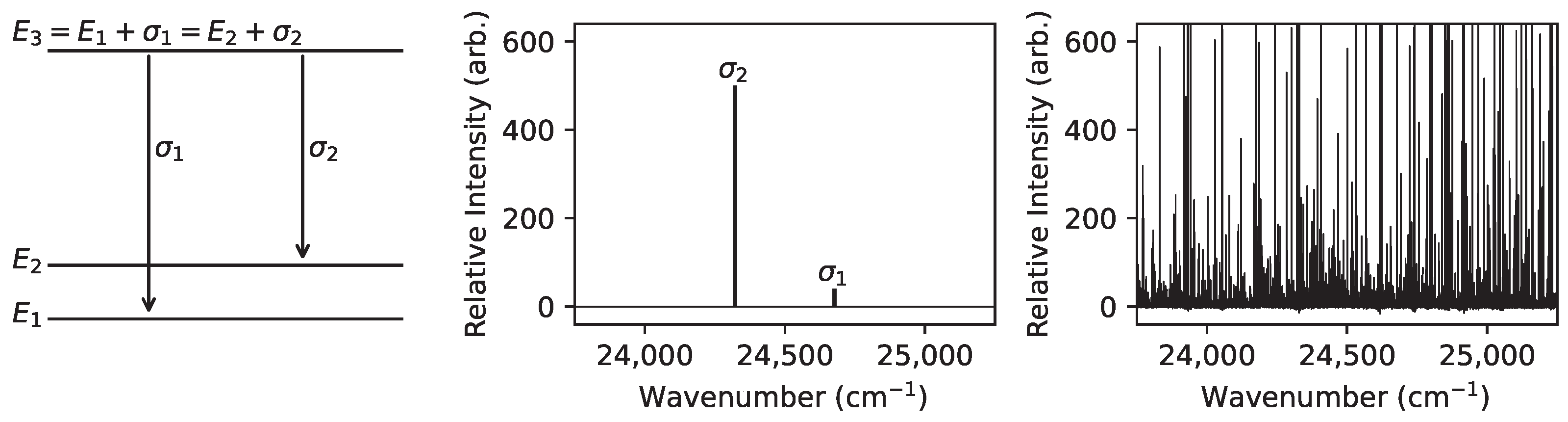
4. Finding Energy Levels from Complex Atomic Spectra
5. Calculating Heavy Element Atomic Structure and Spectra
6. Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atkins, J.F.; Baranov, P.V. Nailing fingerprints in the stars. Nature 2013, 503, 437. [Google Scholar]
- Heiter, U.; Lind, K.; Bergemann, M.; Asplund, M.; Mikolaitis, Š.; Barklem, P.S.; Masseron, T.; de Laverny, P.; Magrini, L.; Edvardsson, B.; et al. Atomic data for the Gaia-ESO survey. Astron. Astrophys. 2021, 645, A106. [Google Scholar] [CrossRef]
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Origin of the heaviest elements: The rapid neutron-capture process. Rev. Mod. Phys. 2021, 93, 015002. [Google Scholar] [CrossRef]
- Wells, M.; Pel, J.W.; Glasse, A.; Wright, G.S.; Aitink-Kroes, G.; Azzollini, R.; Beard, S.; Brandl, B.R.; Gallie, A.; Geers, V.C.; et al. The Mid-Infrared Instrument for the James Webb Space Telescope, VI: The Medium Resolution Spectrometer. Publ. Astron. Soc. Pac. 2015, 127, 646. [Google Scholar] [CrossRef]
- Dekker, H.; D’Odorico, S.; Kaufer, A.; Delabre, B.; Kotzlowski, H. Design, construction, and performance of UVES, the echelle spectrograph for the UT2 Kueyen Telescope at the ESO Paranal Observatory. In Proceedings of the Optical and IR Telescope Instrumentation and Detectors, Munich, Germany, 27–31 March 2000; Volume 4008, pp. 534–545. [Google Scholar]
- Rickman, E.; Rickman, E.; Brown, J. STIS Instrument Handbook, Version 23.0; STScI: Baltimore, MD, USA, 2024; Available online: https://hst-docs.stsci.edu/stisihb (accessed on 26 February 2025).
- Kurucz, R.L. Atomic data for interpreting stellar spectra: Isotopic and hyperfine data. Phys. Scr. 1993, 1993, 110. [Google Scholar] [CrossRef]
- Pickering, J.C.; Belmonte, M.T.; Clear, C.P.; Liggins, F.; Concepcion-Mairey, F. Recent advances in experimental laboratory astrophysics for stellar astrophysics applications and future data needs. Proc. Int. Astron. Union 2019, 15, 220–228. [Google Scholar] [CrossRef]
- Gilmozzi, R.; Spyromilio, J. The European Extremely Large Telescope (E-ELT). Messenger 2007, 127, 3. [Google Scholar]
- The JUST Team; Liu, C.; Zu, Y.; Feng, F.; Li, Z.; Yu, Y.; Bai, H.; Cui, X.; Gu, B.; Gu, Y.; et al. The Jiao Tong University Spectroscopic Telescope Project. Astron. Tech. Instrum. 2024, 1, 16–30. [Google Scholar]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO. Bull. AAS 2019, 51, 035. [Google Scholar]
- Ding, M.; Ryabtsev, A.N.; Kononov, E.Y.; Ryabchikova, T.; Clear, C.P.; Concepcion, F.; Pickering, J.C. Spectrum and energy levels of the low-lying configurations of Nd III. Astron. Astrophys. 2024, 684, A149. [Google Scholar] [CrossRef]
- Ding, M.; Ryabtsev, A.N.; Kononov, E.Y.; Ryabchikova, T.; Pickering, J.C. Spectrum and energy levels of the high-lying singly excited configurations of Nd III—New Nd III experimental energy levels and wavelengths, with transition probability and ionisation energy calculations. Astron. Astrophys. 2024, 692, A33. [Google Scholar] [CrossRef]
- Thorne, A.; Litzén, U.; Johansson, S. Spectrophysics: Principles and Applications; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Thorne, A.P.; Harris, C.J.; Wynne-Jones, I.; Learner, R.C.M.; Cox, G. A Fourier transform spectrometer for the vacuum ultraviolet: Design and performance. J. Phys. E Sci. Instrum. 1987, 20, 54. [Google Scholar] [CrossRef]
- Reader, J. Atomic spectroscopy at NIST: 2001. In Proceedings of the Harnessing Light: Optical Science and Metrology at NIST, San Digeo, CA, USA, 1 August 2001; Volume 4450, pp. 127–139. [Google Scholar]
- De Oliveira, N.; Joyeux, D.; Phalippou, D.; Rodier, J.C.; Polack, F.; Vervloet, M.; Nahon, L. A Fourier transform spectrometer without a beam splitter for the vacuum ultraviolet range: From the optical design to the first UV spectrum. Rev. Sci. Instrum. 2009, 80, 043101. [Google Scholar] [CrossRef]
- Tchang-Brillet, W.Ü.L.; Azarov, V.I. Recent laboratory studies of multiply charged ion spectra using high resolution VUV spectrographs. Phys. Scr. 2002, 2002, 104. [Google Scholar] [CrossRef]
- Zhang, Z.; Svanberg, S.; Palmeri, P.; Quinet, P.; Biémont, E. Measurement of lifetimes by laser-induced fluorescence and determination of transition probabilities of astrophysical interest in Nd III. Astron. Astrophys. 2002, 385, 724–732. [Google Scholar] [CrossRef]
- Kodangil, S.; Domoto, N.; Tanaka, M.; Kato, D.; Gaigalas, G.; Tanuma, H.; Nakamura, N. Measurement of transition probabilities of La II using Laser Induced Breakdown Spectroscopy (LIBS). J. Quant. Spectrosc. Radiat. Transf. 2024, 322, 109011. [Google Scholar] [CrossRef]
- Naoi, Y.; Iwata, M.; Yokota, D.; Gaigalas, G.; Kato, D.; Murakami, I.; Sakaue, H.A.; Sekiguchi, Y.; Tanaka, M.; Tanuma, H.; et al. Laser Induced Breakdown Spectroscopy of Er II for Transition Probability Measurements. Appl. Sci. 2022, 12, 2219. [Google Scholar] [CrossRef]
- Sikström, C.M.; Nilsson, H.; Litzén, U.; Blom, A.; Lundberg, H. Uncertainty of oscillator strengths derived from lifetimes and branching fractions. J. Quant. Spectrosc. Radiat. Transf. 2002, 74, 355–368. [Google Scholar] [CrossRef]
- Mavrodineanu, R. Hollow cathode discharges: Analytical applications. J. Res. Natl. Bur. Stand. 1984, 89, 143. [Google Scholar] [CrossRef]
- Danzmann, K.; Günther, M.; Fischer, J.; Kock, M.; Kühne, M. High current hollow cathode as a radiometric transfer standard source for the extreme vacuum ultraviolet. Appl. Opt. 1988, 27, 4947–4951. [Google Scholar] [CrossRef] [PubMed]
- Finley, D.S.; Jelinsky, P.; Bowyer, S.; Malina, R.F. A Penning discharge source for extreme ultraviolet calibration. In Proceedings of the X-Ray Calibration: Techniques, Sources, and Detectors, San Diego, CA, USA, 19–20 August 1986; Volume 689, pp. 6–10. [Google Scholar]
- Heise, C.; Hollandt, J.; Kling, R.; Kock, M.; Kühne, M. Radiometric characterization of a Penning discharge in the vacuum ultraviolet. Appl. Opt. 1994, 33, 5111–5117. [Google Scholar] [CrossRef] [PubMed]
- Worden, E.F.; Gutmacher, R.G.; Conway, J.G. Use of electrodeless discharge lamps in the analysis of atomic spectra. Appl. Opt. 1963, 2, 707–713. [Google Scholar] [CrossRef]
- Bockasten, K. A study of C III by means of a sliding vacuum spark. Ark Fys. 1955, 9, 457–482. [Google Scholar]
- Castelli, F.; Kurucz, R.L. New Fe II energy levels from stellar spectra. Astron. Astrophys. 2010, 520, A57. [Google Scholar] [CrossRef]
- Dieke, G.H.; Crosswhite, H.M. The spectra of the doubly and triply ionized rare earths. Appl. Opt. 1963, 2, 675–686. [Google Scholar] [CrossRef]
- Cowan, R.D.; Dieke, G.H. Self-absorption of spectrum lines. Rev. Mod. Phys. 1948, 20, 418. [Google Scholar] [CrossRef]
- Johansson, S.; Litzén, U. Possibilities of obtaining laser action from singly ionised iron group elements through charge transfer in hollow cathode lasers. J. Phys. B At. Mol. Phys. 1980, 13, L253. [Google Scholar] [CrossRef]
- Green, J.M.; Webb, C.E. The production of excited metal ions in thermal energy charge transfer and Penning reactions. J. Phys. B At. Mol. Phys. 1974, 7, 1698. [Google Scholar] [CrossRef]
- Nave, G.; Johansson, S. The spectrum of Fe II. Astrophys. J. Suppl. Ser. 2013, 204, 1. [Google Scholar] [CrossRef]
- Reader, J.; Davis, S.P. Fundamental Energy Levels of Neutral Promethium (Pm I). J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1967, 71, 587. [Google Scholar] [CrossRef]
- Learner, R.C.M. A simple (and unexpected) experimental law relating to the number of weak lines in a complex spectrum. J. Phys. B At. Mol. Phys. 1982, 15, L891. [Google Scholar] [CrossRef]
- Nave, G.; Griesmann, U.; Brault, J.W.; Abrams, M.C. Xgremlin: Interferograms and Spectra from Fourier Transform Spectrometers Analysis. Astrophysics Source Code Library, Record ascl:1511.004. 2015. Available online: https://www.ascl.net/1511.004 (accessed on 26 February 2025).
- Engström, L. GFit, A Computer Program to Determine Peak Positions and Intensities in Experimental Spectra; Lund Reports in Atomic Physics; Lund University: Lund, Sweden, 1998; Volume LRAP-232. [Google Scholar]
- Azarov, V.I. Formal approach to the solution of the complex-spectra identification problem. I. Theory. Phys. Scr. 1991, 44, 528. [Google Scholar] [CrossRef]
- Azarov, V.I. Formal approach to the solution of the complex-spectra identification problem. 2. Implementation. Phys. Scr. 1993, 48, 656. [Google Scholar] [CrossRef]
- Azarov, V.I.; Kramida, A.; Vokhmentsev, M.Y. IDEN2—A program for visual identification of spectral lines and energy levels in optical spectra of atoms and simple molecules. Comput. Phys. Commun. 2018, 225, 149–153. [Google Scholar] [CrossRef]
- Johansson, S. Term analysis of a complex spectrum. Phys. Scr. 1996, 1996, 7. [Google Scholar] [CrossRef]
- Kramida, A.E. The program LOPT for least-squares optimization of energy levels. Comput. Phys. Commun. 2011, 182, 419–434. [Google Scholar] [CrossRef]
- Jönsson, P.; Gaigalas, G.; Bieroń, J.; Fischer, C.F.; Grant, I.P. New version: GRASP2K relativistic atomic structure package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Klapisch, M.; Oreg, J. HULLAC, an integrated computer package for atomic processes in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 169–188. [Google Scholar] [CrossRef]
- Badnell, N.R. Autostructure: General Program for Calculation of Atomic and Ionic Properties. Astrophysics Source Code Library, Record ascl:1612.014. 2016. Available online: https://www.ascl.net/1612.014 (accessed on 26 February 2025).
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kurucz, R.L. Including all the lines: Data releases for spectra and opacities. Can. J. Phys. 2017, 95, 825–827. [Google Scholar] [CrossRef]
- Elantkowska, M.; Ruczkowski, J.; Dembczyński, J. Construction of the energy matrix for complex atoms Part I: General remarks. Eur. Phys. J. Plus 2015, 130, 14. [Google Scholar] [CrossRef]
- Uylings, P.; Raassen, T. Orthogonal Operators: Applications, Origin and Outlook. Atoms 2019, 7, 102. [Google Scholar] [CrossRef]
- Rahmouni, S.; Tanaka, M.; Domoto, N.; Kato, D.; Hotokezaka, K.; Aoki, W.; Hirano, T.; Kotani, T.; Kuzuhara, M.; Tamura, M. Revisiting Near-infrared Features of Kilonovae: The Importance of Gadolinium. Astrophys. J. 2025, 980, 43. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; The NIST ASD Team. NIST Atomic Spectra Database, Version 5.12; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024.
- Michalenko, J.J.; Murzyn, C.M.; Zollweg, J.D.; Wermer, L.; Van Omen, A.J.; Clemenson, M.D. Machine learning predictions of transition probabilities in atomic spectra. Atoms 2021, 9, 2. [Google Scholar] [CrossRef]
- Saura, N.; Garrido, D.; Benkadda, S.; Ibano, K.; Ueda, Y.; Hamaguchi, S. Spectroscopic analysis improvement using convolutional neural networks. J. Phys. D Appl. Phys. 2023, 56, 354001. [Google Scholar] [CrossRef]
- Ma, K.; Yang, C.; Zhang, J.; Li, Y.; Jiang, G.; Chai, J. Machine Learning-Assisted Hartree–Fock Approach for Energy Level Calculations in the Neutral Ytterbium Atom. Entropy 2024, 26, 962. [Google Scholar] [CrossRef]
- Zakuskin, A.S.; Labutin, T.A. StarkML: Application of machine learning to overcome lack of data on electron-impact broadening parameters. Mon. Not. R. Astron. Soc. 2024, 527, 3139–3145. [Google Scholar] [CrossRef]
- Ding, M.; Lim, S.Z.J.; Yu, X.; Clear, C.P.; Pickering, J.C. A neural network approach for line detection in complex atomic emission spectra measured by high-resolution Fourier transform spectroscopy. arXiv 2025, arXiv:2501.12276. [Google Scholar]

| FT | Grating | Laser | |
|---|---|---|---|
| Resolving power | ∼ | ∼ | ∼ |
| Sufficient spectral range? | ✓ | ✓ | Not ideal 1 |
| Can measure branching ratios? | ✓ | ✓ | ✓ 1 |
| Can measure hyperfine or isotope structure? | ✓ | Not ideal | ✓ 1 |
| Can measure unstable 2 light sources? | Not ideal | ✓ | ✓ |
| Nd-Ar Hollow Cathode | Nd-Ar Penning Lamp | Nd-Rich Star | Nd-Rich Magnetic Star | Nd Vacuum Spark 1 | |
|---|---|---|---|---|---|
| Temperature 2 | ∼3000 K | ∼7000 K | ∼11,000 K | ∼11,000 K | ∼22,000 K |
| Near IR | FT | FT | Grating | Grating | - |
| Visible | FT | FT | Grating | Grating | - |
| UV | FT | FT | - | - | Grating |
| Vacuum UV | - | - | - | - | Grating |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, M. Challenges in Atomic Spectroscopy of Low-Ionisation-Stage Heavy Elements for Astrophysics. Atoms 2025, 13, 35. https://doi.org/10.3390/atoms13040035
Ding M. Challenges in Atomic Spectroscopy of Low-Ionisation-Stage Heavy Elements for Astrophysics. Atoms. 2025; 13(4):35. https://doi.org/10.3390/atoms13040035
Chicago/Turabian StyleDing, Milan. 2025. "Challenges in Atomic Spectroscopy of Low-Ionisation-Stage Heavy Elements for Astrophysics" Atoms 13, no. 4: 35. https://doi.org/10.3390/atoms13040035
APA StyleDing, M. (2025). Challenges in Atomic Spectroscopy of Low-Ionisation-Stage Heavy Elements for Astrophysics. Atoms, 13(4), 35. https://doi.org/10.3390/atoms13040035








