Benchmark Calculations for Near-Threshold Electron-Impact Excitation of the (1s3s)^3,1S States of Helium

Abstract

We revisit the current status of high-precision calculations for electron-impact excitation of the ${\left(1\mathrm{s}3\mathrm{s}\right)}^{3,1}\mathrm{S}$ states in helium in the low-energy near-threshold regime that is characterized by a large number of resonance features. Having noticed discrepancies between predictions from two previous large-scale calculations for this problem, we report new results and make recommendations regarding the absolute cross-sections that should be used in modeling applications.

1. Introduction

One of the most frequently investigated collision problems in atomic physics is the scattering of electrons from helium atoms. Although often considered a “solved problem”, especially when it comes to modeling applications in plasma or astrophysics, attempts to increase the accuracy of the predictions continue to be reported. Unfortunately, the theoretically favored atomic hydrogen target presents enormous difficulties to experimemtal studies due to the fact that this element prefers to form molecular H₂. Furthermore, the theoretically relatively simple alkali atoms require an oven to bring them into the gas phase, and their high conductivity presents electronic challenges as well. Consequently, helium has been the target of choice in many experimental studies. As a true two-electron system, it can also be treated quite well by state-of-the-art theoretical approaches, albeit a sufficiently accurate nonrelativistic target description, which can reliably be used in a subsequent description of electron collision processes, is by no means trivial due to the importance of electron correlations.

Barry Schneider, to whom this Special Issue is dedicated, was well aware of both the physical and numerical limitations of calculations for structure and, in particular, collision problems. Over his entire career, Schneider worked on the further improvement of theoretical models and their numerical implementation, always keeping in mind what the rapid development of computational hardware would allow ever more sophisticated software to achieve.

This article will compare the predictions of three such computational models, the “Belfast R-matrix” approach [1] employed most recently by Zeng et al. [2] for this problem, the B-spline R-matrix (BSR) method developed by the late Oleg Zatsarinny [3,4], and the convergent-close coupling (CCC) approach [5], which was first extended to the helium target by Fursa and Bray [6]. Even though the original references are 20 or more years old, the resulting computer programs have been continuously modified to run on high-performance supercomputers that allow massively parallelized execution on hybrid OpenMP + MPI architectures and, more recently, have included graphical processing units (GPUs).

This paper is organized as follows: In Section 2, we summarize the most important aspects of the R-matrix and CCC methods. This is followed by our results in Section 3. Our study is the beginning of another joint effort to improve the treatment of the apparently simple electron–helium collision problem to a level that even Barry Schneider might be happy with. Hence, here, we only discuss two of the electron-induced transitions: ${\left(1{\mathrm{s}}^2\right)}^1\mathrm{S}\to {\left(1\mathrm{s}3\mathrm{s}\right)}^3\mathrm{S}$ and ${\left(1{\mathrm{s}}^2\right)}^1\mathrm{S}\to {\left(1\mathrm{s}3\mathrm{s}\right)}^1\mathrm{S}$.

2. Numerical Methods

We now briefly describe the numerical methods used to obtain the results presented below. For more details, the reader should consult the references provided.

2.1. B-Spline R-Matrix

The B-spline R-matrix (BSR) approach [3], developed by the late Oleg Zatarinny, is a general-purpose approach. It is, like the Belfast version [1,7], applicable to any atom or ion, since it treats all $N+1$ electrons explicitly, i.e., N in the target plus the projectile. There are, of course, practical limitations due to the number of configurations and channels that can be handled. An overview of the method and many applications to structure, photo-ionization, and electron collision problems can be found in [4]. The latest version of the programs (including a relativistic D(irac)BSR version) are freely available from Zatsarinny’s GitHub repository [8]. Furthermore, the BSR suite of codes is being preserved through the Atomic, Molecular, and Optical Sciences (AMOS) Gateway [9], where the source code and many sample input files and run scripts for test cases are made available to all interested users.

The BSR results shown below are those reported by Stepanović et al. [10]. This work was performed to support the experiments also reported in that paper. Hence, emphasis was placed on the near-threshold region, with the desire of resolving essentially all resonance structures, independent of how prominent they appear to be. Consequently, all 29 (nonrelativistic) states up to $n=5$ were represented well, while the remaining 40 states were unphysical pseudo-states that were included to account for coupling to the higher Rydberg states, as well as the ionization continuum.

As will be seen below, the choice made at the time for those pseudo-states was not ideal. They were generated by forcing the orbitals into a large R-matrix box of approximately 90 atomic units, and, hence, the energy of the highest-lying state was only about 25 eV. This is too small to generate both an appropriate value for the dipole polarizability of the ground state (important for elastic scattering) and sufficient coupling to the ionization continuum.

At a later stage, a much larger BSR model with a total of 498 states was set up and, indeed, did very well in describing ionization [11] and the even more complex ionization with simultaneous excitation process [12,13,14]. However, that model only had the 11 (nonrelativistic) states up $n=3$ as physical. Hence, it cannot be used for the topic of the present manuscript.

2.2. Convergent Close-Coupling

The convergent close-coupling (CCC) method for electron scattering on helium is detailed by Fursa and Bray [6]. Like the BSR suite of programs, the CCC code is also available on the AMOS Gateway [9].

In brief, as for the hydrogen target [5], the key feature is the underlying Laguerre basis for expanding the total wave function of the electron–atom collision system. The Laguerre basis parameters are the basis size $N_l$ and exponential fall-off ${\lambda }_l$ for $l\le l_{\max }$. Presently, we take $l_{\max }=3$, $N_l=20-l$, and ${\lambda }_l=2.6$. As helium is a two-electron target, we need to specify configurations with Laguerre functions for both the “inner” and the “outer” electrons. To do so, we replace the $1\mathrm{s}, 2\mathrm{s}, 2\mathrm{p}, 3\mathrm{p}$, and $3\mathrm{d}$ (but not $3\mathrm{s}$) functions with those with ${\lambda }_l=8$. These much shorter-ranged functions are put into the configurations for the “inner” electron, while all the Laguerre functions are used for the “outer” electron.

The helium Hamiltonian is diagonalized in all possible configurations, leading to a total of 183 target states, which are subsequently employed to expand the total electron–helium wave function via the CCC formalism [6]. The above Laguerre basis choices yield a helium ionization energy $\approx 0.12$ eV less than the recommended value [15], as well as accurate discrete excited states of principal quantum number $n\le 5$. They also provide a dense discretization of the helium continuum such that an accurate electron-impact total ionization cross-section is obtained similar to that presented by Bray and Fursa [16].

Here, we are only interested in the excitation of the helium ${\left(1\mathrm{s}3\mathrm{s}\right)}^{3,1}\mathrm{S}$ states at energies a few eV above their thresholds. For this purpose, the CCC calculations were performed for partial waves of total orbital angular momentum $0\le L\le 5$ on a fine mesh of incident electron energies.

3. Results and Discussion

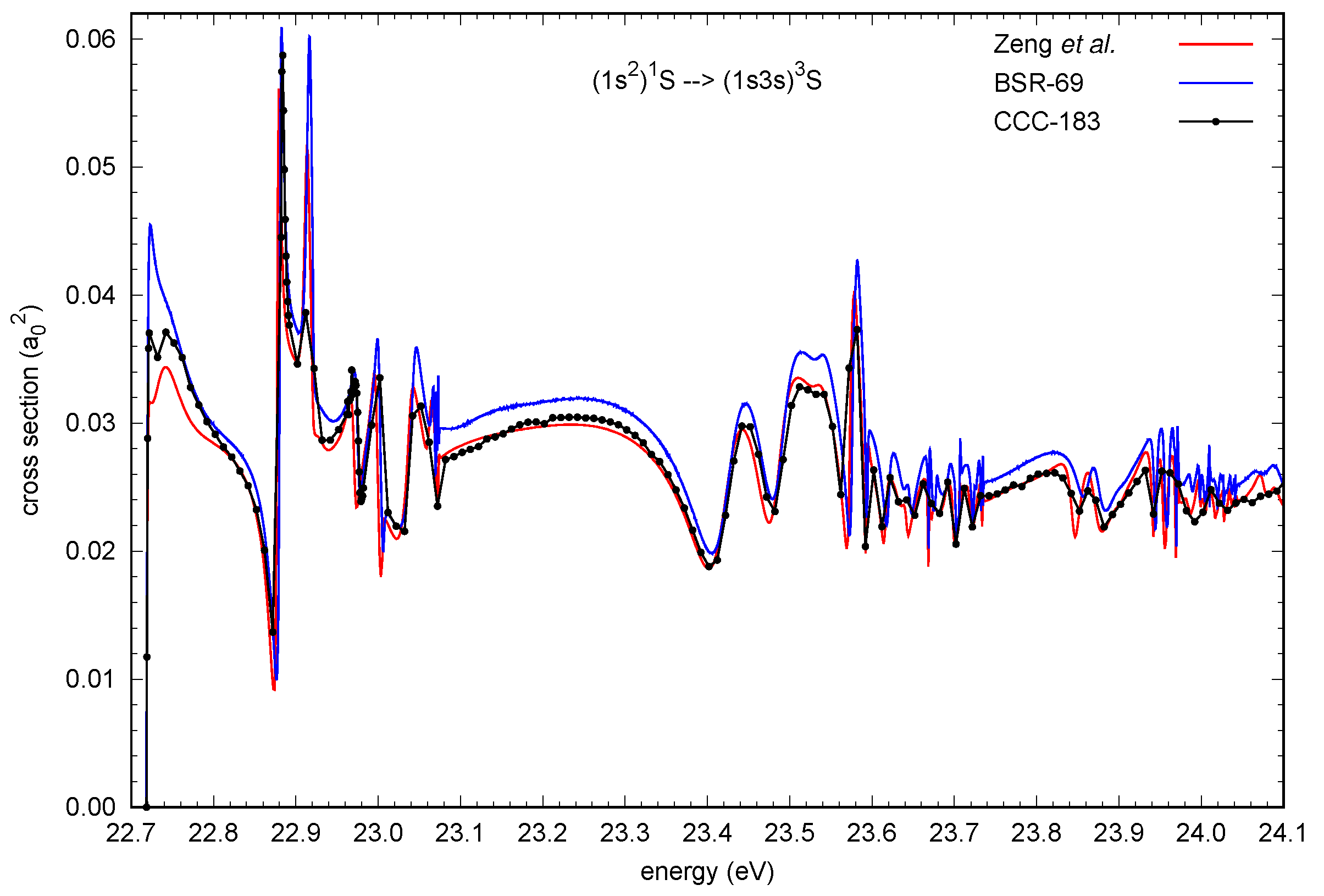
Figure 1 exhibits the predictions for the electron-impact excitation of the ${\left(1{\mathrm{s}}^2\right)}^1\mathrm{S}\to {\left(1\mathrm{s}3\mathrm{s}\right)}^3\mathrm{S}$ transition of helium. As mentioned previously, we are only interested in the near-threshold energy region here. We purposely chose 24.1 eV as the upper limit, which is a little lower than the highest energy plotted by Zeng et al. [2]. It is unlikely that any of the calculations shown would reliably resolve the very detailed resonance structure above 24.1 eV.

We present the results as obtained directly in the collision calculations, except that the energy scale is shifted by about 0.12 eV for CCC-183 and $0.005$ eV for BSR-69 in order to match the experimental excitation energies [15]. In the Belfast code employed by Zeng et al. [2], the theoretical thresholds can be modified to ensure the experimental values.

Looking at the figure, it seems clear that the published BSR-69 results [10], to which the relative experimental data were normalized to provide a good visual fit, overestimate the cross-section by about 10%, thereby confirming the conclusions of Zeng et al. [2]. There is very good, though not perfect, agreement between the latter predictions and those of the CCC-183 model. This is particularly visible in the non-resonant regions. These would contribute substantially to calculations of any rate coefficients, which are the primary parameters of interest for various modeling applications.

Figure 2 depicts the corresponding results for the ${\left(1{\mathrm{s}}^2\right)}^1\mathrm{S}\to {\left(1\mathrm{s}3\mathrm{s}\right)}^1\mathrm{S}$ transition. The conclusions are very similar to those for the previous case, except that the BSR-69 numbers, on average, are about 20% too large.

4. Conclusions

In this contribution, we revisited the current status of ab initio calculations for electron collisions with helium atoms, concentrating on the ${\left(1{\mathrm{s}}^2\right)}^1\mathrm{S}\to {\left(1\mathrm{s}3\mathrm{s}\right)}^{3,1}\mathrm{S}$ transitions in the near-threshold energy region up to just below the thresholds of the $n=6$ manifold. Our principal conclusions are the following:

• We confirm the conclusion of Zeng et al. [2] regarding the likely overestimation of the BSR-69 predictions [10] by about 10% for the ³S and 20% for the ¹S state.
• Even though the energy dependence of the measured cross-sections was in extremely good agreement with the BSR-69 predictions after appropriate convolution with the experimental energy resolution, the experimental data of [10] were relative and normalized to the then presumably best available theory.
• The BSR-69 calculations resolved the resonance features in even more detail than Zeng et al. [2] and the CCC-183 predictions shown here. Hence, despite their shortcoming in the absolute cross-section values, the resonance analysis reported in [10] is likely still the most accurate available today.
• The results of Zeng et al. [2] or the current CCC predictions, after an appropriate shift of the latter to account for the experimental excitation thresholds, should be used for plasma modeling, where generally rate coefficients, i.e., accurate absolute cross-sections integrated over an energy range and weighted with the appropriate electron–energy distribution function, are required.