State-Selective Double Photoionization of Atomic Carbon and Neon
Abstract
1. Introduction
2. Theory
2.1. Single-Photon Double Photoionization (DPI) Amplitudes and Cross Sections
2.2. Describing the Ionized Electrons in the Presence of Other Frozen Electrons
2.3. Computational Details
3. Results
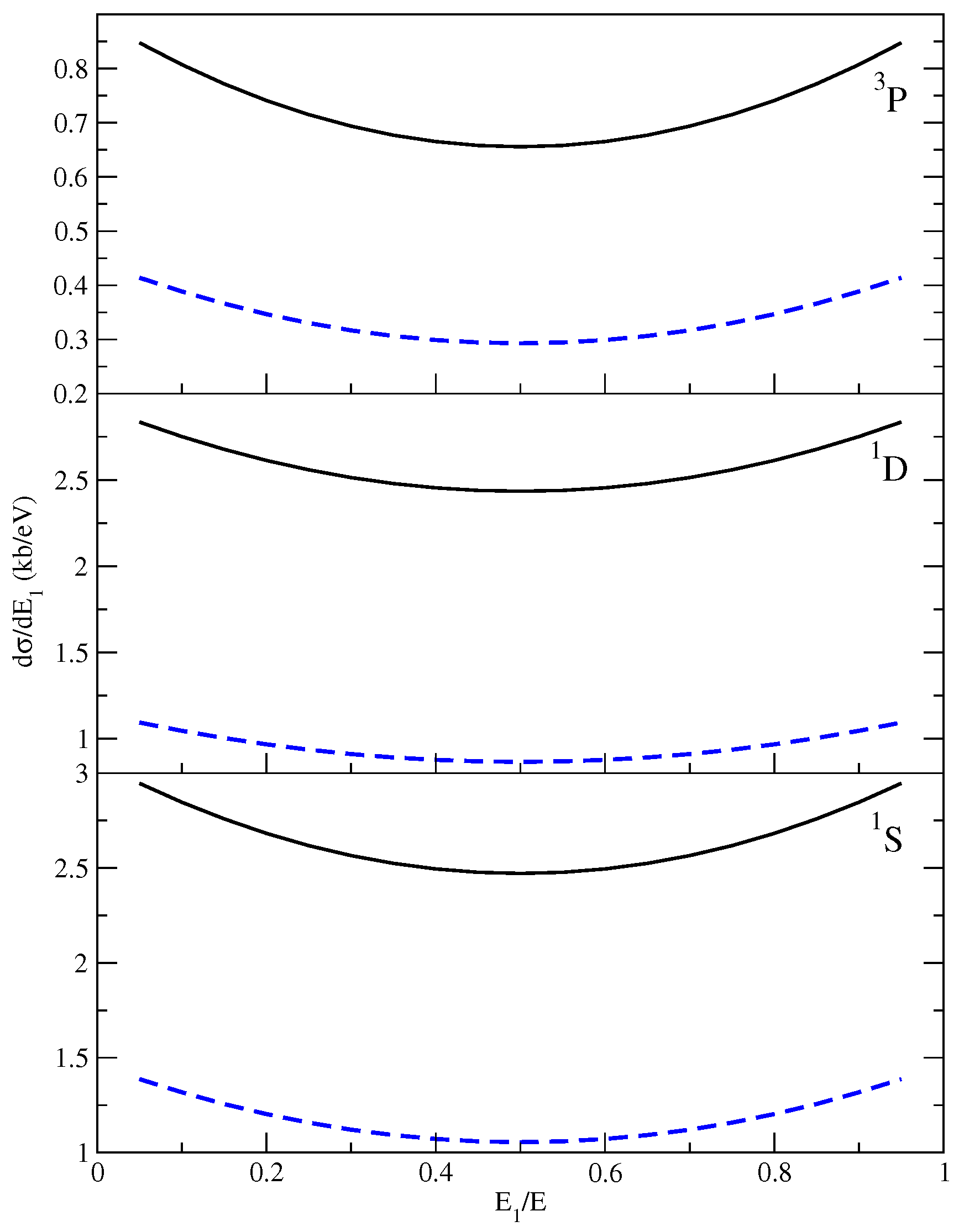
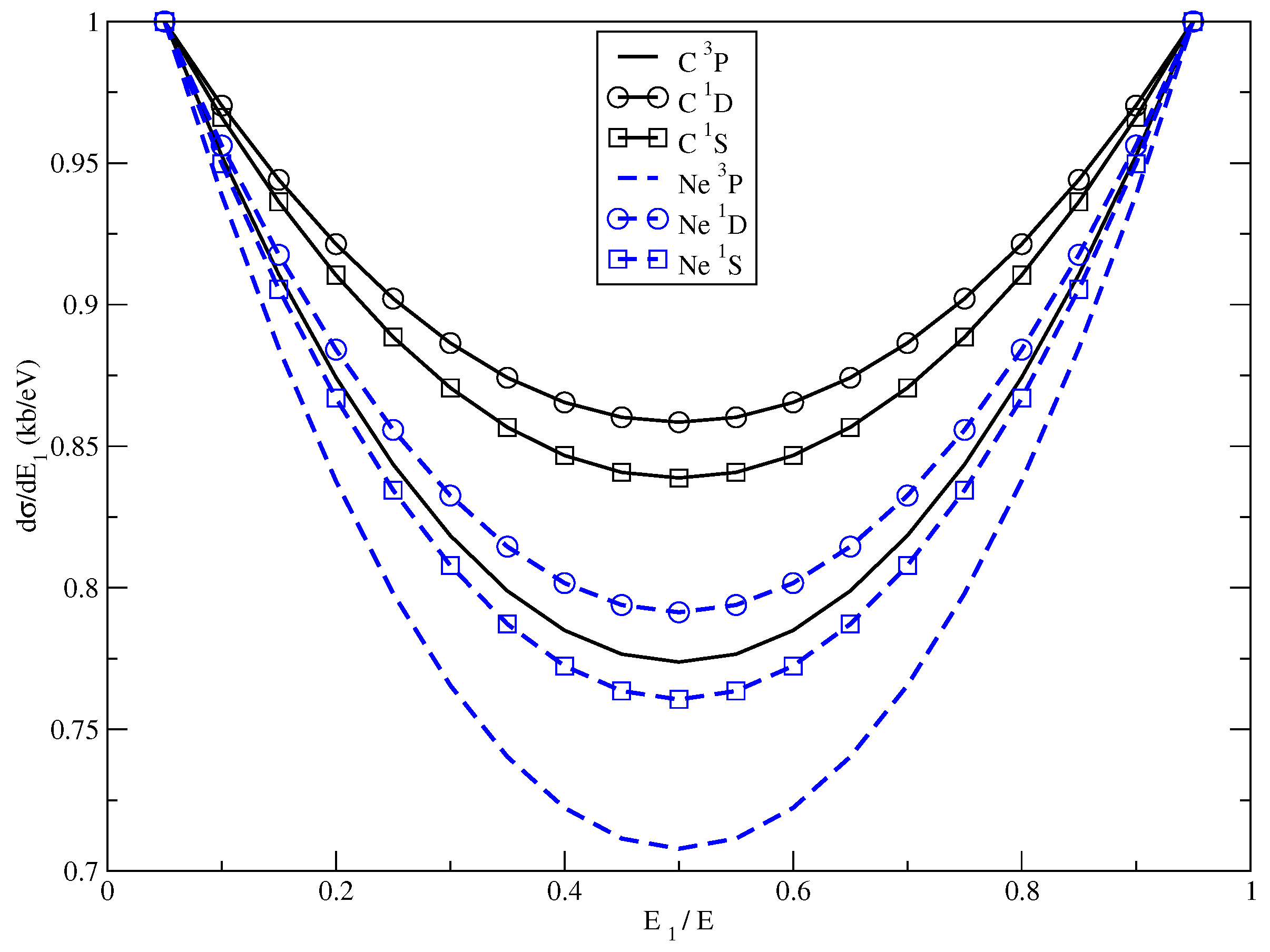
3.1. Single Differential Cross Sections
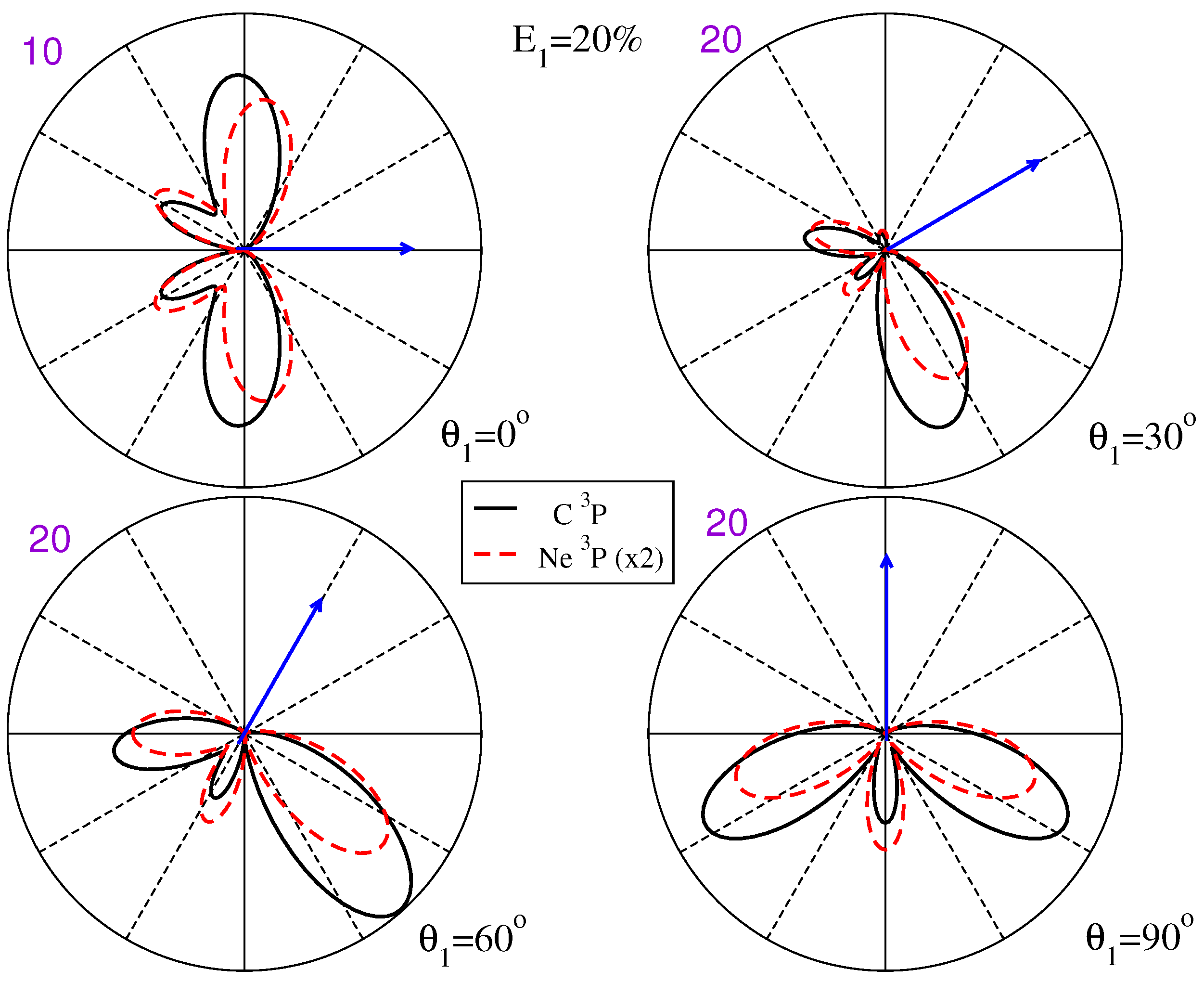
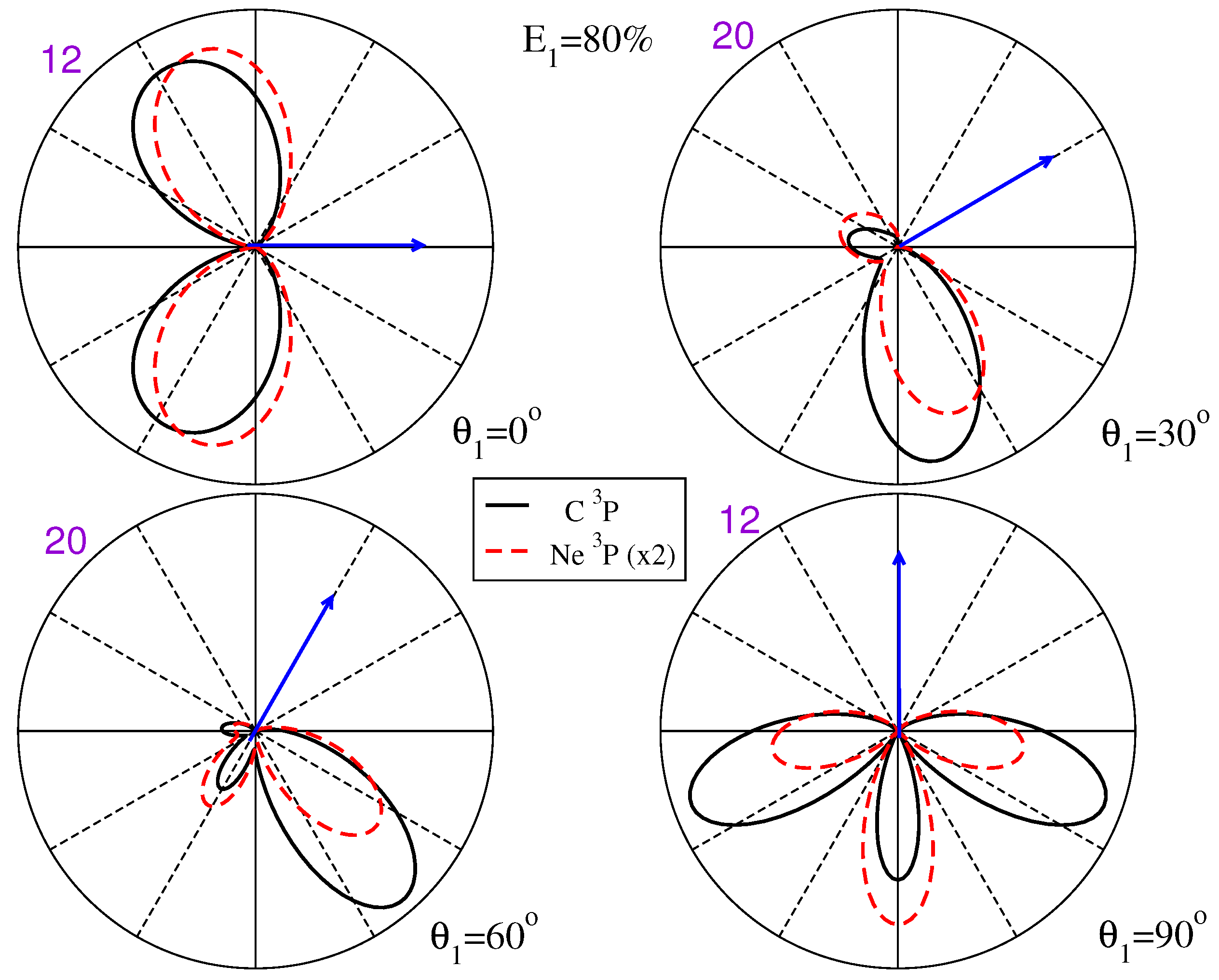
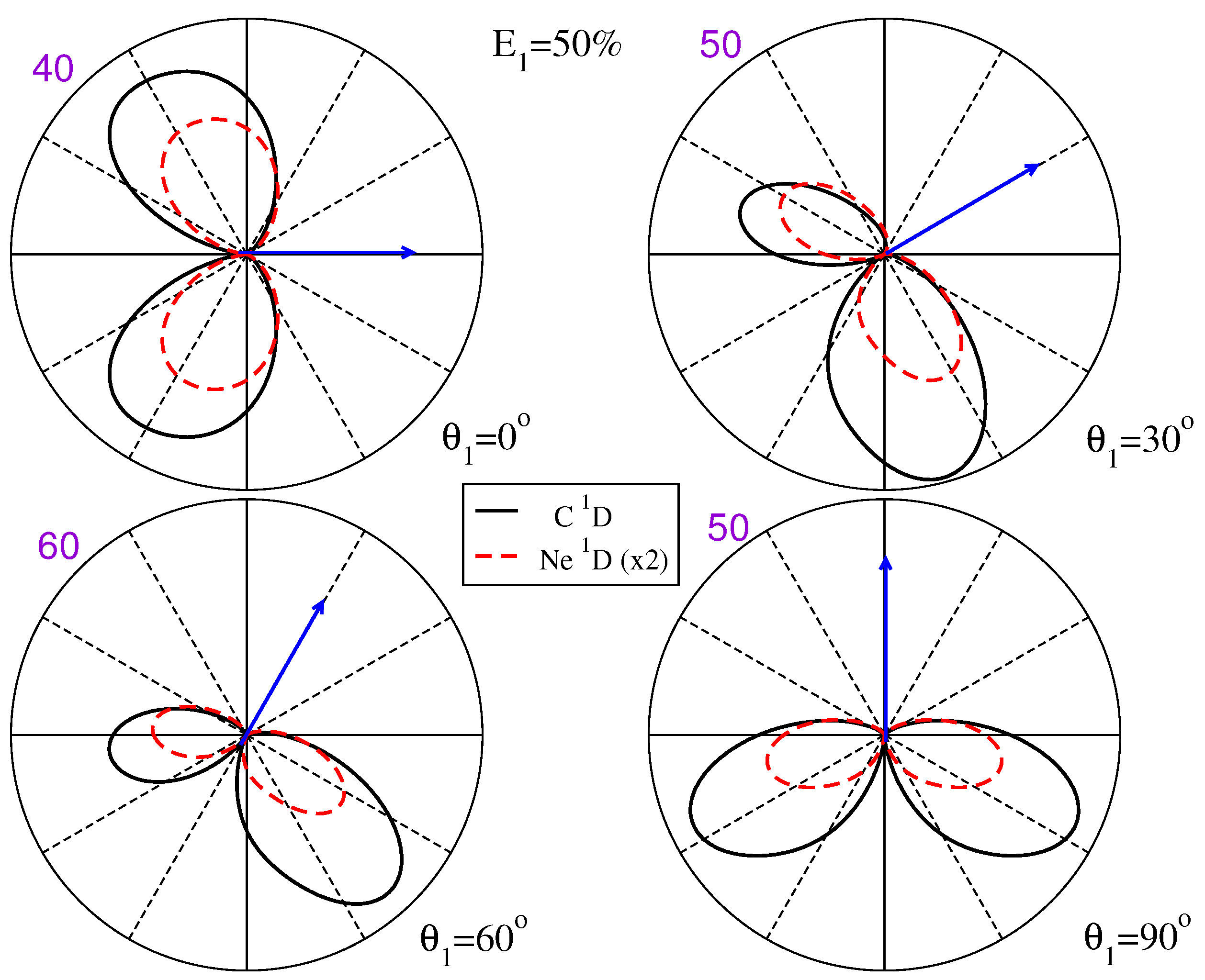
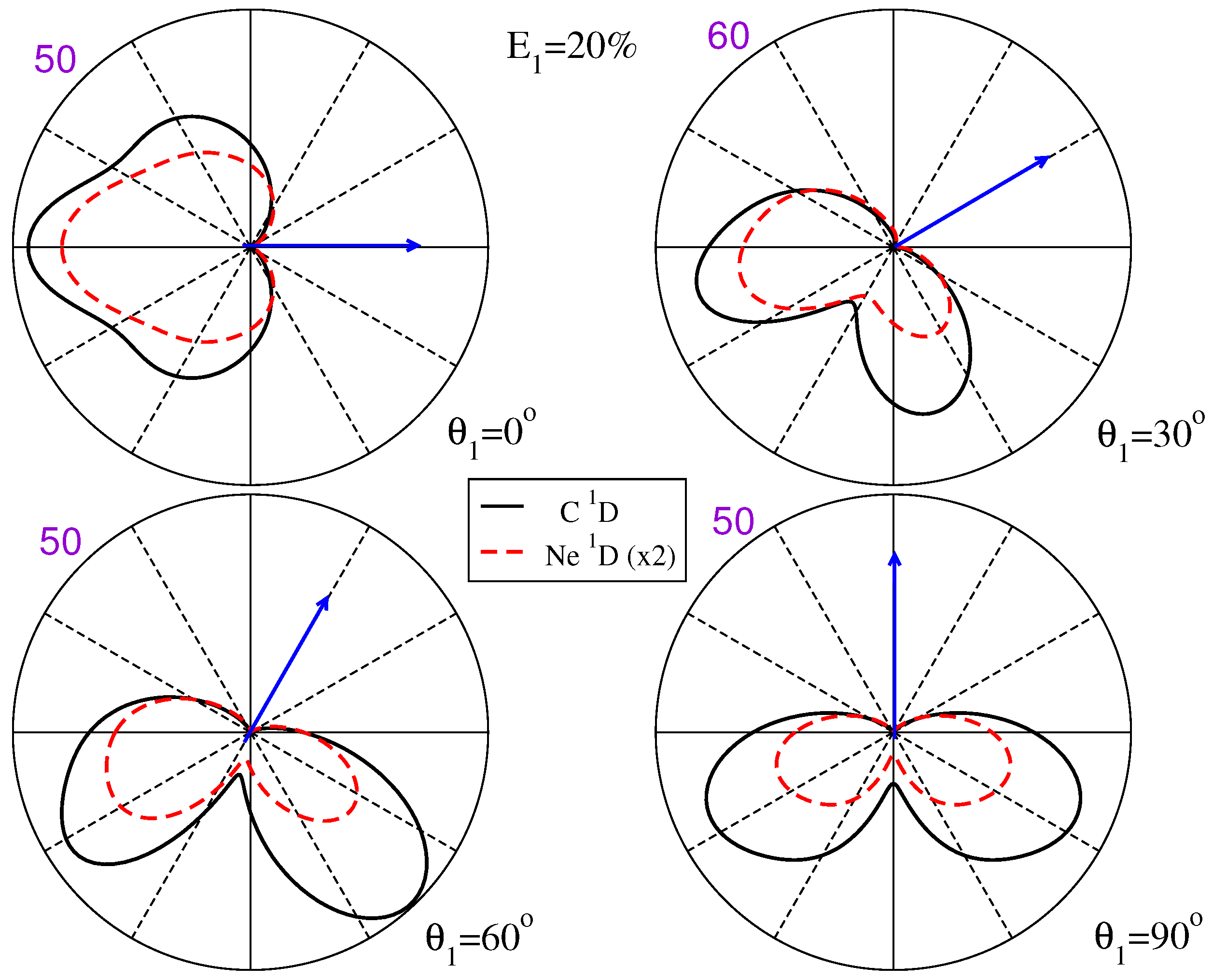
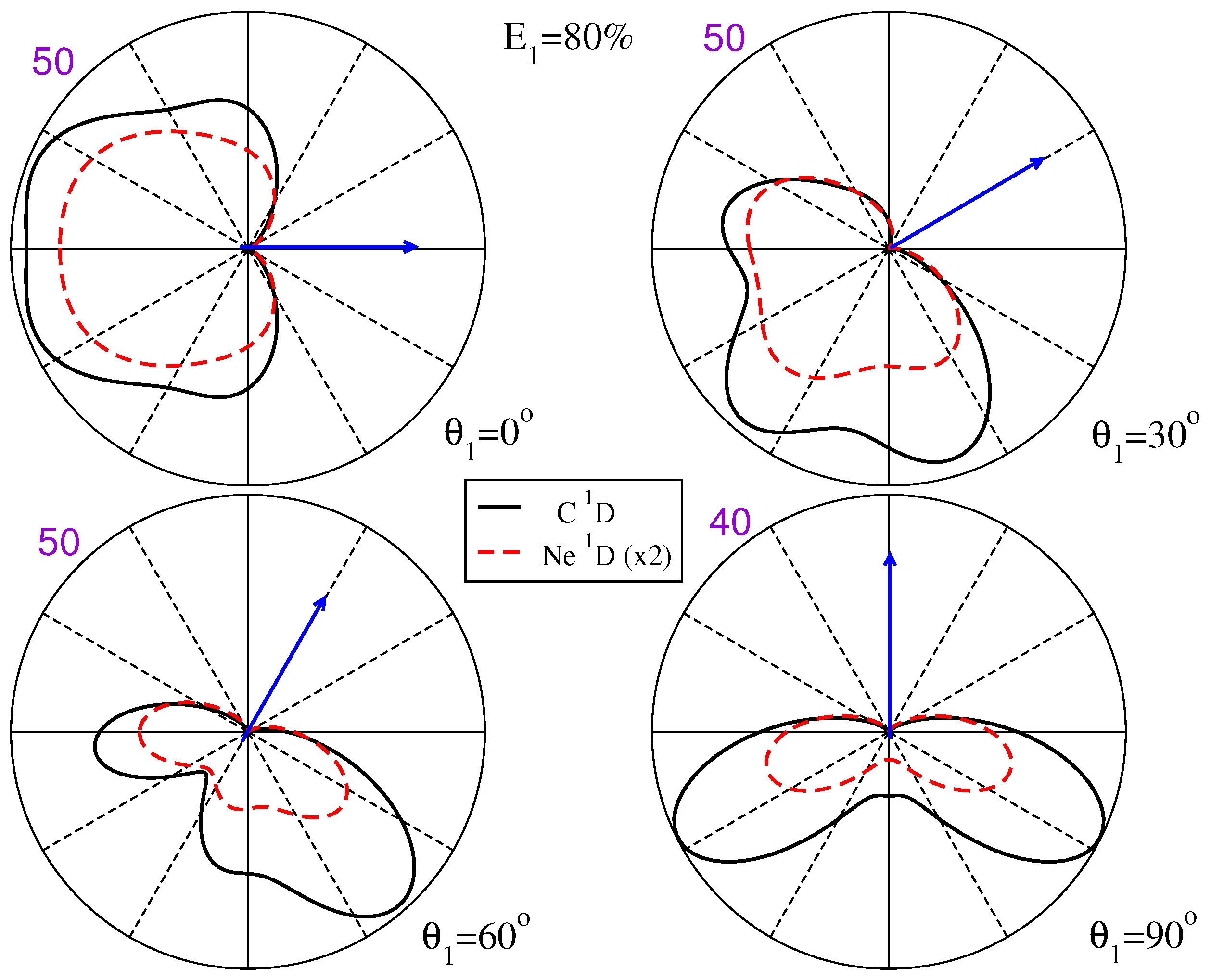
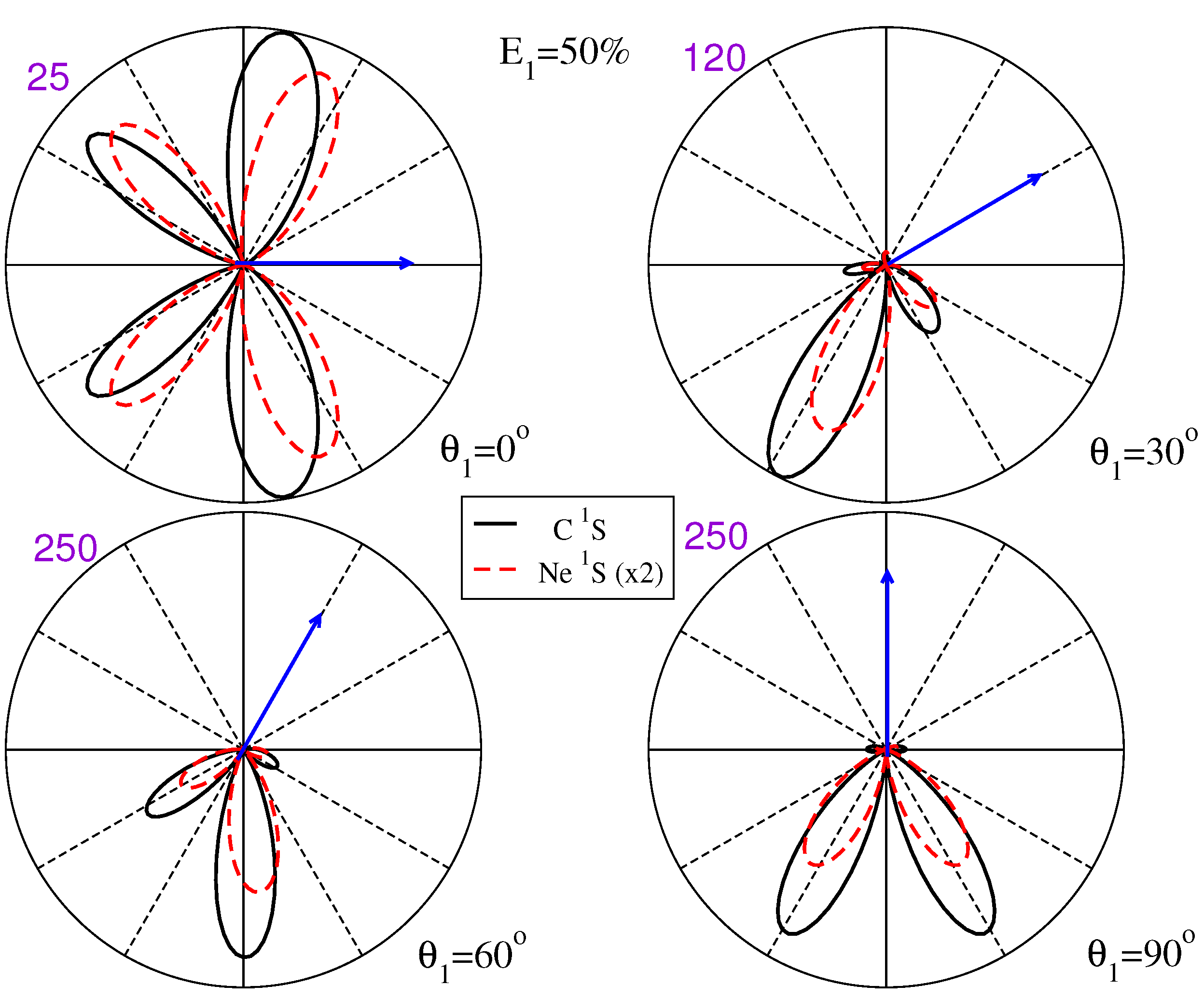
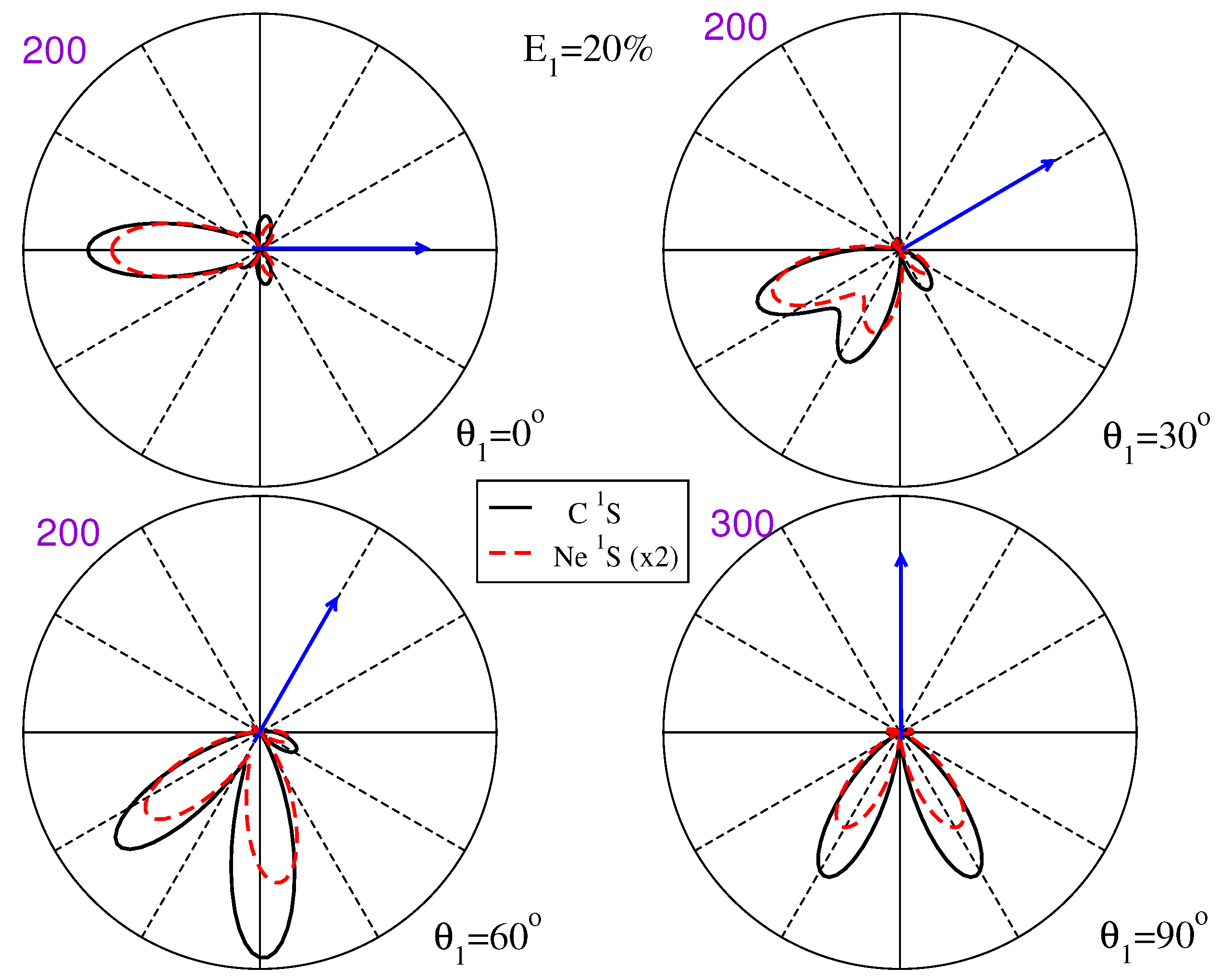
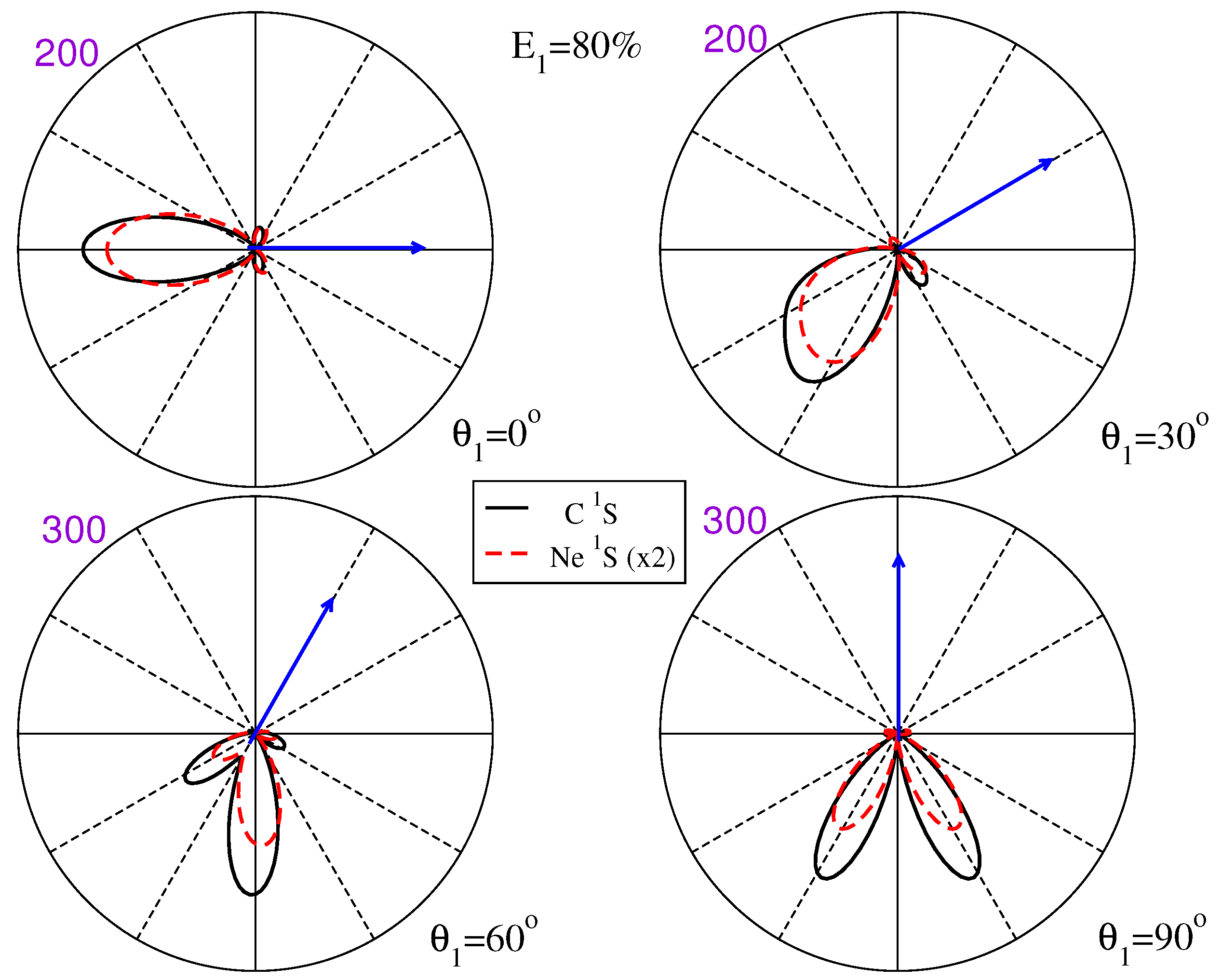
3.2. State-Selective Triple Differential Cross Sections
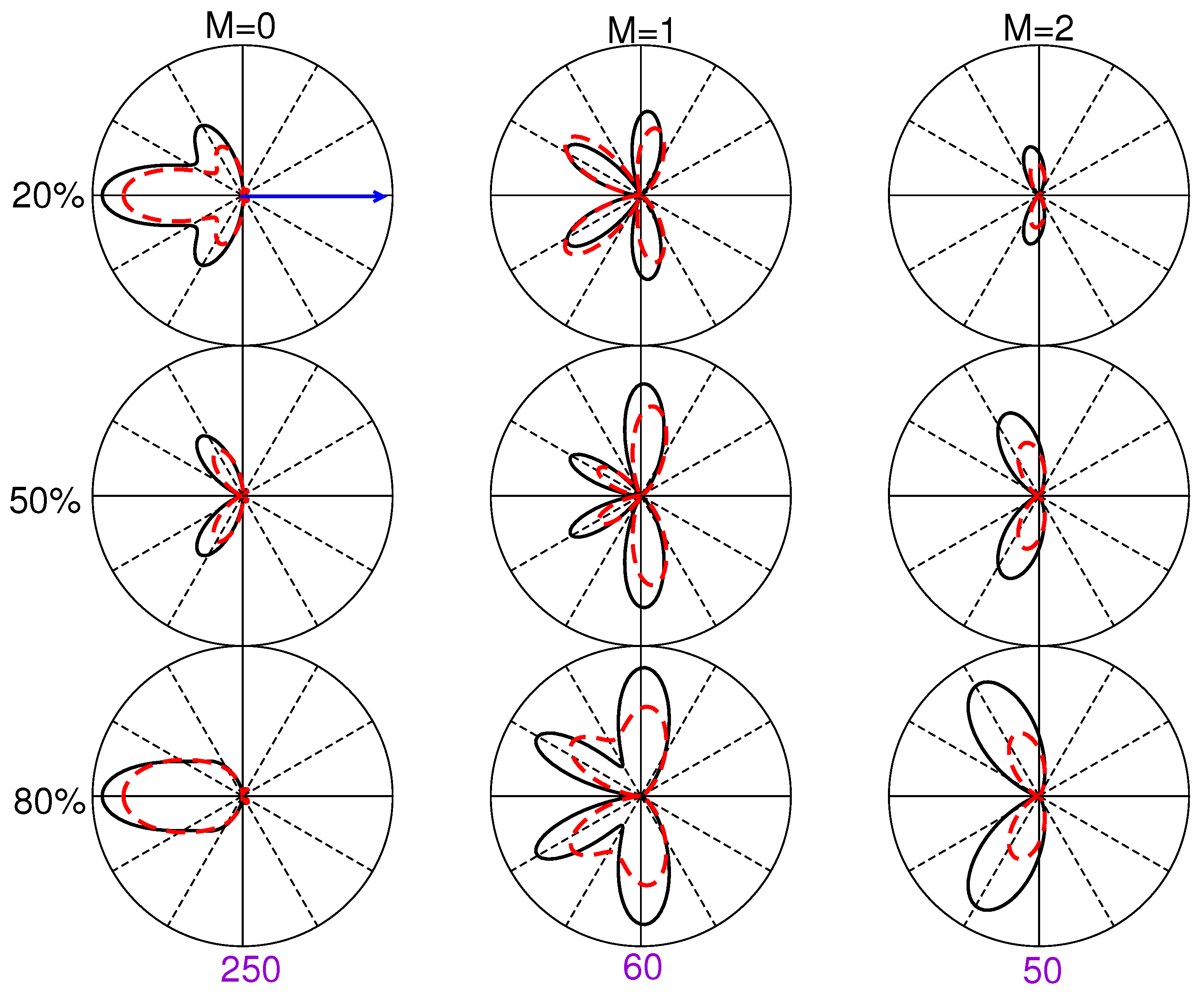
3.3. Examining the Component M States That Constitute the TDCS
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DPI | Double photoionization |
| CI | Configuration interaction |
| TDCS | Triple differential cross section |
| SDCS | Single differential cross section |
| FEM-DVR | Finite element method discrete variable representation |
| ECS | Exterior complex scaling |
| NIST | National Institute of Standards and Technology |
References
- Müller, A.; Borovik, A.; Buhr, T.; Hellhund, J.; Holste, K.; Kilcoyne, A.L.D.; Klumpp, S.; Martins, M.; Ricz, S.; Viefhaus, J.; et al. Observation of a Four-Electron Auger Process in Near-K-Edge Photoionization of Singly Charged Carbon Ions. Phys. Rev. Lett. 2015, 114, 013002. [Google Scholar] [CrossRef] [PubMed]
- Perry-Sassmannshausen, A.; Buhr, T.; Borovik, A.; Martins, M.; Reinwardt, S.; Ricz, S.; Stock, S.O.; Trinter, F.; Müller, A.; Fritzsche, S.; et al. Multiple Photodetachment of Carbon Anions via Single and Double Core-Hole Creation. Phys. Rev. Lett. 2020, 124, 083203. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Double photoionization of He and H2 at unequal energy sharing. Phys. Rev. A 2005, 72, 022703. [Google Scholar] [CrossRef]
- Wehlitz, R.; Heiser, F.; Hemmers, O.; Langer, B.; Menzel, A.; Becker, U. Electron-energy and -angular distributions in the double photoionization of helium. Phys. Rev. Lett. 1991, 67, 3764–3767. [Google Scholar] [CrossRef] [PubMed]
- Avaldi, L.; Huetz, A. Photodouble ionization and the dynamics of electron pairs in the continuum. J. Phys. At. Mol. Opt. Phys. 2005, 38, S861. [Google Scholar] [CrossRef]
- Colgan, J.; Pindzola, M.S. (γ, 2e) total and differential cross-section calculations for helium at various excess energies. Phys. Rev. A 2002, 65, 032729. [Google Scholar] [CrossRef]
- Colgan, J.; Pindzola, M.S.; Robicheaux, F. Time-dependent close-coupling calculations for the double photoionization of He and H2. J. Phys. At. Mol. Opt. Phys. 2004, 37, L377–L384. [Google Scholar] [CrossRef]
- McCurdy, C.W.; Horner, D.A.; Rescigno, T.N.; Martín, F. Theoretical treatment of double photoionization of helium using a B-spline implementation of exterior complex scaling. Phys. Rev. A 2004, 69, 032707. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Robicheaux, F.; Loch, S.D.; Berengut, J.C.; Topcu, T.; Colgan, J.; Foster, M.; Griffin, D.C.; Ballance, C.P.; Schultz, D.R.; et al. The time-dependent close-coupling method for atomic and molecular colli sion processes. J. Phys. At. Mol. Opt. Phys. 2007, 40, R39. [Google Scholar] [CrossRef]
- Guan, X.; Zatsarinny, O.; Noble, C.J.; Bartschat, K.; Schneider, B.I. A time-dependent B-spline R-matrix approach to double ionization of atoms by XUV laser pulses. J. Phys. At. Mol. Opt. Phys. 2009, 42, 134015. [Google Scholar] [CrossRef]
- Dörner, R.; Bräuning, H.; Jagutzki, O.; Mergel, V.; Achler, M.; Moshammer, R.; Feagin, J.M.; Osipov, T.; Bräuning-Demian, A.; Spielberger, L.; et al. Double Photoionization of Spatially Aligned D2. Phys. Rev. Lett. 1998, 81, 5776–5779. [Google Scholar] [CrossRef]
- Feagin, J.M. A helium-like description of molecular hydrogen photo-double ionization. J. Phys. At. Mol. Opt. Phys. 1998, 31, L729–L736. [Google Scholar] [CrossRef]
- Vanroose, W.; Martín, F.; Rescigno, T.N.; McCurdy, C.W. Nonperturbative theory of double photoionization of the hydrogen molecule. Phys. Rev. A 2004, 70, 050703. [Google Scholar] [CrossRef]
- Kheifets, A.S. Single-center model for double photoionization of the H2 molecule. Phys. Rev. A 2005, 71, 022704. [Google Scholar] [CrossRef]
- Vanroose, W.; Martín, F.; Rescigno, T.N.; McCurdy, C.W. Complete Photo-Induced Breakup of the H2 Molecule as a Probe of Molecular Electron Correlation. Science 2005, 310, 1787–1789. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Frozen-core model of the double photoionization of beryllium. Phys. Rev. A 2001, 65, 012710. [Google Scholar] [CrossRef]
- Colgan, J.; Pindzola, M.S. Double photoionization of beryllium. Phys. Rev. A 2002, 65, 022709. [Google Scholar] [CrossRef]
- Citrini, F.; Malegat, L.; Selles, P.; Kazansky, A.K. Direct double photoionization of the valence shell of Be. Phys. Rev. A 2003, 67, 042709. [Google Scholar] [CrossRef]
- Griffin, D.C.; Pindzola, M.S.; Ballance, C.P.; Colgan, J. Double photoionization of Be and Mg atoms using the R-matrix-with-pseudostates method. Phys. Rev. A 2009, 79, 023413. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Bray, I. Valence-shell double photoionization of alkaline-earth-metal atoms. Phys. Rev. A 2007, 75, 042703. [Google Scholar] [CrossRef]
- Laulan, S.; Bachau, H. One- and two-photon double ionization of beryllium with ultrashort ultraviolet laser fields. Phys. Rev. A 2004, 69, 033408. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Ballance, C.P.; Abdel-Naby, S.A.; Robicheaux, F.; Armstrong, G.S.J.; Colgan, J. Single and double photoionization of Be and Mg. J. Phys. At. Mol. Opt. Phys. 2013, 46, 035201. [Google Scholar] [CrossRef]
- McIntyre, M.W.; Kinnen, A.J.; Scott, M.P. Photo-double-ionization of the He and Be isoelectronic sequences within an intermediate-energy R-matrix framework. Phys. Rev. A 2013, 88, 053413. [Google Scholar] [CrossRef]
- Sokell, E.; Bolognesi, P.; Kheifets, A.; Bray, I.; Safgren, S.; Avaldi, L. Signature of Two-Electron Interference in Angular Resolved Double Photoionization of Mg. Phys. Rev. Lett. 2013, 110, 083001. [Google Scholar] [CrossRef]
- Sokell, E.; Bolognesi, P.; Kheifets, A.; Bray, I.; Safgren, S.; Avaldi, L. Photo-double-ionization of Mg studied by electron-electron-coincidence experiments. Phys. Rev. A 2014, 89, 013413. [Google Scholar] [CrossRef]
- Abdel-Naby, S.A.; Pindzola, M.S.; Colgan, J. Differential cross section for the double photoionization of Mg. J. Phys. At. Mol. Opt. Phys. 2014, 48, 025204. [Google Scholar] [CrossRef]
- Yip, F.L.; Rescigno, T.N.; McCurdy, C.W. Fully differential single-photon double photoionization of atomic magnesium. Phys. Rev. A 2016, 94, 063414. [Google Scholar] [CrossRef]
- Yip, F.L. Double Photoionization of Atomic Carbon. Atoms 2022, 10, 23. [Google Scholar] [CrossRef]
- Carter, S.L.; Kelly, H.P. Double photoionization cross section of 3P carbon. J. Phys. At. Mol. Phys. 1976, 9, 1887. [Google Scholar] [CrossRef]
- Yip, F.L.; Rescigno, T.N.; McCurdy, C.W.; Martín, F. Fully Differential Single-Photon Double Ionization of Neon and Argon. Phys. Rev. Lett. 2013, 110, 173001. [Google Scholar] [CrossRef] [PubMed]
- Yip, F.L.; McCurdy, C.W.; Rescigno, T.N. Hybrid orbital and numerical grid representation for electronic continuum processes: Double photoionization of atomic beryllium. Phys. Rev. A 2010, 81, 053407. [Google Scholar] [CrossRef]
- Bello, R.Y.; Yip, F.L.; Rescigno, T.N.; Lucchese, R.R.; McCurdy, C.W. Two-photon double photoionization of atomic Mg by ultrashort pulses: Variation of angular distributions with pulse length. Phys. Rev. A 2020, 102, 053107. [Google Scholar] [CrossRef]
- McCurdy, C.W.; Baertschy, M.; Rescigno, T.N. Solving the three-body Coulomb breakup problem using exterior complex scaling. J. Phys. At. Mol. Opt. Phys. 2004, 37, R137. [Google Scholar] [CrossRef]
- Fischer, C.F. The MCHF atomic-structure package. Comput. Phys. Commun. 2000, 128, 635–636. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. The B-spline R-matrix method for atomic processes: Application to atomic structure, electron collisio ns and photoionization. J. Phys. At. Mol. Opt. Phys. 2013, 46, 112001. [Google Scholar] [CrossRef]
- Rescigno, T.N.; McCurdy, C.W. Numerical grid methods for quantum-mechanical scattering problems. Phys. Rev. A 2000, 62, 032706. [Google Scholar] [CrossRef]
- Krässig, B.; Schaphorst, S.J.; Schwarzkopf, O.; Scherer, N.; Schmidt, V. State dependence of angular correlation patterns in double photoionization. J. Phys. At. Mol. Opt. Phys. 1996, 29, 4255. [Google Scholar] [CrossRef]
- Bolognesi, P.; Zitnik, M.; Malegat, L.; Selles, P.; Turri, G.; Coreno, M.; Camilloni, R.; Avaldi, L. Photo-double ionization of argon at 20 and 40 eV excess energy. J. Phys. At. Mol. Opt. Phys. 2004, 37, 2285. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J. ; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.9); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021. Available online: https://physics.nist.gov/asd (accessed on 15 October 2024).
- Maulbetsch, F.; Briggs, J.S. Selection rules for transitions to two-electron continuum states. J. Phys. At. Mol. Opt. Phys. 1995, 28, 551. [Google Scholar] [CrossRef]
- Gaire, B.; Lee, S.Y.; Haxton, D.J.; Pelz, P.M.; Bocharova, I.; Sturm, F.P.; Gehrken, N.; Honig, M.; Pitzer, M.; Metz, D.; et al. Photo-double-ionization of ethylene and acetylene near threshold. Phys. Rev. A 2014, 89, 013403. [Google Scholar] [CrossRef]
- Bello, R.Y.; Yip, F.L.; Streeter, Z.; Lucchese, R.; McCurdy, C.W. An Orbital Basis Set for Double Photoionization of Atoms and Molecules. J. Chem. Theory Comput. 2024, 20, 9084–9092. [Google Scholar] [CrossRef] [PubMed]


| Carbon | Neon | |||||
|---|---|---|---|---|---|---|
| 3P Double IP | 1D | 1S | 3P Double IP | 1D | 1S | |
| present results | 1.30 | 2.91 | 2.38 | 5.50 | ||
| NIST values [39] | 1.26 | 2.68 | 3.20 | 6.94 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yip, F.L. State-Selective Double Photoionization of Atomic Carbon and Neon. Atoms 2024, 12, 70. https://doi.org/10.3390/atoms12120070
Yip FL. State-Selective Double Photoionization of Atomic Carbon and Neon. Atoms. 2024; 12(12):70. https://doi.org/10.3390/atoms12120070
Chicago/Turabian StyleYip, Frank L. 2024. "State-Selective Double Photoionization of Atomic Carbon and Neon" Atoms 12, no. 12: 70. https://doi.org/10.3390/atoms12120070
APA StyleYip, F. L. (2024). State-Selective Double Photoionization of Atomic Carbon and Neon. Atoms, 12(12), 70. https://doi.org/10.3390/atoms12120070







