Abstract
Structured light encompasses a vast variety of light fields. It has unique properties such as non-uniform transverse intensity and a polarization pattern across their beam cross-sections. In this contribution, we discuss the photoexcitation of a single ionic target system driven by different sets of structured light modes. Specifically, we provide a compilation of transition amplitudes for various structured light modes interacting with atomic systems based on the first-order perturbation theory. To illustrate this, we will choose an electric quadrupole transition () in the target Ca+ ion driven by a structured light field. For this particular interaction, we examine how the beam parameters affect the population of magnetic sub-levels in the atomic excited state.
1. Introduction
Structured light fields have been applied in various applications, including quantum communication [1], microscopy [2], optical tweezers [3], quantum cryptography schemes [4], and many more. These applications have largely benefited by the developments in the production techniques of structured light modes. Modern optical devices, such as spiral phase plates [5], spatial light modulators (SLMs) [6], and Q-plates [7], have significantly simplified the generation of various structured light modes in laboratory settings. Out of various structured light modes, Bessel, Laguerre–Gaussian (LG) and Hermite–Gaussian (HG) modes can be considered to be the prominent ones, while Bessel modes are non-paraxial solutions to the Helmholtz equation in cylindrical coordinates. Moreover, both LG and HG modes are solutions to paraxial equations in cylindrical and Cartesian coordinates, respectively [8].
Bessel, LG and HG modes possess structured transverse intensity profiles [6]. Moreover, Bessel and LG modes carry a projection of orbital angular momentum (OAM) per photon and have helical wavefronts. For this reason, Bessel and LG modes are also called twisted light modes. However, HG modes do not carry orbital angular momentum. In addition, structured light fields can be linearly, circularly or elliptically polarized, similarly to plane waves. However, two or more circularly polarized structured light fields can be combined in a particular fashion to generate so-called vector light fields [9]. These vector light fields exhibit a non-uniform polarization pattern across their beam cross-sections [10].
Over the recent decade, research on structured light atom interactions has flourished immensely in various aspects [11,12,13]. In this contribution, we consider various structured light fields interacting with a single ionic target. Specifically, we provide a compilation of transition amplitudes for different structured light fields interacting with atomic systems. To illustrate this, we will discuss the photoexcitation of the Ca+ ion using structured light fields.
2. Theory of Structured Light Fields
2.1. Bessel Light Modes
Bessel light modes are solutions to the Helmholtz equation in cylindrical coordinates. However, these modes do not satisfy the paraxial condition and also do not undergo diffraction as they propagate in a vacuum [8]. In addition, a twisted light mode exhibits a characteristic transverse intensity profile with multiple rings, as shown in Figure 1a. Now, we provide the vector potential of a circularly polarized Bessel light field propagating along the z axis, such that [14]
where is constant amplitude, is the vector potential of a plane light wave, is helicity, is the projection of the total angular momentum and is a weight function given by
Here, is the azimuthal angle of the momentum vector . Furthermore, the polarization vector can be expressed as a linear combination of the spin basis vectors and , given by
The expansion coefficient is given by , . Furthermore, the Bessel light beam can be described as a superposition of circularly polarized plane waves with helicity in momentum space, as seen in Equation (1). Moreover, the wave vectors of these plane waves with a constant transverse momentum and longitudinal momentum form the surface of a cone with an opening angle (see Figure 1b).
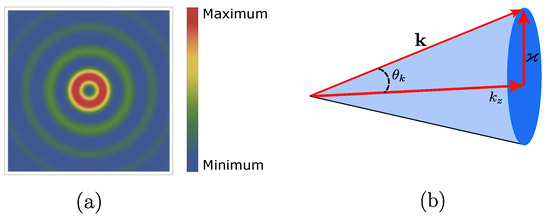
Figure 1.
(a) The transverse intensity profile of a Bessel beam, displaying an infinite number of rings with an opening angle of and . (b) Representation of Bessel beams as a coherent superposition of plane waves with wave vectors confined to the surface of a cone with an opening angle in momentum space.
Although we use the integral representation of the vector potential (1) in our later calculations, it is useful to express in the position space. This representation is particularly helpful for analyzing the polarization of a light field. To achieve this, we substitute the expression (3) into (1) and integrate over using the relation . Additionally, the integral representation of the Bessel function [15] must be used.
Then, the vector potential of the Bessel beam can be expressed in cylindrical coordinates () as [14]
One can also treat the Bessel light fields under the paraxial approximation if one considers a smaller opening angle . Then, one can rewrite the expansion coefficient as and . By incorporating the redefined expansion coefficients and limiting the summation to the leading terms , for which , we obtain the vector potential of a circularly polarized Bessel light field as [16]
Notice that the projection of OAM and helicity are decoupled in the vector potential of a Bessel light field in paraxial approximation (6).
2.2. Laguerre–Gaussian Light Modes
Laguerre–Gaussian modes [17] are solutions to the Helmholtz equation in cylindrical coordinates. In contrast to Bessel modes, they satisfy paraxial approximation [8]. LG modes are mainly characterized by two quantum numbers: projection of OAM and radial index p. As shown in Figure 2, the transverse intensity profile of the LG mode always consists of a number of rings. Moreover, by setting the projection of the orbital angular momentum , one can obtain the well-known Gaussian beam.
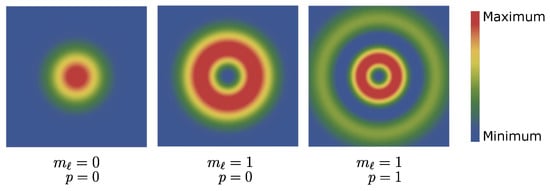
Figure 2.
The transverse intensity profile of the LG beam.
Similar to the construction of the vector potential of Bessel light modes, we can write the vector potential of circularly polarized LG beams as [11]
where is the momentum space wave function and is the vector potential of a plane wave, which is circularly polarized. In the above equation, the momentum space wave function is given by
In the above expression, is the beam width of the LG beam at focus, also called as beam waist, is the binomial coefficient, and is the associated Laguerre polynomial [15]. Moreover, for simplicity, setting the radial index to , one can further simplify the vector potential (7) as [18]
2.3. Hermite–Gaussian Light Modes
The solutions of paraxial wave equations in Cartesian coordinates are Hermite–Gaussian modes [8]. Fundamentally, HG modes are higher-order Gaussian modes. These HG modes can be characterized by two integers , called the mode numbers. Moreover, although the intensity of HG modes is structured (see Figure 3), they do not carry orbital angular momentum like LG or Bessel modes. Since HG and LG families of beams are complete sets of functions, they can be represented in terms of each other. Thus, we express the vector potential of HG modes as
In the above expressions, are mutually orthogonal Cartesian unit vectors. Moreover, we have introduced the coefficient .
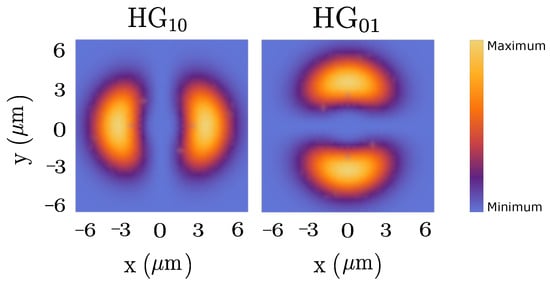
Figure 3.
The transverse intensity profiles of circularly polarized HG modes, HG10 (left) and HG01 (right), with a beam waist of 3 μm.
Even though LG basis is the natural choice to express HG modes, one can also use Bessel basis as discussed in ref. [19].
2.4. Linearly Polarized Structure Light Modes
As an example of a linearly polarized structure light field, we will consider linearly polarized Bessel modes. Specifically, one can write the vector potential of a Bessel light field that is linearly polarized along the x direction as
Notice that in the above expression, we have employed Bessel modes in a paraxial regime to obtain the vector potential expression for linear polarization. Moreover, for larger values, we will not obtain conventional linearly polarized Bessel modes. That is, for larger opening angles, the polarization pattern across the beam cross-section will no longer resemble a linear polarization.
2.5. Vector Structured Light Modes
Vector light fields can be constructed in a similar fashion to a linearly polarized structured light. However, one should also vary the projection of orbital angular momentum of participating twisted light modes in addition to helicity . This results in an interplay between the phase and polarization components of twisted light modes, leading to a light field with a spatially varying polarization pattern across its beam cross-section [10].
The vector potential of a vector Bessel light field can be constructed as
In the above example, we have used a specific case of (). Using (5), we can obtain an explicit expression of the above vector potential as
Note that the above expression is valid for any arbitrary opening angle . For larger values of , the vector beam exhibits a non-zero component of the electric field along the propagation direction.
As discussed earlier, one could obtain a paraxial Bessel beam for a smaller opening angle . Following this logic, the vector potential of a paraxial vector Bessel beam can be written by approximating (14) as
This particular vector Bessel light field exhibits a distinct polarization profile across its beam cross-section, as shown in Figure 4. Since the theory of vector light fields in LG basis is similar to that of in Bessel basis, we will not discuss it in detail here.
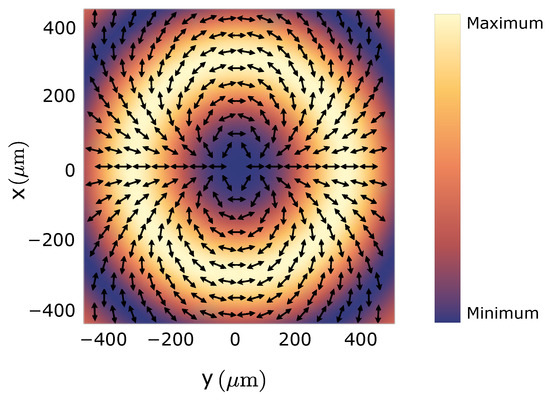
Figure 4.
The intensity and polarization of the vector Bessel beam. Here, , and the opening angle is set to .
2.6. Transition Amplitudes
Let us consider a structured light filed of frequency propagating along the z axis to interact with a single ionic target. Furthermore, this ionic target placed at distance undergoes photoexcitation from an initial state to a final state . For this particular process, we can write the transition amplitude as
where is the Dirac matrix [20] and is the vector potential of the interacting light field.
In this subsection, we will provide a detailed derivation of the transition amplitude for circularly polarized Bessel modes interacting with an atomic target. Using this, we will illustrate how to construct transition amplitudes for linearly polarized and vector Bessel modes.
2.6.1. Bessel Light Modes
If the interacting radiation is a structured light in Bessel basis, then transition amplitude becomes
Before continuing, it is practical to represent the plane wave components present in the vector potential of the Bessel light field using the angular momentum basis. That is, we perform a multipole expansion of the plane wave vector potential to obtain [21,22]
where is the Wigner D function, M is the projection of total angular momentum, and is the multipole parameter. This parameter depends on the total angular momentum of radiation L and () denotes the electric (magnetic) multipole component. Furthermore, represents the vector spherical harmonics of rank L.
Since the transverse intensity profile of a structured light beam is non-uniform, the position of the ionic target is critical. Therefore, we multiply the vector potential of the structured light by displacement operator , where denotes the distance between the atomic target and the beam axis. The transition amplitude after performing the integration over can be written as
where we have employed the Wigner–Eckart theorem [21]; . This helps us to separate the geometrical and atomic parameters in the transition amplitude. That is, the Clebsch–Gordan coefficients characterize the geometrical parameters of the transition amplitude, and the reduced transition amplitude describes the atomic parameters. This reduced transition amplitude can be obtained using the atomic computation package Jena Atomic Calculator (JAC) [23]. That is, all bound-state wave functions that are required are generated within JAC self-consistently, based on the Hartree–Fock–Slater potential. Later, these ab initio wave functions are utilized to evaluate the (many electron) transition amplitudes of electron–photon interactions using the standard angular reduction of symmetry-adapted configuration state functions [24]. The benefits and use of these symmetry-adapted functions have been summarized recently [25] and show how JAC helps to expand the atomic theory towards new light beams and applications.
Furthermore, one can utilize the transition amplitude to obtain an expression for the total rate of excitation as follows:
where is the fine structure constant. Moreover, in the above expression, one has to average over initial projection and summation over final projection . One can also write an expression for a relative sub-level population of the excited state with the help of transition amplitude as follows:
2.6.2. Vector Structured Light Modes
Furthermore, if the interacting light is a vector Bessel beam, then the transition amplitude can be written using (18)
2.6.3. Linearly Polarized Structured Light Modes
The transition amplitude for a linearly polarized Bessel light field interacting with the target atom can be written using (18)
Similarly, one can construct a transition amplitude for HG and LG light modes interacting with an ionic target, as discussed in [19,26].
3. Discussion and Conclusions
Even though our theoretical framework developed in the last section can consider any ionic target, we will choose the Ca+ ion to illustrate this. For this purpose, we will consider circularly polarized and linearly polarized Bessel light fields interacting with the target ion. To be specific, we will consider a 789 nm light field to interact with a Ca+ ion such that it undergoes an electric quadrupole transition from atomic states. For this particular system, we will discuss the relative partial cross-section of the excited state population.
In the first instance, let us consider the incoming radiation to be a circularly polarized Bessel light field. For this light field, if the Ca+ ion is placed on the beam axis, then it will undergo a transition between an initial to a final state (see Figure 5). On the other hand, if the ionic target is displaced from the beam axis, then we will observe an atomic transition between an initial to a final state , as shown in Figure 5.
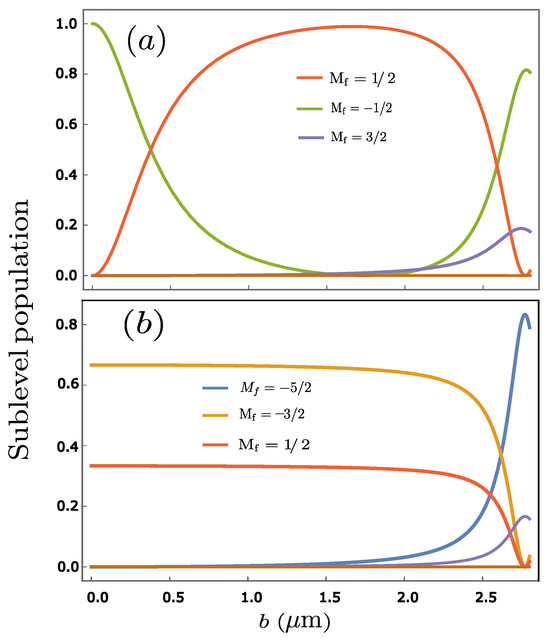
Figure 5.
Relative sub-level population for the electric quadrupole transition in the Ca+ ion. The interacting light field is assumed to comprise (a) circularly and (b) linearly polarized Bessel beams of wavelength 789 nm, , . The ionic target is assumed to be prepared in the ground state and is displaced from the beam axis by b.
Position-dependent atomic transitions can be better understood using the angular momentum selection rule . Specifically, from (18), it is evident that the term determines the value of M across the beam cross-section of structured light beam. For instance, if the target ion is positioned on the beam axis, where , then
That is, on the beam axis, only atomic transitions satisfying the selection rule are allowed. Thus, we observe an atomic transition between an initial to a final state (see Figure 5). On the other hand, if the atomic target is displaced from the beam axis by a distance of b, then the projection of total angular momentum M can take all possible values between and .
Now, let us assume the interacting radiation to be a linearly polarized Bessel beam. For this scenario, if the target ion is positioned on the beam axis, then one observes that two atomic transitions are possible. However, the transition from an initial to a final state is more probable, as seen in Figure 5. Furthermore, for larger b values, we observe a transition from an initial to a final state (see Figure 5).
To summarize our discussion so far, we have explored various structured light beams in terms of their intensity profiles and polarization patterns using their vector potentials. We then derived the transition amplitude for a structured light field interacting with a single ionic target using the first-order perturbation theory. Specifically, we provided a detailed derivation for a Bessel light field interacting with a single target ion. Using this amplitude, we constructed transition amplitudes for linearly and vector-polarized Bessel light beams. To illustrate this, we examined the photoexcitation of a single ionic target by circularly and linearly polarized Bessel light beams. In particular, we focused on electric quadrupole transitions in a Ca+ ion driven by the selected structured light fields. With our results, we analyzed the sub-level population of the excited atomic state and its dependence on the parameters of an incoming structured light field. In particular, it should be noted that these results for circularly and linearly polarized Bessel light fields are calculated for the first time, as previous works have considered LG [11] and vector LG beams [26]. However, these results re-confirm the position-dependent atomic transitions observed in previous works [11,27] with the Ca+ ion interacting with structured light fields. Moreover, these results help us to better understand non-dipole atomic transitions driven by structured light fields, enabling us to build better atomic clocks and quantum information processing devices.
Author Contributions
Conceptualization, S.R.; writing—review and editing, S.R. and S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Research School of Advanced Photon Science (RS-APS) of Helmholtz Institute Jena, Germany.
Data Availability Statement
Data can be made available upon request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LG | Laguerre–Gaussian |
| HG | Hermite–Gaussian |
| SLM | Spatial light modulator |
| OAM | Orbital angular momentum |
References
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light. Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Heintzmann, R.; Gustafsson, M.G.L. Subdiffraction resolution in continuous samples. Nat. Photonics 2009, 3, 362–364. [Google Scholar] [CrossRef]
- Simpson, N.B.; Allen, L.; Padgett, M.J. Optical tweezers and optical spanners with Laguerre–Gaussian modes. J. Mod. Opt. 1996, 43, 2485–2491. [Google Scholar] [CrossRef]
- Souza, C.E.R.; Borges, C.V.S.; Khoury, A.Z.; Huguenin, J.A.O.; Aolita, L.; Walborn, S.P. Quantum key distribution without a shared reference frame. Phys. Rev. A 2008, 77, 032345. [Google Scholar] [CrossRef]
- Kotlyar, V.; Kovalev, A.; Porfirev, A.; Kozlova, E. Orbital angular momentum of a laser beam behind an off-axis spiral phase plate. Opt. Lett. 2019, 44, 3673–3676. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Courtial, J.; Allen, L. Light’s Orbital Angular Momentum. Phys. Today 2004, 57, 35–40. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical Spin-to-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic Media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Babiker, M. The Angular Momentum of Light; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wang, J.; Castellucci, F.; Franke-Arnold, S. Vectorial light–matter interaction: Exploring spatially structured complex light fields. AVS Quantum Sci. 2020, 2, 031702. [Google Scholar] [CrossRef]
- Gbur, G.J. Singular Optics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Peshkov, A.A.; Seipt, D.; Surzhykov, A.; Fritzsche, S. Photoexcitation of atoms by Laguerre-Gaussian beams. Phys. Rev. A 2017, 96, 023407. [Google Scholar] [CrossRef]
- Afanasev, A.; Carlson, C.E.; Solyanik, M. Atomic spectroscopy with twisted photons: Separation of M1–E2 mixed multipoles. Phys. Rev. A 2018, 97, 023422. [Google Scholar] [CrossRef]
- Afanasev, A.; Carlson, C.E.; Mukherjee, A. High-multipole excitations of hydrogen-like atoms by twisted photons near a phase singularity. J. Opt. 2016, 18, 074013. [Google Scholar] [CrossRef]
- Matula, O.; Hayrapetyan, A.G.; Serbo, V.G.; Surzhykov, A.; Fritzsche, S. Atomic ionization of hydrogen-like ions by twisted photons: Angular distribution of emitted electrons. J. Phys. At. Mol. Opt. Phys. 2013, 46, 205002. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1948; Volume 55. [Google Scholar]
- Schulz, S.A.L.; Peshkov, A.A.; Müller, R.A.; Lange, R.; Huntemann, N.; Tamm, C.; Peik, E.; Surzhykov, A. Generalized excitation of atomic multipole transitions by twisted light modes. Phys. Rev. A 2020, 102, 012812. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Peshkov, A.A.; Bidasyuk, Y.M.; Lange, R.; Huntemann, N.; Peik, E.; Surzhykov, A. Interaction of twisted light with a trapped atom: Interplay between electronic and motional degrees of freedom. Phys. Rev. A 2023, 107, 023106. [Google Scholar] [CrossRef]
- Peshkov, A.A.; Jordan, E.; Kromrey, M.; Mehta, K.K.; Mehlstäubler, T.E.; Surzhykov, A. Excitation of Forbidden Electronic Transitions in Atoms by Hermite–Gaussian Modes. Ann. Phys. 2023, 535, 2300204. [Google Scholar] [CrossRef]
- Johnson, W.R. Lectures on Atomic Physics; Notre Dame University Department of Physics: Notre Dame, Indiana, 2006. [Google Scholar]
- Rose, M.E. Elementary Theory of Angular Momentum; Courier Corporation: North Chelmsford, MA, USA, 1995. [Google Scholar]
- Brink, D.M.; Satchler, G.R. Angular Momentum; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Fritzsche, S. A fresh computational approach to atomic structures, processes and cascades. Comput. Phys. Commun. 2019, 240, 1–14. [Google Scholar] [CrossRef]
- Gaigalas, G.; Fritzsche, S.; Grant, I.P. Program to calculate pure angular momentum coefficients in jj-coupling. Comput. Phys. Commun. 2001, 139, 263–278. [Google Scholar] [CrossRef]
- Fritzsche, S. Application of Symmetry-Adapted Atomic Amplitudes. Atoms 2022, 10, 127. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Hofbrucker, J.; Fritzsche, S. Photoexcitation of atoms by cylindrically polarized Laguerre-Gaussian beams. Phys. Rev. A 2022, 105, 033103. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).