Bound–Free and Free–Free Pair Production Channels in Forward Delbrück Scattering
Abstract
1. Introduction
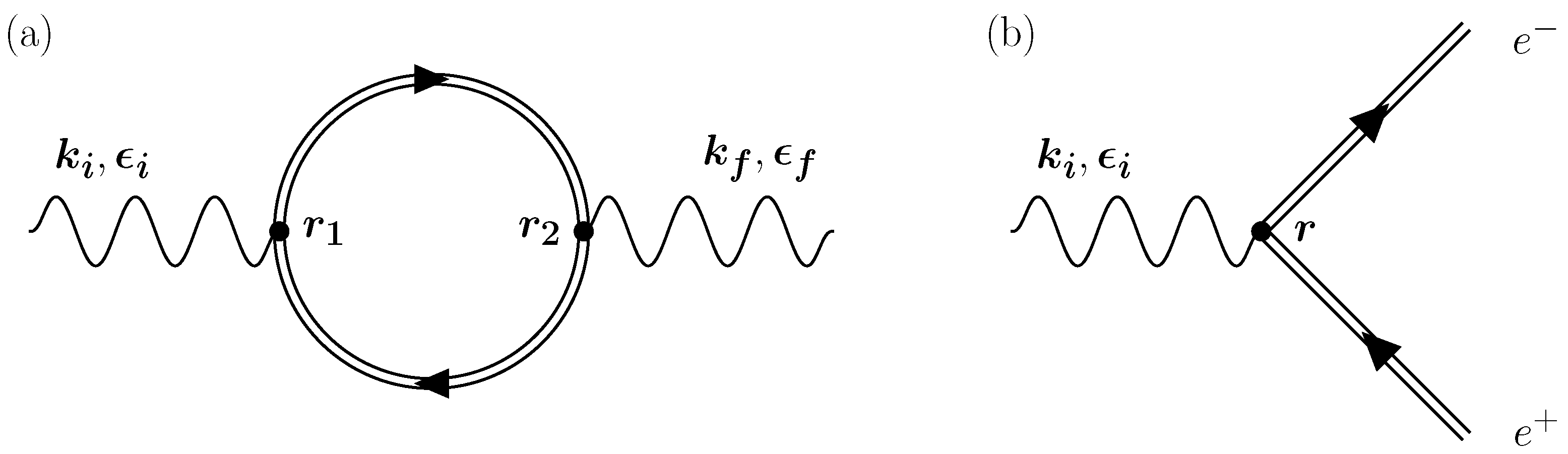
2. Theoretical Background
3. Numerical Results
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schumacher, M. Delbrück scattering. Radiat. Phys. Chem. 1999, 56, 101–111. [Google Scholar] [CrossRef]
- Milstein, A.I.; Schumacher, M. Present status of Delbrück scattering. Phys. Rep. 1994, 243, 183–214. [Google Scholar] [CrossRef]
- Rullhusen, P.; Smend, F.; Schumacher, M. Delbrück scattering of 2754 kev photons by Nd, Ce, I, Sn, Mo and Zn. Phys. Lett. B 1979, 84, 166–168. [Google Scholar] [CrossRef]
- Rullhusen, P.; Smend, F.; Schumacher, M.; Hanser, A.; Rebel, H. Coulomb correction to Delbrück scattering investigated at Z = 94. Z. Phys. A 1979, 293, 287–292. [Google Scholar] [CrossRef]
- Falkenberg, H.; Hünger, A.; Rullhusen, P.; Schumacher, M.; Milstein, A.I.; Mork, K. Amplitudes for Delbrück scattering. At. Data Nucl. Data Tables 1992, 50, 1–27. [Google Scholar] [CrossRef]
- Papatzacos, P.; Mork, K. Delbrück scattering calculations. Phys. Rev. D 1975, 12, 206–218. [Google Scholar] [CrossRef]
- Bar-Noy, T.; Kahane, S. Numerical calculations of Delbrueck scattering amplitudes. Nucl. Phys. A 1977, 288, 132. [Google Scholar] [CrossRef]
- Sommerfeldt, J.; Yerokhin, V.A.; Müller, R.A.; Zaytsev, V.A.; Volotka, A.V.; Surzhykov, A. Calculations of Delbrück scattering to all orders in αZ. Phys. Rev. A 2022, 105, 022804. [Google Scholar] [CrossRef]
- Sommerfeldt, J.; Yerokhin, V.A.; Stöhlker, T.; Surzhykov, A. All-order Coulomb corrections to Delbrück scattering above the pair production threshold. Phys. Rev. Lett. 2023, 131, 061601. [Google Scholar] [CrossRef] [PubMed]
- Sommerfeldt, J.; Yerokhin, V.A.; Surzhykov, A. Delbrück scattering above the pair production threshold: Going beyond the Born approximation. Ann. Phys. 2024, 536, 2300364. [Google Scholar] [CrossRef]
- Rohrlich, F.; Gluckstern, R.L. Forward Scattering of Light by a Coulomb Field. Phys. Rev. 1952, 86, 1. [Google Scholar] [CrossRef]
- Solberg, R.; Mork, K.; Øverbø, I. Coulomb and screening corrections to Delbrück forward scattering. Phys. Rev. A 1995, 51, 359. [Google Scholar] [CrossRef] [PubMed]
- Carney, J.P.J.; Pratt, R.H. Contribution of bound-electron pair production to the dispersion relation for Delbrück scattering. Phys. Rev. A 1999, 60, 3020. [Google Scholar] [CrossRef]
- Kirilin, G.G.; Terekhov, I.S. Coulomb corrections to the Delbrück scattering amplitude at low energies. Phys. Rev. A 2008, 77, 032118. [Google Scholar] [CrossRef]
- Shabaev, V.M. Two-time Green’s function method in quantum electrodynamics of high-Z few-electron atoms. Phys. Rep. 2002, 356, 119–228. [Google Scholar] [CrossRef]
- Øverbø, I. The Coulomb corrections to electron pair production by intermediate-energy photons. Phys. Lett. B 1977, 71, 412–414. [Google Scholar]
- Øverbø, I.; Mork, K.J.; Olsen, H.A. Exact Calculation of Pair Production. Phys. Rev. 1968, 175, 1978. [Google Scholar] [CrossRef]
- Sommerfeldt, J.; Müller, R.A.; Artemyev, A.N.; Surzhykov, A. Polarization effects in bound-free pair production. Phys. Rev. A 2019, 100, 042511. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sommerfeldt, J.; Yerokhin, V.A.; Surzhykov, A. Bound–Free and Free–Free Pair Production Channels in Forward Delbrück Scattering. Atoms 2025, 13, 19. https://doi.org/10.3390/atoms13020019
Sommerfeldt J, Yerokhin VA, Surzhykov A. Bound–Free and Free–Free Pair Production Channels in Forward Delbrück Scattering. Atoms. 2025; 13(2):19. https://doi.org/10.3390/atoms13020019
Chicago/Turabian StyleSommerfeldt, Jonas, Vladimir A. Yerokhin, and Andrey Surzhykov. 2025. "Bound–Free and Free–Free Pair Production Channels in Forward Delbrück Scattering" Atoms 13, no. 2: 19. https://doi.org/10.3390/atoms13020019
APA StyleSommerfeldt, J., Yerokhin, V. A., & Surzhykov, A. (2025). Bound–Free and Free–Free Pair Production Channels in Forward Delbrück Scattering. Atoms, 13(2), 19. https://doi.org/10.3390/atoms13020019





