Prospective Optical Lattice Clocks in Neutral Atoms with Hyperfine Structure
Abstract
1. Introduction
2. Lattice Light Shifts in Optical Lattice Clocks
2.1. An Introduction to AC Stark-Induced Frequency Shifts in OLCs
2.2. Full AC Stark Treatment for Lattice Light Shifts
2.3. Spectroscopy of Forbidden to Transitions of States with the Same Parity
2.4. Spectroscopy between Same-Parity States with , , , and
2.5. New Systematics
2.5.1. Second-Order Zeeman Shift
2.5.2. Hyperpolarizability
3. Neutral Manganese: Atomic Properties and Laser Cooling
3.1. Oscillator Strengths and Lifetimes
3.2. Metastable MOT Operation
Sub-Doppler Cooling and a Novel Continuous Cold Atom Source
3.3. Narrow-Line MOT
4. Mn Clock Transitions
4.1. Allowed E2 Transitions
4.2. Forbidden M1/E2 Transitions
4.2.1. Electric-Field-Induced Forbidden E2 Transitions
4.2.2. Two-Photon Transitions
4.3. Blackbody Radiation-Induced Frequency Shifts
4.4. Magic Wavelengths
4.5. New Systematics and Their Mitigation
4.6. Second-Order Order Zeeman Shift
4.7. Second-Order AC Stark–Hyperpolarizability
5. Prospects for a Copper Clock
5.1. Laser Cooling
5.2. Clock Operation
5.2.1. BBR
5.2.2. AC Stark
5.2.3. Hyperfine Structure Induced Second-Order Shifts
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OLC | Optical Lattice Clock |
| M1 | Magnetic Dipole |
| E2 | Electric Quadrupole |
| MOT | Magneto Optical Trap |
References
- Katori, H. Spectroscopy of strontium atoms in the Lamb-Dicke confinement. In Frequency Standards and Metrology; World Scientific: Singapore, 2002; pp. 323–330. [Google Scholar]
- Ye, J.; Kimble, H.; Katori, H. Quantum state engineering and precision metrology using state-insensitive light traps. Science 2008, 320, 1734–1738. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, T.L.; Campbell, S.; Hutson, R.; Marti, G.E.; Bloom, B.; McNally, R.L.; Zhang, W.; Barrett, M.; Safronova, M.S.; Strouse, G.; et al. Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. Nat. Commun. 2015, 6, 6896. [Google Scholar] [CrossRef] [PubMed]
- McGrew, W.; Zhang, X.; Fasano, R.; Schäffer, S.; Beloy, K.; Nicolodi, D.; Brown, R.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87–90. [Google Scholar] [CrossRef]
- Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.L.; Ye, J.; Kennedy, C.J. JILA SrI optical lattice clock with uncertainty of 2.0 × 10−18. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
- Schioppo, M.; Brown, R.C.; McGrew, W.F.; Hinkley, N.; Fasano, R.J.; Beloy, K.; Yoon, T.; Milani, G.; Nicolodi, D.; Sherman, J.; et al. Ultrastable optical clock with two cold-atom ensembles. Nat. Photonics 2017, 11, 48–52. [Google Scholar] [CrossRef]
- Oelker, E.; Hutson, R.; Kennedy, C.; Sonderhouse, L.; Bothwell, T.; Goban, A.; Kedar, D.; Sanner, C.; Robinson, J.; Marti, G.; et al. Demonstration of 4.8 × 10−17 stability at 1 s for two independent optical clocks. Nat. Photonics 2019, 13, 714–719. [Google Scholar] [CrossRef]
- Delva, P.; Lodewyck, J.; Bilicki, S.; Bookjans, E.; Vallet, G.; Le Targat, R.; Pottie, P.E.; Guerlin, C.; Meynadier, F.; Le Poncin-Lafitte, C.; et al. Test of special relativity using a fiber network of optical clocks. Phys. Rev. Lett. 2017, 118, 221102. [Google Scholar] [CrossRef]
- Kennedy, C.J.; Oelker, E.; Robinson, J.M.; Bothwell, T.; Kedar, D.; Milner, W.R.; Marti, G.E.; Derevianko, A.; Ye, J. Precision metrology meets cosmology: Improved constraints on ultralight dark matter from atom-cavity frequency comparisons. Phys. Rev. Lett. 2020, 125, 201302. [Google Scholar] [CrossRef] [PubMed]
- Barontini, G.; Blackburn, L.; Boyer, V.; Butuc-Mayer, F.; Calmet, X.; López-Urrutia, J.C.; Curtis, E.; Darquie, B.; Dunningham, J.; Fitch, N.; et al. Measuring the stability of fundamental constants with a network of clocks. EPJ Quantum Technol. 2022, 9, 12. [Google Scholar] [CrossRef]
- Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photonics 2020, 14, 411–415. [Google Scholar] [CrossRef]
- Zhang, X.; Bishof, M.; Bromley, S.L.; Kraus, C.V.; Safronova, M.S.; Zoller, P.; Rey, A.M.; Ye, J. Spectroscopic observation of SU(N)-symmetric interactions in Sr orbital magnetism. Science 2014, 345, 1467–1473. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Bromley, S.; Bothwell, T.; Wall, M.; Marti, G.; Koller, A.; Zhang, X.; Rey, A.; Ye, J. Spin–orbit-coupled fermions in an optical lattice clock. Nature 2017, 542, 66–70. [Google Scholar] [CrossRef]
- Oppong, N.D.; Riegger, L.; Bettermann, O.; Höfer, M.; Levinsen, J.; Parish, M.M.; Bloch, I.; Fölling, S. Observation of coherent multiorbital polarons in a two-dimensional Fermi gas. Phys. Rev. Lett. 2019, 122, 193604. [Google Scholar] [CrossRef]
- Aeppli, A.; Chu, A.; Bothwell, T.; Kennedy, C.J.; Kedar, D.; He, P.; Rey, A.M.; Ye, J. Hamiltonian engineering of spin–orbit–coupled fermions in a Wannier-Stark optical lattice clock. Sci. Adv. 2022, 8, eadc9242. [Google Scholar] [CrossRef]
- Bothwell, T.; Kennedy, C.J.; Aeppli, A.; Kedar, D.; Robinson, J.M.; Oelker, E.; Staron, A.; Ye, J. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature 2022, 602, 420–424. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637. [Google Scholar] [CrossRef]
- Brown, R.C.; Phillips, N.B.; Beloy, K.; McGrew, W.F.; Schioppo, M.; Fasano, R.J.; Milani, G.; Zhang, X.; Hinkley, N.; Leopardi, H.; et al. Hyperpolarizability and operational magic wavelength in an optical lattice clock. Phys. Rev. Lett. 2017, 119, 253001. [Google Scholar] [CrossRef]
- Ushijima, I.; Takamoto, M.; Katori, H. Operational magic intensity for Sr optical lattice clocks. Phys. Rev. Lett. 2018, 121, 263202. [Google Scholar] [CrossRef]
- Kim, K.; Aeppli, A.; Bothwell, T.; Ye, J. Evaluation of Lattice Light Shift at Low 10−19 Uncertainty for a Shallow Lattice Sr Optical Clock. Phys. Rev. Lett. 2023, 130, 113203. [Google Scholar] [CrossRef] [PubMed]
- Beloy, K.; Hinkley, N.; Phillips, N.B.; Sherman, J.A.; Schioppo, M.; Lehman, J.; Feldman, A.; Hanssen, L.M.; Oates, C.W.; Ludlow, A.D. Atomic clock with 1 × 10−18 room-temperature blackbody stark uncertainty. Phys. Rev. Lett. 2014, 113, 260801. [Google Scholar] [CrossRef] [PubMed]
- Ushijima, I.; Takamoto, M.; Das, M.; Ohkubo, T.; Katori, H. Cryogenic optical lattice clocks. Nat. Photonics 2015, 9, 185–189. [Google Scholar] [CrossRef]
- Heo, M.S.; Kim, H.; Yu, D.H.; Lee, W.K.; Park, C.Y. Evaluation of the blackbody radiation shift of an Yb optical lattice clock at KRISS. Metrologia 2022, 59, 055002. [Google Scholar] [CrossRef]
- Kozlov, A.; Dzuba, V.; Flambaum, V. Prospects of building optical atomic clocks using Er I or Er III. Phys. Rev. A 2013, 88, 032509. [Google Scholar] [CrossRef]
- Golovizin, A.; Fedorova, E.; Tregubov, D.; Sukachev, D.; Khabarova, K.; Sorokin, V.; Kolachevsky, N. Inner-shell clock transition in atomic thulium with a small blackbody radiation shift. Nat. Commun. 2019, 10, 1724. [Google Scholar] [CrossRef] [PubMed]
- Dzuba, V.; Allehabi, S.O.; Flambaum, V.; Li, J.; Schiller, S. Time keeping and searching for new physics using metastable states of Cu, Ag, and Au. Phys. Rev. A 2021, 103, 022822. [Google Scholar] [CrossRef]
- Safronova, M.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Kastberg, A.; Aoki, T.; Sahoo, B.; Sakemi, Y.; Das, B. Optical-lattice-based method for precise measurements of atomic parity violation. Phys. Rev. A 2019, 100, 050101. [Google Scholar] [CrossRef]
- Eustice, S.; Filin, D.; Schrott, J.; Porsev, S.; Cheung, C.; Novoa, D.; Stamper-Kurn, D.M.; Safronova, M.S. Optical telecommunications-band clock based on neutral titanium atoms. Phys. Rev. A 2023, 107, L051102. [Google Scholar] [CrossRef]
- Westergaard, P.G.; Lodewyck, J.; Lorini, L.; Lecallier, A.; Burt, E.; Zawada, M.; Millo, J.; Lemonde, P. Lattice-induced frequency shifts in Sr optical lattice clocks at the 10−17 level. Phys. Rev. Lett. 2011, 106, 210801. [Google Scholar] [CrossRef]
- Shi, C.; Robyr, J.L.; Eismann, U.; Zawada, M.; Lorini, L.; Le Targat, R.; Lodewyck, J. Polarizabilities of the 87Sr clock transition. Phys. Rev. A 2015, 92, 012516. [Google Scholar] [CrossRef]
- Katori, H.; Takamoto, M.; Pal’Chikov, V.; Ovsiannikov, V. Ultrastable optical clock with neutral atoms in an engineered light shift trap. Phys. Rev. Lett. 2003, 91, 173005. [Google Scholar] [CrossRef]
- Le Kien, F.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to cesium. Eur. Phys. J. D 2013, 67, 92. [Google Scholar] [CrossRef]
- Taichenachev, A.V.; Yudin, V.; Oates, C.; Hoyt, C.; Barber, Z.; Hollberg, L. Magnetic field-induced spectroscopy of forbidden optical transitions with application to lattice-based optical atomic clocks. Phys. Rev. Lett. 2006, 96, 083001. [Google Scholar] [CrossRef]
- Bouchiat, M.; Bouchiat, C.I. Parity violation induced by weak neutral currents in atomic physics. J. Phys. 1974, 35, 899–927. [Google Scholar] [CrossRef]
- Bouchiat, M.; Bouchiat, C. Parity violation induced by weak neutral currents in atomic physics. Part II. J. Phys. 1975, 36, 493–509. [Google Scholar] [CrossRef]
- Alden, E.A.; Moore, K.; Leanhardt, A. Two-photon E1-M1 optical clock. Phys. Rev. A 2014, 90, 012523. [Google Scholar] [CrossRef]
- Beloy, K. Prospects of a Pb2+ ion clock. Phys. Rev. Lett. 2021, 127, 013201. [Google Scholar] [CrossRef] [PubMed]
- Young, A.W.; Eckner, W.J.; Milner, W.R.; Kedar, D.; Norcia, M.A.; Oelker, E.; Schine, N.; Ye, J.; Kaufman, A.M. Half-minute-scale atomic coherence and high relative stability in a tweezer clock. Nature 2020, 588, 408–413. [Google Scholar] [CrossRef]
- Martin, K.W.; Phelps, G.; Lemke, N.D.; Bigelow, M.S.; Stuhl, B.; Wojcik, M.; Holt, M.; Coddington, I.; Bishop, M.W.; Burke, J.H. Compact optical atomic clock based on a two-photon transition in rubidium. Phys. Rev. Appl. 2018, 9, 014019. [Google Scholar] [CrossRef]
- Hertel, I.V.; Schulz, C.P. Atoms, Molecules and Optical Physics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lee, A.C.; Smith, J.; Richerme, P.; Neyenhuis, B.; Hess, P.W.; Zhang, J.; Monroe, C. Engineering large Stark shifts for control of individual clock state qubits. Phys. Rev. A 2016, 94, 042308. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; Number 3; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kramida, A. Cowan code: 50 years of growing impact on atomic physics. Atoms 2019, 7, 64. [Google Scholar] [CrossRef]
- Kurucz, R.L. The Kurucz Smithsonian atomic and molecular database. In Proceedings of the Astrophysical Applications of Powerful New Databases, Hague, The Netherlands, 22–23 August 1994; Volume 78, p. 205. [Google Scholar]
- Metcalf, H.J.; Van der Straten, P. Laser Cooling and Trapping; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Eustice, S.; Cassella, K.; Stamper-Kurn, D. Laser cooling of transition-metal atoms. Phys. Rev. A 2020, 102, 053327. [Google Scholar] [CrossRef]
- Głowacki, P.; Stefańska, D.; Ruczkowski, J.; Elantkowska, M. Estimation of radiative parameters for atomic manganese from the point of view of possible clock transitions and laser cooling schemes. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107898. [Google Scholar] [CrossRef]
- De, S.; Dammalapati, U.; Jungmann, K.; Willmann, L. Magneto-optical trapping of barium. Phys. Rev. A 2009, 79, 041402. [Google Scholar] [CrossRef]
- Berglund, A.J.; Lee, S.A.; McClelland, J.J. Sub-Doppler laser cooling and magnetic trapping of erbium. Phys. Rev. A 2007, 76, 053418. [Google Scholar] [CrossRef]
- Sukachev, D.; Sokolov, A.; Chebakov, K.; Akimov, A.; Kolachevsky, N.; Sorokin, V. Sub-doppler laser cooling of thulium atoms in a magneto-optical trap. JETP Lett. 2010, 92, 703–706. [Google Scholar] [CrossRef][Green Version]
- Meiser, D.; Ye, J.; Carlson, D.; Holland, M. Prospects for a millihertz-linewidth laser. Phys. Rev. Lett. 2009, 102, 163601. [Google Scholar] [CrossRef] [PubMed]
- Cline, J.R.; Schäfer, V.M.; Niu, Z.; Young, D.J.; Yoon, T.H.; Thompson, J.K. Continuous collective strong coupling between atoms and a high finesse optical cavity. arXiv 2022, arXiv:2211.00158. [Google Scholar]
- Katori, H. Longitudinal Ramsey spectroscopy of atoms for continuous operation of optical clocks. Appl. Phys. Express 2021, 14, 072006. [Google Scholar] [CrossRef]
- Chen, C.C.; González Escudero, R.; Minář, J.; Pasquiou, B.; Bennetts, S.; Schreck, F. Continuous Bose–Einstein condensation. Nature 2022, 606, 683–687. [Google Scholar] [CrossRef]
- Safronova, M.S.; Kozlov, M.G.; Clark, C.W. Blackbody radiation shifts in optical atomic clocks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 439–447. [Google Scholar] [CrossRef]
- Mitroy, J.A.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 202001. [Google Scholar] [CrossRef]
- Głowacki, P.; Stefańska, D.; Ruczkowski, J.; Elantkowska, M.; Chomski, M.; Furmann, B. Hyperfine structure investigations of Mn I. J. Quant. Spectrosc. Radiat. Transf. 2022, 287, 108245. [Google Scholar] [CrossRef]
- Farolfi, A.; Trypogeorgos, D.; Colzi, G.; Fava, E.; Lamporesi, G.; Ferrari, G. Design and characterization of a compact magnetic shield for ultracold atomic gas experiments. Rev. Sci. Instrum. 2019, 90, 115114. [Google Scholar] [CrossRef]
- Brewer, S.M.; Chen, J.S.; Hankin, A.M.; Clements, E.R.; Chou, C.w.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R. 27Al+ quantum-logic clock with a systematic uncertainty below 10−18. Phys. Rev. Lett. 2019, 123, 033201. [Google Scholar] [CrossRef]
- Muniz, J.A.; Young, D.J.; Cline, J.R.; Thompson, J.K. Cavity-QED measurements of the 87Sr millihertz optical clock transition and determination of its natural linewidth. Phys. Rev. Res. 2021, 3, 023152. [Google Scholar] [CrossRef]
- Porsev, S.G.; Derevianko, A. Hyperfine quenching of the metastable 3P0,2 states in divalent atoms. Phys. Rev. A 2004, 69, 042506. [Google Scholar] [CrossRef]
- Nemitz, N.; Jørgensen, A.A.; Yanagimoto, R.; Bregolin, F.; Katori, H. Modeling light shifts in optical lattice clocks. Phys. Rev. A 2019, 99, 033424. [Google Scholar] [CrossRef]
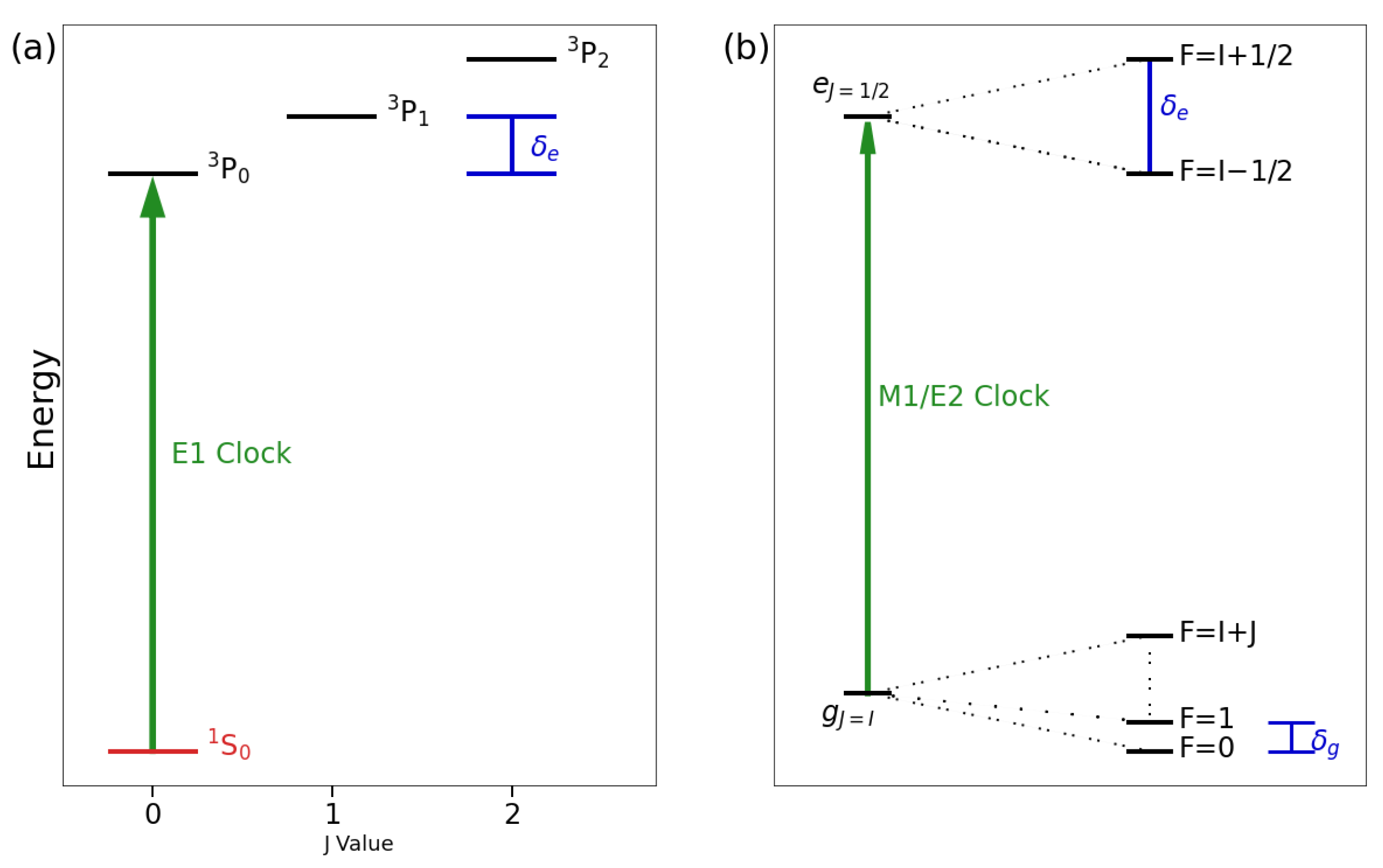


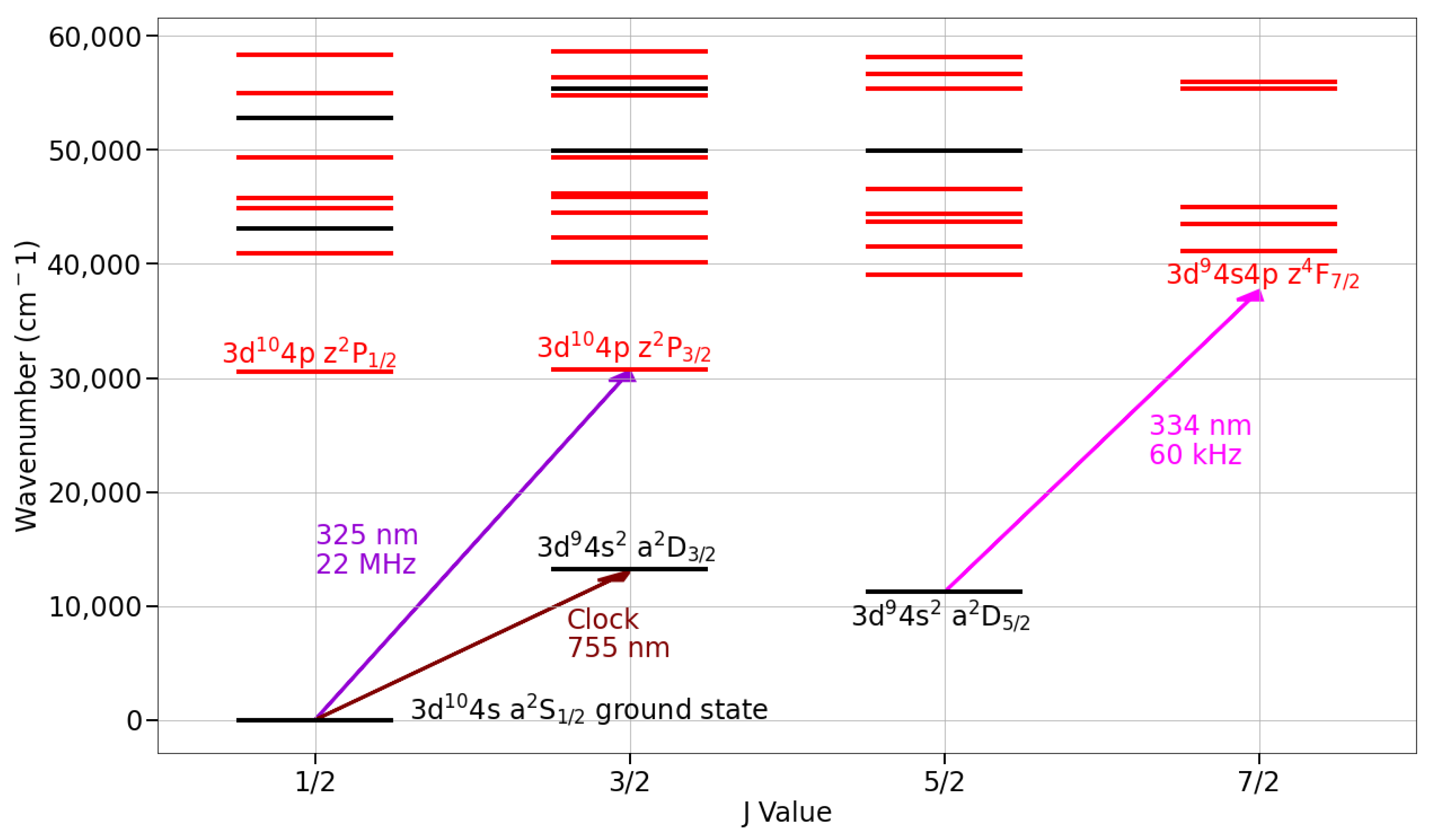
| Atom | Nuclear Spin | Ground State | Excited State | Wavelength (nm) |
|---|---|---|---|---|
| Co * | 7/2 | , | 1509 | |
| La * | 7/2 | , | 2194 | |
| Mn * | 5/2 | , | 573 |
| Atom | Nuclear Spin | Lower State | Excited State | Wavelength (nm) |
|---|---|---|---|---|
| Cu | 3/2 | , | , | 755 |
| Sb | 5/2 | , | , | 1529 |
| As * | 3/2 | , | , | 550 |
| Ir * | 3/2 | , | , | 1187 |
| Re * | 5/2 | , | , | 659 |
| Mn * | 5/2 | , | , | 420 |
| Wavelength (nm) | Lower State | A (s) |
|---|---|---|
| 403.2 | ||
| 1290 | ||
| 1330 | ||
| 1360 |
| Wavelength (nm) | Lower State | A (s) |
|---|---|---|
| 380.7 | ||
| 554.1 | ||
| 554.7 |
| Wavelength (nm) | Lower State | A (s) |
|---|---|---|
| 539.6 | ||
| 6760 | 1.81 |
| Excited State | Wavelength (nm) | Lifetime (s) | BBR Shift (Fractional) |
|---|---|---|---|
| 567 | 1.3 | ||
| 420 | 725 | ||
| 367 | 283 | ||
| 329 | 22 | ||
| 573 | 1.4 | ||
| 425 | 725 |
| Wavelength (nm) | Lower State | A (s) |
|---|---|---|
| 324.8 | ||
| 510.7 | ||
| 570.2 |
| Atom | Lifetime (s) | BBR Shift (Fractional Magnitude) | Hyperpolarizabilty (Fractional at 100 kHz Trap Depth) |
|---|---|---|---|
| Mn * | 1–700 | 1–5 | ≈10 |
| Cu | ≈10 | ||
| Sr | 118 [61] | [17] | [19] |
| Yb | 23 [62] | [17] | [63] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bothwell, T. Prospective Optical Lattice Clocks in Neutral Atoms with Hyperfine Structure. Atoms 2024, 12, 14. https://doi.org/10.3390/atoms12030014
Bothwell T. Prospective Optical Lattice Clocks in Neutral Atoms with Hyperfine Structure. Atoms. 2024; 12(3):14. https://doi.org/10.3390/atoms12030014
Chicago/Turabian StyleBothwell, Tobias. 2024. "Prospective Optical Lattice Clocks in Neutral Atoms with Hyperfine Structure" Atoms 12, no. 3: 14. https://doi.org/10.3390/atoms12030014
APA StyleBothwell, T. (2024). Prospective Optical Lattice Clocks in Neutral Atoms with Hyperfine Structure. Atoms, 12(3), 14. https://doi.org/10.3390/atoms12030014






