Energy Levels and Transition Data of Cs VI

Abid Husain; Haris Kunari; Tauheed Ahmad

doi:10.3390/atoms12030013

,

and

Department of Physics, Aligarh Muslim University, Aligarh 202002, Uttar Pradesh, India

^*

Author to whom correspondence should be addressed.

Atoms2024, 12(3), 13;https://doi.org/10.3390/atoms12030013

Version Notes

Order Reprints

Abstract

Previously reported atomic data (spectral lines, wavelengths, energy levels, and transition probabilities) were collected and systematically analyzed for Cs VI. The present theoretical analysis was supported by extensive calculations made for Cs VI with a pseudo-relativistic Hartree–Fock (HFR) method together with the superposition of configuration interactions implemented in Cowan’s codes. In this work, all previously reported energy levels and their (allowed) transition assignments were confirmed. A critically evaluated set of optimized energy levels with their uncertainties, observed and Ritz wavelengths along with their uncertainties, and theoretical transition probabilities with their estimated uncertainties were presented in the compilation. In addition to this, we determined the radiative transition parameters for several forbidden lines within the ground configuration

5 s^{2} 5 p^{2}

of Cs VI.

Keywords:

atomic spectra; cesium; energy levels; spectral lines; wavelengths; transition probabilities

1. Introduction

In general, accurate atomic data on wavelengths, energy levels, transition probabilities, and oscillator strengths are needed to determine the atmospheric abundances of elements in any astrophysical source or object. By using these atomic data, astronomers have for the first time identified elements heavier than hydrogen and helium in the atmospheres of white dwarfs. These were mostly traces of trans-iron elements (atomic numbers Z ≥ 30) detected in the atmospheres of different hot white dwarfs, such as the hot H-rich (DA-type) white dwarfs G191-B2B, Feige 24, and GD 246 [1], and the hot He-rich (DO-type) white dwarfs HD 149499B, HZ 21, and RE 0503-289 [2,3,4,5]. Recently, Chayer et al. [6] identified the presence of cesium (Z = 55) by means of observing the several absorption lines of Cs IV-VI in the far ultraviolet spectroscopic explorer (FUSE) spectrum of the hot He-rich white dwarf (spectral type DO) HD 149499B. The atomic structure and the radiative transition parameters data for these atomic/ionic species, up to the ionization stage VII, were necessary to obtain accurate stellar atmospheric models for white dwarfs. Chayer et al. [6] calculated oscillator strengths for the bound–bound transitions of Cs IV-VI ions using the multiconfiguration Breit–Pauli and multiconfiguration Dirac–Fock methods, which were implemented in the AUTOSTRUCTURE and GRASP2K atomic structure codes, respectively. Both the AUTOSTRUCTURE and GRASP2K calculations were performed with the same sets of atomic models; however, an extensive radiative transition parameter data set was provided from the AUTOSTRUCTURE calculations only and the GRASP2K results were used for comparison purposes. For the Cs VI spectrum, these are for the

5 s^{2} 5 p^{2} \to {5 s 5 p^{3}

+

5 s^{2} 5 p 5 d

+

5 s^{2} 5 p 6 s

} transitions.

In terms of experimental observations, the first study on the Cs VI spectrum was carried out by Tauheed et al. [7]. They reported the levels of the ground configuration

5 s^{2} 5 p^{2}

and those for the excited

5 s 5 p^{3}

,

5 s^{2} 5 p 5 d

, and

5 s^{2} 5 p 6 s

configurations, with the help of the spectra of cesium photographed in the 325–1400 Å wavelength region on a 3 m normal-incidence vacuum spectrograph at the Antigonish laboratory, Canada. The spectrograph was equipped with a 2400 lines/mm holographic grating giving a reciprocal dispersion of 1.385 Å/mm in the first order of wavelength. The cavities of the aluminum electrodes, filled with pure cesium carbonate and cesium nitrate salts, were used in a triggered spark source, which acted as a light source. A 30 kV trigger unit with a little current to initiate a 6 kV spark discharge in vacuum was used. Additionally, the wavelength information was also supplemented from the previously captured spectra of cesium, which were recorded on a 10.7 m normal incidence vacuum spectrograph at the National Institute of Standards and Technology (NIST), Gaithersburg. Kodak short-wave radiation (SWR) plates were used for all the spectral exposures. The calibrations of the spectrograms were carried out using the known lines of carbon, oxygen, and nitrogen present in the spectra as impurities, and they claimed an accuracy of 0.005 Å for the strong and unperturbed lines in the entire wavelength region mentioned above. The Tauheed et al. [7] findings were included in the latest spectral compilation of Cs I-LV provided by Sansonetti [8], and the same were also available in the NIST’s Atomic Spectra Database (ASD) [9]. In Sansonetti [8]’s compilation, the spectral lines’ observed wavelengths with uncertainties, the line intensities, and their involved energy levels with their energy values, uncertainties, and designations were provided. The transition probabilities were also listed for some spectra but no uncertainty estimates were given. It is not clear how the energy levels were optimized with uncertainties; however, we can only speculate that it was most likely obtained using the widely used “ECALC” code [10]. No Ritz wavelengths and their uncertainties were reported in Sansonetti [8]’s compilation. Thus, a more rigorous and systematic spectral analysis—which has been described and implemented for many spectra in the recent past [11,12,13,14]—would be highly desirable for the spectra described in the above compilation. Recently, we carried out one such for the Cs VII spectrum, in which we reported a critically evaluated atomic data set for Cs VII [15].

In the present work, our motivation is to provide an extensive atomic data set for the Cs VI spectrum, and to carry out critical evaluations for these data by means of their comparison with the existing data in the literature. In addition to these, we aim to compute the radiative transition parameters for the forbidden lines between the levels of the ground configuration

5 s^{2}

5 p^{2}

.

2. HFR Method

To support the present experimental observations, theoretical calculations in this study were made within the framework of a pseudo-relativistic Hartree–Fock (HFR) approach with the superposition of interacting configurations, which were implemented in Cowan’s suite of codes [16]. We use the Windows-based version of the Cowan codes developed by A. Kramida of NIST, Gaithersburg, and distributed through the NIST website [17]. For the present work, we follow the computational procedure laid out in ref. [18]. The particular focus of this work lies on the spectroscopic

5 s^{2} 5 p^{2} \to {5 s 5 p^{3}

+

5 s^{2} 5 p 5 d

+

5 s^{2} 5 p 6 s

} transitions arrays in Cs VI, which were experimentally studied in 1991 [7], with their theoretical transition probabilities recently being reported by Chayer et al. [6]. Further details of the present theoretical calculations are described in Section 3.2.

3. Results and Discussion

The main results of our work on Cs VI are summarized in Table 1 and Table 2. In Table 1, we present the classified lines of Cs VI with their radiative transition parameters and Table 2 describes the optimized energy levels with their LS compositions. The LS composition vectors are computed using the theoretical calculations performed with Cowan’s codes (see Section 3.2). Nevertheless, specific details of the present analysis are discussed in the sections below.

Table 1. Classified lines of Cs VI.

Table 2. Optimized energy levels of Cs VI.

3.1. Optimization of Energy Levels

First, we collected all the experimentally observed wavelength data of Cs VI in the literature [7]. These are for the

5 s^{2} 5 p^{2}

–

5 s 5 p^{3}

,

5 s^{2} 5 p^{2}

–

5 s^{2} 5 p 5 d

, and

5 s^{2} 5 p^{2}

–

5 s^{2} 5 p 6 s

transition arrays. The energy values of the levels involved in transition were computed from their observed spectral line data, i.e., transition wavelengths with uncertainties. In this regard, we used a least-squares level optimization code, ‘LOPT’ [19]. The transition wavelength, its measurement uncertainty, and the unique lower- and upper-level designation for each transition were necessary data inputs to the “LOPT-code”. In the initial stage of the optimization, only the observed wavelengths of Cs VI reported by Tauheed et al. [7] with an uncertainty of 0.005 Å were included as an input to the code. A total of 67 observed lines were included in the LOPT to obtain optimized energy levels (with their uncertainties) of 30 levels involved. For each of the observed wavelengths, their counterpart (precise) Ritz wavelengths with uncertainties were determined from the optimized energy levels. Furthermore, we use the optimized energy levels to derive the accurate Ritz wavelengths for several possibly observable lines of Cs VI (see Table 1) and for the forbidden transitions within the ground configuration (see Section 3.3). We have tabulated all these lines along with their transition probabilities, which are important for detailed plasma models.

3.2. Theoretical Calculations and Transition Probabilities

Two sets of atomic models with varying configuration types, described in Table 3, were considered in this work. In both models the Slater’s parameters were kept at 85% of the HFR-value for the

F^{k}

, 80% for the

G^{k}

, 70% for the

R^{k}

, and the

E_{a v}

and

ζ_{n, l}

parameters were fixed at 100% of their HFR-values. A least-squares parametric fitting (LSF) was performed to minimize the differences between the observed and theoretical energy values in the Cs VI. The standard deviation (SD) of the parametric LSF is given in Table 3 together with the total number of known levels and the number of free parameters involved in the fitting process; the latter is given in curly brackets. All the fitted parameters, together with their values in the LSF of the present HFR-B model, are supplemented by us in Table A1. Using these fitted energy parameters, the transition probabilities (TPs or gA-values) were recalculated for Cs VI. The obtained gA-values from the HFR-B model, along with their cancellation factor (

| C F |

-values), are given in Table 1. The LS percentage compositions of the observed energy levels from the present HFR-B calculations are given in Table 2. We compared our present LS percentage compositions with the previously reported LS percentage compositions in references [7,8] and a good match was found. The LS assignments for most of the levels were found to be good without any ambiguity in our extensive calculation except for two levels of the

5 s^{2} 5 p 5 d

configuration:

{}^{1}D_{2}

at 209,793.6

{cm}^{- 1}

and

{}^{3}D_{2}

at 216,001.6

{cm}^{- 1}

, which were assigned to their second-largest LS percentage component (see Table 2). This observation is in agreement with those made previously by Tauheed et al. [7].

Table 3. Configurations used in HFR models of Cs VI.

Our main purpose for employing two different models—HFR-A and HFR-B with varying configuration types—was to compute and compare the transition probabilities data, and, accordingly, to compare and estimate the uncertainties of the transition probabilities with those reported by Chayer et al. [6] for the transition

5 s^{2} 5 p^{2} \to {5 s 5 p^{3}

+

5 s^{2} 5 p 5 d

+

5 s^{2} 5 p 6 s

} arrays in Cs VI. In their recent work, Chayer et al. [6] used the multiconfiguration Breit–Pauli (MCBP) method to compute the A-values of Cs IV-VI. The MCBP method was implemented in the AUTOSTRUCTURE atomic structure code [20,21]. The configuration sets included in our HFR-A calculations are the same as those used in the MCBP calculations for Cs VI by Chayer et al. [6], whereas those in our HFR-B model are more extensive in terms of the number of interacting configuration sets included in these calculations (see Table 3). Two types of comparison were employed in this work:- (i) a qualitative scheme using gA-values, and (ii) a quantitative scheme, described in refs. [11,12,13,14], based on

d S

-values. The results of these comparisons are illustrated in Figure 1. The agreement between the gA-values obtained from the present HFR-A and HFR-B calculations is shown in Figure 1a, and their comparison with the corresponding S-values is given in Figure 1b. The latter

d S

comparison shows gross disagreements within 26% for the HFR-A and HFR-B models. Indeed the uncertainty for 56 strong lines with S ≥ 0.10 AU (atomic units) was 9% and 47% for the remaining 27 weak lines (see Figure 1b). All of these weak lines are strongly affected by cancellations, i.e., those having

| C F | < 0.10

; as a consequence, their S-values or gA-values are less reliable in comparison to the unaffected ones with

| C F | \geq 0.10

(see details in ref. [16]). There is an alternate method to derive the uncertainty for each S-value by means of generating different sets of LSF calculations with varying parameters within their uncertainty bounds. We use this method to estimate the uncertainty for each of the S-values obtained from the present HFR-B model. A total of six sets of LSF calculations were performed with varying parameters, and the SDs of their S-values were computed and the same were taken to be an estimator for the uncertainties in the S-values. It should be noted that these SDs served as internal uncertainties for the S-values obtained from the present HFR-B model; therefore, they are represented as error bars in our final comparison model (see Figure 1d). Nonetheless, the strong lines with S ≥ 0.10 AU have an average uncertainty of 5% and 18% for the other weak lines. The S-values that suffer strong cancellations have an average uncertainty of about 18% and the unaffected ones were accurate within 3%. Our final comparison model for the gA-values from the HFR-B with those from the MCBP method by Chayer et al. [6] is shown in Figure 1c, and their corresponding S-values comparison is given in Figure 1d. To obtain more reliable estimates, the comparison model illustrated in Figure 1d was selected, and its main results are summarized here. Though the gross disagreements between the two sets of S-values fall within 160%, the strong lines with S ≥ 1 AU are accurate within 24%, 34% for the lines within the mid-range of S ∈ [0.1, 1) AU, about 50% for the weak lines with S ∈ [0.01, 0.1) AU, and the remaining very weak lines are accurate within two to three orders of magnitude. It was found that most of the cancellation affected (25 out of 33) transitions from the HFR-B model with

| C F | < 0.10

fall in the category of accuracy >50%, and they are also weak lines with S < 0.10 AU. All the transitions listed in Table 1 were provided with gA-values and their uncertainty codes and

| C F |

-values. The uncertainty codes are C types with an accuracy ≤25%, D+ with ≤40%, D with ≤50%, and the E types with an accuracy >50%. It should be noted that in the present HFR models of Cs VI, the core–valence electronic interactions are not included. However, the inclusion of such interactions in the HFR model in the form of the core-polarization effect (HFR+CPOL) was found to significantly improve the accuracy of the computed lifetime data (also that of the gA-values) in the Xe V spectrum, which is isoelectronic to Cs VI [22]. In the absence of experimental radiative lifetime data for the Cs VI spectrum, the direct applicability of the HFR+COPL model to this spectrum is limited; however, a semi-empirical method carefully extended from the Xe V may provide reasonable results. Recently, Zainab et al. [23] used such comparison schemes for the Au IV spectrum. Therefore, our present uncertainty estimates for the gA-values of Cs VI quoted above and given in Table 1 should not be taken as absolute.

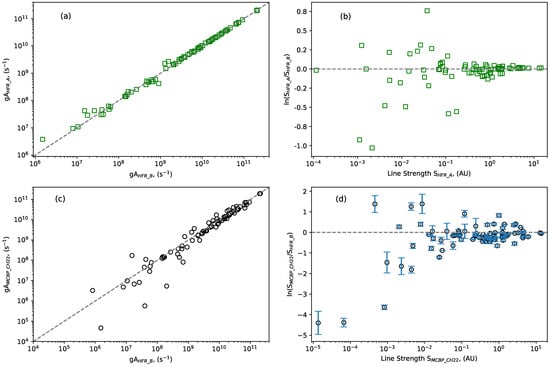
Figure 1. Comparison plots for gA−values and S−values: (a,b) computed with our HFR−A and HFR−B models and (c,d) obtained from HFR−B with those of the MCBP model by Chayer et al. [6]. The error bars in panel (d) represent the internal uncertainties of the S-values obtained from the HFR−B model (see the text).

Curtis [24] previously determined a semi-empirical branching fraction (BF) for lines in the

5 s^{2} 5 p^{2}

–

5 s^{2} 5 p 6 s

transition array in the Sn I isoelectronic sequence (Sn I-Cs VI) by (least-squares) adjusting the energy values of the levels involved, thereby obtaining the optimized values for

F^{2}

and the

ζ_{p p}

parameters for

5 s^{2} 5 p^{2}

and

G^{1}

and

ζ_{p}

for the

5 s^{2} 5 p 6 s

configuration, followed by determination of the mixing angles to compute the relative transition rates (A-values). Recently, Chayer et al. [6] also reported the branching fractions (BFs), which were computed from the MCBP A-values, for the

5 s^{2} 5 p^{2}

–

5 s^{2} 5 p 6 s

transitions. The comparison of these two BF data sets with 13 lines shows a gross disagreement within 300%. The most deviated data points were for the following (mostly) inter-combination transitions: 5

p^{2}

{}^{1}S_{0}

–5p6s

{}^{1, 3}P_{1}^{\circ}

, 5

p^{2}

{}^{3}P_{0}

–5p6s

{}^{1}P_{1}^{\circ}

, 5

p^{2}

{}^{3}P_{1}

–5p6s

{}^{1}P_{1}^{\circ}

, and 5

p^{2}

{}^{1}D_{2}

–5p6s

{}^{3}P_{1}^{\circ}

. This indicates that either the singlet–triplet mixing angles were not computed accurately in the calculations of Curtis [24], or in part some of the MCBP A-values of Chayer et al. [6] are largely uncertain for the

5 s^{2} 5 p^{2}

–

5 s^{2} 5 p 6 s

transitions. To investigate this, we compute the BFs for these transitions from their corresponding gA-values of the present HFR-A and HFR-B models. A good agreement (within 10%) between the BF-values obtained from the HFR-A and HFR-B models was found for the

5 s^{2} 5 p^{2}

–

5 s^{2} 5 p 6 s

transitions. Nevertheless, the BFs from the extensive HFR-B model were selected by us for their consequent comparison with those of Curtis [24] and Chayer et al. [6]. The results of this comparison are shown in Figure 2a. It was found that the general agreement between the BFs of HFR-B and those of Curtis [24] was good except for two inter-combinations, the 5

p^{2}

{}^{1}S_{0}

–5p6s

{}^{3}P_{1}^{\circ}

and 5

p^{2}

{}^{3}P_{0}

–5p6s

{}^{1}P_{1}^{\circ}

transitions, which shows that the computed singlet–triplet mixing angles alone were inadequate to define the A-values for these transitions by Curtis [24]. It should be noted that the intermediate coupling semi-empirical approaches of Curtis [24] are valid in the absence of configuration interaction. However, this assumption is not fully true for complex atomic systems, including Cs VI, in which both intra- and inter-configuration interactions are significant, and particularly for the spin-forbidden inter-combination lines, which are more sensitive to cancellation effects [25]. Figure 2b shows the gross comparison of the BFs from the present HFR-B model with those from the MCBP calculations of Chayer et al. [6] for the transition

5 s^{2} 5 p^{2} \to {5 s 5 p^{3}

+

5 s^{2} 5 p 5 d

+

5 s^{2} 5 p 6 s

} arrays, and their overall agreement is found to be reasonably good.

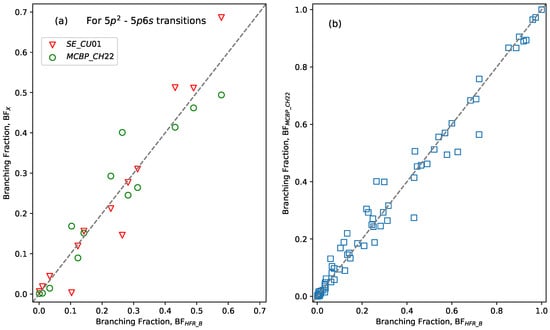
Figure 2. A comparison of (a) theoretical branching fractions BF

_{H F R_B}

obtained from the gA-values of the present HFR−B model with the semi-empirical BF

_{S E_C U 01} -

values (in triangles) reported by Curtis [24] and with the theoretical BF

_{M C B P_C H 22}

(in circles) computed from the MCBP A−values of Chayer et al. [6] for the selected

5 s^{2} 5 p^{2} - 5 s^{2} 5 p 6 s

transitions, and (b) theoretical BF

_{H F R_B}

with the BF

_{M C B P_C H 22}

for the transition

5 s^{2} 5 p^{2} \to {5 s 5 p^{3}

+

5 s^{2} 5 p 5 d

+

5 s^{2} 5 p 6 s

} arrays (see the text).

3.3. Radiative Parameters for Transitions within the Ground Configuration

Biemont et al. [26] reported energy levels and radiative transition probabilities for states within the

5 s^{2} 5 p^{k} (k

= 1–5) configurations of atoms and ions in the indium, tin, antimony, tellurium, and iodine isoelectronic sequences. These transitions are astrophysically important and forbidden types having magnetic-dipole (M1) and/or electric-quadrupole (E2) components. For the Cs VI spectrum, Biemont et al. [26] reported 3 M1 and 4 E2 transitions within the states of the ground configuration

5 s^{2} 5 p^{2}

. We also performed separate HFR calculations [16] with the even parity configurations in our HFR-B model. Our calculations are more extensive than the previous ones performed by Biemont et al. [26] for Cs VI. The obtained line parameters for the 5 M1 and 7 E2 transitions of Cs VI are summarized in Table 4. To estimate the uncertainties of the presently obtained A-values, we performed a Monte Carlo technique suggested by Kramida [27]. This method evaluates the uncertainties of the A-values by randomly varying the Slaters parameters of the known configurations included in the LSF. A total of 20 trials were performed to estimate the uncertainties (%SD) of the A-values of the transitions within the ground configuration and these are also given in Table 4.

Table 4. Radiative rates for forbidden lines within the levels of ground 5s

^{2}

5p

^{2}

configuration in Cs VI.

4. Conclusions

In this work, a thorough critical analysis of the Cs VI spectrum was carried out with the help of extensive HFR calculations performed by us using Cowan’s codes. This compilation provided a set of optimized energy levels (Table 2) of the Cs VI ion with their uncertainties, as well as the observed and Ritz wavelengths with their uncertainties for the levels involved. To the best of our knowledge, the accurate Ritz wavelengths with their uncertainties for this spectrum have been derived for the first time, and the same have been presented in Table 1 along with the gA-values. The uncertainty estimates have been based on gA-values from their comparison with the previous data [6]. In addition, we report the radiative parameters for the forbidden (M1 and E2) lines within the ground configuration 5

s^{2}

5

p^{2}

of Cs VI.

Author Contributions

Conceptualization, H.K.; methodology, H.K.; software, A.H., H.K. and T.A.; validation, A.H. and H.K.; formal analysis, A.H. and H.K.; investigation, A.H. and H.K.; data curation, H.K.; writing—original draft preparation, A.H. and H.K.; writing—review and editing, H.K. and T.A.; visualization, A.H. and H.K.; supervision, H.K. and T.A.; project administration, H.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Supplementary Data

Table A1. Least-squares fitted parameters of Cs VI.

Configuration ^a	Parameter ^a	LSF ^a (cm⁻¹)	Unc ^b (cm⁻¹)	Index ^c	HFR ^a (cm⁻¹)	LSF/HFR ^a (cm⁻¹)
5 $p^{2}$	$E_{a v}$	30,641.00	5		29,620.80	1.034
5 $p^{2}$	$F^{2} (5 p, 5 p)$	49,951.70	58	1	59,884.47	0.834
5 $p^{2}$	$α (5 p)$	−61.30	−6	3	0.00
5 $p^{2}$	$ζ (5 p)$	12,115.30	9	2	11,468.40	1.056
5p6p	$E_{a v}$	308,771.90	fixed		308,771.90	1.000
5p6p	$ζ (6 p)$	12,904.90	10	2	12,215.80	1.056
5p6p	$ζ (p)$	3534.10	fixed		3534.10	1.000
5p6p	$F^{2} (6 p, p)$	19,280.70	fixed		22,683.18	0.850
5p6p	$G^{0} (6 p, p)$	3798.40	fixed		4748.00	0.800
5p6p	$G^{2} (6 p, p)$	5116.30	fixed		6395.38	0.800
5p7p	$E_{a v}$	415,145.50	fixed		415,145.50	1.000
5p7p	$ζ (7 p)$	12,974.90	10	2	12,282.10	1.056
5p7p	$ζ (p)$	1704.40	fixed		1704.40	1.000
5p7p	$F^{2} (7 p, p)$	8550.90	fixed		10,059.88	0.850
5p7p	$G^{0} (7 p, p)$	1317.70	fixed		1647.13	0.800
5p7p	$G^{2} (7 p, p)$	1957.20	fixed		2446.50	0.800
5p8p	$E_{a v}$	469,375.40	fixed		469,375.40	1.000
5p8p	$ζ (8 p)$	13,005.60	10	2	12,311.10	1.056
5p8p	$ζ (p)$	958.40	fixed		958.40	1.000
5p8p	$F^{2} (8 p, p)$	4519.80	fixed		5317.41	0.850
5p8p	$G^{0} (8 p, p)$	641.30	fixed		801.63	0.800
5p8p	$G^{2} (8 p, p)$	991.90	fixed		1239.88	0.800
5p9p	$E_{a v}$	501,140.00	fixed		501,140.00	1.000
5p9p	$ζ (9 p)$	13,020.60	10	2	12,325.30	1.056
5p9p	$ζ (p)$	594.00	fixed		594.00	1.000
5p9p	$F^{2} (9 p, p)$	2686.60	fixed		3160.71	0.850
5p9p	$G^{0} (9 p, p)$	367.50	fixed		459.38	0.800
5p9p	$G^{2} (9 p, p)$	580.70	fixed		725.88	0.800
5p10p	$E_{a v}$	521,411.00	fixed		521,411.00	1.000
5p10p	$ζ (10 p)$	13,028.80	10	2	12,333.10	1.056
5p10p	$ζ (p)$	393.70	fixed		393.70	1.000
5p10p	$F^{2} (10 p, p)$	1730.20	fixed		2035.53	0.850
5p10p	$G^{0} (10 p, p)$	232.10	fixed		290.13	0.800
5p10p	$G^{2} (10 p, p)$	371.60	fixed		464.50	0.800
5p4f	$E_{a v}$	201,858.50	fixed		201,858.50	1.000
5p4f	$ζ (4 f)$	312.40	fixed		312.40	1.000
5p4f	$ζ (5 p)$	11,624.80	9	2	11,004.10	1.056
5p4f	$F^{2} (4 f, 5 p)$	43,435.80	fixed		51,100.94	0.850
5p4f	$G^{2} (4 f, 5 p)$	27,627.30	fixed		34,534.13	0.800
5p4f	$G^{4} (4 f, 5 p)$	20,453.90	fixed		25,567.38	0.800
5p5f	$E_{a v}$	368,464.10	fixed		368,464.10	1.000
5p5f	$ζ (5 p)$	12,751.60	10	2	12,070.70	1.056
5p5f	$ζ (5 f)$	81.20	fixed		81.20	1.000
5p5f	$F^{2} (5 p, 5 f)$	18165.90	fixed		21371.65	0.850
5p5f	$G^{2} (5 p, 5 f)$	4270.90	fixed		5338.63	0.800
5p5f	$G^{4} (5 p, 5 f)$	3606.30	fixed		4507.88	0.800
5p6f	$E_{a v}$	443,747.40	fixed		443,747.40	1.000
5p6f	$ζ (5 p)$	12,907.80	10	2	12,218.60	1.056
5p6f	$ζ (6 f)$	40.10	fixed		40.10	1.000
5p6f	$F^{2} (5 p, 6 f)$	8507.80	fixed		10,009.18	0.850
5p6f	$G^{2} (5 p, 6 f)$	2567.10	fixed		3208.88	0.800
5p6f	$G^{4} (5 p, 6 f)$	2066.50	fixed		2583.13	0.800
5p7f	$E_{a v}$	485,432.70	fixed		485,432.70	1.000
5p7f	$ζ (5 p)$	12,968.80	10	2	12,276.30	1.056
5p7f	$ζ (7 f)$	23.10	fixed		23.10	1.000
5p7f	$F^{2} (5 p, 7 f)$	4703.60	fixed		5533.65	0.850
5p7f	$G^{2} (5 p, 7 f)$	1573.00	fixed		1966.25	0.800
5p7f	$G^{4} (5 p, 7 f)$	1250.40	fixed		1563.00	0.800
5p8f	$E_{a v}$	511,097.80	fixed		511,097.80	1.000
5p8f	$ζ (5 p)$	12,998.00	10	2	12,303.90	1.056
5p8f	$ζ (8 f)$	14.60	fixed		14.60	1.000
5p8f	$F^{2} (5 p, 8 f)$	2887.50	fixed		3397.06	0.850
5p8f	$G^{2} (5 p, 8 f)$	1018.10	fixed		1272.63	0.800
5p8f	$G^{4} (5 p, 8 f)$	805.50	fixed		1006.88	0.800
5p9f	$E_{a v}$	528,022.70	fixed		528,022.70	1.000
5p9f	$ζ (5 p)$	13,013.70	10	2	12,318.80	1.056
5p9f	$ζ (9 f)$	9.80	fixed		9.80	1.000
5p9f	$F^{2} (5 p, 9 f)$	1905.40	fixed		2241.65	0.850
5p9f	$G^{2} (5 p, 9 f)$	693.00	fixed		866.25	0.800
5p9f	$G^{4} (5 p, 9 f)$	547.30	fixed		684.13	0.800
5p10f	$E_{a v}$	539,770.60	fixed		539,770.60	1.000
5p10f	$ζ (5 p)$	13,023.10	10	2	12,327.70	1.056
5p10f	$ζ (10 f)$	6.90	fixed		6.90	1.000
5p10f	$F^{2} (5 p, 10 f)$	1325.70	fixed		1559.65	0.850
5p10f	$G^{2} (5 p, 10 f)$	492.00	fixed		615.00	0.800
5p10f	$G^{4} (5 p, 10 f)$	388.10	fixed		485.13	0.800
4f $^{2}$	$E_{a v}$	384,129.20	fixed		384,129.20	1.000
4f $^{2}$	$F^{2} (4 f, 4 f)$	56,513.40	fixed		66,486.35	0.850
4f $^{2}$	$F^{4} (4 f, 4 f)$	35,065.70	fixed		41,253.77	0.850
4f $^{2}$	$F^{6} (4 f, 4 f)$	25,114.20	fixed		29,546.12	0.850
4f $^{2}$	$α (4 f)$	0.00	fixed		0.00
4f $^{2}$	$β (4 f)$	0.00	fixed		0.00
4f $^{2}$	$G_{a}^{} (4 f)$	0.00	fixed		0.00
4f $^{2}$	$ζ (4 f)$	279.60	fixed		279.60	1.000
5d $^{2}$	$E_{a v}$	400,448.80	fixed		400,448.80	1.000
5d $^{2}$	$F^{2} (5 d, 5 d)$	40,350.20	fixed		47,470.82	0.850
5d $^{2}$	$F^{4} (5 d, 5 d)$	27,593.20	fixed		32,462.59	0.850
5d $^{2}$	$α (5 d)$	0.00	fixed		0.00
5d $^{2}$	$β (5 d)$	0.00	fixed		0.00
5d $^{2}$	$T (5 d)$	0.00	fixed		0.00
5d $^{2}$	$ζ (5 d)$	868.90	fixed		868.90	1.000
6s $^{2}$	$E_{a v}$	514,101.60	fixed		514,101.60	1.000
6p $^{2}$	$E_{a v}$	609,135.60	fixed		609,135.60	1.000
6p $^{2}$	$F^{2} (6 p, 6 p)$	26,654.40	fixed		31,358.12	0.850
6p $^{2}$	$α (6 p)$	0.00	fixed		0.00
6p $^{2}$	$ζ (6 p)$	3888.60	fixed		3888.60	1.000
5p $^{4}$	$E_{a v}$	310,124.60	fixed		310,124.60	1.000
5p $^{4}$	$F^{2} (5 p, 5 p)$	49,940.40	58	1	59,870.94	0.834
5p $^{4}$	$α (5 p)$	−61.30	−6	3	0.00
5p $^{4}$	$ζ (5 p)$	11,969.60	9	2	11,330.50	1.056
5s5p $^{2}$ 6s	$E_{a v}$	387,785.80	fixed		387,785.80	1.000
5s5p $^{2}$ 6s	$F^{2} (5 p, 5 p)$	50,763.20	59	1	60,857.29	0.834
5s5p $^{2}$ 6s	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 6s	$ζ (5 p)$	12,656.30	10	2	11,980.50	1.056
5s5p $^{2}$ 6s	$G^{1} (6 s, 5 p)$	63,423.50	fixed		79,279.38	0.800
5s5p $^{2}$ 6s	$G^{0} (6 s, s)$	3914.20	fixed		4892.75	0.800
5s5p $^{2}$ 6s	$G^{1} (5 p, s)$	5903.20	fixed		7379.00	0.800
5s5p $^{2}$ 7s	$E_{a v}$	518,610.00	fixed		518,610.00	1.000
5s5p $^{2}$ 7s	$F^{2} (5 p, 5 p)$	51,163.00	59	1	61,336.59	0.834
5s5p $^{2}$ 7s	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 7s	$ζ (5 p)$	12,842.60	10	2	12,156.80	1.056
5s5p $^{2}$ 7s	$G^{1} (7 s, 5 p)$	63,846.60	fixed		79,808.25	0.800
5s5p $^{2}$ 7s	$G^{0} (7 s, s)$	1315.10	fixed		1643.88	0.800
5s5p $^{2}$ 7s	$G^{1} (5 p, s)$	1903.80	fixed		2379.75	0.800
5s5p $^{2}$ 8s	$E_{a v}$	582,679.90	fixed		582,679.90	1.000
5s5p $^{2}$ 8s	$F^{2} (5 p, 5 p)$	51,256.90	59	1	61,449.18	0.834
5s5p $^{2}$ 8s	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 8s	$ζ (5 p)$	12,897.40	10	2	12208.70	1.056
5s5p $^{2}$ 8s	$G^{1} (8 s, 5 p)$	63,957.70	fixed		79,947.13	0.800
5s5p $^{2}$ 8s	$G^{0} (8 s, s)$	625.50	fixed		781.88	0.800
5s5p $^{2}$ 8s	$G^{1} (5 p, s)$	902.40	fixed		1128.00	0.800
5s5p $^{2}$ 5d	$E_{a v}$	332,268.40	fixed		332,268.40	1.000
5s5p $^{2}$ 5d	$F^{2} (5 p, 5 p)$	50309.10	58	1	60312.94	0.834
5s5p $^{2}$ 5d	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 5d	$ζ (5 p)$	12,285.10	9	2	11,629.10	1.056
5s5p $^{2}$ 5d	$ζ (5 d)$	868.20	fixed		868.20	1.000
5s5p $^{2}$ 5d	$F^{2} (5 p, 5 d)$	41,905.10	fixed		49,300.12	0.850
5s5p $^{2}$ 5d	$G^{1} (5 s, 5 p)$	62,904.40	fixed		78,630.50	0.800
5s5p $^{2}$ 5d	$G^{2} (5 s, 5 d)$	30,895.30	fixed		38,619.13	0.800
5s5p $^{2}$ 5d	$G^{1} (5 p, 5 d)$	46,326.30	fixed		57,907.88	0.800
5s5p $^{2}$ 5d	$G^{3} (5 p, 5 d)$	29,445.10	fixed		36,806.38	0.800
5s5p $^{2}$ 6d	$E_{a v}$	499,136.40	fixed		499,136.40	1.000
5s5p $^{2}$ 6d	$F^{2} (5 p, 5 p)$	51,137.40	59	1	61,305.88	0.834
5s5p $^{2}$ 6d	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 6d	$ζ (5 p)$	12,803.80	10	2	12,120.10	1.056
5s5p $^{2}$ 6d	$ζ (6 d)$	334.70	fixed		334.70	1.000
5s5p $^{2}$ 6d	$F^{2} (5 p, 6 d)$	14,552.20	fixed		17,120.24	0.850
5s5p $^{2}$ 6d	$G^{1} (5 s, 5 p)$	63,826.90	fixed		79,783.63	0.800
5s5p $^{2}$ 6d	$G^{2} (5 s, 6 d)$	6662.00	fixed		8327.50	0.800
5s5p $^{2}$ 6d	$G^{1} (5 p, 6 d)$	7361.80	fixed		9202.25	0.800
5s5p $^{2}$ 6d	$G^{3} (5 p, 6 d)$	5520.40	fixed		6900.50	0.800
5s5p $^{2}$ 7d	$E_{a v}$	573,135.20	fixed		573,135.20	1.000
5s5p $^{2}$ 7d	$F^{2} (5 p, 5 p)$	51,241.20	59	1	61,430.35	0.834
5s5p $^{2}$ 7d	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 7d	$ζ (5 p)$	12,882.70	10	2	12,194.80	1.056
5s5p $^{2}$ 7d	$ζ (7 d)$	173.50	fixed		173.50	1.000
5s5p $^{2}$ 7d	$F^{2} (5 p, 7 d)$	6844.00	fixed		8051.77	0.850
5s5p $^{2}$ 7d	$G^{1} (5 s, 5 p)$	63,948.90	fixed		79,936.13	0.800
5s5p $^{2}$ 7d	$G^{2} (5 s, 7 d)$	2832.30	fixed		3540.38	0.800
5s5p $^{2}$ 7d	$G^{1} (5 p, 7 d)$	2895.00	fixed		3618.75	0.800
5s5p $^{2}$ 7d	$G^{3} (5 p, 7 d)$	2295.60	fixed		2869.50	0.800
5s5p $^{2}$ 8d	$E_{a v}$	613,658.70	fixed		613658.70	1.000
5s5p $^{2}$ 8d	$F^{2} (5 p, 5 p)$	51,285.40	59	1	61,483.41	0.834
5s5p $^{2}$ 8d	$α (5 p)$	−61.30	−6	3	0.00
5s5p $^{2}$ 8d	$ζ (5 p)$	12,913.40	10	2	12,223.90	1.056
5s5p $^{2}$ 8d	$ζ (8 d)$	102.80	fixed		102.80	1.000
5s5p $^{2}$ 8d	$F^{2} (5 p, 8 d)$	3812.10	fixed		4484.82	0.850
5s5p $^{2}$ 8d	$G^{1} (5 s, 5 p)$	63,999.00	fixed		79,998.75	0.800
5s5p $^{2}$ 8d	$G^{2} (5 s, 8 d)$	1521.70	fixed		1902.13	0.800
5s5p $^{2}$ 8d	$G^{1} (5 p, 8 d)$	1501.30	fixed		1876.63	0.800
5s5p $^{2}$ 8d	$G^{3} (5 p, 8 d)$	1224.10	fixed		1530.13	0.800
5p $^{3}$ 6p	$E_{a v}$	580,567.40	fixed		580,567.40	1.000
5p $^{3}$ 6p	$F^{2} (5 p, 5 p)$	51,057.80	59	1	61,210.47	0.834
5p $^{3}$ 6p	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 6p	$ζ (5 p)$	12,730.70	10	2	12,050.90	1.056
5p $^{3}$ 6p	$ζ (6 p)$	3556.70	fixed		3556.70	1.000
5p $^{3}$ 6p	$F^{2} (5 p, 6 p)$	19,512.30	fixed		22,955.65	0.850
5p $^{3}$ 6p	$G^{0} (5 p, 6 p)$	3622.60	fixed		4528.25	0.800
5p $^{3}$ 6p	$G^{2} (5 p, 6 p)$	5124.70	fixed		6405.88	0.800
5p $^{3}$ 7p	$E_{a v}$	688,292.90	fixed		688,292.90	1.000
5p $^{3}$ 7p	$F^{2} (5 p, 5 p)$	51,209.50	59	1	61,392.35	0.834
5p $^{3}$ 7p	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 7p	$ζ (5 p)$	12,804.30	10	2	12,120.60	1.056
5p $^{3}$ 7p	$ζ (7 p)$	1718.80	fixed		1718.80	1.000
5p $^{3}$ 7p	$F^{2} (5 p, 7 p)$	8636.80	fixed		10,160.94	0.850
5p $^{3}$ 7p	$G^{0} (5 p, 7 p)$	1269.40	fixed		1586.75	0.800
5p $^{3}$ 7p	$G^{2} (5 p, 7 p)$	1957.70	fixed		2447.13	0.800
5p $^{3}$ 8p	$E_{a v}$	743,009.80	fixed		743,009.80	1.000
5p $^{3}$ 8p	$F^{2} (5 p, 5 p)$	51268.70	59	1	61463.29	0.834
5p $^{3}$ 8p	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 8p	$ζ (5 p)$	12,834.40	10	2	12,149.10	1.056
5p $^{3}$ 8p	$ζ (8 p)$	964.00	fixed		964.00	1.000
5p $^{3}$ 8p	$F^{2} (5 p, 8 p)$	4551.00	fixed		5354.12	0.850
5p $^{3}$ 8p	$G^{0} (5 p, 8 p)$	618.20	fixed		772.75	0.800
5p $^{3}$ 8p	$G^{2} (5 p, 8 p)$	989.10	fixed		1236.38	0.800
5p $^{3}$ 9p	$E_{a v}$	774,986.90	fixed		774,986.90	1.000
5p $^{3}$ 9p	$F^{2} (5 p, 5 p)$	51296.20	59	1	61496.35	0.834
5p $^{3}$ 9p	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 9p	$ζ (5 p)$	12,849.00	10	2	12,162.90	1.056
5p $^{3}$ 9p	$ζ (9 p)$	596.90	fixed		596.90	1.000
5p $^{3}$ 9p	$F^{2} (5 p, 9 p)$	2700.90	fixed		3177.53	0.850
5p $^{3}$ 9p	$G^{0} (5 p, 9 p)$	354.40	fixed		443.00	0.800
5p $^{3}$ 9p	$G^{2} (5 p, 9 p)$	578.30	fixed		722.88	0.800
5p $^{3}$ 10p	$E_{a v}$	795,374.50	fixed		795,374.50	1.000
5p $^{3}$ 10p	$F^{2} (5 p, 5 p)$	51,311.20	60	1	61,514.24	0.834
5p $^{3}$ 10p	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 10p	$ζ (5 p)$	12,856.80	10	2	12,170.30	1.056
5p $^{3}$ 10p	$ζ (10 p)$	395.40	fixed		395.40	1.000
5p $^{3}$ 10p	$F^{2} (5 p, 10 p)$	1737.80	fixed		2044.47	0.850
5p $^{3}$ 10p	$G^{0} (5 p, 10 p)$	224.00	fixed		280.00	0.800
5p $^{3}$ 10p	$G^{2} (5 p, 10 p)$	369.80	fixed		462.25	0.800
5p $^{3}$ 4f	$E_{a v}$	459,512.10	fixed		459,512.10	1.000
5p $^{3}$ 4f	$F^{2} (5 p, 5 p)$	49,232.00	57	1	59,021.65	0.834
5p $^{3}$ 4f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 4f	$ζ (4 f)$	329.60	fixed		329.60	1.000
5p $^{3}$ 4f	$ζ (5 p)$	11,449.20	9	2	10,837.80	1.056
5p $^{3}$ 4f	$F^{2} (4 f, 5 p)$	43,149.10	fixed		50,763.65	0.850
5p $^{3}$ 4f	$G^{2} (4 f, 5 p)$	26,815.60	fixed		33,519.50	0.800
5p $^{3}$ 4f	$G^{4} (4 f, 5 p)$	19,940.00	fixed		24,925.00	0.800
5p $^{3}$ 5f	$E_{a v}$	639,346.20	fixed		639,346.20	1.000
5p $^{3}$ 5f	$F^{2} (5 p, 5 p)$	50,879.50	59	1	60,996.71	0.834
5p $^{3}$ 5f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 5f	$ζ (5 p)$	12,589.00	10	2	11,916.80	1.056
5p $^{3}$ 5f	$ζ (5 f)$	81.20	fixed		81.20	1.000
5p $^{3}$ 5f	$F^{2} (5 p, 5 f)$	18,794.20	fixed		22,110.82	0.850
5p $^{3}$ 5f	$G^{2} (5 p, 5 f)$	4918.70	fixed		6148.38	0.800
5p $^{3}$ 5f	$G^{4} (5 p, 5 f)$	4021.50	fixed		5026.88	0.800
5p $^{3}$ 6f	$E_{a v}$	716,416.10	fixed		716,416.10	1.000
5p $^{3}$ 6f	$F^{2} (5 p, 5 p)$	51,137.80	59	1	61,306.35	0.834
5p $^{3}$ 6f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 6f	$ζ (5 p)$	12,740.90	10	2	12,060.60	1.056
5p $^{3}$ 6f	$ζ (6 f)$	40.20	fixed		40.20	1.000
5p $^{3}$ 6f	$F^{2} (5 p, 6 f)$	8708.40	fixed		10,245.18	0.850
5p $^{3}$ 6f	$G^{2} (5 p, 6 f)$	2825.00	fixed		3531.25	0.800
5p $^{3}$ 6f	$G^{4} (5 p, 6 f)$	2236.10	fixed		2795.13	0.800
5p $^{3}$ 7f	$E_{a v}$	758,772.60	fixed		758,772.60	1.000
5p $^{3}$ 7f	$F^{2} (5 p, 5 p)$	51,230.60	59	1	61,417.65	0.834
5p $^{3}$ 7f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 7f	$ζ (5 p)$	12,799.60	10	2	12,116.10	1.056
5p $^{3}$ 7f	$ζ (7 f)$	23.10	fixed		23.10	1.000
5p $^{3}$ 7f	$F^{2} (5 p, 7 f)$	4778.40	fixed		5621.65	0.850
5p $^{3}$ 7f	$G^{2} (5 p, 7 f)$	1688.10	fixed		2110.13	0.800
5p $^{3}$ 7f	$G^{4} (5 p, 7 f)$	1326.60	fixed		1658.25	0.800
5p $^{3}$ 8f	$E_{a v}$	784,756.20	fixed		784,756.20	1.000
5p $^{3}$ 8f	$F^{2} (5 p, 5 p)$	51,272.80	59	1	61,468.24	0.834
5p $^{3}$ 8f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 8f	$ζ (5 p)$	12,827.30	10	2	12,142.40	1.056
5p $^{3}$ 8f	$ζ (8 f)$	14.60	fixed		14.60	1.000
5p $^{3}$ 8f	$F^{2} (5 p, 8 f)$	2922.30	fixed		3438.00	0.850
5p $^{3}$ 8f	$G^{2} (5 p, 8 f)$	1078.20	fixed		1347.75	0.800
5p $^{3}$ 8f	$G^{4} (5 p, 8 f)$	845.60	fixed		1057.00	0.800
5p $^{3}$ 9f	$E_{a v}$	801,855.60	fixed		801,855.60	1.000
5p $^{3}$ 9f	$F^{2} (5 p, 5 p)$	51,295.50	59	1	61,495.41	0.834
5p $^{3}$ 9f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 9f	$ζ (5 p)$	12,842.50	10	2	12,156.70	1.056
5p $^{3}$ 9f	$ζ (9 f)$	9.80	fixed		9.80	1.000
5p $^{3}$ 9f	$F^{2} (5 p, 9 f)$	1923.60	fixed		2263.06	0.850
5p $^{3}$ 9f	$G^{2} (5 p, 9 f)$	728.10	fixed		910.13	0.800
5p $^{3}$ 9f	$G^{4} (5 p, 9 f)$	570.70	fixed		713.38	0.800
5p $^{3}$ 10f	$E_{a v}$	813,709.00	fixed		813,709.00	1.000
5p $^{3}$ 10f	$F^{2} (5 p, 5 p)$	51,308.90	59	1	61,511.53	0.834
5p $^{3}$ 10f	$α (5 p)$	−61.30	−6	3	0.00
5p $^{3}$ 10f	$ζ (5 p)$	12,851.40	10	2	12,165.20	1.056
5p $^{3}$ 10f	$ζ (10 f)$	6.90	fixed		6.90	1.000
5p $^{3}$ 10f	$F^{2} (5 p, 10 f)$	1336.10	fixed		1571.88	0.850
5p $^{3}$ 10f	$G^{2} (5 p, 10 f)$	514.20	fixed		642.75	0.800
5p $^{3}$ 10f	$G^{4} (5 p, 10 f)$	403.00	fixed		503.75	0.800
5d6s	$E_{a v}$	452690.10	fixed		452690.10	1.000
5d6s	$ζ (5 d)$	910.70	fixed		910.70	1.000
5d6s	$G^{2} (5 d, 6 s)$	13,699.00	fixed		17,123.75	0.800
5p $^{2}$ 5d $^{2}$	$E_{a v}$	650,290.10	fixed		650,290.10	1.000
5p $^{2}$ 5d $^{2}$	$F^{2} (5 p, 5 p)$	50,647.10	59	1	60,718.12	0.834
5p $^{2}$ 5d $^{2}$	$α (5 p)$	−61.30	−6	3	0.00
5p $^{2}$ 5d $^{2}$	$F^{2} (5 d, 5 d)$	40,929.00	fixed		48,151.77	0.850
5p $^{2}$ 5d $^{2}$	$F^{4} (5 d, 5 d)$	28,007.90	fixed		32,950.47	0.850
5p $^{2}$ 5d $^{2}$	$α (5 d)$	0.00	fixed		0.00
5p $^{2}$ 5d $^{2}$	$β (5 d)$	0.00	fixed		0.00
5p $^{2}$ 5d $^{2}$	$T (5 d)$	0.00	fixed		0.00
5p $^{2}$ 5d $^{2}$	$ζ (5 p)$	12,437.10	9	2	11,773.00	1.056
5p $^{2}$ 5d $^{2}$	$ζ (5 d)$	910.70	fixed		910.70	1.000
5p $^{2}$ 5d $^{2}$	$F^{2} (5 p, 5 d)$	42,659.30	fixed		50,187.41	0.850
5p $^{2}$ 5d $^{2}$	$G^{1} (5 p, 5 d)$	47,420.90	fixed		59,276.13	0.800
5p $^{2}$ 5d $^{2}$	$G^{3} (5 p, 5 d)$	30,157.50	fixed		37,696.88	0.800
5p $^{2}$ 5d6s	$E_{a v}$	710,849.60	fixed		710,849.60	1.000
5p $^{2}$ 5d6s	$F^{2} (5 p, 5 p)$	51,098.80	59	1	61,259.65	0.834
5p $^{2}$ 5d6s	$α (5 p)$	−61.30	−6	3	0.00
5p $^{2}$ 5d6s	$ζ (5 p)$	12,808.00	10	2	12,124.10	1.056
5p $^{2}$ 5d6s	$ζ (5 d)$	954.30	fixed		954.30	1.000
5p $^{2}$ 5d6s	$F^{2} (5 p, 5 d)$	43,303.30	fixed		50,945.06	0.850
5p $^{2}$ 5d6s	$G^{1} (5 p, 5 d)$	48,198.70	fixed		60,248.38	0.800
5p $^{2}$ 5d6s	$G^{3} (5 p, 5 d)$	30,680.40	fixed		38,350.50	0.800
5p $^{2}$ 5d6s	$G^{1} (5 p, 6 s)$	6003.00	fixed		7503.75	0.800
5p $^{2}$ 5d6s	$G^{2} (5 d, 6 s)$	12,672.40	fixed		15,840.50	0.800
5p $^{2}$ 6s $^{2}$	$E_{a v}$	780,534.60	fixed		780,534.60	1.000
5p $^{2}$ 6s $^{2}$	$F^{2} (5 p, 5 p)$	51,550.30	60	1	61,800.94	0.834
5p $^{2}$ 6s $^{2}$	$α (5 p)$	−61.30	−6	3	0.00
5p $^{2}$ 6s $^{2}$	$ζ (5 p)$	13,194.80	10	2	12,490.20	1.056
5p $^{2}$ 4f $^{2}$	$E_{a v}$	620,435.50	fixed		620,435.50	1.000
5p $^{2}$ 4f $^{2}$	$F^{2} (4 f, 4 f)$	58,660.50	fixed		69,012.35	0.850
5p $^{2}$ 4f $^{2}$	$F^{4} (4 f, 4 f)$	36,480.00	fixed		42,917.65	0.850
5p $^{2}$ 4f $^{2}$	$F^{6} (4 f, 4 f)$	26,150.00	fixed		30,764.71	0.850
5p $^{2}$ 4f $^{2}$	$α (4 f)$	0.00	fixed		0.00
5p $^{2}$ 4f $^{2}$	$β (4 f)$	0.00	fixed		0.00
5p $^{2}$ 4f $^{2}$	$G_{a}^{} (4 f)$	0.00	fixed		0.00
5p $^{2}$ 4f $^{2}$	$F^{2} (5 p, 5 p)$	48,639.00	56	1	58,310.71	0.834
5p $^{2}$ 4f $^{2}$	$α (5 p)$	−61.30	−6	3	0.00
5p $^{2}$ 4f $^{2}$	$ζ (4 f)$	295.70	fixed		295.70	1.000
5p $^{2}$ 4f $^{2}$	$ζ (5 p)$	11,028.30	8	2	10,439.40	1.056
5p $^{2}$ 4f $^{2}$	$F^{2} (4 f, 5 p)$	42,997.20	fixed		50,584.94	0.850
5p $^{2}$ 4f $^{2}$	$G^{2} (4 f, 5 p)$	27,988.40	fixed		34,985.50	0.800
5p $^{2}$ 4f $^{2}$	$G^{4} (4 f, 5 p)$	20,576.60	fixed		25,720.75	0.800
5s5p5d4f	$E_{a v}$	489,764.90	fixed		489,764.90	1.000
5s5p5d4f	$ζ (4 f)$	333.00	fixed		333.00	1.000
5s5p5d4f	$ζ (5 p)$	11,140.20	fixed		11,140.20	1.000
5s5p5d4f	$ζ (5 d)$	812.20	fixed		812.20	1.000
5s5p5d4f	$F^{2} (4 f, 5 p)$	43,531.80	fixed		51,213.88	0.850
5s5p5d4f	$F^{2} (4 f, 5 d)$	30,099.00	fixed		35,410.59	0.850
5s5p5d4f	$F^{4} (4 f, 5 d)$	16,759.80	fixed		19,717.41	0.850
5s5p5d4f	$F^{2} (5 p, 5 d)$	41,003.40	fixed		48,239.29	0.850
5s5p5d4f	$G^{3} (4 f, 5 s)$	28,072.80	fixed		35,091.00	0.800
5s5p5d4f	$G^{2} (4 f, 5 p)$	26,885.40	fixed		33,606.75	0.800
5s5p5d4f	$G^{4} (4 f, 5 p)$	20,054.60	fixed		25,068.25	0.800
5s5p5d4f	$G^{1} (4 f, 5 d)$	17,573.60	fixed		21,967.00	0.800
5s5p5d4f	$G^{3} (4 f, 5 d)$	13,729.40	fixed		17,161.75	0.800
5s5p5d4f	$G^{5} (4 f, 5 d)$	10,405.20	fixed		13,006.50	0.800
5s5p5d4f	$G^{1} (5 s, 5 p)$	62,000.30	fixed		77,500.38	0.800
5s5p5d4f	$G^{2} (5 s, 5 d)$	29,826.00	fixed		37,282.50	0.800
5s5p5d4f	$G^{1} (5 p, 5 d)$	45,114.90	fixed		56,393.63	0.800
5s5p5d4f	$G^{3} (5 p, 5 d)$	28,683.20	fixed		35,854.00	0.800
5p6s	$E_{a v}$	261,854.90	82		262,502.60	0.998
5p6s	$ζ (5 p)$	12,815.20	68	1	12,059.90	1.063
5p6s	$G^{1} (5 p, 6 s)$	5512.50	400	2	7319.63	0.753
5p7s	$E_{a v}$	393,236.40	fixed		393,236.40	1.000
5p7s	$ζ (5 p)$	13,006.60	69	1	12,240.00	1.063
5p7s	$G^{1} (5 p, 7 s)$	1785.60	129	2	2371.00	0.753
5p8s	$E_{a v}$	457,209.10	fixed		457,209.10	1.000
5p8s	$ζ (5 p)$	13,062.80	70	1	12,292.90	1.063
5p8s	$G^{1} (5 p, 8 s)$	849.00	62	2	1127.25	0.753
5p9s	$E_{a v}$	493,662.60	fixed		493,662.60	1.000
5p9s	$ζ (5 p)$	13,086.80	70	1	12,315.50	1.063
5p9s	$G^{1} (5 p, 9 s)$	479.90	35	2	637.25	0.753
5p10s	$E_{a v}$	516,488.70	fixed		516,488.70	1.000
5p10s	$ζ (5 p)$	13,099.20	70	1	12,327.10	1.063
5p10s	$G^{1} (5 p, 10 s)$	300.10	22	2	398.50	0.753
5p5d	$E_{a v}$	208,717.90	95		210,942.20	0.989
5p5d	$ζ (5 p)$	12,445.20	66	1	11,711.70	1.063
5p5d	$ζ (5 d)$	1145.70	72	8	847.20	1.352
5p5d	$F^{2} (5 p, 5 d)$	38,915.30	500	4	48,875.77	0.796
5p5d	$G^{1} (5 p, 5 d)$	41,194.70	272	5	57,132.38	0.721
5p5d	$G^{3} (5 p, 5 d)$	26,056.80	509	6	36,310.50	0.718
5p6d	$E_{a v}$	374,595.20	fixed		374,595.20	1.000
5p6d	$ζ (5 p)$	12,966.40	69	1	12,202.20	1.063
5p6d	$ζ (6 d)$	450.90	28	8	333.40	1.352
5p6d	$F^{2} (5 p, 6 d)$	13,597.30	175	4	17,077.53	0.796
5p6d	$G^{1} (5 p, 6 d)$	6769.70	45	5	9388.88	0.721
5p6d	$G^{3} (5 p, 6 d)$	5019.50	98	6	6994.75	0.718
5p7d	$E_{a v}$	448,002.60	fixed		448,002.60	1.000
5p7d	$ζ (5 p)$	13,047.00	70	1	12,278.00	1.063
5p7d	$ζ (7 d)$	234.20	15	8	173.20	1.352
5p7d	$F^{2} (5 p, 7 d)$	6403.90	82	4	8042.94	0.796
5p7d	$G^{1} (5 p, 7 d)$	2665.40	18	5	3696.63	0.721
5p7d	$G^{3} (5 p, 7 d)$	2088.40	41	6	2910.25	0.718
5p8d	$E_{a v}$	488,324.00	fixed		488,324.00	1.000
5p8d	$ζ (5 p)$	13,078.40	70	1	12,307.60	1.063
5p8d	$ζ (8 d)$	138.90	9	8	102.70	1.352
5p8d	$F^{2} (5 p, 8 d)$	3569.60	46	4	4483.29	0.796
5p8d	$G^{1} (5 p, 8 d)$	1382.10	9	5	1916.88	0.721
5p8d	$G^{3} (5 p, 8 d)$	1113.40	22	6	1551.50	0.718
5p9d	$E_{a v}$	513,098.50	fixed		513,098.50	1.000
5p9d	$ζ (5 p)$	13,094.30	70	1	12,322.50	1.063
5p9d	$ζ (9 d)$	89.40	6	8	66.10	1.352
5p9d	$F^{2} (5 p, 9 d)$	2205.50	28	4	2770.00	0.796
5p9d	$G^{1} (5 p, 9 d)$	823.00	5	5	1141.38	0.721
5p9d	$G^{3} (5 p, 9 d)$	673.70	13	6	938.88	0.718
5p10d	$E_{a v}$	529,448.70	fixed		529,448.70	1.000
5p10d	$ζ (5 p)$	13,103.30	70	1	12,331.00	1.063
5p10d	$ζ (10 d)$	61.00	4	8	45.10	1.353
5p10d	$F^{2} (5 p, 10 d)$	1462.90	19	4	1837.29	0.796
5p10d	$G^{1} (5 p, 10 d)$	534.40	4	5	741.13	0.721
5p10d	$G^{3} (5 p, 10 d)$	442.00	9	6	616.00	0.718
5s5p $^{3}$	$E_{a v}$	158,786.20	108		158,557.30	1.001
5s5p $^{3}$	$F^{2} (5 p, 5 p)$	50,863.20	408	3	59,873.53	0.850
5s5p $^{3}$	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{3}$	$ζ (5 p)$	12,109.70	65	1	11,396.00	1.063
5s5p $^{3}$	$G^{1} (5 s, 5 p)$	57,837.70	167	7	78,111.88	0.740
5s5p $^{2}$ 6p	$E_{a v}$	433,183.30	fixed		433,183.30	1.000
5s5p $^{2}$ 6p	$F^{2} (5 p, 5 p)$	52,014.40	417	3	61,228.71	0.850
5s5p $^{2}$ 6p	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 6p	$ζ (5 p)$	12,889.80	69	1	12,130.10	1.063
5s5p $^{2}$ 6p	$ζ (6 p)$	3539.40	fixed		3539.40	1.000
5s5p $^{2}$ 6p	$F^{2} (5 p, 6 p)$	19,386.70	fixed		22,807.88	0.850
5s5p $^{2}$ 6p	$G^{1} (5 s, 5 p)$	59,036.50	171	7	79,730.88	0.740
5s5p $^{2}$ 6p	$G^{1} (5 s, 6 p)$	5993.30	fixed		7491.63	0.800
5s5p $^{2}$ 6p	$G^{0} (5 p, 6 p)$	3700.10	fixed		4625.13	0.800
5s5p $^{2}$ 6p	$G^{2} (5 p, 6 p)$	5112.80	fixed		6391.00	0.800
5s5p $^{2}$ 7p	$E_{a v}$	540,226.80	fixed		540,226.80	1.000
5s5p $^{2}$ 7p	$F^{2} (5 p, 5 p)$	52,161.50	418	3	61,401.88	0.850
5s5p $^{2}$ 7p	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 7p	$ζ (5 p)$	12,962.00	69	1	12,198.00	1.063
5s5p $^{2}$ 7p	$ζ (7 p)$	1710.70	fixed		1710.70	1.000
5s5p $^{2}$ 7p	$F^{2} (5 p, 7 p)$	8593.70	fixed		10,110.24	0.850
5s5p $^{2}$ 7p	$G^{1} (5 s, 5 p)$	59,171.80	171	7	79,913.63	0.740
5s5p $^{2}$ 7p	$G^{1} (5 s, 7 p)$	2237.30	fixed		2796.63	0.800
5s5p $^{2}$ 7p	$G^{0} (5 p, 7 p)$	1292.30	fixed		1615.38	0.800
5s5p $^{2}$ 7p	$G^{2} (5 p, 7 p)$	1957.00	fixed		2446.25	0.800
5s5p $^{2}$ 8p	$E_{a v}$	594,697.10	fixed		594,697.10	1.000
5s5p $^{2}$ 8p	$F^{2} (5 p, 5 p)$	52,221.70	419	3	61,472.71	0.850
5s5p $^{2}$ 8p	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 8p	$ζ (5 p)$	12,992.50	69	1	12,226.70	1.063
5s5p $^{2}$ 8p	$ζ (8 p)$	960.50	fixed		960.50	1.000
5s5p $^{2}$ 8p	$F^{2} (5 p, 8 p)$	4534.80	fixed		5335.06	0.850
5s5p $^{2}$ 8p	$G^{1} (5 s, 5 p)$	59,228.90	171	7	79,990.75	0.740
5s5p $^{2}$ 8p	$G^{1} (5 s, 8 p)$	1118.30	fixed		1397.88	0.800
5s5p $^{2}$ 8p	$G^{0} (5 p, 8 p)$	629.10	fixed		786.38	0.800
5s5p $^{2}$ 8p	$G^{2} (5 p, 8 p)$	990.10	fixed		1237.63	0.800
5s5p $^{2}$ 4f	$E_{a v}$	319,549.20	fixed		319,549.20	1.000
5s5p $^{2}$ 4f	$F^{2} (5 p, 5 p)$	50,163.10	402	3	59,049.41	0.850
5s5p $^{2}$ 4f	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 4f	$ζ (4 f)$	320.80	fixed		320.80	1.000
5s5p $^{2}$ 4f	$ζ (5 p)$	11,601.30	62	1	10,917.50	1.063
5s5p $^{2}$ 4f	$F^{2} (4 f, 5 p)$	43,297.90	fixed		50,938.71	0.850
5s5p $^{2}$ 4f	$G^{3} (4 f, 5 s)$	28,181.50	fixed		35,226.88	0.800
5s5p $^{2}$ 4f	$G^{2} (4 f, 5 p)$	27,235.30	fixed		34,044.13	0.800
5s5p $^{2}$ 4f	$G^{4} (4 f, 5 p)$	20,205.70	fixed		25,257.13	0.800
5s5p $^{2}$ 4f	$G^{1} (5 s, 5 p)$	57,009.20	165	7	76,992.88	0.740
5s5p $^{2}$ 5f	$E_{a v}$	492,447.80	fixed		492,447.80	1.000
5s5p $^{2}$ 5f	$F^{2} (5 p, 5 p)$	51,824.00	416	3	61,004.59	0.850
5s5p $^{2}$ 5f	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 5f	$ζ (5 p)$	12,741.80	68	1	11,990.80	1.063
5s5p $^{2}$ 5f	$ζ (5 f)$	81.10	fixed		81.10	1.000
5s5p $^{2}$ 5f	$F^{2} (5 p, 5 f)$	18,460.40	fixed		21,718.12	0.850
5s5p $^{2}$ 5f	$G^{1} (5 s, 5 p)$	58,818.50	170	7	79,436.38	0.740
5s5p $^{2}$ 5f	$G^{3} (5 s, 5 f)$	2828.60	fixed		3535.75	0.800
5s5p $^{2}$ 5f	$G^{2} (5 p, 5 f)$	4572.30	fixed		5715.38	0.800
5s5p $^{2}$ 5f	$G^{4} (5 p, 5 f)$	3798.70	fixed		4748.38	0.800
5s5p $^{2}$ 6f	$E_{a v}$	568,603.40	fixed		568,603.40	1.000
5s5p $^{2}$ 6f	$F^{2} (5 p, 5 p)$	52,086.20	418	3	61,313.18	0.850
5s5p $^{2}$ 6f	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 6f	$ζ (5 p)$	12,136.40	fixed		12,136.40	1.000
5s5p $^{2}$ 6f	$ζ (6 f)$	40.10	fixed		40.10	1.000
5s5p $^{2}$ 6f	$F^{2} (5 p, 6 f)$	8604.40	fixed		10,122.82	0.850
5s5p $^{2}$ 6f	$G^{1} (5 s, 5 p)$	59,082.40	171	7	79,792.88	0.740
5s5p $^{2}$ 6f	$G^{3} (5 s, 6 f)$	1647.60	fixed		2059.50	0.800
5s5p $^{2}$ 6f	$G^{2} (5 p, 6 f)$	2691.40	fixed		3364.25	0.800
5s5p $^{2}$ 6f	$G^{4} (5 p, 6 f)$	2148.10	fixed		2685.13	0.800
5s5p $^{2}$ 7f	$E_{a v}$	610,614.10	fixed		610,614.10	1.000
5s5p $^{2}$ 7f	$F^{2} (5 p, 5 p)$	52,182.00	419	3	61,426.00	0.850
5s5p $^{2}$ 7f	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 7f	$ζ (5 p)$	12,956.60	69	1	12,192.90	1.063
5s5p $^{2}$ 7f	$ζ (7 f)$	23.10	fixed		23.10	1.000
5s5p $^{2}$ 7f	$F^{2} (5 p, 7 f)$	4739.30	fixed		5575.65	0.850
5s5p $^{2}$ 7f	$G^{1} (5 s, 5 p)$	59,181.30	171	7	79,926.38	0.740
5s5p $^{2}$ 7f	$G^{3} (5 s, 7 f)$	1031.00	fixed		1288.75	0.800
5s5p $^{2}$ 7f	$G^{2} (5 p, 7 f)$	1629.20	fixed		2036.50	0.800
5s5p $^{2}$ 7f	$G^{4} (5 p, 7 f)$	1287.50	fixed		1609.38	0.800
5s5p $^{2}$ 8f	$E_{a v}$	636,434.50	fixed		636,434.50	1.000
5s5p $^{2}$ 8f	$F^{2} (5 p, 5 p)$	52,225.70	419	3	61,477.41	0.850
5s5p $^{2}$ 8f	$α (5 p)$	−81.50	−36	9	0.00
5s5p $^{2}$ 8f	$ζ (5 p)$	12,984.90	69	1	12,219.60	1.063
5s5p $^{2}$ 8f	$ζ (8 f)$	14.60	fixed		14.60	1.000
5s5p $^{2}$ 8f	$F^{2} (5 p, 8 f)$	2904.50	fixed		3417.06	0.850
5s5p $^{2}$ 8f	$G^{1} (5 s, 5 p)$	59,226.90	171	7	79,988.00	0.740
5s5p $^{2}$ 8f	$G^{3} (5 s, 8 f)$	679.90	fixed		849.88	0.800
5s5p $^{2}$ 8f	$G^{2} (5 p, 8 f)$	1047.70	fixed		1309.63	0.800
5s5p $^{2}$ 8f	$G^{4} (5 p, 8 f)$	825.20	fixed		1031.50	0.800
5p $^{3}$ 6s	$E_{a v}$	536,194.20	fixed		536,194.20	1.000
5p $^{3}$ 6s	$F^{2} (5 p, 5 p)$	51,696.90	415	3	60,854.94	0.850
5p $^{3}$ 6s	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 6s	$ζ (5 p)$	12,653.30	68	1	11,907.50	1.063
5p $^{3}$ 6s	$G^{1} (5 p, 6 s)$	5618.90	407	2	7460.88	0.753
5p $^{3}$ 7s	$E_{a v}$	667,005.40	fixed		667,005.40	1.000
5p $^{3}$ 7s	$F^{2} (5 p, 5 p)$	52,099.20	418	3	61,328.47	0.850
5p $^{3}$ 7s	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 7s	$ζ (5 p)$	12,836.90	69	1	12,080.30	1.063
5p $^{3}$ 7s	$G^{1} (5 p, 7 s)$	1912.60	fixed		2390.75	0.800
5p $^{3}$ 8s	$E_{a v}$	731,155.30	fixed		731,155.30	1.000
5p $^{3}$ 8s	$F^{2} (5 p, 5 p)$	52,194.00	419	3	61,440.12	0.850
5p $^{3}$ 8s	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 8s	$ζ (5 p)$	12,891.20	69	1	12,131.40	1.063
5p $^{3}$ 8s	$G^{1} (5 p, 8 s)$	903.40	fixed		1129.25	0.800
5p $^{3}$ 9s	$E_{a v}$	767,693.80	fixed		767,693.80	1.000
5p $^{3}$ 9s	$F^{2} (5 p, 5 p)$	52,232.30	419	3	61,485.18	0.850
5p $^{3}$ 9s	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 9s	$ζ (5 p)$	12,914.50	69	1	12,153.30	1.063
5p $^{3}$ 9s	$G^{1} (5 p, 9 s)$	509.10	fixed		636.38	0.800
5p $^{3}$ 10s	$E_{a v}$	790,568.10	fixed		790,568.10	1.000
5p $^{3}$ 10s	$F^{2} (5 p, 5 p)$	52,251.70	419	3	61,508.00	0.850
5p $^{3}$ 10s	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 10s	$ζ (5 p)$	12,926.50	69	1	12,164.60	1.063
5p $^{3}$ 10s	$G^{1} (5 p, 10 s)$	317.90	fixed		397.38	0.800
5p $^{3}$ 5d	$E_{a v}$	476,284.60	fixed		476,284.60	1.000
5p $^{3}$ 5d	$F^{2} (5 p, 5 p)$	51,224.20	411	3	60,298.47	0.850
5p $^{3}$ 5d	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 5d	$ζ (5 p)$	12,276.50	66	1	11,552.90	1.063
5p $^{3}$ 5d	$ζ (5 d)$	1204.20	75	8	890.50	1.352
5p $^{3}$ 5d	$F^{2} (5 p, 5 d)$	39,602.70	509	4	49,739.06	0.796
5p $^{3}$ 5d	$G^{1} (5 p, 5 d)$	42,328.30	280	5	58,704.63	0.721
5p $^{3}$ 5d	$G^{3} (5 p, 5 d)$	26,778.50	523	6	37,316.25	0.718
5p $^{3}$ 6d	$E_{a v}$	646,655.70	fixed		646,655.70	1.000
5p $^{3}$ 6d	$F^{2} (5 p, 5 p)$	52,073.50	418	3	61,298.24	0.850
5p $^{3}$ 6d	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 6d	$ζ (5 p)$	12,799.30	68	1	12,044.90	1.063
5p $^{3}$ 6d	$ζ (6 d)$	454.40	28	8	336.00	1.352
5p $^{3}$ 6d	$F^{2} (5 p, 6 d)$	14,588.50	fixed		17,162.94	0.850
5p $^{3}$ 6d	$G^{1} (5 p, 6 d)$	7204.60	fixed		9005.75	0.800
5p $^{3}$ 6d	$G^{3} (5 p, 6 d)$	5440.40	fixed		6800.50	0.800
5p $^{3}$ 7d	$E_{a v}$	721,253.90	fixed		721,253.90	1.000
5p $^{3}$ 7d	$F^{2} (5 p, 5 p)$	52,179.10	419	3	61,422.59	0.850
5p $^{3}$ 7d	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 7d	$ζ (5 p)$	12,877.30	69	1	12,118.30	1.063
5p $^{3}$ 7d	$ζ (7 d)$	235.20	15	8	173.90	1.353
5p $^{3}$ 7d	$F^{2} (5 p, 7 d)$	6853.10	fixed		8062.47	0.850
5p $^{3}$ 7d	$G^{1} (5 p, 7 d)$	2832.40	fixed		3540.50	0.800
5p $^{3}$ 7d	$G^{3} (5 p, 7 d)$	2263.10	fixed		2828.88	0.800
5p $^{3}$ 8d	$E_{a v}$	761,986.60	fixed		761,986.60	1.000
5p $^{3}$ 8d	$F^{2} (5 p, 5 p)$	52,223.70	419	3	61,475.06	0.850
5p $^{3}$ 8d	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 8d	$ζ (5 p)$	12,907.70	69	1	12,146.90	1.063
5p $^{3}$ 8d	$ζ (8 d)$	139.40	9	8	103.10	1.352
5p $^{3}$ 8d	$F^{2} (5 p, 8 d)$	3814.40	fixed		4487.53	0.850
5p $^{3}$ 8d	$G^{1} (5 p, 8 d)$	1469.50	fixed		1836.88	0.800
5p $^{3}$ 8d	$G^{3} (5 p, 8 d)$	1207.30	fixed		1509.13	0.800
5p $^{3}$ 9d	$E_{a v}$	786,954.90	fixed		786,954.90	1.000
5p $^{3}$ 9d	$F^{2} (5 p, 5 p)$	52,246.70	419	3	61,502.12	0.850
5p $^{3}$ 9d	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 9d	$ζ (5 p)$	12,922.70	69	1	12,161.00	1.063
5p $^{3}$ 9d	$ζ (9 d)$	89.70	6	8	66.30	1.353
5p $^{3}$ 9d	$F^{2} (5 p, 9 d)$	2354.60	fixed		2770.12	0.850
5p $^{3}$ 9d	$G^{1} (5 p, 9 d)$	875.70	fixed		1094.63	0.800
5p $^{3}$ 9d	$G^{3} (5 p, 9 d)$	731.20	fixed		914.00	0.800
5p $^{3}$ 10d	$E_{a v}$	803,412.10	fixed		803,412.10	1.000
5p $^{3}$ 10d	$F^{2} (5 p, 5 p)$	52,259.70	419	3	61,517.41	0.850
5p $^{3}$ 10d	$α (5 p)$	−81.50	−36	9	0.00
5p $^{3}$ 10d	$ζ (5 p)$	12,931.10	69	1	12,168.90	1.063
5p $^{3}$ 10d	$ζ (10 d)$	61.10	4	8	45.20	1.352
5p $^{3}$ 10d	$F^{2} (5 p, 10 d)$	1560.20	fixed		1835.53	0.850
5p $^{3}$ 10d	$G^{1} (5 p, 10 d)$	568.40	fixed		710.50	0.800
5p $^{3}$ 10d	$G^{3} (5 p, 10 d)$	479.60	fixed		599.50	0.800
5s5p5d $^{2}$	$E_{a v}$	513,986.70	fixed		513,986.70	1.000
5s5p5d $^{2}$	$F^{2} (5 d, 5 d)$	40,631.80	fixed		47,802.12	0.850
5s5p5d $^{2}$	$F^{4} (5 d, 5 d)$	27,794.90	fixed		32,699.88	0.850
5s5p5d $^{2}$	$α (5 d)$	0.00	fixed		0.00
5s5p5d $^{2}$	$β (5 d)$	0.00	fixed		0.00
5s5p5d $^{2}$	$T (5 d)$	0.00	fixed		0.00
5s5p5d $^{2}$	$ζ (5 p)$	12,602.60	67	1	11,859.80	1.063
5s5p5d $^{2}$	$ζ (5 d)$	1202.30	75	8	889.10	1.352
5s5p5d $^{2}$	$F^{2} (5 p, 5 d)$	39,627.40	509	4	49,770.12	0.796
5s5p5d $^{2}$	$G^{1} (5 s, 5 p)$	58,598.50	170	7	79,139.25	0.740
5s5p5d $^{2}$	$G^{2} (5 s, 5 d)$	31,283.80	fixed		39,104.75	0.800
5s5p5d $^{2}$	$G^{1} (5 p, 5 d)$	42,188.20	279	5	58,510.25	0.721
5s5p5d $^{2}$	$G^{3} (5 p, 5 d)$	26,699.70	522	6	37,206.38	0.718
5s5p5d6s	$E_{a v}$	570,183.00	fixed		570,183.00	1.000
5s5p5d6s	$ζ (5 p)$	12,972.30	69	1	12,207.70	1.063
5s5p5d6s	$ζ (5 d)$	1260.20	79	8	931.90	1.352
5s5p5d6s	$F^{2} (5 p, 5 d)$	40,230.70	517	4	50,527.88	0.796
5s5p5d6s	$G^{1} (6 s, 5 p)$	59,065.50	171	7	79,770.00	0.740
5s5p5d6s	$G^{2} (6 s, 5 d)$	31,715.30	fixed		39,644.13	0.800
5s5p5d6s	$G^{0} (6 s, s)$	3958.50	fixed		4948.13	0.800
5s5p5d6s	$G^{1} (5 p, 5 d)$	42,892.70	284	5	59,487.38	0.721
5s5p5d6s	$G^{3} (5 p, 5 d)$	27,170.00	531	6	37,861.75	0.718
5s5p5d6s	$G^{1} (5 p, s)$	5938.40	fixed		7423.00	0.800
5s5p5d6s	$G^{2} (5 d, s)$	13,219.70	fixed		16,524.63	0.800
5s5p6s $^{2}$	$E_{a v}$	635,459.70	fixed		635,459.70	1.000
5s5p6s $^{2}$	$ζ (5 p)$	13,358.10	71	1	12,570.80	1.063
5s5p6s $^{2}$	$G^{1} (5 s, 5 p)$	59,529.50	172	7	80,396.63	0.740
5s5p4f $^{2}$	$E_{a v}$	491,309.90	fixed		491,309.90	1.000
5s5p4f $^{2}$	$F^{2} (4 f, 4 f)$	57,554.90	fixed		67,711.65	0.850
5s5p4f $^{2}$	$F^{4} (4 f, 4 f)$	35,751.00	fixed		42,060.00	0.850
5s5p4f $^{2}$	$F^{6} (4 f, 4 f)$	25,615.80	fixed		30,136.24	0.850
5s5p4f $^{2}$	$α (4 f)$	0.00	fixed		0.00
5s5p4f $^{2}$	$β (4 f)$	0.00	fixed		0.00
5s5p4f $^{2}$	$G_{a}^{} (4 f)$	0.00	fixed		0.00
5s5p4f $^{2}$	$ζ (4 f)$	287.30	fixed		287.30	1.000
5s5p4f $^{2}$	$ζ (5 p)$	11,196.10	60	1	10,536.20	1.063
5s5p4f $^{2}$	$F^{2} (4 f, 5 p)$	43,131.40	fixed		50,742.82	0.850
5s5p4f $^{2}$	$G^{3} (4 f, 5 s)$	28,729.60	fixed		35,912.00	0.800
5s5p4f $^{2}$	$G^{2} (4 f, 5 p)$	28,380.30	fixed		35,475.38	0.800
5s5p4f $^{2}$	$G^{4} (4 f, 5 p)$	20,822.80	fixed		26,028.50	0.800
5s5p4f $^{2}$	$G^{1} (5 s, 5 p)$	56,322.50	163	7	76,065.50	0.740
5p6s-5p5d	$R_{d}^{2} (5 p, 6 s, 5 p, 5 d)$ ^d	−9894.80	−77	10	−13324.40	0.743
5p6s-5p5d	$R_{e}^{1} (5 p, 6 s, 5 p, 5 d)$	−3800.60	−29	10	−5117.90	0.743
5p6s-5s5p $^{3}$	$R_{d}^{1} (5 s, 6 s, 5 p, 5 p)$	−662.90	−5	10	−892.70	0.743
5p5d-5s5p $^{3}$	$R_{d}^{1} (5 s, 5 d, 5 p, 5 p)$	48226.90	373	10	64942.70	0.743

^a Configurations involved in the calculations and their Slater parameters with the corresponding least-squaresfitted (LSF), Hartree–Fock (HFR) values, and their ratios. ^b Uncertainty of each parameter represents its standard deviation. ^c Parameters in each numbered group were linked together with their ratio fixed at the HFR level. ^d All other configuration-interaction (R^k) parameters for both parities were fixed at 70% of their HFR values.

References

Vennes, S.; Chayer, P.; Dupuis, J. Discovery of Photospheric Germanium in Hot DA White Dwarfs. Astrophys. J. Lett. 2005, 622, L121–L124. [Google Scholar] [CrossRef]
Chayer, P.; Vennes, S.; Dupuis, J.; Kruk, J.W. Abundance of Elements beyond the Iron Group in Cool DO White Dwarfs. Astrophys. J. Lett. 2005, 630, L169–L172. [Google Scholar] [CrossRef]
Rauch, T.; Quinet, P.; Knörzer, M.; Hoyer, D.; Werner, K.; Kruk, J.W.; Demleitner, M. Stellar laboratories. IX. New Se V, Sr IV-VII, Te VI, and I VI oscillator strengths and the Se, Sr, Te, and I abundances in the hot white dwarfs G191-B2B and RE 0503-289. Astron. Astrophys. 2017, 606, A105. [Google Scholar] [CrossRef]
Werner, K.; Rauch, T.; Knörzer, M.; Kruk, J.W. First detection of bromine and antimony in hot stars. Astron. Astrophys. 2018, 614, A96. [Google Scholar] [CrossRef]
Löbling, L.; Maney, M.A.; Rauch, T.; Quinet, P.; Gamrath, S.; Kruk, J.W.; Werner, K. First discovery of trans-iron elements in a DAO-type white dwarf (BD-22°3467). Mon. Not. R. Astron. Soc. 2020, 492, 528–548. [Google Scholar] [CrossRef]
Chayer, P.; Mendoza, C.; Meléndez, M.; Deprince, J.; Dupuis, J. Detection of cesium in the atmosphere of the hot He-rich white dwarf HD 149499B. Mon. Not. R. Astron. Soc. 2023, 518, 368–381. [Google Scholar] [CrossRef]
Tauheed, A.; Joshi, Y.N.; Kaufman, V. Analysis of the four lowest configurations of five times ionized cesium (Cs VI). Phys. Scr. 1991, 44, 579–581. [Google Scholar] [CrossRef]
Sansonetti, J.E. Wavelengths, Transition Probabilities, and Energy Levels for the Spectra of Cesium (Cs I-Cs LV). J. Phys. Chem. Ref. Data 2009, 38, 761–923. [Google Scholar] [CrossRef]
Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database, Version 5.8 (Gaithersburg, MD: National Institute of Standards and Technology). 2020. Available online: http://physics.nist.gov/asd (accessed on 1 July 2023).
Radziemski, L.J., Jr.; Fisher, K.J.; Steinhaus, D.W. Calculation of Atomic-Energy-Level Values; Technical Report Univ. California LA-4402; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1970. [Google Scholar]
Kramida, A. Critical evaluation of data on atomic energy levels, wavelengths, and transition probabilities. Fusion. Sci. Technol. 2013, 63, 313–323. [Google Scholar] [CrossRef]
Kramida, A. Critically evaluated energy levels and spectral lines of singly ionized indium (In II). J. Res. Natl. Inst. Tech. 2013, 118, 52. [Google Scholar] [CrossRef]
Kramida, A. A critical compilation of energy levels, spectral lines, and transition probabilities of singly ionized silver, Ag II. J. Res. Natl. Inst. Tech. 2013, 118, 168. [Google Scholar] [CrossRef]
Haris, K.; Kramida, A.; Tauheed, A. Extended and revised analysis of singly ionized tin: Sn II. Phys. Scr. 2014, 89, 115403. [Google Scholar] [CrossRef][Green Version]
Husain, A.; Haris, K.; Jabeen, S.; Tauheed, A. Critically evaluated energy levels, wavelengths, transition probabilities, and intensities of six-times ionized cesium: Cs VII. J. Res. Natl. Inst. Tech. 2020, 247, 106956. [Google Scholar] [CrossRef]
Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
Kramida, A. A suite of atomic structure codes originally developed by R. D. Cowan adapted for Windows-based personal computers. Natl. Inst. Stand. Technol. 2021, 215, 47–48. [Google Scholar] [CrossRef]
Kramida, A. Cowan Code: 50 Years of Growing Impact on Atomic Physics. Atoms 2019, 7, 64. [Google Scholar] [CrossRef]
Kramida, A.E. The program LOPT for least-squares optimization of energy levels. Comput. Phys. Commun. 2011, 182, 419–434. [Google Scholar] [CrossRef]
Eissner, W.; Jones, M.; Nussbaumer, H. Techniques for the calculation of atomic structures and radiative data including relativistic corrections. Comput. Phys. Commun. 1974, 8, 270–306. [Google Scholar] [CrossRef]
Badnell, N.R. A Breit-Pauli distorted wave implementation for AUTOSTRUCTURE. Comput. Phys. Commun. 2011, 182, 1528–1535. [Google Scholar] [CrossRef]
Biémont, E.; Quinet, P.; Zeippen, C.J. Transition Probabilities in Xe V. Phys. Scr. 2005, 71, 163–169. [Google Scholar] [CrossRef]
Zainab, A.; Haris, K.; Gamrath, S.; Quinet, P.; Tauheed, A. Critically Evaluated Atomic Data for the Au IV Spectrum. Astrophys. J. Suppl. Ser. 2023, 267, 12. [Google Scholar] [CrossRef]
Curtis, L.J. Branching Fractions for the 5s25p2 - 5s25p6s Supermultiplet in the Sn Isoelectronic Sequence. Phys. Scr. 2001, 63, 104–107. [Google Scholar] [CrossRef]
Oliver, P.; Hibbert, A. Energy level classifications and Breit Pauli oscillator strengths in neutral tin. J. Phys. B-At. Mol. Opt. 2008, 41, 165003. [Google Scholar] [CrossRef]
Biemont, E.; Hansen, J.E.; Quinet, P.; Zeippen, C.J. Forbidden transitions of astrophysical interest in the 5p^k(k = 1–5) configurations. Astron. Astrophys. Suppl. 1995, 111, 333. [Google Scholar]
Kramida, A. Assessing Uncertainties of Theoretical Atomic Transition Probabilities with Monte Carlo Random Trials. Atoms 2014, 2, 86–122. [Google Scholar] [CrossRef] [PubMed]
Peck, E.R.; Reeder, K. Dispersion of Air. J. Opt. Soc. Am. 1972, 62, 958. [Google Scholar] [CrossRef]

Figure 1. Comparison plots for gA−values and S−values: (a,b) computed with our HFR−A and HFR−B models and (c,d) obtained from HFR−B with those of the MCBP model by Chayer et al. [6]. The error bars in panel (d) represent the internal uncertainties of the S-values obtained from the HFR−B model (see the text).

Figure 2. A comparison of (a) theoretical branching fractions BF

_{H F R_B}

obtained from the gA-values of the present HFR−B model with the semi-empirical BF

_{S E_C U 01} -

values (in triangles) reported by Curtis [24] and with the theoretical BF

_{M C B P_C H 22}

(in circles) computed from the MCBP A−values of Chayer et al. [6] for the selected

5 s^{2} 5 p^{2} - 5 s^{2} 5 p 6 s

transitions, and (b) theoretical BF

_{H F R_B}

with the BF

_{M C B P_C H 22}

for the transition

5 s^{2} 5 p^{2} \to {5 s 5 p^{3}

+

5 s^{2} 5 p 5 d

+

5 s^{2} 5 p 6 s

} arrays (see the text).

Table 1. Classified lines of Cs VI.

I $_{obs .}$ ^a	$λ_{obs .}$ ^b	$σ$ ^b	Classification	$λ_{Ritz}$ ^b	$δ λ_{o - c}$ ^c	gA ^d	CF ^d	Acc. ^e	gA $_{prev}$ ^f	Line Ref. ^g
(arb. u.)	(Å)	(cm $^{- 1}$ )		(Å)	(mÅ)	(s $^{- 1}$ )			(s $^{- 1}$ )
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s $^{2}$ 5p6s $^{1}$ P $_{1}^{\circ}$	378.4639(21)		5.83 $\times 10^{7}$	0.00	E	7.71 $\times 10^{7}$	TW
22	396.746(5)	252,050(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p6s $^{1}$ P $_{1}^{\circ}$	396.7443(22)	2	2.32 $\times 10^{9}$	0.58	D	9.66 $\times 10^{8}$	T91
38	401.968(5)	248,776(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p6s $^{3}$ P $_{2}^{\circ}$	401.968(3)	0	1.75 $\times 10^{10}$	0.77	D+	1.12 $\times 10^{10}$	T91
15	405.518(5)	246,598(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p6s $^{1}$ P $_{1}^{\circ}$	405.5171(23)	1	8.48 $\times 10^{9}$	0.16	D+	6.03 $\times 10^{9}$	T91
40	410.312(5)	243,717(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s $^{2}$ 5p6s $^{3}$ P $_{1}^{\circ}$	410.310(3)	2	1.44 $\times 10^{10}$	0.45	D+	1.09 $\times 10^{10}$	T91
45	410.976(5)	243,323(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p6s $^{3}$ P $_{2}^{\circ}$	410.976(3)	0	3.03 $\times 10^{10}$	0.76	D+	2.11 $\times 10^{10}$	T91
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s $^{2}$ 5p5d $^{1}$ P $_{1}^{\circ}$	431.007(3)		3.12 $\times 10^{7}$	0.00	E	1.10 $\times 10^{8}$	TW
38	431.883(5)	231,544(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p6s $^{3}$ P $_{1}^{\circ}$	431.884(3)	−1	6.57 $\times 10^{9}$	0.54	D+	6.27 $\times 10^{9}$	T91
50	434.712(5)	230,037(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p6s $^{3}$ P $_{0}^{\circ}$	434.712(5)	0	1.03 $\times 10^{10}$	0.69	D+	9.28 $\times 10^{9}$	T91
52	436.365(5)	229,166(3)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p6s $^{1}$ P $_{1}^{\circ}$	436.365(3)	0	3.98 $\times 10^{10}$	0.69	C	3.33 $\times 10^{10}$	T91
57	442.298(5)	226,092(3)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p6s $^{3}$ P $_{1}^{\circ}$	442.300(3)	−2	1.99 $\times 10^{10}$	0.50	D+	1.71 $\times 10^{10}$	T91
47	442.693(5)	225,890(3)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p6s $^{3}$ P $_{2}^{\circ}$	442.693(3)	0	1.41 $\times 10^{10}$	0.75	D+	1.34 $\times 10^{10}$	T91
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{1}$ P $_{1}^{\circ}$	454.875(3)		4.91 $\times 10^{8}$	0.03	D	3.66 $\times 10^{8}$	TW
25	466.447(5)	214,386.6(23)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{1}$ P $_{1}^{\circ}$	466.445(3)	2	2.29 $\times 10^{9}$	0.04	D+	2.41 $\times 10^{9}$	T91
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s $^{2}$ 5p5d $^{3}$ P $_{1}^{\circ}$	466.887(3)		4.24 $\times 10^{7}$	0.00	E	1.70 $\times 10^{8}$	TW
38	472.107(5)	211,816.4(22)	5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s $^{2}$ 5p6s $^{1}$ P $_{1}^{\circ}$	472.109(3)	−2	1.82 $\times 10^{10}$	0.82	C	2.70 $\times 10^{10}$	T91
55	478.711(5)	208,894.3(22)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{1}$ F $_{3}^{\circ}$	478.709(3)	2	3.57 $\times 10^{10}$	0.13	C	3.00 $\times 10^{10}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p6s $^{3}$ P $_{1}^{\circ}$	479.253(4)		4.92 $\times 10^{8}$	0.01	E	8.14 $\times 10^{7}$	TW
38	490.613(5)	203,826.6(21)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{3}$ D $_{2}^{\circ}$	490.612(3)	1	7.48 $\times 10^{9}$	0.04	D+	1.71 $\times 10^{10}$	T91
65	495.028(5)	202,008.8(20)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{3}$ P $_{1}^{\circ}$	495.024(3)	4	4.62 $\times 10^{10}$	0.51	C	4.43 $\times 10^{10}$	T91
55	498.127(5)	200,752.0(20)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{3}$ P $_{0}^{\circ}$	498.127(5)	0	2.50 $\times 10^{10}$	0.66	C	2.33 $\times 10^{10}$	T91
70	500.502(5)	199,799.4(20)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s $^{2}$ 5p5d $^{3}$ D $_{1}^{\circ}$	500.5033(24)	−1	7.26 $\times 10^{10}$	0.50	C	7.14 $\times 10^{10}$	T91
58	504.097(5)	198,374.5(20)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ D $_{2}^{\circ}$	504.098(3)	−1	2.78 $\times 10^{10}$	0.13	C	3.98 $\times 10^{10}$	T91
66	506.020(5)	197,620.6(20)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{1}$ D $_{2}^{\circ}$	506.024(3)	−4	6.59 $\times 10^{10}$	0.71	C	6.94 $\times 10^{10}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{1}$ P $_{1}^{\circ}$	507.731(4)		2.71 $\times 10^{9}$	0.04	D+	3.68 $\times 10^{9}$	TW
48	508.757(5)	196,557.5(19)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ P $_{1}^{\circ}$	508.757(3)	0	2.03 $\times 10^{10}$	0.43	C	1.89 $\times 10^{10}$	T91
75	514.093(5)	194,517.3(19)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ D $_{3}^{\circ}$	514.090(3)	3	1.96 $\times 10^{11}$	0.71	C	1.93 $\times 10^{11}$	T91
50	514.241(5)	194,461.4(19)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s5p $^{3}$ $^{1}$ P $_{1}^{\circ}$	514.2438(22)	−3	1.28 $\times 10^{10}$	0.17	D+	8.97 $\times 10^{9}$	T91
65	520.375(5)	192,169.1(18)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{1}$ D $_{2}^{\circ}$	520.383(3)	−8	6.53 $\times 10^{10}$	0.48	C	3.76 $\times 10^{10}$	T91
70	522.294(5)	191,463.0(18)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{1}$ F $_{3}^{\circ}$	522.296(4)	−2	2.06 $\times 10^{11}$	0.72	C	1.96 $\times 10^{11}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s $^{2}$ 5p6s $^{3}$ P $_{1}^{\circ}$	522.717(5)		4.77 $\times 10^{9}$	0.28	D+	6.98 $\times 10^{9}$	TW
78m(Cs V)	532.992(10)	187,620(4)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{3}$ D $_{1}^{\circ}$	532.980(2)	12	2.10 $\times 10^{10}$	0.23	C	1.66 $\times 10^{10}$	T91
70	539.366(5)	185,402.9(17)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{3}$ P $_{2}^{\circ}$	539.364(3)	2	7.43 $\times 10^{10}$	0.69	C	5.69 $\times 10^{10}$	T91
45	548.591(5)	182,285.2(17)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{1}$ P $_{1}^{\circ}$	548.5891(21)	2	5.98 $\times 10^{9}$	0.14	D+	9.01 $\times 10^{9}$	T91
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ D $_{1}^{\circ}$	548.933(3)		5.85 $\times 10^{8}$	0.01	D+	1.47 $\times 10^{9}$	TW
64	552.665(5)	180,941.4(16)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ D $_{2}^{\circ}$	552.665(3)	0	9.14 $\times 10^{10}$	0.65	C	7.36 $\times 10^{10}$	T91
63	555.703(5)	179,952.2(16)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ P $_{2}^{\circ}$	555.708(3)	−5	3.54 $\times 10^{10}$	0.21	C	4.51 $\times 10^{10}$	T91
55	556.777(5)	179,605.1(16)	5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s $^{2}$ 5p5d $^{1}$ P $_{1}^{\circ}$	556.779(4)	−2	6.32 $\times 10^{10}$	0.58	C	5.31 $\times 10^{10}$	T91
45	558.268(5)	179,125.4(16)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ P $_{1}^{\circ}$	558.271(3)	−3	1.45 $\times 10^{10}$	0.59	C	1.44 $\times 10^{10}$	T91
52	564.697(5)	177,086.1(16)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ D $_{3}^{\circ}$	564.699(4)	−2	2.18 $\times 10^{10}$	0.14	C	2.02 $\times 10^{10}$	T91
8	565.503(5)	176,833.7(16)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{1}$ P $_{1}^{\circ}$	565.5053(22)	−2	4.21 $\times 10^{8}$	0.00	D	4.44 $\times 10^{8}$	T91
52	569.332(5)	175,644.4(15)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s5p $^{3}$ $^{3}$ S $_{1}^{\circ}$	569.333(3)	−1	8.72 $\times 10^{9}$	0.19	D+	8.67 $\times 10^{9}$	T91
50	572.310(5)	174,730.5(15)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{1}$ D $_{2}^{\circ}$	572.301(3)	9	2.02 $\times 10^{10}$	0.17	C	3.02 $\times 10^{10}$	T91
72	589.477(5)	169,641.9(14)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ F $_{3}^{\circ}$	589.477(5)	0	1.50 $\times 10^{10}$	0.70	C	1.18 $\times 10^{10}$	T91
40	589.691(5)	169,580.3(14)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s $^{2}$ 5p5d $^{3}$ F $_{2}^{\circ}$	589.695(3)	−4	2.70 $\times 10^{9}$	0.60	D+	2.31 $\times 10^{9}$	T91
42	607.020(5)	164,739.2(14)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ D $_{1}^{\circ}$	607.022(3)	−2	6.19 $\times 10^{9}$	0.20	D+	4.72 $\times 10^{9}$	T91
65	609.285(5)	164,126.8(13)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s $^{2}$ 5p5d $^{3}$ F $_{2}^{\circ}$	609.287(3)	−2	5.14 $\times 10^{9}$	0.39	D+	4.22 $\times 10^{9}$	T91
72	611.735(5)	163,469.5(13)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{3}$ S $_{1}^{\circ}$	611.735(3)	0	1.62 $\times 10^{10}$	0.34	C	1.45 $\times 10^{10}$	T91
55	615.320(5)	162,517.1(13)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ P $_{2}^{\circ}$	615.317(3)	3	8.90 $\times 10^{9}$	0.08	C	1.10 $\times 10^{10}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s $^{2}$ 5p5d $^{3}$ P $_{1}^{\circ}$	618.145(5)		4.57 $\times 10^{7}$	0.00	E	5.68 $\times 10^{5}$	TW
75	627.360(5)	159,398.1(13)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{1}$ P $_{1}^{\circ}$	627.352(3)	8	2.72 $\times 10^{10}$	0.37	C	2.65 $\times 10^{10}$	T91
82	632.846(5)	158,016.3(12)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{3}$ S $_{1}^{\circ}$	632.844(3)	2	3.89 $\times 10^{10}$	0.50	C	3.60 $\times 10^{10}$	T91
32	638.762(5)	156,552.8(12)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{1}$ D $_{2}^{\circ}$	638.753(3)	9	5.88 $\times 10^{8}$	0.04	D	5.08 $\times 10^{8}$	T91
68	648.526(5)	154,195.8(12)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s5p $^{3}$ $^{3}$ P $_{1}^{\circ}$	648.518(3)	8	2.04 $\times 10^{9}$	0.05	D+	1.77 $\times 10^{9}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ F $_{3}^{\circ}$	656.992(6)		8.23 $\times 10^{5}$	0.00	E	3.26 $\times 10^{6}$	TW
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{1}$ D $_{2}^{\circ}$	661.804(3)		2.91 $\times 10^{7}$	0.00	E	6.77 $\times 10^{6}$	TW
62	678.479(5)	147,388.5(11)	5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s $^{2}$ 5p5d $^{3}$ D $_{1}^{\circ}$	678.479(4)	0	2.02 $\times 10^{8}$	0.01	E	5.38 $\times 10^{6}$	T91
60	681.699(5)	146,692.3(11)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s $^{2}$ 5p5d $^{3}$ F $_{2}^{\circ}$	681.694(3)	5	3.27 $\times 10^{9}$	0.28	D+	2.71 $\times 10^{9}$	T91
			5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{3}$ P $_{2}^{\circ}$	701.260(5)		3.07 $\times 10^{7}$	0.00	E	4.58 $\times 10^{7}$	TW
80	703.973(5)	142,050.9(10)	5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s5p $^{3}$ $^{1}$ P $_{1}^{\circ}$	703.978(4)	−5	3.83 $\times 10^{9}$	0.08	D+	2.78 $\times 10^{9}$	T91
25	704.104(5)	142,024.5(10)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{3}$ P $_{1}^{\circ}$	704.110(3)	−6	5.84 $\times 10^{9}$	0.19	D+	4.50 $\times 10^{9}$	T91
80bl(Cs VII)	711.313(10)	140,585.1(20)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{3}$ S $_{1}^{\circ}$	711.319(4)	−6	4.69 $\times 10^{8}$	0.01	D	1.40 $\times 10^{8}$	T91
25	711.953(5)	140,458.7(10)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{3}$ P $_{0}^{\circ}$	711.953(5)	0	2.12 $\times 10^{9}$	0.18	D+	1.65 $\times 10^{9}$	T91
78	729.141(5)	137,147.7(9)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{3}$ P $_{2}^{\circ}$	729.141(5)	0	9.94 $\times 10^{9}$	0.13	C	6.79 $\times 10^{9}$	T91
80	732.217(5)	136,571.5(9)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{3}$ P $_{1}^{\circ}$	732.223(3)	−6	2.11 $\times 10^{8}$	0.01	D	1.42 $\times 10^{8}$	T91
88	748.109(5)	133,670.4(9)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{1}$ D $_{2}^{\circ}$	748.115(4)	−6	8.34 $\times 10^{9}$	0.11	D+	4.33 $\times 10^{9}$	T91
72	758.917(5)	131,766.7(9)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$ -5s5p $^{3}$ $^{3}$ D $_{1}^{\circ}$	758.921(4)	−4	3.48 $\times 10^{9}$	0.12	D+	2.68 $\times 10^{9}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s5p $^{3}$ $^{3}$ S $_{1}^{\circ}$	811.466(6)		5.17 $\times 10^{8}$	0.04	D	3.65 $\times 10^{8}$	TW
52	827.035(5)	120,913.9(7)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{3}$ D $_{2}^{\circ}$	827.037(3)	−2	4.03 $\times 10^{9}$	0.11	D+	2.81 $\times 10^{9}$	T91
50	830.465(5)	120,414.5(7)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{3}$ D $_{3}^{\circ}$	830.464(3)	1	3.19 $\times 10^{9}$	0.09	D+	2.04 $\times 10^{9}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{3}$ P $_{2}^{\circ}$	835.320(7)		3.82 $\times 10^{8}$	0.01	D	2.01 $\times 10^{8}$	TW
61	836.190(5)	119,590.0(7)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{3}$ D $_{1}^{\circ}$	836.180(3)	10	4.23 $\times 10^{7}$	0.00	E	8.20 $\times 10^{6}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{3}$ P $_{1}^{\circ}$	839.367(4)		3.79 $\times 10^{6}$	0.00	E	4.62 $\times 10^{4}$	TW
30	866.096(5)	115,460.6(7)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{3}$ D $_{2}^{\circ}$	866.095(3)	1	4.79 $\times 10^{7}$	0.00	D	5.06 $\times 10^{7}$	T91
34	876.127(5)	114,138.7(7)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{3}$ D $_{1}^{\circ}$	876.127(3)	0	2.55 $\times 10^{8}$	0.05	D	2.52 $\times 10^{8}$	T91
54	971.046(5)	102,981.7(5)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{3}$ D $_{3}^{\circ}$	971.047(4)	−1	1.48 $\times 10^{9}$	0.11	D+	9.46 $\times 10^{8}$	T91
4	982.444(5)	101,787.0(5)	5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s5p $^{3}$ $^{3}$ P $_{1}^{\circ}$	982.441(4)	3	1.46 $\times 10^{8}$	0.08	D	1.24 $\times 10^{8}$	T91
75	1020.118(5)	98,027.9(5)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{3}$ D $_{2}^{\circ}$	1020.118(4)	0	6.27 $\times 10^{7}$	0.01	D	2.85 $\times 10^{7}$	T91
22	1034.060(5)	96,706.2(5)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{3}$ D $_{1}^{\circ}$	1034.065(4)	−5	1.38 $\times 10^{8}$	0.05	D	1.49 $\times 10^{8}$	T91
75	1055.929(5)	94,703.3(4)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$ -5s5p $^{3}$ $^{5}$ S $_{2}^{\circ}$	1055.936(4)	−7	1.67 $\times 10^{8}$	0.21	D	1.44 $\times 10^{8}$	T91
73	1120.452(5)	89,249.7(4)	5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$ -5s5p $^{3}$ $^{5}$ S $_{2}^{\circ}$	1120.450(4)	2	1.43 $\times 10^{8}$	0.15	D	1.27 $\times 10^{8}$	T91
			5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$ -5s5p $^{3}$ $^{3}$ D $_{1}^{\circ}$	1260.151(11)		9.42 $\times 10^{6}$	0.01	E	4.85 $\times 10^{6}$	TW
5	1392.432(5)	71,816.8(3)	5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$ -5s5p $^{3}$ $^{5}$ S $_{2}^{\circ}$	1392.430(4)	2	1.09 $\times 10^{7}$	0.03	D	9.74 $\times 10^{6}$	T91

^a Observed relative intensities in arbitrary units, which were taken from T91–Tauheed et al. [7], character of the observed line: bl–blended by a close line, m–masked by a stronger neighboring line. ^b Observed and Ritz wavelengths (in Å) are given in vacuum for all observed wavenumbers (σ) expressed in cm⁻¹ unit. The quantity given in parentheses is the uncertainty in the last digit. ^c Difference between the observed and Ritz wavelengths in mÅ, and 1 mÅ = 10⁻³ Å. ^d Weighted transition probability (gA-value) and absolute cancellation factor from the present HFR-B calculations (see Section 3.2). ^e Accuracy code of the gA-value explained in Section 3.2. ^f gA-values obtained from the A-values reported previously by Chayer et al. [6]. ^g Line reference: T91–Tauheed et al. [7], TW–this work.

Table 2. Optimized energy levels of Cs VI.

Level	Energy ^a	Unc. ^b	Leading Compositions ^c					$Δ$ E $_{o - c}$ ^d	No. of Lines ^e
	(cm $^{- 1}$ )	(cm $^{- 1}$ )	P1	P2	Comp2	P3	Comp3	(cm $^{- 1}$ )
5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{0}$	0.0	0.8	87	12	5s $^{2}$ 5p $^{2}$ $^{1}$ S			4	6
5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{1}$	12,174.5	0.5	98					0	16
5s $^{2}$ 5p $^{2}$ $^{3}$ P $_{2}$	17,627.3	0.3	62	36	5s $^{2}$ 5p $^{2}$ $^{1}$ D			−8	18
5s $^{2}$ 5p $^{2}$ $^{1}$ D $_{2}$	35,060.26	0.20	61	36	5s $^{2}$ 5p $^{2}$ $^{3}$ P			5	17
5s $^{2}$ 5p $^{2}$ $^{1}$ S $_{0}$	52,410.4	0.5	86	12	5s $^{2}$ 5p $^{2}$ $^{3}$ P			−1	5
5s5p $^{3}$ $^{5}$ S $_{2}^{\circ}$	106,877.18	0.24	91	7	5s5p $^{3}$ $^{3}$ P $^{\circ}$			26	3
5s5p $^{3}$ $^{3}$ D $_{1}^{\circ}$	131,766.0	0.5	74	12	5s5p $^{3}$ $^{3}$ P $^{\circ}$	7	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$	-260	4
5s5p $^{3}$ $^{3}$ D $_{2}^{\circ}$	133,088.1	0.4	72	14	5s5p $^{3}$ $^{3}$ P $^{\circ}$	6	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$	−63	3
5s5p $^{3}$ $^{3}$ D $_{3}^{\circ}$	138,041.9	0.4	91	8	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$			112	2
5s5p $^{3}$ $^{3}$ P $_{0}^{\circ}$	152,633.2	1.0	92	7	5s $^{2}$ 5p5d $^{3}$ P $^{\circ}$			−99	1
5s5p $^{3}$ $^{3}$ P $_{1}^{\circ}$	154,197.7	0.5	75	12	5s5p $^{3}$ $^{3}$ D $^{\circ}$	5	5s $^{2}$ 5p5d $^{3}$ P $^{\circ}$	88	4
5s5p $^{3}$ $^{3}$ P $_{2}^{\circ}$	154,774.9	0.9	42	23	5s5p $^{3}$ $^{1}$ D $^{\circ}$	14	5s5p $^{3}$ $^{3}$ D $^{\circ}$	130	1
5s5p $^{3}$ $^{1}$ D $_{2}^{\circ}$	168,729.5	1.3	34	27	5s5p $^{3}$ $^{3}$ P $^{\circ}$	27	5s $^{2}$ 5p5d $^{1}$ D $^{\circ}$	196	2
5s5p $^{3}$ $^{3}$ S $_{1}^{\circ}$	175,644.1	0.8	64	27	5s5p $^{3}$ $^{1}$ P $^{\circ}$			−9	4
5s $^{2}$ 5p5d $^{3}$ F $_{2}^{\circ}$	181,753.6	0.9	86	8	5s5p $^{3}$ $^{1}$ D $^{\circ}$			95	3
5s $^{2}$ 5p5d $^{3}$ F $_{3}^{\circ}$	187,269.2	1.4	89	5	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$			−205	1
5s5p $^{3}$ $^{1}$ P $_{1}^{\circ}$	194,460.3	0.9	48	24	5s5p $^{3}$ $^{3}$ S $^{\circ}$	15	5s $^{2}$ 5p5d $^{1}$ P $^{\circ}$	−112	5
5s $^{2}$ 5p5d $^{3}$ P $_{2}^{\circ}$	197,578.0	1.0	45	22	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$	15	5s $^{2}$ 5p5d $^{1}$ D $^{\circ}$	105	3
5s $^{2}$ 5p5d $^{3}$ F $_{4}^{\circ}$	(199,500)	(400)	98					0
5s $^{2}$ 5p5d $^{3}$ D $_{1}^{\circ}$	199,798.9	0.8	60	16	5s $^{2}$ 5p5d $^{3}$ P $^{\circ}$	8	5s5p $^{3}$ $^{1}$ P $^{\circ}$	98	4
5s $^{2}$ 5p5d $^{1}$ D $_{2}^{\circ}$	209,793.6	1.8	35	37	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$	15	5s5p $^{3}$ $^{1}$ D $^{\circ}$	−90	3
5s $^{2}$ 5p5d $^{3}$ D $_{3}^{\circ}$	212,145.7	1.4	76	7	5s $^{2}$ 5p5d $^{3}$ F $^{\circ}$	7	5s $^{2}$ 5p5d $^{1}$ F $^{\circ}$	−46	2
5s $^{2}$ 5p5d $^{3}$ P $_{0}^{\circ}$	212,926.5	2.0	91	6	5s5p $^{3}$ $^{3}$ P $^{\circ}$			−34	1
5s $^{2}$ 5p5d $^{3}$ P $_{1}^{\circ}$	214,184.8	1.2	66	21	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$	6	5s5p $^{3}$ $^{3}$ P $^{\circ}$	24	3
5s $^{2}$ 5p5d $^{3}$ D $_{2}^{\circ}$	216,001.6	1.1	27	44	5s $^{2}$ 5p5d $^{3}$ P $^{\circ}$	11	5s $^{2}$ 5p5d $^{1}$ D $^{\circ}$	42	3
5s $^{2}$ 5p5d $^{1}$ F $_{3}^{\circ}$	226,522.6	1.5	87	9	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$			−76	2
5s $^{2}$ 5p5d $^{1}$ P $_{1}^{\circ}$	232,015.0	1.4	74	10	5s5p $^{3}$ $^{1}$ P $^{\circ}$	6	5s $^{2}$ 5p5d $^{3}$ D $^{\circ}$	84	2
5s $^{2}$ 5p6s $^{3}$ P $_{0}^{\circ}$	242,212	3	98					98	1
5s $^{2}$ 5p6s $^{3}$ P $_{1}^{\circ}$	243,718.4	1.6	73	21	5s $^{2}$ 5p6s $^{1}$ P $^{\circ}$			16	3
5s $^{2}$ 5p6s $^{3}$ P $_{2}^{\circ}$	260,950.5	1.6	98					−109	3
5s $^{2}$ 5p6s $^{1}$ P $_{1}^{\circ}$	264,226.0	1.4	73	23	5s $^{2}$ 5p6s $^{3}$ P $^{\circ}$			−9	4

^a Optimized energy values obtained using LOPT code [19]. The value given in parentheses and its uncertainty are the theoretical ones from the LSF of Cowan’s code (see Section 3.2). ^b Uncertainties resulting from the level optimization procedure include the D1 uncertainty (D1 is close to the minimum estimated dispersion relative to any other term; see further details in ref. [19]). ^c The LS-coupling percentage compositions determined in this work were made by parametric least-squares fitting with Cowan’s codes (see text), wherein P1 refers to the first percentage value of the configuration and term given in the first column of the table. The remaining percentage (P2, P3) values are provided with their corresponding components. ^d Differences between the observed and calculated energies in the parametric least-squares fitting. Blank for unobserved levels. ^e Number of observed lines determining the level in the level optimization.

Table 3. Configurations used in HFR models of Cs VI.

Even Parity		Odd Parity
Model: HFR-A
$5 s^{2} 5 p^{2}$ , $5 p^{4}$		$5 s 5 p^{3}$
$5 s^{2} 5 p 6 p$		$5 s^{2} 5 p {(5, 6) d + (6, 7) s}$
$5 s 5 p^{2} {(5, 6) d + (6, 7) s}$		$5 s 5 p^{2} 6 p$
$5 p^{3} 6 p$		$5 p^{3} {(5, 6) d + (6, 7) s}$
$5 s^{2} 5 d^{2}$ , $5 s^{2} 6 s^{2}$ , $5 s^{2} 5 d 6 s$		$5 s 5 p 5 d^{2}$ , $5 s 5 p 6 s^{2}$
$5 p^{2} 5 d^{2}$ , $5 p^{2} 6 s^{2}$ , $5 p^{2} 5 d 6 s$		$5 s 5 p 5 d 6 s$
.......		.......
No. of Levels ^a = 5{4}		No. of Levels ^a = 25{13}
SD = 15 cm $^{- 1}$		SD = 276 cm $^{- 1}$
Model: HFR-B
$5 s^{2} 5 p^{2}$ , $5 p^{4}$		$5 s 5 p^{3}$
$5 s^{2} 5 p n l (n \leq 10$ , $l = p, f)$		$5 s^{2} 5 p n l (n \leq 10$ , $l = s, d)$
$5 s 5 p^{2} n l (n \leq 8$ , $l = s, d)$		$5 s 5 p^{2} n l (n \leq 8$ , $l = p, f)$
$5 p^{3} n l (n \leq 10$ , $l = p, f)$		$5 p^{3} n l (n \leq 10$ , $l = s, d)$
$5 s^{2} 4 f^{2}$ , $5 s^{2} 5 d^{2}$ , $5 s^{2} 6 s^{2}$ , $5 s^{2} 6 p^{2}$
$5 s^{2} 5 d 6 s$ , $5 p^{2} 5 d 6 s$ , $5 p^{2} 5 d^{2}$		$5 s 5 p 5 d^{2}$ , $5 s 5 p 6 s^{2}$
$5 p^{2} 6 s^{2}$ , $5 p^{2} 4 f^{2}$ , $5 s 5 p 5 d 4 f$		$5 s 5 p 4 f^{2}$ , $5 s 5 p 5 d 6 s$
.......		.......
No. of Levels ^a = 5{4}		No. of Levels ^a = 25{13}
SD = 10 cm $^{- 1}$		SD = 155 cm $^{- 1}$

^a Total number of known levels and the number of free parameters in the LSF; the latter quantity is given in parentheses.

Table 4. Radiative rates for forbidden lines within the levels of ground 5s

^{2}

5p

^{2}

configuration in Cs VI.

Table 4. Radiative rates for forbidden lines within the levels of ground 5s

^{2}

5p

^{2}

configuration in Cs VI.

	This Work				Previous Work ^d
Transitions	$λ_{Ritz}$ ^a	A $_{M 1}$ ^b	A $_{E 2}$ ^b	%SD ^c	A $_{M 1}$	A $_{E 2}$	${BF}_{{abs}^{f}}$
	(Å)	( $s^{- 1}$ )	( $s^{- 1}$ )		( $s^{- 1}$ )	( $s^{- 1}$ )
$^{3}$ P $_{1}$ – $^{1}$ S $_{0}$	2484.59(4)	4.170 $\times 10^{2}$		0.15			0.947
$^{3}$ P $_{0}$ – $^{1}$ D $_{2}$	2851.39(5)		1.29 $\times 10^{- 2}$	3.00		1.511 $\times 10^{- 2}$	0.000
$^{3}$ P $_{2}$ – $^{1}$ S $_{0}$	2874.12(5)		2.096 $\times 10^{1}$	0.30			0.048
$^{3}$ P $_{1}$ – $^{1}$ D $_{2}$	4368.30(6)	6.032 $\times 10^{1}$	6.001 $\times 10^{- 1}$	0.20	5.996 $\times 10^{1}$	5.768 $\times 10^{- 1}$	0.545
$^{3}$ P $_{0}$ – $^{3}$ P $_{2}$	5671.44(21)		2.6035 $\times 10^{- 1}$	0.04		2.542 $\times 10^{- 1}$	0.159
$^{3}$ P $_{2}$ – $^{1}$ D $_{2}$	5734.67(10)	5.027 $\times 10^{1}$	6.655 $\times 10^{- 1}$	0.08			0.455
$^{1}$ D $_{2}$ – $^{1}$ S $_{0}$	5762.04(21)		2.4906 $\times 10^{0}$	0.08			0.006
$^{3}$ P $_{0}$ – $^{3}$ P $_{1}$	8211.6(5)	2.8743 $\times 10^{1}$		0.02	2.884 $\times 10^{1}$		1.000
$^{3}$ P $_{1}$ – $^{3}$ P $_{2}$	18,334.2(12)	1.3804 $\times 10^{0}$	7.889 $\times 10^{- 4}$	0.12	1.406 $\times 10^{0}$	7.896 $\times 10^{- 4}$	0.841

^a Ritz wavelengths (in standard air [28]) and the quantity given in parentheses is the uncertainty in the last digit. The wavelength uncertainties are determined in the level optimization procedure (see Section 3.1). ^b The scaled A-values for the M1 and E2 components from the present HFR-B calculations (see Section 3.3). The scaling was carried out with the help of experimental transition energies computed from Table 2. ^c Uncertainties (%SD) of the A-values for the M1 and E2 components, obtained using the Monte Carlo method (see the text). ^d A-values for the M1 and E2 components previously reported by Biemont et al. [26]. ^f Absolute branching fractions for the spectral lines are calculated from the present A-values given in columns 3 and 4.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Energy Levels and Transition Data of Cs VI

Abstract

1. Introduction

2. HFR Method

3. Results and Discussion

3.1. Optimization of Energy Levels

3.2. Theoretical Calculations and Transition Probabilities

3.3. Radiative Parameters for Transitions within the Ground Configuration

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A. Supplementary Data

References

Article Metrics

Citations

Article Access Statistics